Skip to main content

Advertisement

SpringerLink
Log in

A Comparison of Deterministic and Stochastic Plant-Vector-Virus Models Based on Probability of Disease Extinction and Outbreak

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

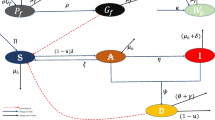
In this investigation, we formulate and analyse a stochastic epidemic model using the continuous-time Markov chain model for the propagation of a vector-borne cassava mosaic disease in a single population. The stochastic model is based upon a pre-existing deterministic plant-vector-virus model. To see how demographic stochasticity affects the vector-borne cassava mosaic disease dynamics, we compare the disease dynamics of both deterministic and stochastic models through disease extinction process. The probability of disease extinction and therefore the major outbreak are estimated analytically using the multitype Galton–Watson branching process (GWbp) approximation. Also, we have found the approximate probabilities of disease extinction numerically based on 30000 sample paths, and it is shown to be good estimate with the calculated probabilities from GWbp approximation. In particular, it is observed that there is a very high probability of disease extinction when the disease is introduced via the infected vectors rather than through infected plants.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

There is no associated data.

References

  • Alabi O. J, Kumar P. L, NaiduR. A,(2011) Cassava mosaic disease: A curse to food security in subsaharan africa, APSnet Features

  • Allen LJS (2008) An introduction to stochastic epidemic models. Springer, Mathematical epidemiology, pp 81–130

  • Allen L. J. S,(2015) Stochastic population and epidemic models, Mathematical biosciences lecture series, stochastics in biological systems

  • Allen LJS (2007) An introduction to mathematical biology. Upper Saddle River, New Jersey

    Google Scholar 

  • Allen LJS (2010) An introduction to stochastic processes with applications to biology. CRC Press, Boca Raton

    Book  Google Scholar 

  • Allen LJ (2012) Branching processes. Encyclopedia of theoretical ecology. University of California Press, Berkeley, pp 112–119

    Google Scholar 

  • Allen LJS (2017) A primer on stochastic epidemic models: formulation, numerical simulation, and analysis. Infect Dis Model 2(2):128–142

    Google Scholar 

  • Allen LJS, van den Driessche P (2013) Relations between deterministic and stochastic thresholds for disease extinction in continuous-and discrete-time infectious disease models. Math Biosci 243(1):99–108

    Article  MathSciNet  MATH  Google Scholar 

  • Allen LJS, Lahodny GE Jr (2012) Extinction thresholds in deterministic and stochastic epidemic models. J Biol Dyn 6(2):590–611

    Article  MATH  Google Scholar 

  • Allen L. J. S, Burgin A. M,(2000) Comparison of deterministic and stochastic SIS and SIR models in discrete time, Math Biosci 163 (1) 1-33. doi:https://doi.org/10.1016/S0025- 5564(99)00047-4. URL https://www.sciencedirect.com/science/article/pii/S0025556499000474

  • Athreya K, Ney P, (1972)Springer-Verlag; Newyork: Branching processes. [Google Scholar]

  • Atiri G, Ogbe F, Dixon AG, Winter S, Ariyo O (2004) Status of cassava mosaic virus diseases and cassava begomoviruses in sub-Saharan Africa. J Sustain Agric 24(3):5–35

    Article  Google Scholar 

  • Bartlett M,(1960) Stochastic population models (methuen & co, Ltd., London, UK)

  • Bartlett MS (2020) Deterministic and stochastic models for recurrent epidemics. Contributions to biology and problems of health. University of California Press, Berkeley, pp 81–110

    Google Scholar 

  • Bokil VA, Allen LJS, Jeger MJ, Lenhart S (2019) Optimal control of a vectored plant disease model for a crop with continuous replanting. J Biol Dyn 13(sup1):325–353

    Article  MathSciNet  MATH  Google Scholar 

  • Carter S, Fresco L, Jones P, Fairbairn J, (1993)Introduction and diffusion of cassava in Africa

  • Chan M.-S, Jeger M. J,(1994) An analytical model of plant virus disease dynamics with roguing and replanting, J Appl Ecol 413-427

  • Chen Y, Yang J (2016) Global stability of an SEI model for plant diseases. Math Slovaca 66(1):305–311

    Article  MathSciNet  MATH  Google Scholar 

  • Diekmann O, Heesterbeek J, Roberts MG (2010) The construction of next-generation matrices for compartmental epidemic models. J Royal Soc Interf 7(47):873–885

    Article  Google Scholar 

  • Fargette D, Vié K et al (1995) Simulation of the effects of host resistance, reversion, and cutting selection on incidence of african cassava mosaic virus and yield losses in cassava. Phytopathology 85(3):370–375

    Article  Google Scholar 

  • Fargette D, Thresh J, Otim-Nape GW et al (1994) The epidemiology of African cassava mosaic geminivirus: reversion and the concept of equilibrium. Trop Sci 34(1):123–133

    Google Scholar 

  • Fauquet C, Fargette D et al (1990) African cassava mosaic virus: etiology, epidemiology and control. Plant Dis 74(6):404–411

    Article  Google Scholar 

  • Fereres A,Thresh J, Irwin M, (2000)et al., Plant virus epidemiology: challenges for the twenty-first century, almeria, spain, 11-16 april 1999., Virus Research 71 (1/2)

  • Gao S, Xia L, Liu Y, Xie D (2016) A plant virus disease model with periodic environment and pulse roguing. Stud Appl Math 136(4):357–381

    Article  MathSciNet  MATH  Google Scholar 

  • Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81(25):2340–2361

    Article  Google Scholar 

  • Guthrie J,(2003) Controlling African cassava mosaic disease, Technical Centre for Agricultural and Rural Cooperation,

  • Harris TE et al (1963) The theory of branching processes, vol 6. Springer, Berlin

    Book  MATH  Google Scholar 

  • Hebert MP, Allen LJS (2016) Disease outbreaks in plant-vector-virus models with vector aggregation and dispersal. Discrete Contin Dyn Syst-B 21(7):2169

    Article  MathSciNet  MATH  Google Scholar 

  • Heesterbeek J, Roberts M (2007) The type-reproduction number T in models for infectious disease control. Math Biosci 206(1):3–10

    Article  MathSciNet  MATH  Google Scholar 

  • Hilker FM, Allen LJ, Bokil VA, Briggs CJ, Feng Z, Garrett KA, Gross LJ, Hamelin FM, Jeger MJ, Manore CA et al (2017) Modeling virus coinfection to inform management of maize lethal necrosis in kenya. Phytopathology 107(10):1095–1108

    Article  Google Scholar 

  • Holt J, Jeger M, Thresh J, Otim-Nape G,(1997) An epidemilogical model incorporating vector population dynamics applied to African cassava mosaic virus disease, J Appl Ecol 793-806

  • Imran M, Hassan M, Dur-E-Ahmad M, Khan A (2013) A comparison of a deterministic and stochastic model for hepatitis c with an isolation stage. J Biol Dyn 7(1):276–301

    Article  MathSciNet  MATH  Google Scholar 

  • Jeger M, Holt J, Van Den Bosch F, Madden L (2004) Epidemiology of insect-transmitted plant viruses: modelling disease dynamics and control interventions. Physiol Entomol 29(3):291–304

    Article  Google Scholar 

  • Jennings D et al (1994) Breeding for resistance to African cassava mosaic geminivirus in East Africa. Trop Sci 34(1):110–122

    MathSciNet  Google Scholar 

  • Karlin S, Taylor H,(I960) A first course in stochastic process, Academic Press, second edition. New York. Kendall. DG, “Birth and death processess and the theory of carcinogenesis”, Biometrika 47 (1975) 13-21

  • Khan A, Hassan M, Imran M, (2013)The effects of a backward bifurcation on a continuous time markov chain model for the transmission dynamics of single strain dengue virus

  • Kirupaharan N, Allen LJS (2004) Coexistence of multiple pathogen strains in stochastic epidemic models with density-dependent mortality. Bull Math Biol 66(4):841–864

    Article  MathSciNet  MATH  Google Scholar 

  • Lahodny GE, Allen LJS (2013) Probability of a disease outbreak in stochastic multipatch epidemic models. Bull Math Biol 75(7):1157–1180

    Article  MathSciNet  MATH  Google Scholar 

  • Lahodny G Jr, Gautam R, Ivanek R (2015) Estimating the probability of an extinction or major outbreak for an environmentally transmitted infectious disease. J Biol Dyn 9(sup1):128–155

    Article  MathSciNet  MATH  Google Scholar 

  • Lloyd AL, Zhang J, Root AM (2007) Stochasticity and heterogeneity in host-vector models. J Royal Soc Interf 4(16):851–863

    Article  Google Scholar 

  • Maliyoni M (2021) Probability of disease extinction or outbreak in a stochastic epidemic model for west nile virus dynamics in birds. Acta Biotheor 69(2):91–116

    Article  Google Scholar 

  • Maliyoni M, Chirove F, Gaff HD, Govinder KS (2017) A stochastic tick-borne disease model: exploring the probability of pathogen persistence. Bull Math Biol 79(9):1999–2021

    Article  MathSciNet  MATH  Google Scholar 

  • Maliyoni M, Chirove F, Gaff HD, Govinder KS (2019) A stochastic epidemic model for the dynamics of two pathogens in a single tick population. Theor Popul Biol 127:75–90

    Article  MATH  Google Scholar 

  • Mandal PS, Allen LJ, Banerjee M (2014) Stochastic modeling of phytoplankton allelopathy. Appl Math Model 38(5–6):1583–1596

    Article  MathSciNet  MATH  Google Scholar 

  • McQuaid CF, Gilligan CA, van den Bosch F (2017) Considering behaviour to ensure the success of a disease control strategy. Royal Soc Open Sci 4(12):170721

    Article  Google Scholar 

  • Nandi A, Allen LJ (2019) Stochastic multigroup epidemic models: duration and lnal size. Modeling, stochastic control, optimization, and applications. Springer, Berlin, pp 483–507

    Chapter  MATH  Google Scholar 

  • Nipa KF, Allen LJ (2020) Disease emergence in multi-patch stochastic epidemic models with demographic and seasonal variability. Bull Math Biol 82(12):1–30

    Article  MathSciNet  MATH  Google Scholar 

  • Nipa KF, Jang SR-J, Allen LJ (2021) The effect of demographic and environmental variability on disease outbreak for a dengue model with a seasonally varying vector population. Math Biosci 331:108516

    Article  MathSciNet  MATH  Google Scholar 

  • Njie D, Rumsey T, Singh R (1998) Thermal properties of cassava, yam and platain. J Food Eng 37(1):63–76

    Article  Google Scholar 

  • Oke O, Redhead J, Hussain M,(1990) Roots, tubers, plantains and bananas in human nutrition, FAO food and nutrition series 24

  • Pénisson S,(2010) Conditional limit theorems for multitype branching processes and illustration in epidemiological risk analysis

  • Roberts M, Heesterbeek J (2003) A new method for estimating the effort required to control an infectious disease. Proc Royal Soc London Series B Biol Sci 270(1522):1359–1364

    Article  Google Scholar 

  • Sani A, Kroese D, Pollett P (2007) Stochastic models for the spread of HIV in a mobile heterosexual population. Math Biosci 208(1):98–124

    Article  MathSciNet  MATH  Google Scholar 

  • Seal S, Jeger M, Van den Bosch F (2006) Begomovirus evolution and disease management. Adv Virus Res 67:297–316

    Article  Google Scholar 

  • Shi R, Zhao H, Tang S (2014) Global dynamic analysis of a vector-borne plant disease model. Adv Diff Equ 2014(1):1–16

    Article  MathSciNet  MATH  Google Scholar 

  • Thresh J,(1983) Progress curves of plant virus disease

  • Thresh J, Cooter R (2005) Strategies for controlling cassava mosaic virus disease in Africa. Plant Pathol 54(5):587–614

    Article  Google Scholar 

  • Thresh J, Otim-Nape G (1994) Strategies for controlling african cassava mosaic geminivirus. Advances in disease vector research. Springer, Berlin, pp 215–236

    Chapter  Google Scholar 

  • Thresh J, Otim-Nape G, Fargette D,(1998) The control of african cassava mosaic virus disease: Phytosanitation and/or resistance?

  • Van den Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180(1–2):29–48

    Article  MathSciNet  MATH  Google Scholar 

  • Waterworth H, Hadidi A (1998) Economic losses due to plant viruses. Plant virus disease control. APS, St. Paul

  • Wenjun O, Maofen L, Aye TM, Srey S (2016) Current situation of cassava production, constraints and opportunities in cambodia. Agric For Fisher 5(3):64–70

    Google Scholar 

  • Zhang X-S, Holt J, Colvin J (2000) A general model of plant-virus disease infection incorporating vector aggregation. Plant Pathol 49(4):435–444

    Article  Google Scholar 

Download references

Acknowledgements

Sunil Maity’s research is supported by research fellowship from MHRD, Government of India, Partha Sarathi Mandal’s research is supported by MATRICS Project, DST, SERB, India [File No:MTR/2019/000317].

Author information

Authors and Affiliations

  1. Department of Mathematics, NIT Patna, Patna, Bihar, India

    Sunil Maity & Partha Sarathi Mandal

Authors
  1. Sunil Maity
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Partha Sarathi Mandal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Partha Sarathi Mandal.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maity, S., Mandal, P.S. A Comparison of Deterministic and Stochastic Plant-Vector-Virus Models Based on Probability of Disease Extinction and Outbreak. Bull Math Biol 84, 41 (2022). https://doi.org/10.1007/s11538-022-01001-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11538-022-01001-x

Keywords

Search

Navigation