Global dynamic analysis of a vector-borne plant disease model

Abstract

An epidemic model which describes vector-borne plant diseases is proposed with the aim to investigate the effect of insect vectors on the spread of plant diseases. Firstly, the analytical formula for the basic reproduction number $R_0$ is obtained by using the next generation matrix method, and then the existence of disease-free equilibrium and endemic equilibrium is discussed. Secondly, by constructing a suitable Lyapunov function and employing the theory of additive compound matrices, the threshold for the dynamics is obtained. If $R_0\le 1$, then the disease-free equilibrium is globally asymptotically stable, which means that the plant disease will disappear eventually; if $R_0>1$, then the endemic equilibrium is globally asymptotically stable, which indicates that the plant disease will persist for all time. Finally some numerical investigations are provided to verify our theoretical results, and the biological implications of the main results are briefly discussed in the last section.

1 Introduction

In the natural world, plants are very important, since they are the survival foundation for all kinds of creatures, including human being, animals, and even microbes. However, there are a lot of plant diseases which affect the health of plants, such as Cucumber mosaic virus, Broad bean wilt virus, Beet curly top virus, and Maize streak virus [1]. A serious potato disease destroyed almost all the potatoes of the Irish and caused a great famine in 1845-1846. In fact, in human history, plant diseases were not recognized until very late. In the late 18th century, there were many scientists who began to research the essence of plant diseases. For example, Marthieu Tillet experimentally proved that Wheat bunt is caused by a kind of black powder; Adolf Mayer found that Tobacco mosaic disease can be spread by the juice of infected leafs; and many other plant diseases have been found and researched. It was confirmed that insect vectors (such as aphids, leafhoppers, plant hopper, mealworm etc.) have close relations with many kinds of plant diseases [2, 3].

Recently vector-borne plant diseases have attracted the interest of many mathematical modeling researchers. For instance, F van den Bosch and MJ Jeger have researched plant virus’ propagation characteristics and population dynamics in [4, 5], and they evaluated the influence of insects’ various transmission types and migration on the spread of virus plant diseases in [6]; MP Grill discussed the influence of the timings of insects mediators feeding on plant virus’ infection rate in [7]; MJ Jeger et al., presented some control strategies in [8], and they pointed out that biological control method has become an important part of the integrated pest management. In [9], NJ Cunniffe and CA Gilligan considered the effect of biological control on soil-borne plant pathogens. An antagonist is included in their model to control plant diseases. They obtained invasion criteria for all three species: host, pathogen and antagonist.

The research of plant diseases is also attractive to epidemiologists. They need to establish a simple plausible mechanism to protect susceptible hosts, allowing coexistence of pathogens and hosts, which is consistent with empirical studies of diseases in plant populations. The dynamics of these host-pathogen systems are routinely modeled by compartmental susceptible-infected-removed (SIR) epidemic models. Some criteria were derived for the invasion and persistence of both the pathogen and the host [10, 11]. In [12, 13], the authors considered plant disease models with impulsive effects.

Although early investigations of the epidemics caused by plant pathogens seldom included the demographics of the host population, replenishment of susceptible hosts is common in those models [4, 5, 14, 15]. Motivated by references [10, 11, 14, 15], in this paper, we will develop and analyze the dynamics of a vector-borne plant disease model. The organization of this paper is as follows: In Section 2, the model is constructed and the basic reproduction number is obtained by using the next generation matrix method. In Section 3, we consider the local stability of the equilibria by the Jacobian matrix method; and by the method of constructing a Lyapunov function and employing the theory of competitive systems, the global stability of the disease-free equilibrium and endemic equilibrium are investigated. In Section 4, we give some numerical simulations to prove our theoretical results, and a brief discussion is also provided in this section.

2 Model formulation and the basic reproduction number

To construct the model, we make the following assumptions.

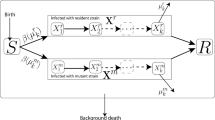
(A1) For an insect vector population, the total population is divided into two categories, X and Y, which denote the densities of the susceptible vector and infective vector at time t, respectively. For the plant host population, the total population is divided into three categories S, I, and R, which denote the numbers of the susceptible, infective, and recovered host plant population at time t, respectively. The total number of plants $K=S+I+R$ is a positive constant. Here, the assumption that the number of plants in one area is fixed is reasonable. In fact, one can always keep the total number fixed by adding a new plant when a plant has died. Further, we assume that those new plants are susceptible, i.e., we chose the birth rate of susceptible plant host as $f(S,I)=\mu K+dI$.

(A2) The susceptible plants can be infected not only by the infected insect vectors but also by the infected plants.

(A3) A susceptible vector can be infected only by an infected plant host, and after it is infected, it will hold the virus for the rest of its life. Further, there is no vertical infection being considered.

(A4) The replenishment rate of insect vectors is a positive constant, and all of the new born vectors are susceptible.

(A5) A nonlinear incidence rate of the disease is included in the model.

According to the principle of the compartmental model, the model is formulated as follows:

$$\{\begin{array}{c}\dot{S}=f(S,I)-\mu S-(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S,\hfill \\ \dot{I}=(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S-(d+\mu +\gamma )I,\hfill \\ \dot{R}=\gamma I-\mu R,\hfill \\ \dot{X}=\mathrm{\Lambda }-\frac{{\beta }_{1}IX}{1+{\alpha }_{1}I}-mX,\hfill \\ \dot{Y}=\frac{{\beta }_{1}IX}{1+{\alpha }_{1}I}-mY.\hfill \end{array}$$

(1)

Here the dimensionless variables and parameters (with parameter values) are given in Table 1.

Table 1 Dimensionless variables and parameters (with illustrative parameter values) in system ( 1 )

By adding the fourth and fifth equations of system (1), we get

$$\dot{N}=\mathrm{\Lambda }-mN,$$

(2)

where $N=X+Y$. From Eq. (2), we easily get $N\to \frac{\mathrm{\Lambda }}{m}$ as $t\to \mathrm{\infty }$.

Note that $S+I+R=K$. Therefore, we only need to consider the dynamics of the following subsystem:

$$\{\begin{array}{c}\dot{S}=\mu (K-S)-(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S+dI,\hfill \\ \dot{I}=(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S-\omega I,\hfill \\ \dot{Y}=\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}(\frac{\mathrm{\Lambda }}{m}-Y)-mY,\hfill \end{array}$$

(3)

where $\omega =d+\mu +\gamma$. Obviously,

$$\mathrm{\Omega }=\{(S,I,Y)\in R_{+}^3:0\le S+I\le K,0\le Y\le \frac{\mathrm{\Lambda }}{m}\}$$

(4)

is the positively invariant set for system (3).

Now, we will calculate the basic reproduction number of system (3) by the next generation method [16]. The rate at which new infections are created is determined by the matrix F, and the rates of transfer into and out of the class of infected states are represented by the matrix V; these are given by

$$F=\left(\begin{array}{cc}{\beta }_{s}K& {\beta }_{p}K\\ 0& 0\end{array}\right)$$

and

$$V=\left(\begin{array}{cc}\omega & 0\\ -\frac{{\beta }_1\mathrm{\Lambda }}{m}& m\end{array}\right).$$

Therefore, the next generation matrix is

$$F{V}^{-1}=\left(\begin{array}{cc}\frac{{\beta }_{s}K}{\omega }+\frac{{\beta }_1{\beta }_p\mathrm{\Lambda }K}{m^2\omega }& \frac{{\beta }_{p}K}{m}\\ 0& 0\end{array}\right),$$

from which we get the basic reproduction number as

$$R_0=\frac{{\beta }_{s}K}{\omega }+\frac{{\beta }_1{\beta }_p\mathrm{\Lambda }K}{m^2\omega }.$$

3 The equilibria and their stability

3.1 The existence of equilibria

In this subsection, we investigate the existence of equilibria of system (3). It is easy to see that system (3) always has a disease-free equilibrium $E_0$, and $E_0=(K,0,0)$. Next, we consider the existence of endemic equilibrium.

Let the right equations of system (3) be equal to 0; we obtain algebraic equations as follows:

$$\{\begin{array}{c}\mu (K-S)-(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S+dI=0,\hfill \\ (\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S-\omega I=0,\hfill \\ \frac{{\beta }_{1}I}{1+{\alpha }_{1}I}(\frac{\mathrm{\Lambda }}{m}-Y)-mY=0.\hfill \end{array}$$

(5)

By adding the first and the second equations of (5), one finds

$$\mu (K-S)-(\mu +\gamma )I=0,$$

and from which we get

$$S=K-(1+\frac{\gamma }{\mu })I.$$

(6)

By the third equation of (5), we get

$$Y=\frac{{\beta }_{1}I\mathrm{\Lambda }}{m{\beta }_{1}I+m^2(1+{\alpha }_{1}I)}.$$

(7)

Substituting Eqs. (6) and (7) into the second equation of (5), we obtain

$$A{I}^2+BI+C=0,$$

(8)

where

$$\begin{array}{r}A=(\mu +\gamma )({\beta }_p{\beta }_1{\alpha }_s\mathrm{\Lambda }+m{\beta }_1{\beta }_s+m^2{\beta }_s{\alpha }_1+{\beta }_s{\beta }_p{\beta }_1\mathrm{\Lambda })>0,\\ B=(\mu +\gamma )({\beta }_p{\beta }_1\mathrm{\Lambda }+{\beta }_s{m}^2)-\mu K(m{\beta }_1{\beta }_s+{\alpha }_1{\beta }_s{m}^2+{\beta }_p{\beta }_s{\beta }_1\mathrm{\Lambda }+{\beta }_p{\beta }_1{\alpha }_s\mathrm{\Lambda })\\ \phantom{B=}+\mu \omega (m{\beta }_1+{\alpha }_1{m}^2+{\alpha }_p{\beta }_1\mathrm{\Lambda }+m^2{\alpha }_s),\\ C=\mu m^2\omega (1-R_0).\end{array}$$

If $R_0>1$, then $C<0$, and Eq. (8) has a unique positive root. Accordingly, for system (3) there exists a unique endemic equilibrium $E^{\ast }$ in the interior of Ω, denoted by $E^{\ast }=(S^{\ast },I^{\ast },Y^{\ast })$, and

$$\begin{array}{r}{S}^{\ast }=K-(1+\frac{\gamma }{\mu })I^{\ast },\\ I^{\ast }=\frac{-B+\sqrt{B^2-4AC}}{2A},\\ Y^{\ast }=\frac{{\beta }_1\mathrm{\Lambda }{I}^{\ast }}{m{\beta }_1{I}^{\ast }+m^2(1+{\alpha }_1{I}^{\ast })}.\end{array}$$

3.2 Local stability of the equilibria

In this subsection, we will investigate the local properties of the equilibria of system (3). The Jacobian matrix of system (3) is

$$J=\left(\begin{array}{ccc}-\mu -(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})& d-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}& -\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\\ \frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}& \frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}-\omega & \frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\\ 0& (\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}& -\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m\end{array}\right).$$

Thus, the characteristic equation at the disease-free equilibrium $E_0$ is

$$\left|\begin{array}{ccc}\lambda +\mu & -d+{\beta }_{s}K& +{\beta }_{p}K\\ 0& \lambda -{\beta }_{s}K+\omega & -{\beta }_{p}K\\ 0& -\frac{\mathrm{\Lambda }}{m}{\beta }_1& \lambda +m\end{array}\right|=0.$$

(9)

It is easy to see that one of the roots with respect to λ of (9) is −μ. The other two roots are determined by the following quadratic equation:

$${\lambda }^2+(m+\omega -{\beta }_{s}K)\lambda +m\omega -m{\beta }_{s}K-\frac{\mathrm{\Lambda }}{m}{\beta }_1{\beta }_{p}K=0.$$

(10)

If $R_0<1$, we know that both of the roots of Eq. (10) have a negative real part; if $R_0>1$, there exists at least one root with positive real part. Therefore, we get the following result.

Theorem 3.1 The disease-free equilibrium $E_0$ is locally asymptotically stable if $R_0<1$, and unstable if $R_0>1$. In addition, when $R_0>1$, the unique endemic equilibrium $E^{\ast }$ emerges in  Ω.

The Jacobian matrix at the endemic equilibrium $E^{\ast }$ is

$$J\left(E^{\ast }\right)=\left(\begin{array}{ccc}-\mu -(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})& d-\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}& -\frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}\\ \frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }}& \frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}-\omega & \frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}\\ 0& (\frac{\mathrm{\Lambda }}{m}-Y^{\ast })\frac{{\beta }_1}{{(1+{\alpha }_1{I}^{\ast })}^2}& -\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}-m\end{array}\right),$$

and the second additive compound matrix of $J(E^{\ast })$ is given by

$$J^{[2]}\left(E^{\ast }\right)=\left(\begin{array}{ccc}{a}_{11}& \frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}& \frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}\\ (\frac{\mathrm{\Lambda }}{m}-Y^{\ast })\frac{{\beta }_1}{{(1+{\alpha }_1{I}^{\ast })}^2}& a_{22}& d-\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}\\ 0& (\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})& a_{33}\end{array}\right),$$

where

$$\begin{array}{r}{a}_{11}=-\mu -(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})+\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}-\omega ,\\ a_{22}=-\mu -(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }}+\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}+m),\\ a_{33}=\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}-\omega -\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}-m.\end{array}$$

To demonstrate the local stability of the positive equilibrium $E^{\ast }$, we need the following lemma.

Lemma 3.2 [17, 18]

Let M be a $3\times 3$ real matrix. If $tr(M)$, $det(M)$ and $det(M^{[2]})$ are all negative, then all of the eigenvalues of M have negative real part.

Theorem 3.3 The endemic equilibrium $E^{\ast }$ of system (3) is locally asymptotically stable if $R_0>1$.

Proof Note that

$$tr\left(J\left(E^{\ast }\right)\right)=-\mu -(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})+\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}-\omega -\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}-m,$$

and it is easy to calculate by the second equation of system (3) that

$$\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}<\frac{{\beta }_s{S}^{\ast }}{(1+{\alpha }_s{I}^{\ast })}<\omega .$$

Thus

$$tr\left(J\left(E^{\ast }\right)\right)<0.$$

By a simple calculation we have

$$\begin{array}{r}det\left(J\left(E^{\ast }\right)\right)\\ =-(\mu +\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})\\ \times [(\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}-\omega )(-\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}-m)-(\frac{A}{m}-Y^{\ast })\frac{{\beta }_1}{{(1+{\alpha }_1{I}^{\ast })}^2}\frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}]\\ -(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})\\ \times [d-\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}(-\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}-m)+(\frac{A}{m}-Y^{\ast })\frac{{\beta }_1}{{(1+{\alpha }_1{I}^{\ast })}^2}\frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}].\end{array}$$

By the second and third equations of system (3) we get

$$\frac{{\beta }_p{S}^{\ast }{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}=(-\frac{{\beta }_s{S}^{\ast }}{1+{\alpha }_s{I}^{\ast }}+\omega )I^{\ast },$$

and

$$\frac{\mathrm{\Lambda }}{m}\frac{{\beta }_1{I}^{\ast }}{(1+{\alpha }_1{I}^{\ast })}=(\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}+m)Y^{\ast }.$$

Thus

$$det\left(J\left(E^{\ast }\right)\right)<0.$$

Further, we have

$$\begin{array}{r}det\left(J^{[2]}\left(E^{\ast }\right)\right)\\ =-(\mu +\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }}+\omega -\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2})\\ \times [(\mu +\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }}+\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}+m)(\omega -\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}+\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}+m)\\ -(d-\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2})(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})]-(\frac{A}{m}-Y^{\ast })\frac{{\beta }_1}{{(1+{\alpha }_1{I}^{\ast })}^2}\\ \times [\frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}(\frac{{\beta }_s{S}^{\ast }}{{(1+{\alpha }_s{I}^{\ast })}^2}-\omega -\frac{{\beta }_1{I}^{\ast }}{1+{\alpha }_1{I}^{\ast }}-m)\\ -\frac{{\beta }_p{S}^{\ast }}{{(1+{\alpha }_p{Y}^{\ast })}^2}(\frac{{\beta }_p{Y}^{\ast }}{1+{\alpha }_p{Y}^{\ast }}+\frac{{\beta }_s{I}^{\ast }}{1+{\alpha }_s{I}^{\ast }})]\\ <0.\end{array}$$

Therefore, it follows from Lemma 3.2 that the proof is complete. □

3.3 Global stability of the equilibria

In this subsection, we will investigate the global stability of the equilibria of system (3).

Theorem 3.4 If $R_0\le 1$, then the disease-free equilibrium $E_0$ is globally asymptotically stable in Ω.

Proof From the second and third equations of system (3), we have

$$\{\begin{array}{c}\dot{I}\le {\beta }_{p}KY+{\beta }_{s}KI-\omega I,\hfill \\ \dot{Y}\le \frac{{\beta }_1\mathrm{\Lambda }}{m}I-mY.\hfill \end{array}$$

(11)

Consider the following comparison system:

$$\{\begin{array}{c}\dot{Z_1}={\beta }_{p}K{Z}_2+({\beta }_{s}K-\omega )Z_1,\hfill \\ \dot{Z_2}=\frac{{\beta }_1\mathrm{\Lambda }}{m}{Z}_1-m{Z}_2.\hfill \end{array}$$

(12)

From $R_0\le 1$, we have

$$m^2{\beta }_{s}K+{\beta }_1{\beta }_{p}K\mathrm{\Lambda }\le m^2\omega .$$

(13)

It is easy to show that if condition (13) holds, then any solutions of system (12) with nonnegative initial values will satisfy

$$\underset{t\to \mathrm{\infty }}{lim}{Z}_i(t)=0,i=1,2.$$

Let $0<I(0)\le Z_1(0)$, $0<Y(0)\le Z_2(0)$. If $(Z_1(t),Z_2(t))$ is a solution of system (12) with nonnegative initial values $(Z_1(0),Z_2(0))$, then by the comparison principle for differential equations, we have $I(t)\le Z_1(t)$, $Y(t)\le Z_2(t)$ for all $t\ge 0$. Hence, together with the positivity of the solution, we have

$$\underset{t\to \mathrm{\infty }}{lim}I(t)=0,\underset{t\to \mathrm{\infty }}{lim}Y(t)=0.$$

Then, the limit equations of system (3) become

$$\{\begin{array}{c}\dot{S}=\mu (K-S),\hfill \\ \dot{I}=0,\hfill \\ \dot{Y}=0,\hfill \end{array}$$

(14)

and it is easy to see that $S\to K$ as $t\to \mathrm{\infty }$. Therefore, by the LaSalle invariance principle [19] we conclude that all trajectories starting in Ω approach $E_0$ for $R_0\le 1$.

Together with the result of Theorem 3.1, we complete the proof of this theorem. □

Now we will investigate the global stability of the endemic equilibrium $E^{\ast }$ in the positively invariant set Ω. To do so, we will use the results for the three dimensional competitive systems that live in convex sets [20–22] and a powerful theory of additive compound matrix to prove asymptotic orbital stability of periodic solutions [16, 23]. The approach has been adopted by many authors (see [24, 25] and the references cited therein) to show the global stability of the endemic equilibrium in the three dimensional competitive systems. Before proving our main result, we give the following useful lemma.

Lemma 3.5 [25]

Consider the system of differential equations

$$U^{\prime }=F(U),U\in D,$$

(15)

where $U=(u_1,u_2,u_3)$ is a three-dimensional vector, D is an open subset on $R^3$, and F is twice continuously differentiable in D. Assume D is convex and bounded, and system (15) is competitive and permanent and has the property of stability of periodic orbits. If $U^{\ast }$ is the only equilibrium point in intD and if it is locally asymptotically stable, then it is globally asymptotically stable in intD.

Theorem 3.6 If $R_0>1$, then system (3) is uniformly persistent, i.e., there exists $\epsilon >0$ (independent of the initial conditions), such that ${lim\hspace{0.17em}inf}_{t\to \mathrm{\infty }}S(t)>\epsilon$, ${lim\hspace{0.17em}inf}_{t\to \mathrm{\infty }}I(t)>\epsilon$, ${lim\hspace{0.17em}inf}_{t\to \mathrm{\infty }}Y(t)>\epsilon$.

Proof Let π be the semi-dynamics in ${(R_0^{+})}^3$ defined by system (3), χ a locally compact metric space and ${\mathrm{\Gamma }}_0=\{(S,I,Y)\in \mathrm{\Omega }:Y=0\}$. It is easy to show that the set ${\mathrm{\Gamma }}_0$ is a compact subset of Ω and $\mathrm{\Omega }\setminus {\mathrm{\Gamma }}_0$ is a positively invariant set of system (3). Let $F:\chi \to R_0^{+}$ be defined by $F(S,I,Y)=Y$ and set $M=\{(S,I,Y)\in \mathrm{\Omega }:F(S,I,Y)<\rho \}$, where ρ is sufficiently small so that $\frac{R_0(1-\frac{m}{\mathrm{\Lambda }}\rho )}{1+{\alpha }_1\rho }>1$. Assume that there is a solution $x\in M$ such that for any $t>0$, we have $F(\pi (x,t))<F(x)<\rho$. Let us consider the auxiliary function

$$L(t)=\frac{{\beta }_{p}K(1-{\delta }^{\ast })}{m}Y+I,$$

(16)

where ${\delta }^{\ast }$ is a sufficiently small constant such that $\frac{R_0(1-\frac{m}{\mathrm{\Lambda }}\rho )(1-{\delta }^{\ast })}{1+{\alpha }_1\rho }>1$. By direct calculation, we have

$$\begin{array}{rl}\dot{L}(t)& =\frac{{\beta }_{p}K(1-{\delta }^{\ast })}{m}[\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}(\frac{\mathrm{\Lambda }}{m}-Y)-mY]+(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})S-\omega I\\ \ge \frac{{\beta }_{p}K(1-{\delta }^{\ast })}{m}[\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}(\frac{\mathrm{\Lambda }}{m}-Y)-mY]-\omega I\\ \ge \omega [\frac{K(m^2{\beta }_s+{\beta }_1{\beta }_p\mathrm{\Lambda })(1-\frac{m}{\mathrm{\Lambda }}\rho )(1-{\delta }^{\ast })}{m^2\omega (1+{\alpha }_1\rho )}-1]I+{\beta }_{p}K{\delta }^{\ast }Y\\ =\omega [\frac{K(m^2{\beta }_s+{\beta }_1{\beta }_p\mathrm{\Lambda })(1-\frac{m}{\mathrm{\Lambda }}\rho )(1-{\delta }^{\ast })}{m^2\omega (1+{\alpha }_1\rho )}-1]I+\frac{m{\delta }^{\ast }}{1-{\delta }^{\ast }}\frac{{\beta }_{p}K(1-{\delta }^{\ast })}{m}Y.\end{array}$$

(17)

Denote $\delta =min\{\omega [\frac{K(m^2{\beta }_s+{\beta }_1{\beta }_P\mathrm{\Lambda })(1-\frac{m}{\mathrm{\Lambda }}\rho )(1-{\delta }^{\ast })}{m^2\omega (1+{\alpha }_1\rho )}-1],\frac{m{\delta }^{\ast }}{1-{\delta }^{\ast }}\}>0$. Then, we have

$$\dot{L}(t)\ge \delta L(t).$$

(18)

The inequality (18) implies that $L(t)\to \mathrm{\infty }$ as $t\to \mathrm{\infty }$. However, $L(t)$ is bounded on the set Ω. According to Theorem 1 in reference [20], we get the result of this theorem. □

Theorem 3.7 If $R_0>1$, then system (3) has the property of stability of periodic orbits.

Proof Let $P(t)=(S,I,Y)$ be a periodic solution whose orbit is contained in intΩ. In accordance with the criterion given by Muldowney in [16], for the asymptotic orbital stability of a periodic orbit of a general autonomous system, it is sufficient to prove that the linear non-autonomous system

$$\dot{W}(t)=\left(J^{[2]}(P(t))\right)W(t)$$

(19)

is asymptotically stable, where $J^{[2]}$ is the second additive compound matrix of the Jacobian matrix J. The Jacobian matrix of system (3) is given by

$$J=\left(\begin{array}{ccc}-\mu -(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})& d-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}& -\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\\ (\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})& \frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}-\omega & \frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\\ 0& (\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}& -\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m\end{array}\right).$$

For the solution $P(t)$, Eq. (19) becomes

$$\begin{array}{r}{\dot{W}}_1(t)=-(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}+\omega )W_1(t)\\ \phantom{{\dot{W}}_1(t)=}+\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}{W}_2(t)+\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}{W}_3(t),\\ {\dot{W}}_2(t)=(\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}{W}_1(t)+(d-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2})W_3(t)\\ \phantom{{\dot{W}}_2(t)=}-(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}+\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}+m)W_2(t),\\ {\dot{W}}_3(t)=(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})W_2(t)+(\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m-\omega )W_3(t).\end{array}$$

(20)

To prove that system (20) is asymptotically stable, we will use the following Lyapunov function:

$$V(W_1(t),W_2(t),W_3(t),S,I,Y)=\parallel (W_1(t),\frac{I}{Y}{W}_2(t),\frac{I}{Y}{W}_3(t))\parallel ,$$

(21)

where $\parallel \cdot \parallel$ is the norm in $R^3$ defined by

$$\parallel (W_1(t),W_2(t),W_3(t))\parallel =sup\{|W_1(t)|,|W_2(t)+W_3(t)|\}.$$

From Theorem 3.6, we see that the orbit of $P(t)$ remains at a positive distance from the boundary of Ω. Therefore, we have

$$I(t)\ge \eta ,Y(t)\ge \eta ,$$

with $0<\eta <min\{K,\frac{\mathrm{\Lambda }}{m}\}$. Hence, the function $V(t)$ is well defined along $P(t)$ and

$$V(W_1(t),W_2(t),W_3(t),S,I,Y)\ge \eta \parallel (W_1(t),W_2(t),W_3(t))\parallel .$$

(22)

Along the positive solution $(W_1(t),W_2(t),W_3(t))$ of system (20), $V(t)$ becomes

$$V(t)=sup\{|W_1(t)|,\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right)\}.$$

(23)

Similarly to what was done in [25–27], we obtain the following inequalities:

$$\begin{array}{r}{D}_{+}{W}_1(t)\le -(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}+\omega )|W_1(t)|\\ \phantom{D_{+}{W}_1(t)\le }+\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\left(|W_2(t)+W_3(t)|\right)\\ \phantom{D_{+}{W}_1(t)}=-(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}+\omega )|W_1(t)|\\ \phantom{D_{+}{W}_1(t)\le }+\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\frac{Y}{I}\left(\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right)\right),\\ D_{+}{W}_2(t)\le (\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}|W_1(t)|\\ \phantom{D_{+}{W}_2(t)\le }-(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}+\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}+m)|W_2(t)|\\ \phantom{D_{+}{W}_2(t)\le }+(d-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2})|W_3(t)|,\\ D_{+}{W}_3(t)\le (\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})|W_2(t)|\\ \phantom{D_{+}{W}_3(t)\le }+(\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m-\omega )|W_3(t)|\\ \phantom{D_{+}{W}_3(t)}\le (\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})|W_2(t)|\\ \phantom{D_{+}{W}_3(t)\le }+(\gamma +\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m-\omega )|W_3(t)|.\end{array}$$

(24)

From the second and third inequality of system (24), we have

$$\begin{array}{rl}{D}_{+}\left(|W_2(t)+W_3(t)|\right)\le & (\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}|W_1(t)|\\ -(\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}+m+\mu )\left(|W_2(t)+W_3(t)|\right).\end{array}$$

Thus, we obtain

$$\begin{array}{r}{D}_{+}\left(\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right)\right)\\ =(\frac{\dot{I}}{I}-\frac{\dot{Y}}{Y})\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right)\\ +\frac{I}{Y}{D}_{+}\left(|W_2(t)+W_3(t)|\right)\\ \le (\frac{\dot{I}}{I}-\frac{\dot{Y}}{Y})\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right)\\ +\frac{I}{Y}[(\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}|W_1(t)|\\ -(\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}+m+\mu )\left(|W_2(t)+W_3(t)|\right)]\\ =(\frac{\dot{I}}{I}-\frac{\dot{Y}}{Y})\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right)\\ +\frac{I}{Y}(\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}|W_1(t)|\\ -\frac{I}{Y}(\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}+m+\mu )\left(|W_2(t)+W_3(t)|\right)\\ =\frac{I}{Y}(\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}|W_1(t)|\\ +(\frac{\dot{I}}{I}-\frac{\dot{Y}}{Y}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m-\mu )\frac{I}{Y}\left(|W_2(t)+W_3(t)|\right).\end{array}$$

(25)

From the first equation of (24) and the above equation, we obtain

$$D_{+}V(t)\le sup\{g_1(t),g_2(t)\}W(t),$$

(26)

where

$$\begin{array}{r}{g}_1(t)=-(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}-\frac{{\beta }_{s}S}{{(1+{\alpha }_{s}I)}^2}+\omega )+\frac{{\beta }_{p}S}{{(1+{\alpha }_{p}Y)}^2}\frac{Y}{I},\\ g_2(t)=\frac{I}{Y}\frac{\mathrm{\Lambda }}{m}\frac{{\beta }_1}{{(1+{\alpha }_{1}I)}^2}+(\frac{\dot{I}}{I}-\frac{\dot{Y}}{Y}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m-\mu ).\end{array}$$

The second and third equations of system (3) can be rewritten as follows:

$$\frac{\dot{I}}{I}=(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})\frac{S}{I}-\omega$$

(27)

and

$$\frac{\dot{Y}}{Y}=\frac{{\beta }_{1}I(\frac{\mathrm{\Lambda }}{m}-Y)}{(1+{\alpha }_{1}I)Y}-m.$$

(28)

Thus, from Eqs. (27) and (28), we have

$$\begin{array}{rl}{g}_1(t)& \le -(\mu +\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I}-\frac{{\beta }_{s}S}{(1+{\alpha }_{s}I)}+\omega )+\frac{{\beta }_{p}S}{1+{\alpha }_{p}Y}\frac{Y}{I}\\ \le -(\mu -\frac{{\beta }_{s}S}{(1+{\alpha }_{s}I)}\frac{I}{I}+\omega )+\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}\frac{S}{I}\\ =-\mu +(\frac{{\beta }_{p}Y}{1+{\alpha }_{p}Y}+\frac{{\beta }_{s}I}{1+{\alpha }_{s}I})\frac{S}{I}-\omega \\ =-\mu +\frac{\dot{I}}{I}\end{array}$$

(29)

and

$$\begin{array}{rl}{g}_2(t)& \le \frac{I}{Y}(\frac{\mathrm{\Lambda }}{m}-Y)\frac{{\beta }_1}{(1+{\alpha }_{1}I)}+(\frac{\dot{I}}{I}-\frac{\dot{Y}}{Y}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}-m-\mu )\\ =-\mu +\frac{\dot{I}}{I}+\frac{I}{Y}\frac{\mathrm{\Lambda }}{m}\frac{{\beta }_1}{(1+{\alpha }_{1}I)}-\frac{{\beta }_{1}I(\frac{\mathrm{\Lambda }}{m}-Y)}{(1+{\alpha }_{1}I)Y}+m-m-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}\\ =-\mu +\frac{\dot{I}}{I}-\frac{{\beta }_{1}I}{1+{\alpha }_{1}I}\\ \le -\mu +\frac{\dot{I}}{I}.\end{array}$$

(30)

Namely,

$$sup\{g_1(t),g_2(t)\}\le -\mu +\frac{\dot{I}}{I}.$$

Therefore, from Eq. (26) and Gronwall’s inequality, we obtain

$$V(t)\le V(0)I(t)exp(-\mu t)\le V(0)Kexp(-\mu t),$$

which implies that $V(t)\to 0$ as $t\to \mathrm{\infty }$. By Eq. (22), it shows that $(W_1(t),W_2(t),W_3(t))\to 0$ as $t\to \mathrm{\infty }$, which implies that the linear system (20) is asymptotically stable.

This completes the proof. □

Theorem 3.8 If $R_0>1$, then the unique endemic equilibrium $E^{\ast }$ is globally asymptotically stable for system (3).

Proof Combining the results of Theorems 3.3, 3.6, and 3.7 with Lemma 3.5, we can complete the proof. □

4 Numerical analysis and discussion

4.1 Numerical simulations

In this subsection, we will illustrate the influence of insect vector on the spread of plant disease by numerical simulations.

To do this, let ${\beta }_1=0.0025$, ${\beta }_p=0.0025$, ${\beta }_s=0.0001$, $\mu =0.1$, $\gamma =0.4$, $K=1\text{,}000$, $\mathrm{\Lambda }=5$, ${\alpha }_1=0.1$, ${\alpha }_p=0.2$, ${\alpha }_s=0.2$, $m=0.3$, $d=0.1$, then by a simple calculation we have $R_0=0.89444<1$. It follows from Figure 1 that the disease-free equilibrium of system (3) is globally asymptotically stable.

Figure 1

Stability of disease-free equilibrium. The parameters are fixed as follows: ${\beta }_1=0.0025$, ${\beta }_p=0.0025$, ${\beta }_s=0.0001$, ${\alpha }_1=0.1$, ${\alpha }_p=0.2$, ${\alpha }_s=0.2$, $\mu =0.1$, $\gamma =0.4$, $K=1\text{,}000$, $\mathrm{\Lambda }=5$, $m=0.3$, $d=0.1$, and the initial values are $(S_0,I_0,Y_0)=(700,200,10)$. The time series charts for $S(t)$, $I(t)$, $Y(t)$ and the phase diagram are given in (A), (B), (C), and (D), respectively.

If we fixed all parameter values as follows: ${\beta }_1=0.01$, ${\beta }_p=0.02$, ${\beta }_s=0.01$, $\mu =0.1$, $\gamma =0.4$, $K=1\text{,}000$, $\mathrm{\Lambda }=5$, ${\alpha }_1=0.1$, ${\alpha }_p=0.2$, ${\alpha }_s=0.2$, $m=0.3$, $d=0.1$, then $R_0=26.222>1$. For this parameter set Figure 2 indicates that the endemic equilibrium of system (3) is globally asymptotically stable.

Figure 2

Stability of endemic equilibrium. The parameters are fixed as follows: ${\beta }_1=0.01$, ${\beta }_p=0.02$, ${\beta }_s=0.01$, ${\alpha }_1=0.1$, ${\alpha }_p=0.2$, ${\alpha }_s=0.2$, $\mu =0.1$, $\gamma =0.4$, $K=1\text{,}000$, $\mathrm{\Lambda }=5$, $m=0.3$, $d=0.1$, and the initial values are $(S_0,I_0,Y_0)=(700,200,10)$. The time series charts for $S(t)$, $I(t)$, $Y(t)$, and the phase diagram are given in (A), (B), (C), and (D), respectively.

4.2 Discussion

In this paper, we propose a differential system to model a vector-borne plant disease. Our main object is to investigate the effect of the insect vector on the dynamics of the plant disease. We get the basic reproduction number $R_0$ by the next generation matrix method in Section 2. In detail, the existence, local stability, and global stability of the disease-free equilibrium and endemic equilibrium are investigated in Section 3. By employing a suitable Lyapunov function, and the second additive compound matrix method, the main results as shown in Theorems 3.4 and 3.8 have been derived. Our main results indicate that if $R_0\le 1$, then the disease-free equilibrium is globally asymptotically stable in Ω, and the unique endemic equilibrium is globally asymptotically stable provided that $R_0>1$. It follows from these results that the basic reproduction number $R_0$ plays an important role in determining the persistence or dying out of the disease.

Note that the basic reproduction number, $R_0$, is a strictly increasing function with respect to the parameters ${\beta }_1$, ${\beta }_p$, ${\beta }_s$, whereas it decreases the function with respect to parameters m, ω. The parameters ${\alpha }_1$, ${\alpha }_p$, ${\alpha }_s$ have no relations to the value of $R_0$. That is, the total number of the host plant, birth rate of the vector, and incidence rate of the disease can positively affect the value of $R_0$; while the death rate of the host plant, the death rate of the vector, and the disease-induced death rate can negatively affect the value of $R_0$; but the saturation rate of the incidence has no relation to the value of $R_0$. Those results are useful and could help us to design optimal control strategies for disease control. For example, if under natural conditions the value of $R_0$ is greater than 1, then it follows from Theorem 3.8 that the endemic equilibrium is globally stable. This means that the disease will be an endemic. However, we can take measures to reduce the values of incidence rate ${\beta }_1$, ${\beta }_p$, and (or) ${\beta }_s$, such that the value of $R_0$ can be reduced until it is less than 1.