1 Introduction

Malaria is a life-threatening infectious disease caused by Plasmodium parasites that are transmitted to humans through the bites of infected female Anopheles mosquitoes. P. falciparum, P. malariae, P. ovale, P. vivax and P. knowlesi are five known species of human malaria parasites among which P. falciparum is responsible for the vast majority of malaria cases and deaths worldwide. The data released by the World Health Organization (WHO) indicates that there were about 228 million malaria cases including 405,000 deaths in 2018 (World Health Organization 2019). No dramatic reduction in malaria incidence rate in the period of 2015–2018. Over 40% of the world’s population in more than 80 countries and areas is still at risk of contracting malaria. Nowadays malaria is preventable, treatable and curable. Reducing the contacts of people with mosquitoes is the core strategy to prevent and control the spread of malaria. A number of precautions such as decreasing mosquito breeding sites, sleeping under insecticide-treated nets and indoor residual spraying with insecticides, are used for reducing malaria vectors and their bites. The artemisinin-based combination therapies are recommended by WHO as the fist-line treatments for uncomplicated P. falciparum malaria (World Health Organization 2015). So far there is only one approved malaria vaccine (RTS, S) with a relatively low efficacy, but requiring four injections (RTS, S Clinical Trials Partnership et al. 2011).

Mathematical models towards an understanding of the transmission dynamics of malaria have a history of over 100 years. The earliest model was proposed by Ross in 1911 who was awarded the Nobel Prize in Physiology or Medicine in 1902 for being the discoverer of the life cycle of malarial parasite (Ross 1911). Macdonald extended Ross’ basic model by considering superinfection and developed the entomological theory and the quantitative theory of malaria control (Macdonald 1957). The so-called Ross–Macdonald model captures the essential feature of malaria transmission and the modeling framework has been widely adopted to study the epidemiology of malaria and other mosquito-borne or even vector-borne diseases (Reiner et al. 2013). Dietz et al. (1974) and Aron (1988) conducted a modeling study on acquired immunity for whom has ever suffered from malaria. Aron and May (1982) formed an SIRS model with constant infection rate to fit data on age-prevalence curves. Ngwa and Shu (2000) established a compartmental model with an SEIRS pattern for humans and an SEI pattern for mosquitoes. Their model was later extended by Chitnis et al. (2006) through including constant immigration of susceptible humans and generalizing mosquito biting rate. Hasibeder and Dye (1988) and Gao et al. (2019) showed that nonhomogeneous mixing between humans and mosquitoes leads to a higher basic reproduction number using Lagrangian and Eulerian approaches, respectively. Ruan et al. (2008) proposed a delayed Ross–Macdonald model in consideration of the incubation periods of parasites within both humans and mosquitoes. Abu-Raddad et al. (2006) and Mukandavire et al. (2009) studied the influence of the interaction between HIV and malaria in a community. Differences in susceptibility, exposedness and infectivity between non-immune and semi-immune human hosts for malaria transmission were investigated by Ducrot et al. (2009). Chamchod and Britton (2011) introduced a vector-bias model with vital dynamics to account for the greater attractiveness of infectious humans to mosquitoes. A theoretical model for evaluating the effectiveness of malaria control using genetically modified mosquitoes was developed and analyzed by Diaz et al. (2011). In addition, environmental changes (Li et al. 2002; Parham and Michael 2010), seasonal human migration (Gao et al. 2014b) and drug resistance (Koella and Antia 2003) were also considered in malaria models.

Quarantine is a public health control strategy in containing infectious diseases by separating exposed or sick persons from the healthy population. As early as the 14th century, ships arriving in Venice from areas infected with plague were required to wait forty days before landing. The essential of quarantine is to prevent infectious individuals from contacting with susceptible individuals. This measure is effective even for newly emerging infectious diseases caused by unidentified infectious agents. Quarantine has been widely used in the control of COVID-19, SARS, Ebola, Bubonic plague, measles, tuberculosis, H7N9, typhoid fever, etc. Many studies have shown the effectiveness of quarantine for controlling and eliminating infectious diseases. Feng and Thieme (1995) formulated a perfect quarantine model where a proportion of infected people stay at home and do not infect anybody and showed that the model can give rise to sustained oscillations. Hethcote et al. (2002) analyzed six types of SIQS and SIQR models to explore which one can produce periodic solutions. Gumel et al. (2004) used models to examine the effectiveness of quarantine and isolation on the control of SARS outbreaks. Tang et al. (2012) proposed a dynamic model to evaluate the influence of campus quarantine for curbing the H1N1 outbreak in the Chinese city of Xi’an during the 2009 H1N1 pandemic. Pandey et al. (2014) developed a compartmental model for Ebola transmission to assess the effectiveness of non-pharmaceutical interventions (e.g., quarantine, case isolation, and sanitary burial practices) for curtailing the epidemic in Liberia. Erdem et al. (2017) studied the impact of imperfect quarantine on the dynamics of an SIR-type model.

Although malaria is still a serious threat to public health, the disease burden has been sharply reduced over the past two decades due to global efforts. A number of countries are on the road to malaria elimination. However, imported infections pose the greatest threat for maintaining the elimination status. For example, a National Malaria Elimination Programme was launched in China in 2010, aiming at achieving national malaria elimination by 2020 (Ministry of Health of the People’s Republic of China 2010). Imported cases account for over 98% of the total malaria cases in China since 2014 (Feng et al. (2018), see Fig. 1). The situation leads to the theme of National Malaria Day in China since 2015 being “Malaria eradication: preventing imported cases”. For a malaria-free or low transmission country or region, it is feasible to quarantine sporadic imported or autochthonous cases to limit the disease transmission from humans to mosquitoes. Meanwhile, malaria patients get less mosquito bites when they receive treatment and health care in hospitals or at homes.

Fig. 1
figure 1

Indigenous and imported malaria cases in China during 2011–2018 (Color figure online)

Full size image

The main purpose of this work is to explore the role of quarantine-like intervention on malaria control and elimination. In Sect. 2, we formulate a Ross–Macdonald type malaria model with imperfect quarantine. Sections 3 and 4 are devoted to dynamical behavior analysis of the model with standard and bilinear incidence rates, respectively. Sensitivity analysis and numerical simulations are given in Sect. 5 to illustrate the impact of quarantine on malaria control. Finally, we summarize the main results, address the limitations of the present study and list some future research topics.

2 Model Formulation

In the Ross–Macdonald model for malaria transmission, the total human population H is split into susceptible humans \(S_h=H-I_h\) and infectious humans \(I_h\), and the total mosquito population V is divided into susceptible mosquitoes \(S_v=V-I_v\) and infectious mosquitoes \(I_v\). The model takes the following form

$$\begin{aligned} \begin{aligned} \dfrac{\hbox {d}I_h}{\hbox {d}t}&= ab\dfrac{I_v}{H}(H-I_h)-\gamma I_h,\\ \dfrac{\hbox {d}I_v}{\hbox {d}t}&= ac\dfrac{I_h}{H}(V-I_v)-\mu I_v. \end{aligned} \end{aligned}$$
(1)

Here a denotes the number of bites on humans per mosquito per unit time, b is the probability of transmission of infection from an infectious mosquito to a susceptible human per bite, c is the probability of transmission of infection from an infectious human to a susceptible mosquito per bite, \(\gamma \) is the human recovery rate, and \(\mu \) is the death rate for mosquitoes. Let \(m=V/H\) denote the ratio of mosquito to human populations. The basic reproduction number of model (1) is defined as

$$\begin{aligned} \mathcal {R}_0= \sqrt{\dfrac{a^2bcm}{\gamma \mu }}. \end{aligned}$$
Fig. 2
figure 2

Flow diagram of the malaria model with quarantine (Color figure online)

Full size image

The model exhibits global threshold dynamics, i.e., the origin is globally asymptotically stable (GAS) if \(\mathcal {R}_0\le 1\) and there is a unique GAS positive equilibrium if \(\mathcal {R}_0>1\).

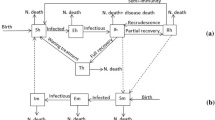
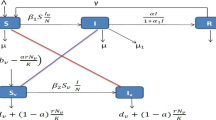
People who have malaria usually suffer chill, fever, sweating, and headache, and may develop severe complications such that they need to seek medical care in hospitals or take breaks at homes. Hospital or home stay plus health education campaign could reduce patient exposure to mosquitoes. In countries approaching malaria elimination, timely quarantine of detected cases is especially feasible. We thus introduce a compartment \(Q_h\) representing quarantined people who get fewer mosquito bites. Let \(\sigma \) be the proportion of bites that is reduced via quarantine. Then \(\sigma =1\) corresponds to perfect quarantine, \(\sigma =0\) corresponds to no quarantine, and \(\sigma \in (0,1)\) corresponds to imperfect quarantine. Let \(A_v(I_h, Q_h, I_v)\) be the mosquito biting rate, i.e., the number of bites per mosquito per unit time, and \(A_h(I_h, Q_h, I_v)\) be the human biting rate, i.e., the number of bites per non-quarantined human per unit time. By the conservation of bites, we have

$$\begin{aligned} A_v V=A_h(H-Q_h)+(1-\sigma )A_hQ_h=A_h(H-\sigma Q_h). \end{aligned}$$

The forces of infection on humans and mosquitoes are

$$\begin{aligned} \begin{aligned} \lambda _h&=A_h\cdot \dfrac{I_v}{V}\cdot b =\dfrac{A_v V}{H-\sigma Q_h}\cdot \dfrac{I_v}{V}\cdot b= A_v\cdot \dfrac{I_v}{H-\sigma Q_h}\cdot b, \\ \lambda _v&=A_v\cdot \dfrac{A_hI_h+(1-\sigma )A_hQ_h}{A_h(H-Q_h)+(1-\sigma )A_hQ_h}\cdot c=A_v\cdot \dfrac{I_h+(1-\sigma )Q_h}{H-\sigma Q_h}\cdot c, \end{aligned} \end{aligned}$$
(2)

respectively. Based on the Ross–Macdonald model (1) and the flow diagram illustrated in Fig. 2, the transmission dynamics of malaria in the presence of quarantine are described by the following system

$$\begin{aligned} \dfrac{\hbox {d}S_h}{\hbox {d}t}= & {} -\lambda _hS_h+(1-\theta )\gamma I_h+\gamma _2 Q_h, \nonumber \\ \dfrac{\hbox {d}I_h}{\hbox {d}t}= & {} \lambda _h S_h-(\theta \gamma _1+(1-\theta )\gamma )I_h, \nonumber \\ \dfrac{\hbox {d}Q_h}{\hbox {d}t}= & {} \theta \gamma _1I_h-\gamma _2Q_h, \\ \dfrac{\hbox {d}S_v}{\hbox {d}t}= & {} \mu V-\lambda _v S_v-\mu S_v, \nonumber \\ \dfrac{\hbox {d}I_v}{\hbox {d}t}= & {} \lambda _vS_v-\mu I_v.\nonumber \end{aligned}$$
(3)

Since \(H=S_h+I_h+Q_h\) and \(V=S_v+I_v\) are constant, the model system (3) can be reduced to a three-dimensional system

$$\begin{aligned} \begin{aligned} \dfrac{\hbox {d}I_h}{\hbox {d}t}&= \lambda _h (H-I_h-Q_h)-(\theta \gamma _1+(1-\theta )\gamma )I_h,\\ \dfrac{\hbox {d}Q_h}{\hbox {d}t}&= \theta \gamma _1I_h-\gamma _2Q_h,\\ \dfrac{\hbox {d}I_v}{\hbox {d}t}&= \lambda _v(V-I_v)-\mu I_v. \end{aligned} \end{aligned}$$
(4)

The descriptions and ranges for model parameters are summarized in Table 1. In particular, \(\theta \) is defined in order that \({\hat{\theta }}\) of infectious humans are quarantined, that is,

$$\begin{aligned} {\hat{\theta }}=\dfrac{\theta \gamma _1}{\theta \gamma _1+(1-\theta )\gamma }, \quad \text{ or } \quad \theta =\dfrac{{\hat{\theta }}\gamma }{{\hat{\theta }}\gamma +(1-{\hat{\theta }})\gamma _1}. \end{aligned}$$

The present approach for modeling quarantine follows the very influential work on Ebola models by Legrand et al. (2007). Throughout the manuscript, we assume that quarantine does not affect the infectious period, i.e.,

$$\begin{aligned} \dfrac{1}{\gamma }=\dfrac{1}{\gamma _1}+\dfrac{1}{\gamma _2}. \end{aligned}$$
Table 1 Ranges of the model parameters (time unit is day)
Full size table

Assume that \(A_v(I_h,Q_h,I_v)\) is continuously differentiable in all state variables. The model (4) is mathematically and epidemiologically well-posed.

Theorem 1

System (4) has a unique bounded solution for all time with initial condition lying in

$$\begin{aligned} \varOmega =\left\{ (I_h,Q_h,I_v)\in {\mathbb {R}}_+^3\ | \ I_h+Q_h\le H,\ I_v\le V \right\} . \end{aligned}$$

Moreover, the compact set \(\varOmega \) is positively invariant with respect to system (4).

Proof

The vector field described by the right-hand sides of (4) is Lipschitz continuous in \(\varOmega \), so there exists a unique solution for \(t\ge 0\). If \(I_h=0\), then \(I_h^{\prime }\ge 0\). Similar arguments apply to \(Q_h\) and \(I_v\). If \(I_v=V\), then \(I_v^{\prime }\le 0\). If \(I_h+Q_h=H\), then \(I_h^{\prime }+Q_h^{\prime }\le 0\). It follows that all solutions of system (4) starting from \(\varOmega \) stay in \(\varOmega \). \(\square \)

3 Model with Standard Incidence

When the mosquito population is small relative to the human population, the blood source for mosquitoes is abundant. It is reasonable to assume that the mosquito biting rate is constant, denoted by \(A_v=a\). Thus, we can rewrite the forces of infection (2) as

$$\begin{aligned} \lambda _h = a\cdot \dfrac{I_v}{H-\sigma Q_h}\cdot b \quad \text{ and } \quad \lambda _v =a\cdot \dfrac{I_h+(1-\sigma )Q_h}{H-\sigma Q_h}\cdot c. \end{aligned}$$
(5)

Substituting (5) into (4) gives a standard incidence malaria model

$$\begin{aligned} \begin{aligned} \dfrac{\hbox {d}I_h}{\hbox {d}t}&= ab\dfrac{I_v}{H-\sigma Q_h}(H-I_h-Q_h)-\big (\theta \gamma _1+(1-\theta )\gamma \big )I_h,\\ \dfrac{\hbox {d}Q_h}{\hbox {d}t}&= \theta \gamma _1I_h-\gamma _2Q_h,\\ \dfrac{\hbox {d}I_v}{\hbox {d}t}&= ac\dfrac{I_h+(1-\sigma )Q_h}{H-\sigma Q_h}(V-I_v)-\mu I_v. \end{aligned} \end{aligned}$$
(6)

3.1 Basic Reproduction Number

It is clear that system (6) always has a unique disease-free equilibrium (DFE) at \(E_0=(0,0,0)\). Following the next generation matrix method (Diekmann et al. 1990; van den Driessche and Watmough 2002), the new infection and transition matrices are

$$\begin{aligned}F_1=\begin{pmatrix} 0 &{} \quad 0 &{} \quad ab \\ 0 &{} \quad 0 &{} \quad 0 \\ acm &{} \quad (1-\sigma )acm &{} \quad 0 \\ \end{pmatrix} \quad \text{ and } \quad \ V_1=\begin{pmatrix} \theta \gamma _1+(1-\theta )\gamma &{} \quad 0 &{} \quad 0 \\ -\theta \gamma _1 &{} \quad \gamma _2 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \mu \end{pmatrix}, \end{aligned}$$

respectively. The basic reproduction number of model (6) is

$$\begin{aligned} \mathcal {R}_{10}&= \rho (F_1V_1^{-1}){\,{=}\,\sqrt{\dfrac{a^2bcm(\theta (1-\sigma )\gamma _1+\gamma _2)}{\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )}}}= \sqrt{(\mathcal {R}_{10i})^2+(\mathcal {R}_{10q})^2}\\&= \sqrt{\dfrac{acm}{\theta \gamma _1+(1-\theta )\gamma }\cdot \dfrac{ab}{\mu } + \dfrac{\theta \gamma _1}{\theta \gamma _1+(1-\theta )\gamma }\cdot \dfrac{(1-\sigma )acm}{\gamma _2}\cdot \dfrac{ab}{\mu }} , \end{aligned}$$

where \(\mathcal {R}_{10i}\) and \(\mathcal {R}_{10q}\) are the number of secondary cases produced by an infectious human at non-quarantined and quarantined stages, respectively. It is worth noting that \(\mathcal {R}_{10}\le \mathcal {R}_0\) with equality if and only if \(\theta =0\) or \(\sigma =0\) (no quarantine or it does not work) and \(\mathcal {R}_{10}\) depends on all model parameters.

Theorem 2

For model (6), the disease-free equilibrium \(E_0\) is locally asymptotically stable if \(\mathcal {R}_{10}<1\) and unstable if \(\mathcal {R}_{10}>1\). Moreover, \(E_0\) is globally asymptotically stable if \(\mathcal {R}_{0}\le 1\).

Proof

The local stability of \(E_0\) immediately follows from Theorem 2 in van den Driessche and Watmough (2002). We next turn to prove the global asymptotic stability of the disease-free equilibrium as \(\mathcal {R}_{0}\le 1\). Using the facts that

$$\begin{aligned} ab\frac{I_v}{H-\sigma Q_h}(H-I_h-Q_h)\le abI_v \end{aligned}$$

and

$$\begin{aligned} ac\dfrac{I_h+(1-\sigma )Q_h}{H-\sigma Q_h}(V-I_v)\le ac\dfrac{I_h+Q_h}{H}(V-I_v)\le ac\dfrac{I_h+Q_h}{H}V, \end{aligned}$$

we have

$$\begin{aligned} \left( \dfrac{\hbox {d}I_h}{\hbox {d}t},\dfrac{\hbox {d}Q_h}{\hbox {d}t},\dfrac{\hbox {d}I_v}{\hbox {d}t} \right) ^T\le (F-V)\left( I_h, Q_h,I_v\right) ^T, \end{aligned}$$

where

$$\begin{aligned} F=\begin{pmatrix} 0 &{} \quad 0 &{} \quad ab \\ 0 &{} \quad 0 &{} \quad 0 \\ acm &{} \quad acm &{} \quad 0 \end{pmatrix}\ge F_1 \quad \text{ and } \quad V=\begin{pmatrix} \theta \gamma _1+(1-\theta )\gamma &{} \quad 0 &{} \quad 0 \\ -\theta \gamma _1 &{} \quad \gamma _2 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \mu \end{pmatrix}=V_1. \end{aligned}$$

One can verify by direct calculation that \(V^{-1}F\) is a nonnegative and irreducible matrix and \(\rho (V^{-1}F)=\mathcal {R}_0\). It follows from the Perron–Frobenius theorem that \(V^{-1}F\) has a positive left eigenvector \({\varvec{v}}\) associated with \(\mathcal {R}_0\), i.e.,

$$\begin{aligned} {\varvec{v}} V^{-1}F=\mathcal {R}_{0}{\varvec{v}}. \end{aligned}$$

Since \({\varvec{v}} V^{-1}\) is a positive vector, we consider a Lyapunov function

$$\begin{aligned} L_1={\varvec{v}}V^{-1}\left( I_h, Q_h,I_v\right) ^T. \end{aligned}$$

Differentiating \(L_1\) along the solutions of (6) gives

$$\begin{aligned} \begin{aligned} L_1^\prime&= {\varvec{v}}V^{-1}\left( \dfrac{\hbox {d}I_h}{\hbox {d}t}, \dfrac{\hbox {d}Q_h}{\hbox {d}t}, \dfrac{\hbox {d}I_v}{\hbox {d}t} \right) ^T\le {\varvec{v}}V^{-1}(F-V)\left( I_h, Q_h,I_v\right) ^T \\&= (\mathcal {R}_0-1){\varvec{v}}\left( I_h, Q_h,I_v\right) ^T. \end{aligned} \end{aligned}$$

Denote \(\varGamma _1\) the largest invariant set contained in \(\{(I_h,Q_h,I_v)\in \varOmega : L_1^\prime =0\}\).

  1. (i)

    \(\mathcal {R}_{0}<1\). Since \({\varvec{v}}\gg 0\), then \(L_1^\prime =0\) implies that \(I_h=Q_h=I_v=0\). Thus \(\varGamma _1=\{E_{0}\}\).

  2. (ii)

    \(\mathcal {R}_{0}=1\). The equality \(L_1^\prime =0\) implies that

    $$\begin{aligned} \left( \dfrac{\hbox {d}I_h}{\hbox {d}t},\dfrac{\hbox {d}Q_h}{\hbox {d}t},\dfrac{\hbox {d}I_v}{\hbox {d}t} \right) ^T=(F-V)\left( I_h, Q_h,I_v\right) ^T, \end{aligned}$$

    or equivalently,

    $$\begin{aligned} \begin{aligned}&\dfrac{I_v}{H-\sigma Q_h}(H-I_h-Q_h)=I_v,\\&\dfrac{I_h+(1-\sigma )Q_h}{H-\sigma Q_h}(V-I_v)=\dfrac{I_h+Q_h}{H}V. \end{aligned} \end{aligned}$$
    (7)

    We conclude from the first equation of (7) that \(I_v=0\), or \(I_h=0\) and \((1-\sigma )Q_h=0\). If \(I_v=0\), then \(I_h'=-((1-\theta )\gamma +\theta \gamma _1)I_h\) and hence \(I_h=0\). The second equation of (6) gives \(Q_h'=-\gamma _2Q_h\). Thus \(Q_h=0\) and hence \(\varGamma _1=\{E_0\}\). If \(I_h=0\), then the second and third equations of (6) imply \(Q_h=0\) and \(I_v=0\), respectively. Once again we have \(\varGamma _1=\{E_{0}\}\).

By LaSalle’s invariance principle (Lasalle 1976), the disease-free equilibrium \(E_0\) is globally asymptotically stable with respect to \(\varOmega \) if \(\mathcal {R}_0\le 1\). \(\square \)

Since \(\mathcal {R}_{10}\le \mathcal {R}_0\le 1\) means that the disease becomes extinct in the absence of quarantine. It is not surprising that under quarantine the disease still dies out if \(\mathcal {R}_0\le 1\). However, based on the analysis below, the disease-free equilibrium \(E_0\) can be locally asymptotically stable but not globally asymptotically stable for system (6) as \(\mathcal {R}_{10}<1\).

3.2 Endemic Equilibrium

Let \(E^*=(I_h^*, Q_h^*, I_v^*)\) denote an endemic equilibrium of system (6). Solving the equilibrium equations associated with (6) gives

$$\begin{aligned} \begin{aligned} I_h^{*}&=\dfrac{\gamma _2\lambda _h^{*}}{\gamma _2(\theta \gamma _1+(1-\theta )\gamma )+(\theta \gamma _1+\gamma _2)\lambda _h^{*}}H, \\ Q_h^{*}&=\dfrac{\theta \gamma _1\lambda _h^{*}}{\gamma _2(\theta \gamma _1+(1-\theta )\gamma )+(\theta \gamma _1+\gamma _2)\lambda _h^{*}}H, \\ I_v^{*}&=\dfrac{\lambda _v^{*}}{\mu +\lambda _v^{*}}V, \end{aligned} \end{aligned}$$
(8)

where the forces of infection on humans and mosquitoes at \(E^*\) are

$$\begin{aligned} \lambda _h^{*}=ab\dfrac{I_v^{*}}{H-\sigma Q_h^{*}} \quad \text{ and } \quad \lambda _v^{*}=ac\dfrac{I_h^{*}+(1-\sigma )Q_h^{*}}{H-\sigma Q_h^{*}}, \end{aligned}$$
(9)

respectively. By substituting (8) into (9), we eventually obtain a quadratic equation in terms of \(\lambda _h^{*}\) as follows

$$\begin{aligned} c_2(\lambda _h^{*})^2+c_1\lambda _h^{*}+c_0=0, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} c_2\,=\,&(ac+\mu )(\theta \gamma _1(1-\sigma )+\gamma _2)^2H, \\ c_1\,=\,&((ac+2\mu )\gamma _2(\theta \gamma _1+(1-\theta )\gamma )H-a^2bc(\theta \gamma _1+\gamma _2)V) (\theta \gamma _1(1-\sigma )+\gamma _2), \\ c_0\,=\,&\mu \gamma _2^2(\theta \gamma _1+(1-\theta )\gamma )^2(1-(\mathcal {R}_{10})^2) H. \end{aligned} \end{aligned}$$

Obviously, \(c_2>0\) and the terms \(c_0\) and \(\mathcal {R}_{10}-1\) have opposite signs. Therefore, the following result is established.

Proposition 1

The model (6) can have up to two endemic equilibria, i.e.,

  1. (i)

    a unique endemic equilibrium if \(c_0<0\);

  2. (ii)

    a unique endemic equilibrium if \(c_1<0\), and \(c_0=0\) or \(c_1^2-4c_0c_2=0\);

  3. (iii)

    two endemic equilibria if \(c_0>0, c_1<0\ \text{ and } \ c_1^2-4c_0c_2>0\);

  4. (iv)

    no endemic equilibrium otherwise.

Moreover, differing from the classical Ross–Macdonald model (1), we find that the phenomenon of backward bifurcation (i.e., the stable disease-free equilibrium coexists with a stable endemic equilibrium) can occur when quarantine is considered.

Theorem 3

The model (6) undergoes backward bifurcation at \(\mathcal {R}_{10}=1\) if

$$\begin{aligned} ac(\theta \gamma _1(1-\sigma )+\gamma _2)+\mu (\theta \gamma _1(1-2\sigma )+\gamma _2)<0. \end{aligned}$$

Proof

The Jacobian matrix of system (6) at \(E_0\) is

$$\begin{aligned} J(E_{0})=F_1-V_1=\begin{pmatrix} -\theta \gamma _1-(1-\theta )\gamma &{} \quad 0 &{} \quad ab \\ \theta \gamma _1 &{} \quad -\gamma _2 &{} \quad 0 \\ acm &{} \quad (1-\sigma )acm &{} \quad -\mu \\ \end{pmatrix}. \end{aligned}$$

We choose the ratio of mosquitoes to humans \(m=V/H\) as a bifurcation parameter. Solving m from \(\mathcal {R}_{10}=1\) gives

$$\begin{aligned} m^*=\dfrac{\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )}{a^2bc(\theta (1-\sigma )\gamma _1+\gamma _2)}. \end{aligned}$$

Denote the Jacobian matrix \(J(E_0)\) at \(m=m^*\) by \(J_{m^*}\). It is easy to see that \(J_{m^*}\) has a simple zero eigenvalue and all other eigenvalues have negative real parts. Since \(J_{m^*}\) is essentially nonnegative and irreducible, it has a positive right eigenvector \(\varvec{\omega }\) and a positive left eigenvector \(\varvec{\nu }\) corresponding to the zero eigenvalue. More specifically,

$$\begin{aligned} \varvec{\omega }=(\omega _1,\omega _2, \omega _3)^T \quad \text{ and } \quad \varvec{\nu }=(\nu _1,\nu _2,\nu _3), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \omega _1&=\dfrac{ab}{\theta \gamma _1+(1-\theta )\gamma },\ \omega _2=\frac{ab\theta \gamma _1}{\gamma _2(\theta \gamma _1+(1-\theta )\gamma )},\ \omega _3=1, \\ \nu _1&=\frac{\mu }{ab},\ \nu _2=\dfrac{\mu (1-\sigma )(\theta \gamma _1+(1-\theta )\gamma )}{ab(\theta \gamma _1(1-\sigma )+\gamma _2)},\ \nu _3=1. \end{aligned} \end{aligned}$$

Following the notations and method developed by Castillo-Chavez and Song (2004), we get

$$\begin{aligned} \begin{aligned} \mathbf {a}&= -\dfrac{2ab(ac(\theta \gamma _1(1-\sigma )+\gamma _2)+\mu (\theta \gamma _1(1-2\sigma )+\gamma _2))}{\gamma _2(\theta \gamma _1+(1-\theta )\gamma )H},\\ \mathbf {b}&=\dfrac{a^2bc(\theta \gamma _1(1-\sigma )+\gamma _2)}{\gamma _2(\theta \gamma _1+(1-\theta )\gamma )}>0. \end{aligned} \end{aligned}$$

Thus, the proof is complete by applying Theorem 4.1 in Castillo-Chavez and Song (2004). \(\square \)

3.3 Uniform Persistence

We now prove the uniform persistence of the disease when \(\mathcal {R}_{10}>1\).

Theorem 4

Assume that \(\mathcal {R}_{10}>1\), then system (6) is uniformly persistent, i.e., there exists an \(\varepsilon >0\) such that every solution \(\varphi _t(x_0)=(I_h(t), Q_h(t), I_v(t))\) of system (6) with initial value \(x_0=(I_h(0), Q_h(0), I_v(0))\in \varOmega \backslash \{E_0\}\) satisfies

$$\begin{aligned} \liminf _{t\rightarrow \infty }\ (I_h(t),Q_h(t),I_v(t))>(\varepsilon ,\varepsilon ,\varepsilon ). \end{aligned}$$

Proof

Define

$$\begin{aligned} \begin{aligned} {\mathring{\varOmega }}&=\{(I_h,Q_h,I_v)\in \varOmega \ |\ I_h>0,\ Q_h>0,\ I_v>0\}, \\ \partial \varOmega&=\varOmega \backslash {\mathring{\varOmega }}=\{(I_h,Q_h,I_v)\in \varOmega \ |\ I_h=0\ \text{ or } \ Q_h=0 \ \text{ or }\ I_v=0\}. \end{aligned} \end{aligned}$$

One can easily check that \(\varOmega \) and \({\mathring{\varOmega }}\) are positively invariant, and \(\partial \varOmega \) is relatively closed in \(\varOmega \). Since \(\varOmega \) is a compact set, system (6) is point dissipative. Denote

$$\begin{aligned} M_\partial =\{x_0\in \partial \varOmega : \varphi _t(x_0)\in \partial \varOmega \ \text { for }\ t\ge 0 \}. \end{aligned}$$

Clearly, \(\{E_0\}\subseteq M_\partial \subseteq \partial \varOmega \). Meanwhile, for any \(x_0\in \partial \varOmega \backslash \{E_0\}\), by the irreducibility of system (6), we have \(\varphi _t(x_0)\in {\mathring{\varOmega }}\) for all \(t>0\). Therefore, \(x_0\notin M_\partial \) and \(M_\partial =\{E_0\}\).

We claim that \(W^s(E_0)\cap {\mathring{\varOmega }}=\emptyset \) where \(W^s(E_0)\) is the stable manifold of \(E_{0}\). Denote

$$\begin{aligned} M_\varepsilon =\varepsilon \begin{pmatrix} 0 &{} \quad 0 &{} \quad \dfrac{2ab}{H} \\ 0&{} \quad 0 &{} \quad 0 \\ \dfrac{ac}{H} &{} \quad \dfrac{ac(1-\sigma )}{H} &{} \quad 0 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} J_\varepsilon =F_1-V_1-M_\varepsilon =\begin{pmatrix} -\theta \gamma _1-(1-\theta )\gamma &{} \quad 0 &{} \quad \dfrac{ab(H-2\varepsilon )}{H} \\ \theta \gamma _1 &{} \quad -\gamma _2 &{} \quad 0 \\ \dfrac{ac(V-\varepsilon )}{H} &{} \quad \dfrac{ac(1-\sigma )(V-\varepsilon )}{H} &{} \quad -\mu \end{pmatrix}. \end{aligned}$$

Since \(s(F_1-V_1)>0\) if and only if \(\mathcal {R}_{10}>1\), by the continuity of spectral bound, there exists a sufficiently small \(\varepsilon _1>0\) such that \(s(J_\varepsilon )>0\) for \(\varepsilon \in [0,\varepsilon _1]\). We now show

$$\begin{aligned} \limsup _{t\rightarrow \infty }\ \Vert \varphi _t(x_0)-E_0\Vert _2>\varepsilon _1, \quad \forall x_0\in {\mathring{\varOmega }}, \end{aligned}$$

where \(\Vert \cdot \Vert _2\) is the Euclidean norm.

Assume the contrary, for some \(x_0\in {\mathring{\varOmega }}\), up to a translation, we have

$$\begin{aligned} \Vert \varphi _t(x_0)-E_0\Vert _2=\Vert \varphi _t(x_0)\Vert _2\le \varepsilon _1 \quad \text{ for } \,\, \forall \ t\ge 0 \end{aligned}$$

and hence

$$\begin{aligned} \left( \dfrac{\hbox {d}I_h}{\hbox {d}t},\dfrac{\hbox {d}Q_h}{\hbox {d}t},\dfrac{\hbox {d}I_v}{\hbox {d}t}\right) ^T \ge J_{\varepsilon _1}(I_h, Q_h, I_v)^T. \end{aligned}$$

Since \(J_{\varepsilon _1}\) is irreducible and essentially nonnegative, it has a positive eigenvector associated with \(s(J_{\varepsilon _1})>0\). By the standard comparison principle, each component of the solution \(\varphi _t(x_0)\) tends to infinity as \(t\rightarrow \infty \), this is a contradiction. The claim is proved.

The singleton \(M_{\partial }=\{E_0\}\) is an isolated invariant set and acyclic. By Theorem 4.6 in Thieme (1993), we conclude that system (6) is uniformly persistent in \({\mathring{\varOmega }}\) whenever \(\mathcal {R}_{10}>1\). \(\square \)

4 Model with Bilinear Incidence

When the ratio of mosquitoes to humans is large, the odds of successful blood feeding increases in the number of blood sources (human hosts). Since mosquitoes make less bites towards individuals who are quarantined, the contact rate between mosquitoes and humans depends on those available for mosquitoes rather than the total human population. Thus, we assume that the mosquito biting rate is proportional to the adjusted or effective number of humans that mosquitoes can contact in the environment, i.e.,

$$\begin{aligned} A_v={\tilde{a}}(S_h+I_h+(1-\sigma )Q_h)={\tilde{a}}(H-\sigma Q_h), \end{aligned}$$

where \({\tilde{a}}\) is a proportional coefficient. For simplicity, we denote

$$\begin{aligned} \alpha ={\tilde{a}}b \ \text{ and } \ \beta ={\tilde{a}}c. \end{aligned}$$

The forces of infection (2) can then be written as

$$\begin{aligned} \lambda _h =\alpha I_v \ \text{ and } \ \lambda _v =\beta (I_h+(1-\sigma )Q_h). \end{aligned}$$
(10)

By substituting (10) into (4), we obtain a bilinear incidence malaria model with quarantine

$$\begin{aligned} \begin{aligned} \dfrac{\hbox {d}I_h}{\hbox {d}t}&= \alpha I_v (H-I_h-Q_h)-(\theta \gamma _1+(1-\theta )\gamma )I_h,\\ \dfrac{\hbox {d}Q_h}{\hbox {d}t}&= \theta \gamma _1I_h-\gamma _2Q_h,\\ \dfrac{\hbox {d}I_v}{\hbox {d}t}&= \beta (I_h+(1-\sigma )Q_h)(V-I_v)-\mu I_v. \end{aligned} \end{aligned}$$
(11)

4.1 Basic Reproduction Number

Again following the next generation matrix method (van den Driessche and Watmough 2002), the linearization of (11) at the disease-free equilibrium \(E_0=(0,0,0)\) gives

$$\begin{aligned}F_2=\begin{pmatrix} 0 &{} \quad 0 &{} \quad \alpha H \\ 0 &{} \quad 0 &{} \quad 0 \\ \beta V &{} \quad \beta V(1-\sigma ) &{} \quad 0 \\ \end{pmatrix}\ \text{ and } \ V_2=\begin{pmatrix} \theta \gamma _1+(1-\theta )\gamma &{} \quad 0 &{} \quad 0 \\ -\theta \gamma _1 &{} \quad \gamma _2 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \mu \end{pmatrix}. \end{aligned}$$

Then we define the basic reproduction number of model (11) as

$$\begin{aligned} \begin{aligned} \mathcal {R}_{20}&=\rho (F_2V_2^{-1}){ = \sqrt{\dfrac{\alpha \beta HV(\theta \gamma _1(1-\sigma )+\gamma _2)}{\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )}} } =\sqrt{(\mathcal {R}_{20i})^2+(\mathcal {R}_{20q})^2}\\&=\sqrt{\dfrac{\alpha V}{\theta \gamma _1+(1-\theta )\gamma }\cdot \dfrac{\beta H}{\mu } + \dfrac{\theta \gamma _1}{\theta \gamma _1+(1-\theta )\gamma }\cdot \dfrac{(1-\sigma )\alpha V}{\gamma _2}\cdot \dfrac{\beta H}{\mu }}, \end{aligned} \end{aligned}$$

where \(\mathcal {R}_{20i}\) and \(\mathcal {R}_{20q}\) represent infections attributed to an infected person during non-quarantined and quarantined stages, respectively. Note that \(\mathcal {R}_{20}\) also depends on all model parameters.

Theorem 5

For system (11), the disease-free equilibrium \(E_{0}\) is globally asymptotically stable whenever \(\mathcal {R}_{20}\le 1\).

Proof

We can again obtain the local stability of \(E_0\) by using Theorem 2 in van den Driessche and Watmough (2002). Consider a Lyapunov function

$$\begin{aligned} L_2= & {} \beta V(\theta \gamma _1(1-\sigma )+\gamma _2)I_h+\beta V(\theta \gamma _1+(1-\theta )\gamma )(1-\sigma )Q_h\\&+\gamma _2(\theta \gamma _1+(1-\theta )\gamma )I_v \end{aligned}$$

on \(\varOmega \), then computing the derivative of \(L_2\) along solutions of system (11) gives

$$\begin{aligned} \begin{aligned} L_2'&= \beta V(\theta \gamma _1(1-\sigma )+\gamma _2)(\alpha I_v (H-I_h-Q_h)-(\theta \gamma _1+(1-\theta )\gamma )I_h)\\&\quad +\beta V(1-\sigma )(\theta \gamma _1+(1-\theta )\gamma )(\theta \gamma _1I_h-\gamma _2Q_h)\\&\quad +\gamma _2(\theta \gamma _1+(1-\theta )\gamma )(\beta (I_h+(1-\sigma )Q_h)(V-I_v)-\mu I_v)\\&=\alpha \beta V(\theta \gamma _1(1-\sigma )+\gamma _2)(H-I_h-Q_h)I_v -\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )I_v \\&\quad -\beta \gamma _2(\theta \gamma _1+(1-\theta )\gamma )(I_h+(1-\sigma )Q_h)I_v\\&\le \alpha \beta HV(\theta \gamma _1(1-\sigma )+\gamma _2)I_v -\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )I_v\\&= \dfrac{1}{\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )}((\mathcal {R}_{20})^2-1)I_v. \end{aligned} \end{aligned}$$

Denote the largest invariant set contained in \(\{(I_h,Q_h,I_v)\in \varOmega : L_2'=0\}\) by \(\varGamma _2\).

  1. (i)

    \(\mathcal {R}_{20}<1\). Then \(L_2^\prime =0\) if and only if \(I_v=0\). Following from the first and second equations of (11), we know \(I_h=0\) and \(Q_h=0\), respectively. Thus \(\varGamma _2=\{E_0\}\).

  2. (ii)

    \(\mathcal {R}_{20}=1\). \(L_2^\prime =0\) implies that \(I_v=0\) or \(I_h=Q_h=0\). The first case can proceed as before. For the second case, the third equation of (11) indicates that \(I_v=0\). Hence \(\varGamma _2=\{E_0\}\).

According to LaSalle’s invariance principle, we find that the disease-free equilibrium of model (11) is globally asymptotically stable in \(\varOmega \). \(\square \)

4.2 Endemic Equilibrium

Let \(E^{**}=(I_h^{**}, Q_h^{**},I_v^{**})\) denote the endemic equilibrium of model system (11). A direct but tedious calculation gives

$$\begin{aligned} \begin{aligned} I_h^{**}&=\dfrac{\mu \gamma _2^2(\theta \gamma _1+(1-\theta )\gamma )((\mathcal {R}_{20})^2-1)}{\beta (\theta \gamma _1(1-\sigma )+\gamma _2) (\alpha V(\theta \gamma _1+\gamma _2)+ \gamma _2(\theta \gamma _1+(1-\theta )\gamma ))},\\ Q_h^{**}&=\dfrac{\theta \gamma _1}{\gamma _2}I_h^{**},\\ I_v^{**}&=\dfrac{\beta V(\theta \gamma _1(1-\sigma )+\gamma _2)I_h^{**}}{\beta (\theta \gamma _1(1-\sigma )+\gamma _2)I_h^{**}+\mu \gamma _2}. \end{aligned} \end{aligned}$$

Thus there exists a unique endemic equilibrium \(E^{**}\) if and only if \(\mathcal {R}_{20}>1\).

Theorem 6

The endemic equilibrium \(E^{**}\) of model (11) is locally asymptotically stable when it exists.

Proof

The Jacobian matrix of system (11) at the positive equilibrium \(E^{**}=(I_h^{**},Q_h^{**},I_v^{**})\) is

$$\begin{aligned} J(E^{**})\!=\!\begin{pmatrix} -\alpha I_v^{**}-\theta \gamma _1-(1-\theta )\gamma &{} \quad -\alpha I_v^{**} &{} \quad \alpha S_h^{**} \\ \theta \gamma _1 &{} \quad -\gamma _2 &{} \quad 0 \\ \beta S_v^{**} &{} \quad \beta (1-\sigma )S_v^{**} &{} \quad -\beta \big (I_h^{**}+(1-\sigma )Q_h^{**}\big )-\mu \\ \end{pmatrix}, \end{aligned}$$

where \(S_h^{**}=H-I_h^{**}-Q_h^{**}\) and \(S_v^{**}=V-I_v^{**}\). The equilibrium equations of system (11) are

$$\begin{aligned} \begin{aligned}&\alpha I_v^{**}S_h^{**}=(\theta \gamma _1+(1-\theta )\gamma )I_h^{**},\\&\theta \gamma _1I_h^{**}=\gamma _2Q_h^{**},\\&\beta (I_h^{**}+(1-\sigma )Q_h^{**})S_v^{**}=\mu I_v^{**}, \end{aligned} \end{aligned}$$

which imply that

$$\begin{aligned} \alpha \beta (\theta \gamma _1(1-\sigma )+\gamma _2)S_h^{**}S_v^{**} =\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma ). \end{aligned}$$

The matrix \(J(E^{**})\) can be rewritten as

$$\begin{aligned} J(E^{**})=\begin{pmatrix} -(\theta \gamma _1+(1-\theta )\gamma )\left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) &{} \quad -\alpha I_v^{**} &{} \quad \alpha S_h^{**} \\ \theta \gamma _1 &{} \quad -\gamma _2 &{} \quad 0 \\ \beta S_v^{**} &{} \quad \beta (1-\sigma )S_v^{**} &{} \quad -\mu \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) \end{pmatrix}. \end{aligned}$$

The characteristic equation of \(J(E^{**})\) is

$$\begin{aligned} \begin{aligned} P_2(\lambda )=\,&(\lambda +\gamma _2)(\lambda ^2+b_1\lambda +b_0)\\&+\theta \gamma _1\left( \alpha I_v^{**}\left( \lambda +\mu \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) \right) -\alpha \beta (1-\sigma )S_h^{**}S_v^{**}\right) =0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} b_1=\,&(\theta \gamma _1+(1-\theta )\gamma )\left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) +\mu \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right)>\mu \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) ,\\ b_0=\,&\mu (\theta \gamma _1+(1-\theta )\gamma )\left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) -\alpha \beta S_h^{**}S_v^{**}\\ =\,&\mu (\theta \gamma _1+(1-\theta )\gamma )\left( \left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) -\dfrac{\gamma _2}{\theta \gamma _1(1-\sigma )+\gamma _2}\right) >0. \end{aligned} \end{aligned}$$

Expanding the characteristic polynomial \(P_2(\lambda )\) yields

$$\begin{aligned} P_2(\lambda )=\lambda ^3+B_2\lambda ^2+B_1\lambda +B_0=0, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} B_2=\,&b_1+\gamma _2>0,\\ B_1=\,&b_0+b_1\gamma _2+\alpha \theta \gamma _1I_v^{**}>0,\\ B_0=\,&b_0 \gamma _2 +\alpha \theta \gamma _1\left( \mu I_v^{**}\left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) - \beta (1-\sigma )S_h^{**}S_v^{**} \right) \\ =\,&\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )\left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) -\alpha \beta \gamma _2 S_h^{**}S_v^{**}\\&+\alpha \theta \gamma _1\left( \mu I_v^{**}\left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) - \beta (1-\sigma )S_h^{**}S_v^{**} \right) \\>\,&\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )\left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) \\&-\alpha \beta (\theta \gamma _1(1-\sigma )+\gamma _2) S_h^{**}S_v^{**}\\ =\,&\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )\left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) -\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )\\ =\,&\mu \gamma _2(\theta \gamma _1+(1-\theta )\gamma )\left( \left( 1+\dfrac{I_h^{**}}{S_h^{**}}\right) \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) -1 \right) >0 \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} B_1B_2-B_0=\,&(b_0+b_1\gamma _2+\theta \alpha \gamma _1I_v^{**})(b_1+\gamma _2)-b_0\gamma _2\\&-\theta \gamma _1\left( \alpha \mu I_v^{**}\left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) - \alpha \beta (1-\sigma )S_h^{**}S_v^{**}\right) \\>\,&b_1 \theta \alpha \gamma _1I_v^{**}-\alpha \mu \theta \gamma _1\left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) I_v^{**}\\ =\,&\theta \gamma _1\alpha \left( b_1-\mu \left( 1+\dfrac{I_v^{**}}{S_v^{**}}\right) \right) I_v^{**}>0. \end{aligned} \end{aligned}$$

The Routh–Hurwitz criterion implies that all eigenvalues of \(J(E^{**})\) have negative real parts and hence the endemic equilibrium \(E^{**}\) is locally asymptotically stable. \(\square \)

Similar to the proof of Theorem 4, we can show that the disease persists for the model with bilinear incidence provided that \(\mathcal {R}_{20}>1\).

Theorem 7

If \(\mathcal {R}_{20}>1\), then system (11) is uniformly persistent. That is, there exists a positive constant \(\eta \) such that for all initial conditions \(x_0=(I_h(0), Q_h(0), I_v(0))\in \varOmega \backslash \{E_0\}\), the solution of system (11), denoted by \(\psi _t(x_0)\) \(=(I_h(t), Q_h(t), I_v(t))\), satisfies

$$\begin{aligned} \liminf _{t\rightarrow \infty }(I_h(t),Q_h(t),I_v(t))>(\eta ,\eta ,\eta ). \end{aligned}$$

Finally, we establish a sufficient condition under which all nontrivial solutions of system (11) converge to the unique endemic equilibrium.

Theorem 8

Assume that \(\mathcal {R}_{20}>1\). If \(\gamma _2-\alpha V+\beta (2-\sigma )\eta >0\), then the unique endemic equilibrium \(E^{**}\) for system (11) is globally asymptotically stable in \(\varOmega \backslash \{E_0\}\).

Proof

We use the second additive compound matrix method developed by Li and Muldowney (1996) to prove the global asymptotic stability of \(E^{**}\). The domain \(\varOmega \) is simply connected and \(E^{**}\) is the unique equilibrium of system (11) in the interior of \(\varOmega \). It follows from the uniform persistence of system (11) that there exists a compact absorbing set in \({\mathring{\varOmega }}\). The second additive compound matrix of the Jacobian matrix of system (11) is

$$\begin{aligned} J^{[2]}=\begin{pmatrix} - \alpha I_v-\theta \gamma _1-(1-\theta )\gamma -\gamma _2 &{} \quad 0 &{} \quad -\alpha (H-I_h-Q_h)\\ \beta (1-\sigma )(V-I_v) &{} \quad J_{22}^{[2]} &{} \quad -\alpha I_v\\ -\beta (V-I_v) &{} \quad \theta \gamma _1 &{} \quad -\beta \big (I_h+(1-\sigma )Q_h\big )-\gamma _2-\mu \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} J_{22}^{[2]}=-\alpha I_v-\beta \big (I_h+(1-\sigma )Q_h\big )-\theta \gamma _1-(1-\theta )\gamma -\mu . \end{aligned}$$

Choose a matrix function

$$\begin{aligned} A(I_h,Q_h,I_v)=\mathop {\mathrm {diag}}\left\{ 1,\,\,\dfrac{I_h}{I_v},\,\,\dfrac{I_h}{I_v}\right\} . \end{aligned}$$

Let f denote the vector field described by (11) and \(A_f\) be the matrix obtained by replacing each entry of A by its derivative in the direction of f. Then

$$\begin{aligned} A_fA^{-1}=\mathop {\mathrm {diag}}\left\{ 0,\,\,\dfrac{I_h'}{I_h}-\dfrac{I_v'}{I_v},\dfrac{I_h'}{I_h}-\dfrac{I_v'}{I_v}\right\} . \end{aligned}$$

and the matrix \(B=A_fA^{-1}+AJ^{[2]}A^{-1}\) can be written in block form

$$\begin{aligned} B= \begin{pmatrix} B_{11} &{} \quad B_{12}\\ B_{21} &{} \quad B_{22}\\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} B_{11}&=-\alpha I_v-\theta \gamma _1-(1-\theta )\gamma -\gamma _2,\ \ B_{12}=\left( 0,-\alpha (H-I_h-Q_h)\dfrac{I_v}{I_h}\right) ,\\ B_{21}&=\begin{pmatrix} \beta (1-\sigma )(V-I_v)\dfrac{I_h}{I_v} \\ -\beta (V-I_v)\dfrac{I_h}{I_v} \end{pmatrix},\ \ B_{22}=\begin{pmatrix} \dfrac{I_h^\prime }{I_h}-\dfrac{I_v^\prime }{I_v}+J_{22}^{[2]}\ \ &{} \quad -\alpha I_v\\ \theta \gamma _1\ \ &{} \quad B_{22}^{22} \end{pmatrix}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} B_{22}^{22}=\dfrac{I_h^\prime }{I_h}-\dfrac{I_v^\prime }{I_v}-\beta \big (I_h+(1-\sigma )Q_h\big )-\gamma _2-\mu . \end{aligned}$$

The vector norm \(\Vert \cdot \Vert \) in \({\mathbb {R}}^3\cong {\mathbb {R}}^{\genfrac(){0.0pt}1{3}{2}} \) is chosen as

$$\begin{aligned} \Vert (u,v,w)\Vert =\sup \{\Vert u\Vert ,\Vert v\Vert +\Vert w\Vert \}. \end{aligned}$$

The Lozinskiĭ measure \(\mu (B)\) with respect to \(\Vert \cdot \Vert \) can be estimated as follows

$$\begin{aligned} \mu (B)\le \sup \{g_1,g_2\}, \end{aligned}$$

where

$$\begin{aligned} g_1=\mu _1(B_{11})+\Vert B_{12}\Vert \ \text{ and } \ g_2=\Vert B_{21}\Vert +\mu _1(B_{22}). \end{aligned}$$

The terms \(\Vert B_{12}\Vert \) and \(\Vert B_{21}\Vert \) are matrix norms with respect to the \(l_1\) vector norm, and \(\mu _1\) denotes the Lozinskiĭ measure with respect to the \(l_1\) vector norm. Furthermore, we have

$$\begin{aligned} \begin{aligned} \mu _1(B_{11}) =\,&-\alpha I_v-\theta \gamma _1-(1-\theta )\gamma -\gamma _2, \\ \Vert B_{12}\Vert =\,&\alpha (H-I_h-Q_h)\dfrac{I_v}{I_h}, \ \Vert B_{21}\Vert =\beta (V-I_v)\dfrac{I_h}{I_v},\\ \mu _1(B_{22}) =\,&\dfrac{I_h^\prime }{I_h}-\dfrac{I_v^\prime }{I_v}-\beta \left( I_h+\left( 1-\sigma \right) Q_h \right) -\mu \\&+\max \{-\alpha I_v-(1-\theta )\gamma , \ \alpha I_v-\gamma _2\}. \end{aligned} \end{aligned}$$

Applying the first and third equations in (11), we have

$$\begin{aligned} \begin{aligned} g_1=\,&\dfrac{I_h^\prime }{I_h}-\alpha I_v-\gamma _2,\\ g_2 =\,&\dfrac{I_h^\prime }{I_h}-\beta (1-\sigma )Q_h\dfrac{V}{I_v} -\beta I_h+\max \{-\alpha I_v-(1-\theta )\gamma , \alpha I_v-\gamma _2\}. \end{aligned} \end{aligned}$$

If \(\kappa =\gamma _2-\alpha V+\beta (2-\sigma )\eta >0\), then

$$\begin{aligned} \begin{aligned}&\dfrac{1}{t}\int _0^t \left( -\beta (1-\sigma )Q_h\dfrac{V}{I_v} -\beta I_h+\alpha I_v-\gamma _2\right) \hbox {d}s \\&\quad \le \dfrac{1}{t}\int _0^t \left( -\beta (1-\sigma )\eta -\beta \eta +\alpha V-\gamma _2\right) \hbox {d}s=-\kappa \end{aligned} \end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned}&\dfrac{1}{t}\int _0^t \mu (B)\hbox {d}s\le \dfrac{1}{t}\int _0^t \sup \{ g_1,g_2\} \hbox {d}s \\&\quad \le \dfrac{1}{t}\ln \left( \dfrac{I_h(t)}{I_h(0)}\right) -\min \{\kappa ,\alpha \eta +\gamma _2,\alpha \eta +(1-\theta )\gamma \}<0, \end{aligned} \end{aligned}$$

as \(t\rightarrow \infty \), for all \(x_0=(I_h(0),Q_h(0),I_v(0))\in {\mathring{\varOmega }}\). This completes the proof. \(\square \)

5 Numerical Results

In this section, we numerically analyze the standard incidence malaria model (6) since standard incidence rate is more frequently used in modeling mosquito-borne disease transmission (Chamchod and Britton 2011; Chitnis et al. 2008; Ducrot et al. 2009; Gao et al. 2014a; Hasibeder and Dye 1988; Ngwa and Shu 2000). The parameter values are mainly chosen from Anderson and May (1991), Chitnis et al. (2008), Gao et al. (2014a), Mandal et al. (2011), Mwanga et al. (2015) and the references cited therein. The default time unit is day. Recall that the infectious period is assumed to be unaffected by quarantine, i.e., \(\gamma _1^{-1}+\gamma _2^{-1}=\gamma ^{-1}\).

Fig. 3
figure 3

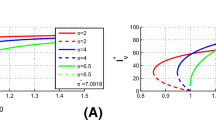
Bifurcation diagram for the \(I_h^*\)-component of the equilibrium solutions of model (6) versus the total number of mosquitoes, V. The solid blue line indicates a stable equilibrium point while the red dashed line represents an unstable equilibrium point (Color figure online)

Full size image

Example 1

Backward bifurcation To illustrate the bifurcation analysis, we set the values of model parameters as follows:

$$\begin{aligned} \begin{aligned}&a=0.15, \quad b=0.32, \quad c=0.43, \quad H=10000, \quad \mu =0.19, \\&\gamma =\frac{1}{55}, \quad \gamma _1=\frac{1}{2}, \quad \gamma _2=\frac{1}{53}, \quad \theta =0.49, \quad \sigma =0.89, \end{aligned} \end{aligned}$$

and let the total mosquito population V vary from 30,000 to 70,000. The bifurcation diagram of the component \(I_h^*\) of the endemic equilibrium \(E^*\) against V is shown in Fig. 3. The model system (6) has two endemic equilibria when V is between 41,482 and 64,260: the equilibrium point with larger \(I_h^*\) is locally asymptotically stable while the equilibrium point with smaller \(I_h^*\) is unstable. For example, if we fix V at 50,000, then the corresponding basic reproduction number \(\mathcal {R}_{10}\) equals 0.88 and there are two endemic equilibria \(E^*\approx (279,3628,1645)\) and (640, 8314, 8437). Solution curves of \(I_h(t)\) under different initial values are illustrated in Fig. 4. It can be seen that the disease dies out when the initial number of infections is small and the disease persists when the initial number of infections is large. In other words, both the threshold quantity \(\mathcal {R}_{10}\) and the initial condition are important in determining the outcome of disease transmission when backward bifurcation appears. The occurrence of backward bifurcation means that reducing \(\mathcal {R}_{10}\) to less than one cannot guarantee disease elimination. Furthermore, within the parameter ranges in Table 1, we use the Latin hypercube sampling (LHS) method to generate \(10^5\) random parameter sets among which 508 scenarios exhibiting backward bifurcation. For these 508 scenarios, we calculate the corresponding quarantine ratio \({\hat{\theta }}\) and find that the average quarantine ratio is approximately 95% with the minimum of 69%. Moreover, if the quarantine is perfect, i.e., \(\sigma =1\), then 5252 scenarios have backward bifurcation with the average and minimum quarantine ratio being around 95% and 64%, respectively. In reality, it is very difficult to achieve such a high quarantine ratio and hence backward bifurcation is less likely to happen for model (6).

Fig. 4
figure 4

Numerical solutions of system (6) with initial conditions a \((I_h(0), Q_h(0), I_v(0))=(50,20,80)\) and b \((I_h(0), Q_h(0), I_v(0))=(2500, 200, 3000)\). The solution in a tends to the disease-free equilibrium, but the solution in b approaches an endemic equilibrium (Color figure online)

Full size image

Example 2

Impact of quarantine on disease prevalence We consider model (6) with the following baseline parameter setting:

$$\begin{aligned} \begin{aligned}&a=0.29, \quad b=0.1, \quad c=0.3, \quad H=10000, \quad V=20000, \quad \mu =0.08, \\&\gamma =\frac{1}{20},\quad \gamma _1=\frac{1}{7},\quad \gamma _2=\left( \frac{1}{\gamma }-\frac{1}{\gamma _1}\right) ^{-1}=\frac{1}{13},\quad \theta =0.2,\quad \sigma =0.27. \end{aligned} \end{aligned}$$

By keeping two of the three quarantine-related parameters \(\theta , \gamma _1\) and \(\sigma \) fixed at the baseline values and letting the remaining one vary over the range in Table 1, the curves of the number of non-quarantined infectious humans, \(I^*_h\), quarantined infectious humans, \(Q^*_h\), and the total infectious humans, \(I^*_h+Q^*_h\), at the endemic equilibrium \(E^*\) versus \(\gamma _1, \theta \) and \(\sigma \) are plotted in Fig. 5. Both \(I^*_h\) and \(I^*_h+Q^*_h\) are monotone decreasing with respect to all three parameters. However, \(Q^*_h\) decreases in terms of \(\sigma \) but initially increases then decreases in terms of \(\gamma _1\) and \(\theta \). Overall, reducing the bites on quarantined humans is the most crucial factor in accomplishing a successful quarantine.

Fig. 5
figure 5

Number of non-quarantined infectious humans, \(I^*_h\), quarantined infectious humans, \(Q^*_h\), and the total infectious humans, \(I^*_h+Q^*_h\), at the endemic equilibrium \(E^*\) versus a per capita rate of transition from symptom onset to quarantine \(\gamma _1\), b adjusted quarantine ratio \(\theta \), and c biting reduction ratio \(\sigma \), respectively (Color figure online)

Full size image

Example 3

Sensitivity analysis Sensitivity index is a measure of the change of a variable with a parameter in a system (Chitnis et al. 2008). The normalized forward sensitivity index of the basic reproduction number \(\mathcal {R}_{10}\) with respect to a parameter p is defined as

$$\begin{aligned} \varUpsilon _{p}^{\mathcal {R}_{10}}=\dfrac{\partial \mathcal {R}_{10}}{\partial p}\times \dfrac{p}{\mathcal {R}_{10}}. \end{aligned}$$

Direct calculations yield

$$\begin{aligned} \varUpsilon _{a}^{\mathcal {R}_{10}}&=1, \quad \varUpsilon _{b}^{\mathcal {R}_{10}}=\varUpsilon _{c}^{\mathcal {R}_{10}}=\varUpsilon _{m}^{\mathcal {R}_{10}}=\frac{1}{2}, \quad \varUpsilon _{\mu }^{\mathcal {R}_{10}}=-\frac{1}{2},\\ \varUpsilon _{\gamma }^{\mathcal {R}_{10}}&=-\dfrac{(\theta \gamma _1+(1-\theta )\gamma )^2 +\theta \sigma (\gamma (\gamma -2\gamma _1)-\theta (\gamma -\gamma _1)^2)}{2(\theta \gamma _1+(1-\theta )\gamma )(\gamma +\theta (1-\sigma )(\gamma _1-\gamma ))}\\&=-\frac{1}{2}-\varUpsilon _{\gamma _1}^{\mathcal {R}_{10}}>-\frac{1}{2}, \\ \varUpsilon _{\gamma _1}^{\mathcal {R}_{10}}&=-\dfrac{\theta \sigma \gamma \gamma _1}{2(\theta \gamma _1+(1-\theta )\gamma )(\gamma +\theta (1-\sigma )(\gamma _1-\gamma ))}>-\frac{1}{2}, \\ \varUpsilon _{\theta }^{\mathcal {R}_{10}}&=-\dfrac{\theta \sigma \gamma \gamma _1}{2(\theta \gamma _1+(1-\theta )\gamma )(\theta \gamma _1(1-\sigma )+\gamma _2)}>-\dfrac{1}{2},\\ \varUpsilon _{\sigma }^{\mathcal {R}_{10}}&=-\dfrac{\theta \sigma \gamma _1}{2(\theta \gamma _1(1-\sigma )+\gamma _2)}. \end{aligned}$$

Therefore, \(\mathcal {R}_{10}\) is most sensitive to the regular mosquito biting rate a.

Choosing the same set of parameter values as in Example 2 except that \(a=0.33\) and \(\sigma =0.5\), we use the above formulae to calculate their sensitivity indices (see Fig. 6a). In this scenario, \(\mathcal {R}_{10}\) is most sensitive to mosquito biting rate, followed by transmission probabilities, mosquito-to-human ratio, and mosquito mortality rate. Moreover, based on the parameter ranges in Table 1, we generate \(10^6\) random parameter sets with the LHS method and calculate the partial rank correlation coefficients for \(\mathcal {R}_{10}\) to model parameters (see Fig. 6b). Thus we can draw a similar conclusion through global sensitivity analysis. It is worth mentioning that the biting reduction ratio, \(\sigma \), is the most sensitive parameter among the three quarantine-related parameters. Biologically speaking, the quarantine effect on initial disease transmission is primarily determined by the amplitude of reduction in mosquito bites.

Fig. 6
figure 6

Sensitivity indices (SI) and partial rank correlation coefficients (PRCC) of \(\mathcal {R}_{10}\) with respect to model parameters for the standard incidence malaria model (6)

Full size image

6 Discussion

In this paper, we proposed a dynamic model for malaria transmission to investigate the potential role of quarantine on malaria control and elimination. The human population is divided into three classes: susceptible, infectious, and quarantined, while the mosquito population is divided into two classes: susceptible and infectious. We analyzed the dynamical behavior of the model in term of the basic reproduction number. Specifically, for the model with standard incidence, we obtained a sufficient condition for the global asymptotic stability of the disease-free equilibrium \(E_0\) and showed that the model can exhibit both forward and backward bifurcations at \({\mathcal {R}}_{10}=1\). In addition, the disease is uniformly persistent and there exists a unique endemic equilibrium when \({\mathcal {R}}_{10}>1\). In contrast, the model with bilinear incidence obeys the regular threshold dynamics. Namely, if \(\mathcal {R}_{20}\le 1\), then the disease dies out; if \({\mathcal {R}}_{20}>1\), then the disease persists and the unique endemic equilibrium is locally asymptotically stable. We also used the second additive compound matrix method to establish the global stability of the endemic equilibrium under certain condition. Finally, three numerical examples on the standard incidence model were carried out to further explore the impact of quarantine on malaria persistence and control. The first example confirmed the occurrence of backward bifurcation with biologically acceptable parameter settings. The efficacies of the change in the three quarantine-related parameters, \(\theta ,\,\gamma _1\) and \(\sigma \), on reducing malaria cases were compared in the second example. In the last example, we performed both local and global sensitivity analyses on the basic reproduction number \({\mathcal {R}}_{10}\) and found that the most sensitive parameter is the mosquito biting rate. Results suggest that the most important factor in achieving a successful quarantine for malaria is to reduce the biting rate of the quarantined people other than to quarantine more infected people at earlier infection stage. It is therefore very important to provide health advice (e.g., wear protective clothing and stay in mosquito-free accommodation) and essential supplies (e.g., insecticide-treated bed nets and mosquito repellent) to malaria patients such that the possibility of exposure to mosquito bites is dramatically reduced.

The two malaria models with quarantine only differ in incidence rate, but their dynamical behaviors can be substantially different, which highlights the importance of choosing the right biting rate or incidence rate function in mathematical modeling (Yang et al. 2017). Generally speaking, if the ratio of mosquitoes to humans is small, then it is proper to choose the standard incidence. Otherwise, the bilinear or saturated incidence rate is a preferred choice (Chitnis et al. 2006). Note that the Ross–Macdonald model (1) exhibits the global threshold dynamics in terms of \(\mathcal {R}_0\), so quarantine is a new mechanism of backward bifurcation in mosquito-borne disease models (Gumel 2012). The quarantine strategy is traditionally used for controlling diseases that are transmissible from human to human. We must address that quarantine is applicable to the control and elimination of malaria only if a low transmission region with a limited number of imported or autochthonous cases is concerned. For mosquito-borne diseases, we quarantine suspected and confirmed cases not these who have contacts with patients or have been exposed to malaria parasites with no symptoms. Moreover, quarantine becomes more practical if fast, low-cost and highly sensitive diagnostic kits for malaria are available.

To better evaluate the effect of quarantine for malaria control, we need to extend the current model by incorporating more biological and epidemiological factors. For example, the extrinsic incubation period in mosquitoes and intrinsic incubation period in humans, seasonal fluctuations in the mosquito population, acquired immunity in humans, differential susceptibility and infectivity of humans to malaria infection, imperfect malaria vaccine, differences in attractiveness to mosquitoes, and spatial heterogeneity. Quarantined people who receive better treatment and care may have a shorter period of infectiousness or a lower parasitemia level. The use of quarantine is less beneficial when there is a high proportion of asymptomatic or subclinical infections. It is worth mentioning that modeling quarantine and/or isolation under exponential distribution assumption (EDA) may result in biased outcomes in understanding dynamic behaviors and assessing control measures (Feng et al. 2007). Models that make no contradiction in terms of the basic reproduction number, endemic equilibrium, infectious period and other epidemiological characteristics, but remain mathematically tractable are most desirable. Non-exponential distribution assumptions such as gamma distribution assumption (GDA) may yield an improvement on the model under EDA (Feng et al. 2007, 2016). The framework of the current work can be adopted to the study of the prevention and control of other mosquito-borne or vector-borne diseases, especially these having a relatively short infectious period.