1 Introduction

Elastoplasticity builds on additive decomposition of strain rates into elastic and plastic. The decomposition of the strain rate into elastic and plastic requires that each component be described with certain assumptions. The elastic portion of the strain rate is assumed to be uniquely determined by the corresponding stress increments, where the elastic moduli are assumed known. For metals, a positive definite elastic stiffness tensor with constant moduli is often assumed. For soils, rocks and similar materials, the elastic moduli are assumed to depend on several factors such as the void ratio, effective confining pressure and history of loading [37]. In addition, the definition of elasticity for discontinuous materials such as soils is somewhat arbitrary—it might rather be considered an elastic tendency. On the other hand, the plastic strain rate is assumed to depend on the current stress state in some way (not on the stress increment). This property was originally postulated by Saint-Venant [9]. Later, von Mises proposed a potential function of stress whose gradient with respect to stresses is assumed to give the direction of plastic flow. Assumption of coaxiality of principal stresses and principal plastic strain rates was then introduced. Drucker [10] presented his postulate of material stability in which the plastic potential function has to be identical to the yield function which a stress state obeys and that the yield function has to be convex. This branch of elastoplasticity where the yield function serves as a plastic potential function as well is called associated plasticity. Even though associated plasticity is a well-established theoretical framework with several elegant mathematical theorems and its success in its application for metals, with yield functions that are based on Coulomb's shear strength theory, the application of associated plasticity to the modelling of soils, rocks and concrete leads to unrealistic plastic volumetric strains during plastic deformation [42]. This necessitated establishing a plastic potential function that is different from the yield function for realistic prediction of shear induced plastic volumetric strains. This second type of plasticity framework is called non-associated plasticity. Technically, associated plasticity is a special class of non-associated plasticity. The limitation of associated plasticity to reproduce the observed deformation behavior of soils and similar materials is often identified as a limitation of the framework itself. This is not necessarily true. For the most part, it is the limitation of Coulomb's formula for the description of shear strength of soils—which is also carried over to several of its extended forms. This limitation was recognized when Schofield and Wroth [31] established the original Cam clay model and in part the original Cam clay model was developed to correct the pitfalls the Mohr–Coulomb yield function has when employed in the associated plasticity framework.

Coulomb [6] described the shear strength of soils in terms of their friction angle and cohesion as1

$$\tau \mathop = \limits^{1} \sigma_{n} \tan \varphi + c\mathop = \limits^{2} (\sigma_{n} + a)\tan \varphi,$$
(1)

where \({\sigma }_{n}\) is the effective stress normal to the \(\tau\) -plane, \(\varphi\) is the friction angle or angle of internal friction, \(c\) is cohesion and \(a=c\mathrm{cot}\varphi\) is attraction [15]. Coulomb's shear strength theory held a central place in traditional earth-pressure theories, but it ignores the fact that soils contain grains [35]—which renders them with certain peculiar properties when sheared. Reynolds [26] recognized the limitation of Coulomb's shear strength theory after his discovery of the property of dilatancy which manifests from the particulate nature of sands. Reynolds then envisaged that the consideration of the property of dilatancy would place earth-pressure theories on a true foundation.

The first attempt to apply the principles of dilatancy to earth pressure problems appear in Jenkin [17]. Shortly after, Casagrande [4] discussed the dilatancy behavior of sands in line with his critical state porosity concept. One of the earliest attempts to describe dilatancy behavior of frictional materials in terms of the energy dissipation was due to Taylor [34]. Reynolds also considered a work hypothesis, but he was rather interested in frictionless particles. The work of Taylor has been a basis of various dissipation equations and stress–dilatancy formalisms. The other interesting theoretical framework for describing the relationship between stress ratio and dilatancy ratio is due to Rowe [27]. Rowe developed his theory for plane strain and axisymmetric deformation modes based on hypothesis of minimum energy ratio. Taylor’s and Rowe’s theories are endowed with simplicity and descriptive power and have been modified, extended and reinterpreted in the literature [41]. The former has also been used for establishing a plastic potential function in the associated plasticity framework [31]. Both consider loading in shear, i.e., mobilizing away from isotropic stress state. This is one of the major drawbacks of these theories for application in the modelling of deformation behaviour soils subjected to cyclic shear.

In this paper, a theoretical framework is put forward as a unifying viewpoint and for tackling the limitation of the stress–dilatancy theories for the modelling of deformation behavior of soils under cyclic shear. Both loading and unloading in shear are explicitly considered while establishing stress–dilatancy relations and further when deriving plastic potential functions. Towards this end, first plastic dissipation is discussed in its generality, stress–dilatancy conjugates contained in the plastic work are identified and the role of stress–dilatancy relations in the plastic dissipation is pointed out. Hypothesis of complementarity of stress–dilatancy conjugates is then put forward. With this hypothesis, the writer aims at establishing a common viewpoint for both Taylor's work hypothesis, and Rowe's minimum energy ratio hypothesis and further extending and generalizing them. Then, stress–dilatancy relations are derived considering both loading and unloading in shear first for axisymmetric and plane strain conditions and further for the general stress–strain conditions. Loading and unloading in shear are identified through a state variable which assumes a value of 1 when a stress state is tending away from isotropic stress condition and assumes a value of -1 when a stress state is tending towards isotropic stress condition.

Note that:

  • Strain rates defined in this paper refer generally to an artificial time increment and can likewise be considered infinitesimal strain increments.

  • All stress quantities are effective without distinguishing them with a prime or not necessarily using the adjective "effective".

  • Sign convention of soil mechanics is adopted, i.e., compression is positive.

2 Plastic dissipation and complementarity of stress–dilatancy conjugates

For an isothermal condition, the average energy variation in a deforming body may be written as

$$\dot{F} + {\mathcal{D}} - \dot{W} = 0,\,{\mathcal{D}} \ge 0$$
(2)

where \(\dot{F}\) is the rate of Helmholtz free energy, \(\mathcal{D}\) is the rate of dissipation and \(\dot{W}\) is the rate of work.

The general conception is that the free energy can depend on both elastic and plastic strains. Under certain assumptions, the free energy can be decomposed into elastic and plastic parts. Furthermore, considering that the elastic free energy rate is equal to the elastic rate of work, one ends up with the result that the plastic rate of work is the sum of the plastic free energy rate and the dissipation rate. The physical basis of the plastic part of the free energy rate for geomaterials is explained in [5, 45] for example. This framework is considered a convenient approach for kinematically hardening elastoplastic models with the back stress playing a stress like variable associated with the plastic part of the Helmholtz free energy rate.Footnote 1

Considering the additive decomposition of the strain rate into elastic and plastic, the rate of work of a continuum body may be written as

$$\dot{W} = \sigma_{ij} \dot{\varepsilon }_{ij} = \sigma_{ij} \dot{\varepsilon }_{ij}^{e} + \sigma_{ij} \dot{\varepsilon }_{ij}^{p} = p\dot{\varepsilon }_{v}^{e} + c_{\Delta }^{e} q\dot{\varepsilon }_{q}^{e} + p\dot{\varepsilon }_{v}^{p} + c_{\Delta }^{p} sq\dot{\varepsilon }_{q}^{p}$$
(3)

where

  • \({\sigma }_{ij}\) is Cauchy's stress tensor, \(p=\frac{1}{3}{\sigma }_{ij}{\delta }_{ij}\) is the isotropic stress, also called mean effective stress, effective confining stress or effective confining pressure, \({\delta }_{ij}\) is Kronecker’s delta with a property \({\delta }_{ij}=1, i=j\) and \({\delta }_{ij}=0, i\ne j\) and Einstein’s summation rule over repeated indices applies.

  • \({s}_{ij}={\sigma }_{ij}-{\sigma }_{ij}{\delta }_{ij}/3\) is the deviatoric stress tensor, it is a traceless tensor that contains all the shear components. The magnitude of the deviatoric stress is given by \(||{\varvec{s}}||=\sqrt{{s}_{ij}{s}_{ij}}=q\sqrt{2/3}\), and \(q\) is called deviatoric stress.

  • \({\dot{\varepsilon }}_{v}={\dot{\varepsilon }}_{ij}{\delta }_{ij}\) is the volumetric strain rate.

  • \({\dot{e}}_{ij}\) is distortional or deviatoric strain rate tensor which is the deviation from mean isotropic straining. It is thus obtained by subtracting the mean normal strain rate from the total strain rate tensor as \({\dot{e}}_{ij}={\dot{\varepsilon }}_{ij}-{\dot{\varepsilon }}_{v}{\delta }_{ij}/3\), and its magnitude is given by \(||\dot{{\varvec{e}}}||=\sqrt{{\dot{e}}_{ij}{\dot{e}}_{ij}}=\sqrt{3/2}{\dot{\varepsilon }}_{q}\), where \({\dot{\varepsilon }}_{q}\) is the deviatoric strain rate.

  • \({c}_{\Delta }\) is the degree of coaxiality between the respective stress and strain increments (\({c}_{\Delta }=1\) when they are coaxial.)

  • s is a state variable and assumes a value of 1 for stress state mobilization away from isotropic stress condition (for shear loading) and assumes a value of –1 for stress states  mobilizing towards isotropic stress condition (shear unloading).

  • The superscripts e and p, respectively, indicate elastic and plastic.

Elastic strain increments are often assumed to be coaxial with stress increments, i.e.,

$$c_{\Delta }^{e} = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} \frac{{s_{ij} \dot{s}_{ij} }}{{q\parallel \dot{s}_{ij} \parallel }} = \sqrt {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}} \frac{{\dot{q}}}{{\parallel \dot{s}_{ij} \parallel }},\,{\text{for}}\,\parallel \dot{s}_{ij} \parallel > 0.$$
(4)

Let us define, according to Gutierrez and Ishihara [14],

$$s_{ij} = q\tilde{m}_{ij} \,{\text{and}}\,\dot{e}_{ij}^{p} = \dot{\varepsilon }_{q}^{p} \tilde{n}_{ij}$$
(5)

such that

$$c_{\Delta }^{p} = \parallel \tilde{m}_{ij} \tilde{n}_{ij} \parallel ,\,s = {\text{sgn}} \left( {\tilde{m}_{ij} \tilde{n}_{ij} } \right),$$
(6)

where \(\mathrm{sgn}()\) denotes a signum function, and \({\widetilde{m}}_{ij}\) and \({\widetilde{n}}_{ij}\) are, respectively, given by

$$\tilde{m}_{ij} = \frac{2}{3}\left[ {T_{i1}^{\sigma } T_{j1}^{\sigma } \sin \left( {\theta_{\sigma } + {{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-\nulldelimiterspace} 3}} \right) + T_{i2}^{\sigma } T_{j2}^{\sigma } \sin \left( {\theta_{\sigma } + {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-\nulldelimiterspace} 3}} \right) + T_{i2}^{\sigma } T_{j2}^{\sigma } \sin \left( {\theta_{\sigma } } \right)} \right],\,{\text{and}}$$
(7)
$$\tilde{n}_{ij} = T_{i1}^{{\dot{\varepsilon }^{p} }} T_{j1}^{{\dot{\varepsilon }^{p} }} \sin \left( {\theta_{{\dot{\varepsilon }}}^{p} + {{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-\nulldelimiterspace} 3}} \right) + T_{i2}^{{\dot{\varepsilon }^{p} }} T_{j2}^{{\dot{\varepsilon }^{p} }} \sin \left( {\theta_{{\dot{\varepsilon }}}^{p} + {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-\nulldelimiterspace} 3}} \right) + T_{i2}^{{\dot{\varepsilon }^{p} }} T_{j2}^{{\dot{\varepsilon }^{p} }} \sin \left( {\theta_{{\dot{\varepsilon }}}^{p} } \right).$$
(8)

\({T}_{ik}^{\sigma }\) and \({T}_{ik}^{\dot{\varepsilon }}\) are matrices that transform the stress tensor and the plastic strain rate tensors into their respective principals, \({\theta }_{\sigma }\) is the Lode angle of the stress tensor; \({\theta }_{\dot{\varepsilon }}^{p}\) is the Lode angle of the plastic strain rate tensor. If \({T}_{ik}^{\sigma }\ne {T}_{ik}^{\dot{\varepsilon^p }}\), then principal stresses and principal plastic strain rates are said to be non-coaxial and the condition is referred to as non-coaxiality.

Let us focus on the plastic part of the energy rate in Eq. (2). We assume that the total plastic dissipation is due to mobilization of interparticle friction, dilation and cohesion. Interparticle friction resists interparticle gliding and its mobilization relates to the stress ratio in the soil body. On the other hand, dilation depends on the ratio of transversal plastic strain increments in the soil body and indirectly measures the amount of energy invested to overcome interlocking (geometric interference). Cohesion between soil particles tends to resist interparticle gliding. One of the most convenient interpretations of cohesion is in terms of Janbu's attraction, as shown in Eq. (1). Attraction acts to suppress plastic work and dilatancy in just the same manner as an effective confining pressure does—the difference is that confining pressure/stress is external to the material and attraction is internal, innate behaviour of the material. Attraction can be envisaged as an internal force that exerts a pullback force when particles tend to move apart from each other. In other words, attraction works against plastic volumetric expansion and suppresses mobilization of friction. Attraction may then be introduced as added isotropic compression which tends to resist interparticle gliding and volumetric expansion and may consequently be introduced as an isotropic shift in effective stresses such that the plastic dissipation is written as

$$D^{p} = \overline{p}c_{\Delta }^{p} d \dot{\varepsilon }_{q}^{p} \ge 0,\,d = \frac{{\dot{\varepsilon }_{v}^{p} }}{{c_{\Delta }^{p} \dot{\varepsilon }_{q}^{p} }} + s\frac{q}{{\overline{p}}},\,\overline{p} = p + a$$
(9)

where in addition nonnegativity of the plastic dissipation rate, i.e., \({D}^{p}\ge 0\) is assumed, \({d}\) is here called a stress–dilatancy function and contains the stress ratio, (\(q/\overline{p })\), and its conjugate dilatancy ratio, \({\dot{\varepsilon }}_{v}^{p}/{c}_{\Delta }^{p}{\dot{\varepsilon }}_{q}^{p}\). In this paper, non-coaxiality will not be considered in further details and accordingly \({c}_{\Delta }^{p}\) is set to unity, i.e., principal stresses and principal plastic strain rates are assumed coaxial; and we will focus on the coaxial plastic dissipation in terms of other convenient stress and conjugate plastic strain increments or their invariants, and for special modes of deformation of interest.

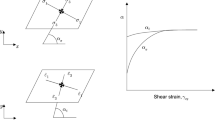
The work hypotheses due to Taylor [34] is based on consideration of deformation of a sand sample in a direct shear box test apparatus. Figure 1(left) and (right) are from Taylor's book [34] and, respectively, illustrate the typical stress–strain behavior observed in a direct shear box test and in a drained triaxial compression tests of a sand sample of different initial void ratios.

Fig. 1
figure 1

Left: Typical –plots of direct shear tests: Samples of Ottawa Sand, Right: Plots of typical triaxial compression tests: Samples of Fort Peck Sand(after Taylor [34])

Full size image

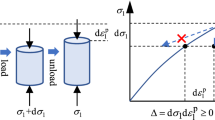
Considering deformation of sand in a direct shear box, Taylor [34] hypothesized that part of the strain energy used to overcome interlocking and result in volume expansion is supplied by a portion of the total shear stress. This allowed Taylor to split the total strain energy rate into energy expended due to shear and due to dilation, which led him to write a relationship between dilatancy ratio and stress ratio such that their sum is a constant. Let us look this more closely by writing the plastic dissipation for a soil specimen subjected to normal stress, \({\sigma }_{n},\) and shear stress, \(\tau\), in a direct shear box, as

$$D^{p} = \overline{\sigma }_{n} d_{T} |\dot{\gamma }^{p} | \ge 0,\,\overline{\sigma }_{n} = \sigma_{n} + a,\,d_{T} = \frac{{\dot{\varepsilon }_{n}^{p} }}{{|\dot{\gamma }^{p} |}} + s\frac{|\tau |}{{\overline{\sigma }_{n} }},$$
(10)

where \({\dot{\varepsilon }}_{n}^{p}\) and \({\dot{\gamma }}^{p}\) are the corresponding work conjugate plastic strain rates, \({d}_{T}\) is the stress–dilatancy function and contains the conjugate stress ratio (\(\frac{|\tau |}{{\tilde{\sigma }}_{n}}\)) and dilatancy ratio (\(\frac{{\dot{\varepsilon }}_{n}^{p}}{{\dot{\gamma }}^{p}}\)). In simple terms, Taylor's work hypothesis is setting \({d}_{T}\) a constant. However, Taylor considered only loading in shear and therefore \(s\) =1 which makes the resulting stress–dilatancy relationship applicable only to conditions that involve loading in shear (mobilizing away from isotropic stress condition.)

Taylor's work hypothesis may be generalized for an arbitrary stress state using the multilaminate framework [12, 25, 29, 44, 46]. Suppose a virtual sphere of unit radius is assumed around the stress point and the unit sphere is divided into several planes; and further each plane is assigned a weight factor, say \({w}_{i}\), according to the proportion of its sector relative to the unit sphere. The stress tensor can be transformed into a normal stress and a shear stress on arbitrary plane \(\mathrm{k}\) with a unit normal \(\mathbf{n}={\left[\begin{array}{ccc}{n}_{1}& {n}_{2}& {n}_{3}\end{array}\right]}^{T}\), the traction on the surface is defined by \(\mathbf{t}={\varvec{\upsigma}}\widehat{\mathbf{n}}\), Figure 2. The scalar product between the traction and the unit normal gives the normal stress, \({\sigma }_{n}=\mathbf{t}\widehat{\mathbf{n}}\). With further consideration of symmetry of the stress tensor, the normal stress can be written as

$$\sigma_{n} = n_{1}^{2} \sigma_{11} + n_{2}^{2} \sigma_{22} + n_{3}^{2} \sigma_{33} + 2n_{1} n_{2} \sigma_{12} + 2n_{2} n_{3} \sigma_{23} + 2n_{1} n_{3} \sigma_{13}.$$
(11)
Fig. 2
figure 2

Global stress components in a Cartesian coordinate system and depiction of the traction vector, the normal and shear stresses on an arbitrary plane

Full size image

The normal stress \({\sigma }_{n}\) can alternatively be written as

$$\sigma_{n} = {{\varvec{\upsigma}}}:\frac{{\partial \sigma_{n} }}{{\partial {{\varvec{\upsigma}}}}} = {{\varvec{\upsigma}}}:{\hat{\mathbf{n}}},$$
(12)

where \(\widehat{\mathbf{n}}\) is obtained as

$$\hat{n}_{ij} = \frac{{\partial \sigma_{n} }}{{\partial \sigma_{ij} }} = \left\{ {\begin{array}{*{20}c} {n_{i}^{2} ;} & {i = j} \\ {2n_{i} n_{j} ;} & {i \ne j} \\ \end{array} } \right.$$
(13)

The shear stress on the plane is obtained by subtracting the normal stress vector from the traction vector as

$${{\varvec{\uptau}}} = {\mathbf{t}} - ({\mathbf{n\sigma n}}){\mathbf{n}} = \tau {\mathbf{\underline {n} }}$$
(14)

and its magnitude, \(\tau = {||}{{\varvec{\uptau}}}{||}\) is given by

$$\tau = \sqrt {\left( {n_{1} s_{11} + n_{2} \sigma_{12} + n_{3} \sigma_{13} } \right)^{2} + \left( {n_{2} s_{22} + n_{1} \sigma_{12} + n_{3} \sigma_{23} } \right)^{2} + \left( {n_{3} s_{33} + n_{1} \sigma_{13} + n_{2} \sigma_{23} } \right)^{2} },$$
(15)

where \(s_{ij} = \left\{ {\begin{array}{*{20}l} {\sigma_{ij} - \sigma_{n} \delta_{ij} ,\quad i = j} \hfill \\ {0,\quad \quad \quad \quad \;\,i \ne j} \hfill \\ \end{array} } \right.\).

The shear stress on the plane can alternatively be written as

$${{\varvec{\uptau}}} = {{\varvec{\upsigma}}}:\frac{\partial \tau }{{\partial {{\varvec{\upsigma}}}}} = {{\varvec{\upsigma}}}:{\mathbf{\underline {n} }}.$$
(16)

The vector \({\mathbf{\underline {n} }}\) can be specified by differentiating Eq. (15) with respect to stress, \({\varvec{\upsigma}}\) as

$$\underline {n}_{ij} = \frac{\partial \tau }{{\partial \sigma_{ij} }} = \frac{1}{\tau }\left\{ {\begin{array}{*{20}l} {n_{i} t_{i} - n_{i}^{2} \sigma_{n} ;\,i = j} \hfill \\ {n_{j} t_{i} + n_{i} t_{j} - 2n_{i} n_{j} \sigma_{n} ;\,i \ne j} \hfill \\ \end{array} } \right. \, ,\,\tau \ne 0.$$
(17)

The plastic dissipation on each plane can be obtained as a scalar product of the transformed stresses on each plane and their codirectional plastic strain increments multiplied by the weight factor, \({w}_{i}\), of the plane. Suppose the plastic strain increments in the normal and tangential directions are denoted, respectively, by \({\dot{\varepsilon }}_{n}^{p}\) and \({\dot{\gamma }}^{p}\), the total plastic dissipation may then be given as

$$D^{p} = \sum\limits_{i = 1}^{m} {\overline{\sigma }_{ni} d_{Ti} |\dot{\gamma }_{i}^{p} |w_{i} } \ge 0,\,d_{Ti} = \frac{{\dot{\varepsilon }_{ni}^{p} }}{{|\dot{\gamma }_{i}^{p} |}} + s\frac{{|\tau_{i} |}}{{\overline{\sigma }_{ni} }},$$
(18)

where \(m\) is the number of integration planes. In such a way, the Multilaminate framework may offer a comprehensive way of generalizing Taylor's work hypothesis, but it can be relatively computationally costly. We may choose shear stresses and effective normal stresses on a single "representative" plane instead of multiple planes. One of such planes which is conveniently employed in constitutive modelling of geomaterials is the spatial mobilized plane proposed by Matsuoka and Nakai [22]. The Matsuoka–Nakai's spatial mobilized plane, Figure 3, is a plane that is formed by planes of maximum mobilization due to combinations of principal stresses \({\sigma }_{1},{\sigma }_{2}\), \({\sigma }_{2},{\sigma }_{3}\) and \({\sigma }_{1},{\sigma }_{3}\), and is thus defined by a unit normal vector

$${\mathbf{n}} = \sqrt {\frac{{I_{3\sigma } }}{{I_{2\sigma } }}} \left\{ {\begin{array}{*{20}c} {\sigma_{1}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \\ {\sigma_{2}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \\ {\sigma_{3}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \\ \end{array} } \right\}$$
(19)
Fig. 3
figure 3

The Matsuoka–Nakai spatial mobilized plane [22]

Full size image

Substitution of Eq. (19) into Eqs. (11) and (17) and dropping \({\sigma }_{ij}\) terms with \(i\ne j\) leads, respectively, to a normal stress

$$\sigma_{n,MN} = 3\frac{{I_{3\sigma } }}{{I_{2\sigma } }},$$
(20)

and a shear stress

$$\tau_{MN} = \frac{1}{{I_{2\sigma } }}\sqrt {I_{1\sigma } I_{2\sigma } I_{3\sigma } - 9I_{3\sigma }^{2} },$$
(21)

where \({I}_{1\sigma }\), \({I}_{2\sigma }\) and \({I}_{3\sigma }\) are the first, the second and the third stress invariants which are given in terms of the principal stresses, respectively, as \({I}_{1\sigma }={\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}\), \({I}_{2\sigma }={\sigma }_{1}{\sigma }_{2}+{\sigma }_{2}{\sigma }_{3}+{\sigma }_{3}{\sigma }_{1}\) and \({I}_{3\sigma }={\sigma }_{1}{\sigma }_{2}{\sigma }_{3}\).

Considering the Matsuoka-Nakai spatial mobilized plane, the plastic dissipation may be written as

$$D^{p} = \overline{\sigma }_{{n,{\text{MN}}}} d_{{{\text{MN}}}} \dot{\varepsilon }_{\gamma }^{p} \ge 0,\,d_{{{\text{MN}}}} = \frac{{\dot{\varepsilon }_{n}^{p} }}{{\dot{\varepsilon }_{\gamma }^{p} }} + s\frac{{\tau_{{{\text{MN}}}} }}{{\overline{\sigma }_{{n,{\text{MN}}}} }},$$
(22)

where \({\overline{\sigma }}_{n,\mathrm{MN}}\) and \({\tau }_{\mathrm{MN}}\), respectively, are the effective normal stress and the shear stress on the Matsuoka–Nakai spatial mobilized plane, \({\dot{\varepsilon }}_{n}^{p}\) and \({\dot{\varepsilon }}_{\gamma }^{p}\) are the corresponding work conjugate plastic strain rates.

We have so far shown how Taylor's work hypothesis, which was conceived based on deformation in a direct shear box apparatus, could be adopted to a general stress state. The other work hypothesis of interest in our further discourse is Rowe's [27]. Rowe [27] looked at triaxial compression and plane strain deformation modes in formulating his minimum energy ratio hypothesis. For a plane strain and triaxial conditions, the plastic dissipation may be written as

$$D^{p} = r_{1} \overline{\sigma }_{1} \dot{\varepsilon }_{1}^{p} + r_{3} \overline{\sigma }_{3} \dot{\varepsilon }_{3}^{p} = r_{1} \overline{\sigma }_{1} \dot{\varepsilon }_{1}^{p} d_{R} \ge 0,\,d_{R} = 1 + m_{s} \frac{{\overline{\sigma }_{3} }}{{\overline{\sigma }_{1} }}\frac{{\dot{\varepsilon }_{3}^{p} }}{{\dot{\varepsilon }_{1}^{p} }}$$
(23)

wherein \({\sigma }_{i}={\overline{\sigma }}_{i}-a\) and \({\dot{\varepsilon }}_{i}^{p}\) are principal stress and plastic strain rate components respectively (\(i=1\) for major, and \(i=3\) for minor) and are assumed coaxial, \({r}_{i}\) depend on mode of shear \(({r}_{1}={r}_{3}=1\) for plane strain, \({r}_{1}=2{r}_{3}=2\) for triaxial extension and \(2{r}_{1}={r}_{3}=2\) for triaxial compression), \({m}_{s}=\frac{{r}_{3}}{{r}_{1}}\) and \(a\) is attraction [15], and \(\frac{{\overline{\sigma }_{3} }}{{\overline{\sigma }_{1} }} = \frac{{\sigma_{3} + a}}{{\sigma_{1} + a}}\) is the shifted stress ratio that is conjugate to the dilatancy ratio \(\frac{{\dot{\varepsilon }}_{3}^{p}}{{\dot{\varepsilon }}_{1}^{p}}\).

The minimum energy ratio hypothesis that Rowe [27] proposed for linking the stress–dilatancy conjugates, in effect, is setting the stress–dilatancy function, \({d}_{R}\) constant, which in principle agrees with that of Taylor's except their difference in form.

In general, the stress–dilatancy function, \({d}_{i}\), that contains the stress ratio and its conjugate dilatancy ratio can be established by rearranging the plastic dissipation systematically. The stress–dilatancy formalism seeks for the relationship between the stress–dilatancy conjugates in the stress–dilatancy function. One of the simplest relationships is when the stress–dilatancy function, \({d}_{i}\), is just a constant, and this is the underlying hypothesis in both Taylor's and Rowe's stress–dilatancy theories. This may be stated in a more generalized hypothesis as follows.

Let di be the stress–dilatancy function that contains the stress–dilatancy conjugates in the plastic dissipation as described above. Then, for a soil mass that is subjected to continuous shearing, the variation of the stress–dilatancy function, i.e., δdi, vanishes and the plastic dissipation is nonnegative both when the stress state mobilizing away from isotopic stress state (loading in shear) and when the stress state is mobilizing towards isotropic stress state (unloading in shear.)

According to this hypothesis, the stress–dilatancy conjugates contained in the stress–dilatancy function di complement/supplement each other such that di is a constant. That is, they interplay in such a way that when one is less the other is more for di to be a constant. This hypothesis is here called complementarity of stress–dilatancy conjugates or in short complementarity hypothesis. The complementarity hypothesis yields stress–dilatancy relations depending on the choice of the stress–dilatancy conjugates. The hypothesis agrees with both Taylor's work hypothesis and Rowe's minimum energy ratio hypothesis and generalizes them for the case of loading and unloading in shear and it is also found suitable for introducing non-coaxiality between eigen directions of stresses and plastic strain rates and critical state into the stress–dilatancy theories [37,38,39].

3 Relations between stress–dilatancy conjugates and derivation of plastic flow potential

Next, the complementarity hypothesis is employed to formulate stress–dilatancy relations and further deriving plastic potential functions in the associated plasticity framework. First, plane strain and axisymmetric conditions are considered. The theoretical framework is applied for the general stress–strain condition considering Lode angle dependency of the shear strength of soils, the multilaminate framework and the Matsuoka–Nakai spatial mobilized plane.

3.1 Plane strain and axisymmetric

Consider the Mohr–Coulomb theory for describing the shear strength of soils (illustrated in Fig. 4). The relationship between principal stress components may then be written as

$$\sigma_{1} + a = N_{\varphi } (\sigma_{3} + a)$$
(24)

where \({N}_{\varphi }\) is the shifted stress ratio.

Fig. 4
figure 4

a Normalized Mohr’s stress circle, dimensionless quantities and Coulomb's criterion [16], b Illustration of angles and orientation of principal stresses in critical elements in the active Rankine and passive Rankine zones in classical geometry of bearing capacity mechanism of a vertically loaded foundation; \({{\varvec{\sigma}}}_{1}\) and \({{\varvec{\sigma}}}_{3}\) are, respectively, the major and the minor effective principal stresses [37]

Full size image

We also assume that orthogonal plastic strain rates are related as

$$\dot{\varepsilon }_{3}^{p} = - N_{\psi } \dot{\varepsilon }_{1}^{p} ,$$
(25)

where \({N}_{\psi }\) is the dilatancy ratio. The plastic dissipation in Eq. (22) can now be written as

$$D^{p} = r_{1} (\sigma_{1} + a)\dot{\varepsilon }_{1}^{p} d_{R} ,$$
(26)

where \({d}_{R}\) is the stress–dilatancy function given by

$$d_{R} = 1 - m_{s} \frac{{N_{\psi } }}{{N_{\varphi } }},\,m_{s} = {{r_{3} } \mathord{\left/ {\vphantom {{r_{3} } {r_{1} }}} \right. \kern-\nulldelimiterspace} {r_{1} }}.$$
(27)

The complementarity hypothesis implies that the stress–dilatancy function, \({d}_{R}\), is a constant or its variation is zero, i.e.,

$$\delta d_{R} = - N_{\varphi } \delta (m_{s} N_{\psi } ) + m_{s} N_{\psi } \delta N_{\varphi } = 0$$
(28)

which yields [37]

$$C_{N} m_{s} N_{\psi } = N_{\varphi } ,$$
(29)

where \({C}_{N}\) is a ‘constant’ which may have different values for different modes of shearing, fabric and sample density. As stated earlier, although phrased in a more advantageous form, the variation in Eq. (28) is equivalent to Rowe’s minimum energy ratio or least work hypothesis.

From Eqs. (26) and (29), the plastic dissipation is obtained as

$${\mathcal{D}}_{N}^{p} = r_{1} \left( {\sigma_{1} + a} \right)\dot{\varepsilon }_{1}^{p} \left( {\frac{{C_{N} - 1}}{{C_{N} }}} \right) \ge 0.$$
(30)

Assuming nonnegative plastic dissipation, the inequality

$$C_{N} = \langle - s\rangle C_{N}^{U} + \langle s\rangle C_{N}^{L} ,\,\,s = {\text{sgn}} \left( {\dot{\varepsilon }_{1}^{p} } \right),\,0 < C_{N}^{U} = {1 \mathord{\left/ {\vphantom {1 {C_{N}^{L} }}} \right. \kern-\nulldelimiterspace} {C_{N}^{L} }} \le 1$$
(31)

is proposed in [37, 38], where \(\langle \rangle\) is the Macaulay bracket, the superscripts \(L\) and \(U\), respectively, indicate loading and unloading in shear. Note that \({C}_{N}^{U}\) does not need to be the inverse of the \({C}_{N}^{L}\) but its value must be less than unity for making sure that the plastic dissipation is nonnegative during unloading. The inverse relationship is just one of the possibilities.

Considering the stress–dilatancy relation in Eq. (29) and further assuming \({{r}_{1}\mathrm{d}{\sigma }_{1}\dot{\varepsilon }}_{1}^{p}+{{r}_{3}\mathrm{d}{\sigma }_{3}\dot{\varepsilon }}_{3}^{p}=0\), i.e., assuming that the stress increments are orthogonal to the plastic strain increments (associated plasticity) we get

$$C_{N} \frac{{{\text{d}}\sigma_{1} }}{{{\text{d}}\sigma_{3} }} = N_{\varphi } ,\,m_{s} N_{\psi } = \frac{{{\text{d}}\sigma_{1} }}{{{\text{d}}\sigma_{3} }}.$$
(32)

The solution of this differential equation is:

$$\sigma_{1} + a = C\left( {\sigma_{3} + a} \right)^{{\frac{1}{{C_{N} }}}} ,$$
(33)

where \(C\) is the constant of integration which may be established by considering a boundary condition along the curves described by Eq. (33). A boundary condition considered here is where along the curve defined by Eq. (33) the stress state is isotropic, i.e., \({\sigma }_{1}={\sigma }_{3}={p}_{c}\). \({p}_{c}\) is here called the apparent pre-consolidation stress and the constant of integration \(C\) can now be specified as

$$C = \left( {p_{c} + a} \right)^{{\frac{{C_{N} - 1}}{{C_{N} }}}}.$$
(34)

Combining Eqs. (33) and (34), we have:

$$\frac{{\sigma_{1} + a}}{{p_{c} + a}} = \left( {\frac{{\sigma_{3} + a}}{{p_{c} + a}}} \right)^{{\frac{1}{{C_{N} }}}}.$$
(35)

The stress ratio, \({N}_{\varphi }\), can now be given as:

$$N_{\varphi } = \frac{{\sigma_{1} + a}}{{\sigma_{3} + a}} = \left( {\frac{{\sigma_{3} + a}}{{p_{c} + a}}} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}}.$$
(36)

Or, the plastic potential function, which is here called a Cyclic State Dilatancy (CStaD) plastic potential function, can be written as

$$f = \frac{{\sigma_{1} + a}}{{p_{c} + a}} - \left( {\frac{{\sigma_{3} + a}}{{p_{c} + a}}} \right)^{{\frac{1}{{C_{N} }}}} = 0.$$
(37)

For a given stress state defined by stress components \(({\sigma }_{1},{\sigma }_{3}\)), suppose the apparent pre-consolidation stresses of the respective loading and unloading plastic potential pairs are, respectively, \({p}_{cl}\) and \({p}_{cu}\), one finds the identity

$$\frac{{(\sigma_{1} + a)(\sigma_{3} + a)}}{{(p_{cl} + a)(p_{cu} + a)}} = 1.$$
(38)

Here, plastic potential pairs are defined as loading and unloading curves that intersect at a given stress state for that stress state.

The mobilized dilatancy angle may also be written as

$$\sin \psi_{m} : = \frac{{m_{s} N_{\psi } - 1}}{{m_{s} N_{\psi } + 1}} = - \frac{{\left( {\sigma_{3} + a} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}} - C_{N} \left( {p_{c} + a} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}} }}{{\left( {\sigma_{3} + a} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}} + C_{N} \left( {p_{c} + a} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}} }}.$$
(39)

Conversely, the apparent pre-consolidation stress can also be related to the dilatancy angle as

$$p_{c} + a = \left( {\frac{1}{{C_{N} }}\frac{{1 - \sin \psi_{m} }}{{1 + \sin \psi_{m} }}} \right)^{{\frac{{C_{N} }}{{1 - C_{N} }}}} \left( {\sigma_{3} + a} \right).$$
(40)

The plastic potential function in Eq. (36) is visualized in Figs. 5 and 6. In Figure 5, the plastic potential function is plotted both for shear loading and shear unloading for \({C}_{N}\) =3 and \({p}_{c}=400 \mathrm{kPa}\). The figure shows the conjugate dilatancy ratio and the stress ratio as geometric properties of the plastic potential function. In the figure, the curve that lies above the isotropic axis is valid for stress states where the effective radial stress \(\left({\sigma }_{r}\right)\) is less than the radial effective stress \(({\sigma }_{a})\) while the conjugate curve that lies bellow the isotropic axis is valid for stress states \({\sigma }_{a}<{\sigma }_{r}\). The extension of each yield function beyond \({p}_{c}\) is valid for unloading in shear. For the case of loading, the stress-states contained within phase transformation lines are for contractive states where as the stress-states on the outside of the phase transformation lines are for the dilative states. For this framework, mobilizing towards isotropy (unloading in shear) is always contractive. The curves are also plotted in Fig. 6 in \(s-t\) space (defined in the figure) where the dilatancy angle is interpreted as a tangent to the plastic potential curves. In Fig. 7, plastic potential curves described by Eq. (36) are plotted in \({\sigma }_{a}- {\sigma }_{r}\) space (left) and \(s-t\) space (right) for both loading and unloading for a constant \({C}_{N}\) and varying values of apparent pre-consolidation stress (\({p}_{c}\)). The increase in the apparent \({p}_{c}\) results in an increase in the size of the plastic potential function. In Fig. 8, the plastic potential function is plotted, for \({p}_{c}\) = 400 kPa and varying values of \({C}_{N},\) for both loading and unloading in shear. A general picture may be obtained by recognizing the plot of plastic potential pairs through the same apparent \({p}_{c}\) give a picture that resembles fish form (a fish curve) where the tail is valid for unloading in shear and the rest is valid for loading in shear.

Fig. 5
figure 5

Plot of the CStaD loading-unloading potential pairs in axial stress radial stress space for \({p}_{c}=400 kPa\) and \({C}_{N}=3\)

Full size image
Fig. 6
figure 6

Plots of the CStaD plastic potential curves in s-t space for \({C}_{N}=3\). Geometric interpretation of dilatancy angle, identification of dilative and contractive regions. The solid lines are for shear loading (mobilizing away from stress isotropy) and the dotted lines are for shear unloading (mobilizing towards stress isotropy)

Full size image
Fig. 7
figure 7

CStaD plastic potential curves for loading (solid lines), unloading (dotted lines) for varying \({p}_{c}\) values and constant \({C}_{N}=3\) and CS is phase transformation /critical state line

Full size image
Fig. 8
figure 8

CStaD plastic potential curves for loading (solid lines) and unloading (dotted lines) for constant \({p}_{c}=300\) kPa and varying \({C}_{N}\) values

Full size image

The tangent line anywhere along the plastic potential function defined in Eq. (37) is:

$$\sigma_{1} = \frac{1}{{C_{N} }}\left( {\frac{{\sigma_{3} + a}}{{p_{c} + a}}} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}} \sigma_{3} + c_{a} ,\,m_{s} N_{\psi } = - \frac{1}{{C_{N} }}\left( {\frac{{\sigma_{3} + a}}{{p_{c} + a}}} \right)^{{\frac{{1 - C_{N} }}{{C_{N} }}}},$$
(41)

where \({c}_{a}\) is called the apparent cohesion and is given as

$$c_{a} = \left( {N_{\varphi } - N_{\psi } } \right)\sigma_{3}.$$
(42)

Equation (41) may serve as both a yield function and a plastic potential function [19] given the apparent cohesion is incrementally derived according to Eq. (42).

The critical state can now be investigated by considering \({m}_{s}{N}_{\psi }=1\), which leads to

$$\sigma_{1ct} + a = \left( {C_{N} } \right)^{{\frac{1}{{1 - C_{N} }}}} \left( {p_{c} + a} \right)\,{\text{and}}\,\sigma_{3ct} + a = \left( {C_{N} } \right)^{{\frac{{C_{N} }}{{1 - C_{N} }}}} (p_{c} + a).$$
(43)

The stress ratio at the critical state is therefore as expected

$$\frac{{\sigma_{1ct} + a}}{{\sigma_{3ct} + a}} = C_{N}.$$
(44)

The writer's concern in this paper is mainly loading and unloading in shear. Purely isotropic compression loading is, therefore, outside the scope of the theory laid out here. But, it may be worth pointing out one aspect of the theory when considering isotropic compression. Let us consider the direction of plastic strain increment for a purely isotropic compression stress state at \(p={p}_{c}\). At this point, considering normality of the plastic strain increment to the plastic potential for loading in shear alone, the plastic strain increment appears to have a shear component as well. However, at this point, both loading and unloading are equally legitimate and, therefore, Koiter's rule [6] may be considered such that:

$$\sin \psi_{m} = \left. {\sin \psi_{m,L} } \right|_{{at\,p_{c} }} + \left. {\sin \psi_{{m,{\text{U}}}} } \right|_{{at\,p_{c} }} = \frac{{1 - C_{N} }}{{1 + C_{N} }} + \frac{{C_{N} - 1}}{{1 + C_{N} }} = 0,$$
(45)

i.e., the net effect is such that there will not be plastic shear strain increment for isotropic stress increments.

Let us consider a Mohr–Coulomb (MC) material where the mobilized stress ratio and the critical state stress ratio are defined as

$$N_{\varphi }^{{{\text{MC}}}} \mathop = \limits^{1} \frac{{1 + \sin \varphi_{m} }}{{1 - \sin \varphi_{m} }}\,{\text{and}}\,C_{N}^{{L,\,{\text{MC}}}} \mathop = \limits^{2} \frac{{1 + \sin \varphi_{c} }}{{1 - \sin \varphi_{c} }},$$
(46)

in which \({\varphi }_{m}\) and \({\varphi }_{c}\) are, respectively, the mobilized friction angle and the critical state friction angle. The stress–dilatancy relationship can now be derived for both loading and unloading in shear considering Eq. (46)1,2 into Eq. (39).

3.1.1 Mobilizing away from isotropy (loading in shear)

The stress–dilatancy relationship is obtained by substituting the relations in Eq. (46) into Eq. (29) as

$$C_{N}^{{L,\,{\text{MC}}}} m_{s} N_{\psi } = N_{\varphi }^{{{\text{MC}}}}$$
(47)

Then, the negative of the sine of the mobilized dilatancy angle is given as [41]

$$- \sin \psi_{m} \, = \,\,\frac{{N_{\varphi }^{{{\text{MC}}}} - C_{N}^{{L,\,{\text{MC}}}} }}{{N_{\varphi }^{{{\text{MC}}}} + C_{N}^{{L,\,{\text{MC}}}} }}.$$
(48)

After some simple rearrangement one is led to:

$$- \sin \psi_{m} \, = \,\,\,\frac{{\sin \varphi_{m} - \sin \varphi_{c} }}{{1 - \sin \varphi_{m} \sin \varphi_{c} }}.$$
(49)

For \({\varphi }_{c}={\varphi }_{\mu }\), where \({\varphi }_{\mu }\) is interparticle friction angle, Eq. (49) simplifies to the original Rowe’s stress–dilatancy relationship. Rowe [27, 28] established his stress–dilatancy relationship for granular materials by considering the kinematics and the stress state of a pack of orderly arranged steel rods, Fig. 9. The relationship has been widely applied in constitutive models for soils either as it is or with some modifications, for example in [30, 32, 40, 43]. It has also been re-derived from some other assumptions, for example [8, 24].

Fig. 9
figure 9

Stress and kinematics of a pack of orderly arranged cylindrical bars (after Rowe [27])

Full size image

3.1.2 Mobilizing towards isotropy (unloading in shear)

For the case of unloading in shear, considering Eq. (29), i.e., \({C}_{N}^{U}=\frac{1}{{C}_{N}^{L}}\), the stress–dilatancy relationship is obtained as

$$- \sin \psi_{m} \, = \frac{{N_{\varphi }^{{{\text{MC}}}} C_{N}^{{L,\,{\text{MC}}}} - 1}}{{N_{\varphi }^{{{\text{MC}}}} C_{N}^{{L,\,{\text{MC}}}} + 1}}.$$
(50)

Considering the definitions in Eq. (46), Eq. (50) simplifies to

$$\, - \sin \psi_{m} \, = \,\,\frac{{\sin \varphi_{m} + \sin \varphi_{c} }}{{1 + \sin \varphi_{m} \sin \varphi_{c} }}.$$
(51)

Note that the minus sign in Eq. (49) changes into a plus sign in Eq. (51). According to Eq. (51), the plastic strain increments in plastic shear unloading are strictly contractive. The loading and unloading stress–dilatancy relations can then be combined as [37]

$$\, - \sin \psi_{m} \, = \,\,\frac{{\sin \varphi_{m} - s\sin \varphi_{c} }}{{1 - s\sin \varphi_{m} \sin \varphi_{c} }},$$
(52)

where \(s=1\) during loading in shear and \(s=-1\) during unloading in shear (in general \({s}_{l}{s}_{u}=-1\), in which the subscripts l and u represent loading and unloading in shear respectively).

The stress–dilatancy relationship may also be enhanced by considering

$$N_{\varphi }^{{{\text{MC}}}} \mathop = \limits^{1} \frac{{1 + \sin \varphi_{m} }}{{1 - \sin \varphi_{m} }}\,{\text{and}}\,{,}\,C_{N}^{{L,\,{\text{MC}}}} \mathop = \limits^{2} \frac{{1 + f_{sd} \sin \varphi_{c} }}{{1 - f_{sd} \sin \varphi_{c} }},\,0 \le f_{sd} \sin \varphi_{c} < 1,$$
(53)

here again \({\varphi }_{m}\) is the mobilized friction angle, \({\varphi }_{c}\) is the critical state friction angle, and \({f}_{sd}\) is an ad-hoc void ratio dependency function introduced into Equation (46)2. The corresponding stress–dilatancy relationship will then be

$$\, - \sin \psi_{m} \, = \,\,\frac{{\sin \varphi_{m} - sf_{sd} \sin \varphi_{c} }}{{1 - sf_{sd} \sin \varphi_{m} \sin \varphi_{c} }}.$$
(54)

Equation (54) is the enhanced form of Rowe’s [27] stress–dilatancy equation proposed by Wan and Guo [43] with one important difference, i.e., the stress–dilatancy relationship in Eq. (54) takes into consideration both loading and unloading in shear. In addition, \({f}_{sd}\mathrm{sin}{\varphi }_{c}\in (\left.\mathrm{0,1}\right)\) needs to be satisfied so as not to violate geometric and physical properties. Furthermore, \({f}_{sd}\) needs to evolve to unity when the stress state mobilizes towards the critical state. The phase transformation point, defined as a point where the deformation state changes from contractive to dilative, can then be reached before reaching the critical state. There are several candidate functions in literature that can be used for \({f}_{sd}\). One possible function that can be used to define \({f}_{sd}\) is the Gudehus-Bauer [2, 13] void ratio dependency function [37], which can be written in terms of the Been and Jefferies [3] state parameter, \(\Psi\), as:

$$f_{sd} = \left( {1 - \frac{\Psi }{{\Psi_{\max } }}} \right)^{\beta } ;\Psi = e - e_{c} ;\,\,\Psi_{\max } = e_{d} - e_{c} ,$$
(55)

where \({e}_{c}\) and \({e}_{d}\) are, respectively, the critical sate void ratio and the minimum void ratio at the current effective confining pressure, \(\beta\) is a material parameter. At the minimum void ratio, \({C}_{N}=1\) is obtained. That is, it implies no further plastic volumetric contraction is allowed. In this way, the minimum void ratio guarantees that unlimited volumetric contraction will not be produced during high number cycles of shear strains/ shear stresses. Introducing a non-constant \({f}_{sd}\) overrules the constancy \({C}_{N}\) we set out postulating. However, it seems to be the case that the stress ratio at the phase transformation depends on the density of the sample and on the fabric of the soil medium. If \({C}_{N}\) depends on the initial void ratio, consistency demands that it must also be dependent on subsequent void ratios during shearing. The effect of fabric may be accounted by considering the Li-Dafalias [7, 21] state parameter which adds a fabric term on the Been and Jefferies state parameter.

Let us demonstrate the working mechanism of the enhanced model using symmetric and asymmetric cycles of \(\mathrm{sin}{\varphi }_{m}\) in the following figures, Figs. 10, 11, 12, and 13. In the example plots, a critical state friction angle of 30 degrees and \({f}_{sd}\) defined by the Gudehus-Bauer void ratio dependency function in Eq. (55) are considered; the minimum void ratio and the critical state void ratio are assumed to be pressure dependent and that both follow Bauer's compression rule [37]. The hardening rule is not explicitly given here, as it requires a thorough treatment of its own and, in the process, will take us away from the central theme of this paper. For now, it suffices to state that the hardening rule is a mathematical function that describes incremental relationship between the mobilized friction angle and the plastic shear strain. It is represented by the \(\mathrm{sin}{\varphi }_{m}-{\alpha }_{G}^{p}{\gamma }^{p}\) curves in the figures and the curves can, for the present purpose, be considered as inputs to the model (\({\alpha }_{G}^{p}\) is a unitless parameter—may also be called normalized plastic modulus).

Fig. 10
figure 10

Accumulation of plastic volumetric strain (\(-{\varepsilon}_{v}^{p}\)) during cyclic mobilization of constant amplitude friction angle with plastic shear strain (γp)

Full size image
Fig. 11
figure 11

Accumulation of plastic volumetric strain (\(-{\varepsilon}_{v}^{p}\)) with plastic shear strain (γp) in one-sided oscillation of loading and unloading with a decreasing amplitude of the mobilized friction angle

Full size image
Fig. 12
figure 12

Accumulation of plastic volumetric strain (\({-{\varvec{\varepsilon}}}_{{\varvec{v}}}^{{\varvec{p}}}\)) during combined one-sided and two-sided loading-unloading mobilization of constant amplitude friction angle with plastic shear strain (γp)

Full size image
Fig. 13
figure 13

Accumulation of plastic volumetric strain (\(-{\varepsilon}_{v}^{p}\)) during small unloading-reloading steps superimposed on a varying amplitude sinusoidally cyclic mobilization of friction angle with plastic shear strain (γp)

Full size image

3.2 General stress–strain condition

In the previous section, we have derived stress–dilatancy relations and plastic potential functions considering axisymmetric and plane strain conditions. The resulting stress–dilatancy relations did not reflect the effect of intermediate stress state. Here, we will consider other stress invariants which are convenient for establishing stress–dilatancy relations and plastic potential function in the general stress space.

Considering Eq. (3) and assuming coaxiality between eigen directions of stresses and plastic strain increments, the plastic dissipation may be written as

$$D^{p} = \overline{p}\dot{\varepsilon }_{v}^{p} + s\cos (\theta_{\sigma } - \theta_{{\dot{\varepsilon }}}^{p} )q\dot{\varepsilon }_{q}^{p}$$
(56)

where \({\theta }_{\sigma }\) is the Lode angle of the effective stress tensor; \({\theta }_{\dot{\varepsilon }}^{p}\) is the Lode angle of the plastic strain increment tensor; \(s=1\) for loading in shear (mobilizing away from stress isotropy) and \(s=-1\) for unloading in shear (mobilizing towards stress isotropy) (in general \({s}_{l}{s}_{u}=-1)\).

Let \({M}_{\sigma }^{\theta }\) be the stress ratio mobilized for a given level of plastic deviatoric strain (iso-distortional plastic strain contours) and depend on the Lode angle (schematized in Fig. 14) and \({M}_{\psi }^{\theta }\) be the conjugate dilatancy ratio such that

$$q = M_{\sigma }^{\theta } \overline{p}\,{\text{and}}\,\dot{\varepsilon }_{v}^{p} = - M_{\psi }^{\theta } \dot{\varepsilon }_{q}^{p}$$
(57)
Fig. 14
figure 14

a Plots of a linear yield line for the intermediate shear mode in p-q plane, b iso-distortional plastic strain contours in \(\pi\)-plane, TC: triaxial compression, TE: triaxial extension, \({\theta}_{\sigma}\): Lode angle

Full size image

From Eqs. (56) and (57), the plastic dissipation can be written as

$$D^{p} = \overline{p}\dot{\varepsilon }_{q}^{p} \cos (\theta_{\sigma } - \theta_{{\dot{\varepsilon }}}^{p} )d_{M} ,$$
(58)

where

$$d_{M} = - \tilde{M}_{\psi }^{\theta } + \tilde{M}_{\sigma }^{\theta }$$
(59)

is a function that contains the stress–dilatancy conjugates, \({\widetilde{M}}_{\sigma }^{\theta }={M}_{\sigma }^{\theta }\) and \({\widetilde{M}}_{\psi }^{\theta }={M}_{\psi }^{\theta }/\mathrm{cos}\left({{\theta }_{\sigma }-\theta }_{\dot{\varepsilon }}^{p}\right)\).

Postulating the variation \(\delta {d}_{M}\) to vanish following the complementarity hypothesis [37] yields \({d}_{M}\) a constant, say \({d}_{M}={C}_{M}^{\theta }\). The stress–dilatancy relationship is therefore

$$\tilde{M}_{\psi }^{\theta } = \tilde{M}_{\sigma }^{\theta } - C_{M}^{\theta } ,$$
(60)

or

$$M_{\psi }^{\theta } = \cos (\theta_{\sigma } - \theta_{{\dot{\varepsilon }}}^{p} )\left( {sM_{\sigma }^{\theta } - C_{M}^{\theta } } \right).$$
(61)

\({C}_{M}^{\theta }\) may be evaluated at \({\dot{\varepsilon }}_{v}^{p}\approx {\dot{\varepsilon }}_{v}\to 0\), i.e., assuming elastic strain rates to be small. Equation (60) assumes that the sum of the stress ratio and its conjugate dilatancy ratio is a constant for a given mode of shear [23].

From Eqs. (58) and (61), the plastic dissipation is given by

$${\mathcal{D}}_{M}^{p} = \overline{p}C_{M}^{\theta } \cos (\theta_{\sigma } - \theta_{{\dot{\varepsilon }}}^{p} )\dot{\varepsilon }_{q}^{p} \ge 0,\,C_{M}^{\theta } \ge 0,$$
(62)

and when \({\theta }_{\sigma }={\theta }_{\dot{\varepsilon }}^{p}\) and \(a=0\), the original Cam clay [31, 36] plastic dissipation is recovered.

As pointed out earlier for the stress–dilatancy relationship in the axisymmetric and plane strain conditions, here too, unloading in shear, i.e., mobilizing towards isotropic stress condition, is necessarily contractive [37]. Let us see this more closely. Considering the stress–dilatancy relationship in Eq. (61). For the same, the plastic dissipation may be rewritten as

$${\mathcal{D}}_{M}^{p} = \overline{p}\dot{\varepsilon }_{v}^{p} \frac{{C_{M}^{\theta } }}{{C_{M}^{\theta } - sM_{\sigma }^{\theta } }}$$
(63)

For plastic unloading in shear, \(s=-1\) and \({C}_{M}^{\theta }>0\), \({C}_{M}^{\theta }-s{M}_{\sigma }^{\theta }>0\) is always valid. This implies that for nonnegative plastic dissipation \(p{\dot{\varepsilon }}_{v}^{p}\ge 0\) must be satisfied, where sign convention of soil mechanics applies and therefore \({\dot{\varepsilon }}_{v}^{p}\) must be positive (i.e., contractive).

Typical stress–strain results from cyclic undrained simple shear and triaxial compression-extension tests show a significant pore pressure generation during unloading in shear under undrained conditions and volumetric contraction during drained unloading in shear, Figs. 15, 16, and 17 for instance. This constraint may need to be relaxed should some anisotropic soil media are observed to behave dilative during unloading in shear. 

Fig. 15
figure 15

Plots of effective normal stress versus shear stress for cyclic undrained simple shear tests on Fraser Delta Sand of varying relative density [33]

Full size image
Fig. 16
figure 16

Plots of a stress ratio versus deviatoric strain and b void ratio versus stress ratio of a constant effective confining pressure (at p =196 kPa) unloading reloading drained triaxial compression test results on Toyoura Sand [20]

Full size image
Fig. 17
figure 17

Plots of a stress ratio versus deviatoric strain and b void ratio versus stress ratio of a constant effective confining pressure (at p =196 kPa) cyclic triaxial compression extension tests under drained conditions of Toyoura Sand [20]

Full size image

Let us find the plastic potential function assuming associated flow, i.e., \(\mathrm{d}\overline{p}{\dot{\varepsilon } }_{v}^{p}+\mathrm{cos}\left({\theta }_{\sigma }-{\theta }_{\dot{\epsilon }}^{p}\right)\mathrm{ d}q{\dot{\varepsilon }}_{q}^{p}=0\) and setting,

$$\frac{{M_{\psi }^{\theta } }}{{\cos (\theta_{\sigma } - \theta_{{\dot{\varepsilon }}}^{p} )}} = \frac{{{\text{d}}q}}{{{\text{d}}\overline{p}}} = \left( {s\frac{q}{{\overline{p}}} - C_{M}^{\theta } } \right),$$
(64)

where \(\overline{p} = p + a\).

This leads us to a plastic potential function (holding \({C}_{M}^{\theta } \mathrm{a constant})\)

$$f = q - sC_{M}^{\theta } \overline{p}\left( {1 - \ln \frac{{\overline{p}}}{{\overline{p}_{cs} }}} \right) = 0,$$
(65)

where \({p}_{cs}\) is the effective confining pressure at the critical state, i.e., the critical state is to remain on \(q=s{C}_{M}^{\theta }\overline{p }\) line. Note that when \(s=-1\), the critical state line is defined by an image deviatoric stress \(q\) which has a negative value. The plastic potential function in Eq. (65) is here called Generalized Cyclic State Dilatancy plastic potential function and is abbreviated GCStaD. Note that when \(a=0\) and \(s=1\), it reduces to just the original Cam clay yield function. The dilatancy ratio can now be obtained in the from

$$- \tilde{M}_{\psi }^{\theta } = - \frac{{{\text{d}}q}}{{{\text{d}}\overline{p}}} = sC_{M}^{\theta } ln\frac{{\overline{p}}}{{\overline{p}_{cs} }}.$$
(66)

Equation (65) implies that the plastic potential function contains cohesion component defined by attraction, \(a\), frictional component defined by \({C}_{M}^{\theta }\) and a dilatancy component defined by \({\widetilde{M}}_{\psi }^{\theta }\).

Suppose we define the point at which the plastic potential function defined by Eq. (65) intercepts the p-axis as an apparent pre-consolidation stress, \({p}_{c}\), the following relation holds:

$$\ln \overline{p}_{cs} = \ln \overline{p}_{c} - 1,$$
(67)

The plastic potential function can also be written in terms of \({\overline{p} }_{c}\) as

$$f = q + \overline{p}sC_{M}^{\theta } \ln \frac{{\overline{p}}}{{\overline{p}_{c} }} = 0$$
(68)

An interesting identity can be obtained considering the loading and the unloading potential pairs. Suppose a stress state whose loading and unloading plastic potential pairs are described, respectively, by the apparent pre-consolidation stresses \({p}_{cl}\) and \({p}_{cu}\). Then, the square of the shifted effective octahedral stress is the product of \({\overline{p} }_{cl}\) and \({\overline{p} }_{cu}\), i.e., \({\overline{p} }^{2}/{\overline{p} }_{cu}{\overline{p} }_{cl}=1\). Considering this identity, the plastic potential function for loading in shear, i.e., for \(s=1\), can be written as

$$f = q + C_{M}^{\theta }\sqrt {\overline{p}_{cu} \overline{p}_{cl} } \ln \sqrt {\frac{{\overline{p}_{cu} }}{{\overline{p}_{cl} }}} = 0.$$
(69)

\({C}_{M}^{\theta }\) may be given as

$$C_{M}^{\theta } = 6\ell_{\theta } \frac{{f_{sd} \sin \varphi_{c} }}{{3 - f_{sd} \sin \varphi_{c} }} \ge 0,$$
(70)

where \({\varphi }_{c}\) is the critical sate friction angle for triaxial compression condition, \({\mathcal{l}}_{\theta }\) is the Lode angle dependency function and \({f}_{sd}\) is an ad hoc density dependency function (given in Eq. (55) for instance.) For \({\mathcal{l}}_{\theta }=1\), \({C}_{M}^{\theta }\) defines the stress ratio for the triaxial compression condition according to the Mohr–Coulomb criterion. There are several Lode angle dependency functions that have frequently been applied in constitutive modelling of soils. For instance, Bardet [1] derived a Lode angle dependent function

$$\ell_{B}^{\theta } = \frac{\sqrt 3 \omega }{{2\sqrt {\omega^{2} - \omega + 1} }}\frac{1}{\cos \vartheta }$$
(71)

for the Matsuoka–Nakai criterion, where

$$\omega = \frac{{3 - f_{sd} \sin \varphi_{c} }}{{3 + f_{sd} \sin \varphi_{c} }},$$
(72)

and the angle \(\vartheta\) is here defined in terms of the Lode angle of the plastic strain increment tensor,\({\theta }_{\dot{\varepsilon }}^{p}\), as

$$\vartheta = \frac{\pi }{3}\langle {\text{sgn}} \theta_{{\dot{\varepsilon }}}^{p} \rangle - \frac{1}{6}{\text{sgn}} \theta_{{\dot{\varepsilon }}}^{p} \arccos \left( { - 1 + \frac{{27\omega^{2} (1 - \omega )^{2} }}{{2(\omega^{2} - \omega + 1)^{3} }}\sin^{2} 3\theta_{{\dot{\varepsilon }}}^{p} } \right){,}$$
(73)

in which \(\mathrm{sgn}{\theta }_{\dot{\varepsilon }}^{p}={\theta }_{\dot{\varepsilon }}^{p}/\left|{\theta }_{\dot{\varepsilon }}^{p}\right|, {\theta }_{\dot{\varepsilon }}^{p}\ne 0\), is -1 for \({\theta }_{\dot{\varepsilon }}^{p}\le 0\) and +1 for \({\theta }_{\dot{\varepsilon }}^{p}>0\) and \(\langle .\rangle\) is the Macaulay bracket with a property \(\langle a\rangle =a\) if \(a>0\) and \(\langle a\rangle =0\) if \(a\le 0\). For the case of proportional monotonic loading, the Lode angle of the effective stress and that of the Lode angle of the plastic strain increment may be set equal.

The solutions provided here are generalization of the original Cam clay yield function. One of the limitations constitutive modellers looked away from the original Cam clay yield function is the direction of plastic strain increments during isotropic compression. When the original Cam clay yield function is used as a plastic potential function, pure isotropic compression loading would lead to accumulation of deviatoric plastic strain increments which seems unphysical. A new insight is obtained with the consideration of unloading in shear. That is, it can be clearly seen that the loading and unloading curves of the same \({p}_{c}\) are intersecting along the isotropic axis and for any plastic compression along this axis both are equally likely. In other words, one direction is not any preferable than the other and uniqueness of the direction of plastic flow is lost for plastic deformation at this point. As we did for the axisymmetric and plane strain case, we may then consider Koiter's rule [18] and sum the plastic strain increments in both directions which then gives

$$\left( { - \frac{{{\text{d}}q}}{{{\text{d}}\overline{p}}}} \right)_{{\text{L}}} + \left( { - \frac{{{\text{d}}q}}{{{\text{d}}\overline{p}}}} \right)_{{\text{U}}} = C_{M}^{\theta } ln\frac{{\overline{p}_{c} }}{{\overline{p}_{cs} }} - C_{M}^{\theta } ln\frac{{\overline{p}_{c} }}{{\overline{p}_{cs} }} = 0,$$
(74)

for the plastic shear strain increment. While this consideration may remove one of the main limitations of the plastic potential function derived here, this does not fully address the limitation of the plastic dissipation for the case of plastic volumetric deformations under isotropic stress states, in which the model could accumulate plastic volumetric strain without any plastic dissipation. This may be tackled by introducing additional terms into the plastic dissipation such that it is a function of the plastic volumetric strain increment as well. This lies outside the objective of this paper.

Example plots of GCStaD plastic potential curves for loading in shear and unloading in shear for constant critical state friction angle and varying apparent pre-consolidation stress are presented in Fig. 18. Part of each curve that is produced beyond its respective apparent pre-consolidation stress is valid only for unloading in shear. Note here as well that the plastic potential is of fish form where unloading in shear is described by the tail and the rest is for loading in shear. For this model, the hardening function may conveniently be established in terms of the stress ratio, \({M}_{\sigma }^{\theta }\), instead of \(\mathrm{sin}{\varphi }_{m}\), but with the same characteristics as demonstrated in Figs. 10, 11, 12, and 13.

Fig. 18
figure 18

GCStaD plastic potential curves described by Equation (65). Considering the likeness of the geometric form with the fish curve, the tails (broken lines) are valid for unloading in shear and manifest when the stress state mobilizes towards isotropic stress state and CS is phase transformation /critical state line. Both the unloading and the loading plastic potential curves are continued to space defined by \(-{q}/{C}_{M}^{\theta}\)

Full size image

The theoretical framework laid out here can be utilized in the multilaminate framework with a plastic potential function given for each plane as

$$f_{i} = \tau_{i} + s_{i} \overline{\sigma }_{ni} \tan \varphi_{ci} \ln \frac{{\overline{\sigma }_{ni} }}{{\overline{p}_{ci} }} = 0,$$
(75)

where \(i\) is plane counter, \({\varphi }_{ci}\) and \({p}_{ci}\), respectively, are the critical state friction angle and the apparent pre-consolidation stress for the \(i\) th plane. In this case, the possible anisotropy of the critical state friction angle may be easily accommodated. In addition, \({f}_{sd}{\mathrm{tan}\varphi }_{ci}\) may be used in place of \({\mathrm{tan}\varphi }_{ci}\), where \({f}_{sd}\) is a carefully chosen ad hoc void ratio dependency function.

The theory can also be directly applied considering shear stresses and effective normal stresses on the Matsuoka–Nakai spatial mobilized plane. Such a consideration leads to a plastic potential function of the form:

$$f = \sqrt {\overline{I}_{1\sigma } \overline{I}_{2\sigma } \overline{I}_{3\sigma } - 9\overline{I}_{3\sigma }^{2} } + 2s\tan \varphi_{c} \overline{I}_{3\sigma } ln\left( {3\frac{{\overline{I}_{3\sigma } }}{{\overline{I}_{2\sigma } \overline{p}_{c} }}} \right) = 0,$$
(76)

which is here called GCStaD-MN, where \({I}_{1\sigma }\), \({I}_{2\sigma }\) and \({I}_{3\sigma }\) are the first, the second and the third stress invariants which are given in terms of the principal stresses, respectively, as \({\overline{I} }_{1\sigma }={\tilde{\sigma }}_{1}+{\tilde{\sigma }}_{2}+{\tilde{\sigma }}_{3}\), \({\overline{I} }_{2\sigma }={\tilde{\sigma }}_{1}{\tilde{\sigma }}_{2}+{\tilde{\sigma }}_{2}{\tilde{\sigma }}_{3}+{\tilde{\sigma }}_{3}{\tilde{\sigma }}_{1}\) and \({I}_{3\sigma }={\tilde{\sigma }}_{1}{\tilde{\sigma }}_{2}{\tilde{\sigma }}_{3}\), in which \({\tilde{\sigma }}_{i}={\sigma }_{i}+a\), \({\varphi }_{c}\) is the critical state friction angle, and as discussed above ad hoc void ratio dependency function, say \({f}_{sd}{\mathrm{tan}\varphi }_{c}\), may be used in place of \({\mathrm{tan}\varphi }_{c}\) for capturing density dependency of the friction angle at the phase transformation.

4 Summary and conclusions

Soils can be subjected to repetitive (cyclic) loads of varying magnitude which may affect their stiffness and load carrying capacity and further have consequences on the state of the structures they carry. The modelling of deformation behavior of soils subjected to repetitive (cyclic) loading conditions has therefore been a subject of continuous interest in the geotechnical engineering community. Theoretical frameworks that were regarded to hold good for the modelling of deformation behavior of soils subjected to monotonic loading need to be reconsidered and extended for the modelling of deformations under cyclic loading. The stress–dilatancy theory is one of them. Several advanced models do consider complex mathematical functions for describing the stress–dilatancy behavior of soils under cyclic loading conditions and succeeded to a degree, but many of them lack clarity and descriptiveness in their abstraction. The classical stress–dilatancy theories, such as Taylor's and Rowe's have the clarity in their abstraction and are endowed with descriptive power but consider only loading in shear and therefore they fall short for describing changes in volumetric strain of soil specimens subjected to loading-unloading in shear or cyclic shear. In this paper, a theoretical framework is put forward for establishing stress–dilatancy relations and shear-induced plastic dissipations in both loading in shear (mobilizing away from isotropic stress state) and unloading in shear (mobilizing towards isotropic stress state) while maintaining the simplicity and descriptiveness of the classical stress–dilatancy theories. The hypothesis of complementarity of stress–dilatancy conjugates proposed in this treatise proved useful for unifying and further extending Taylor's work hypothesis and Rowe's minimum energy ratio hypothesis. Then, cyclic stress–dilatancy relations and plastic potential functions are established first for axisymmetric and plane strain conditions and further for the general stress–strain conditions. In the latter, Lode angle dependency of shear strength of soils is considered. The theory is also applied considering shear mobilization in a multilaminate framework and further considering the Matsuoka–Nakai spatial mobilized plane.

In the framework, plastic dissipation is considered nonnegative in both loading and unloading in shear where loading in shear is defined as mobilizing away from isotropic stress condition and unloading in shear is defined as mobilizing towards isotropic stress condition. The resulting stress–dilatancy relations and plastic potential functions are shown to have the following properties.

  • The plastic potential curve that is produced beyond the apparent pre-consolidation stress and its image mirrored about the isotropic stress axis make a fish like shape and, in that, the tail that lies beyond the pre-consolidation stress is the part of the plastic potential curve that is realized during unloading in shear (moving towards stress isotropy) while the rest of the urve that is contained within the pre-consolidation stress is realized during loading in shear (moving away from stress isotropy).

  • While the plastic volumetric strain increments during loading in shear can be either contractive or dilative depending on the level of mobilization relative to the phase transformation stress ratio, the plastic strain increments during unloading in shear are contractive. This implies, for undrained conditions, plastic unloading in shear will generate pore pressures.

The cyclic stress–dilatancy relations are further enhanced by introducing a void ratio dependency function into the phase transformation stress ratio. For the same, the Gudehus–Bauer void ratio dependency function, which can further be linked to the Been and Jefferies state parameter, is considered. With this enhancement, while the stress ratio at the critical state is maintained unique for a given mode of shear,

  • Changes in the stress–dilatancy behavior and non-uniqueness of the stress ratio at the phase transformation with different initial void ratio and effective confining pressure of soil samples can be taken into account.

  • The amount of plastic volumetric contraction during application of cyclic shear is limited by the minimum void ratio contained in the Gudehus–Bauer void ratio dependency function. The introduction of minimum void ratio helps avoid accumulation of unrealistically high volumetric strain under application of several cycles of shear streses/ shear strain amplitudes.

The explicit consideration of both loading and unloading in shear extends the applicability of the framework in constitutive models that aim at the modelling of the deformation behavior of soils subjected to cyclic shear. The plastic potential functions derived in this paper, having similar geometric properties as that of the original Cam clay plastic potential function, would have given an unreasonable prediction of plastic shear strain increments under isotropic stress condition if unloading in shear were not considered. With the consideration of unloading in shear, it is proven that the plastic strain increments are purely volumetric when the stress state is purely isotropic. This takes the framework one step closer to accommodating loading and unloading under isotropic stress states which the writer wishes to follow up in more details in the future. The writer also wishes to follow up the current exposition with applications in examining soil stress states created by unloading in shear and extension of the theory to noncoaxial plastic flow and anisotropic conditions.