Improving binary diffing speed and accuracy using community detection and locality-sensitive hashing: an empirical study

Abstract

Binary diffing is a commonly used technique for detecting syntactic and semantic similarities and/or differences between two programs’ binary executables (not source code). Here we present REveal, a binary diffing application. REveal is based on the detection of Function Call Graph (FCG) approximate isomorphism and improves both speed and accuracy, mainly by the use of two techniques. First, we propose the use of hierarchical Community Detection (CD) in executables’ FCGs, for the purpose of detecting groups of densely connected functions, thus partitioning them in smaller groups. Moreover, we use Locality-Sensitive Hashing (LSH) for further grouping of similar functions in hash buckets. Both techniques are used in a divide-and-conquer fashion to simplify the diffing process of the programs being compared, practically reducing it to diffing of their FCG communities and LSH buckets.

1 Introduction

Binary diffing is a commonly used technique for detecting syntactic and semantic similarities or, equivalently, differences, between two programs’ binary executables, when access to their source code is not an option. In most real world applications, binary diffing involves using various reverse engineering techniques to recover information from the subject executables, representing the recovered knowledge as a series of labeled graphs and computing a form of bijection between the latter. Examples of such graphs include the Function Call Graph (FCG), the Control Flow Graph (CFG), the Program Dependence Graph (PDG) and others. The said bijection is usually some form of graph isomorphism and this often means computing the Maximum Common Subgraph or Multiple Common Subgraphs of the two compared graphs. Generally, the graph isomorphism problem belongs to the NP class and, consequently, related problems can only be solved approximately, by compromising precision in favor of acceptable running times.

A common technique, implemented in many binary diffing tools, including our prototype REveal, is approaching the problem of computing the Multiple Common Subgraphs of compared FCGs using function matching. In function matching, functions, that uniquely stand out based on their characteristics, are first matched, effectively creating an initial partial mapping of vertices between the compared graphs. Following that, functions “related to” already matched functions are compared and matched in an attempt to maximize the aforementioned mapping. This can be done (a) by using the recovered program structure (e.g by matching successors and predecessors in the FCG [14, 15, 17]) and/or (b) by exploiting the locality characteristics inherent in the program linking process performed by most compilers (e.g. by matching functions nearby in the program’s address space [28]). When no more new vertices can be matched, the process ends. In the literature, the former phase is usually referred to as the pre-filtering phase, while the latter as the propagation phase.

This paper presents two techniques for improving both the speed and accuracy of the overall binary diffing process as described in the previous paragraph. First, we propose the use of hierarchical Community Detection (CD) in executables’ FCGs, for the purpose of detecting groups of densely connected functions, thus partitioning them in smaller groups. Moreover, we propose the use of Locality-Sensitive Hashing (LSH) for further grouping of similar, in terms of features, functions in hash buckets. Effectively, CD and LSH can be seen as complementary forms of partitioning; the former groups functions with respect to how they relate to their neighbors, while the latter probabilistically groups functions based on a hashing scheme of their features’ values. In practice, this is equivalent to a 2-stage partitioning scheme where functions are divided into smaller groups by two mutually independent processes. Both techniques are used in a divide-and-conquer fashion to simplify the diffing process of the programs being compared, practically reducing it to diffing of their FCG communities and LSH buckets.

Overall, in this paper we make the following contributions:

• We present a fast and reliable hierarchical CD algorithm, based on Node Similarity-based Algorithm (NSA) [9] and Louvain [3, 16], for partitioning FCGs in non-overlapping clusters of densely-connected functions. To our knowledge, use of CD algorithms in binary diffing has not been previously studied.

• We examine further splitting of communities in hash buckets of similar, in terms of characteristics, functions using LSH and, more specifically, a form of minhashing. [4]

• Based on the previous constructs, we develop a divide-and-conquer algorithm for binary diffing, which results, not only in speed improvements, but also in increased matching precision. We prove this by comparing our algorithms, implemented in REveal, against other binary diffing tools of the public domain, namely Diaphora and YaDiff, as well as an older version of REveal [28].

The rest of this paper is organized as follows. Section 2 gives an overview of previous work in the fields of binary diffing, CD as well as LSH. Preliminaries on graph theory and the notations used in this paper are given in Sect. 3. Section 4 presents the overall proposed CD and LSH based binary diffing algorithm, while Sect. 5 delves into its CD aspects and Sect. 6 elaborates on its LSH implementation. Last but not least, in Sect. 7 we evaluate our algorithm against those implemented in other tools and we conclude in Sect. 8 with a summary of current work and an overview of future research directions.

2 Previous work

When two graphs are similar, it is highly likely that their community structure will be similar as well. Based on this simple observation, many graph theoretical problems can be approached as follows:

• 1. decompose the subject graph in smaller, but more compact, structures,

• 2. look for local solutions in the decomposed components,

• 3. form a global solution by combining local solutions.

This divide-and-conquer methodology has been successfully applied to many graph problems including (relevantly to our problem) the approximate graph isomorphism problem [1, 24, 32]. Even though community detection has been extensively used for tasks like knowledge extraction and graph classification, in various scientific domains, little has been done on computing the Maximum Common Subgraph of two graphs.

The idea of comparing two networks, by gradually compressing them in more compact representations, is presented at [42]. Using spatial clustering, cluster alignment using Earth Moving Distance (EMD) and Graph Convolutional Networks (GCNs), the authors essentially perform hierarchical community detection, based on label propagation, and matching of communities between the compared graphs. The Hierarchical Graph Matching Network (HGMN), as it is termed, can be used on any network, including CFGs and FCGs recovered from binary executables, as long as each vertex in the network can be abstractly represented by a feature vector (otherwise a feature vector of all-ones can be used). The effectiveness of HGMN is showcased in a series of experiments, where it is proven that it outperforms other graph-theoretic, as well as learning-based, approaches both in accuracy and efficiency.

Surprisingly, public literature on hierarchical graph isomorphism is very limited, with most research focused on graph classification. For example, seminal work on malware clustering is presented at [31]. First, the authors define cost functions for primitive graph edit operations and propose the use of GED for computing the similarity between two FCGs. Two major clustering algorithms are evaluated, namely k-medoids and DBSCAN. The authors conclude that DBSCAN is more promising for the task of partitioning malware samples or, equivalently, their FCGs into a set of an unknown number of clusters.

In [30], authors classify Android malware applications in clusters using DBSCAN. When a new malware sample is received, 4-tuples, holding structural information of methods, are first extracted. The 4-tuples of the new sample are matched with those of the representative mean of each cluster. A similarity score is computed as the ratio of matched methods over the total number of methods and the sample is added in the cluster with the highest matching score.

Community detection in FCGs is demonstrated in [37]. The authors investigate the potential of extracting cohesion information on classes of object-oriented programs based on method communities recovered using a variety of algorithms including Louvain. Despite the fact that [37] is focused on computing software quality metrics, its conclusions might as well be applied for binary diffing purposes, especially when type information is available in the binary executables under comparison.

Yet another interesting technique of detecting components in binary code is presented in [29]. The authors construct a Decomposition Graph which is, in fact, the union of three other graphs, namely the Sequence Graph (SG), the Data Reference Graph (DRG) and the FCG. Newman’s community detection algorithm with modularity optimization is used to recover the resulting graph’s community structure in a hierarchical approach.

LSH was first introduced in [25]. This paper discusses the problem of nearest neighbor search and proposes LSH as a means of dealing with the Curse of Dimensionality (i.e., the fact that as the number of dimensions of the input space grows, nearest neighbor search algorithms become less and less efficient, to the point where they do no better than brute-force linear search). The techniques in [25] have a query time complexity of $\mathcal {O}(dn^{\frac{1}{\epsilon }})$ (where n is the number of points, and d the dimensionality). This was later improved by Gionis et al. [22] resulting in a query time of $\mathcal {O}(dn^{\frac{1}{\epsilon + 1}})$.

More recently, LSH was used for binary diffing purposes in [35]. Basic blocks are first represented as a bag-of-words and converted to a large vector whose length is equal to the length of the alphabet (i.e., the number of instruction types of a given computer architecture). Each element in the aforementioned vector holds the number of occurrences of the corresponding instruction. Then, an arbitrary number of random hyperplanes of the same dimensionality are created. For each basic block, the angle it forms with each of the aforementioned hyperplanes is computed and the sign of the cosine of the angle is saved as a single bit (e.g. 0 means negative cosine, 1 positive). The concatenation of these bits, is effectively a hash of a basic block, which is used to group similar blocks and speed-up the nearest-neighbor search.

Binary diffing [14, 15, 17] is actively used, by researchers in various scientific domains, for tasks like malware classification [6, 7, 23], patch analysis [26], plagiarism detection [33], propagation of profiling information [40] and others. Various high quality tools for performing binary diffing tasks can be found in the public domain with [2, 11, 43] being some of them. An interesting summary of the capabilities of many modern binary diffing solutions is given in [12]. In this paper we extend REveal [27, 28], our prototype tool which is being actively developed and tested.

3 Preliminaries

In the following sections we use uppercase letters to represent sets, and lowercase letters to represent primitive objects. Furthermore, we use the notation ${\left\lceil {x}\right\rceil }_P$ to indicate that x is rounded up to the nearest prime number.

3.1 Graph theory

We represent digraphs (i.e., directed graphs) with the notation $G = \big \langle V, E \big \rangle$, where V (or V(G)) is the digraph’s vertex set and $E \subseteq V \times V$ (or E(G)) is the digraph’s edge set. In what follows we will usually say, for brevity, graph when we actually mean digraph. Given a vertex $v \in V$, we define the set of successors of v as $succ(v) = \{s \mid (v,\ s) \in E\}$ and the set of predecessors of v as $pred(v) = \{p \mid (p,\ v) \in E\}$. The set of all neighbors of v is represented as $neigh(v) = succ(v) \cup pred(v)$.

We assume that, succ(v), pred(v) and neigh(v) hold the corresponding vertex sets ordered by an arbitrary total ordering relation defined over V i.e., if $succ(v) = \{s_0, s_1, ..., s_{n-1}\}$, for some $v \in V$, then $r(s_0) \le r(s_1) \le ... \le r(s_{n-1})$, where $r : V \rightarrow \mathbb {R}$ is a sorting function defined over the vertex set, that returns vertex ordinals; numbers via which the aforementioned total ordering is achieved. If, for a given sorting function r, $r(s_0)< r(s_1)< ... < r(s_{n-1})$ holds, then r is said to be strict. Notice that from the previous definition, it follows that $r(s_i) \ne r(s_j)\ \forall \ i,\ j$ and $i \ne j$, that is, no two vertices should have the same ordinal number. Ordinals can be assigned to vertices in an application-specific manner.

We allow vertices and edges of a graph to carry attributes which can take arbitrary values. We use the notation v.attr to refer to the value of attribute attr of vertex v and (u, v).attr to refer to the attribute of edge (u, v).

For each graph G, we define a feature function $f: V \rightarrow \mathbb {R}^d$ mapping each vertex of G to a feature vector of dimension d. Feature vectors are assumed to hold the characteristics of the objects represented by the corresponding vertices. When domain-specific features are not available, simple centrality metrics might be used (e.g. a feature vector of one element holding the vertex’s degree). Similarly, we define the inverse of f, $f^{-1}: \mathbb {R}^d \rightarrow \mathcal {P}(V)$, which returns the set of all vertices of G that are characterized by a given feature vector.

Given a graph $G = \big \langle V, E \big \rangle$, we can partition vertices of G in non-overlapping communities $C_i \subseteq V$, $0 \le i < N_C$, where $N_C$ is the number of communities and $C_i \cap C_j = \varnothing ,\ \forall \ i,\ j$ with $i \ne j$. The process via which communities are detected is referred to as Community Detection (CD). Furthermore, we can define the Community Graph (CG) to be a graph whose set of vertices is $V = \{C_i \mid 0 \le i < N_C\}$ and there is an edge from $C_i$ to $C_j$ iff $\{succ(v)\ \mid \ v \in C_i\}\ \cap \ \{pred(v)\ \mid \ v \in C_j\}\ \ne \ \varnothing$ (i.e., there’s at least one edge in G from a vertex in $C_i$ to a vertex in $C_j$ and this holds for $i = j$ as well). Hierarchical CD algorithms repeat the same process on the resulting CG, thus producing another, higher level CG where vertices represent communities of communities. This process can be repeated $N_L$ times, to generate a set of communities $C_{li}$, where $0 \le l < N_L$ is the level index and i the index of a community in that level. In this case $N_L$ CGs can be computed, one for each level. Notice that, usually, levels have different number of communities. More specifically, the higher the level, the less the number of communities, otherwise hierarchical community detection would make no sense.

3.2 Program representations

We define a program P to be a set of $N_F$ functions $P = \{F_i \mid 0 \le i < N_F\}$, a function F to be a set of $N_B$ basic blocks (straight-line machine code sequences with no branches in, except to the entry, and no branches out, except at the exit) $F = \{B_i \mid 0 \le i < N_B\}$ and a basic block B to be a set of $N_I$ instructions $B = \{I_i \mid 0 \le i < N_I\}$. Binary diffing involves comparing two programs, namely $P_1$, the primary subject, and $P_2$, the secondary subject, and forming a 1-1 mapping M, that corresponds functions of $P_1$ to functions of $P_2$, $M = \{F_1 \rightarrow F_2 \mid F_1 \in P_1,\ F_2 \in P_2\}$. Similar mappings can be further created for function basic blocks and instructions, depending on the required level of detail.

For each function F, in a program P, we define a digraph $CFG = \big \langle V,\ E \big \rangle$, where V is the set of F’s basic blocks, while the set of edges E denotes the possible execution flow paths between the function’s basic blocks. If $e = (B_i,\ B_j) \in E$, then control flow can reach basic block $B_j$ immediately after $B_i$ (i.e., $B_j \in succ(B_i)$). Digraph CFG is usually referred to as F’s Control Flow Graph (CFG).¹

A program P can also be treated as a digraph of program functions, referred to as the program’s Function Call Graph (FCG). FCG of program P is a digraph whose vertices correspond to individual functions (or, equivalently of function CFGs), that is $V = \{F \mid F \in P\}$. For each control transfer instruction in basic block $B_k \in F_i$, that transfers execution to basic block $B_l \in F_j$ (this also covers the case of $F_i = F_j$), an edge $(F_i,\ F_j)$ exists in E. Multiple such edges $(F_i,\ F_j)$ can be replaced with a single weighted edge with a weight equal to the number of calls from $F_i$ to $F_j$.

As uniquely identifying vertices by centrality measures is generally not possible, a common ordering of vertices in program related graphs (like FCGs and CFGs) can be based on the address, in program memory, of the structure represented by each vertex (like functions or basic block accordingly). That is r, defined in the previous section, is $r_{address}: V \rightarrow \mathbb {N}$, where $r_{address}(v)$ is a function that returns the address of vertex v in program memory. For CGs, an address can be assigned to each vertex based on the minimum or the maximum address of the elements contained in each community.

Furthermore, we define a dataset as $D = \big \langle G,\ S,\ r,\ f \big \rangle$, where G is a CG (i.e., community graph) or FCG, $S \subseteq V(G)$, r a sorting function defined over V(S) and f the feature function of G. Generally, the presented algorithms process functions of P in datasets using various strategies. For example, given a function $F \in P$, a dataset can be constructed consisting of P’s FCG, $S = neigh(F)$, $r_{address}$ and the FCG’s feature function. When G is a FCG, the corresponding dataset is referred to as a function dataset, in the opposite case it is termed a community dataset.

Last but not least, for a previous discussion on feature selection for vertices of a FCG the reader is referred to [27, 28] and [39].

3.3 Locality sensitive hashing

Locality Sensitive Hashing (LSH) is a process by which similar inputs are hashed to the same bucket. Unlike normal cryptographic hash functions, that need to minimize the number of hash collisions, LSH functions attempt to maximize them for inputs which are “close to each other” in a given metric space $\mathcal {M}$. More specifically, given two points $p,\ q \in \mathcal {M}$ and a LSH function $h: \mathcal {M} \rightarrow \mathbb {N}$, mapping points in $\mathcal {M}$ to hash bucket indexes, the following should hold:

• 1. If $d(p, q) < R$, then $h(p) = h(q)$ with probability at least $p_1$

• 2. If $d(p, q) \ge cR$, then $h(p) = h(q)$ with probability no more than $p_2 \ll p_1$

In the above relations, R is a distance threshold, below which points are considered to be “close by”, while $c > 1$ is the approximation factor. The first relation indicates that, when p and q are nearby, according to a distance function d defined on $\mathcal {M}$’s points, then they should hash to the same bucket with probability at least $p_1$. The second relation represents the case of a hash collision for inputs which are not nearby. Obviously, for the LSH function h to be meaningful, $p_1$ must be much higher than $p_2$, so that hashing dissimilar objects in the same bucket is less probable than the opposite case.

Among its many applications, LSH is commonly used for solving the k-nearest neighbor problem. A family of L LSH functions $H = \{h_i \mid 0 \le i < L\}$ (e.g. minhashing [4], based on min-wise independent permutations, or simhashing [8], based on random projections) is first constructed. Inputs are hashed using all such functions and eventually are split up in buckets. Given an input query point q, its k-nearest neighbors can be found by hashing q using all hash functions in H and looking for neighbors in the resulting L buckets. Search stops when k candidates have been found, or k “best” points have been drawn from the overall result set.

4 A community-based function matching algorithm

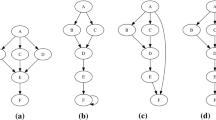
We begin by giving a high level overview of the overall matching process, carried out by REveal, in Algorithm 1 and a call-graph of the most essential procedures, presented in this paper, in Fig. 1.

Before proceeding to a detailed description of the above blocks (in separate subsections), let us give a brief overview of the workflow described in Fig. 1.

• At the top of the diagram we have match_programs which, upon conclusion, will return the mapping MF of functions of program $P_1$ to functions of program $P_2$. This function calls match_comms and match_funcs.

• match_comms is called first to detect the community structure of programs $P_1$ and $P_2$, effectively aggregating functions into groups (i.e. communities). It returns a mapping MC of communities of program $P_1$ to communities of program $P_2$.

• Given MC, populated by match_comms, match_funcs begins the actual function matching process. It basically executes consecutive rounds of exact and inexact matching of functions within the matched communities (in MC) until no more new matches can be found.

• match_funcs_in_comms is the actual workhorse used by match_funcs. It is able to perform rounds of exact and inexact function matching by utilizing the information in MC. A boolean argument passed to match_funcs_in_comms determines whether exact or inexact matching will take place.

• match, called by match_comms and match_funcs_in_comms, matches datasets (as defined in Sect. 3.2), in an abstract manner. It expects two datasets as inputs and uses the data features to match dataset elements. It does not distinguish between community datasets and function datasets, as the underlying matching strategies and algorithms are the same. It keeps applying various matching strategies (described below) until new matches cannot be found.

• Blocks named *_matcher implement the actual matching strategies as described in [28]. Matching strategies are, practically, ways of constructing “smaller” datasets of related functions, so that those smaller datasets can be matched for speed and efficiency purposes. For example, structural_matcher will construct temporary datasets, consisting of neighbors of already matched functions, and will attempt to match these to expand MF with new entries.

• match_datasets takes these smaller datasets, generated by the abovementioned blocks, and calls match_datasets_inexact or match_datasets_exact to actually populate a mapping with new entries. The said mapping can either be MC or MF since, as it was previously mentioned, the same abstract algorithms are used for both community and function matching.

Before proceeding, it is also useful to detail the ways in which the current implementation of REveal improves upon the previous one [27, 28]. Briefly, the new version of REveal:

• Implements community detection and matching using the algorithms presented in Sect. 5.

• Performs inexact matching, in addition to exact implemented in the previous version.

• Increases matching speed using LSH (Sect. 6).

We continue by elaborating on the various functional blocks of Fig. 1.

Fig. 1

Call-graph of most essential algorithms presented in this paper

4.1 Algorithm 1: match_programs

Algorithm 1 expects the two programs under comparison, namely $P_1$ and $P_2$, to be given as inputs. The output of Algorithm 1 is the set MF (stands for Matched Functions), with elements of the form $F_1 \rightarrow F_2$, mapping function $F_1$ of $P_1$ to function $F_2$ of $P_2$.

Given input programs $P_1$ and $P_2$, match_programs begins by constructing the corresponding datasets $D_1$ and $D_2$ at lines 2 and 3. These datasets hold the two programs’ FCGs, while the sorting functions are set to $r_{address}$ and the feature functions, $f_{P1}$ and $f_{P2}$, return program function features (e.g. [27, 28, 39]) of $P_1$ and $P_2$ respectively. The algorithm continues by detecting and matching communities in the programs’ FCGs, by means of match_comms (line 4), and proceeds by using the recovered community structure, in MC (stands for Matched Communities), in order to match program functions via match_funcs (line 5). Algorithm 1 terminates by returning MF.

4.2 Algorithm 2: match_comms

Algorithm 2, begins by initializing MC to an empty list (line 2). More specifically, MC is a list of sets, with the set at index i holding elements of the form $C_1 \rightarrow C_2$, where $C_1 \subseteq P_1$ and $C_2 \subseteq P_2$, representing matched communities at level $num\_levels - 1 - i$ of the community hierarchy of the compared programs. The community hierarchies themselves are recovered at lines 3–4, using techniques and algorithms presented in Sect. 5, and implemented by detect_comms. The aforementioned function returns a list of community datasets, with the i-th set holding information on the community structure at level i in the corresponding program’s community hierarchy. The higher the value of i the bigger (i.e. more abstract) the communities. For example, assuming P1 consists of a 2-level community hierarchy, $CD_{1,0}$ represents communities of functions, while $CD_{1,1}$ communities consisting of $CD_{1,0}$’s communities. Evidently, the process of community detection is repeated for both programs and the results are stored in $CD_1$ and $CD_2$ for the first and second programs respectively.

With a $N_{L1}$-level community hierarchy having been recovered from $P_1$ and a $N_{L2}$-level from $P_2$, a process of matching the communities in each level begins, with only $min(N_{L1}, N_{L2})$ (line 5) levels actually being considered. The process of matching communities is carried out level by level starting from higher ones (i.e. larger, more abstract communities) to lower ones (i.e. smaller, more concrete communities). Notice how the following loop iterates from 1 to $num\_levels$ (line 6), but indices in $CD_{1,-i}$ and $CD_{2,-i}$ are negative signifying reverse element access (i.e. $-1$ is the last set, $-2$ the second to last etc.). In each iteration a new empty set $MC_i$ is initialized (line 7) and match (defined later on) is invoked to match communities in the community datasets. A round of exact matching (last argument of match is false) follows a round of inexact matching (last argument of match set to true) and the whole process repeats until no more communities can be matched (lines 8–17). In each iteration $MC_i$ is appended in MC (line 18). Ultimately, MC is returned (line 20) for use by match_funcs.

4.3 Algorithm 3: match_funcs

The entry point to function matching can be seen in Algorithm 3. The two function datasets $D_1$ and $D_2$, as well as the matched community hierarchy information in MC, returned by match_comms, are expected as inputs. MF, is a set that holds matched function pairs and is initially set to the empty set (line 2), while the loop, at lines 4–12, repeatedly appends new entries in it. At the core of the aforementioned loop, match_funcs_in_comms (defined later on) is called twice at lines 6 and 9. The last argument determines the type of function matching round that will take place; false means exact matching, while true inexact. In essence, once no more functions can be matched exactly, inexact matches are looked up and if that generates new findings, the exact matching round needs to be repeated. When the loop breaks, MF is returned (line 13).

4.4 Algorithm 4: match_funcs_in_comms

Algorithm 4, which is at the heart of our divide-and-conquer approach, expects 5 input parameters; two function datasets $D_1$ and $D_2$, the set of sets of matched communities, as returned by match_comms (defined previously), an initially empty set of matched functions MF and a boolean argument $is\_inexact$, whose value determines whether the current matching round will be an exact or inexact one. The main logic of Algorithm 4 is implemented in two nested loops at lines 6–14 and 7–13. The outer loop iterates over all sets of matched communities (one for each level in the community hierarchy). The inner loop iterates over all matched communities of each such set. Given a valid match $C_1 \rightarrow C_2$, two new function datasets $D_1'$ and $D_2'$ are created. The vertex subsets, in these datasets, are set to the functions contained in $C_1$ and $C_2$ respectively, effectively forming a smaller set of potential match candidates. It’s essential to note that, since the outer loop, at lines 6–14, iterates through all community levels, all but the last level hold communities of communities. In this case, $\{F \mid F \in C \}$ practically means “all functions which belong to communities of community C transitively”. The new, smaller datasets are passed to function match, which populates MF with matched function pairs of the form $F_1 \rightarrow F_2$, where $F_1 \in C_1$ (and, of course, $F_1 \in P_1$) and $F_2 \in C_2$ (and $F_2 \in P_2$). Once all community levels have been handled, a final attempt to match functions in $D_1$ and $D_2$ is made at line 15. Note that $D_1$ and $D_2$ are the initial function datasets and that this step accounts for any potential discrepancies in the way communities were recovered, by giving a chance to functions, erroneously identified as belonging to different communities, to be matched if they are the same (exact matching case) or similar (inexact matching case). A third, outmost loop, at lines 4–18, guarantees that the overall process repeats as long as new findings are detected. Finally the total number of additional matched function pairs, appended in MF, is returned at line 19.

4.5 Algorithm 5: match

The pseudocode for method match is given in Algorithm 5. It is comprised of an outer loop (lines 4–15) that executes as long as singleton_matcher, structural_matcher or monotonic_matcher return an integer greater than 0. For brevity, the pseudocode and semantics of the three aforementioned methods are omitted (for more information readers are referred to [28]).

5 Community detection

5.1 Introductory remarks

Before we present in more detail the components of Algorithm 2 (match_comms), let us briefly discuss the community detection problem.

An important aspect of graphs is their community structure which can be recovered by vertex clustering. By this we mean the separation of vertices into clusters, with many edges joining vertices of the same cluster and comparatively few edges joining vertices of different clusters. The community detection problem is not well posed, because there are many possible definitions of cluster (i.e., community) and choosing a particular definition is to some degree arbitrary. Hence many different approaches appear in the related literature [19, 20]. However it is worth noting that intuitively, we can recognize that many real-life graphs do exhibit community structure. That is, while detecting groups of densely-connected or related vertices may indeed be possible by visual inspection, no universal algorithm is currently known to reliably do this.

Choosing a community detection algorithm for graph analysis applications is a task that requires many parameters to be taken into account. Apart from an algorithm’s ability to detect high quality communities, its capability to handle large networks, possibly with millions of vertices, and the memory footprint, execution time is also an essential aspect and a major criterion for making the final choice. One of the most popular community detection algorithms, is the Louvain algorithm [3, 16], characterized by its capability to handle very large graphs with reasonable time and memory requirements. Hence we have decided to use this algorithm as a core component of our REveal algorithm, the reference implementation presented in this paper.

Despite its good performance, it is well known that the Louvain community detection algorithm suffers from some weaknesses. To begin with, according to [38], a vertex acting as a “bridge” between two groups of vertices in a community, may, for modularity optimization purposes, be moved in a different community, resulting in the former being disconnected. Iteratively applying Louvain may further worsen the problem. Furthermore, being a Local Modularity Optimization (LMO) algorithm, the Louvain algorithm may fail to discover small communities due to the resolution limit problem, described by Fortunato and Barthelemy [18]. To highlight another weakness of the Louvain algorithm consider the following: given two versions of the same program, community detection in their FCGs can be thought of as the problem of detecting communities in a dynamic graph$^{1}$. In this case, due to its inherent randomness, the Louvain algorithm produces unstable partitionings, for t and $t+1$, and is thus unsuitable for this purpose. This “instability” problem is further explored in [10].²

Due to the aforementioned problems, in certain applications ([21, 34]), the Louvain algorithm is only used to improve the modularity of an existing partitioning, instead of generating one from scratch. That is, in the first iteration of the Louvain algorithm, graph vertices are already grouped in a set of preliminary initial communities, possibly produced by other means, as opposed to forming singleton communities. Then, Louvain is applied to fine-tune the initial partitioning. In [34], for example, the authors present a divisive community detection algorithm, referred to as MILPA, which uses the Louvain algorithm in such a post-processing fashion.

Following this approach, we propose the use of a Label Propagation Algorithm (LPA), for the purpose of computing an initial set of communities on a given FCG, followed by an application of the Louvain algorithm for improving the aforementioned community structure’s modularity score. The LPA algorithm used is a modified and trimmed down version of Node Similarity-based Algorithm (NSA) described by Cheng et al [9]. The process is repeated as long as the number of detected communities changes. Our final community detection algorithm is summarized in Algorithm 6. As it will become apparent in the following sections, to “stabilize” the partitionings produced, the community detection algorithms were modified to introduce determinism in the overall process.

Let us now discuss, in separate subsections, the algorithms invoked by Algorithm 2 (match_comms).

5.2 Algorithm 6: detect_comms

Algorithm 6 expects a function dataset D as input, recovers the community hierarchy of D’s FCG and, finally, computes and returns a list of community datasets (one element per level of the community hierarchy). detect_comms begins by initializing CD (i.e. community datasets) to the empty list (line 2). CD is a list of sets, with the i-th element holding the community dataset at level i of the program’s community hierarchy. Procedures compute_vertex_ranks (line 4) and compute_edge_ranks (line 5) are, then, called to assign vertex and edge ranks respectively to the FCG. The input dataset D, which holds the program FCG, is then converted to a new dataset (line 6) where FCG vertices are ordered by sorting function $r_{rank}$, which in turn sorts graph vertices according to the ranks assigned previously. The concept and rationale behind vertex ranking is further analyzed in Sect. 5.3. In this context, vertex ranking effectively results in functions, that process datasets that use $r_{rank}$, accessing vertices of the dataset’s graph in order of increasing rank (e.g. in succ(v), pred(v) or neigh(v) for a $v \in V(G)$).

Community hierarchy recovery is an iterative process (lines 8–17) which is repeated as long as the number of detected communities changes between levels. In each iteration, the modified NSA algorithm (detect_initial_comms, line 9) is applied on the current dataset $CD_{i-1}$ (with $D_0$ being a function dataset holding the FCG, sorted using $r_{rank}$). The result is a set of communities, which is given as input to the directed Louvain algorithm [16] (improve_comms, line 10). The latter’s task is to improve the quality of the partitioning, using local modularity optimization heuristics. Next, the induced graph of communities is computed (line 12). In this graph, vertices correspond to $G_{i-1}$’s communities and edges connect communities of neighboring vertices. More specifically, given $G_{i-1}$ and its decomposition into communities $C_i$, compute_induced_graph constructs a new graph $G_i$ with the following characteristics;

• 1. $V(G_i)$ is the set of communities of $G_{i-1}$; $V(G_i) = \{C_0,\ C_1,\ ...\ C_{N_C}\}$

• 2. $C_i.rank = \sum _{v \in C_i}{v.rank}$ where $v \in V(G_{i-1})$, that is, vertex ranks of $G_i$ are computed by summing the ranks of vertices in the corresponding community.

• 3. Edge ranks in the new graph are computed as the sum of the ranks of the original graph’s edges as follows: $(C_i, C_j).rank = \sum _{u \in C_i,\ v \in C_j,\ (u,v) \in E(G_{i-1})}{(u, v).rank}$.

Last but not least, in each iteration, a new community dataset is created, to hold the results of the current partitioning (line 13) and is appended in the list of community datasets (line 17).

5.3 Vertex and edge ranking

The results produced by many agglomerative community detection algorithms, including [9], as well as [3], depend on the order that graph vertices are traversed. More specifically, in [3] the authors claim that preliminary results on several test cases seem to indicate that the ordering of the vertices does not have a significant influence on the modularity that is obtained. However, traversal order may impact performance, and more importantly, the structure of the communities produced as output. In [9] the authors traverse graph vertices in order of decreasing degree. Ties are broken by choosing an arbitrary vertex from a set of vertices with the same degree. Consequently, applying the algorithm twice, even on the same graph, might produce two different results.

For graph comparison purposes, the communities of the compared graphs, detected by whatever algorithm is used for that purpose, should be as similar as possible. Unlike other scientific domains, where detected communities are more valuable when community vertices are semantically related, for graph isomorphism related problems, communities do not have to make sense, as long as the community structures, recovered from the binaries under comparison, are as identical as possible. In an attempt to minimize the effect of randomness in community detection algorithms, a high quality ordering of graph vertices should be adopted.

Ideally the corresponding sorting function should be strict, but this is not easy in practice. Given two programs $P_1$ and $P_2$, one needs to find a sorting function r, defined over $F_1 \cup F_2$, such that $r(F_1) = r(F_2)$, with $F_1 \in P_1$ and $F_2 \in P_2$, whenever $F_1$ and $F_2$ are the same function. This however has many problems in practice. First and foremost, it might be the case that $F_1$ and $F_2$ are byte-by-byte equal but are not the same function (e.g. this is quite common in binary code that makes extensive use of C++ templates). Furthermore, finding such an r requires that all mappings $F_1 \rightarrow F_2$ are known in advance, which is impossible, as this is the problem we are asked to solve in the first place. Consequently, only approximations can be made, that is we need a sorting function r that produces $r(F_1) = r(F_2)$ with a high probability if $F_1$ and $F_2$ are equal.

5.3.1 Algorithms 7–9: compute_vertex_ranks and associated algorithms

Our sorting function r is based on the notion of vertex ranks. Vertex ranks are integer values, and more specifically prime numbers, assigned to vertices of the program FCG by compute_vertex_ranks, shown in Algorithm 7.

Given a function dataset, Algorithm 7 computes initial rank values for each function in the dataset’s FCG (lines 3–5) and then executes 16 Weisfeiler–Lehman [41] rounds (lines 6–18) to obtain a high quality coloring based on these ranks (16 was chosen empirically, so that each vertex’ color is affected by that of neighbors at most 16 “steps” away). Ranks are, in fact, stored as vertex attributes and their initial value is set to the quantity returned by $r_{inf}$ (defined later on) rounded up to the next prime number. Each Weisfeiler–Lehman round (lines 7–13) computes the new rank of each vertex based on the ranks of its neighbors, using plain integer product, which is guaranteed to be unique for vertices that have similarly ranked neighbors. The new rank value is stored in attribute $rank'$ and eventually replaces attribute rank (lines 14–17) after being rounded up to the next prime number. Once all 16 iterations have completed, Algorithm 7 returns and rank attributes hold a high quality coloring of the FCG vertices. An interesting observation is that the for loops at lines 3–5, 7–13 and 14–17 traverse the set of graph vertices in order of increasing address. Indeed, dataset D passed to compute_vertex_ranks in Algorithm 6 uses $r_{address}$ as a sorting function. Even though this fact alone is not pivotal for the results produced by Algorithm 7, it is essential for understanding the notion of datasets and sorting functions.

Initial vertex ranks in Algorithm 7 are computed by rounding the return value of $r_{inf}$ to the next prime integer. Algorithm 8 shows how $r_{inf}$ is actually implemented. The input to Algorithm 8 is a vertex of either a FCG or CG. The if condition, at lines 3–13, distinguishes between the two aforementioned cases; if v is a function (i.e. a vertex in a FCG), the return value is computed by summing $\log {p_{instruction}}$ for each instruction in the function’s body (lines 4–8). Quantity $\log {p_{instruction}}$ is, in fact, the Shannon information content of an instruction computed on the random variable $X = P_1 \cup P_2$ i.e. the logarithm of the probability of occurrence of each instruction in the union of instructions of the programs under comparison which, practically, highlights functions that are composed of “rare” instructions. Returning back to the if clause, if v is a community of functions (or a community of communities), $r_{inf}$ is called recursively for each element (lines 10–13). Finally, the computed value r is returned at line 14.

Finally, $r_{rank}$, the sorting function used in Algorithm 6, can be seen in Algorithm 9. Since vertex ranks, assigned by compute_vertex_ranks, are stored as vertex attributes, $r_{rank}$ returns that attribute value. This, effectively, means that, functions that process datasets, whose sorting function is set to $r_{rank}$, traverse graph vertices in increasing vertex ranks. This is especially true for functions detect_initial_comms and improve_comms used by Algorithm 6.

5.3.2 Algorithm 10: compute_edge_ranks

Once vertex ranks have been determined, compute_edge_ranks of Algorithm 10 is used to compute edge ranks. First, the PageRank [36] algorithm is used, at line 3, to compute initial rank values. We assume these values are stored in an attribute named pagerank of each edge of G. Then, at line 6, the rank of each edge (u, v) is set to a linear combination of the ranks of u and v, with the coefficients being the pagerank values of u and v respectively.

5.4 Algorithm 11: detect_initial_comms

Algorithm 11 shows the pseudocode for detect_initial_comms, our modified NSA community detection procedure. Recall that NSA is used to detect initial communities in each iteration of Algorithm 6.

For each vertex (function or community of functions) in the dataset’s graph (FCG or CG respectively) (line 4), it is first checked whether the vertex in question already belongs to a community (line 5). In this case, processing continues with the next vertex in the graph G(D). It is crucial to mention that vertices of G(D) are iterated based on the dataset’s ordering function, which, in this case, happens to be $r_{rank}$ (see how detect_initial_comms is invoked in Algorithm 6). Orphan vertices (i.e. vertices with no successors and predecessors) are always added in the same community, namely community 0 (lines 8–11), as this greatly simplifies the overall recovered community structure. The process continues by considering the next vertex according to $r_{rank}$. For each v, the vertex most similar to v (as reported by max_similarity_neighbor, Algorithm 12, presented below) is returned in u (line 12) and the two are added in the same community (lines 13–14). However if u.comm is not set (i.e. u does not belong to a community), a new community is created and v and u are both assigned to that community (lines 16–18).

Assigning vertices to communities is performed based on vertex similarity. The procedure that actually computes the similarity score between two vertices is given in Algorithm 12. For a vertex v, max_similarity_neighbor works as follows:

• 1. The ratio of common neighbors, between v and each of its neighbors u, over the union of their neighbors is computed (line 2). The neighbors of v with the highest ratio are added in set S and, if $\Vert S\Vert = 1$, the single element u of S is returned (line 9).

• 2. If $\Vert S\Vert > 1$, S is reduced to the set of those vertices with the smallest degree. If there are no ties (i.e. $\Vert S\Vert = 1$), u from S is returned (line 9).

• 3. If still $\Vert S\Vert > 1$, the vertex $u \in S$ whose address is nearest to v is picked. There can be no ties in this case. In case D represents a community dataset, address() can be made to return an arbitrary community characteristic (e.g. the lowest address member of the community).

5.5 Algorithm improve_comms

Algorithm 6 invokes improve_comms to fine-tune the partitioning returned by detect_initial_comms, using LMO heuristics. As it has already been mentioned, the former uses the directed Louvain algorithm. We will presently explain in detail the operation of this algorithm, but let us remark that it is the algorithm presented in [16], with a single modification: graph vertices are traversed in a deterministic way, based on the ordinals of $r_{rank}$, as opposed to random traversal proposed in the literature (refer to improve_comms, invoked in Algorithm 6).

For brevity purposes, we present our directed Louvain variant in verbal rather than pseudocode form. The algorithm can be summarized as follows:

• 1. Assign each vertex v of graph G in its own singleton community.

• 2. For each node v in G:

  • (a) Compute the potential increase in modularity by moving a neighbor u of v in the same community as v.

  • (b) Only move the vertex u that produces the maximum increase in modularity, if any.

• 3. Build induced graph of updated communities.

• 4. Repeat until modularity does not increase above a certain threshold.

The order, by which vertices in G are traversed in step 2, is arbitrary and might, as well, be random. This order, however, greatly affects the community structure recovered, and, so, for more deterministic results, a way of ordering nodes should be agreed upon before using Louvain to group functions in programs $P_1$ and $P_2$. Sorting functions $r_{rank}$ aim to partially tackle this problem, by assigning ranks to graph vertices and edges. Ranks are ordinals, which are used for sorting graph vertices and edges. As already mentioned, our Louvain variant traverses the graph vertices in that order, at step 2, as opposed to any other arbitrary order. This way, the more $P_1$ and $P_2$ “look alike“, the more their community structure, as recovered by our Louvain variant, does too.

6 LSH

6.1 Introductory remarks

Algorithm 5 delegates actual dataset matching to the following algorithms; singleton_matcher, structural_matcher and monotonic_matcher. The aforementioned procedures implement matching strategies and their semantics are discussed in [28]. In this work, we extend these semantics, by appending an additional parameter in their argument lists; a boolean value, named $is\_inexact$, which signifies whether exact or inexact matching is to be performed.

In earlier versions of our work, to detect exact matches, a greedy $\mathcal {O}(nm)$ algorithm was used, where n was the size of the primary dataset and m that of the secondary. The algorithm iterated through both datasets and matched singleton elements (elements appearing only once in their respective datasets) with numerically identical feature vectors. This algorithm was, in turn, used to implement the three aforementioned matching strategies (singleton matching, structural matching and monotonic matching). Greedy exact matching, which has been the standard practice in binary diffing tools, gives good results but performance drops dramatically as n and m increase. When inexact matching is also considered, $\mathcal {O}(nm)$ becomes prohibitively expensive, as distance computations between feature vectors cannot be assumed to take $\mathcal {O}(1)$ time (as assumed in the exact matching case).

Locality Sensitive Hashing (LSH) is a data clustering technique, which can remedy the greedy algorithm problems in the following ways:

• 1. Dimensionality reduction—LSH schemes can be used to approximate the Jaccard similarity of compared elements directly, by only considering the elements’ hash values. These hash values can be seen as the new set of the elements’ reduced dimensions.

• 2. Bucketing—LSH can aid in clustering data in smaller buckets, which can, then, be processed by divide and conquer algorithms to amortize the cost of $\mathcal {O}(nm)$.

REveal exploits the advantages offered by hashing as explained below:

• 1. In the inexact matching case, REveal implements a form of minhashing, based on universal hash functions [5] instead of permutations. Minhashing is used to split input datasets into smaller datasets consisting of elements that “look alike” according to their numerical features. Matching of elements between datasets is performed using the $\mathcal {O}(mn)$ greedy algorithm on the reduced datasets.

• 2. In the exact matching case, LSH does not offer any benefits. Instead plain hashing is used to split input datasets in smaller datasets consisting of elements with equal features. The new, smaller datasets are then processed by the $\mathcal {O}(mn)$ greedy algorithm.

6.2 Algorithm 13: match_datasets

The entry point of dataset matching logic is given in Algorithm 13.

At line 2, the value of $is\_inexact$ is checked. This boolean determines whether datasets will be matched exactly (line 3) or approximately (line 5).

6.2.1 Algorithm 14: match_datasets_inexact

Given two datasets $D_1$ and $D_2$, Algorithm 14 begins by iterating through the vertices of graph $G(D_1)$, the primary dataset’s graph, and hashing the feature vector of each vertex using all hash functions $h_i$ in H (lines 3–8). All $h_i$ are simple universal hash functions of the following form:

$$\begin{aligned} h_i(x) = (a_ix + b_i)\ mod\ p \end{aligned}$$

Where p is a prime integer. Note that $G(D_1)$ can be either be a FCG or a CG, depending on the diffing phase, while H is assumed to be a set of randomly chosen universal hash functions. Next, for each k-shingle (k can be 1) w of the set of hashes S, a mapping $w \rightarrow v$ is created in the hash table $T_1$ (line 6) and, consequently, vertex v might be stored in several buckets of $T_1$. The aforementioned process is then repeated for the graph of the secondary dataset $G(D_2)$ (lines 10–15). This time, hashed elements are added in hash table $T_2$.

In the following loop (lines 17–21), only the set of keys that both $T_1$ and $T_2$ have in common are considered. For each such key w, a temporary dataset $D_1'$, consisting of $D_1$’s vertices in $T_1[w]$ (line 18), and a temporary dataset $D_2'$, consisting of $D_2$’s vertices in $T_2[w]$ (line 19), are constructed and a greedy matching algorithm (function greedy) is invoked to solve the resulting reduced problem. We assume that given two datasets, greedy produces a matching of vertices with a low (but not necessarily the lowest) cost, adds matched pairs in M, removes matched vertices from their respective datasets and returns the number of matches n.

6.2.2 Algorithm 15: match_datasets_exact

For exact matching purposes, match_datasets_exact uses an arbitrary hash function h. This can be either a cryptographic hash function, or even a CRC code computed over f(v), the feature vector of a vertex v. This is done for all v in datasets $D_1$ (lines 3–6) and $D_2$ (lines 8–11) with hashed elements ending up in hash tables $T_1$ and $T_2$ respectively. The loop at lines 13–17 is similar to that of Algorithm 14. We again assume that greedy populates M with the newly matched pairs, removes vertices from their datasets and returns the number n of matched pairs.

7 Experimental results

7.1 Baseline

In this section we compare REveal, our binary diffing framework, against two popular tools of the same domain, namely, Diaphora and YaDiff. All three run on IDA Pro; the first two as IDA Python plug-ins, while the latter as a native plug-in. Furthermore, for evaluating the efficiency of CD and LSH, we also compare the current version of REveal against its older version that lacks inexact matching capabilities and the algorithm implementations presented in the previous sections.

REveal is the name of our binary diffing software, first introduced in [27]. It implements all algorithms presented in [27, 28], as well as the ones of the present paper. As our research progresses, we extend it with new algorithms and features, constantly improving its matching efficiency and speed. Even though REveal is not yet in the public domain, we plan to release it once its code base matures and becomes stable. For the time being, access, for non-commercial use and for preview purposes, can be granted, on request, to interested researchers and reverse engineers.

Diaphora is a free and open-source binary diffing tool, which is probably the most widespread of its kind in the reverse engineering community. It was first released during SyScan 2015 and is still actively maintained. Diaphora works by exporting function information, from IDA Pro databases under comparison, into portable SQLite files. This per-function information includes the number of basic blocks, the number of connected components, a signature synthesized by the function’s instructions and many more. Diaphora is also capable of utilizing the power offered by the IDA decompiler. If the latter is detected, Diaphora uses it to create a filtered version of each function’s decompiled C code and and stores the result as yet another function feature. Diaphora compares the exported databases using a set of predetermined SQL queries, which compare various combinations of function features. These queries are able to detect both exact, as well as inexact matches. In the latter case, a similarity score is also returned. It is worth noting that Diaphora also comes with a graphical user interface that allows reverse engineers to explore the diffing results interactively.

YaDiff is a binary diffing tool, part of YaCo, a collaborative reverse engineering plug-in for IDA Pro. YaDiff was developed for the purpose of porting information between two IDA Pro databases. That is, given two IDBs, it applies a binary diffing algorithm for the purpose of merging information, from the former to the latter, and writes the result in a new database, so as not to trash the original inputs. Merged information includes, symbol names, comments, bookmarks and all sorts of annotations usually found in an IDA Pro database. That said, YaDiff is not a generic, interactive binary diffing tool (like Diaphora which allows users to examine the list of symbols that were matched between the two databases), it merely performs the information merging process in a fully automated manner, giving no insights on the actual matching results. However, since YaDiff is open source and function matching is an integral part of its binary diffing engine, we were able to modify it and make it expose the required information. With the said modifications in place, YaDiff’s matching power is now measurable.

7.2 Evaluation

All experiments were performed on IDA Pro 7, running IDA Python based on Python 2.7. For this purpose, the version of Diaphora used is the latest from the diaphora-1.2 branch, with a series of patches manually backported from the master branch, to fix minor bugs in the former. Unfortunately, running the latest version of Diaphora, requires a new IDA Pro license, as both have recently moved to using Python 3 instead. When it comes to YaDiff, the latest commits in its master branch appear to be about 3 years old. For the purpose of running our experiments, the latest version of YaDiff was modified, as already mentioned in the previous paragraph, and was manually compiled using the IDA Pro SDK. Last but not least, it should be noted that all experiment instances were carried out on a Mac laptop equipped with a Core i7 2.4Ghz and 8Gb of RAM. We plan to perform comparisons against the latest Diaphora version (as well as against additional binary diffing tools) in the near future and report them in another publication.

Fig. 2

Experimental results for our custom dataset. Rows correspond to programs (ncmc, nmap, ffmpeg-android, vmlinux) and columns correspond to measurements (execution time, number of matches, number of mismatches). For the total number of functions in each case refer to Table 1

In the following, all binary diffing tools were used to find both exact and inexact function matches in the compared subjects. Debugging information, present in the experiment corpus, is used as a ground truth for verifying the correctness of the results and classifying them as either valid matches or mismatches. For the sake of fairness, function names in IDA Pro databases were scrambled (using simple IDA Python scripts) before executing the diffing engines. Note that the time it takes for the compared tools to export information is not measured; only the diffing process is timed and displayed in the following tables.

To demonstrate the efficiency of our new, divide-and-conquer approach in binary diffing, as well as the improvements in REveal’s diffing engine for that matter, we reused the same dataset as in [28]. The dataset consists of binary executables for ncmc, nmap, ffmpeg-android and the Linux kernel. The aforementioned programs are of increasing complexity, with ncmc executables having the least number of functions ($\approx 1000$) and vmlinux binaries the most ($\approx 40000$). The dataset contains two versions of each of the aforementioned programs, for example, Linux kernel 4.4.1 and 4.4.40, which are diffed with one another. Furthermore, for each pair of versions of each program, executables for all four computer architectures, namely i386, amd64, arm and aarch64 are compared. The above combinations result in a total of 16 experiment instances summarized in Fig. 2. For each experiment, we measure the time it takes for the diffing process to complete (ignoring latencies introduced during information exporting), the number of successful function matches, as well as the number of mismatches, that is, functions that were matched, but according to ground truth, they are not the same.

Additionally, we evaluate the abovementioned diffing tools in a subset of the DeepBinDiff [13] dataset, which is publicly available at the project’s GitHub repository. This dataset contains several precompiled binary executables, generated by compiling various versions of coreutils, diffutils and findutils, using optimization levels ranging from O0 to O3. More specifically, during our evaluation, we considered the following; coreutils version 8.1 against 8.30 (102 binaries), diffutils version 3.4 against 3.6 (4 binaries) and findutils version 4.41 against 4.6 (3 binaries). Executables, compiled with optimization levels from O0 to O3, were used, resulting in a total of 12 experiment instances summarized in Fig. 3. For each experiment, we take the exact same measurements as previously (execution time, number of matches and mismatches). Due to lack of historical data, the performance of REveal’s predecessor is not shown. Note that Fig. 3 shows only the accumulated execution time, number of matches and mismatches, not the individual diffing results of each diffed binary executable pair.

7.3 Results

7.3.1 Custom dataset

Experimental results are shown in Fig. 2 (see also Table 1 for the total number of functions contained in each program and architecture). We observe that REveal has the highest number of correctly matched functions in all experiment instances apart from one (ffmpeg_android for i386). Starting with ncmc (Fig. 2, 1st row), Reveal successfully matches 691, 651, 798 and 685 functions, when comparing aarch64, amd64, arm and i386 binary executables respectively. Diaphora comes second with 609, 568, 650 and 500 matches. The matching power of REveal, compared to this of its previous version, presented in [28], has evidently risen, at the expense of slightly increased running time. YaDiff comes third with respect to number of matches, but has shorter running times than its two competitors. REveal produces the most false positives, with an average of about 132 mismatches in each instance of this first round of experiments.

Table 1 Number of functions in our custom dataset

The second series of experiments (Fig. 2, 2nd row) concerns nmap. The subject binaries, in this batch of experiments, are larger, with the number of functions being increased from a few hundreds, compared to ncmc, to a few thousands. Once again we see a higher number of successful matches detected by REveal, which beats YaDiff by 1522, 1637, 2063 and 1814 matches. Interestingly, in the first three instances, the updated version of REveal finds a few thousand extra matches, compared to its previous version, about 10–40 s faster. As the size of the compared programs increases, YaDiff’s execution time advantage becomes more marked, with its running times being an order of magnitude shorter that those of its competitors. It’s also obvious that, in this series of experiment, YaDiff outperforms Diaphora in terms of correctly matched functions. Last but not least, when it comes to mismatches, REveal is again the loser, with an average of about 1844 mismatches per run.

The next four experiment instances (Fig. 2, 3rd row) concern ffmpeg binaries for Android. The number of functions have now doubled, compared to nmap. We begin by noting that, for i386, YaDiff outperforms both Diaphora and REveal, with a score of 18151 matches and a running time of 86 s. The new version of REveal is both faster and more efficient, in terms of matches, than its predecessor and is the winner in the remaining runs. When it comes to mismatches, REveal is again the loser, but the percentages of erroneous matches have fallen to more tolerable values, compared to the total number of functions. YaDiff performs exceptionally well, even outperforming Diaphora in some runs, with impressive speed efficiency, making it ideal for quick binary diffing tasks.

The vmlinux series of experiments (Fig. 2, 4th row) highlight REveal’s power to match binary executables, when these are very similar. First and foremost, we can see that REveal is once again the winner when looking at the numbers of correctly matched functions. Additionally, even though the number of mismatches, found by REveal, is evidently higher than this of YaDiff, we can see that, generally, it’s Diaphora that makes the most mistakes in this batch. In terms of execution time, YaDiff is followed by REveal, which in turn wins Diaphora, while the obsolete version of REveal comes last. Evidently REveal has greatly benefited by CD and LSH, when it comes to execution speed compared to its predecessor. The second and fourth experiment instances highlight this, with the new version executing about 6 to 7 times faster.

Fig. 3

Experimental results for the DeepBinDiff dataset. Rows correspond to programs (coreutils, diffutils, findutils) and columns correspond to measurements (execution time, number of matches, number of mismatches). For the total number of functions in each case refer to Table 2

7.3.2 DeepBinDiff dataset

As previously mentioned, the DeepBinDiff dataset consists of several ELF binary executables which are, generally, small in size (as opposed to our custom dataset that mainly consists of a few large executables). One conclusion, that can be quickly drawn by looking at Fig. 3 (and Table 2 that shows the total number of functions for each program and optimization level), is that, REveal is about 2 to 5 times slower when compared to its competitors. CD and LSH both require “setup” times, whose cost is amortized for larger executables, but becomes more evident when the compared subjects are smaller. As it can be seen, in all experiment instances (Fig. 3, 1st column) REveal takes 17 to 364 s to complete, while both Diaphora and YaDiff are much faster, with running times ranging from 2 to 108 s for the former and from 1 to 126 s for the latter.

Focusing on the number of correctly matched functions (Fig. 3, 2nd column), we can see how REveal wins the race, with more noticeable leverage in the cases of coreutils and diffutils (rows 1 and 2 respectively). Of course, this additional precision comes with the time penalty mentioned in the previous paragraph. Diaphora and YaDiff also perform well, but come second and third respectively, with the former winning the latter in 8 out of the 12 experiment instances (more specifically YaDiff wins in diffutils O1, O2 and O3, as well as in findutils O0).

Finally, when it comes to mismatches (Fig. 3, 3rd column), we again experience high numbers of false positives generated by REveal, especially in the coreutils and findutils cases, with the O0 and O2 findutils experiments being the most notable ones. In these two cases, REveal generates a number of false positives almost equal to the number of true positives. On the contrary, Diaphora and YaDiff are more resilient and generate acceptable false positive percentages. This time, YaDiff wins by generating the least mismatches in 9 out of 12 runs, with Diaphora winning the O1 and O2 coreutils run, as well as the O2 findutils one.

7.4 On the number of false positives

From Figs. 2 and 3, and the analysis of the previous section, it is clear that REveal has a high false positive rate. During its inexact matching rounds, REveal will keep matching as many functions as it can, even if the similarity score is very low (i.e., distance is high), as long as unique score matches can be found and, consequently, this may lead to increased numbers of false positives. Trying to avoid this by hardcoding distance thresholds, below which matches are considered legitimate, and dropping all matches above that threshold, is generally not an acceptable solution.

Table 2 Number of functions in DeepBinDiff dataset (for reasons unknown to us, findutils O1 consists of a single binary, hence the inconsistency in the numbers)

However, the high false positive rate is not an acute problem. Among others, binary diffing tools aid in manual reverse engineering and REveal is not an exception. Since all results are provided to the user, matches can be filtered using application-specific and domain-specific knowledge at a later time. Indeed, as a reverse engineer makes use of the results produced by a diffing tool, he or she can decide whether a match has been identified correctly or not. Based on manual effort, user-identified matches can be specified and guide the overall matching process. Furthermore, research on more reliable community detection and community matching algorithms that will allow to, at least partially, tackle this problem, is currently underway.

8 Conclusion

We have empirically proven that binary diffing can benefit from divide-and-conquer approaches, using techniques like CD and LSH, both in terms of speed efficiency as well as matching precision. However, we believe this merits further research. Dataset partitioning during binary diffing is still an unpopular approach, so we hope to have inspired researchers and reverse engineers to look into it. Several community detection and, generally, graph partitioning algorithms can be found in the public literature; their systematic testing and formal evaluation in binary diffing applications will definitely advance the current state of the art.