Communication, networks and asset price dynamics: a survey

Abstract

In this paper, we provide a wide-ranging survey of the state of the art in the area of communication and asset price dynamics. We start out by documenting empirical evidence that social communication influences investment decisions and asset prices, before turning to the main modelling approaches in the literature (both past and present). We discuss models of belief-updating based on observed performance; models of herd behaviour; and models with social interactions that arise from preferences for conformity or contrarianism. Our main contribution is to introduce readers to a social network approach which has been widely used in the opinion dynamics literature, but only recently applied to asset pricing. In the final part, we show how recent contributions to both modelling and empirical work are using the social network approach to improve our understanding of financial markets and asset price dynamics. We conclude with some thoughts on fruitful avenues for future research.

Investing in speculative assets is a social activity. Investors spend a substantial part of their leisure time discussing investments, reading about investments, or gossiping about others’ successes or failures in investing. It is thus plausible that investors’ behaviour (and hence prices of speculative assets) would be influenced by social movements. (Shiller 1984)

[T]he time has come to move beyond behavioural finance to ‘social finance’, which studies the structure of social interactions, how financial ideas spread and evolve, and how social processes affect financial outcomes. (Hirshleifer 2015)

1 Introduction

Asset prices defy easy explanation but affect the fortunes of individuals and entire economies. When asset prices increase, investors make capital gains and firms can raise more financial capital by issuing shares. Conversely, if asset prices fall sharply, aggregate wealth takes a hit and the resulting losses are widespread, from professional investors, to workers trying to supplement their income, to the old whose pensions depend on the value of the stock market. The ripple effect to the wider economy is a ‘financial accelerator’ in reverse. Therefore, understanding the determinants of asset prices is a worthwhile endeavour.

Following the seminal paper of Shiller (1984), attention turned to communication as a potential determinant of asset prices. In short, the idea is that investors are influenced not only by ‘fundamentals’ or personal judgement about an asset’s value, but also by the opinions of others they come into contact with, such as friends and relatives, well-known successful investors or industry experts. There is a large empirical literature which has found that social factors influence investment decisions, and alongside this literature has developed a model-based literature that studies the impact of communication on asset prices.

In this paper, we survey the literature that models communication and asset price dynamics. We start out by documenting empirical evidence that social communication influences investment decisions and asset prices, before turning to the main modelling approaches in the literature. As a benchmark, we first study an asset pricing model with rational expectations and no communication. We then set out an alternative framework based on heterogeneous expectations and communication between investors, and highlight some important implications. We emphasize heterogeneous expectations because, in most models, communication between investors happens at the level of individual beliefs or asset demands. We also highlight what the main approaches in the literature have in common, such as the assumed use of rule-of-thumb behaviours, or heuristics, by agents in financial markets.

We consider in detail how communication has been modelled in the literature. In particular, we discuss models with updating of belief types (chartist or fundamentalist) based on the observed performance of other investors; models of herd behaviour; and models with ‘social interactions’ due to preferences for conformity or contrarianism at the individual level. Our main departure from previous literature is to highlight a social network approach, which has been widely used in the opinion dynamics literature, but only recently applied to asset pricing. We introduce some key concepts and notation in relation to networks, thus providing readers with the tools needed to understand this growing area of the literature.

In the final part, we show how the most recent contributions to modelling and empirical work are using the social network approach to good effect. We include here works that extend social interactions models via the inclusion of local social networks; models that build directly on the opinion dynamics approach by adding a financial market and performance-based updating of beliefs; and diffusion-based models in which beliefs spread, like a virus, in the population of investors. We highlight some advantages of these modern approaches, and we also show how social network models of asset prices can be—and are being—taken to the data by leading researchers with cutting-edge methods in hand. We conclude by discussing some promising avenues for future research.

2 Motivation

Interest in communication and asset prices was sparked by the work of Shiller (1984). Shiller argued that since investing in speculative assets is a social activity, investor behaviour (and hence asset prices) will be influenced by collective social movements, such as ‘fads’ and fashions. Shiller also pointed to ‘local’ social influences that could affect investor decisions and asset prices, such as group pressure to conform with the opinions of one’s peers or the exchange of information through word-of-mouth communication.

Many empirical studies have considered this social influence hypothesis. In an early paper, Shiller and Pound (1989) surveyed 131 investors and found that many stock purchases were influenced by interactions with personal contacts, such as friends and relatives. In a German study, Arnswald (2001) surveyed 275 fund managers and found that information exchange with industry experts was cited as the most important source of information for their work, followed by conversations with colleagues and media reports.

Focusing on investment portfolios, Hong et al. (2005) show that mutual fund managers in the US have similar asset holdings to those of other fund managers in the same city, while Ivković and Weisbenner (2007) show that US households are more likely to purchase stocks from a particular industry if their neighbours did so. Shive (2010) investigated the impact of social influence using trading data for the 20 most active stocks in Finland; socially influenced trades were found to predict stock returns. In a similar vein, Ozsoylev et al. (2014) found that investors in the Istanbul Stock Exchange are connected in an empirical investor network and that more central investors earn higher returns with respect to information events.

More recently, there has been attention on social media as a medium of communication that affects investment decisions and asset prices. For example, Jiao et al. (2020) study the impact of traditional news media and social media on turnover and stock volatility and find that traditional news coverage predicts decreases in subsequent turnover and volatility, whereas social media coverage predicts increases in subsequent turnover and volatility. They also show that these patterns are consistent with a model of ‘echo chambers’ in which social networks repeat news, but some investors interpret repeated news as new information. By comparison, Semenova and Winkler (2021) study text data from online discussions on the investor forum WallStreetBets and find that discussions about particular stocks can be self-perpetuating and that peer influence on retail investors is primarily through consensus formation and belief contagion by shifting investor attention to particular stocks.

Finally, there are also several ‘lab experiments’ that study the impact of communication on asset prices. For example, Oechssler et al. (2011) study the implications of inside information and communication among traders in an experimental asset market; they find that having traders with an information advantage can create bubbles, but communication is counterproductive for bubble formation. Schoenberg and Haruvy (2012) studied traders in an experimental asset market who received communication about their relative performance; this information had a significant impact on market prices and boom duration. Communication and price bubbles is revisited by Steiger and Pelster (2020), who find that face-to-face communication leads to significantly larger asset price bubbles than standard laboratory markets and increases size of bubbles more than communication via social media ‘likes’.

In short, there is compelling evidence that communication affects investment decisions and asset prices. This observation raises important questions for researchers interested in financial markets. How should social interactions between investors be modelled? Which social interactions, specifically, are most useful in explaining price volatility and stylized facts of empirical stock returns? In the next sections, we first set out a benchmark asset pricing model in which communication plays no role. We then add heterogeneous expectations in the model and use this framework to introduce the reader to the various approaches to modelling social communication in the literature, including the most recent developments.

3 Asset pricing without communication

Let us start by considering a benchmark model of asset prices with no social influence. We assume that investors have common rational expectations, consistent with the efficient market hypothesis (see e.g. Fama 1970). We refer to this as the ‘conventional approach’.

The conventional approach stresses economic fundamentals as the key determinant of asset prices. These fundamentals include, among others, interest rates on bonds and dividends paid out to shareholders. Note that dividends should be considered stochastic since future profitability of firms is uncertain ex ante and firms are not required to pay dividends to shareholders even if they earn a profit. As a result, investors must form expectations of future fundamentals, such as dividends, which are random variables.

To make this concrete, suppose there are N investors and two assets, a share and a bond. The first asset (shares, x) pays a stochastic dividend $d_t$ in each period $t \in {\mathbb {N}}$; we assume $d_t$ is exogenous and has a fixed conditional variance. Shares can be purchased at a known price $p_t$ and their (unknown) resale price one period ahead is $p_{t+1}$. The second asset (bonds) is riskless: it pays a fixed return $r>0$ and has a price normalized to 1. Shares are in zero net supply, whereas bonds have a flexible supply. As a result, investors are not liquidity constrained and may take arbitrarily large positive or negative asset positions.

Investors want a portfolio of shares and bonds that maximizes their utility. Following Markowitz (1952), we give each investor $i\in {\mathcal {N}}$ a mean-variance utility function with risk aversion parameter $a>0$, where ${\mathcal {N}}$ denotes the set of all investors. We also give all investors common rational expectations $E_t[.]=E[.|I_t]$, where $E_t[.]$ is the conditional expectations operator and $I_t = \{p_t,p_{t-1},\ldots ;d_t, d_{t-1},\ldots \}$ is the information set of investors at time t.

The optimal portfolio choice of investor $i\in {\mathcal {N}}$ solves the problem:

$$\begin{aligned} \max \limits _{x_t^i} \hspace{2.84544pt}E_t[w_{t+1}^i] - \frac{a}{2}V_t[w_{t+1}^i] \end{aligned}$$

(1)

where $w_{t+1}^i = (p_{t+1} + d_{t+1} ) x_t^i + (1+r)(w_t^i - p_t x_t^i)$ is the future wealth, $w_t^i - p_t x_t^i$ is holdings of the riskless asset (bonds), and $V_t$ denotes conditional variance. Let $R_{t}= p_{t}+d_{t} - (1+r)p_{t-1}$ denote the excess return on shares.

The first-order condition for problem (1) is:

$$\begin{aligned} x_t^i = \frac{ E_t[R_{t+1}] }{a V_t[R_{t+1}]} = \frac{E_t[p_{t+1}+d_{t+1}] - (1+r)p_t}{a \sigma ^2} \end{aligned}$$

(2)

where we set $V_t[R_{t+1}]=\sigma ^2>0$ because under standard assumptions about dividends, there is a fundamental rational expectations solution with constant conditional variance.¹

Equation (2) says that the optimal demand for shares equals the ratio of the expected excess return to the (scaled) conditional return variance; intuitively, the latter is the product of the aversion to risk a and the quantity of risk $\sigma ^2$. Because all these terms are common knowledge to investors with rational expectations, the demand for shares is homogeneous.

Market-clearing requires that the aggregate demand for shares equal the zero net supply, or $\sum _i x_t^i = 0$, which implies that $p_t = \frac{E_t[p_{t+1}] + E_t[d_{t+1}]}{1+r}$. Assuming that rational bubbles are ruled out, the asset price is given by²

$$\begin{aligned} p_t = \sum _{j=1}^\infty \frac{E_t d_{t+j}}{(1+r)^j} \end{aligned}$$

(3)

i.e. price equals the expected present-discounted-value of the future dividend stream.

Hence, the rational expectations asset pricing model set out above implies that:

• Investors have common expectations, such that all investors value the asset equally and take the same asset position (given the absence of liquidity constraints);

• The price can be determined using the expectations of a ‘representative agent’ and these expectations reflect all available (useful) information about asset payoffs;

• Price depends on expected future fundamentals (dividends and interest rates) in all future periods and is equal to the risky asset’s intrinsic value.

According to this textbook model of asset pricing, social factors play no role for the simple reason that no investor can learn anything useful from interactions with others: all investors share the same information and beliefs, and thus take the same investment decisions.

The conventional approach clearly makes strong assumptions and has strong implications. For instance, because investors value the asset equally and take identical asset positions, there is no trade between investors. From an empirical standpoint, both Shiller (1981) and LeRoy and Porter (1981) pointed to problems with the simple present-discounted-value model of asset prices in (3): historical US stock prices have been far too volatile to be explained by observed changes in dividends, so there is an excess volatility puzzle.

A further implication of the present-value model in (3) is that changes in stock prices should be due solely to unanticipated news about future fundamentals (e.g. dividends). However, large declines in the stock market have been observed even when there has been little or no extra news about fundamentals, and stock prices often seem to be at odds with events in the real economy, to which the profitability of firms is presumably linked.

If fundamentals are not volatile enough to explain the observed variation in share prices, it may be that expectations of future payoffs are excessively volatile. For example, in a well-known passage of the General Theory, Keynes compares the stock market to a newspaper ‘beauty contest’ in which the participants attempt to guess the average opinion, knowing that other readers are participating in the same guessing game. If investors in the stock market are indeed anticipating the expectations of others when forming their own expectations, then expectations need not coordinate on rational expectations, and thus behavioural and psychological influences on investors become relevant considerations. Keynes’ analogy also suggests that investors may prefer to be informed about the expectations of others before making their own investment decisions; this could be achieved, for example, if investors communicate and share information about their beliefs as we discuss below.

These three ingredients—heterogeneous expectations, behavioural influences, and social communication—provide the foundations of an alternative approach to asset pricing that has received considerable interest in recent decades. In the remainder of this paper, we set out this approach and then take the reader to the forefront of this literature.

4 Asset pricing with communication

In this section, we introduce a benchmark asset pricing model in which the investors have heterogeneous expectations about asset payoffs. We then add social communication in the model and use this framework to discuss the main modelling approaches in the literature.

4.1 Heterogeneous expectations

Early work in the literature emphasized heterogeneous expectations across different groups of investors. However, there are many ways in which expectations could differ across individuals, and each could have different asset pricing implications. Research has therefore been informed by psychological evidence that real-world decisions are based on rules-of-thumb, or heuristics, rather than full optimization by unboundedly rational agents (see e.g. Gigerenzer and Todd 1999). This behavioural approach to expectations formation emphasizes simple forecasting rules that may differ across individual investors.

Suppose, therefore, that our model is unchanged, except that investors differ in expectations. We denote the subjective expectation of investor i as $\tilde{E}_t^i[.]$, where the ‘tilde’ indicates that the expectation is boundedly-rational, in the sense of Simon (1957), to reflect cognitive limitations of investors.³ Similarly, ${\tilde{V}}_t^i[.]$ is the subjective variance of investor i.

The optimal portfolio choice of investor $i \in {\mathcal {N}}$ now solves the problem⁴

$$\begin{aligned} \max \limits _{x_t^i} \hspace{2.84544pt}{\tilde{E}}_t^i[w_{t+1}^i] - \frac{a}{2}{\tilde{V}}_t^i[w_{t+1}^i] \end{aligned}$$

(4)

The demand of investor i is therefore amended from (2) to

$$\begin{aligned} x_t^i = \frac{{\tilde{E}}_t^i[R_{t+1}]}{a {\tilde{V}}_t^i[R_{t+1}] } = \frac{{\tilde{E}}_t^i[p_{t+1}+d_{t+1}] - (1+r)p_t}{a {\tilde{\sigma }}_{i,t}^2} \end{aligned}$$

(5)

where ${\tilde{\sigma }}_{i,t}^2$ is the subjective return variance of investor i at date t.

Equation (5) makes clear that if investors differ in expectations, then they will generally take different investment decisions. For example, optimistic investors will have higher (risk-adjusted) valuations than pessimistic investors and thus find it optimal to invest more in the risky asset.⁵ Aggregating asset demands across investors and equating aggregate demand with the zero (net) supply of shares, we find that the market-clearing asset price is

$$\begin{aligned} p_t = \frac{ \frac{1}{\sum _{i=1}^N (a {\tilde{\sigma }}_{i,t}^2)^{-1}} \sum _{i=1}^N \frac{{\tilde{E}}_t^i[p_{t+1}+d_{t+1}]}{a {\tilde{\sigma }}_{i,t}^2} }{1+r}. \end{aligned}$$

(6)

Some papers consider heterogeneous, time-varying conditional variances as in (5) and (6). In this case, both an investor’s expectations about payoffs ${\tilde{E}}_t^i[p_{t+1}+d_{t+1}]$ and their subjective return variance ${\tilde{\sigma }}_{i,t}^2$ need to be specified (see De Grauwe and Grimaldi 2006; Ap Gwilym 2010). However, most papers have preferred to focus on heterogeneous expectations of payoffs by assuming subjective variances are homogeneous across agents. In this case, (6) simplifies to

$$\begin{aligned} p_t = \frac{ \frac{1}{N} \sum _{i=1}^N {\tilde{E}}_t^i[p_{t+1}+d_{t+1}] }{1+r}. \end{aligned}$$

(7)

Equation (7) simply says that the asset price equals the average expected payoff (across all investors), discounted by gross return on the riskless asset. There are some notable differences relative to the fundamental price under rational expectations in Eq. (3).

First, the rational expectations price (3) equals the expected discounted present value of future dividends—i.e. the intrinsic value of the risky asset. The price under heterogeneous expectations, (7), will coincide with the latter only if subjective expectations are on average equal to the rational expectation. Second, to the extent that average opinion determines asset prices, the asset price in (7) is in line with Keynes’ beauty-contest view of the stock market: speculative asset prices depend on average opinion, which consists of the subjective assessments of individual investors, rather than strictly rational valuations. Finally, note that each expectation has an equal weight of 1/N, so investors whose subjective expectations are strongly optimistic or pessimistic may ‘bias’ the price in one direction or another.

A common approach in the literature has been to focus on heterogeneous price expectations $E_t^i[p_{t+1}]$ by holding expected dividends ${\tilde{E}}_t^i[d_{t+1}]$ equal across investors.⁶ Price expectations ${\tilde{E}}_t^i[p_{t+1}]$ are often assumed to be of two types: chartist and fundamentalist. The basic idea is that at any given point in time, investors may make either a chartist (or trend-following) forecast of asset prices or a ‘fundamentalist’ forecast which conditions on fundamental indicators such as dividends and interest rates. The key difference between the two forecasting approaches is that the chartist approach is backward-looking (relying on past prices), whereas the fundamental approach is forward-looking: investors use information on current and projected future fundamentals such as dividends and interest rates.

A chartist forecasting rule c has the general form:

$$\begin{aligned} {\tilde{E}}_t^c[p_{t+1}] = f_c(p_{t-1},\ldots ,p_{t-L}) \end{aligned}$$

(8)

where the function $f_c: {\mathbb {R}}^L \rightarrow {\mathbb {R}}$ describes how the chartist forecast relates to past prices.

The parameter $L \ge 1$ in (8) is the longest price lag that is taken into account by chartists. The function $f_c$ may be linear or nonlinear, but linearity is often assumed in the literature for the sake of analytical tractability. Note that the above specification nests both extrapolative rules (that consider the size and direction past price changes) and level rules (that consider the absolute level of prices). Hence, (8) allows a range of behaviours associated with the trend-following and technical analysis popularized by Charles Dow.

A fundamentalist forecasting rule f has the form:

$$\begin{aligned} {\tilde{E}}_t^f[p_{t+1}] = E_t[p_{t+1}^*] \end{aligned}$$

(9)

where $E_t[p_{t+1}^*]$ is the expected future fundamental price.

Note that the forecast $E_t[p_{t+1}^*]$ would equal the (actual) expected future price if all investors were fundamentalists with rational expectations; it is thus equal to the one-period-ahead conditional expectation of (3). Equivalently, $E_t[p_{t+1}^*]$ is the price that is expected to clear fundamental demand at date $t+1$,⁷ Note that (9) implies that fundamentalists base price forecasts on fundamental information only, even if the market is populated by some chartists; hence such fundamentalist forecasts are behavioural in the sense that they ignore (or are ignorant of) the presence of chartists in the market. This ‘fundamentals-only’ approach appears to be a good (rough) description of some prominent investors.⁸

Early works that modelled both chartist and fundamental investors, include Zeeman (1974), Beja and Goldman (1980) and Chiarella (1992). These papers showed that the presence of chartist investors in the market provides an explanation for the unstable short run behaviour of stock prices. For example, in the model of Zeeman (1974), there is endogenous switching of asset prices between bull and bear markets that can be traced to the behaviour of fundamentalists and chartists, whereas Beja and Goldman (1980) show that with sufficiently strong trend-following in their model, the dynamic system is unstable with exploding price oscillations, such that speculative trading of chartists destabilizes asset prices. In Chiarella (1992), the Beja-Goldman model is generalized such that the demand of chartists is nonlinear, increasing and S-shaped; as a result, a unique stable limit cycle exists along which the asset price and chartists’ assessment of the price trend fluctuate over time.⁹

The focus on chartists and fundamentalists is consistent with evidence on the forecasting strategies of real-world investors. For example, Frankel and Froot (1990) provide survey evidence from foreign exchange forecasting firms: some firms described themselves as focusing on economic fundamentals, whereas others said they relied on chartist analysis or a combination of the two approaches. Interestingly, the relative proportion of firms using chartist forecasting approaches increased substantially over the decade from 1978 to 1988—a period of substantial Dollar appreciation which is difficult to explain using economic fundamentals.

Further evidence is provided by Taylor and Allen (1992) using questionnaire surveys of foreign exchange dealers in London: both chartist (technical) and fundamentalist forecasting approaches are cited, but there is a skew towards chartist, as opposed to fundamentalist, analysis at shorter horizons, which is steadily reversed as the forecast horizon is increased. In a review, Menkhoff and Taylor (2007) find the overall shares of chartist and fundamentalist approaches in foreign exchange forecasting are quite similar, whereas Menkhoff (2010) finds that the pattern of greater reliance on technical analysis at short horizons applies also to fund managers, with the pattern again reversed at longer horizons such as months and years.

The survey evidence above indicates that the popularity of chartist versus fundamentalist forecasting strategies is not fixed over time and seems to be linked to the relative performance of these forecasting approaches (see Frankel and Froot 1990). In the early models with chartists and fundamentalists discussed above, the population shares of the two groups were taken as fixed, and hence updating of forecasting strategies was neglected. Note that specifying such updating requires us to take a stand on communication between investors, since adoption of a different forecasting rule based on performance implies that investors know both the forecasting rules of others and their relative performance.

These are some key themes that have been taken up in the subsequent literature.

4.2 Social communication models

We now introduce asset pricing models with heterogeneous expectations and communication, including type updating based on performance, herding models, and social interactions.

4.2.1 The Brock–Hommes model

The Brock and Hommes (1998) model brings together some key ingredients discussed so far. In the simplest version of the model, a large population of investors may choose between a chartist forecasting rule and a fundamentalist forecasting rule. It is assumed that each investor can observe the performance (i.e. profitability) of all other investors and the forecasting rule they follow. The key dynamic in the model is the updating of forecasting strategies: in any period, the better-performing rule will have a higher rate of adoption in the population of investors (as we show below).¹⁰ The Brock–Hommes model can be interpreted as a simple model of communication: social comparisons matter for belief updating.

Investors are boundedly-rational. The price forecast of investor i is denoted by $\tilde{E}_t^i[p_{t+1}]$ (as in Sect. 5.1 above), and all investors are assumed to have a common subjective return variance which is fixed at ${\tilde{\sigma }}^2>0$. Dividends follow an exogenous process of the form $d_t = {\bar{d}} + \varepsilon _t$, where ${\bar{d}}>0$ and $\varepsilon _t$ is IID and mean zero. It assumed that all investors know the dividend process, such that $\tilde{E}_t^i[d_{t+1}]={\bar{d}}$ for all $i\in {\mathcal {N}}$. In any period $t \in {\mathbb {N}}$, an investor must adopt either a chartist forecasting rule or a fundamental forecasting rule for the price.

Given the above assumptions, the demand of investor i at date t (see (5)) is

$$\begin{aligned} x_t^i = \frac{{\tilde{E}}_t^i[p_{t+1}] + {\overline{d}} - (1+r)p_t}{a {\tilde{\sigma }}^2} \end{aligned}$$

(10)

where ${\tilde{E}}_t^i[p_{t+1}]$ is the expectation of investor i given their forecasting rule at date t.

The fundamental forecasting rule can be derived by finding the price $p_t^*$ that would clear the market if all investors were fundamentalists with common rational expectations, such that ${\tilde{E}}_t^i[p_{t+1}] = E_t[p_{t+1}^*]$ for all $i\in {\mathcal {N}}$. Using this expression in (10) and noting that market-clearing requires $x_t^i (p_t^*) = 0$ $\forall i\in {\mathcal {N}}$ gives the fundamental price as¹¹

$$\begin{aligned} p_t^* = {\bar{p}}: = {\bar{d}} / r \end{aligned}$$

(11)

such that the fundamental forecasting rule (9) simplifies to

$$\begin{aligned} {\tilde{E}}_t^f[p_{t+1}] = {\bar{p}}. \end{aligned}$$

(12)

Here, ${\overline{p}}$ is the fundamental price in (3) when expected dividends equal ${\bar{d}}$ in every period. It says that in the absence of rational bubbles, an asset that is expected to pay a fixed dividend ${\overline{d}}$ in perpetuity has a price (= intrinsic value) given by the presented discounted value of the dividend stream. The fundamental forecast (12) is based upon this intrinsic value.

The chartist forecasting rule is given by a special case of (8) when there are $L=1$ lags and the function $f_c$ is linear:

$$\begin{aligned} {\tilde{E}}_t^c[p_{t+1}] = (1-g) {\bar{p}} + gp_{t-1} \end{aligned}$$

(13)

where $g>0$ is the trend-following parameter.

Note that the forecasting rule (13) has the interpretation that chartists expect the future deviation of price from the fundamental price to be linked to its past value $(p_{t-1} - {\bar{p}})$ via the trend-following parameter g; hence, chartists extrapolate from the past to the future. Note that the one-lag chartists are myopic in contrast to the fundamentalists who are farsighted.

The key mechanism in the model is the adoption of types via evolutionary competition. In particular, at a given date t, each investor must be either a chartist or a fundamentalist, and the probabilities of being each type are depend on the relative performance of the two forecasting rules. In a large population $N \rightarrow \infty$, only the population shares of investors of each type need to be tracked. Brock and Hommes therefore assume the population shares are determined by a discrete choice logistic updating equation:

$$\begin{aligned} n_{t+1}^c = \frac{\text {exp}(\beta U_{t}^c )}{ \text {exp}(\beta U_{t}^c ) + \text {exp}(\beta U_{t}^f ) }, \hspace{17.07182pt}n_{t+1}^f = 1 -n_{t+1}^c \end{aligned}$$

(14)

where $\beta \ge 0$ is the intensity of choice and $U_{t}^h \in {\mathbb {R}}$ is the fitness of predictor h at date t.

Equation (14) says that the share of the population using the chartist predictor c at date $t+1$ depends on its relative performance against the fundamentalist predictor f, as judged by the past observed levels of fitness $U_{t}^c$ and $U_{t}^f$. The intensity of choice parameter $\beta$ determines how fast agents switch to better-performing predictors. In the special case $\beta =0$, the population shares are fixed and equal to 1/2; in this case, performance is ignored by investors and they are split equally between the two predictors. At the other extreme $\beta \rightarrow \infty$, all investors will adopt in period $t+1$ the best-performing predictor in period t.¹²

Note that for any $\beta \in (0, \infty )$, the better-performing predictor will be adopted by a larger share of the population, which is apparent if we write (14) as $n_{t+1}^c = \frac{ 1 }{ 1 + e^{\beta (U_{t}^f - U_{t}^c)} }$.

The model is closed with the fitness measures $U_{t,c}$ and $U_{t,f}$. Brock and Hommes (1998) use the realized profits under a given predictor $h \in \{c,f\}$ net of a predictor cost¹³

$$\begin{aligned} \begin{aligned} U_t^h&= {\tilde{R}}_t x_{t-1}^h - C^h \\&= (p_t + d_t - (1+r)p_{t-1}) x_{t-1}^h - C^h \end{aligned} \end{aligned}$$

(15)

where ${\tilde{R}}_t:=p_t + d_t - (1+r)p_{t-1}$ is the realized excess return on shares at date t and $C^h \ge 0$ is the cost of obtaining predictor h.

Brock and Hommes assume that only the fundamental predictor is costly: $C^c = 0$, $C^f = C \ge 0$. The basic idea here is that fundamental information may be more costly to obtain because it relies on more than past prices (which are readily observable). The asset price $p_t$ is determined by market-clearing, given an assumption of zero outside supply, such that $\sum _{h \in \{c,f\}} n_t^h x_t^h=0$. The market-clearing asset price is

$$\begin{aligned} {\tilde{p}}_t = \frac{n_t^c g}{1+r} {\tilde{p}}_{t-1} \end{aligned}$$

(16)

where $\tilde{p}_t: = p_t - {\bar{p}}$ is the deviation of price from the fundamental price.

Brock and Hommes (1998) establish several properties of the dynamical system (10)–(16):

• For $0<g<1+r$, the model has a unique, globally stable steady state. At this (fundamental) steady state, the asset price p is equal to the fundamental price ${\bar{p}}$.

• For $g>2(1+r)$, there are three steady states: two non-fundamental steady states with (resp.) positive and negative price deviation, and a fundamental steady state where $p={\bar{p}}$, such that $\tilde{p}=0$. The fundamental steady state is unstable.

• For $1+r<g<2(1+r)$, there are two possibilities: either (i) there are three steady states (as above) and the fundamental steady state is unstable, or (ii) the fundamental steady state is the unique, globally stable steady state.¹⁴

• For $1+r<g<2(1+r)$, there is a pitchfork bifurcation at some $\beta = \beta ^*>0$, and as the intensity of choice increases further there is a Hopf bifurcation at some $\beta =\beta ^{**}$. The non-fundamental steady states are unstable for $\beta > \beta ^{**}$.

Fig. 1

Bifurcation diagram for price deviation $\tilde{p}_t$ in the two-type model (chartists and fundamentalists). Parameters are $g=1.2$, $r=0.1$, $C=1$, $a {\tilde{\sigma }}^2=1$ and we simulate the deterministic skeleton, i.e. $d_t = {\overline{d}}$ for all t. For each $\beta$ we plot 350 points following a transitory of 4000 periods from initial values $\tilde{p}_{-1} \in (0,2)$

In Fig. 1, we show a numerical bifurcation diagram for the case $1+r<g<2(1+r)$. For low enough intensity of choice $\beta$, the fundamental steady state $\tilde{p}=0$ is stable. As the intensity of choice increases, the fundamental steady state becomes unstable due to a pitchfork bifurcation ($\beta ^* \approx 2.37$) in which two extra (non-fundamental) steady states $\tilde{p}^*<0<\tilde{p}^*$ are created (since we assume $\tilde{p}_{-1}>0$, only the upper ‘fork’ appears in the diagram). As the intensity of choice increases further, the non-fundamental steady states become unstable due to a Hopf bifurcation ($\beta ^{**} \approx 3.33$), giving more complicated dynamics, including stable limit cycles and quasi-periodic attractors. For intensity of choice above (approx.) 3.6, there is a positive Lyapunov exponent, indicating chaotic price dynamics.

The social aspect of the model (switching based on observable differences in performance) is essential for these dynamics. If the population shares of chartists were instead exogenous and fixed at some ${\bar{n}}^c \in [0,1]$, then for any initial condition $p_{-1} \ne {\bar{p}}$ the price would converge monotonically to the fundamental price if $0 \le {\bar{n}}^c g < 1+r$; remain fixed and equal to $p_{-1}$ if ${\bar{n}}^c g = 1+r$; and diverge monotonically to $+\infty$ or $-\infty$ if ${\bar{n}}^c g > 1+r$.

Several papers have provided empirical support for the two-type Brock–Hommes model. For example, Boswijk et al. (2007) estimate an empirical version of the model on annual US stock price data from 1871 to 2003. The estimation supports the existence of heterogeneous expectations that differ in the extent of fundamentalist or trend-following behaviour, and the model offers an explanation for the run-up in stock prices after 1990 in terms of increased trend-following among investors. The estimated two-type model of fundamentalists and chartists in Chiarella et al. (2014) also supports the assumption of heterogeneous expectations, and the model can explain endogenously the rise and collapse of asset prices in a bubble-like fashion, as seen in the dot-com bubble.¹⁵ The importance of heterogeneous expectations for asset price fluctuations has also been highlighted by ‘learning to forecast’ experiments in laboratory asset markets: evolutionary selection between behavioural expectation rules improves out-of-sample predictive performance and endogenous bubbles are related to trend-chasing behaviour (Hommes et al. 2008; Anufriev and Hommes 2012).

4.2.2 Herding models

We now turn to models of herd behaviour among investors. We confine our attention to behavioural herding models, which have been widely used in the asset pricing literature.¹⁶

An early contribution was Kirman’s stochastic recruitment model (see Kirman 1993). The model was motivated by a puzzle in biology concerning the behaviour of ants: when faced with two identical food sources, ants concentrate more on one of the two food sources, but after a period they would switch their attention to the other food source. Thus, ants facing a symmetric situation behave collectively in an asymmetric way. Similar asymmetry has been observed in humans choosing between restaurants of similar price and quality situated on either side of a street: a large majority choose the same restaurant. Here, we consider a financial markets version of the Kirman (1993) model, as in the survey by Hommes (2006).

There are N investors who form an expectation about the future asset price $p_{t+1}$, which may be either optimistic or pessimistic. An investor’s expectation depends on the outcome of random meetings with other investors. Let $k_t \in \{0,1,\ldots ,N\}$ denote the number of investors that hold the optimistic view at date t; the initial number of optimistic investors $k_0$ is given. Beliefs in periods $t \ge 1$ are formed as follows. When two investors meet, the first investor is converted to the other investor’s belief with probability $(1-\delta )$, where $\delta \in [0,1]$. There is also a small probability $\epsilon$ that the first investor will change their view independently.

Given the above assumptions, the number of optimistic investors $k_t$ is updated as follows:

$$\begin{aligned} k_{t+1} = {\left\{ \begin{array}{ll} k_t+1 &{} \hbox {} \quad \hbox {with probability} P_t^+ = \left( 1-\frac{k_t}{N}\right) \left( \epsilon + (1-\delta )\frac{k_t}{N-1} \right) \\ k_t-1 &{} \hbox { }\ \quad \textrm{with probability }P_t^- = \frac{k_t}{N} \left( \epsilon + (1-\delta )\frac{N-k_t}{N-1} \right) \\ k_t &{} \hbox {} \quad \hbox {with probability} 1-P_t^+ - P_t^- \end{array}\right. } \end{aligned}$$

(17)

where $P_t^+$ and $P_t^-$ are the state-contingent probabilities of a change in optimism, which depend on the prevailing number of optimists $k_t$.

In Fig. 2, we simulate the fraction of optimistic investors $k_t/N$ over 60,000 periods (left panel) and the ‘optimism distribution’ over a long time horizon (right panel). The fraction of optimistic investors starts out close to zero and remains below 10% for the first third of simulated periods (left panel), i.e. there is strong and persistent herding on the pessimistic belief. In the middle of the simulation, the fraction of optimistic investors rises due to a run of ‘optimism shocks’ and at one point exceeds 50% before becoming very volatile and then strongly pessimistic again. In the final third of the simulation, however, we see a sudden switch from herding on the pessimistic belief to persistent herding on the optimistic belief.

Fig. 2

Fraction k/N in the Kirman (1993) model with parameters $\epsilon = 0.002$, $\delta = 0.01$, $k_0=0$, $N=100$. Left panel: $T=60$,000 periods. Right panel: $T=5\times 10^7$ periods

The herd-like behaviour of beliefs is also clear from the simulated distribution of the fraction of optimists (right panel). The distribution is bimodal with peaks at the extremes of 0 and 1, for which all investors are either pessimistic or optimistic. Although the average fraction of optimistic investors is one-half, the share of optimistic investors spends least time at this value and most time near the extremes of 0 and 1. There is a U-shaped distribution for the population share of optimists, as in Fig. 2, provided that $\epsilon$ (the probability of an independent change in an investor’s beliefs) is small enough; in particular, we require $\epsilon < (1-\delta )/(N-1)$ for a U-shaped distribution (see Kirman 1993, p. 144).

Kirman (1991) adds this simple herding mechanism in an asset pricing model, such that the population share of chartists $n_t^c$ is determined by stochastic recruitment as in (17). Hence, unlike the Brock–Hommes model, population shares are determined by pure social dynamics, without any reference to profitability. The forecasting rules in the model are similar to the fundamentalist and chartist rules (12)–(13).¹⁷ Price volatility is high when chartist beliefs dominate the market ($n_t^c$ close to 1) and low when fundamental beliefs dominate ($n_t^c$ close to 0). As the population share of chartists switches from low to high values as in Fig. 2, price volatility switches from a low volatility regime to a high volatility regime. The model thus provides a qualitative explanation for volatility clustering in returns.

Cont and Bouchaud (2000) also construct a herding model and assess its implications for stock market returns. In their model, investors interact through a random communication structure to determine the asset price (see below). In each period the investors $i \in \{1,\ldots ,N\}$ receive a random signal $\phi _i(t) \in \{-1,0,1\}$. If $\phi _i(t)=+1$, investor i buys the asset in period t; if $\phi _i(t)=-1$, investor i sells the asset; and if $\phi _i(t)=0$, then investor i does not trade in period t. Aggregate excess demand for the asset at date t is thus:

$$\begin{aligned} D_t = \sum _{i=1}^N \phi _i(t). \end{aligned}$$

(18)

The evolution of $\phi _i(t)$ is described by

$$\begin{aligned} \phi _i(t) = {\left\{ \begin{array}{ll} +1 &{} \hbox { with probability}\ b \\ -1 &{} \hbox { with probability}\ b \\ 0 &{} \hbox { with probability}\ 1-2b \\ \end{array}\right. }, \quad \quad \text {where }b \in (0,1/2]. \end{aligned}$$

(19)

A value of $b <1/2$ allows a finite fraction of traders not to trade, with positive probability, in a given period. Given the assumption of a symmetric marginal distribution in (19), expected excess demand is zero. Thus, in any given period t, excess demand will vary around zero due to random variations in the aggregate sentiment $\sum _{i=1}^N \phi _i(t)$.

The asset price $p_t$ is given by a market-maker equation in which the change in price is a linear function of the past excess demand:

$$\begin{aligned} p_t - p_{t-1} = \frac{1}{\lambda } D_{t-1} \quad \implies \quad p_t = p_{t-1} + \frac{1}{\lambda } \sum _{i=1}^N \phi _i(t-1) \end{aligned}$$

(20)

where parameter $\lambda >0$ is referred to as the market depth.

Cont and Bouchaud (2000) first consider the case where individual demands $[\phi _i(t)]_{1 \le i \le N}$ are IID random variables with finite variance. Since this assumption implies that individual demands are statistically independent, they call this the ‘independent agents’ hypothesis. In the case, the joint distribution of the demands is the product of the individual distributions, and the change in price $\Delta p = p_t-p_{t-1}$ is a sum of N IID random variables with finite variance (and hence $p_t$ is a random walk; see 20). For large N, the distribution of $\Delta p$ is well-approximated by a normal distribution via the central limit theorem.

Is this a good model of stock market returns? The basic answer is no. Empirical distributions of asset returns and price changes are strongly non-normal, exhibiting fat tails and excess kurtosis; moreover, the tails of the empirical distributions are heavy with finite variance (see Pagan 1996; Mandelbrot and Hudson 2010). Accordingly, Cont and Bouchaud conclude that the ‘independent agents’ hypothesis is at odds with the data and turn to the hypothesis that individual demands are determined by communication between investors.

Cont and Bouchaud (2000) suppose that investors organize into groups which are given by forming independent binary links with probability c/N, where $0<c<1$ is a connectivity parameter. The components of the so-formed Erdös and Rényi random network (see Sect. 6.1.2) then determine the trading groups. Investors in a particular group (or cluster) coordinate their actions in a herd-like manner, such that all members of a group act in unison to buy or sell (or to not trade).

For the case of $n_g$ groups, the price equation is adjusted from (20) to

$$\begin{aligned} p_t = p_{t-1} + \frac{1}{\lambda } \sum _{\alpha =1}^{n_g} D_{\alpha ,t} \end{aligned}$$

(21)

where $D_{\alpha ,t} = N_\alpha \phi _\alpha (t)$ is the demand of group $\alpha$ at date t, $N_\alpha$ is the number of investors in group $\alpha$, and $\phi _\alpha (t)$ is the common individual demand of each member of the group.

Cont and Bouchaud assume that the demands of each cluster $\phi _\alpha (t)$ are independently random variables with a symmetric distribution analogous to (19), i.e.

$$\begin{aligned} P(\phi _\alpha (t)=+1)= P(\phi _\alpha (t)=-1)=b, \quad \quad P(\phi _\alpha (t)=0)=1-2b. \end{aligned}$$

The parameter b is taken as proportional to order flow in a given time period and inversely proportional to the number of investors N; this implies that only a finite number of investors trade at the same time when the number of investors increases without bound.

Under the above assumptions, Cont and Bouchaud (2000) show that the distribution of price changes as $N \rightarrow \infty$ has the following properties:

• The density of price changes $\Delta p = p_t - p_{t-1}$ has a heavy, non-Gaussian tail

• The heaviness of the tails, as measured by the kurtosis of the price change, is inversely related to the order flow (i.e. liquidity of the market)

In summary, Cont and Bouchaud show that the ‘independent agents’ version of their model is rejected by the data, but adding communication between investors through a simple herding mechanism allows the model to generate a distribution of price changes that shares some key features of the empirical distribution of stock market returns.

4.2.3 Herding plus performance-based updating

In a series of papers, Lux and co-authors combine herding mechanisms with endogenous updating of investor types based on the evolution of asset prices. In particular, these works combine herd-like behaviour as in the Kirman and Cont and Bouchaud models with performance-based updating as in the Brock and Hommes model, such that there is a coupled dynamics of prices, trader sentiment and investor types.

The herding mechanism, known as mimetic contagion, is set out in Lux (1995).¹⁸ Time is continuous and there is a fixed number of chartist investors 2N. Investors may be either optimistic or pessimistic, such that $n_+ + n_- = 2N$, where $n_+$ ($n_-$) is the prevailing number of optimistic (pessimistic) chartist investors. Chartists are assumed to react to the prevailing sentiment $m = n/N$, where $n = (n_+ - n_-)/2$, such that $m \in [-1,1]$. Lux assumes the probability of switching from pessimism to optimism $P_{+-}$ is higher the larger the prevailing share of optimistic chartists, and vice versa for a switch in the opposite direction:

$$\begin{aligned} P_{+-} = v \exp (bm), \quad \quad P_{-+} = v \exp (-bm) \end{aligned}$$

(22)

where $v>0$ and the parameter $b > 0$ measures the strength of herd behaviour.¹⁹

Given the above assumptions, the dynamics of the sentiment index s is given by

$$\begin{aligned} \begin{aligned} dm/dt&= (1-m)P_{+-} - (1+m)P_{-+} \\&= 2v[\text {Tanh}(bm)-m]\text {Cosh}(bm). \end{aligned} \end{aligned}$$

(23)

For $b \le 1$, there is a unique stable steady state at $m=0$, whereas for $b>1$ , the steady state at $m=0$ is unstable and two extra, stable, steady states $m_+>0$, $m_{-}=-m_+<0$ exist.

Thus, if the herd effect is relatively weak ($0<b\le 1$), then the dynamics return to a balanced sentiment $m=0$ after a disturbance. On the other hand, for $b>1$ small disturbances will make a majority of speculative investors bullish or bearish through mutual contagion, such that the steady state $m=0$ is unstable and the dynamics lead to an unbalanced steady state ($m_+$ or $m_{-}$) in which the majority has either an optimistic or a pessimistic opinion, with the majority being bigger for a larger herding parameter b.

Stock market dynamics are introduced through demand and supply for shares. At any instant, a chartist investor may either buy or sell a fixed amount of stock $t_N>0$; the optimistic chartists are the buyers and the pessimistic chartists are the sellers. Under these assumptions, the net demand of chartist investors is

$$\begin{aligned} D_N = n_+ \hspace{0.56917pt}t_N - n_{-} \hspace{0.56917pt}t_N = m T_N \end{aligned}$$

(24)

where $T_N= 2N t_N$ is the trading volume of chartists.

Only if $m=0$ would all trades of speculators be carried out within the group. Therefore, to close the model, Lux (1995) also introduces fundamentalists. Fundamental demand depends on the difference between the prevailing price p and a fundamental price ${\overline{p}}$:

$$\begin{aligned} D_F = T_F({\overline{p}}-p) \end{aligned}$$

(25)

where $T_F>0$ represents the trading volume of fundamentalists.

A market-maker sets the price in response to excess demand, such that

$$\begin{aligned} {\text {d}}p/{\text {d}}t = \mu [D_N + D_F] = \mu [m T_N + T_F({\overline{p}}-p)] \end{aligned}$$

(26)

with $\mu >0$ being a speed of adjustment coefficient.

To allow feedback from the market price to the disposition of chartists, Lux (1995) amends the switching probabilities in (22) as follows:

$$\begin{aligned} P_{+-} = v \exp (b_1 {\dot{p}}/v + b_2 m), \quad \quad P_{-+} = v \exp (-b_1 {\dot{p}}/v -b_2 m) \end{aligned}$$

(27)

where $b_1,b_2 > 0$, ${\dot{p}}$ denotes the time derivative of the price (i.e. the price trend), and the parameter $b_1$ is a weight that describes how the probability of switching disposition is affected by the price trend (as opposed to the prevailing sentiment, m, among chartists).

With this amendment, the system of contagion and price dynamics is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{m}} = 2v[\text {Tanh}(b_1 {\dot{p}}/v + b_2 m)-m]\text {Cosh}(b_1 {\dot{p}}/v + b_2 m) \\ {\dot{p}} = \mu [m T_N + T_F({\overline{p}}-p)] \end{array}\right. }. \end{aligned}$$

(28)

System (28) allows a rich variety of dynamic behaviours (see Lux 1995, Proposition 2):

• (i) For $b_2 \le 1$, there exists a unique (fundamental) steady state $E_f = (0,{\overline{p}})$

• (ii) For $b_2 > 1$, two additional steady states exist: $E_+ = (m_+,p_+)$, $E_{-} = (m_{-},p_{-})$, where $m_+>0$, $m_{-}=-m_+$ and $p_+-{\overline{p}}=-(p_{-}-{\overline{p}})>0$. If $E_{\pm }$ exist, $E_f$ is always unstable.

• (iii) When $E_f$ is a unique steady state, it may either be stable or unstable.

• (iv) If $E_f$ is unique and unstable, at least one stable limit cycle exists and all trajectories of the system converge to a periodic orbit.

Note that stability of the zero-contagion steady state ($E_f$) is no longer guaranteed when the herding parameter $b_2 \le 1$. Stability is favoured by low ‘responsiveness to trend’ $b_1$ and by high (low) values of the trading volume of fundamentalists $T_F$ (chartists $T_N)$.

As noted in part (iv), a cyclic motion prevails when $E_f$ is a unique steady state (i.e. $b_2 \le 1$) and the local stability condition is violated. In this case, the price switches between undervaluation and overvaluation as the disposition of chartists switches between pessimism and optimism. The price trend and sentiment reinforce each other in the upward and downward phases of the cycle; however, stationary majorities are avoided because contagion reaches a climax and declines thereafter, as illustrated in Fig. 3.²⁰

Fig. 3

Contagion and price dynamics: a non-fundamental steady states, b cycles

Finally, Lux (1995) shows that cycles are not ruled out when herding is strong ($b_2>1$) if the switching probabilities are amended with an ‘mood term’ that depends on average returns relative to average expected returns.²¹ This switching between bull and bear markets is related to opinion reversals of the speculative traders (i.e. chartists). In particular, as stock prices increase, the ‘mood’ is initially positive due to positive realized returns; however, once the overwhelming majority of chartists are bullish, the mood switches because the pool of potential buyers is exhausted, such that price increases start to diminish. Ultimately, this change in sentiment causes the bubble to collapse, and chartists then become more pessimistic and prices fall until the next bull market is triggered by diminishing deflation.

In Lux (1998) and Lux and Marchesi (1999), switching based on profit is introduced. The mechanism is similar to that in Brock and Hommes (1998), except that there are two types of chartists—optimistic and pessimistic—and the switching probabilities of these types are allowed to differ. In particular, the probabilities to switch from fundamentalist to optimistic chartist, from optimistic chartist to fundamentalist, from fundamentalist to pessimistic chartist, and from pessimistic chartist to fundamentalist are:

$$\begin{aligned} P_{+f}=\, & {} v_0 \frac{n_+}{2N} \exp (\beta U_1), \quad \quad P_{f+} = v_0 \frac{n_f}{2N} \exp (-\beta U_1) \\ P_{-f}=\, & {} v_0 \frac{n_{-}}{2N} \exp (\beta U_2), \quad \quad P_{f-} = v_0 \frac{n_f}{2N} \exp (-\beta U_2) \end{aligned}$$

where $v>0$ and $\beta \ge 0$ is the sensitivity of traders to the fitness measures $U_1$ and $U_2$.

The fitness measures $U_1$ and $U_2$ are based on the difference in profits between chartists and fundamentalists—in particular, the realized excess profit per share of chartists and the expected (discounted) profit of fundamentalists. There are two fitness measures $U_1$ and $U_2$ because optimistic chartists buy shares, while pessimistic chartists sell shares. Note that $n_+/2N$ ($n_{-}/2N$) is the probability of a fundamentalist meeting an optimistic chartist (pessimistic chartist), and $n_f/2N$ is the probability of a chartist meeting a fundamentalist.

Lux (1998) shows that the model with herding and performance-based updating has chaotic attractors for a wide range of parameter values. Consistent with empirical evidence, the distribution of price returns implied by the chaotic trajectories has higher peaks around the mean than the Normal distribution and fat tails. In a similar vein, Lux and Marchesi (1999) show that a version of the model with IID-Normal news arrival in the fundamental price generates volatility clustering in returns, a plausible frequency of extreme events, and other features of the empirical distribution of stock returns, such as a slower than exponential fall-off in the density of large price fluctuations that ‘dies out’ under time aggregation.

In short, a simple model that combines herding and performance-based type updating does well at replicating some key empirical regularities of stock market returns. The social aspects of the model—herding related to aggregate sentiment and updating of types based on meeting other investors—play a central role in the empirical performance of the model.

We now consider some alternatives to the models discussed above, which are based on social interactions. We then turn to network approaches to social communication.

4.2.4 Social interactions

Social interaction refers to a situation where the utility or payoff of an individual depends directly upon the choices of other individuals in their ‘reference group’. Note that such interactions differ from the (indirect) dependencies between individuals that occur through, say, market prices or congestion effects when all agents have ‘selfish’ utility. Social interactions include, for example, the behaviours of conformity and contrarianism. We first introduce a simple discrete choice model of social interactions (Brock and Durlauf 2001), and we then discuss how this approach has been used in the context of asset pricing.

Each individual in a population of N agents makes a binary choice $\omega _i \in \{-1,+1\}$. In an asset pricing context this could be the choice to buy or sell a stock, or the choice between two different price predictors. Let $\omega _{-i} = \{\omega _1,\ldots ,\omega _{i-1}, \omega _{i+1},\ldots ,\omega _N\}$ denote the choices of all agents other than i. The utility that agent i derives from choice $\omega _i$ has three components:

$$\begin{aligned} V(\omega _i) = u(\omega _i) + S(\omega _i,\mu _i^e(\omega _{-i})) + \epsilon (\omega _i) \end{aligned}$$

(29)

where $u(\omega _i)$ is private utility, $S(\omega _i,\mu _i^e(\omega _{-i}))$ is social utility that depends on i’s choice $\omega _i$ and on a generic conditional probability measure $\mu _i^e(\omega _{-i})$ that agent i places on the choices of other agents, and $\epsilon (\omega _i)$ is a random utility term that is assumed to be IID across agents.

A common specification for $\mu _i^e(\omega _{-i})$ is the mean expected choice of all other agents²²:

$$\begin{aligned} \mu _i^e(\omega _{-i}) = {\bar{m}}_i^e:= \frac{1}{N-1} \sum _{j \ne i} \omega _{i,j}^e \end{aligned}$$

(30)

where $\omega _{i,j}^e$ is the expected choice of agent j as forecast by agent i.

Brock and Durlauf (2001) consider a simple specification for the social utility term:

$$\begin{aligned} S(\omega _i,\mu _i^e(\omega _{-i})) = J \omega _i {\bar{m}}_i^e, \quad \quad J>0. \end{aligned}$$

(31)

Since $J>0$, the specification in (31) implies a positive externality from conforming to the average. In fact, maximizing (31) by choosing $\omega _i$ is equivalent to maximizing a conformity-based specification $S(\omega _i,\mu _i^e(\omega _{-i}))=-\frac{J}{2}(\omega _i-{\bar{m}}_i^e)^2$, since $\omega _i^2 = 1$ is independent of $\omega _i$.

The random utility terms $\epsilon (-1)$ and $\epsilon (1)$ are assumed to be independent with an extreme-value distribution, such that the differences in the errors follow a logistic distribution:

$$\begin{aligned} P(\epsilon (-1)-\epsilon (1) \le x) = \frac{1}{1+\exp (-\beta x)}, \quad \quad \beta \ge 0. \end{aligned}$$

Under these assumptions, the probability of individual choices follows a logistic model:

$$\begin{aligned} P(\omega _i) = \frac{\exp (\beta [u(\omega _i) + J \omega _i {\bar{m}}_i^e])}{\sum _{\omega _i \in \{-1,1\}} \exp (\beta [u(\omega _i) + J \omega _i {\bar{m}}_i^e])} \end{aligned}$$

(32)

where $\beta$ can be interpreted as the intensity of choice.

Note that the exponents in (32) may be nonlinear in $\omega _i$ due to the private utility $u(\omega _i)$. However, since $\omega _i \in \{-1,1\}$, the private utility can be replaced with a linear utility function ${\tilde{u}}(\omega _i) = k + h \omega _i$, where h and k are parameters that satisfy $h+k = u(1)$ and $k-h=u(-1)$, such that $h=(u(1)-u(-1))/2$. Note that the function ${\tilde{u}}(\omega _i)$ recovers $u(\omega _i)$ exactly, such that the probabilities in (32) can be simplified by replacing $u(\omega _i)$ with $k + h \omega _i$.²³

Using (30), the expected value of $\omega _i$ is given by

$$\begin{aligned} \begin{aligned} E[\omega _i]&= 1 \cdot \frac{\exp (2\beta [h + J {\bar{m}}_i^e])}{1 + \exp (2\beta [h + J {\bar{m}}_i^e])} + (-1) \cdot \frac{1}{1 + \exp (2\beta [h + J {\bar{m}}_i^e])} \\&= \text {Tanh} \left( \beta h + \frac{\beta J}{N-1} \sum _{j \ne i} \omega _{i,j}^e \right) . \end{aligned} \end{aligned}$$

(33)

Under common rational expectations, $\omega _{i,j}^e= E[\omega _i]$ for all i, j, so $E[\omega _i]=E[\omega _j]:= m^*$ for all i, j. In this case, (33) simplifies to

$$\begin{aligned} m^*= \text {Tanh} \left( \beta h + \beta J m^* \right) . \end{aligned}$$

(34)

Brock and Durlauf (2001) show that a rational expectations equilibrium $m^*$ always exists and, depending on parameters, there may be multiple solutions. For $\beta J<1$, (34) has a unique solution, whereas for $\beta J > 1$ , (34) has three solutions if either $h=0$ or $h \ne 0$ and $|\beta h|<H$ (where threshold H depends on $\beta J$) and a unique solution if $|\beta h|>H$.

With a dynamic model in discrete time $t \in {\mathbb {N}}$ and myopic expectations based on past mean choices, we have $\omega _{i,j,t}^e= m_{t-1}$ for all i, j and $\omega _{i,t}^e = m_{t}$ for all $i\in {\mathcal {N}}$, so by (33), we have:

$$\begin{aligned} m_t = \text {Tanh} (\beta h + \beta J m_{t-1} ). \end{aligned}$$

(35)

The steady states of (35) correspond to the rational expectations solutions $m^*$ discussed above. When there is a unique steady state (e.g. $\beta J<1$ or $|\beta h|>H$), this steady state is globally stable. On the other hand, if (35) has three steady states, then the middle one is locally unstable, whereas the other steady states are locally stable (see Hommes 2006). Thus, when there are multiple steady states, the system will settle at one of the extremes in which there is herd behaviour: all agents choose either $\omega _i=-1$ or $\omega _i=1$. In such cases, small differences in individual utility may lead to large changes in aggregate choices.

The social interactions approach is applied to asset pricing in Chang (2007, 2014). In these papers, the Brock–Hommes model is extended with myopic global interactions (see (35)), such that parameter h is the difference in fitness of chartists and fundamentalists. Interestingly, Chang (2007) shows that the strength of social interactions depends not just on the parameter J, but also on an ‘endogenous coefficient’ that reflects the characteristics of the predictors, such that the steady state version of (35) reads as:

$$\begin{aligned} m^* = \text {Tanh} (\beta J_g + \beta (J_b+J) m^* ) \end{aligned}$$

(36)

where $J_g,J_b$ are coefficients that depend on $m^*$ and $J_b$ generally differs from zero.²⁴

For the two-type model with chartists and fundamentalists Chang (2007) shows that additional steady states may exist if the strength of social interactions J is strong enough (i.e. if $\beta J > 1$), while weak social interactions ($\beta J < 1$) can give rise to attractors where the population share and asset price have a cyclical behaviour. Further, local stability of steady states can be quite sensitive to the strength of social interactions. In Chang (2014), herd behaviour and price bubbles are examined. The main finding is that for strong enough social interactions, a small deviation from the fundamental price may lead to herding that results in a price ‘bubble’ and causes the price-type dynamics to settle at a new steady state where herding is permanent and the asset is mispriced relative to fundamentals.²⁵

5 Networks and opinion dynamics

In the papers introduced so far, communication or social interactions are global. Empirical evidence, however, suggests that the interactions determining financial investment decisions are usually local; see Sect. 3. To model local interaction, some recent papers on communication and asset price dynamics employ results from the literature on opinion dynamics and the spread of diseases on networks.

This social network approach to communication has been widely used in the opinion dynamics literature and has some important advantages. First, networks provide a precise description of social connections that is general enough to nest many different communication structures observed in practice. Second, given increased availability of computing power and big data, there is now an empirical literature that estimates social networks directly. Third, networks are convenient both analytically and computationally because they can be analysed using the tools of linear algebra.

Despite these attractions, social networks have not been widely used in asset pricing models until recently. We therefore introduce useful network concepts in this section, before turning to recent literature that embeds social networks in asset pricing models.

5.1 Networks and notation

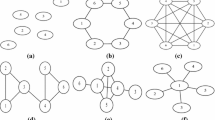
A network is fully described by the set of vertices and edges, which satisfies the definition of a graph in mathematics. In the context of economics and financial markets, the vertices represent the interacting agents or investors and are usually assumed to stay fixed over time. Hence, we use the same notation for the set of vertices that we used for the set of investors, i.e. ${\mathcal {N}}=\{1,\ldots ,N\}$. In this paper, we will not use the set-theoretic notation of the set of edges, but rather describe a network by its $N\times N$ adjacency matrix ${\textbf{A}}$. Figure 4 gives some example networks and their adjacency matrices where

$$\begin{aligned} {\textbf{A}}_a=\begin{bmatrix} 0&{}1&{}1&{}1\\ 1&{}0&{}1&{}0\\ 1&{}1&{}0&{}0\\ 1&{}0&{}0&{}0 \end{bmatrix},\; {\textbf{A}}_b=\begin{bmatrix} 0&{}1&{}0&{}0\\ 1&{}0&{}1&{}0\\ 1&{}0&{}0&{}0\\ 1&{}0&{}0&{}0 \end{bmatrix} \text { and } {\textbf{A}}_c=\begin{bmatrix} 0.5&{}0.5&{}0&{}0\\ 0.4&{}0.4&{}0.2&{}0\\ 0.6&{}0&{}0.4&{}0\\ 0.1&{}0&{}0&{}0.9 \end{bmatrix}. \end{aligned}$$

Fig. 4

a Undirected network ${\textbf{A}}_a$, b directed network ${\textbf{A}}_b$, and c weighted network ${\textbf{A}}_c$

In many applications, networks are binary such that the modeller only cares about whether two agents i and j influence each other or not. In this case, each entry $a_{ij}$ is of binary nature such that the restriction $a_{ij}\in \{0,1\}$ is imposed and an entry $a_{ij}=1$ denotes a link from agent i to agents j. Examples where the direction of the link matters include information flow, citations, or following behaviour in social media. Such a network can be represented by its directed edges as in Fig. 4b). A further restriction may require the network to be undirected which best describe bilateral relations like friendship, cooperations, or co-authorship. In this case, the adjacency matrix is restricted to be symmetric such that $a_{ij}=a_{ji}$ for all $i,j\in {\mathcal {N}}$ and an entry $a_{ij}=a_{ji}=1$ is referred to as a link between agents i and j. An example of an undirected network is given in Fig. 4a. Non-binary or weighted networks play a role for opinion dynamics to determine relative influences. In this case, a weighted network is required to be row stochastic to account for relative influences such that $\sum _{j\in {\mathcal {N}}}a_{ij}=1$ for all $i\in {\mathcal {N}}$ is imposed. While binary networks often impose the assumption that there are no self-links, i.e. $a_{ii}=0$ $\forall i\in {\mathcal {N}}$, this is often not the case for row-stochastic influence matrices, as these loops represent self-trust. An example of a weighted, row-stochastic network is drawn in Fig. 4c.

In the application of financial markets, information flow plays a crucial role. If the network represents information flow or influence between agents, then agents can only influence each other directly if they are connected by a link in the network ${\textbf{A}}$. To account for the direction of information flow, define $N^i({\textbf{A}}):=\{j\in {\mathcal {N}}:a_{ij}>0\}$ as the set of agents that i observes and let $M^i({\textbf{A}}):=\{j\in {\mathcal {N}}:a_{ji}>0\}$ be the set of agents that observe i. For example, in Fig. 4b, $N_1=\{2\}$ while $M_1=\{2,3,4\}$. Clearly for undirected networks, $N^i=M^i$ for all $i\in N$. In this case, the number of neighbours is called the degree and denoted by $\eta _i:=|N^i|$ for all $i\in {\mathcal {N}}$.

Agents can also influence each other indirectly via multiple connections. To capture this, define a walk from node i to node j of length $k\in {\mathbb {N}}$ by a sequence of connected nodes $(i^1,\ldots i^k)$ such that $a_{i^l,i^{l+1}}=1$ for all $1\le l\le k-1$ and $i^1=i$ and $i^k=j$. Note that a walk of length k from i to j exists, if and only if we have $({\textbf{A}}^k)_{ij}>0$ where ${\textbf{A}}^k$ denotes the k-th power of the matrix ${\textbf{A}}$. The set of nodes that lie on a walk that starts in node i are defined as ${\mathcal {W}}^i:=\{j\in N|\exists k\in {\mathbb {N}}: ({\textbf{A}}^k)_{ij}>0\}.$ Clearly, ${\mathcal {W}}^j\subseteq {\mathcal {W}}^i$ for all $j\in {\mathcal {W}}^i$. For instance, ${\mathcal {W}}^4=\{1,2,3,4\}$ in ${\textbf{A}}_b$ in Fig. 4c and ${\mathcal {W}}^j=\{1,2,3\}$ for $j=1,2,3$.

A subset of agents ${\mathcal {C}}\subset {\mathcal {N}}$ is said to be strongly connected if there is a walk from any $i\in {\mathcal {C}}$ to any $j\in {\mathcal {C}}$, i.e. $j\in {\mathcal {W}}^i$ for all $i,j\in {\mathcal {C}}$. Thus, information can flow between any two agents of a strongly connected subset. For instance, the sets $\{1,2\}$ and $\{1,2,3\}$ are the only strongly connected (non-singleton) sets in Fig. 4a–c. A subset of agents ${\mathcal {C}}\subset {\mathcal {N}}$ is said to be closed if there exists no walk from any $i\in {\mathcal {C}}$ to any outsider $j\in {\mathcal {N}}\setminus {\mathcal {C}}$, i.e. ${\mathcal {W}}^i\subseteq {\mathcal {C}}$ for all $i\in {\mathcal {C}}$. Note, that the sets $\{1,2,3\}$ and $\{1,2,3,4\}$ are the only closed sets in Fig. 4a–c. Thus, the notion of walks induces a partition of the set of agents into communication classes $\Pi ({\mathcal {N}},{\textbf{A}})=\{{\mathcal {C}}_1,{\mathcal {C}}_2,\ldots ,{\mathcal {C}}_K,{\mathcal {R}} \}$ such that the sets ${\mathcal {C}}_k$ are strongly connected and closed and ${\mathcal {R}}$ denotes the (possibly empty) rest of the world of agents not belonging to a strongly connected and closed set. Note that there always exists at least one non-empty strongly connected and closed set ${\mathcal {C}}$ for each network. A network is called strongly connected if ${\mathcal {N}}$ is strongly connected. In the examples of Fig. 4a–c, the set $\{1,2,3\}$ is the only closed and strongly connected communication class and the singleton set $\{4\}$ is the rest of the world.

The distance between two nodes i and j in network ${\textbf{A}}$ is defined as the minimal walk length denoted by $d(i,j):=\min \{k\in {\mathbb {N}}:({\textbf{A}}^k)_{ij}>0\}$. A path between two nodes i and j is a shortest walk, i.e. a walk with distance d(i, j). If two nodes are not connected by a walk, we set $d(i,j)=\infty$. Clearly a network is strongly connected if $d(i,j)<\infty$ for all $i,j\in N$. The diameter of the network is given by $D({\textbf{A}})=\max _{i,j\in N}d(i,j)$.

5.1.1 Network centrality

In many applications, the centrality of nodes (e.g. investors) in a network plays an important role. This is also true if we think about opinion dynamics, information flow, and influence in networks as discussed later. Before economists paid attention to networks, a large body of literature in sociology introduced measures to assess how central an agent is in a network.

The most straightforward way to define a node’s centrality is to count the neighbours, which is also called the degree centrality of an agent. Clearly, such a centrality measure ignores large parts of the network structure and may be too simple for many applications. More elaborated centrality measures take into account more structural properties of the network which may be intuitively thought of as assessing network ‘flows’ (Borgatti 2005).

Taking into account only the shortest possible network flows, i.e. paths between nodes in the network, Freeman (1979) defines the seminal measures of Closeness and Betweenness centrality. Closeness centrality simply discounts the distance d(i, j) between any two nodes such that agents with many short paths to others receive a high closeness centrality. Betweenness centrality, on the other hand, considers all paths between any two nodes and counts for each node $i\in {\mathcal {N}}$ the respective share of paths which pass through i.²⁶

Reducing network flows to only the shortest possible ones may be relevant in some applications, but often this assumption is a bit restrictive. For instance, Betweenness centrality only takes into account the paths between any two nodes. Potential outside options via walks of greater distance play no role. Similarly, information flows usually take place not only along walks of minimum distance, but also along all possible walks in a network.

Seminal notions of centrality taking into account all network flows, were developed by Katz (1953) and Bonacich (1987). In a similar spirit as Freeman closeness centrality, Bonacich centrality discounts the length of all possibly walks between any two nodes by a parameter $0<\delta <\lambda _1({\textbf{A}})^{-1}$ where $\lambda _1({\textbf{A}})$ is the eigenvalue of ${\textbf{A}}$ having largest modulus. The idea is that agents with many short walks to others receive a high Bonacich centrality. This centrality measure can be alternatively expressed by a self-referential notion such that the centrality index proposed by Bonacich (1987), $b_i({\textbf{A}})$, is given by, $b_i({\textbf{A}},\delta )=1+\delta \sum _{j\in N^i({\textbf{A}})}b_{j}({\textbf{A}},\delta )$ for all nodes $i\in {\mathcal {N}}$. This self-referential notion expresses the idea that an agent is central, if the neighbours are central (see e.g. Hellmann 2021, for more details). Similar ideas trace back to Katz (1953) who defined status of a node to be high if the status of observing neighbours $M^i$ is high. The most straightforward way to define this is to directly impose the condition that centrality is proportional to the sum of centralities of neighbours, i.e. $c_i({\textbf{A}})=\frac{1}{\lambda }\sum _{j\in M^i}c_j({\textbf{A}})$, with $\lambda$ being some constant. This system of equations can be rewritten in matrix notation such that

$$\begin{aligned} \lambda {\textbf{c}}({\textbf{A}})={\textbf{c}}({\textbf{A}}){\textbf{A}}. \end{aligned}$$

(37)

For this system of equations to have a solution, $\lambda$ must be an eigenvalue and ${\textbf{c}}({\textbf{A}})$ must be a (left) eigenvector of ${\textbf{A}}$. Usually, $\lambda$ is assumed to be the largest eigenvalue such that all entries of the eigenvector are guaranteed to be real (by Perron Frobenius). For instance, the principal eigenvalue of the weighted network in Fig. 4c is $\lambda =1$ (since ${\textbf{A}}_c$ is row stochastic) and the eigenvector normalized such that entries sum to unity is ${\textbf{c}}({\textbf{A}}_c)=(\frac{18}{38},\frac{15}{38},\frac{5}{38},0)'$. Note that nodes from the rest of the world always receive eigenvector centrality of 0. PageRank developed by Google founder Larry Page uses similar ideas (but introduces additional scaling factors) and helped Google dominate over other search engines.

One advantage of the eigenvector based centrality measures defined in Eq. (37) is that it not only applies to binary networks, but can also be applied for weighted and directed networks. We show in Sects. 6.3.3 and 7.2.2 that these centrality measures appear in applications of opinion formation and belief formation in financial markets.

5.1.2 Random networks

The networks discussed so far have deterministic links. When the modeler does not know the entire network or wants to use degree distributions rather than the precise structure of the network, a simplifying assumption is that network formation is random. The most straightforward way to model random networks is to assume that all links in an (undirected) network form with some probability p which is identical and independent across all links. Erdös and Rényi advanced the findings for such models in such a way that these types of random networks are often referred to as Erdös and Rényi networks; see e.g. Erdös and Rényi (1959, 1960). Due to their simplicity, Erdös and Rényi random networks provide a good benchmark to compare with empirical facts in order to find out how real-world networks differ from purely random networks (see also Sect. 6.2).

For Erdös and Rényi networks, it is quite easy to calculate the degree distribution as this is binomial. The probability that a given node has exactly $\eta$ neighbours is given by

$$\begin{aligned}P(\eta )=\begin{pmatrix} N-1 \\ \eta \end{pmatrix} p^{\eta }(1-p)^{N-1-\eta } \end{aligned}$$

For large N and small p, this degree distribution is well approximated by a Poisson distribution such that the fraction of nodes that have $\eta$ links is given by $\frac{\exp (-(N-1)p)\left( (N-1)p\right) ^\eta }{\eta !}$.

Erdös and Rényi networks already appear in Cont and Bouchaud (2000) where trading groups are determined by the random network (see Sect. 5.2.2). More recently, Granha et al. (2022) apply these types of random graphs in an agent-based model to analyse opinion dynamics of noise traders and fundamentalists.

Other approaches to random networks aiming to capture some real-world phenomenon directly impose degree distributions. One example is the class of scale-free networks where the degree distribution follows a power law, i.e. which can be written as

$$\begin{aligned} P(\eta )=k\eta ^{-\kappa } \end{aligned}$$

(38)

where k is a constant ensuring that the probabilities sum to unity and $\kappa \in {\mathbb {R}}_+$. In a log-log plot mapping degrees to probabilities (or relative frequencies of observations), such a distribution is given by a straight line. Scale-free networks seem to better capture some stylized facts about real world networks which we present subsequently and which play an important role in diffusion models; see Sect. 6.3.

5.2 Stylized facts of real-world networks

Many real-world networks across different contexts share common properties. In this section, we only sketch some stylized facts about real-world networks and refer the reader to textbooks such as Watts (1999) or Jackson (2008) and references therein for more details.

• Connectivity Social networks with many participants are often quite sparse, i.e. each node is only connected to a very small subset of nodes. As a case in point, Ugander et al. (2011) study Facebook data from 2011 and find that out of 721 million users, the median friend count is 99 with most users having less than 200 friends (out of a possible 721 million connections).

• High clustering Clustering refers to the likelihood that three connected nodes in an undirected network form a ‘clique’ which means that they are completely connected. To put it simply, it is a measure determining the likelihood that two neighbours of a node are neighbours themselves. In Erdös and Rényi networks where links form independently, two friends of a given node are not more likely to be friends themselves than any two random nodes. Instead, in real-world networks, this is clearly not the case and clustering is quite high. For instance while the global Facebook network is quite sparse, the clustering coefficient is independent of the number of friends and is estimated at 0.14, which is quite high compared to the relative frequency of links (see above).

• Small worlds The small world property refers to the fact that many real-world networks have small diameters relative to the number of nodes and small average distances although networks are sparse and highly clustered. This was observed by Milgram (1967) in the famous letter experiments where participants had to send a letter to unknown persons within the USA by only sending and forwarding letters to acquaintances. The experiments seemed to confirm the phrase ‘six degrees of separation’ since the median number of steps for a letter to reach a target was 5, although this phrase was not used by the authors themselves. Modern studies (Backstrom et al. 2012) using global Facebook data (with more than 1.59 billion facebook users) estimate the average distance to be 4.57, corresponding to 3.57 intermediaries or ‘degrees of separation’.

• Degree distribution The distribution of (the number of) neighbours in a network usually does not follow a Poisson distribution as would be expected for sparse but large networks if links form with IID probability, as in Erdös and Rényi networks. Instead, the distribution of degrees in real-world networks often exhibits fat tails: nodes with very high degrees and with very low degrees occur a lot more frequently than expected from a Poisson distribution. Some studies find that the degree distributions of real-world networks are well-approximated by scale-free power law distributions, see (38). For instance, Liljeros et al. (2001) study the network of human sexual contacts in Sweden and conclude that the degree distribution is well approximated by a power law. Multiple studies also confirm that the world wide web has a scale-free degree distribution (Albert et al. 1999, 2000; Caldarelli et al. 2000; Medina et al. 2000). In particular, scale-free networks satisfy the fat tails property, though not all studies on the degree distribution of real-world networks confirm a strict power law.²⁷

• Assortativity Many studies have found real-world networks to exhibit positive assortativity with respect to degrees. In other words, nodes with many neighbours will be connected to other nodes with many neighbours with higher probability than under pure random network formation. For instance, Newman (2003) finds a high correlation of neighbouring nodes’ degrees in scientific co-authorship networks. One network structure with positive assortativity is the core-periphery structure composed of a well-connected core and a sparse periphery of nodes (see Borgatti and Everett 2000,and references therein); this structure is observed quite frequently in social and financial contexts—e.g. the institutional funds market has this sort of hierarchical structure (Alfarano et al. 2013). An example core-periphery structure is presented in Fig. 5.

Fig. 5

A core periphery network with core $\{1,\ldots ,5\}$ and periphery $\{6,\ldots ,9\}$

5.3 Models of diffusion and opinion formation in networks

Particularly relevant for communication and asset prices is the theory of how information (respectively diseases) or opinions and beliefs spread through a network. We present here two models in epidemiology, the SIR model and the SIS model, and a model of opinion formation, the so-called DeGroot model, that have recently been used to model the spread of information or types within models of communication on networks and asset prices.

The SIR and the SIS model are diffusion models originating in epidemiology and use networks to model local interaction. In this case, networks are usually assumed to be random to allow aggregation over transmission probabilities or use of mean-field approaches. Typical questions include infection rates and diffusion thresholds at which a phase transition occurs from only a small fraction of the population being infected to the large parts of the population catching the disease. Such approaches have been applied to find relative frequencies of chartist and fundamentalist types and diffusion thresholds in asset pricing models.

The DeGroot model instead assumes a fixed network that is allowed to be directed and weighted, thus modeling relative influences. Research focuses on long-run opinions, consensus, time to convergence, and wisdom of the crowds. This approach has been recently applied model the dynamics of investor types and asset prices.

5.3.1 The SIR model

The most widely used model of the spread of diseases like the recent Covid-19 pandemic, influenza virus, or sexually transmitted diseases is the susceptible-infected-removed (SIR) model. Individuals can be in one of three states: (a) susceptible which means that they are susceptible to becoming, (b) infected upon contact with other infected (which entails that they stay infected for some time) before getting, and (c) removed (e.g. becoming immune) such that they cannot become infected anymore and, therefore, cannot infect others. Such models date back to the 1920 s but have been studied using networks in the last two decades. Newman (2002) studies a large class of randomly generated networks and assumes pair-specific transmission rates. This extension of the classical SIR model also nests the more complex disease transmission models such as SEIR models in which there is an infected but-not-infective period (E). Depending on the network-generating function, Newman (2002) characterizes the outbreak sizes, the epidemic transition, threshold and the fraction of infected individuals (infection rate).

Newman applies this methodology to the spread of sexually transmitted diseases assuming a scale-free power law distribution as in Liljeros et al. (2001) and shows that these types of networks have a lower epidemic transition threshold than the fully mixed SIR model where no network is assumed. In the SIS model, which we introduce in more detail in the next section, the epidemic threshold is zero in scale-free networks, and this explains why scale-free networks are particularly susceptible to diffusion.

The SIR model on random networks has been used beyond epidemiology to model, e.g. social influence and, more relevant in our context, communication and investment behaviour. The idea is that being infected can be viewed as holding a positive opinion about investing, an optimistic expectation of asset returns, or a buy signal. For instance, Shive (2010) shows that the infection rate in the SIR model is a good predictor of investment decisions and returns of investors in the Finnish stock market, as we explain in Sect. 7.4.²⁸

5.3.2 The SIS model

The other seminal model from epidemiology is the so-called SIS model which stands for susceptible-infected-susceptible. Compared to the SIR model which assumes removal (immunity, death) after infection, the SIS model has only two possible states: susceptible and infected. In other words, this implies that after infection, individuals become susceptible again which makes this model useful to model the spread of diseases that only have a short-term immune reaction (or no immune reaction at all) as with the common cold or computer viruses (Pastor-Satorras and Vespignani 2001).

The model has found some application in economics (Jackson and Rogers 2007; López-Pintado 2008) as the SIS model can easily be interpreted as diffusion of behaviour like adopting a product where adoption rates depend on the number of others using the same product. In most contexts of diffusion of economic actions, the SIS model is a better choice than the SIR model if economic agents can easily switch between actions (and hence do not obtain immunity). Such switching is easy, for example, in liquid financial markets, and there is evidence that investors trade too often to maximize profit (Odean 1999).

A general treatment of the SIS model can be found Bailey et al. (1975) and has been applied to scale-free networks by Pastor-Satorras and Vespignani (2001). To show how the SIS model works with networks, we follow the presentation of López-Pintado (2008): at any time $t\in {\mathbb {N}}$ each individual $i\in {\mathcal {N}}$ is either susceptible, denoted by $s_{i,t}=0$ or infected denoted by $s_{i,t}=1$. The state of the system at time $t\in {\mathbb {N}}$ is described by a vector ${\textbf{s}}_t=(s_{i,t})_{i\in {\mathcal {N}}}$ with $s_{i,t}\in \{0,1\}$ for all $i\in {\mathcal {N}}$. Agents are connected by a random network according to some degree distribution $P(\eta )$. A susceptible agent i with a number of infected neighbours $a_i$ becomes infected with probability

$$\begin{aligned} F(\nu ,\eta _i,a_i)=\nu f(\eta _i,a_i) \end{aligned}$$

where $\nu$ is the spreading rate and f is called the diffusion function. A very simple example of a diffusion function is $f(\eta _i,a_i)=a_i$ as in Jackson and Rogers (2007) where the infection probability is linear in the number of infected neighbours. After infection, individuals ‘heal’ with probability $\delta$ in each period—i.e. an infected agent j becomes susceptible again with probability $\delta$ independently of neighbours’ infection status. The effective spreading rate is then denoted by $\lambda =\nu /\delta$.

Although the dynamical system is clearly a time-homogeneous continuous Markov Chain, closed-form characterizations become intractable quickly for arbitrary network structures. The literature often reverts to a mean-field approximation (Pastor-Satorras and Vespignani 2001; Jackson and Rogers 2007; López-Pintado 2008). An important underlying assumption in using the mean-field approach is that the random network is re-generated at every time step, meaning that an agent with degree $\eta$ makes $\eta$ new and independent draws from the population ${\mathcal {N}}$ at each time step $t\in {\mathbb {N}}$. Further, the mean-field approximation only holds for large populations (infinite N); hence, it is an approximation for most contexts.

Denoting by $\theta (t)$ the probability that a given link is to an infected individual, we get that the number of infected neighbours is binomial which implies that the transition probability from susceptible to infected is given by $g_{\nu ,\eta }(\theta (t))=\sum _{a=1}^\eta \nu f(\eta ,a)\begin{pmatrix} \eta a \end{pmatrix}\theta (t)^a(1-\theta (t))^{\eta -a}$.²⁹

The mean-field equation for the relative density of infected agents at time t with a degree $\eta$, denoted by $\rho _\eta (t)$, can be written as

$$\begin{aligned} \frac{\partial \rho _\eta (t)}{\partial t}= (1-\rho _\eta (t)){\tilde{g}}_{\nu ,\eta }(\theta _t)-\rho _\eta (t)\delta . \end{aligned}$$

(39)

The first part of (39) is the fraction of susceptible nodes that become infected and the second part is the fraction of infected nodes that recover to become susceptible.

A steady state is such that $\frac{\partial \rho _\eta (t)}{\partial t}=0$ and, hence, requires $\rho _\eta =\frac{{\tilde{g}}_{\nu ,\eta }(\theta )}{\frac{1}{\delta }+{\tilde{g}}_{\nu ,\eta }(\theta )}.$ Averaging over all relative frequencies $\rho _\eta$ implies that for a steady-state probability of linking to an infected node $\theta$ we get $\theta =\frac{1}{E_P(\eta )}\sum _{\eta \ge 1}\eta P(\eta )\rho _\eta$, where $E_P(\eta )=\sum _{\eta }\eta P(\eta )$ denotes the average degree given degree distribution $P(\eta )$. Together this gives

$$\begin{aligned} \theta =\frac{1}{E_P(\eta )}\sum _{\eta \ge 1}\eta P(\eta )\frac{{\tilde{g}}_{\nu ,\eta }(\theta )}{\frac{1}{\delta }+{\tilde{g}}_{\nu ,\eta }(\theta )}. \end{aligned}$$

(40)

Any solution to the recursive Eq. (40) is a steady state of the dynamical system. For any degree distribution and any diffusion function f, there may exist multiple steady states. For instance, $\theta =\rho _\eta =0$ for all degrees $\eta$ is always a steady-state infection level, but there can also exist steady states with positive infection rates.

Whether a positive steady state exists is determined by the effective spreading rate $\lambda =\frac{\nu }{\delta }$ inherent in the disease (or: economic behaviour). If the effective spreading rate $\lambda$ exceeds a critical threshold $\lambda _c$, then a positive steady state exists (assuming that infection requires infected neighbours, i.e. $f(\eta ,0)=0$). If multiple steady states exist, the only stable steady state is a nonzero one, if the diffusion function f is weakly concave as shown in López-Pintado (2008). In other words, the critical threshold marks a phase transition in the sense that if starting from an infinitesimally small part of the population, the disease dies out when the effective spreading rate is below the critical threshold, but it infects a positive fraction of the population at any point in time otherwise.

The following holds for the threshold $\lambda _c$ under weakly concave diffusion functions:

• The critical threshold is given by

  $$\begin{aligned} \lambda _c=\frac{E_P(\eta )}{\sum _{\eta }\eta ^2P(\eta )f(\eta ,1)} \end{aligned}$$

  and thereby depends on the network via the degree distribution $P(\eta )$ and is independent of the diffusion function $f(\eta ,a)$ for all $a>1$. For the simple case of the diffusion function being independent of $\eta$ (Jackson and Rogers 2007), this implies $\lambda _c=\frac{E_P(\eta )}{E_P(\eta ^2)}$.

• In the case of a scale-free network, where the degree distribution $P(\eta )$ follows a power law (see (38)), we have $V_P(\eta ^2)=E_P(\eta ^2)=\infty$, which implies that $\lambda _c=0$. In other words, the infection can spread regardless of how small the effective spreading rate $\lambda$ is. Hence, there is no epidemic threshold in scale-free networks meaning that any disease will spread to a positive fraction of the population, which was already pointed out by Pastor-Satorras and Vespignani (2001) and which is empirically confirmed for computer viruses. The intuition behind this is that there are many hubs (high-degree nodes) in scale-free networks which are likely to become infected because of their high exposure and then spread the disease/virus to many other nodes.

• Other types of networks can be compared in terms of epidemic thresholds, and comparative statics results between degree distributions are obtained in López-Pintado (2008) and Jackson and Rogers (2007) using mean-preserving spreads and stochastic dominance relations.

In the context of communication and asset price dynamics, the SIS model has been used to study the adoption of chartist behaviour in a network of investors (Gong and Diao 2022), as we discuss in more detail in Sect. 7.3.1.

5.3.3 The DeGroot model

While both the SIR and the SIS model have their origins in epidemiology and have been applied as models of social influence, a more direct and straightforward way to model opinion dynamics has been proposed by DeGroot (1974). Suppose each individual $i\in {\mathcal {N}}$ initially holds an opinion or a belief $g^i_0$ about some underlying state of nature. At discrete time steps $t\in {\mathbb {N}}$, individuals communicate with each other. How individuals take each other’s opinions into account is described by a weighted network ${\textbf{A}}$ where the entry $a_{ij}$ denotes the updating weight. Since only relative influences matter, the network ${\textbf{A}}$ is assumed to be row stochastic such that $a_{ij}\ge 0$ and $\sum _{j\in {\mathcal {N}}}a_{ij}=1$ for all $i\in {\mathcal {N}}$.

The most radical assumption in DeGroot (1974) is that individuals update according to the same network ${\textbf{A}}$ at each time step $t\in {\mathbb {N}}$. Thus, given individuals hold opinions $g^j_t$ in period $t\in {\mathbb {N}}$ for each $j\in {\mathcal {N}}$, we get that individual $i's$ opinion in period $t+1$ is given by

$$\begin{aligned} g_i(t+1)=\sum _{j\in {\mathcal {N}}}a_{ij}g_j(t). \end{aligned}$$

(41)

This assumption entails that opinions are updated naïvely and influence does not vary over time. While rational updating is beyond the scope of this article,³⁰ we briefly present the literature dealing with time-varying updating matrices/networks below.

Denoting the vector of opinions at time step $t\in {\mathbb {N}}$ by $\textbf{g}_t=(g^1_t,\ldots , g^N_t)$, (41) can be written as a power series of the network ${\textbf{A}}$ such that

$$\begin{aligned} \textbf{g}(t+1)={\textbf{A}}\textbf{g}(t)={\textbf{A}}^{t+1} \textbf{g}(0) \end{aligned}$$

(42)

Steady states of this dynamical system are such that $\textbf{g}={\textbf{A}}\textbf{g}$. In other words, a vector of opinions is a steady state of the opinion dynamics if and only if it is a unit eigenvector of the matrix ${\textbf{A}}$. An eigenvalue equal to 1 always exists since ${\textbf{A}}$ is row stochastic and, hence, has a spectral radius equal to 1.

Not all row stochastic matrices imply that opinions converge to a steady state. For instance, the $2\times 2$ matrix ${\textbf{A}}$ with entries $a_{ii}=0$ and $a_{ij}=1$ for $i\not =j$ has opinions alternating and never obtaining a steady state if initial opinions differ. Such a matrix is called periodic. A common assumption to rule out periodicity is to assume that the diagonal of ${\textbf{A}}$ is strictly positive, which seems reasonable in many contexts of communication.

If ${\textbf{A}}$ is aperiodic, the opinion dynamics always converges to a steady state $\textbf{g}(\infty )$ such that the following holds (see e.g. Golub and Jackson 2010; Buechel et al. 2015):

• Each closed and strongly connected communication class ${\mathcal {C}}_i$ obtains a long-run consensus which is given by $g_{j}(\infty )={\textbf{v}}_{{\mathcal {C}}_i}'\textbf{g}_{{\mathcal {C}}_i}(0)$ for all $j\in {\mathcal {C}}_i$ where ${\textbf{v}}_{{\mathcal {C}}_i}$ is the left unit eigenvector of the matrix ${\textbf{A}}_{{\mathcal {C}}_i}$ which has its entries sum to 1.³¹ In other words, the consensus obtained in each closed and strongly connected group is the weighted average of the initial opinions of its members where the weights are determined by the eigenvector centrality of each group member; see (37). The more central an individual is in the network within a closed and strongly connected communication class, the higher the influence of this individual’s initial opinion on the consensus. Each closed and strongly connected communication class is not influenced by opinions outside this class. Further, the absolute value of the second largest eigenvalue $\lambda$ of ${\textbf{A}}_{{\mathcal {C}}_i}$ is a measure of how fast opinions in ${\mathcal {C}}_i$ converge to consensus. Greater values of $|\lambda |$ imply slower convergence of opinions and can be thought of as a measure of how similar individuals are connected.³²

• The opinions in the rest of the world are formed as weighted averages of the consensuses reached in the closed and strongly connected communication classes according to the connections that each member of the rest of the world has. Since these may differ, the rest of the world usually does not obtain a consensus if there is more than one closed and strongly connected group. Formally, the long-run vector of opinions in the rest of the world is given by,

  $$\begin{aligned} \textbf{g}_{\mathcal {R}}(\infty )=\sum _{i=1}^K(I-{\bar{{\textbf{A}}}}_{{\mathcal {R}}{\mathcal {R}}} )^{-1}{\bar{{\textbf{A}}}} _{{\mathcal {R}}{\mathcal {C}}_i}\textbf{g}_{{\mathcal {C}}_i}(\infty ) \end{aligned}$$

  where $\textbf{g}_{{\mathcal {C}}_i}(\infty )=g_{i}(\infty )\textbf{1}_{{\mathcal {C}}_i}={\textbf{v}}_{{\mathcal {C}}_i}'\textbf{g}_{{\mathcal {C}}_i}(0)\textbf{1}_{{\mathcal {C}}_i}$ is the consensus vector in each ${\mathcal {C}}_i$ such that $\textbf{1}_{{\mathcal {C}}_i}$ denotes the $|{\mathcal {C}}_i|\times 1$ vector with all entries equal to 1.

The classical model of opinion dynamics dating back to DeGroot (1974) has been extended in multiple directions in recent decades. For instance, Golub and Jackson (2010) study how well this naïve model of opinion formation performs in terms of information aggregation when there is an underlying true state of nature and initial opinions are unbiased random variables. Golub and Jackson show that there is wisdom of the crowds when there are many non-central individuals. Other studies allow the influence matrix ${\textbf{A}}$ to vary over time in models where individuals only update from others with close opinions Hegselmann and Krause (2002); when self-trust varies over time (DeMarzo et al. 2003); when cultural traits are transmitted across generations (Buechel et al. 2014); or when opinions can be misrepresented to account for conformity or contrarianism (Buechel et al. 2015). A general treatment of time-varying influence matrices in the model of opinion dynamics can be found in a series of studies by Lorenz (see e.g. Lorenz 2005, 2007). A time-inhomogeneous version of the DeGroot model is used to model communication between different investor types in Hatcher and Hellmann (2022), which we discuss in more detail in Sect. 7.2.2.

6 The state of the art: networks and asset prices

In this final section we review recent contributions the literature on communication in social networks and asset price dynamics. We focus on works that build on the network approaches outlined in the previous section by setting out asset pricing models with local social networks of some kind. We then discuss leading empirical work that has estimated social network models using financial data, thus giving an empirical perspective on these models. Finally, we conclude with some thoughts on useful directions for future research.

6.1 An early model

Yang (2009) studies opinion formation in an asset market. There are N investors, and $p_t$ is the asset price in period t. Investor i’s forecast of the future price is $\tilde{E}_t^i[p_{t+1}]$, dividends are zero, and there is no risk-free asset. Therefore, the demand of investor i is a simple function of their price forecast (see (10)). Let $k_t^i$ be the exogenous capital ratio of investor i at time t, with $\sum _{i=1}^N k_t^i=1$. Note that $k_t^i$ may be interpreted either as the relative capital available to a single investor, or the share of total capital available to a particular investor type. Given these assumptions and a fixed asset supply, the pricing equation is³³

$$\begin{aligned} p_t = \sum _{i=1}^N k_{t}^i \tilde{E}_t^i[p_{t+1}] \end{aligned}$$

(43)

An investor’s price expectation $\tilde{E}_t^i[p_{t+1}]$ is influenced by their social network. Analogous to the DeGroot model, the social network weights ${\tilde{a}}_{ij} \in [0,1]$ measure the (relative) influence of agent j on agent i such that $\sum _{j\in {\mathcal {N}}}{\tilde{a}}_{ij}=1$ holds, giving rise to the row stochastic network $\tilde{{\textbf{A}}}$.

Investor i’s price expectation is given by the weighted opinion of their neighbours:

$$\begin{aligned} \tilde{E}_t^i[p_{t+1}] = \sum _{j=1}^N {\tilde{a}}_{ij} F_t^j \end{aligned}$$

(44)

where $F_t^j$ is investor j’s date-t opinion about the future price $p_{t+1}$ and depends, in a chartist manner, on past prices up to some lag:

$$\begin{aligned} F_t^j = f(p_{t-1},\ldots ,p_{t-m_j}), \quad \quad 1 \le m_j \le M \end{aligned}$$

(45)

with $m_j$ being the ‘memory span’ of investor j and M being the longest memory span.

Thus, past prices combined with memory spans determine investor opinions, which in turn determine price expectations (by (44)) and therefore the current asset price by (43). Hence, there is feedback from past prices to investor opinions and to current prices, with the feedback strength depending on the influence weights in the matrix ${\tilde{{\textbf{A}}}}$.

Substitution of (44) and (45) into (43) shows that the price dynamics are given by a difference equation with maximum order M. Letting $\mathbf{{P}}_t:= (p_t,p_{t-1},\ldots ,p_{t-M+1})'$, (45) can be written as $F_t^j = f_j(\mathbf{{P}}_{t-1})$ and, therefore, the price equation (43) can be written as

$$\begin{aligned} p_t = \sum _{i=1}^N k_{t}^i \left( \sum _{j=1}^N {\tilde{a}}_{ij} f_j(\mathbf{{P}}_{t-1}) \right) \end{aligned}$$

(46)

such that the price vector $\mathbf{{P}}_t$ is given by a first-order difference equation:

$$\begin{aligned} \mathbf{{P}}_t = \Phi (\mathbf{{P}}_{t-1}):= \begin{bmatrix} \sum _{i=1}^N k_{t}^i \left( \sum _{j=1}^N {\tilde{a}}_{ij} f_j(\mathbf{{P}}_{t-1}) \right) \\ (\mathbf{{I}}_{M-1} \quad \mathbf{{0}}_{M-1}) \mathbf{{P}}_{t-1} \end{bmatrix} \end{aligned}$$

(47)

where $\mathbf{{I}}_{M-1}$ is the identity matrix of size $M-1$ and $\mathbf{{0}}_{M-1}$ is an ($M-1$)-vector of zeros.

The stability of the price dynamics depends on the Jacobian matrix ${\textbf{J}}$ of (47). Proposition 1 in Yang (2009) provides a general stability condition of the form $||\mathbf{{Q}}_t|| < R({\textbf{J}}_{Q_t})$, where $\mathbf{{Q}}_t = [q_t^1 \hspace{7.11317pt}q_t^2\ldots q_t^M]$ is the first row of the Jacobian matrix and $R({\textbf{J}}_{Q_t})$ is the stability radius of the characteristic equation. As an example, Yang (2009) considers the L-1 norm $||{\textbf{x}}||_1 = \sum _{i=1}^N |x_i|$ and shows the stability condition in this case amounts to $||\mathbf{{Q}}_t||_1 < 1/M$. The social weighting matrix $\tilde{{\textbf{A}}}$ matters for price stability as it influences the value of $||\mathbf{{Q}}_t||$.

The relative influences in ${\tilde{{\textbf{A}}}}$ are assumed to result from an undirected network structure ${\textbf{A}}$ where each investor $i\in {\mathcal {N}}$ has degree of at least 1, i.e. $\eta _i\ge 1$. The degree matrix is given by ${\textbf{H}}= \text {diag}[\eta _1,,\ldots ,\eta _N]$, which is an $N \times N$ diagonal matrix with degrees on the diagonal.

The influence matrix ${\tilde{{\textbf{A}}}}$ is then given by

$$\begin{aligned} {\tilde{{\textbf{A}}}} = \alpha {\textbf{H}}^{-1} {{{\textbf{A}}}} + (1-\alpha )\mathbf{{I}}_N, \quad \quad 0< \alpha \le 1. \end{aligned}$$

(48)

The parameter $\alpha$ can be interpreted as the relative weight on other connected investors’ opinions versus the investor’s own opinion. Because ${\tilde{{\textbf{A}}}}$ is row stochastic, 1 is an eigenvalue of ${\tilde{{\textbf{A}}}}$ and all eigenvalues lie in the unit circle.

Yang (2009) illustrates the implications of different network structures with numerical examples. The four chosen networks of size $N=5$ and are called power law network (abusing notation) ${\textbf{A}}^{PL}$, star network ${\textbf{A}}^{S}$, ring network ${\textbf{A}}^{R}$, and complete network ${\textbf{A}}^{C}$.³⁴ Further, the functional form for investors beliefs is assumed to be linear:

$$\begin{aligned} F_t^i = \frac{1}{m_i}( p_{t-1}+\ldots +p_{t-m_i} ), \quad \text { for } i=1,\ldots ,5. \end{aligned}$$

Investor (node) $i\in \{1,\ldots ,5\}$ is given a price memory of length $m_i=i+1$, such that $M=6$. Yang (2009) considers three values of the relative weight $\alpha$: 0.1, 0.5 and 0.9, where higher values mean more emphasis on opinions of others versus own opinion.

The numerical results are relatively tricky to interpret. One observation is that the complete network has a comparatively larger stability space that the other networks, i.e. it is more likely that the dynamic system will be stable.³⁵ There is no clear pattern in terms of dynamic stability when the other networks are compared against each other. Further, the stability space was larger for higher values of $\alpha$, meaning influence from other agents. Thus, opinion exchange is most effective if agents are well connected, are equally important, and place high weight on others which may ‘diffuse’ potentially destabilizing beliefs of individual investors. In a second experiment, the central node in the star network was given a longer memory horizon and the stability space in this case was close to that of the complete network, suggesting that a central investor with more feedback data from the past is stabilizing relative to having a central but myopic agent.

The results of Yang (2009) show the potential of social network asset pricing models. At the same time, there are some clear limitations of the analysis—for instance, the implications of different network structures for price stability can be difficult to interpret, and the performance of social connections is ignored by investors.³⁶ As discussed below, some recent works have tried to fill this gap by providing models in which asset price dynamics depend on the financial performance of social contacts and can easily be related to properties of networks, such as degree, eigenvector centrality and network diameter.

6.2 Performance-based updating in social networks

Both Panchenko et al. (2013) and Hatcher and Hellmann (2022) set out asset pricing models in which investor types depend on the relative performance of neighbours on a social network. We discuss these papers in this section, starting with Panchenko et al. (2013).

6.2.1 Brock–Hommes model with local networks

Panchenko et al. (2013) extend the two-type Brock and Hommes model with local social networks. Recall that in the original model (see Sect. 5.2.1) investors are either chartist or fundamentalist and update their type after observing differences in profit across a large population of investors. The profitability of each investor—and their type— is thereby visible to every other investor (i.e. public information). Seen this way, it is clear that the original Brock–Hommes model uses a specific social structure: a complete network.

To investigate local social interactions, Panchenko et al. study four different networks: the complete network (which nests the Brock–Hommes model); a regular lattice where each agent has degree $d=4$; a Erdös and Rényi random graph; and a small world network. The small worlds network is adapted from Watts and Strogatz (1998) and results from a regular lattice with additional random links, and can be motivated by the observation that real-world networks are sparse and clustered, and have a small diameter (see Sect. 6.2).³⁷

The investors are represented by the nodes of the social network and can observe the performance (past profitability) only of those investors who reside on the nodes directly connected to them. Hence, an investor who is connected to investors of a different type has the possibility to switch type, whereas an investor connected only to investors of the same type will not update at that time step. Let $P_{i,t}$ denote the probability that investor i adopts the chartist type in period t, and let $I_{i,t}$ be an indicator variable equal to 1 (0) if investor i has the chartist (fundamentalist) type at date t. The evolution of $P_{i,t}$ is described by

$$\begin{aligned} P_{i,t} = {\left\{ \begin{array}{ll} 0 &{} \hbox { if}\ I_{j,t-1} = 0 \quad \forall j \in N^i \\ 1 &{} \hbox { if}\ I_{j,t-1} = 1 \quad \forall j \in N^i \\ \Delta _t: = \frac{\text {exp}(\beta U_{t}^c )}{ \text {exp}(\beta U_{t}^c ) + \text {exp}(\beta U_{t}^f ) } &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(49)

where $N^i$ is the set of investors that i observes (including herself), $\Delta _t \in (0,1)$ is a probability with $U_t^h$ being past profit associated with belief type h, and $\beta \ge 0$ is the intensity of choice.

Equation (49) states that i does not update their type at date t if either they are a chartist and all their neighbours are chartists, or if they are a fundamentalist and all their neighbours are fundamentalists. If investor i has at least one neighbour with a different type to herself, then her probability of updating to the chartist type is given by the discrete choice logistic probability $\Delta _t \in (0,1)$ as in the original Brock–Hommes model; see (14). Note that $\Delta _t$ does not depend on the number of chartist neighbours that investor i has.

For the case of a complete network, the set of neighbours of any given investor i is all other investors, such that $P_{i,t} = \Delta _t$ for all $i\in {\mathcal {N}}$ and t (excluding degenerate cases where all investors start with, or adopt by chance, the same type). If we then let the number of investors increase without bound, then by the law of large numbers we recover original Brock–Hommes model in which $n_t^c= \Delta _t$ is the chartist population share.

In the case of local social networks, tractable analytics are hard to come by. However, Panchenko et al. (2013) show that for a random graph and an infinitely large population of investors, the population share of chartists is approximated by

$$\begin{aligned} n_t^c = (n_{t-1}^c)^{k+1} + [1-(n_{t-1}^c)^{k+1}-(1-n_{t-1}^c)^{k+1}]\Delta _t \end{aligned}$$

(50)

where k is the average degree of the random graph.

As k increases the population share dynamics approximate complete network case, and for $k \rightarrow \infty$ we recover the original Brock–Hommes population dynamics: $\lim _{k \rightarrow \infty } n_t^c= \Delta _t$. In this case, the price-type dynamics are given by the original model (10)–(16). For small values of k, however, the population dynamics—and hence the price dynamics in (16)—can be very different to the original Brock–Hommes model.

Panchenko et al. (2013) establish the following results for existence and stability of steady states in the case of the degree-k random graph³⁸

• Case 1: $0<g<1+r$. For $\beta <\beta ^{tr}$ there are three fundamental steady states: one with all chartists $E_1$; one with all fundamentalists $E_0$; and one ${\overline{E}}$ with chartist share ${{\overline{n}}}^c \in [0.5,1)$. ${\overline{E}}$ is stable and $E_0,E_1$ are unstable. At $\beta = \beta ^{tr}$, a transcritical bifurcation occurs. For $\beta > \beta ^{tr}$, ${\overline{E}}$ does not exist, $E_1$ becomes stable, and $E_0$ remains unstable.

• Case 2: $1+r< g < 2(1+r)$. For $\beta < \beta ^*$, there are three fundamental steady states: $E_0$, $E_1$, ${\overline{E}}$. $E_0,E_1$ are unstable and ${\overline{E}}$ is stable. At $\beta = \beta ^*$, a pitchfork bifurcation occurs, ${{\overline{E}}}$ loses stability and two non-fundamental steady states $E_+$ and $E_{-}$ emerge. For $\beta ^*< \beta < \beta ^{**}$, $E_+$ and $E_{-}$ are stable. At $\beta =\beta ^{**}$ there is a Neimark-Sacker bifurcation and $E_+$, $E_{-}$ lose stability for $\beta >\beta ^{**}$. $E_0$ and $E_1$ are unstable for any $\beta$.

• Case 3: $g > 2(1+r)$. There are three fundamental steady states $E_0$, $E_1$, ${\overline{E}}$ and two non-fundamental steady states, $E_+$ and $E_{-}$. All the fundamental steady states are unstable. The two non-fundamental steady states are stable for $\beta < \beta ^{**}$.

Relative to the original Brock–Hommes model, the main differences are as follows. First, for a relatively small trend-following parameter $g <1+r$, there are now two ‘corner’ fundamental steady states where all investors have a single type (either all chartist or all fundamentalist). Second, for intermediate values of the trend-following parameter $g \in ((1+r),2(1+r))$, the bifurcation values $\beta ^*$ and $\beta ^{**}$ are lower than in the original Brock–Hommes model. The bifurcation values are increasing in k, and in the limit as $k \rightarrow \infty$ they converge on the original bifurcation values. Finally, for strong trend extrapolation $g>2(1+r)$, the non-fundamental steady state is stable for $0< \beta < \beta ^{**}$, but this region may be relatively small as just noted.

The implications of the other two networks—regular lattice and small world—are studied using numerical bifurcation diagrams in which the intensity of choice $\beta$ is increased. The results indicate that the regular lattice and small world networks have similar bifurcation values to the random network, which are much smaller than those for the complete network (i.e. the original Brock–Hommes model for the same parameter values). Hence, the price dynamics are more sensitive to investors willingness to switch type in response to past performance, and market stability in the sense of convergence to the fundamental price is far less robust to increases in $\beta$ once we deviate from the complete network assumption.

Panchenko et al. (2013) also document the impact of the networks on some time series properties such as return autocorrelations (both squared and in levels), but stop short of a full empirical assessment of the different networks. In light of this, a useful exercise for future research would be to identify which types of network structures perform best empirically. Since a complete network can be nested in the above model, explanatory power will at least match the original Brock and Hommes (1998) model, but we would hope to identify empirically-plausible networks for which the model’s quantitative performance is improved.

6.2.2 Repeated-averaging in networks and performance weights

The discrete belief types approach in Brock and Hommes (1998) can be contrasted with belief updating in the opinion dynamics literature. The latter approach allows individuals to form beliefs (or ‘types’) which are continuous and may potentially differ from those of all other individuals. In an asset pricing context this means that—depending on the network structure—investors with initially different types may either converge to a long-run type consensus or remain permanently heterogeneous in terms of types (as explained below).

Hatcher and Hellmann (2022) take this approach. In their model, there are N investors who are connected via a social network in each period $t \in {\mathbb {N}}$. The links between investors are described by the network matrix ${\textbf{A}}$, with $a_{ij} =1$ if i observes j and $a_{ij}=0$ otherwise. The network diameter is denoted $D({\textbf{A}})$. Each investor observes herself, so $a_{ii} = 1$ for all $i\in {\mathcal {N}}$. Note that $a_{ij} =1$ has the interpretation that investor i receives advice from investor j before taking investment decisions. The risky asset is in fixed net supply $X \ge 0$.

Individual demands $x_t^i$ follow the Brock and Hommes and Panchenko et al. models (see (10)); however, an important difference is that investors adopt personal subjective beliefs rather than being restricted to two polar types (chartist or fundamentalist). Investors update their beliefs based on observed relative performance in their social network using repeated-average updating rather than a discrete choice approach. In particular, beliefs are determined by individual-specific types on the spectrum from pure fundamentalist to arbitrarily strong chartist; it is these types which are updated and ultimately determine an investor’s beliefs.

Specifically, an investor’s price expectation (or belief) is a type-weighted combination of the chartist and fundamentalist beliefs. Investor i’s type is denoted by $g^i_t \in {\mathbb {R}}_+$. Accordingly, the price expectation of investor i is given by

$$\begin{aligned} \begin{aligned} \tilde{E}_t^i[p_{t+1}]&=g^i_t\tilde{E}_t^c[p_{t+1}] +(1-g^i_t)\tilde{E}_t^f[p_{t+1}] \\&= g^i_t p_{t-1} +(1-g^i_t) {\overline{p}} \end{aligned} \end{aligned}$$

(51)

where ${\overline{p}}$ is the fundamental price and $p_{t-1}$ is an (unbiased) chartist belief.³⁹

Note that the beliefs in (51) generalize the two-type model in which an investor must adopt either a chartist or a fundamentalist belief in a given period. Investors can thus differ in terms of how strongly chartist or fundamentalist they are in their thinking—i.e. they form an expectation on the range between fundamentalist and arbitrary strong chartist.

Types are updated according to

$$\begin{aligned} g_{t+1}^i= \sum _{j\in N^i} \frac{\exp (\beta U_t^j)}{\sum _{k\in N^i}\exp (\beta U_t^k)} \ g_t^j, \qquad \forall i \in {\mathcal {N}}\end{aligned}$$

(52)

where $N^i$ is the set of neighbours of investor i, $U_t^j$ is the past profit earned by investor j given their belief type, and $\beta \ge 0$ is a performance-weight parameter.

The type updating in (52) bears some resemblance to the discrete choice approach. In particular, the updating weights, $\exp (\beta U_t^j)/\sum _{k\in N^i}\exp (\beta U_t^k)$, for each neighbour have the interpretation that investor j’s type is weighted according to their relative performance against other neighbours of investor i. However, in contrast to the local-networks version of the Brock–Hommes model in Panchenko et al. , an investor i is not restricted to two fixed types (fundamentalist or chartist) but instead takes a weighted average of types among their neighbours. As a result, both the types and the fractions of investors adopting a given type are endogenously determined in the model.

The parameter $\beta$ is similar to the intensity of choice in the discrete choice approach. For finite $\beta$, investors consider the belief types of all investors in their social network, and better-performing investors receive a higher weight for $\beta >0$. If $\beta =0$, performance is irrelevant and the types of every neighbour in i’s social network are given the same weight $\frac{1}{ |N^i|}$ in the updating Eq. (52); i.e. updating is purely social. For the other polar case $\beta \rightarrow \infty$, investors update only from the best-performers in their social network in each period.⁴⁰

The vector of types ${\textbf{g}}(t)=(g_1(t),\ldots ,g_n(t))'$ is thus updated according to

$$\begin{aligned} {\textbf{g}}({t+1})={\tilde{{\textbf{A}}}}(t){\textbf{g}}({t}) \end{aligned}$$

(53)

where ${\tilde{{\textbf{A}}}}(t)=\left[ {\tilde{a}}_{ij}(t)\right] _{i,j\in {\mathcal {N}}}$ and ${\tilde{a}}_{ij}(t):= a_{ij} \frac{\exp (\beta U_t^j)}{\sum _{k\in N^i}\exp (\beta U_t^k)}$ are the updating weights.

Given price beliefs of the form (51), market-clearing $\sum _{i=1}^N x_t^i = X$ determines the price of the risky asset. With $\tilde{p}_t:= p_t - {\overline{p}}$ denoting the deviation of the price from the fundamental price, the price equation has a simple form:

$$\begin{aligned} \tilde{p}_t = \frac{ {\overline{g}}_t}{1+r} \tilde{p}_{t-1} \end{aligned}$$

(54)

where ${\overline{g}}_t = \frac{1}{N} \sum _{i=1}^N g_i(t)$ is the average type in the population. The initial price is $\tilde{p}_0 \ne 0$.

Relative to the Brock and Hommes model, the average type in the population enters in place of the population share of chartists scaled by the fixed trend-following parameter. As a result, the long-run price dynamics will depend crucially on whether the average type ${\overline{g}}_t$ converges to a limit as $t \rightarrow \infty$, and the on value of the limit when it exists.

By (53) and (54), we have the following: (i) price converges to the fundamental price ${\tilde{p}}=0$ if $\lim _{t \rightarrow \infty } {\overline{g}}_t < 1+r$; and price diverges to $+\infty$ or $-\infty$ if $\lim _{t \rightarrow \infty } {\overline{g}}_t > 1+r$; (ii) if $\lim _{t \rightarrow \infty } {\overline{g}}_t =1+r$, price converges to some $\tilde{p} \in {\mathbb {R}}$. Note that if ${\overline{g}}_t$ does not converge to a finite limit, then price may converge, price may diverge to $+\infty$ or $-\infty$, or there may be permanent price oscillations. Price is guaranteed to converge for any initial price $\tilde{p}_0$ if all investors are initially weak chartists ($g_i(0) \le (1+r)$ $\forall i\in {\mathcal {N}}$) and is guaranteed to diverge to either $+\infty$ or $-\infty$ for any $\tilde{p}_0$ if all types are initially strong chartists ($g_i(0) > (1+r)$ $\forall i\in {\mathcal {N}}$).⁴¹

With initial types either side of $1+r$, price oscillations occur if ${\overline{g}}_t$ fluctuates between values $>(1+r)$ and $<(1+r)$ as $t \rightarrow \infty$, and the long-run price dynamics depend on how strongly chartist is the long-run average type in the population. The latter depends on the coupled price-type dynamics (53) and (54), whose evolution depends on the social network ${\textbf{A}}$ and performance-weighted updating in response to realized returns that include stochastic dividends. In the polar cases $\beta =0$ and $\beta \rightarrow \infty$, there are tractable analytical results.

Since for $\beta =0$ performance of neighbours is ignored, the type dynamics (53) are independent of the price dynamics. In this case, type updating from neighbours is purely social as in the time-homogeneous DeGroot (1974) model and the type dynamics follow a process akin to that described in Sect. 6.3.3.⁴² In the long-run, each closed and strongly connected group ${\mathcal {C}}$ forms a consensus $g_{{\mathcal {C}}}(\infty )$ that is a weighted average of initial types such that these weights are given by eigenvector centrality and the rest of the world forms an average of the consensuses in the closed and strongly connected groups. A simple conclusion in terms of price stability is the following:

• Price stability can be fully characterized in terms of the network structure (via eigenvector centrality of the investors) and the initial types by taking the long-run average type ${\bar{g}}_{\infty }=\sum _{i\in {\mathcal {N}}}g_i(\infty )$.

• For instance, price divergence to $+\infty$ or $-\infty$ is likely if strong chartists ($g_i(0)>1+r$) are central in the network or have a large population share, whereas price stability is more likely if more fundamental types ($g_i(0)<1+r$) are influential or many. At the knife-edge ${\bar{g}}_{\infty }=1+r$ where strong chartists and fundamentalists are offsetting, the price will converge to a value that may deviate from the fundamental price.

For $\beta \rightarrow \infty$, investors update only from best-performing neighbours (given realized profit). In this case, average initial sentiment ${\bar{g}}_0$ is crucial as it determines whether chartists or fundamentalists perform better, and the initial price $\tilde{p}_0$ also matters if the risky asset is in positive net supply. Hatcher and Hellmann (2022) focus on the case of deterministic dividends and give analytical results for consensus. Here, we concentrate on the results under zero net supply $X=0$, which can be summarized as follows⁴³:

• If ${\bar{g}}_0<(1+r)^2$, any investor $i\in {\mathcal {N}}$ adopts the most fundamental type within the set ${\mathcal {W}}^i$ in finite time and keeps this type forever, implying closed and strongly connected groups form a consensus on the most fundamental type. Analogous conclusions hold with respect to adoption of the most chartist type within the set ${\mathcal {W}}^i$ if ${\bar{g}}_0>(1+r)^2$.

• The time to adoption of such an extreme type depends on the distance to an investor carrying the extreme type initially. In a strongly connected network, all investors will have adopted the most fundamental, respectively the most chartist type, by time step $t\ge 2D({\textbf{A}})-1$ which depends on network diameter $D({\textbf{A}})$.

• Price always diverges if ${\bar{g}}_0>(1+r)^2$ or if $g_0^{\min }<(1+r)$. Price always converges to the fundamental price if $g_0^{\min }<(1+r)$ and ${\bar{g}}_0<(1+r)^2$. In a strongly connected network, the other direction of both statements holds, too (i.e. if and only if holds).

Relative to the case $\beta =0$, there are some dramatic differences. The in-group consensuses no longer depend on eigenvector centrality, but instead go to the maximum or minimum initial type in the group (depending on whether ${\bar{g}}_0<(1+r)^2$ or ${\bar{g}}_0>(1+r)^2$ which determines whether high or low types earn higher profit). Hence, the network only has an indirect impact on consensus by determining group membership. With consensus on extreme types, price stability is likely if initial chartist sentiment is low (${\bar{g}}_0<(1+r)^2$) and impossible if initial chartist sentiment is high (${\bar{g}}_0>(1+r)^2$).

Though network structure plays little role in determining the type consensuses when investors are strongly focused on performance, network diameter influences time to convergence. To see the implications, suppose the network is strongly connected and there exists at least one pure fundamentalist, i.e. $g_i(0) =0$ for some i. If ${\bar{g}}_0<(1+r)^2$, consensus is on the pure fundamental type of 0, so $\tilde{p}_t = 0$ for all $t\ge 2D({\textbf{A}})-1$ (see (53)). In this case, the market is efficient in the long run, but not in the short run, and the maximum distance between investors gives an upper bound on the date when mispricing is eliminated.

For intermediate $0<\beta <\infty$, Hatcher and Hellmann (2022) show by simulation that agents adopt a long-run type that is a weighted average between the eigenvector centrality based type (network determined type) and one of the extreme types (performance determined type). The weights depend on the intensity of choice $\beta$ in a continuous but non-linear way such that the intensity of choice $\beta$ scales between the network determined type and the performance determined type.

There are also two further numerical applications. First, Hatcher and Hellmann show that if $\beta \rightarrow \infty$ and the dividend shock variance is large enough, the consensus is hard to predict and may differ substantially from the ‘extreme type’ prediction in the deterministic case because the performance ranking will switch if dividend shocks change the sign of realized returns. At the same time, time to convergence varies dramatically and is highest for intermediate shock variances, so even small noise is enough to delay the ‘long run’ substantially. In a second exercise, they consider a deterministic model with positive outside supply and both a stubborn fundamentalist and a stubborn chartist who are followed by others but do not change their type. Here, permanent price fluctuations arise when $\beta$ is sufficiently large; the reason is that with positive outside supply, the performance ranking of types can switch endogenously when price moves either side of a price threshold which is itself endogenous.

While the above results are interesting, it is an open question whether belief updating is better modelled by a discrete-choice approach as in Brock and Hommes (1998) or by the approach in Hatcher and Hellmann (2022). Future empirical work may be of help here.

6.3 Diffusion models with social networks

A third strand of recent modelling work has considered diffusion-based models of investor beliefs with explicit social networks. We focus, in particular, on the theoretical paper of Gong and Diao (2022) and the empirical contribution of Nicolas (2022).⁴⁴

6.3.1 A SIS-type model

Gong and Diao (2022) consider a model with imitation and performance-based updating. There are N investors in the population, where N is large. Investors are connected in an undirected random network. Let $\eta _i$ denote the degree of investor i and $P(\eta )$ the degree distribution. Investors have either a chartist or a fundamentalist type, and there are two groups of investors, A and B. Investors in group A care about what their neighbours do but ignore strategy performance; investors in group B follow a Brock–Hommes updating rule.

In group A the investors imitate each other according to a SIS mechanism. The degree distribution of group A satisfies $\sum _{i \in A}P_A(\eta _i)=1$, where $P_A(\eta _i)$ is the fraction of the population in group A with $\eta _i$ neighbours. The population fractions of groups A and B are $\delta$ and $(1-\delta )$ (respectively); under these assumptions we have the interpretation that investors imitate other investors’ trading strategies with (herding) probability $\delta$ and consider past profit with probability $(1-\delta )$. Investors who update type based on profitability compare profit under the chartist and fundamentalist trading strategies and select the chartist strategy with the usual discrete choice probability $\Delta _t$ in (49), with $U_t^h$ being the (net) profit of type h.⁴⁵ Given the assumption of a large population, the fraction of chartists in group B is $\Delta _t$.

Asset demands are determined as in the Brock and Hommes (1998) model (see (10)). For investors in group B, beliefs are determined by profits as just discussed. For investors in group A, the imitation dynamics determine their belief at each t (and hence their demand). The diffusion framework is based on the SIS model (see Sect. 6.3) adopted from López-Pintado (2008), with $v_f$ being the probability that a chartist type switches to a fundamentalist type after contact with a fundamentalist. Analogously, $v_c$ is the switching probability of a fundamentalist type that meets a chartist.

For an investor $i \in A$ with $\eta _i$ neighbours, we have $\eta _i = a_i + b_i$, where $a_i$ ($b_i$) is the number of fundamentalist (chartist) neighbours. Gong and Diao (2022) assume that investor i’s imitation decision depends on the conditional probabilities $\nu _h$ and the number ($\eta _i$) of neighbours and their composition ($a_i,b_i$). In particular, the respective probabilities of switching from the fundamentalist type to the chartist type at time $t+1$, and vice versa, are:

$$\begin{aligned} F(\nu _c,\eta _i,b_i) = \nu _c \frac{b_i}{\eta _i^\lambda }, \quad \quad F(\nu _f,\eta _i,a_i) = \nu _f \frac{a_i}{\eta _i^\lambda } \end{aligned}$$

(55)

where $\lambda \ge 0$ represents a neighbourhood effect.

The larger is $\lambda$, the more attention investors pay to the relative number of neighbours who have different trading strategies. For $\lambda =0$, the imitation mechanism matches the standard SIS model, in which the switching probability is proportional to the number of neighbours with the other type. Note that the parameters $\nu _c$ and $\nu _f$ in the diffusion functions (55) are the spreading rates of the trading strategies. Let $\theta _t$ be the probability of meeting an investor adopting the fundamental strategy at date t. Via the binomial distribution, the rates at which an investor in group A with $\eta$ neighbours switches state from chartist to fundamentalist is $\nu _f \theta _t \eta ^{1-\lambda }$, and the switching rate fundamentalist to chartist is $\nu _c (1-\theta _t) \eta ^{1-\lambda }$.

Gong and Diao (2022) show the mean-field equations for the switching dynamics are⁴⁶

$$\begin{aligned} \rho _{\eta ,t+1} - \rho _{\eta ,t} = (1-\rho _{\eta ,t})\nu _f \theta _t \eta ^{1-\lambda } - \rho _{\eta ,t}\nu _c (1-\theta _t) \eta ^{1-\lambda } \end{aligned}$$

(56)

$$\begin{aligned} \theta _t = \delta \sum _{\eta >0} \frac{P_A(\eta ) \eta }{\langle \eta \rangle } \rho _{\eta ,t} + (1-\delta )(1-\Delta _t) \end{aligned}$$

(57)

where $\rho _{\eta ,t}$ is the share of degree-$\eta$ investors adopting the fundamental strategy at date t, and $1-\Delta _t$ is the share of fundamentalists in group A. Note that the population share of fundamental investors in group A is $\rho _t:= \sum _{\eta >0} P_A(\eta ) \rho _{\eta ,t}$.

Equation (56) is the population dynamics of investors in group A, while (57) is the probability $\theta _t$ of meeting a fundamentalist in the entire population. Recall that an investor picked at random is in group A with probability $\delta$ and group B with probability $(1-\delta )$. Given the assumption of a large number of investors, the market population shares are:

$$\begin{aligned} n_t^f = \delta \rho _t + (1-\delta )(1-\Delta _t), \quad \quad n_t^c = \delta (1-\rho _t) + (1-\delta )\Delta _t. \end{aligned}$$

(58)

It follows that per-investor demand for the risky asset at date t is $x_t = n_t^c x_t^c + n_t^f x_t^f$. The price is set by a market-maker who updates the price in response to past excess demand according to $p_{t+1} = p_t + \mu x_t$, such that the deviation of price from the fundamental price is:

$$\begin{aligned} {\tilde{p}}_{t+1} = {\tilde{p}}_t + \mu x_t, \quad \quad \mu >0. \end{aligned}$$

(59)

Gong and Diao (2022) first consider steady states of the above system. There exist only fundamental steady states with ${\tilde{p}} = 0$ and $\rho _k^* = \frac{\nu _f \theta ^*}{\nu _f \theta ^*+\nu _c (1-\theta ^*)}$, where $\theta ^* = n^f$, such that $\rho _k^*$ is independent of the degree $\eta$ (and hence network structure). They also show the following:

• If the spreading rates $\nu _c$ and $\nu _f$ differ, or if $\nu _c=\nu _f$ and $\delta \in [0,1)$, then there is a unique fundamental steady state. Otherwise, there are infinitely many steady states corresponding to the many different values of $\theta ^*$ such that $\rho _k^* = \theta ^*$.

• When $\nu _f > \nu _c$ and $\delta \in [0,1)$, the fundamental strategy is adopted with higher probability in the market than warranted by its relative performance (i.e. $\theta ^*>n^f$).

Having studied steady states, Gong and Diao (2022) proceed to stability analysis. For $\lambda =1$, only the composition of neighbours matters for imitation (see (55)) and network structure is irrelevant. In this case, stability is favoured if the price adjustment parameter $\mu$ is small, if $\delta$ is large, and if the intensity of choice $\beta$ is not too large or too small; further, herding can aid market stability, even if herding is on the chartist strategy. For $\lambda \ne 1$ the network structure matters and stability is weakened as the Jacobian has a unit eigenvalue. Further, a market with conservative investors ($\lambda >1$) is more likely to be stable than one with aggressive investors ($\lambda <1$), like the standard SIS model, where $\lambda =0$ and only the absolute number of neighbours matters for contagion. Finally, Gong and Diao show that for small $\lambda$, the stability condition is less likely to be satisfied for large variance of the degree distribution, $\langle \eta ^2 \rangle$. In such cases, network structure is important for market stability.

6.3.2 An estimated Lux-type model with sentiment data

A diffusion-based asset pricing model is taken to the data in Nicolas (2022). In particular, the Lux herding model is adapted to include a social network and is estimated using a sentiment index based on 15 US stocks and five cryptocurrencies. Fundamental investors are absent, so the population of investors consists of chartists (i.e. speculators) who may be either optimistic or pessimistic. Accordingly, at time t there are $n_+$ optimistic investors and $n_{-}$ pessimistic investors; the overall population size is therefore $2N = n_+ + n_{-}$.⁴⁷

The prevailing sentiment $m \in [-1,1]$ is given by

$$\begin{aligned} m = \frac{n}{N} = \frac{n_+ - n_{-}}{2N}, \quad \quad \text {where }n:= (n_+ - n_{-})/2. \end{aligned}$$

(60)

If $m >0$ ($<0$) then optimistic (pessimistic) investors are predominant in the population; hence $m>0$ can be interpreted as positive sentiment and $m<0$ as negative sentiment. Switches between optimism and pessimism are governed by transition probabilities analogous to those in (22), except for the inclusion of an ‘intercept term’ $b_0$:

$$\begin{aligned} P_{+-} = v \exp (b_0 + b_1 m), \quad \quad P_{-+} = v \exp (-b_0 - b_1 m). \end{aligned}$$

(61)

where $b_1:= \kappa N$, such that $\kappa$ can be interpreted as a ‘strength of herding’ parameter.

In the Lux (1995) model, each individual forms their opinion knowing the current societal configuration, which is equivalent to investors being fully connected via a complete network. Accordingly, the coefficient $b_1$ in (61) is proportional to N, reflecting more interactions in a large population. In a model with large N, however, this assumption is hard to justify because individuals can only participate in a limited number of interactions (e.g. due to congestion). Further, as discussed in Sect. 6, real-world networks have properties such as clustering and sparsity, which are inconsistent with a complete network.

Nicolas (2022) therefore augments the model with local social networks. Given the definition of n in (60), the social configuration of neighbours of investor i is defined by

$$\begin{aligned} n(i,N^i) = (n_+(i,N^i) - n_{-}(i,N^i))/2 \end{aligned}$$

(62)

where $N^i$ is defined as the set of investors to which i is connected (excluding self).

For tractability, a mean-field approximation is used as in Alfarano and Milaković (2009). Under this assumption, heterogeneity is negligible and (62) can be approximated by

$$\begin{aligned} \langle n(i) \rangle = (\langle n_+(i) \rangle - \langle n_{-}(i)\rangle )/2. \end{aligned}$$

(63)

Define ${\bar{\eta }}$ as the average number of neighbours per investor ($=$ average degree of the network). At the mean-field approximation, every investor has ${\bar{\eta }}$ neighbours. Therefore, taking $n_+/2N$ and $n_{-}/2N$ as approximations to the unconditional probabilities that a neighbour of investor i is, respectively, optimistic or pessimistic, yields:

$$\begin{aligned} \langle n_+(i) \rangle = {\bar{\eta }} \frac{n_+}{2N}, \quad \quad \langle n_{-}(i)\rangle = {\bar{\eta }} \frac{n_{-}}{2N}, \end{aligned}$$

such that (63) is given by

$$\begin{aligned} \langle n(i) \rangle = {\bar{\eta }} ( n_+ - n_{-})/2N = \frac{{\bar{\eta }}}{2} m \end{aligned}$$

The transition probabilities are therefore amended from (61) to

$$\begin{aligned} P_{+-} = v \exp (b_0 + {\tilde{b}}_1 m), \quad \quad P_{-+} = v \exp (-b_0 - {\tilde{b}}_1 m) \end{aligned}$$

(64)

where ${\tilde{b}}_1:= \kappa {\bar{\eta }}$ is independent of the number of investors (i.e. does not depend on N).

The key difference between (64) and (61) can be seen by letting $N \rightarrow \infty$. The transition probabilities (61) in the original Lux model depend on the coefficient $b_1$, which explodes as N is increased. By comparison, the transition probabilities in (64) depend on ${\tilde{b}}_1$, which is scale-independent due to the fixed average number of interactions ${\bar{\eta }}$ of each investor.

There are two important advantages of this approach. First, the problem of N-dependence highlighted by Alfarano and Milaković (2009) is avoided, such that increasing the number of agents does not lead to a lack of robustness in the macroscopic properties of the model. Second, because the coefficient ${\tilde{b}}_1$ does not explode, it becomes feasible to estimate the herding parameter using a dataset with large N. Both these properties are important from an empirical perspective since real-world markets—and datasets—often have many investors.

Nicolas (2022) estimates the model using data extracted from the StockTwits social media platform. The sample period is daily 1 Jan 2018 to 1 Jan 2021, and the sample consists of 15 US stocks and five cryptocurrencies which trended on the platform during the sample period (based on discussion activity). To construct a sentiment index m, sentiment analysis was used to classify messages as either bullish, bearish or neutral, giving a weekly measure of overall sentiment. Alongside this, price and returns data for the assets was also obtained at weekly frequency. The model was estimated using maximum likelihood methods.

The estimation results for the parameter $\tilde{b}_1$ indicate a strong influence of investor interactions in the formation of sentiment that is stronger for high volatility assets, consistent with the hypothesis that herding behaviour is linked to higher volatility levels. Further, for the five cryptocurrencies that experienced a bubble in late 2017, the herding effects were found to be particularly strong during this bubble period. As noted by Nicolas (2022), these results cast doubt on the efficient markets view that traders make decisions independently of one another and ignore non-fundamental information such as investor sentiment.

6.4 Empirical work and model estimation

As we have seen, recent work has added explicit social networks in asset pricing models. Alongside these new models there have been attempts to estimate real-world investor networks and asset pricing models in which social networks are embedded. In this section, we discuss these leading empirical works as well as recent developments in methods for estimating financial market models with heterogeneous agents.

Early work which investigated the impact of social influences in investment decisions found that investors rely on advice from close contacts, such as friends and relatives, and consider communication with industry experts as one of the most important factors in their decisions. This initial work relied on surveys of investors, but subsequent literature also identified social connections based on asset holdings: mutual fund managers have similar asset holdings to those of other fund managers in the same city, while households are more likely to purchase stocks from a particular industry if their neighbours did so.⁴⁸

Shive (2010) sets out an epidemic model of the stock market: the basic idea is that investors with a strong opinion about a stock are likely to take a position (infection) and share their opinion with others (spread the ‘infection’). Consistent with the SIR model, the infection rate is assumed to be proportional to product of the populations of infective and susceptible. Shive tests this hypothesis using data on investor trades in the leading stocks in Finland from Dec 1994 to Jan 2004. The empirical results support the ‘social influence hypothesis’: a 1% increase in the intensity of social meetings is associated with a 2% increase in subsequent buys or sells, and socially-motivated trades help to predict stock returns. In a similar vein, estimated models of herd behaviour in financial markets, such as Franke and Westerhoff (2011) and Cipriani and Guarino (2014), find that social connections exert an influence on investment decisions, and a recent paper by Granha et al. (2022) sets out a model of opinion dynamics via random networks that has impressive empirical performance.

The interconnectedness of the financial system—as shown by the Global Financial Crisis—has focused attention on the implications of networks for financial stability. Detailed studies of investor social networks include Ozsoylev et al. (2014), in which the authors uncover an empirical investor network in the Istanbul Stock Exchange; and Ahern (2017), which provides evidence of illegal insider-trading networks in the USA, with links formed through family, friends and geographical proximity. In addition, Rossi et al. (2018) document a positive relationship between network centrality and risk-adjusted performance of delegated portfolio managers, whereas Li and Jiang (2022) find that well-connected institutional investors in China contribute to an increase in stock price crash risk.

Some recent papers have estimated asset pricing models with social networks directly. For example, the model of Nicolas (2022), discussed in the previous section, was estimated using maximum likelihood and data on 15 US stocks, five cryptocurrencies and a measure of sentiment. The estimation results show a strong impact of herding behaviour on sentiment for highly volatile assets. Interestingly, financial returns appear to have limited impact on sentiment for high-volatility assets, but exert an important influence for low-volatility assets; hence the relative importance of pure social effects versus financial performance seems to depend on return volatility. Clearly, such estimation exercises are important to determine the relative contribution of modelling social networks in asset pricing models.

In general, there are several methods available for estimating structural asset pricing models with heterogeneous agents and social interactions. Two broad approaches have been used in the literature (see Lux and Zwinkels 2018). The first approach is based on some form of simulated method of moments estimation. For example, Boswijk et al. (2007) use nonlinear least squares to estimate a two-type Brock–Hommes model with time-varying population shares, while Amilon (2008) uses simulated method of moments to estimate a three-type model. An alternative approach is to use maximum likelihood estimation. Chiarella et al. (2014) estimate a simplified two-type model using quasi maximum likelihood, while some recent contributions (see below) use filtering techniques to approximate the conditional densities that enter into the likelihood function. The main advantage of the latter approach is the precision of parameter estimates and the possibility of inferring the trajectories of latent variables, such as the fundamental price or sentiment index, in heterogeneous-agent models.

In Lux (2018), a sequential Monte Carlo method with the particle filter is used to estimate two such models. The first model is based on Alfarano et al. (2008) and is essentially a discrete-time Kirman–Lux model in which the fundamental price follows a random walk, speculative traders have fixed trading volume, and the overall disposition of sentiment-prone traders (as measured by the sentiment index) is determined by transition probabilities that allow herding on an optimistic or pessimistic sentiment alongside occasional shifts in opinion, as in Kirman’s ant recruitment model. The second estimated model is inspired by Franke and Westerhoff (2012); it is similar in spirit to the previous model but allows trading volume to depend on the past price trend, and agents can switch between chartist and fundamental types. The results of a Monte Carlo exercise on both models are encouraging, although the intensity of using the particle filter increases computation time substantially relative to other approaches. The empirical application which estimates both models suggests that goodness-of-fit is better for the Alfarano et al. (2008) model.

In Majewski et al. (2020), a Bayesian filtering approach is used—in conjunction with the Unscented Kalman Filter—to estimate a version of the Chiarella (1992) model with non-linear demand of fundamentalists. The estimation uses monthly time series on a range of asset classes since 1800, including a US stock price index. A key advantage of this approach is that it reduces computational burden relative to the particle filter while allowing the identification of latent variables. For example, the fundamental price is estimated without using any external information such as dividends or a pricing equation, and the resulting fundamental value is endogenous since it is treated as a ‘reference point’ that can be filtered out from the time series of prices. This feature is attractive given the difficulty of finding plausible equations to describe the level and dynamics of fundamental values.

In summary, the estimation of heterogeneous-agent model remains a challenge, and many papers have considered models with a small number of investor types. However, recent developments in both modelling and estimation techniques give cause for optimism, and this is only reinforced when one factors in likely improvements in data availability, computing power and the potential of machine-learning and other artificial intelligence methods.

6.5 Future research

As impressive as the literature on communication and asset price dynamics is, there are some clear gaps in our understanding and several interesting directions for future research.

First, models which incorporate explicit social networks are in their infancy, and hence, there is a need for future work that explores the potential of this approach for explaining price dynamics and empirical stylized facts of stock market returns. If such models are useful from an empirical perspective—as initial work suggests—then the next step will be to discipline such models with social networks and investor behaviour that are supported by real-world data. In this case, it will be important to have rich data on social connections for both professional and retail investors. As shown, several works have estimated investor networks using real-world data and improved our understanding of investment decisions.

Ultimately, such works may make it possible to adapt financial market models to specific settings, in which case they may eventually be useful guides, or testing grounds, for forecasting or the design of robust regulatory policies. Admittedly, we are some distance from this right now, but with increasing computing power, and the promise of artificial intelligence and big data, modelling investor networks makes sense precisely because they may (plausibly) be disciplined by real-world data. In a similar vein, experimental and survey evidence are shedding light on how investors form expectations and the relative importance of social communication for events such as financial market booms and crashes.

Second, many recent models of communication and asset prices can be viewed as extensions of earlier models, but with the addition of social networks. Nevertheless, different models can have very different implications for asset price dynamics, and it is therefore important to understand conditions under which alternative models produce similar or different results. As an example, some approaches emphasize past profitability as an important factor in belief updating on social networks whereas others ignore this possibility; and even among approaches that emphasize performance, the details of the updating can matter a lot for beliefs and asset prices. More work is also needed to evaluate the importance of past performance for investment decisions and to shed light on the ‘memory length’ of investors.

While most of this survey article has focused on communication between investors with respect to price expectation, there may also be other parts of investors’ utility that drive investment decisions. One example is a preference for environmental or socially-focused investments such as green tastes (Pástor et al. 2021). A general finding (without communication) is that if investors have preferences for certain assets that are unrelated to prices, then these assets are overvalued because investors enjoy holding them. When investors instead communicate and their tastes evolve accordingly, what are the implications for the performance of the associated assets? Should financial institutions and fund managers invest in accordance with these tastes, if they have a strong preference for financial performance?

Last but not least, there have been dramatic changes in how investors communicate over the past 20 years—including social media, online forums and retail investing—yet our understanding of how these modern developments impact financial markets is limited. Some important questions are: do online forums facilitate herd behaviour by making it easier for investors to observe and imitate the opinions of others? Do amateurs (i.e. retail investors) tend to rely on the opinions of others to a greater or lesser extent than professional investors, and what are the implications of this for market stability and financial regulation? How does online communication compare with face-to-face in terms of influence on investment decisions? Answering questions like these is important not only for regulators, but to ensure that the next generation of asset pricing models are useful and draw on relevant data.

7 Conclusion

In this paper, we provided a survey of the state of the art in the area of communication and asset price dynamics. We focused in particular on attempts to model asset prices as the outcome of various social communication protocols, and on how this growing literature has evolved over time. One common feature among studies is that communication between agents is modelled at the level of investors expectations or demands, which follow simple rules-of-thumb or heuristics. A robust finding from the literature is that simple investor behaviour, combined with social communication, gives rise to complex asset price dynamics.

By taking communication seriously, these models can explain several stylized facts which challenge the efficient markets hypothesis. Early contributions to the literature focused on herding or adoption of the most successful investment strategies, and showed these models do well empirically. Recent work has modelled communication using explicit social networks which specify connections between individual investors, as in the opinion dynamics literature. In these models, investor beliefs influence both the asset price and the beliefs of other investors, so communication plays an important role in price determination. On top of this, recent work allows belief updating from an investor’s (local) social network to depend on performance, thus extending an important tradition from the early models.

This modern approach appears to have much potential, and we discussed some leading examples which support this view. The most interesting questions relate to the empirical value of this approach and how researchers can build better models of asset pricing. Promising avenues for future research include attempts to better understand the consequences of communication for asset prices and regulation of financial markets, including the roles of performance-based social updating and ‘influencers’; work to assess how well different communication models of asset prices perform empirically via model estimation, evaluation against stylized facts, or asset pricing experiments; and research that documents social connections between investors and thus facilitates the calibration of models with social networks. Admittedly, this is a list of highly ambitious goals, but with continuing developments in big data and artificial intelligence, much of this may soon be feasible for ordinary researchers.