Entropy and discrimination measures based q-rung orthopair fuzzy MULTIMOORA framework for selecting solid waste disposal method

Abstract

Fastest growing population, rapid urbanization, and growth in the disciplines of science and technology cause continually development in the amount and diversity of solid waste. In modern world, evaluation of an appropriate solid waste disposal method (SWDM) can be referred as multi-criteria decision-making (MCDM) problem due to involvement of several conflicting quantitative and qualitative sustainability indicators. The imprecision and ambiguity are usually arisen in SWDM assessment problem, and the q-rung orthopair fuzzy set (q-ROFS) has been recognized as one of the adaptable and valuable ways to tackle the complex uncertain information arisen in realistic problems. In the context of q-ROFSs, entropy is a significant measure for depicting fuzziness and uncertain information of q-ROFS and the discrimination measure is generally used to quantify the distance between two q-ROFSs by evaluating the amount of their discrimination. Thus, the aim of this study is to propose a novel integrated framework based on multi-attribute multi-objective optimization with the ratio analysis (MULTIMOORA) method with q-rung orthopair fuzzy information (q-ROFI). In this approach, an integrated weighting process is presented by combining objective and subjective weights of criteria with q-ROFI. Inspired by the q-rung orthopair fuzzy entropy and discrimination measure, objective weights of criteria are estimated by entropy and discrimination measure-based model. Whereas, the subjective weights are derived based on aggregation operator and the score function under q-ROFS environment. In this respect, novel entropy and discrimination measure are proposed for q-ROFSs. Furthermore, to display the feasibility and usefulness of the introduced approach, a case study related to SWD method selection is presented under q-ROFS perspective. Finally, comparison and sensitivity investigation are presented to confirm the robustness and solidity of the introduced approach.

Introduction

Solid waste is the unnecessary or unusable solid product produced from human activities in residential, industrialized, or commercial areas. These wastes can pose harmful effects on population and the environment; thus, it should be managed with great care (Geda et al., 2020). Solid waste can be divided into “urban solid wastes (USWs),” “special wastes (SWs),” and “industrial wastes (IWs).” The USWs usually contain non-hazardous wastes, while SWs refer to radioactive, medical, and toxic wastes, and IWs refer to industrial wastes, which can be produced from industry or municipal. USWs are also called municipal solid wastes (Li et al., 2021).

Industrialization, economic growth, and improving life standards have resulted into increased amount of solid wastes; as a result, the proper management of these wastes is a challenging task for urban communities, particularly in developing countries (Habib et al., 2019). The development and structure of “solid waste management (SWM)” can be categorized into assessment of waste treatment methods, distribution of solid wastes and its residues from the producer to the treatment or disposal sites, and assessment of transportation directions (Li et al., 2021; Bilgilioglu et al., 2022). Selection of “solid waste disposal method (SWDM)” is an intricate “multi-criteria decision-making (MCDM)” problem because of the participation of many tangible and intangible criteria related to politics, socio-cultural, technical, economic, and environmental aspects (Rahimi et al., 2020). To achieve the sustainable development goals, it is essential to select the most suitable SWDM alternative for the government and environmentalists. The considered criteria involved in this process may fluctuate based on the variety of considered product, and often in conflict with each other. In view of that, it is very significant to discover a suitable tool to precise evaluation information and employ this tool in the evaluation of SWD method selection.

During the process of SWDM selection process, the data available for an alternative by means of several attributes may be qualitative linguistic values or imprecise or incomplete in nature. To handle the imprecise and unclear data, Zadeh (1965) gave the notion of “fuzzy set (FS)” and applied to several decision-making applications by considering various perspectives. The notion of FSs has presented its own measures of qualitative information, which finds relevance in different fields (Bozanic et al., 2021; Kumar et al., 2022; Pamučar et al. 2022a). As an extended version of FS theory, the concept of “q-rung orthopair fuzzy set (q-ROFS)” (Yager, 2017) has been proven as more flexible and superior way to model the imprecision and ambiguity of highly complex MCDM problems. The constraint condition of q-ROFS is that the sum of qth powers of belongingness and non-belongingness degrees is restricted to 1. With parameter q, the q-ROFSs portray a wider range of information than the classical FSs (Zadeh, 1965), “intuitionistic fuzzy sets (IFSs)” (Atanassov, 1986), “Pythagorean fuzzy sets (PFSs)” (Yager, 2014), and “Fermatean fuzzy sets (FFSs)” (Senapati and Yager, 2020). As a result, this theory has received a great attention in the field of MCDM (Liao et al., 2020; Cheng et al. 2021a; Mishra and Rani, 2021; Saha et al., 2022; Hu et al., 2022).

Motivated by this idea, we have focused this study under the context of q-ROFSs. In the literature, many MCDM methods have been proposed within q-ROFSs setting, but there is no investigation in the literature regarding the MULTIMOORA method under q-ROFS perspective. Entropy and discrimination measure, as the information measures, have been proven as important tools in the doctrine of Zadeh’s FS and its generalizations. Although, very few authors (Peng and Liu, 2019; Verma, 2020; Khan et al., 2021a; Mishra and Rani, 2021) have concentrated their interest in the development of “q-rung orthopair fuzzy (q-ROF)” information measures. Also, no one has employed the concepts of entropy and discrimination measure to estimate the objective criteria weights for evaluation of SWDM selection problem. Here, we develop a hybridized approach with the MULTIMOORA model and novel information measures under q-ROFS setting, and employ to assess the SWDM selection problem with wholly unidentified information about the criteria and DEs.

Research challenges

On the basis of existing studies, the following challenges have been identified:

• The idea of entropy and discrimination measure has been identified as one of the key research topics in many fields including machine learning, artificial intelligence, texture analysis, and MCDM. Moreover, the theory of q-ROFSs is proven as more flexible and superior way to model the vagueness and imprecision of complex MCDM problems. In the literature, very few authors (Peng and Liu, 2019; Verma, 2020; Chakraborty and Kumar, 2021; Khan et al. 2021a; Mishra and Rani, 2021) have concentrated their interest in the development of q-rung orthopair fuzzy entropy and discrimination measure, but these measures have some counter intuitive cases.

• In the literature (Darko and Liang, 2020; Garg and Chen, 2020; Khan et al., 2021a,b; Arsu and Ayçin, 2021; Kumar and Chen, 2022; Deveci et al., 2022a), the weight of each DE was directly assigned by the authors, which can cause subjective uncertainty. Consequently, how to determine the DE weights is also a significant challenge during the MCDM process.

• In the studies (Aydemir and Gündüz, 2020; Wang et al., 2020; Bakır et al., 2021; Kakati and Rahman, 2022; Kumar and Chen, 2022; Deveci et al., 2022a), the researchers have considered the direct values for criteria weights. On the other hand, diverse weights of criteria will lead to different decision outcomes. Accordingly, it is very significant to compute the criteria weights in realistic MCDM problems.

• Aydemir and Gündüz (2020) extended the classical MULTIMOORA approach from q-ROFS setting. On the other hand, this approach is unable to handle the objective and subjective weights of criteria, and multiple preferences of experts under q-ROF information.

• In the literature, very few MCDM methods have been introduced for evaluating the suitable and sustainable SWD method under uncertain context; however, existing methods have limitations in handling the multi-faceted SWD method selection problem from q-ROF perspective.

Contributions of this study

The novel contributions of the manuscript are elucidated by the following:

• New entropy and discrimination measure are developed with their desirable characteristics.

• A formula is presented to determine the DE weights under q-ROFS environment.

• To evade the adverse effects of objective and subjective aspects, an integrated weighting model is developed by combining objective weight-determining procedure using entropy and discrimination measure, and subjective weight-determining process using the aggregation operator and score function to estimate the criteria weights with q-ROF information.

• To avoid the shortcomings of extant MULTIMOORA methods, an extended version of MULTIMOORA approach is put forward for solving complex MCDM problems on the q-ROFSs setting.

• A case study of SWD method selection problem is taken to show the usefulness and efficiency of the present MULTIMOORA on q-ROFSs. Comparison and sensitivity investigation are made to validate the results.

Organizations of this study

The remaining study is planned as “Literature review” section presents the comprehensive literatures realted to current study. “Proposed entropy and discrimination measures” section introduces new entropy and discrimination measure for q-ROFSs. “Proposed q-ROF-MULTIMOORA approach” section presents an innovative q-ROF-MULTIMOORA framework based on entropy and discrimination measure. “An empirical study: solid waste disposal (SWD) method selection” section discusses a case study of SWD method selection problem with q-ROFI. Further, comparative and sensitivity investigation are conferred to verify the results. “Conclusions” section concludes the study and shows the scope for further research.

Literature review

This section presents the comprehensive literature review related to the present study.

q-ROFSs

Owing to the subjectivity of human mind and increasing complications of realistic applications, the DEs are unable to provide the exact numerical values for assessment information. To manage the uncertainty and vagueness of realistic applications, Atanassov (1986) originated the doctrine of “intuitionistic fuzzy set (IFS),” which is an advance version of FS. IFS is portrayed by the “belongingness degree (BD),” “non-belongingness degree (ND),” and “hesitancy degree (HD)” with the characteristic that the sum of BD and ND is $\le 1$. Nonetheless, based on the complexity and ambiguity of human’s subjective cognition, the assessment information given by the specialists does not assure the requirement of IFS. To surmount this limitation, Yager (2014) had proven the system of Pythagorean fuzzy set (PFS) with the condition that square sum of BD and ND is $\le 1$. The theories of IFS and PFS can articulate the knowledge of DEs more scientifically. Thus, the PFSs are more dominant than IFSs to designate the uncertain behavior of practical problems (Alipour et al., 2021; Zhang et al., 2021; Osintsev et al., 2021).

On the other hand, there may be a case wherein the DEs may offer the BD to which an alternative ${N}_{i}$ fulfills that the constraint ${P}_{j}$ is 0.7 and degree to which an alternative ${N}_{i}$ dissatisfies the constraint is 0.9. Under this circumstance, the theories of IFS and PFS are unable to give evaluation results because $0.7+0.9>1$ and ${0.7}^{2}+{0.9}^{2}>1.$ Further, Yager (2017) projected the doctrine of q-rung orthopair fuzzy set (q-ROFS) and showed by the BD, ND, and HD with the condition that the sum of qth powers of the BD and ND is $\le 1,$ where q ≥ 1. Since the space of q-ROFSs is wider than the PFSs in accordance with the variation of parameter q (q ≥ 1), therefore, it expands the representation scope of decision making information. Recently, some authors (Garg and Chen, 2020; Darko and Liang, 2020; Seikh and Mandal, 2021; Kumar and Chen, 2022; Kakati and Rahman, 2022) have proposed the series of “q-rung orthopair fuzzy (q-ROF)” aggregation operators, namely, hamacher, neutrality, frank, weighted averaging, hamacher-generalized Shapley choquet integral operators, and so on.

Liao et al. (2020) put forward an improved “gained and lost dominance score (GLDS)” model to tackle with the MCDM problems from q-ROFSs. They introduced their model by combining dominance flows and order scores of alternatives, and proposed weighting models. Rani and Mishra (2020) firstly proposed a novel score function and measure of similarity for q-ROFSs. Further, they established a similarity measure-based decision-making framework for selecting an appropriate alternative fuel technology from q-ROF perspective. Khan et al. (2021b) developed the cosine inverse function-based q-ROF knowledge measure and its properties to consider the information precision and information content. Then, they presented an application of the proposed knowledge measure in MCDM problem under q-ROFS context. Based on prospect theory, Liang et al. (2022) gave an innovative q-ROF information-based tri-reference point model for solving the MCDM problems. In addition, they considered Bayesian network to estimate the interaction between criteria and a new technique to compare two q-ROFSs. In a study, Deveci et al. (2022b) studied a hybrid framework by integrating the “combinative distance-based assessment (CODAS)” method with q-ROFSs and applied for evaluating the “socially responsible rehabilitation activities (SRRAs)” in mining sites. Their outcomes concluded that the rehabilitation and social transition subsidy are the most appropriate candidates among the list of selected alternatives. Till now, no one has introduced the q-ROFS-based decision-making methodology for SWDM selection problem.

Entropy and discrimination measure

Entropy is a measure of uncertainty occurring in information wherein a higher value implies more information in the process being considered. In the process of MCDM, it is employed to estimate the objective weights of the criteria based on the data in the decision matrix. In FS theory, entropy is used to measure the degree of fuzziness of a set. De Luca and Termini (1972) firstly gave the axiom construction for fuzzy entropy based on Shannon’s probability entropy. In the context of q-ROFS, Peng and Liu (2019) gave the definition of entropy and presented several entropy measures for q-ROFS. To quantify the degree of fuzziness of q-ROFS, Verma (2020) put forward two novel parametric q-ROF entropy measures of order $\alpha$ with their applicability in MCDM. Liu et al. (2020) considered a new q-ROF entropy measure and its desirable properties. Mishra and Rani (2021) presented a new entropy function for measuring the fuzziness of q-ROFS and its applicability to derive the sustainability indicators’ weights in recycling partner selection.

The discrimination measure, as an information measure, is one of the research hotspots in FS theory and its extensions. It quantifies the degree of divergence between two sets. In the recent past, the discrimination measure has broadly been used in many fields, like medical diagnosis, decision-making, pattern recognition, and so on. In terms of q-ROFSs, the concept of discrimination measure was firstly introduced by Verma (2020) based on order $\alpha$. Further, Khan et al. (2021a) introduced some axiomatically supported discrimination measures for q-ROFSs to avoid the shortcomings of Verma’s discrimination measure. Recently, Mishra and Rani (2021) proposed different discrimination measure and its application in MCDM problems. However, there is no study regarding the criteria weights in the assessment of SWDM using q-ROF entropy and discrimination measures.

MULTIMOORA approach

With the expansion of socio-economic settings, the real-life MCDM problems are becoming progressively complicated. Accordingly, numerous MCDM methods have successfully been discussed and implemented in realistic applications (Cali et al., 2022; Pamucar et al., 2022a,b; Deveci et al., 2022b,c; Wu et al., 2022). The “multi-objective optimization method by ratio analysis (MOORA) (Brauers and Zavadskas, 2006)” is a one of the effective and prominent MCDM techniques, which consists of “ratio system (RS)” and “reference point (RP)” model. In order to show the strength of MOORA approach, Brauers and Zavadskas (2010) proposed a novel technique, named as “multi-attribute multi-objective optimization on the basis of ratio analysis (MULTIMOORA),” consisting of the “ratio system (RS),” the “reference point (RP),” and the “full multiplicative form (FMF)” procedures. Compared to “analytic hierarchy process (AHP),” “technique for order performance by similarity to ideal solution (TOPSIS),” “VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR),” “preference ranking organization method for enrichment evaluation (PROMETHEE),” “linear programming technique for multi-dimensional analysis of preference (LINMAP),” “elimination and choice translating reality (ELECTRE),” “complex proportional assessment (COPRAS),” “measurement alternatives and ranking according to the compromise solution (MARCOS),” and “weighted aggregated sum product assessment,” the MULTIMOORA has more higher stability, simple mathematical process, less computational time, and higher robustness (Rani and Mishra, 2021).

In the recent past, various theories and applications based on MULTIMOORA method have been developed. For example, Aydemir and Gündüz (2020) developed an integrated MULTIMOORA method by combining the “aggregation operators (AOs)” with q-ROFSs, and employed for treating MCDM problems. Rani and Mishra (2021) established a decision-making system based on MULTIMOORA method, discrimination measure, and Einstein-weighted AOs under the context of Fermatean fuzzy sets (FFSs). In order to assess the sustainable community-based tourism locations, He et al. (2021) recommended a hybrid MULTIMOORA model with the integration of “step-wise weight assessment ratio analysis (SWARA)” model and interval-valued Pythagorean fuzzy information.

Motivated by MULTIMOORA technique, Sarabi and Darestani (2021) introduced an MCDM model for treating the logistics service providers’ problem with fuzzy information. Qin and Ma (2022) proposed a hybridized method by integrating third-generation prospect theory and MULTIMOORA model with “interval type-2 fuzzy sets (IT2FSs)” and employed for emergency response plans assessment during COVID-19. Shang et al. (2022) designed an improved fuzzy MULTIMOORA method-based decision support system for solving supplier selection problem from sustainability perspective. Further, numerous generalizations of MULTIMOORA model have been presented within the context of uncertainty (Luo et al., 2019; Rahimi et al., 2020; Wang et al., 2021); however, no one has utilized the concept of entropy and discrimination measure-based q-ROF-MULTIMOORA method for solving solid waste disposal (SWD) method selection problem.

Methods for SWM systems

In recent times, several articles have been presented in the literature for the treatment and management of solid wastes. For instance, Singh (2019) firstly studied the rationale and background of the “municipal solid waste (MSW)” disposal problems. Further, they presented the applications of fuzzy analysis technique and incorporated waste management for handling the uncertainty problems of waste disposal. Kumar and Agrawal (2020) studied a comprehensive review summarizing the current solid waste management status identifying the related challenges and deriving possible solutions for the MSW management in the Indian perspective. Al-Ghouti et al. (2021) discussed the characterizations, leaching mechanisms, and pretreatment methods for MSW bottom and fly ashes. Furthermore, they presented the current trends and applications of MSW bottom and fly ashes, and explored their potential insights into sustainable development. Cheng et al. (2021b) proposed the reliability analysis-based framework to deal with the uncertainties for the multiple-stage solid waste management structure. In addition, the authors have presented a mathematical model to maximize the reliability of solid waste management systems and constructed an event tree to analyze the failure mode of the entire system. In the recent past, many studies have been conducted for SWM including healthcare and food wastes under different fuzzy environments (see Table 1). In this study, the authors have firstly introduced the q-ROF entropy and discrimination measure-based MULTIMOORA method in the evaluation of SWDMs under uncertain context.

Table 1 Recent studies related to solid waste management systems

The leading question of this work is “which one is the most suitable SWDM from sustainable perspective?” In order to deal with this issue, the following concerns need to be solved.

• What are the main criteria to select the most suitable SWDM candidate with uncertain information?

• Which is the most important criteria for SWDMs assessment?

• Which is the most significant framework to choose and rank the suitable SWDM option in order to ensure the sustainable development goals?

The key objectives of this work are as follows:

• Define the main criteria to choose the most suitable SWDM alternative through literature survey and DE opinions. In addition, find the importance weights of each criterion with uncertainty.

• Develop a model to compute the weights of considered evaluation criteria.

• Develop a hybrid MCDM methodology to prioritize the SWDMs under highly uncertain environment.

Proposed entropy and discrimination measures

In the doctrine of q-ROFSs, entropy and discrimination measures have widely been applied to cope with uncertain information arises in MCDM, medical diagnosis, and so on. Based on the advantages of these measures, we develop novel q-ROF-entropy and q-ROF-discrimination measures in the current section.

New entropy for q-ROFSs

Let $M\text{}\in \text{}q-ROFS\left(O\right).$ Then, an entropy measure for q-ROFS M is

$$h\left(M\right)=1-\frac{1}{n}\sum_{i=1}^{n}\left[\left({t}_{M}^{q}\left({o}_{i}\right)-{f}_{M}^{q}\left({o}_{i}\right)\right){I}_{\left[{t}_{M}^{q}\left({o}_{i}\right)\ge {f}_{M}^{q}\left({o}_{i}\right)\right]}\right.+\left.\left({f}_{M}^{q}\left({o}_{i}\right)-{t}_{M}^{q}\left({o}_{i}\right)\right){I}_{\left[{t}_{M}^{q}\left({o}_{i}\right)<{f}_{M}^{q}\left({o}_{i}\right)\right]}\right].$$

(1)

Theorem 3.1. The measure $h\left(M\right)$ is valid entropy for q-ROFS $\left(O\right).$  

Proof: To do this, the measure in Eq. (1) must fulfill the postulates given in Definition 5 (see Appendix).

(p1). In q-ROFS, $0\text{}\le {t}_{M}^{q}\left({o}_{i}\right)+{f}_{M}^{q}\left({o}_{i}\right)\le 1,$ therefore, from Eq. (1), we observe that $0\text{}\le h\left(M\right)\le 1.$  

(a2). Let M be a crisp set, i.e., ${t}_{M}\left({o}_{i}\right)=1, {f}_{M}\left({o}_{i}\right)=0$ or ${t}_{M}\left({o}_{i}\right)=0, {f}_{M}\left({o}_{i}\right)=1.$ Thus, from Eq. (1), we obtain $h\left(M\right)=0.$  

Conversely, suppose $h\left(M\right)=0.$ Then, Eq. (1) turn into zero iff ${t}_{M}^{q}\left({o}_{i}\right)=1={t}_{M}\left({o}_{i}\right), {f}_{M}^{q}\left({o}_{i}\right)=0={f}_{M}\left({o}_{i}\right)$ or ${t}_{M}^{q}\left({o}_{i}\right)=0={t}_{M}\left({o}_{i}\right), {f}_{M}^{q}\left({o}_{i}\right)=1={f}_{M}\left({o}_{i}\right), \forall {o}_{i}\in O,$ it implies M is a crisp set.

(p3). It is evident from definition that if ${t}_{M}({o}_{i})={f}_{M}({o}_{i}),\forall {o}_{i}\in O,$ then $h\left(M\right)=1.$  

Again, if $h\left(M\right)=1,$ then from Eq. (1), we get

$$1-\frac{1}{n}\sum_{i=1}^{n}\left[\left({t}_{M}^{q}\left({o}_{i}\right)-{f}_{M}^{q}\left({o}_{i}\right)\right){I}_{\left[{t}_{M}^{q}\left({o}_{i}\right)\ge {f}_{M}^{q}\left({o}_{i}\right)\right]}\right.+\left.\left({f}_{M}^{q}\left({o}_{i}\right)-{t}_{M}^{q}\left({o}_{i}\right)\right){I}_{\left[{t}_{M}^{q}\left({o}_{i}\right)<{f}_{M}^{q}\left({o}_{i}\right)\right]}\right]=1.$$

It implies that

$\left(\left({t}_{M}^{q}\left({o}_{i}\right)-{f}_{M}^{q}\left({o}_{i}\right)\right){I}_{\left[{t}_{M}^{q}\left({o}_{i}\right){f}_{M}^{q}\left({o}_{i}\right)\right]}+\left({f}_{M}^{q}\left({o}_{i}\right)-{t}_{M}^{q}\left({o}_{i}\right)\right){I}_{\left[{t}_{M}^{q}\left({o}_{i}\right)<{f}_{M}^{q}\left({o}_{i}\right)\right]}\right)=0,\forall {o}_{i}\in O,$ which gives ${t}_{M}\left({o}_{i}\right)={f}_{M}\left({o}_{i}\right),\forall {o}_{i}\in O.$  

(a4). From Eq. (1), we obtain that $h\left(M\right)=h\left({M}^{c}\right).$  

(a5). Let

$$\psi \left(\alpha ,\beta \right)=1-\left[\left\{\alpha -\beta \right\}{I}_{\left[\alpha \ge \beta \right]}+\left\{\beta -\alpha \right\}{I}_{\left[\alpha <\beta \right]}\right].$$

(2)

From Eq. (2), we obtain ${\psi }_{\alpha }^{^{\prime}}\ge 0$ when $\alpha <\beta$ and ${\psi }_{\alpha }^{^{\prime}}\le 0$ when $\alpha \ge \beta .$ Thus, for $\alpha ,\beta \in \left[0,1\right],$ the function $\psi \left(\alpha ,\beta \right)$ increases over $^{^{\prime}}{\alpha }^{^{\prime}}$ as $\alpha <\beta$ and decreases over $^{^{\prime}}{\alpha }^{^{\prime}}$ as $\alpha \ge \beta .$ Similarly, it can simply confirm that the mapping $\psi \left(\alpha ,\beta \right)$ decreases with respect to $^{^{\prime}}{\beta }^{^{\prime}}$ as $\alpha <\beta$ and increases with respect to $^{^{\prime}}{\beta }^{^{\prime}}$ as $\alpha \ge \beta .$  

Let $M,N\in q-ROFSs\left(O\right)$ with $M\subseteq N$ and ${t}_{M}({o}_{i})\le {f}_{M}({o}_{i}),$ for each ${o}_{i}\in O.$ Divide the finite universe O into two disjoint sets ${O}_{1}$ and ${O}_{2}$ where $\phi ={O}_{1}\cap {O}_{2}$ and $O={O}_{1}\cup {O}_{2}.$ Furthermore, assume that ${o}_{i}\in {O}_{1}$ with ${t}_{M}({o}_{i})\le {t}_{N}({o}_{i})\le {f}_{N}({o}_{i})\le {f}_{M}({o}_{i})$ and ${o}_{i}\in {O}_{2}$ with ${t}_{M}({o}_{i})\ge {t}_{N}({o}_{i})\ge {f}_{N}({o}_{i})\ge {f}_{M}({o}_{i}).$ Then, by the monotonicity of $\psi \left(\alpha ,\beta \right),$ we observe that $h\left(M\right)\le h\left(N\right).$ Hence, the function $h\left(M\right)$ is entropy for q-ROFS(O).

New q-ROF-discrimination measure

Let $M,N\in q-ROFSs(O).$ Then, a novel discrimination measure for q-ROFSs M and N is

$$J\left(M,N\right)=\frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\sum_{i=1,\gamma >0,\gamma \ne 2}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{2}+{\left({t}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{2}+{\left({f}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right].$$

(3)

Theorem 3.2: The measure $J\left(M,N\right),$ given in Eq. (3), is a discrimination measure for q-ROFSs(O).

Proof: For this, the function $J\left(M,N\right),\;\gamma >0,\gamma \ne 2,$ has to be satisfying all the postulates of Definition 6 (see Appendix).

(a1). For any two real number $\alpha ,\beta \in {\mathbb{R}},$ the following inequalities satisfy:

$$\left(\frac{\alpha^2+\beta^2}2\right)^{\gamma/2}\geq\frac{\alpha^\gamma+\beta^\gamma}2\;\text{for }\gamma<2\;\mathrm{and}\;\left(\frac{\alpha^2+\beta^2}2\right)^{\gamma/2}\leq\frac{\alpha^\gamma+\beta^\gamma}2\;\mathrm{for}\;\gamma>2.$$

(4)

Also, we have

$$\frac1{n\left(2^{\left(1-\gamma/2\right)}-1\right)}>0\;\;\mathrm{for}\;\;\gamma<2\;\;\mathrm{and}\;\;\frac1{n\left(2^{\left(1-\gamma/2\right)}-1\right)}<0\;\;\mathrm{for}\;\;\gamma>2.$$

(5)

In q-ROFSs(O), we know that $0\le {t}_{M}^{q}\left({o}_{i}\right),{f}_{M}^{q}\left({o}_{i}\right),{\pi }_{M}^{q}\left({o}_{i}\right)\le 1$ and $0\le {t}_{N}^{q}\left({o}_{i}\right),{f}_{N}^{q}\left({o}_{i}\right),{\pi }_{N}^{q}\left({o}_{i}\right)\le 1.$  

Therefore, we have

$$\left.\begin{array}{c}\left(\frac{\left(t_M^q(o_i)\right)^2+\left(t_N^q(o_i)\right)^2}2\right)^{\gamma/2}\geq\frac{\left(t_M^q(o_i)\right)^\gamma+\left(t_N^q(o_i)\right)^\gamma}2,\\\left(\frac{\left(f_M^q(o_i)\right)^2+\left(f_N^q(o_i)\right)^2}2\right)^{\gamma/2}\geq\frac{\left(f_M^q(o_i)\right)^\gamma+\left(f_N^q(o_i)\right)^\gamma}2,\\\left(\frac{\left(\pi_M^q(o_i)\right)^2+\left(\pi_N^q(o_i)\right)^2}2\right)^{\gamma/2}\geq\frac{\left(\pi_M^q(o_i)\right)^\gamma+\left(\pi_N^q(o_i)\right)^\gamma}2\end{array}\right\}\mathrm{for}\;\gamma\;<2$$

(6)

and

$$\left.\begin{array}{c}\left(\frac{\left(t_M^q(o_i)\right)^2+\left(t_N^q(o_i)\right)^2}2\right)^{\gamma/2}\leq\frac{\left(t_M^q(o_i)\right)^\gamma+\left(t_N^q(o_i)\right)^\gamma}2,\\\left(\frac{\left(f_M^q(o_i)\right)^2+\left(f_N^q(o_i)\right)^2}2\right)^{\gamma/2}\leq\frac{\left(f_M^q(o_i)\right)^\gamma+\left(f_N^q(o_i)\right)^\gamma}2,\\\left(\frac{\left(\pi_M^q(o_i)\right)^2+\left(\pi_N^q(o_i)\right)^2}2\right)^{\gamma/2}\leq\frac{\left(\pi_M^q(o_i)\right)^\gamma+\left(\pi_N^q(o_i)\right)^\gamma}2\end{array}\right\}\mathrm{for}\;\gamma\;> 2.$$

(7)

Therefore, for each ${o}_{i}\in O,$ we combine Eqs. (5)–(7) as follows:

$$\frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\sum_{i=1,\gamma >0,\gamma \ne 2}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{2}+{\left({t}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{2}+{\left({f}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right]\ge 0.$$

(8)

From Eq. (3), we obtain $J\left(M,N\right)\ge 0.$  

(a2). Consider that $M=N,$ therefore, ${t}_{M}\left({o}_{i}\right)={t}_{N}\left({o}_{i}\right),{f}_{M}\left({o}_{i}\right)={f}_{N}\left({o}_{i}\right)$ and ${\pi }_{M}\left({o}_{i}\right)={\pi }_{N}\left({o}_{i}\right).$ Then, Eq. (3) becomes

$$J\left(M,N\right)=\frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\sum_{i=1,\gamma >0,\gamma \ne 2}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{2}+{\left({t}_{M}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{2}+{\left({f}_{M}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right]=0.$$

Conversely, assume $J\left(M,N\right)=0,$

$$\begin{array}{c}\iff \frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\sum_{i=1,\gamma >0,\gamma \ne 2}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{2}+{\left({t}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{2}+{\left({f}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right]=0,\\ \iff {\left(\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{2}+{\left({t}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}+{\left(\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{2}+{\left({f}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}+{\left(\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}\\ -\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}-\frac{{\left({t}_{N}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{N}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}=0.\end{array}$$

This is possible if and only if ${t}_{M}\left({o}_{i}\right)={t}_{N}\left({o}_{i}\right),{f}_{M}\left({o}_{i}\right)={f}_{N}\left({o}_{i}\right)$ and ${\pi }_{M}\left({o}_{i}\right)={\pi }_{N}\left({o}_{i}\right).$ Thus, we have $M=N.$  

(a3). It is obvious from Definition 6 (see Appendix).

(a4)–(a5). In order to prove these properties, firstly, we will prove $J\left(M\cup N,M\cap N\right)=J\left(M,N\right),$ for all $M,N\in q-ROFSs\left(O\right).$  

Now, we divide the universe of discourse O into two disjoint parts ${O}_{1}$ and ${O}_{2},$ where ${O}_{1}=\left\{{o}_{i}\left|{o}_{i}\in O,M\left({o}_{i}\right)\subseteq N\left({o}_{i}\right)\right.\right\}$ and ${O}_{2}=\left\{{o}_{i}\left|{o}_{i}\in O,N\left({o}_{i}\right)\subseteq M\left({o}_{i}\right)\right.\right\}.$  

Then,

$$\begin{array}{c}J\left(M\cup N,M\cap N\right)=\frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\\ \sum_{i=1,\gamma >0,\gamma \ne 2}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{M\cup N}^{q}({o}_{i})\right)}^{2}+{\left({t}_{M\cap N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{M\cup N}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{M\cap N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{M\cup N}^{q}({o}_{i})\right)}^{2}+{\left({f}_{M\cap N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{M\cup N}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{M\cap N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{M\cup N}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{M\cap N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{M\cup N}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{M\cap N}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right]\\ \begin{array}{c}=\frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\sum_{i=1,{o}_{i}\in {O}_{1}}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{N}^{q}({o}_{i})\right)}^{2}+{\left({t}_{M}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{N}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{2}+{\left({f}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right]\\ +\frac{1}{n\left({2}^{\left(1-\gamma /2\right)}-1\right)}\sum_{i=1,{o}_{i}\in {O}_{2}}^{n}\left[\begin{array}{c}{\left(\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{2}+{\left({t}_{N}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({t}_{M}^{q}({o}_{i})\right)}^{\gamma }+{\left({t}_{N}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({f}_{N}^{q}({o}_{i})\right)}^{2}+{\left({f}_{M}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({f}_{N}^{q}({o}_{i})\right)}^{\gamma }+{\left({f}_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}\\ +{\left(\frac{{\left({\pi }_{N}^{q}({o}_{i})\right)}^{2}+{\left({\pi }_{M}^{q}({o}_{i})\right)}^{2}}{2}\right)}^{\gamma /2}-\frac{{\left({\pi }_{N}^{q}({o}_{i})\right)}^{\gamma }+{\left({\pi }_{M}^{q}({o}_{i})\right)}^{\gamma }}{2}\end{array}\right].\end{array}\end{array}$$

This implies that

$$J\left(M\cup N,M\cap N\right)=J\left(M,N\right).$$

(9)

To prove (a4) and (a5), the universal set O is partitioned into the following eight subsets:

$$\begin{array}{c}O=\left\{{o}_{i}\in O|\text{M}\left({o}_{i}\right)\le N\left({o}_{i}\right)=T\left({o}_{i}\right)\right\}\cup \left\{{o}_{i}\in O|\text{M}\left({o}_{i}\right)=N\left({o}_{i}\right)\le T\left({o}_{i}\right)\right\}\\ \cup \left\{{o}_{i}\in O|\text{M}\left({o}_{i}\right)\le \text{N}\left({o}_{i}\right)<T\left({o}_{i}\right)\right\}\cup \left\{{o}_{i}\in O|\text{M}\left({o}_{i}\right)\le T\left({o}_{i}\right)<\text{N}\left({o}_{i}\right)\right\}\\ \begin{array}{c}\cup \left\{{o}_{i}\in O|\text{N}\left({o}_{i}\right)<M\left({o}_{i}\right)\le T\left({o}_{i}\right)\right\}\cup \left\{{o}_{i}\in O|\text{N}\left({o}_{i}\right)\le T\left({o}_{i}\right)<M\left({o}_{i}\right)\right\}\\ \cup \left\{{o}_{i}\in \text{O|}\text{T}\left({o}_{i}\right)<\text{M}\left({o}_{i}\right)\le N\left({o}_{i}\right)\right\}\cup \left\{{o}_{i}\in O|\text{T}\left({o}_{i}\right)<\text{N}\left({o}_{i}\right)<\text{M}\left({o}_{i}\right)\right\},\end{array}\end{array}$$

which are denoted by ${\Delta }_{1},{\Delta }_{2},...,{\Delta }_{8}.$ According to Montes et al. (2015), for each ${\Delta }_{j},\;j=1,2,...,8, \;\left|\left(M\cup T\right)\left({o}_{i}\right)-\left(N\cup T\right)\left({o}_{i}\right)\right|\le \left|M\left({o}_{i}\right)-N\left({o}_{i}\right)\right|$ and $\left|\left(M\cap T\right)\left({o}_{i}\right)-\left(N\cap T\right)\left({o}_{i}\right)\right|\le \left|M\left({o}_{i}\right)-N\left({o}_{i}\right)\right|.$  

Therefore, from Eq. (8), we obtain.

$J\left(M\cup T,N\cup T\right)\le J\left(M,N\right)$ and $J\left(M\cap T,N\cap T\right)\le J\left(M,N\right),\forall \,T\in q-ROFS\left(O\right).$ since the measure $J\left(M,N\right)$ holds all the essential postulates of Definition 6. Hence, $J\left(M,N\right)$ is a valid q-ROF-discrimination measure.

Theorem 3.3: The discrimination measure $J\left(M,N\right)$ fulfills the following properties:

• (R1). $J\left({M}^{c},N\right)=J\left(M,{N}^{c}\right),$  

• (R2). $J\left(M,N\right)=J\left({M}^{c},{N}^{c}\right),$  

• (R3). $J\left(M\cup N,T\right)\le J\left(M,T\right)+J\left(N,T\right),\forall\, T\in q-ROFS\left(O\right),$  

• (R4). $J\left(M\cap N,T\right)\le J\left(M,T\right)+J\left(N,T\right),\forall \,T\in q-ROFS\left(O\right).$  

Proof: The proofs of these properties are omitted.

Proposed q-ROF-MULTIMOORA approach

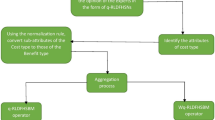
The MULTIMOORA method uses the vector normalization procedure for making comparable ratings and three subordinate ranking techniques: “ratio system, reference point approach, and full multiplicative form.” Due to its good stability and high robustness , the MULTIMOORA approach has been expanded into different forms and applied in different areas. Moreover, the q-ROFSs could be considered as one of the feasible tools to cope with high uncertainty because they can maximize the accuracy and integrity of fuzzy information. The use of q-ROFS enables the DEs to express their opinions more flexibly and precisely under uncertainty environment. However, no one has proposed the entropy and divergence measure-based MULTIMOORA for MCDM problems with q-rung orthopair information. To utilize the benefits of classical MULTIMOORA and q-ROFS theory, this section presents an integrated q-ROF-MULTIMOORA approach, which are derived from the combination of q-ROF-entropy and q-ROF-discrimination measure-based formula. In this sense, the proposed method is more robust than a single approach, such as the q-ROF-TOPSIS, the q-ROF-VIKOR, and the q-ROF-AHP methods. In addition, the present method provides more preferences to the DEs by changing the values of the parameter “q,” which offers another layer of flexibility. The evaluation structure of this technique is described by (see Fig. 1).

• Step 1: Initiate the options and attributes.

Fig. 1

Graphical representation of the proposed approach

In MCDM problem, let $N=\left\{{N}_{1},{N}_{2},...,{N}_{m}\right\}$ and $P=\left\{{P}_{1},{P}_{2},...,{P}_{n}\right\}$ be the sets of alternatives and criteria/attributes. A set of DEs $\left\{{\alpha }_{1},{\alpha }_{2},...,{\alpha }_{l}\right\}$ presents their views on each option ${N}_{i}$ over the attribute ${P}_{j}$ by means of q-ROFNs. Assume that $R={\left({\xi }_{ij}^{\left(k\right)}\right)}_{m\times n}$ be the “q-ROF-decision matrix (q-ROF-DM)” given by kth “decision expert (DE),” where ${\xi }_{ij}^{\left(k\right)}$ shows the assessment of an option ${N}_{i}$ over an attribute ${P}_{j}$ for kth expert.

• Step 2: Estimate the DE weights.

The determination of DE weights is a crucial concern in realistic MCDM problems. Firstly, the DE weights are given by the experts on the basis of their knowledge as ${B}_{k}=\left({t}_{ij},{f}_{ij}\right), \;k=1\left(1\right)\mathcal{l}.$ For the purpose of determining their relative significance in MCDM procedure, the crisp weights of DEs are derived as

$$\varpi_k=\frac{t_k^q\left(2-t_k^q-f_k^q\right)}{\sum\limits_{k=1}^{\mathcal l}\left[t_k^q\left(2-t_k^q-f_k^q\right)\right]},\;\mathrm{where}\;\;\varpi_k\geq0\;\;\mathrm{and}\;\sum\limits_{k=1}^{\mathcal l}\varpi_k=1.$$

(10)

• Step 3: Obtain the “aggregated q-ROF-DM (A-q-ROF-DM).”

To form the A-q-ROF-DM, each individual matrix requires to be merged into single decision matrix. For this purpose, the “q-rung orthopair fuzzy weighted averaging operator (q-ROFWAO)” is used and then ${\mathbb{R}}={\left({\vartheta }_{ij}\right)}_{m\times n}$ is the A-q-ROF-DM, wherein

$${\vartheta }_{ij}=q-{\mathrm{ROFWA}}_{\varpi }\left({\xi }_{ij}^{(1)},{\xi }_{ij}^{(2)},...,{\xi }_{ij}^{(\mathcal{l})}\right)=\left(\sqrt[q]{1-\prod_{k=1}^{\mathcal{l}}{\left(1-{t}_{k}^{q}\right)}^{{\varpi }_{k}}},\prod_{k=1}^{\mathcal{l}}{\left({f}_{k}\right)}^{{\varpi }_{k}}\right).$$

(11)

• Step 4: Integrated weight-determining model for attribute weights.

We consider that each attribute has different significance degree. Let $\varphi ={\left({\varphi }_{1},{\varphi }_{2},...,{\varphi }_{n}\right)}^{T}$ be the weight vector of attributes set, satisfying ${\sum }_{j=1}^{n}{\varphi }_{j}=1$ and ${\varphi }_{j}\in \left[0,1\right].$ Consecutively, to compute ${\varphi }_{j},$ we utilize the integrated objective and subjective weighting processes:

• Case I: Create the objective weight ${\varphi }_{j}^{o}$ of jth attribute by employing the following entropy and discrimination measure-based procedure:

$${\varphi }_{j}^{o}=\frac{\sum\limits_{i=1}^{m}\left[\frac{1}{m-1}\sum\limits_{t=1,t\ne i}^{m}J\left({\vartheta }_{ij},{\vartheta }_{tj}\right)+\left(1-h\left({\vartheta }_{ij}\right)\right)\right]}{\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\left[\frac{1}{m-1}\sum\limits_{t=1,t\ne i}^{m}J\left({\vartheta }_{ij},{\vartheta }_{tj}\right)+\left(1-h\left({\vartheta }_{ij}\right)\right)\right]},j=1,2,...,n.$$

(12)

Here, $J\left({\vartheta }_{ij},{\vartheta }_{tj}\right)$ presents the discrimination measure between ${\vartheta }_{ij}$ and ${\vartheta }_{tj},$ and $h\left({\vartheta }_{ij}\right)$ expresses the measure of entropy of ${\vartheta }_{ij}.$

• Case II: Evaluate the subjective weight ${\varphi }_{j}^{s}$ of each attribute.

Firstly, form the subjective weighted matrix $\left({w}_{j}^{s}\right)$ for kth DE which as

$${\varphi }_{j}^{s}={\left[{\varphi }_{j\left(k\right)}^{s}\right]}_{n\times 1}=\left[\begin{array}{c}{\varphi }_{1\left(k\right)}^{s}\\ {\varphi }_{2\left(k\right)}^{s}\\ \vdots \\ {\varphi }_{n\left(k\right)}^{s}\end{array}\right],$$

(13)

where ${\varphi }_{j\left(k\right)}^{s},\;j=1,2,...,n,k=1,2,...,\mathcal{l}$ denotes subjective weight of ${P}_{j}$ provided by kth expert, and we have

$${\omega }_{j}^{s}={\vartheta }_{ij}=q-ROFW{A}_{\varpi }\left({\varphi }_{j\left(1\right)}^{s},{\varphi }_{j\left(2\right)}^{s},...,{\varphi }_{j\left(\mathcal{l}\right)}^{s}\right).$$

(14)

Let ${\omega }_{j\left(k\right)}^{s}=\left({b}_{ijk}\right)$ be the decision weight of kth DE, where ${b}_{ijk}=\left({t}_{ijk},{f}_{ijk}\right)$ is a q-ROFN. To find the aggregated subjective criterion weight, the formula is given as

$${\omega }_{j}^{s}=\left({t}_{ij*},{f}_{ij*}\right)=\left(\sqrt[q]{1-\prod_{k=1}^{\mathcal{l}}{\left(1-{t}_{ijk}^{q}\right)}^{{\varpi }_{k}}},\prod_{k=1}^{\mathcal{l}}{\left({f}_{ijk}\right)}^{{\varpi }_{k}}\right).$$

(15)

Here, $\omega_j^s=\left(t_{ij\ast},f_{ij\ast}\right)$ is a q-ROFN.

Next, we estimate the score value ${\mathbb{S}}^{*}\left({\omega }_{j}^{s}\right)$ by Eq. (2) of ${\omega }_{j}^{s}=\left({t}_{ij*},{f}_{ij*}\right).$ Thus, we obtain the subjective weight of attribute as follows:

$${\varphi }_{j}^{s}=\frac{{\mathbb{S}}^{*}\left({\omega }_{j}^{s}\right)}{{\sum }_{j=1}^{n}{\mathbb{S}}^{*}\left({\omega }_{j}^{s}\right)},\;j=1,2,...,n.$$

(16)

• Case III: Estimate the combined weight of attribute.

Based on case I and case II, the DEs want to combine the objective and subjective weights of attributes. Thus, the combined weight of jth attribute is given by Eq. (17).

$${\varphi }_{j}=\gamma {\varphi }_{j}^{s}+\left(1-\gamma \right){\varphi }_{j}^{o},\;j=1,2,...,n,$$

(17)

where $\gamma$ is the aggregation parameter of decision precision lies between 0 to 1.

• Step 5: Obtain the priority order the alternatives with the RS model.

The RS process can be articulated in the following points:

• Step 5.1: Compute the significance of ith option by using Eqs. (20) and (21).

$${Y}_{i}^{+}=\left(\sqrt[q]{1-\prod_{j\in {P}_{b}}{\left(1-{\left({t}_{ij}\right)}^{q}\right)}^{{\varphi }_{j}}},\prod_{j\in {P}_{b}}{\left({f}_{ij}\right)}^{{\varphi }_{j}}\right),$$

(18)

$${Y}_{i}^{-}=\left(\sqrt[q]{1-\prod_{j\in {P}_{n}}{\left(1-{\left({t}_{ij}\right)}^{q}\right)}^{{\varphi }_{j}}},\prod_{j\in {P}_{n}}{\left({f}_{ij}\right)}^{{\varphi }_{j}}\right),$$

(19)

where ${P}_{b}$ and ${P}_{n}$ signify the beneficial and non-beneficial attributes, respectively.

• Step 5.2: Find the score values of ${Y}_{i}^{+}$ and ${Y}_{i}^{-},$ where

$${y}_{i}^{+}={\mathbb{S}}^{*}\left({Y}_{i}^{+}\right)\; \mathrm{and}\;\; {y}_{i}^{-}={\mathbb{S}}^{*}\left({Y}_{i}^{-}\right).$$

(20)

• Step 5.3: Estimate the complete significance value of alternatives as follows:

$${y}_{i}={y}_{i}^{+}-{y}_{i}^{-}.$$

(21)

• Step 5.4: Determine the preferences of the alternatives.

• Determine the priority order of alternatives by RP model.

The RP model involves the following steps:

• Step 6.1: Calculate the RP.

In this step, each coordinate of the RP ${p}^{*}=\left\{{p}_{1}^{*},{p}_{2}^{*},...,{p}_{n}^{*}\right\}$ is a q-ROFN, wherein

$$p_j^\ast=\left\{\begin{array}{l}\left(\max_it_{ij},\min_if_{ij}\right),\;\mathrm{for}\;\mathrm{beneficial} \,\mathrm{criterion}\;P_b\\\left(\min_it_{ij},\max_if_{ij}\right),\;\mathrm{for}\;\mathrm{non-beneficial}\,\mathrm{criterion}\;P_n\end{array}\right.\mathrm{for}\;j=1,2,...,n.$$

(22)

• Step 6.2: By using Eq. (23), estimate the discrimination from each alternative to all the references of the RP

  $${J}_{ij}={\varphi }_{j}\left(J\left(\vartheta_{ij},{p}_{j}^{*}\right)\right),$$

  (23)

  where ${J}_{ij}$ signifies the maximum discrimination of the option ${N}_{i}$ associated to criterion ${P}_{j},$ given by Eq. (3).

• Step 6.3: Compute the maximum discrimination of each option.

  $${d}_{i}=\underset{j}{\mathrm{max}}{\;J}_{ij},\;i=1,2,...,m.$$

  (24)

• Step 6.4: Rank the alternatives.

• Determine the preferences order of the options using FMF process.

The FMF process consists of the following steps:

• Step 7.1: Calculate L_i and K_i by using Eqs. (25) and (26).

$${L}_{i}=\left(\prod_{j\in {P}_{b}}{\left({t}_{ij}\right)}^{{\varphi }_{j}},\sqrt[q]{1-\prod_{j\in {P}_{b}}{\left(1-{\left({f}_{ij}\right)}^{q}\right)}^{{\varphi }_{j}}}\right),$$

(25)

$${K}_{i}=\left(\prod_{j\in {P}_{n}}{\left({t}_{ij}\right)}^{{\varphi }_{j}},\sqrt[q]{1-\prod_{j\in {P}_{n}}{\left(1-{\left({f}_{ij}\right)}^{q}\right)}^{{\varphi }_{j}}}\right),$$

(26)

where ${L}_{i}$ and ${K}_{i}$ are q-ROFNs.

• Step 7.2: Obtain the ${\chi }_{i}$ and ${\beta }_{i}$ using the improved score value given by Definition 3 (see appendix) and is given by

$${\chi }_{i}={\mathbb{S}}^{*}\left({J}_{i}\right)\;\mathrm{and} \;\;{\beta }_{i}={\mathbb{S}}^{*}\left({K}_{i}\right).$$

(27)

• Step 7.3: Compute the “utility degree (UD)” for each option, given as

$${u}_{i}=\frac{{\chi }_{i}}{{\beta }_{i}}$$

(28)

• Sep 7.4: Estimate the ranking of alternatives.

• Computation of the “overall utility degree (OUD)” of each alternative.

First, we obtained the normalized RS, RP, and FMF scores of each alternative with the use of vector normalization, and we obtain ${y}_{i}^{*}, {d}_{i}^{*},$ and ${u}_{i}^{*},$ correspondingly. In accordance with modified Borda rule, the assessment value of ith option is computed as

$$I\left({N}_{i}\right)={y}_{i}^{*}\cdot \frac{m-\rho \left({y}_{i}^{*}\right)+1}{\left(m\left(m+1\right)/2\right)}-{d}_{i}^{*}\cdot \frac{\rho \left({d}_{i}^{*}\right)}{\left(m\left(m+1\right)/2\right)}+{u}_{i}^{*}\cdot \frac{m-\rho \left({u}_{i}^{*}\right)+1}{\left(m\left(m+1\right)/2\right)}, i=1, 2, ..., m.$$

(29)

where ${y}_{i}^{*}=\frac{{y}_{i}}{\sqrt{{\sum }_{i=1}^{m}{\left({y}_{i}\right)}^{2}}},{u}_{i}^{*}=\frac{{u}_{i}}{\sqrt{{\sum }_{i=1}^{m}{\left({u}_{i}\right)}^{2}}},$ and $\rho \left({y}_{i}^{*}\right), \rho \left({d}_{i}^{*}\right)$, and $\rho \left({u}_{i}^{*}\right)$ are the priority order sets of RS, RP, and FMF models, respectively. The utmost value of $I\left({N}_{i}\right)$ determines the most appropriate alternative.

• Step 9: End.

An empirical study: solid waste disposal (SWD) method selection

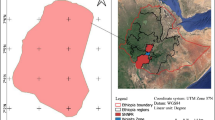
Because of the advancing lifestyles of societies together with unintended growing activities, industrialization, and urbanization, the management and treatment of USW have acquired alarming dimensions in India. In India, over 377 million urban people live in 7935 towns and cities and generate 62 MT of USW every year. Out of which, only 43 MT of the waste is assembled, 11.9 MT is treated, and 31 MT is dumped in landfill locations. SWD is one of the major fundamental facilities offered by the municipal systems in the nation to keep urban regions clean. It comprises the whole procedure of handling the SWs, beginning from the generation, collection from the prime source to final disposal in a hygienic and systematic way. Though, practically all municipal systems dispose the SW at a dump yard inside or outside the city arbitrarily, which creates environmental and public health-related issues. Specialists consider that India is following a faulty structure of waste management and disposal. In this study, an empirical study of SWD method assessment in Delhi, India, is taken to reveal the practicality and efficacy of introduced method as Delhi is the capital of India and administrative hub, offering job opportunities which have enhanced the pace of urbanization. Over 9500 t of waste is generated in this city every day. About 8000 t of waste is composed and transported to three landfill locations at Bhalswa, Okhla, and Ghazipur every day. As per the Master Plan for Delhi: 2020–21, these landfill locations had surpassed their capacity way back in 2008. Most of these locations have polluted the aquifers and groundwater in and around their neighborhoods. As the mountain of garbage in this city is gaining an enormous size, there is a need of an appropriate SWD management system which reduces the negative impacts on the environment and provides solutions for recycling items that do not belong to garbage. However, there are some commonly used SWD methods, but they are not efficient and environmentally safe.

In this case study, we have considered five SWD method options of Delhi, which are incineration (N₁), composting (N₂), plasma gasification (N₃), bioremediation (N₄), and landfill (N₅) and tried to find the suitable SWD method by employing the present q-ROF-MULTIMOORA approach.

Incineration (N₁): In this procedure, the waste material transforms into, ash, heat, and gases. Incineration reduces the waste mass by 95 to 96%. This process can be a good choice for the places that have land shortage (Arıkan et al. 2017; Liu et al., 2022).

Composting (N₂): It is one of the well-known and easy methods for solid waste disposal. Through this process, the organic wastes are disintegrated by microorganisms into simpler forms. The microorganisms use the carbon in the waste as an energy source (Arıkan et al. 2017).

Plasma gasification (N₃): It is a process of SWM that uses high ionized gases called plasma within a vessel to transform carbon-based materials into fuels. It is a promising method to handle the hazardous wastes by altering incinerator ash or chemicals into non-hazardous slag (Chen et al., 2022).

Bioremediation (N₄): It is an environmental and low-cost process of solid waste disposal that make the atmosphere free of pollution using eco-friendly microbes. By means of this process, the hazardous waste can be transferred to non-toxic materials in a long time (Waghmare et al., 2014).

Landfill (N₅): It is a well-engineered and managed method for solid waste disposal. Landfills should be created in places with low groundwater levels and far from sources of flooding, because once this process is completed, the area is declared unfit for construction of buildings for the next 20 years (Liu et al., 2022).

To evaluate the criteria and alternatives, a team of four DEs (B₁, B₂, B₃, B₄) is formed who are responsible for this SWDM selection. These experts are from municipality, sustainable development, and environmental sector. Out of 4 DEs, 2 experts are from environmental sector, other two experts are from sustainable development and municipality. Educational backgrounds of two experts are PhD, and others are masters’ and post doctorate. The team of DEs has prepared a questionnaire to estimate the significance of criteria in the assessment of SWDMs. The goal of this survey is to choose the significant sustainability indicators influencing the SWDM selection process. The criteria that may affect the SWDMs evaluation process are collected by reviewing the literature. On the basis of literature review, online questionnaire. and open interviews, a set of sustainability perspectives and indicators are collected to select the best SWDM. Thus, this MCDM problem includes 12 attributes or criteria, which are initial investment cost (P₁), operating costs (P₂), transportation costs (P₃), environmental risks (P₄), emissions (P₅), air pollution control (P₆), feasibility (P₇), technical reliability (P₈), capacity (facility) (P₉), efficiency (waste reduction) (P₁₀), waste recovery (P₁₁), and energy recovery (P₁₂). Here, P₁, P₂, P₃, P₄, P₅, and P₆ are of non-beneficial type, and others are of beneficial-type attributes. After reviewing the broadway of all SWD method alternatives, each DE provided their views for the evaluation of each alternative over each attribute in terms of q-ROFNs. The explanation of attributes is specified in Table 2.

Table 2 Detail description of the criteria to evaluate the SWDM selection

First of all, experts decide the significance value of each decision expert in terms of q-ROFNs, given as {(0.80, 0.50, 0.7133), (0.85, 0.45, 0.6655), (0.90, 0.40, 0.6655), and (0.75, 0.60, 0.7128)}. Since the DE weights are q-ROFSs, therefore, the numeric weights are assessed by utilizing Eq. (10) as $\left\{{\varpi }_{1}=0.2368, {\varpi }_{2}=0.2698,{\varpi }_{3}=0.2985, {\varpi }_{4}=0.1949\right\}$. Table 3 presents the individual opinion of each DE for the assessment of each alternative with respect to each attribute. With the use of Eq. (11), the aggregated decision matrix is created and given in Table 4.

Table 3 Evaluation ratings of competitive SWDM selection

Table 4 A-q-ROF-DM matrix for SWD method selection

To estimate the objective weights of attribute, use Eqs. (1) and (3) in Eq. (12), and hence ${\varphi }_{j}^{o}=$(0.1453, 0.1333, 0.0881, 0.1187, 0.0596, 0.1024, 0.0748, 0.0618, 0.0697, 0.0521, 0.0392, 0.0551).

To obtain the subjective weights of attribute, we create Table 5, which shows the “linguistic values (LVs)” and their corresponding q-ROFNs to measure the relative importance of each evaluation criterion.

Table 5 Linguistic term to q-ROFNs

For subjective weights of attributes, we apply Eqs. (13)–(16), and hence, we obtain (see Table 6) as follows:

Table 6 Subjective weights of criteria based on DEs and score function

${\varphi }_{j}^{s}=$(0.1044, 0.0979, 0.1030, 0.0735, 0.0916, 0.0801, 0.0859, 0.0946, 0.0730, 0.0697, 0.0580, 0.0683).

By means of Eq. (17), the combined weights of attribute is calculated ($\gamma =0.5$), and thus, we get.

${\varphi }_{j}=$(0.1249, 0.1156, 0.0955, 0.0961, 0.0756, 0.0912, 0.0804, 0.0782, 0.0713, 0.0609, 0.0486, 0.0617).

The procedural steps of RS model by means of Eqs. (18)–(21) are shown in Table 7.

Table 7 The priority order of SWDMs based on RS model

Using Eq. (22), each coordinate of reference point is calculated as.

${p}_{j}^{*}=$ {(0.524, 0.776, 0.730), (0.589, 0.768, 0.701), (0.562, 0.753, 0.734), (0.614, 0.750, 0.703), (0.631, 0.725, 0.717), (0.638, 0.778, 0.646), (0.749, 0.673, 0.650), (0.725, 0.664, 0.687), (0.731, 0.684, 0.662), (0.714, 0.679, 0.685), (0.710, 0.679, 0.689), (0.732, 0.668, 0.676)}.

With the use of Eqs. (23)–(24), the discrimination of each option to all the reference points is calculated, and further, the maximum discrimination is computed in Table 8. Finally, the prioritization order of SWDMs are obtained and shown in Table 8.

Table 8 The preference order of SWDMs using the RP model

In accordance with Eqs. (25)–(28), the results of the FMF model are computed and given in Table 9.

Table 9 The prioritization of alternatives using the FMF model

Using Eq. (29), the OUD $I\left({N}_{i}\right)$ of each SWDM option is computed in Table 10. Thus, the priority order of the SWDMs is ${N}_{1}\succ {N}_{5}\succ {N}_{3}\succ {N}_{2}\succ {N}_{5}.$ And, hence the optimal SWDM is incineration $\left({N}_{1}\right).$

Table 10 Final ranking of the SWDMs

Comparative study

In order to prove the robustness of the presented approach, we compare the presented q-ROF-MULTIMOORA approach with existing TOPSIS (Liu et al., 2019) and COPRAS (Krishankumar et al., 2019) methods from q-rung orthopair fuzzy perspective.

q-ROF information-based TOPSIS approach

This approach comprises the following steps:

• Steps 1–4: Follow the steps of q-ROF-MULTIMOORA.

• Step 5: In the following, determine the “q-rung orthopair fuzzy ideal solution (q-ROF-IS)” and “q-rung orthopair fuzzy anti ideal solution (q-ROF-AIS)”:

ϕ⁺={(0.524, 0.776, 0.730), (0.589, 0.768, 0.701), (0.562, 0.753, 0.734), (0.614, 0.750, 0.703), (0.631, 0.725, 0.717), (0.638, 0.778, 0.646), (0.749, 0.673, 0.650), (0.725, 0.664, 0.687), (0.731, 0.684, 0.662), (0.714, 0.679, 0.685), (0.710, 0.679, 0.689), (0.732, 0.668, 0.676)},

ϕ⁻={(0.650, 0.703, 0.723), (0.680, 0.705, 0.695), (0.685, 0.658, 0.732), (0.643, 0.725, 0.706), (0.665, 0.650, 0.755), (0.648, 0.719, 0.710), (0.654, 0.748, 0.671), (0.648, 0.748, 0.676), (0.628, 0.747, 0.695), (0.649, 0.727, 0.700), (0.673, 0.738, 0.664), (0.705, 0.672, 0.701)}, respectively. Next, we assess the distances between the alternative ${N}_{i}\left(i=1\left(1\right)m\right)$ from q-ROF-IS and q-ROF-AIS over the attribute ${P}_{j}.$

• Step 6: Obtain the relative “closeness index (CI).”

The relative CI of each SWD method is determined as

$${\mathbb{C}}\left({N}_{i}\right)=\frac{D\left({N}_{i},{\phi }^{-}\right)}{D\left({N}_{i},{\phi }^{+}\right)+D\left({N}_{i},{\phi }^{-}\right)},$$

(30)

where

$$D\left({N}_{i},{\phi }^{+}\right)=\frac{1}{2}\sum_{j=1}^{n}\left[{\varphi }_{j}\left(\left|{t}_{{\vartheta }_{ij}}^{q}-{t}_{{\phi }_{j}^{+}}^{q}\right|+\left|{f}_{{\vartheta }_{ij}}^{q}-{f}_{{\phi }_{j}^{+}}^{q}\right|+\left|{\pi }_{{\vartheta }_{ij}}^{q}-{\pi }_{{\phi }_{j}^{+}}^{q}\right|\right)\right]$$

and

$$D\left({N}_{i},{\phi }^{-}\right)=\frac{1}{2}\sum_{j=1}^{n}\left[{\varphi }_{j}\left(\left|{t}_{{\vartheta }_{ij}}^{q}-{t}_{{\phi }_{j}^{-}}^{q}\right|+\left|{f}_{{\vartheta }_{ij}}^{q}-{f}_{{\phi }_{j}^{-}}^{q}\right|+\left|{\pi }_{{\vartheta }_{ij}}^{q}-{\pi }_{{\phi }_{j}^{-}}^{q}\right|\right)\right].$$

Next, the revised CI of each option is defined by

$$\Lambda \left({N}_{i}\right)=\frac{D\left({N}_{i},{\phi }^{-}\right)}{{D}_{\mathrm{max}}\left({N}_{i},{\phi }^{-}\right)}-\frac{D\left({N}_{i},{\phi }^{+}\right)}{{D}_{\mathrm{min}}\left({N}_{i},{\phi }^{+}\right)}, \;\mathrm{where}\;\, {D}_{\mathrm{min}}\left({N}_{i},{\phi }^{+}\right)=\underset{1\le i\le m}{\mathrm{min}}D\left({N}_{i},{\phi }^{+}\right), {D}_{\mathrm{max}}\left({N}_{i},{\phi }^{-}\right)=\underset{1\le i\le m}{\mathrm{max}}D\left({N}_{i},{\phi }^{-}\right).$$

The overall computational results and prioritization order of the SWDM options are presented in Table 11. Hence, the desirable method is incineration $\left({N}_{1}\right)$.

Table 11 Priority order of q-ROF-TOPSIS for SWDM selection

q-ROF information-based COPRAS method

This approach comprises the following steps:

• Steps 1–4: Analogous to earlier framework.

• Step 5: Aggregate the benefit-type and cost-type attribute. We calculate the maximum degrees to beneficial type and minimum degree ${\upsilon }_{i}=\stackrel{n}{\underset{j=l+1}{\oplus }}{\varphi }_{j}\;{\vartheta }_{ij},$ to non-beneficial-type criteria, which are given as ${\iota }_{i}=${(0.560, 0.854, 0.586), (0.528, 0.874, 0.570), (0.520, 0.875, 0.574), (0.508, 0.879, 0.575), (0.533, 0.869, 0.576)} and ${\upsilon }_{i}=$ {(0.497, 0.835, 0.665), (0.543, 0.827, 0.650), (0.555, 0.836, 0.626), (0.551, 0.815, 0.663), (0.533, 0.827, 0.656)}.

• Step 6: The relative degree ${\gamma }_{i}=\tau {\mathbb{S}}^{*}\left({\iota }_{i}\right)+\left(1-\tau \right)\frac{\sum_{i=1}^{m}{\mathbb{S}}^{*}\left({\upsilon }_{i}\right)}{{\mathbb{S}}^{*}\left({\upsilon }_{i}\right)\sum_{i=1}^{m}\left(1/{\mathbb{S}}^{*}\left({\upsilon }_{i}\right)\right)},$ where ${\mathbb{S}}^{*}\left({\iota }_{i}\right)$ and ${\mathbb{S}}^{*}\left({\upsilon }_{i}\right)$ are the score degrees of ${\iota }_{i}$ and ${\upsilon }_{i},$ respectively, and the parameter $\tau \in \left[\mathrm{0,1}\right]$ is the decision mechanism parameter of the DEs. Therefore, we obtain ${\gamma }_{1}=0.300,{\gamma }_{2}=0.266,{\gamma }_{3}=0.267,{\gamma }_{4}=0.252,$ and ${\gamma }_{5}=0.262.$

• Step 7: The ranking of the SWDMs is ${\gamma }_{1}\succ {\gamma }_{3}\succ {\gamma }_{2}\succ {\gamma }_{5}\succ {\gamma }_{4}.$_s The ranking reflects that the SWDM ${N}_{1}$ (incineration) is the best among the others.

• Step 8: Estimate the “utility degree (UD)” ${\delta }_{i}=\frac{{\gamma }_{i}}{{\gamma }_{\mathrm{max}}}\times 100\%,i=1\left(1\right)m,$ which reveals the degree of utility between each SWDMs and the desirable SWDM. Then, we obtain ${\delta }_{1}=$ 100%, ${\delta }_{2}=$ 88.67%, ${\delta }_{3}=$ 89.00%, ${\delta }_{4}=$ 84.00%, and ${\delta }_{5}=$ 87.33%.

Next, Table 12 shows the preference orders of the SWDMs in accordance with present and existing methods. By applying each method, we get that the Incineration $\left({N}_{1}\right)$ is the optional SWDM. Figure 2 presents the correlation plot of preference orders obtained by proposed and existing methods. From Fig. 2, the histograms of approaches perform along with the matrix diagonal; scatter designs of approach pairs seem off diagonal. The slopes of the least-squares reference lines in the scatter designs are similar as the shown correlation degree. It is noticeable that the uniformity of the q-ROF-MULTIMOORA is higher than extant frameworks. The spearman correlation values of proposed q-ROF-MULTIMOORA method (improved Borda rule), RS model, RP model, FMF model, Krishankumar et al. (2019), and Liu et al. (2019) with overall assessment solutions are given by (1.00, 0.60, 0.90, 0.90, 70, 0.90).

Table 12 Preference order of SWDM option from different approaches

Fig. 2

Correlation plot of preference order obtained by proposed framework and existing methods

In comparison with some of the existing studies for ranking of alternatives (Liu et al., 2019; Krishankumar et al., 2019; Ali, 2022) and criteria weight-determining procedures (Pamucar et al., 2018; Žižović and Pamucar, 2019), the merits of the proposed MCDM methodology are as follows:

• Existing q-ROF-TOPSIS and q-ROF-COPRAS methods consider the direct weights of criteria. While, in the present methodology, the combined weight-determining procedure is based on the combination of objective weighting and subjective weighting techniques for criteria weights, which makes the present method more practical, accurate, and flexible. The introduced entropy in this study quantifies the degree of fuzziness of q-ROFS, while q-ROF-discrimination measure depicts the degree of discrimination between two q-ROFSs. Thus, there is no threat of information loss as it considers the entropy of criteria as well as the discrimination between the criteria.

• In q-ROF-MARCOS (Ali, 2022), the reference points are considered through the q-ROF-IS and q-ROF-AIS, and then, the degree of utility is determined for each alternative with respect to both set solutions. Thus, the ranking of each alternative is derived based on degree of utility. While, the proposed MULTIMOORA method is based on three model: RS, RP, and FMF. In this method, the rank of each alternative is computed individually for each model, and based on the results, the final preference ordering of each alternative is determined using the dominance theory. Consideration of three models determines the more precise results in making a decision. In other words, we can say that as the proposed MULTIMOORA approach contains three subordinate models; therefore, it determines a more reliable and robust result than other single methods in the assessment of alternatives.

• The q-ROF-MULTIMOORA model has higher operability than the q-ROF-TOPSIS method when the numbers of criteria and criteria are large. In proposed method, there is no need to compute the q-ROF-IS and q-ROF-AIS. The results are computed by dealing with the real data, which reveals that the proposed method can deal with more intricate and realistic MCDM problems.

• In the present method, the entropy and discrimination measure-based model is presented to derive the objective (data-based) weights of criteria under q-ROFS environment. While the “level-based weight assessment (LBWA)” (Žižović and Pamucar, 2019) and “full consistency method (FUCOM)” (Pamucar et al., 2018) are unable to determine the objective weights of criteria.

Sensitivity assessment (SA)

In the present section, the SA is executed to confirm the stability of the outcomes obtained by the introduced approach. From Table 13 and Fig. 3, the results show that the overall assessment degree ${I}_{B}\left({N}_{i}\right),\left(i=1(1)5\right)$ of SWDMs with respect to different values of parameter $\gamma .$ For $\gamma =0.0$ (objective weight) and $\gamma =0.2,$ we obtain the following preference order: ${N}_{1}\succ {N}_{5}\succ {N}_{2}\succ {N}_{3}\succ {N}_{4}$, and ${N}_{1}$ is the optimal method, while for $\gamma =0.5$ (combined weight) $\gamma =0.8,$ and $\gamma =1.0$ (subjective weight), we get the following preference order: ${N}_{1}\succ {N}_{5}\succ {N}_{3}\succ {N}_{2}\succ {N}_{4}$, and ${N}_{1}$ is the optimal option. Hence, we observe that the preference order of SWDM options slightly varies with respect to the parameter values. Henceforth, we observe that the SWDM evaluation is dependent on and delicate to specified values of parameter $\gamma$. Thus, the introduced q-ROF-MULTIMOORA approach has an ample stability over diverse sets of attribute weights. Also, Fig. 4 depicts the correlation plot of preference orders obtained over the parameter values. From Fig. 4, histograms of the each value of parameter $\gamma$ perform with the matrix diagonal; scatter designs of parameter $\gamma$ value pairs perform off diagonal. The slopes of the least-squares reference lines in the scatter designs are same to the presented correlation degrees. It is obvious that the uniformity of the present methodology is high with respect to different parameter values. The spearman correlation values of proposed q-ROF-MULTIMOORA method for $\gamma =0.0$ (objective weight), $\gamma =0.2,$ $\gamma =0.5$ (combined weight), $\gamma =0.8$ and $\gamma =1.0$ (subjective weight) with the $\gamma =0.5$ (combined weight) are given by (0.90, 0.90, 1.00, 1.00, 1.00).

Table 13 Assessment values and preference ordering of SWDMs with respect to the parameter $\left(\gamma \right)$

Fig. 3

Sensitivity results of SWDMs with respect to the parameter $\left(\gamma \right)$

Fig. 4

Correlation plot of preference order SWDM options with respect to the parameter $\left(\gamma \right)$

Discussion and implications

SWM is one of the leading challenges to the municipal authorities of both small and large cities in most countries worldwide. A proper and sustainable SWM system requires to follow various key objectives. First of all, the SWM system has to take the advantage of environmental sustainability by minimizing the related costs and carbon emissions . Then, the system requires to enhance social sustainability by increasing the healthcare facilities near populated residential areas (Fidelis et al. 2020). Further, SWM system may facilitate energy recovery and power generation (Cucchiella et al. 2017). SWM directly relates to the economic development, social development, and environmental development .

The results of the proposed MULTIMOORA approach proves that initial investment cost (P₁) is the most important criterion with a weight value 0.1044, transportation cost (P₃) is the second most important criterion with a weight value 0.1030, and operating cost (P₂) is the third most important criterion with a weight value 0.0979. From Table 10, we observe that incineration (N₁) is the most suitable SWDM for given case study under q-rung orthopair fuzzy environment. Landfill (N₅) has secured the second position, plasma gasification (N₃) is at the third position, composing (N₂) is at the fourth position, and bioremediation (N₅) is at the fifth position. The managerial implications of this research are mainly to facilitate decision-making under highly uncertain environment. DEs often have concerns regarding the events that they expected to happen. The application of this work assures that the proposed MULTIMOORA model offers an effective SWM system. Thus, the policymakers feel more confident with the ranking of SWDM alternatives. A suitable and robust weight-determining formula will definitely decrease unnecessary costs owing to improper, vague, and indeterminate judgments in the weight determination process. Furthermore, the selection of improper SWDM may have negative consequences on society, environment, and economic growth of the nations. The presented method helps the DEs and policymakers to identify reliable and robust SWDM alternative among a set of alternatives concerning multiple sustainability criteria. In the process of multi-criteria SWDM problems, data are very often imprecise, fuzzy, and difficult to quantify. A DE may encounter difficulty in quantifying such data. The decision-making method introduced in this paper is very useful, advantageous, and superior to other models because it has the potential to deal with uncertain information. This method consists of an effective processes to weigh the DEs and criteria, and to rank the SWDM options. The finding of this study explains the significance of the weights of the numerous sustainability indicators in order to choose the most suitable SWDM candidate. Thus, the proposed method not only assesses the significant degrees of various indicators but also handles the ambiguity and fuzziness arisen through the SWDM assessment problem in the emerging economies.

Conclusions

With the increasing environmental concerns and subjectivity of human thinking, the selection of SWDM can be considered as a MCDM problem due to involvement of several criteria. For this purpose, a novel hybridized MCDM approach has proposed to find the most appropriate SWDM from sustainable perspective. Here, we have extended the classical MULTIMOORA approach to q-rung orthopair fuzzy context by means of q-ROF entropy and discrimination measures. In this method, the objective weights of criteria have derived by the proposed information measure-based model and the subjective weights of criteria have determined based on DEs’ information and score function. Then, a combined weighting model is presented to obtain the final weights of the criteria. Further, a case study of SWDM assessment problem has been implemented under q-ROFI, which expresses the usefulness and practicability of the introduced methodology. In this case study, an integrated framework for SWDM selection is presented based on 12 criteria, which are broadly considered from the literatures, research reports, and DEs’ information. Comparison with exiting methods has presented to reveal the validity and stability of the obtained results. To demonstrate the robustness of the results, sensitivity analysis has discussed over different values of parameter. The findings of the outcomes prove that the presented framework has good solidity, and is well consistent than the various extant approaches.

However, some limitations must be addressed in further studies.

• ○ In reality, there are different types of composting process, but this study considered composting in general.

• ○ In this study, the considered sustainability indicators/criteria were selected based on related literature review and discussion with experts. This study does not guarantee that there are no other SWDMs that are better than ordered storing (N₁). It only means that N₁ is the most suitable SWDM among all considered five alternatives.

• ○ The final ranking could change when more evaluation criteria and alternatives are taken into consideration.

• ○ The proposed method ignores the interrelationships between the sustainability factors.

• ○ The present method ignores the target-based criteria.

• ○ This study does not consider the indeterminate and inconsistent information during SWDM assessment problem.

In further study, we will try to address the aforesaid limitations. In addition, this study ignores the target-based criteria in the process of MCDM. In Future, we will try to consider these points:

• Different methods of composing and its objective will be considered.

• Society education and training programs on the available policies and guidelines of SWDM are urgently required;

• More aspects of sustainability can be considered in the evaluation criteria index system;

• More alternatives such as open burning, dumping into the sea, ploughing in fields, hog feeding, grinding and discharging into sewers, salvaging, fermentation, and biological digestion should be included in further studies;

• New methods such as multi-normalization multi-distance assessment (TRUST), Operational Competitiveness Rating (OCRA), simple weighted sum-product (WISP) methods can be combined with criteria weighting models including criteria importance through intercriteria correlation (CRITIC) and method based on the removal effects of criteria (MEREC) for solving MCDM problems under uncertain environment;

• The developed framework can be extended to other uncertain environments including q-rung orthopair fuzzy soft rough set, interval-valued q-rung orthopair fuzzy set, and probabilistic linguistic hesitant fuzzy set.

• The proposed approach is not limited to SWDM selection problem but can also be implemented on other complex MCDM problems such as water distillation selection, sustainable biomass crop selection, low carbon supplier selection, and others.

Appendix 1 Preliminaries

The current section briefly presents the fundamental notions and information measures for q-ROFSs.

Definition 1 (Yager, 2017). Let $O=\left\{{o}_{1},{o}_{2},...,{o}_{n}\right\}$ be a finite discourse set. Then, the q-ROFS M on O is defined by

$$M=\left\{\left.\langle {o}_{i},{t}_{M}\left({o}_{i}\right),{f}_{M}\left({o}_{i}\right)\rangle \right|{o}_{i}\in O\right\},$$

where in ${t}_{M},{f}_{M}:O\to \left[0,1\right]$ imply the BD and ND of the element ${o}_{i}\in O,$ respectively, with the constraints $0\le {t}_{M}\left({o}_{i}\right)\le \mathrm{1,0}\le {f}_{M}\left({o}_{i}\right)\le \mathrm{1,0}\le {\left({t}_{M}\left({o}_{i}\right)\right)}^{q}+{\left({f}_{M}\left({o}_{i}\right)\right)}^{q}\le 1,q\ge 1,\forall {o}_{i}\in O.$ Next, the indeterminacy degree is presented as ${\pi }_{M}\left({o}_{i}\right)=\sqrt[q]{1-{\left({t}_{M}\left({o}_{i}\right)\right)}^{q}-{\left({f}_{M}\left({o}_{i}\right)\right)}^{q}}.$ For convenience, $\left({t}_{M}\left({o}_{i}\right),{f}_{M}\left({o}_{i}\right)\right)$ is known as a “q-rung orthopair fuzzy number (q-ROFN)” and represented by $\theta =\left({t}_{\theta },{f}_{\theta }\right).$  

Definition 2 (Liu and Wang, 2018). Let $\theta =\left({t}_{\theta },{f}_{\theta }\right),{\theta }_{1}=\left({t}_{{\theta }_{1}},{f}_{{\theta }_{1}}\right),{\theta }_{2}=\left({t}_{{\theta }_{2}},{f}_{{\theta }_{2}}\right)\in q-ROFNs\left(O\right)$, then operations on q-ROFNs are discussed as.

• ${\theta }^{c}=\left({f}_{\theta },{t}_{\theta }\right),$  

• ${\theta }_{1}\oplus {\theta }_{2}=\left(\sqrt[q]{{t}_{{\theta }_{1}}^{q}+{t}_{{\theta }_{2}}^{q}-{t}_{{\theta }_{1}}^{q}{t}_{{\theta }_{2}}^{q}},{f}_{{\theta }_{1}}{f}_{{\theta }_{2}}\right),$  

• ${\theta }_{1}\otimes {\theta }_{2}=\left({t}_{{\theta }_{1}}{t}_{{\theta }_{2}},\sqrt[q]{{f}_{{\theta }_{1}}^{q}+{f}_{{\theta }_{2}}^{q}-{f}_{{\theta }_{1}}^{q}{f}_{{\theta }_{2}}^{q}}\right),$  

• $\lambda \theta =\left(\sqrt[q]{1-{\left(1-{t}_{\theta }^{q}\right)}^{\lambda }},{f}_{\theta }^{\lambda }\right),\lambda >0,$  

• ${\theta }^{\lambda }=\left({t}_{\theta }^{\lambda },\sqrt[q]{1-{\left(1-{f}_{\theta }^{q}\right)}^{\lambda }}\right),\lambda >0.$  

Definition 3 (Liu and Wang, 2018). Let $\theta =\left({t}_{\theta },{f}_{\theta }\right)\in q-ROFS\left(O\right).$ Then, the functions ${\mathbb{S}}\left(\theta \right)={t}_{\theta }^{q}-{f}_{\theta }^{q}$ and $\hslash \left(\theta \right)={t}_{\theta }^{q}+{f}_{\theta }^{q}$ are defined as the score and accuracy values of $\theta$ such that ${\mathbb{S}}\left(\theta \right)\in \left[-1,1\right]$ and $\hslash \left(\theta \right)\in \left[\mathrm{0,1}\right].$ Since ${\mathbb{S}}\left(\theta \right)\in \left[-\mathrm{1,1}\right],$ therefore, the improved score function is defined by

$${\mathbb{S}}^{*}\left(\theta \right)=\frac{1}{2}\left({\mathbb{S}}\left(\theta \right)+1\right), \;\mathrm{ where}\;\; {\mathbb{S}}^{*}\left(\theta \right)\in \left[\mathrm{0,1}\right].$$

(A1)

The larger the score value, the higher the q-ROFN.

Next, the modified accuracy function is defined as

$${\hslash }^{^\circ }\left(\theta \right)=1-\hslash \left(\theta \right),\; \mathrm{where }\;\;{\hslash }^{^\circ }\left(\theta \right)\in \left[\mathrm{0,1}\right].$$

(A2)

The larger the accuracy function, the bigger the q-ROFN. The most significant contributions of Definition 3 is that it provides a process to compare two q-ROFNs.

On the basis of score and accuracy functions, a comparative scheme is given for any two q-ROFNs ${\theta }_{1}=\left({t}_{1},{f}_{1}\right)$ and ${\theta }_{2}=\left({t}_{2},{f}_{2}\right),$ which as

• (i) If ${\mathbb{S}}^{*}\left({\theta }_{1}\right)>{\mathbb{S}}^{*}\left({\theta }_{2}\right),$ then ${\theta }_{1}>{\theta }_{2},$  

• (ii) If ${\mathbb{S}}^{*}\left({\theta }_{1}\right)<{\mathbb{S}}^{*}\left({\theta }_{2}\right),$ then ${\theta }_{1}<{\theta }_{2},$  

• (iii) If ${\mathbb{S}}^{*}\left({\theta }_{1}\right)={\mathbb{S}}^{*}\left({\theta }_{2}\right),$ then

• (a) if ${\hslash }^{^\circ }\left({\theta }_{1}\right)>{\hslash }^{^\circ }\left({\theta }_{2}\right),$ then ${\theta }_{1}>{\theta }_{2},$  

• (b) if ${\hslash }^{^\circ }\left({\theta }_{1}\right)<{\hslash }^{^\circ }\left({\theta }_{2}\right),$ then ${\theta }_{1}<{\theta }_{2},$

• (c) if ${\hslash }^{^\circ }\left({\theta }_{1}\right)={\hslash }^{^\circ }\left({\theta }_{2}\right),$ then ${\theta }_{1}={\theta }_{2}.$  

Definition 4 (Liu et al., 2019). Let ${\theta }_{1}=\left({t}_{{\theta }_{1}},{f}_{{\theta }_{1}}\right),{\theta }_{2}=\left({t}_{{\theta }_{2}},{f}_{{\theta }_{2}}\right)\in q-ROFNs\left(O\right).$ Then, the distance measure for q-ROFSs is given by

$$d\left({\theta }_{1},{\theta }_{2}\right)=\frac{1}{2}\left(\left|{t}_{{\theta }_{1}}^{q}-{t}_{{\theta }_{2}}^{q}\right|+\left|{f}_{{\theta }_{1}}^{q}-{f}_{{\theta }_{2}}^{q}\right|+\left|{\pi }_{{\theta }_{1}}^{q}-{\pi }_{{\theta }_{2}}^{q}\right|\right).$$

(A3)

Definition 5 (Peng and Liu, 2019). Let $M,N\in q-ROFSs\left(O\right).$ A real-valued function $h:q-ROFS\left(O\right)\to [0,1]$ is called q-ROF-entropy if it fulfils the following axioms:

• (p1). $0\le h\left(M\right)\le 1,$  

• (p2). $h\left(M\right)=0\iff$  M is a crisp set,

• (p3). $h\left(M\right)=1\iff {t}_{M}\left({o}_{i}\right)={f}_{M}\left({o}_{i}\right),$  

• (p4). $h\left(M\right)=h\left({M}^{c}\right),$  

• (p5). $h\left(M\right)\le h\left(N\right)$ if M is less fuzzy than N, i.e., ${t}_{M}\left({o}_{i}\right)\le {t}_{N}\left({o}_{i}\right)\le {f}_{N}\left({o}_{i}\right)\le {f}_{M}\left({o}_{i}\right)$ or ${f}_{M}\left({o}_{i}\right)\le {f}_{N}\left({o}_{i}\right)\le {t}_{N}\left({o}_{i}\right)\le{t}_{M}\left({o}_{i}\right).$  

Definition 6 (Mishra and Rani, 2021). Let $M,N,T\in q-ROFSs\left(O\right).$ A q-ROF-discrimination measure is a real-valued mapping $J:q-ROFSs\left(O\right)\times q-ROFSs\left(O\right)\to {\mathbb{R}}$ which fulfills the following assumptions:

• (a1). $J\left(M,N\right)\ge 0,$  

• (a2). $J\left(M,N\right)=0\iff M=N,$  

• (a3). $J\left(M,N\right)=J\left(N,M\right),$  

• (a4). $J\left(M\cup T,N\cup T\right)\le J\left(M,N\right),\forall T\in q-ROFS\left(O\right),$  

• (a5). $J\left(M\cap T,N\cap T\right)\le J\left(M,N\right),\forall T\in q-ROFS\left(O\right).$