A Compressive Sensing Based Computationally Efficient High-Resolution DOA Estimation of Wideband Signals Using Generalized Coprime Arrays

Abstract

Most recent state-of-the-art wideband direction of arrival (DOA) estimation techniques achieve reasonable accuracy at the expenses of high computational complexity. In this paper, a new computationally efficient approach based on compressive sensing (CS) is introduced for high resolution wideband DOA estimation. The low software complexity is achieved utilizing CS with deterministic chaotic Chebyshev sensing matrices that allow reducing the measurement vector dimension, while the high-resolution DOA estimation is acquired utilizing an efficient generalized coprime array configuration. The effectiveness of the introduced approach in enhancing the DOA estimation precision and reducing the computational complexity is studied along with a detailed comparison between three state-of-the-art wideband DOA estimation techniques, namely incoherent signal subspace method (ISSM), focusing signal subspace (FSS), and modified test of orthogonality of projected subspaces (mTOPS) with and without applying the proposed CS technique. The performance is examined utilizing various assessment metrics such as the spatial spectrum, the computational time, and the root mean square error between estimated and actual DOAs when varying the signal-to-noise ratio and number of elements. Results reveal that applying the proposed CS technique to the three algorithms (ISSM, FSS, and mTOPS) provides significant reduction in the execution time needed for the DOA estimation without affecting the resolution accuracy under various set of parameters. This reveals the importance of the proposed approach in wideband wireless communication systems.

1 Introduction

Direction of arrival (DOA) estimation plays an important role in array signal processing, explored in several wireless applications, including radar systems, mobile communications, and seismic sensing [1, 2]. DOA estimation algorithms can be used for array pattern synthesis of various antenna arrays with arbitrary configurations [3,4,5,6]. In practical applications, most wireless systems require wideband signals rather than narrowband signals. Despite the efficiency of narrowband DOA estimation techniques such as multiple signal classification (MUSIC) and maximum likelihood [7,8,9,10], they cannot be employed directly to wideband DOA estimation because the steering vectors are not only function of the DOA but also function of the frequency [11]. Wideband DOA estimation is more complex than narrowband DOA estimation because a pre-processing step is required before the estimation process, in which the wideband signals are decomposed into multiple narrowband signals using filter bank or discrete Fourier transform (DFT) [12].

Wideband DOA estimation techniques differ from each other on how they exploit the narrowband components to get the final DOAs of the signals. Incoherent signal subspace method (ISSM) is a simple wideband DOA estimation technique that applies narrowband DOA estimation methods independently to each of frequency bins acquired from wideband signal decomposition. Then, the results from all frequency bins are averaged to acquire the final DOAs of the received wideband signals [13]. Although ISSM is a straightforward wideband DOA estimation technique, its performance degrades for low signal-to-noise ratio (SNR) of some frequency bins, which leads to low estimation accuracy of the final DOAs [14].

To avoid the drawbacks of ISSM and to enhance the DOA estimation accuracy, coherent signal subspace method (CSSM) was proposed [15]. In CSSM processing, the covariance matrices of the received signals at each frequency bin are focused to a reference frequency using focusing matrices. Then, the focused covariance matrices are averaged to get a new covariance matrix that can be processed using narrowband DOA estimation techniques to obtain the final DOA estimations of incoming wideband signal sources [16, 17]. The main drawback of CSSM is the performance dependency on the pre-estimated DOAs so that errors in the pre-estimation of DOAs will degrade the DOA estimation accuracy [18]. To overcome this drawback, several techniques were proposed such as autofocusing algorithm for DOA estimation [19] and focusing signal subspace (FSS) algorithm [20]. In FSS algorithm, a unitary focusing matrix is constructed by combining the eigenvector of signal subspace at the reference frequency with the eigenvector of signal subspace at discrete frequencies. The resulted focusing matrix does not require any pre-estimation of DOAs.

The test of orthogonality of projected subspaces (TOPS) algorithm is a modern wideband DOA estimation technique that exploits the signal and noise subspaces of various frequency bins and provides good DOA estimation performance without requiring initial estimations of the DOAs [21]. In TOPS, the DOAs are estimated by measuring the orthogonality between the signal and the noise subspaces of various frequency components of the sources at different angles [22]. Despite the good DOA estimation performance of TOPS, it suffers from spurious peaks in the TOPS spatial spectrum (pseudospectrum) at all SNR levels which leads to difficulty in estimating the true DOAs of signal sources. A modification on TOPS technique, denoted by modified-TOPS (mTOPS), was proposed to reduce spurious peaks in the pseudospectrum by incorporating signal-subspace projection instead of null-space projection utilized in TOPS [23].

Recent studies investigated new techniques for enhancing the accuracy of wideband DOA estimation [24,25,26]. In [24], a modern wideband DOA estimation technique was developed by computing the largest principal angle (LPA) between the signal subspace and the subspace spanned by a new augmented array manifold which contains all frequency bins. In [25], the DOA estimation is obtained by measuring the orthogonality between the signal and the noise subspaces of some sub-bands that have better spatial information. In [26], a frequency group decision strategy (FGDS) was employed to provide the DOA estimations at each frequency bin under the condition of distinct frequency bins with distinct angles. However, this method suffers from inaccurate DOA estimation at low SNR conditions.

Some wireless applications require high resolution DOA estimation, where very closely spaced sources can be separated successfully. The estimation resolution depends mainly on the aperture size of the antenna array. Several antenna array configurations can be employed for wideband DOA estimation. Uniform linear array (ULA) configuration requires huge number of elements to obtain the large array aperture needed for high resolution, which increases both the hardware/software complexity [27, 28]. Nonuniform antenna arrays can be utilized to overcome the ULA drawback of small array aperture and achieve higher array aperture than ULA using reduced number of elements [29, 30].

While most of the recent wideband DOA estimation techniques achieve reasonable accuracy, they suffer from high computational burden and hardware/software complexity. The aim of this research study is to introduce a new enhanced wideband DOA estimation approach with high resolution and low system complexity. Enhancing the DOA estimation resolution is obtained utilizing an efficient generalized coprime array configuration, while the low system complexity is acquired using compressive sensing (CS) with deterministic chaotic sensing matrices [31] that allows reducing the measurement vector dimension. The robustness of the introduced method in improving the DOA estimation performance is studied along with a simultaneously held comparison between three state-of-the-art wideband DOA estimation techniques, namely ISSM, FSS, and mTOPS.

The rest of paper is organized as follows. In section II,the wideband DOA estimation techniques, namely ISSM, FSS, and mTOPS are explained, followed by applying the proposed CS technique to the three wideband DOA estimation algorithms. Afterwards, the proposed generalized coprime antenna array configurations are described. Section III shows the results utilizing various assessment metrics to investigate the performance of the introduced approach, followed by comparing the DOA estimation performance of the three techniques under investigation. Section IV provides the conclusion of this research.

2 Methodology

The superscripts and operators used in paper are as follows: $\left( \cdot \right)^{T}$ indicates the transpose, ${(\cdot)}^{H}$ represents the Hermitian transpose, $\left( \cdot \right)^{ - 1}$ represents the inverse of the matrix, $E(\cdot)$ is the expectation operator, ${\Vert \cdot\Vert }_{F}$ denotes the Frobenius norm, $tr(\cdot)$ is the trace, and $Re(\cdot)$ represents the real part.

Consider $R$ uncorrelated wideband signals in the frequency range${[f}_{L} , {f}_{H}$], $P$ antenna elements for the reception of signals assuming isotropic antenna elements, and $K$ number of samples. The received signal at time sample $k$ with the antenna element $p$ is modelled as following:

$$ x_{p} \left( k \right) = \mathop \sum \limits_{r = 1}^{R} s_{r} (k - \frac{{d_{p} }}{c}sin\theta_{r} ) + n_{p} \left( k \right) $$

(1)

where ${s}_{r}$ is the r^th signal waveform, ${d}_{p}$ is the spacing between the p^th antenna element and the first element, ${\theta }_{r}$ is the DOA of the rth signal, $c$ is the propagation velocity, and ${n}_{p}$ is the noise added to the received signal by the pth element. By passing the signals received by antenna elements through filter bank or by using Discrete Fourier Transform (DFT), the signals can be decomposed into $I$ frequency bins, so the received signal by the pth sensor at frequency bin $i$ can be written as following

$$ X_{p} \left( {\omega_{i} } \right) = \mathop \sum \limits_{r = 1}^{R} e^{{ - j\omega_{i} \frac{{d_{p} }}{c}sin\theta_{r} }} S_{r} \left( {\omega_{i} } \right) + N_{p} \left( {\omega_{i} } \right) $$

(2)

where ${\omega }_{i}\in [2\pi {f}_{L,}2\pi {f}_{H}]$. The measurement vector $X$ at frequency bin $i$ is given by

$${\varvec{X}}\left({\omega }_{i}\right)={\varvec{A}}\left({\omega }_{i},{\varvec{\Theta}}\right){\varvec{S}}\left({\omega }_{i}\right)+{\varvec{N}}({\omega }_{i})$$

(3)

where ${\varvec{\Theta}}$ is the array of DOA of sources ${\varvec{\Theta}}$=${{[\theta }_{1},\ldots ,{\theta }_{R}]}^{T}$, ${{\varvec{S}}\left({\omega }_{i}\right)=[{S}_{1}\left({\omega }_{i}\right),{S}_{2}\left({\omega }_{i}\right),{S}_{R}\left({\omega }_{i}\right)]}^{T}$ is the vector of the sources at frequency ${\omega }_{i}$ and ${\varvec{A}}\left({\omega }_{i},\Theta \right)$ is the steering matrix which has the dimension $P\times R$ and consists of

$${\varvec{A}}\left({\omega }_{i},{\varvec{\Theta}}\right)=[{\varvec{a}}\left({\omega }_{i},{\theta }_{1}\right),{\varvec{a}}\left({\omega }_{i},{\theta }_{2}\right)\cdots ,{\varvec{a}}\left({\omega }_{i},{\theta }_{R}\right)]$$

(4)

Each column of it corresponds to the steering vector

$${\varvec{a}}\left({\omega }_{i},{\theta }_{r}\right)={[1 {e}^{-j{\omega }_{i}\frac{{d}_{2}}{c}sin{\theta }_{r} }\cdots {e}^{-j{\omega }_{i}\frac{{d}_{P}}{c}sin{\theta }_{r} }]}^{T}$$

(5)

With the use of the measurement vector at each frequency bin, several methods can be employed to estimate the DOAs such as ISSM, FSS, and mTOPS.

2.1 ISSM Algorithm

In ISSM, the measurement vector ${\varvec{X}}\left({\omega }_{i}\right)$ received at frequency bin $i$ is used to compute the covariance matrix ${{\varvec{R}}}_{i}$ at the corresponding frequency bin as follows:

$${{\varvec{R}}}_{i}=E[{\varvec{X}}\left({\omega }_{i}\right){{\varvec{X}}}^{H}\left({\omega }_{i}\right)]$$

(6)

In practice, when the observation interval is divided into $J$ segments, ${{\varvec{R}}}_{i}$ can be estimated as follows [16]:

$$ \hat{\user2{R}}_{i} = \frac{1}{J}\mathop \sum \limits_{j = 1}^{J} {\varvec{X}}_{j} \left( {\omega_{i} } \right){\varvec{X}}_{j}^{H} \left( {\omega_{i} } \right) $$

(7)

By applying the eigenvalue decomposition to ${\widehat{{\varvec{R}}}}_{i}$, signal subspace ${{\varvec{F}}}_{i}$, which contains eigenvectors corresponding to largest R eigenvalues, and noise subspaces ${{\varvec{W}}}_{i}$, consisting of the remaining eigenvectors, are obtained. For angles within angle search interval $\theta \epsilon [{\theta }_{1},{\theta }_{f}]$, spatial spectrum ${{\varvec{S}}}_{i}$ can be constructed as follows [10]:

$${S}_{i}\left(\theta \right)=\frac{{{\varvec{a}}}^{H}\left({\omega }_{i},\theta \right){\varvec{a}}\left({\omega }_{i},\theta \right)}{{{\varvec{a}}}^{H}\left({\omega }_{i},\theta \right){{\varvec{W}}}_{i} {{{\varvec{W}}}_{i}}^{H}{\varvec{a}}\left({\omega }_{i},\theta \right)}$$

(8)

Finally, the estimated angles are obtained by identifying the maximum $R$ peaks in the total spectrum ${{\varvec{S}}}_{{\varvec{I}}{\varvec{S}}{\varvec{S}}{\varvec{M}}}$ which is given by [14]:

$${S}_{ISSM}\left(\theta \right)=\frac{1}{I}\sum_{i=1}^{I}{S}_{i}\left(\theta \right)$$

(9)

The implementation of ISSM algorithm is summarized in Table 1.

Table 1 Implementation of ISSM algorithm

2.2 FSS Algorithm

In FSS, the general covariance matrix ${{\varvec{R}}}_{{\varvec{x}}}$ at the reference frequency is obtained by [22]:

$${{\varvec{R}}}_{{\varvec{x}}}=\frac{1}{I}\sum_{i=1}^{I}{\varvec{T}}\left({f}_{i}\right){\widehat{{\varvec{R}}}}_{i}{ {\varvec{T}}}^{H}\left({f}_{i}\right)$$

(10)

where ${\varvec{T}}\left({f}_{i}\right)$ is the transformation matrix at frequency bin ${f}_{i}$ which can be reached by minimizing the error between array manifold at frequency bin ${f}_{i}$ and the one at reference frequency ${f}_{0}$. Note that signal subspace at each frequency bin has the same span of array manifold of signals at this frequency bin. This allows obtaining the transformation matrix ${\varvec{T}}\left({f}_{i}\right)$ by solving the following problem [20]:

$${}_{{\varvec{T}}({f}_{i})}{}^{min} {||{{\varvec{F}}}_{0}-{\varvec{T}}\left({f}_{i}\right){{\varvec{F}}}_{i}||}_{F}^{2}$$

(11)

With the constraint

$${{\varvec{T}}}^{H}\left({f}_{i}\right){\varvec{T}}\left({f}_{i}\right)={\varvec{I}}$$

(12)

where ${\varvec{I}}$ is the identity matrix. The Frobenius norm in Eq. (11) is equivalent to the following [20]:

$${\left|\left|{{\varvec{F}}}_{0}-{\varvec{T}}\left({f}_{i}\right){{\varvec{F}}}_{i}\right|\right|}_{F}^{2}=tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{0}^{H}\right)+tr\left({{\varvec{F}}}_{i}{{\varvec{F}}}_{i}^{H}\right)-2Re[tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)]$$

(13)

This means that the problem can be transformed to the maximization of $Re[tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)]$, where the following relation is hold [20]:

$$Re\left[tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)\right]\le |tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)|$$

(14)

The Singular Value Decomposition (SVD) is applied to the matrix ${{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}$ as follows:

$$ {\varvec{F}}_{0} {\varvec{F}}_{i}^{H} = {\varvec{U}}_{i} \sum_{i} {\varvec{V}}_{i}^{H} $$

(15)

where ${{\varvec{U}}}_{i}$ an ${{\varvec{V}}}_{i}$ are the left and right singular vectors of ${{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}$, respectively. ${\sum }_{i}$ is the diagonal matrix of singular values ${\sigma }_{pp}$ of ${{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}$, where $p=1, 2, 3, \dots P$. By substituting from (15) into (14), Eq. (14) can be rewritten as [20]:

$$Re\left[tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)\right]\le |tr\left({{\varvec{U}}}_{i}{\sum }_{i}{{\varvec{V}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)|$$

$$\le |tr\left({\sum }_{i}{{\varvec{V}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right){{\varvec{U}}}_{i}\right)|$$

(16)

Let ${{\varvec{Z}}}_{i}={{\varvec{V}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right){{\varvec{U}}}_{i}$ is unitary matrix with diagonal elements ${|z}_{pp}|\le 1$, then Eq. (16) can be rewritten as [20]:

$$Re\left[tr\left({{\varvec{F}}}_{0}{{\varvec{F}}}_{i}^{H}{{\varvec{T}}}^{H}\left({f}_{i}\right)\right)\right]\le |tr\left({\sum }_{i}{{\varvec{Z}}}_{i}\right)|$$

$$\le \sum_{p=1}^{P}{|z}_{pp}|{\sigma }_{pp}$$

(17)

This reveals that the maximization occurs when ${|z}_{pp}|$ =1, and hence ${\varvec{T}}\left({f}_{i}\right)$ can be computed as follows:

$${\varvec{T}}\left({f}_{i}\right)={{\varvec{U}}}_{i}{{\varvec{V}}}_{i}^{H}$$

(18)

The implementation of FSS algorithm is illustrated in Table 2.

Table 2 Implementation of FSS algorithm

2.3 mTOPS Algorithm

Unlike FSS, transformation matrices in TOPS technique are not used to transform the covariance matrices into a general covariance matrix ${{\varvec{R}}}_{{\varvec{x}}}$, and instead other transformation matrices are employed to transform a reference signal subspace ${{\varvec{F}}}_{0}$ computed at a selected reference frequency bin ${\omega }_{0}$ to other frequency bins [21]. The reference frequency should be selected to obtain the best accuracy which can be found when achieving the maximum difference between the smallest eigenvalue of signal subspace and largest eigenvalue of noise subspace [22].

Use the transformation matrix ${\varvec{\beta}}(\Delta {\omega }_{i},\theta )$ to get the transformed signal subspaces ${{\varvec{\gamma}}}_{{\varvec{i}}}\left(\theta \right)$, with the pth element of the diagonal matrix ${\varvec{\beta}}\left(\Delta {\omega }_{i},\theta \right)$ equals to ${e}^{-j\Delta {\omega }_{i}\frac{dp}{c}sin\theta }$, as follows [21]:

$${{\varvec{\gamma}}}_{i}\left(\theta \right)={\varvec{\beta}}\left(\Delta {\omega }_{i},\theta \right){{\varvec{F}}}_{0}$$

(19)

where $\Delta {\omega }_{i}={\omega }_{i}-{\omega }_{0}$. Define the matrix ${\varvec{D}}(\theta )$ as [21]:

$$ {\varvec{D}}\left( \theta \right) = \left[ {{\varvec{\gamma}}_{1}^{H} {\varvec{W}}_{1} \left| {{\varvec{\gamma}}_{2}^{H} {\varvec{W}}_{2} } \right| \ldots \ldots \ldots {\varvec{\gamma}}_{I - 1}^{H} {\varvec{W}}_{I - 1} } \right] $$

(20)

${\varvec{D}}\left(\theta \right)$ can be modified to increase the estimation accuracy by decreasing the leakage of noise subspace in signal subspace that could happen due to errors in the estimation of the covariance matrix. In TOPS, a projection matrix ${{\varvec{P}}}_{i}(\theta )$, which projects the transformed signal subspaces onto the null space of ${{\varvec{a}}}_{i}(\theta )$, is defined as [23]:

$${{\varvec{P}}}_{i}\left(\theta \right)={{\varvec{I}}-{{\varvec{a}}}_{i}\left(\theta \right)\left({{\varvec{a}}}_{i}^{H}\left(\theta \right){{\varvec{a}}}_{i}\left(\theta \right)\right)}^{-1}{{\varvec{a}}}_{i}^{H}(\theta )$$

(21)

The modified version of ${\varvec{D}}\left(\theta \right)$ is denoted by $\widehat{{\varvec{D}}}(\theta )$ and it can be computed by replacing each matrix ${{\varvec{\gamma}}}_{i}\left(\theta \right)$ with the projected one $\stackrel{`}{{{\varvec{\gamma}}}_{i}}(\theta )$ which is defined as follows [22]:

$$\stackrel{`}{{{\varvec{\gamma}}}_{i}}\left(\theta \right)={{\varvec{P}}}_{i}\left(\theta \right){{\varvec{\upgamma}}}_{i}\left(\theta \right)$$

(22)

The estimated DOA can be found when the matrix $\widehat{{\varvec{D}}}(\theta )$ loses its rank. In other words, when $\theta ={\theta }_{r}$, the matrix $\widehat{{\varvec{D}}}(\theta$) becomes rank deficient. In TOPS, the DOAs are estimated by finding the angles that cause $R$ local maxima of the following spectrum [14]:

$${S}_{TOPS}\left(\theta \right)=\frac{1}{{\sigma }_{min}(\theta )}$$

(23)

where ${\sigma }_{min}(\theta$) is the smallest singular value of $\widehat{{\varvec{D}}}(\theta$).

The TOPS algorithm suffers from spurious peaks in the TOPS spatial spectrum at all SNR levels which leads to difficulty in estimating the true DOAs of signal sources. A modified version of TOPS technique, called mTOPS, was proposed to reduce spurious peaks in the pseudospectrum by performing two main modifications to TOPS. The first modification is to replace null-space projection utilized in TOPS with signal-subspace (${{\varvec{P}}}_{mi}\left(\theta \right),{{\varvec{\gamma}}}_{mi}\left(\theta \right))$ using the following equations [23]:

$${{\varvec{P}}}_{mi}\left(\theta \right)={{{\varvec{a}}}_{i}\left(\theta \right)\left({{\varvec{a}}}_{i}^{H}\left(\theta \right){{\varvec{a}}}_{i}\left(\theta \right)\right)}^{-1}{{\varvec{a}}}_{i}^{H}(\theta )$$

(24)

$${{\varvec{\gamma}}}_{mi}\left(\theta \right)={{\varvec{P}}}_{mi}\left(\theta \right){{\varvec{\gamma}}}_{i}\left(\theta \right)$$

(25)

A new matrix ${{\varvec{D}}}_{{\varvec{m}}}(\theta )$ is constructed by replacing ${{\varvec{\gamma}}}_{i}\left(\theta \right)$ with ${{\varvec{\gamma}}}_{mi}\left(\theta \right)$ in Eq. (20). The second modification is to estimate DOAs by finding the $R$ local maxima in the following spectrum [23]:

$${S}_{mTOPS}\left(\theta \right)=\frac{1}{tr[{{\varvec{D}}}_{{\varvec{m}}}\left(\theta \right){{\varvec{D}}}_{{\varvec{m}}}^{H}\left(\theta \right)]}$$

(26)

The implementation of mTOPS algorithm is shown in Table 3.

Table 3 Implementation of mTOPS algorithm

2.4 CS Using Chaotic Matrix

The system complexity represents a main issue in achieving wideband DOA estimation with high resolution. Note that as the number of antenna array elements increases, the number of RF front-end chains increases, where each RF chain is used to amplify, filter and transform from analog to digital if needed, which causes high hardware system complexity [27, 32]. Also, most wideband DOA estimation techniques suffer from high computational burden caused by executing extensive mathematical operations at each frequency bin. These mathematical operations include eigen value decomposition (EVD), SVD, estimation of the covariance matrix, and spatial spectrum construction in the angle search interval. The computational time of such mathematical operations increases when dealing with high-dimensional matrices. In this study, the CS is investigated to alleviate the system complexity of wideband DOA estimation with high resolution.

The CS theorem states that a sparse signal can be perfectly reconstructed even though it is sampled at a much lower rate than the requirements indicated by the Nyquist theorem [33]. The computational efficiency of DOA estimation can be enhanced by employing CS techniques to reduce the measurement vector dimension through some projections [27]. The use of compressed measurements provides comparable performance compared to the use of uncompressed measurements, while keeping the same number of the receiving antenna array elements. This allows preserving the array aperture and controlling the resolution of DOA estimation [31]. The CS can be employed utilizing random and some deterministic sensing matrices. However, deterministic sensing matrices are easier to generate and store than random sensing matrices, leading further support for their use in CS [34].

In this work, the CS utilizing deterministic chaotic sensing matrices is investigated for wideband DOA estimation to reduce the dimension of the measurement vector, and hence decrease the computational burden. CS is applicable in DOA estimation problem because the signal sources exist only in $R$ points within the angle search interval $\theta \in [{\theta }_{1},{\theta }_{f}]$, which means that signals are sparse in the angular domain [35]. Based on the sparsity of the signals, the measurement vector ${\varvec{X}}$ can be expressed as [35]:

$${\varvec{X}}({\omega }_{i})={\varvec{\Psi}}({\omega }_{i}){\varvec{Z}}({\omega }_{i})$$

(27)

where ${\varvec{\Psi}}({\omega }_{i})$ is the sparsity basis which corresponds to the steering matrix of the angles in the angle search interval and ${\varvec{Z}}({\omega }_{i})$ is the sparsity vector that contains the Fourier transformation (FT) values of signal amplitudes with only $R$ non-zero values within $\theta \in [{\theta }_{1},{\theta }_{f}]$. It can be noted that the application of CS to DOA estimation process allows reconstructing the ${\varvec{Z}}$ vector without degrading the original accuracy.

For wideband DOA estimation, the measurement vector ${\varvec{X}}$, which contains FT of signals received by the antenna array at any frequency bin, can be compressed into lower-dimensional vector ${\varvec{Y}}$ by multiplying it with a sensing matrix ${\varvec{\phi}}$ as follows:

$${\varvec{Y}}({\omega }_{i})={\varvec{\phi}}{\varvec{X}}({\omega }_{i})$$

(28)

where ${\varvec{X}}$ has a dimension of $P\times 1$ at a single frequency bin and the dimension of the sensing matrix ${\varvec{\phi}}$ is$Q\times P$. Note that the dimension of the compressed vector ${\varvec{Y}}$ is reduced to $Q\times 1$ with $Q$ << $P$ , and consequently the dimension of the estimated covariance matrix ${\widehat{{\varvec{R}}}}_{iY}$ is decreased to $Q\times Q$ instead of $P\times P$ without using CS, where $Q$ < < $P$. This reduction in covariance matrix dimension allows faster execution of all mathematical operations including the covariance matrix, which leads to reduction in the computational time and the software complexity.

In wideband DOA estimation techniques, the CS is employed by multiplying the steering vector ${{\varvec{a}}}_{i}\left(\theta \right)$ by the sensing matrix $\varnothing$ to get a compressed vector ${{\varvec{b}}}_{i}\left(\theta \right)$ as follows:

$$ {\varvec{b}}_{i} \left( \theta \right) = \phi \;{\varvec{a}}_{i} \left( \theta \right) $$

(29)

Note that the transformation matrix ${\varvec{\beta}}\left(\Delta {\omega }_{i},\theta \right)$ is multiplied by the sensing matrix ${\varvec{\phi}}$ to get a compressed matrix. The choice of appropriate sensing matrix ${\varvec{\phi}}$ is very important as it should satisfy the conditions of incoherence and restricted isometry property (RIP) [33]. Sensing matrices that satisfy these conditions can be classified into random and deterministic. The most common random sensing matrices are Gaussian, Rademacher, and Bernoulli but they require tedious generation and storage. On contrast, the generation and storage of deterministic sensing matrices are easier than random sensing matrices [34, 36]. Chaotic sensing matrices are efficient deterministic sensing matrices that satisfy the conditions of incoherence and RIP using several equations such as logistic map, quadratic map, and Chebyshev map. This allows their use in CS for wideband DOA estimation [36]. In this work, deterministic chaotic sensing matrices using Chebyshev map is investigated for wideband DOA estimation. The Chebyshev map is described using the following recursive formula [36]:

$${x}_{n+1}={\text{cos}}(r{cos}^{-1}\left({x}_{n}\right))$$

(30)

where ${x}_{n}$ denotes the n^th term of the developed sequence and $r$ is the bifurcation parameter. Note that the generated sequence exists only when $r$ lies in the interval $[2,\infty ]$. Figure 1 illustrates the bifurcation diagram of Chebyshev map by plotting the chaotic sequence ${x}_{n}$ versus $r$. Figure 1 was plotted using a fixed initial value ${x}_{0}=0.6$ for 5000 terms of chaotic sequence versus every value of $r$.

Fig. 1

Bifurcation diagram of Chebyshev map with ${x}_{0}=0.6$

The chaotic sensing matrix can be formed based on the Chebyshev sequence as follows [36]:

$${v}_{m}={x}_{1000+md}-median({{\varvec{x}}}_{{\varvec{s}}{\varvec{e}}{\varvec{q}}})$$

(31)

where ${{\varvec{x}}}_{{\varvec{s}}{\varvec{e}}{\varvec{q}}}$ is a vector consisting of the elements of ${x}_{1000+md}$ with ignoring the first 1000 elements of the Chebyshev sequence, $d$ denotes the down sampling factor, and $m$ is a counter, where $m=0, 1, 2, 3,\dots .$.. The chaotic sensing matrix ${\varvec{\phi}}$ is developed using the elements of the sequence of ${v}_{m}$ as follows:

$$ \phi = \sqrt{\frac{2}{Q}} \left[ {\begin{array}{*{20}l} {v_{0} } \hfill & {v_{Q} } \hfill & \ldots \hfill & {v_{{Q\left( {P - 1} \right)}} } \hfill \\ {v_{1} } \hfill & {v_{Q + 1} } \hfill & \ldots \hfill & {v_{{Q\left( {P - 1} \right) + 1}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {v_{Q - 1} } \hfill & {v_{2Q - 1} } \hfill & \ldots \hfill & {v_{QP - 1} } \hfill \\ \end{array} } \right] $$

(32)

2.5 Wideband DOA estimation with Generalized Coprime Array

Various antenna array configurations can be utilized for wideband DOA estimation. ULA is a simple antenna array configuration with a fixed spacing between the elements. However, this array configuration suffers from low aperture size of $(P-1)\lambda$/2, where $P$ is the number of antenna elements and $\lambda$ is the wavelength [37]. This reveals that in ULA, increasing the array aperture needed for high resolution requires huge number of antenna elements, which increases the system complexity [27, 28]. Nonuniform large-spaced antenna arrays can be utilized to acquire higher array aperture than ULA using reduced number of elements [29]. An example of nonuniform antenna array configurations is the coprime array [30].

In coprime arrays, two uniform subarrays with coprime integer number of elements $N$ and $M$ are combined to construct the coprime array. The $N$ elements of the first subarray are placed with a fixed spacing of$M\lambda /2$, yielding positions of $\left\{ {0,\frac{M\lambda }{2}, \frac{2M\lambda }{2}, \ldots \ldots ., \frac{{\left( {N - 1} \right)M\lambda }}{2}} \right\}$, while the $M$ elements of second subarray are placed with a fixed spacing of$N\lambda /2$, yielding positions of $\left\{ {0,\frac{N\lambda }{2}, \frac{2N\lambda }{2}, \ldots \ldots ., \frac{{\left( {M - 1} \right)N\lambda }}{2}} \right\}$. Since the first element of the two subarrays is overlapped, the total number of antenna elements is $P=M+N-1$ and the aperture size is the maximum of$((M-1)N\lambda /2$,$(N-1)M\lambda /2$) [30, 37].

Two generalized array configurations can be obtained from coprime arrays based on how the elements of the two subarrays are placed. In the first configuration denoted by coprime array with compressed inter-element spacing (CACIS), the interelement spacing of the first subarray is compressed to $\widehat{M}\lambda /2$ with $\widehat{M}=M/C$ where $C$ is a compression factor within the extent $[2, M]$. This results in placing the elements of the first subarray in the positions $\{0,\frac{ \widehat{M}\lambda }{2}, \frac{2 \widehat{M}\lambda }{2},\dots \dots ., \frac{\left(N-1\right) \widehat{M}\lambda }{2}\}$, while achieving higher array aperture of $\frac{(M-1)N\lambda }{2}$ than the ULA. The second configuration, namely coprime array with displaced subarrays (CADiS), includes a displacement of $L\lambda /2$ between the two subarrays, where $L\ge {\text{min}}(\widehat{M},N)$. In CADiS configuration, the first subarray consists of $N$ elements with inter-element spacing of $\widehat{M}\lambda /2$, while the second subarray contains $M-1$ elements with inter-element spacing of $N\lambda /2$. This leads to an array aperture of $\left(MN+\widehat{M}N-\widehat{M}-2N+L\right)\lambda /2$ that exceeds CACIS and ULA layouts [29].

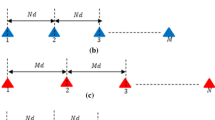
Figure 2 illustrates the distribution of antenna elements for ULA, CACIS, and CADiS array layouts using the same number of array elements and assuming unity wavelength. Figure 2a demonstrates that the ULA layout with $P$ = 16 antenna element achieves an array aperture of 7.5. Figure 2b demonstrates the CACIS layout with N = 9, M = 8, and C = 2, yielding an array aperture of 31.5. The CADiS layout is illustrated in Fig. 2c using C = 2 with N = 9 and M − 1 = 7, where $L=\widehat{M}+N=13$. This leads to an array aperture of 49.5 which is higher than both ULA and CACIS layouts. CADiS layout has the largest array aperture, followed by CACIS layout, and finally ULA layout provides the lowest array aperture. In this work, the three antenna array layouts are examined with and without applying the introduced CS technique under various set of parameters.

Fig. 2

a ULA configuration with $P$ = 16. b CACIS layout with N = 9, M = 8, and C = 2. c CADiS layout with N = 9, M = 8, L = 13, and C = 2

3 Results

The performance of the introduced technique is assessed by executing MATLAB simulations under several conditions and parameters. Two wideband chirp signals of sampling frequency 12 kHz were employed. One of the two signals is upchirp with a start frequency of 2 kHz and an end frequency of 4 kHz, while the other one is uncorrelated downchirp signal as shown in Fig. 3. The two signals are bandlimited with a centre frequency of 3 kHz and bandwidth of 2 kHz. Each signal is partitioned into 50 segments, each with a specified length of 128 samples. The spectrum of the received signal is obtained and divided into 23 frequency bins using DFT.

Fig. 3

Spectrograms of a upchirp and b downchirp signals

The proposed approach is applied to three wideband DOA estimation techniques, namely ISSM, FSS, and mTOPS, in an angle search interval from − 90° to 90° with a step angle of 0.01°. The CS is employed utilizing chaotic sequence with initial value ${x}_{0}=0.3$, bifurcation parameter $r=4$, and down sampling factor $d=10$. The efficiency of wideband DOA estimation is evaluated utilizing three metrics, including the spatial spectrum, the Root Mean Square Error (RMSE) between estimated and true DOAs, and the computational time. Note that The RMSE value is calculated by averaging the RMSE values of 100 simulation rounds for each parameter using the following formula:

$$ RMSE = \frac{1}{R}\mathop \sum \limits_{r = 1}^{R} \sqrt {\frac{1}{100}\mathop \sum \limits_{l = 1}^{100} \left( {\hat{\theta }_{r,l} - \theta_{r} } \right)^{2} } $$

(33)

where ${\widehat{\theta }}_{r,l}$ is the estimated DOA of the rth source in the simulation round l and ${\theta }_{r}$ is the actual DOA of the rth source.

All evaluation metrics were obtained for both generalized coprime array and ULA configurations with and without CS using the three wideband DOA estimation techniques (ISSM, FSS, and mTOPS). The effect of changing the SNR level and the number of antenna array elements is also studied for all metrics under investigation.

3.1 ISSM

The spatial spectrum of the ISSM algorithm is investigated utilizing three different antenna array layouts, namely ULA, CACIS, and CADiS. The ISSM technique is employed to estimate DOAs of two closely spaced wideband sources arrived at angles 41° and 41.5° with SNR = 20 dB for ULA, CACIS, and CADiS layouts using 14 antenna array elements with N = 11, M = 4, L = 13, and $C$ = 2. CS is applied to the ISSM algorithm utilizing Chaotic Chebyshev sensing matrix ${\varvec{\phi}}$ of dimension $8\times 14$ to reduce the measurement vector from length 14 to 8. Figure 4 shows the spatial spectrum of ISSM algorithm using ULA, CACIS, and CADiS layouts. The ULA layout failed to estimate the DOAs of the two closely spaced received signals, while CACIS and CADIS generalized coprime array configurations succeeded to separate the same two sources because of their higher aperture than the ULA. Figure 4 shows that CADiS configuration achieves the best estimation resolution because of its highest aperture compared to both ULA and CACIS configurations for the same number of antenna array elements. The spatial spectrum resolution is also examined with CS utilizing ULA, CACIS, and CADiS layouts, and the results revealed that the ISSM algorithm can estimate accurately the DOAs of the two sources with the application of CS when the resolution of the array aperture is sufficient. This shows that the estimation resolution is not affected when utilizing the compressed measurement vector instead of the actual measurement vector.

Fig. 4

Spatial spectrum of ISSM with CS for DOA estimation of two wideband signals received at angles 41° and 41.5° with SNR = 20 dB using ULA, CACIS, and CADiS layouts

The effectiveness of the ISSM method is further examined with and without CS by computing the the RMSE between estimated and true DOAs when varying the SNR and the number of elements (see Fig. 5). The results are validated by computing the average RMSE over 100 trials for each parameter value. Note that different number of trials are tested, and the results reveal no significant difference between using 100 trials and other cases of higher number of trials. Empirically, it is found that 100 iterations are sufficient for accurate analysis. Consider two wideband signals received at angles of 61°and 61.4° for ULA, CACIS, and CADiS layouts using 16 elements with N = 11, M = 6, L = 13, and $C$ = 3. CS is applied to the ISSM method using Chaotic Chebyshev sensing matrix of size $7\times 16$ to reduce the length of the measurement vector. The average RMSE is plotted when changing the input SNR from 0 to 28 dB with a step of 2 dB as shown in Fig. 5a. The average RMSE is calculated at each SNR value when using the standalone ISSM, and when using the compressed measurement vector resulted from combining the ISSM algorithm with CS. Results demonstrate that the average RMSE decreases with the SNR increase when utilizing the compressed or the actual measurement vector. The ULA layout provides the lowest array aperture and hence fails to separate the two closely spaced wideband sources, which leads to high RMSE values for the whole range of the input SNR values. On contrast, CACIS and CADiS configurations succeeded to separate accurately the two wideband sources with low RMSE values. CADiS configuration achieves lower RMSE values than CACIS configuration because of its higher aperture, which demonstrates its efficiency. Figure 5a shows comparable RMSE values when using the compressed and the actual measurement vectors over the whole range of the input SNR values, which demonstrates the successful combining of the ISSM algorithm with CS without deteriorating the DOA estimation accuracy.

Fig. 5

a RMSE versus SNR and b RMSE versus number of antenna array elements for the ISSM algorithm with and without CS using ULA, CACIS, and CADiS layouts

The impact of changing the number of antenna elements on the average RMSE values for the ISSM algorithm is investigated with and without CS. Figure 5b shows the RMSE variations with varying the number of antenna elements from 10 to 28 elements with a step of 2 for the DOA estimation of closed wideband sources arrived at angles 75° and 76° at fixed SNR of 20 dB using ULA, CACIS, and CADiS layouts. The measurement vector length is compressed to be 8 by applying CS to the ISSM technique. Figure 5b shows high constant RMSE values for ULA configuration when increasing the number of antenna elements within the range of tested number of elements, which reveals the low DOA estimation accuracy of ULA. On contrast, for CACIS and CADiS layouts, the RMSE decreases with increasing the number of antenna array elements. Figure 5b demonstrates that for any fixed number of antenna elements, CADiS configuration achieves lower RMSE values and higher estimation resolution than CACIS configuration. It can be noted that for any number of elements using either CACIS or CADiS configurations, the RMSE of ISSM algorithm is comparable with and without CS, which demonstrates the efficiency of applying the CS in wideband DOA estimation.

3.2 FSS

The spatial spectrum of the FSS technique combined with CS is obtained using ULA, CACIS, and CADiS layouts. It is utilized to estimate DOAs of two closed wideband sources arrived at angles 0.3°and 0.5° with SNR = 15 dB using 16 antenna array elements with N = 9, M = 8, L = 13, and $C$ = 2. CS is applied to the FSS technique using a sensing matrix ${\varvec{\phi}}$ of dimension $6\times 16$ to reduce the measurement vector length from 16 to 6. Figure 6 demonstrates the spatial spectrum of FSS technique combined with CS for ULA, CACIS, and CADiS layouts. Results demonstrate that the CADiS layout achieves the highest estimation resolution, followed by CACIS layout, and finally ULA layout which failed to distinguish the DOAs of the two wideband sources due to its low resolution. Like ISSM algorithm, the application of CS to FSS algorithm does not deteriorate the DOA estimation accuracy which is controlled only by the aperture of the used antenna array configuration (see Fig. 6).

Fig. 6

Spatial spectrum of FSS with CS for DOA estimation of two wideband sources received at angles − 0.3° and 0.5° with SNR = 15 dB using ULA, CACIS, and CADiS layouts

The average RMSE of the FSS technique is calculated over 100 trials when changing the SNR and the number of elements (see Fig. 7). Figure 7a demonstrates the average RMSE against the input SNR extending from 0 to 20 dB for DOA estimation of two closely spaced wideband signals received at angles of − 0.5° and 0.2° for ULA, CACIS, and CADiS layouts using 12 elements with N = 7, M = 6, L = 10, and $C$ = 2. The CS is applied utilizing a sensing matrix ${\varvec{\phi}}$ of dimension $6\times 12$ to reduce the size of measurement vector. The average RMSE is obtained with and without CS at each input SNR value for the three array configurations. It can be noted that for either standalone FSS or FSS combined with CS, CADiS configuration achieves the lowest RMSE, followed by CACIS configuration and lasty ULA configuration which has the highest RMSE for the whole range of the input SNR values. Results reveal that for both CADiS and CACIS configurations, the average RMSE of standalone FSS is close to the combined FSS with CS over wide range of input SNR values.

Fig. 7

a RMSE versus SNR and b RMSE versus number of antenna array elements for the FSS algorithm with and without CS using ULA, CACIS, and CADiS layouts

The change of RMSE with increasing the number of antenna elements at fixed SNR is examined when using both the actual and the compressed measurement vectors. Figure 7b illustrates the average RMSE against the number of antenna elements at fixed SNR of 25 dB when estimating the DOAs of two wideband sources arrived at angles 61° and 61.7° using ULA, CACIS, and CADiS layouts. The results are obtained when the standalone FSS is employed and when CS is applied to the FSS technique to compress the measurement vector to be of length 8. Figure 7b shows that ULA configuration has the highest RMSE compared to CACIS and CADiS layouts utilizing either the original or compressed measurement vector. It can be noted that for both CACIS and CADiS layouts, the average RMSE decreases with increasing the number of antenna elements from 12 to 18, while it is almost constant when increasing the number of elements above 18. Results reveal a slight negligible increase in the average RMSE of FSS technique combined with CS in comparing with the standalone FSS technique for both CACIS and CADiS layouts. This elucidates the effectiveness of applying CS to the FSS wideband estimation technique.

3.3 mTOPS

The spatial spectrum of mTOPS technique combined with CS is examined for ULA, CACIS, and CADiS antenna array layouts. A compressed measurement vector of length 8 is obtained by applying CS to the mTOPS algorithm with a Chebyshev sensing matrix ${\varvec{\phi}}$ of dimension $8\times 16$. Figure 8 shows the spatial spectrum of mTOPS combined with CS for DOA estimation of two wideband sources received at angles − 41° and 41.5° at SNR = 16 dB using 16 antenna array elements with N = 11, M = 6, L = 13, and $C$ = 2. It can be noted that CACIS and CADIS configurations succeeded to separate the two closely spaced wideband sources, while ULA configuration failed to distinguish them. This is because the apertures of CACIS and CADIS configurations are larger than the ULA configuration. Also, the DOAs of closely spaced wideband sources were estimated successfully when applying CS to the mTOPS technique, which demonstrates that the usage of CS does not degrade the estimation performance. This reveals that the used type of antenna array configuration is the only controlling factor in the DOA estimation resolution, where CADiS configuration achieves the highest estimation resolution, followed by CACIS configuration and lastly ULA configuration.

Fig. 8

Spatial spectrum of mTOPS with CS for DOA estimation of two wideband sources received at angles − 41° and − 41.5° with SNR = 16 dB using ULA, CACIS, and CADiS layouts

The influence of varying the SNR and the number of elements on the average RMSE is investigated for ULA, CACIS, and CADiS layouts with and without applying the suggested CS technique (see Fig. 9). Figure 9a shows the average RMSE of the mTOPS technique calculated over 100 trials when changing the SNR from 0 to 20 dB for estimating the DOAs of two wideband signals received at angles of − 0.5° and 0.2° using 16 elements with N = 13, M = 4, L = 15, and $C$ = 2. A Chebyshev sensing matrix ${\varvec{\phi}}$ of size $6\times 16$ is utilized to reduce the measurement vector length. Figure 9a shows that the SNR increase leads to reduction in the average RMSE for both CACIS and CADiS layouts, while it has almost no effect on ULA configuration. It can be noted that for either the standalone mTOPS algorithm or the combined mTOPS with CS, CADiS configuration outperforms CACIS configuration in terms of RMSE for the whole range of input SNR. Like ISSM and FSS techniques, the DOA estimation accuracy of mTOPS is not significantly affected when using the compressed measurement vector instead of the actual measurement vector for all antenna array configurations. This reveals the successful application of the introduced CS approach to the three wideband DOA estimation techniques under investigation.

Fig. 9

a RMSE versus SNR and b RMSE versus number of antenna array elements for the mTOPS algorithm with and without CS using ULA, CACIS, and CADiS layouts

Figure 9b shows the average RMSE of the mTOPS technique calculated over 100 trials when varying the number of elements from 12 to 30 at fixed SNR of 15 dB for estimating the DOAs of two wideband sources received at angles of 30° and 30.4°.The results are obtained for ULA, CACIS and CADiS layouts utilizing the original measurement vector and the compressed version of length 8. Figure 9b shows that for CACIS and CADiS configurations, increasing the number of elements leads to array aperture increase, and hence provides RMSE reduction. On contrast, the RMSE of ULA configuration is high and almost constant when increasing the number of antenna elements because the ULA aperture in this region is not sufficient to distinguish closely spaced wideband sources. Results also demonstrate the superior performance of CADiS configuration over CACIS and ULA configurations in terms of average RMSE over a wide range of number of antenna elements. Like FSS and ISSM methods, the application of CS to the mTOPS technique does not affect the DOA estimation accuracy of resolving closely spaced wideband sources compared to the standalone mTOPS technique, which reveals the advantage of combining the proposed CS technique with several wideband DOA estimation techniques to achieve accurate DOA estimation with low computational complexity.

3.4 Performance Analysis

To effectively evaluate the performance of applying the introduced CS technique to the three wideband DOA estimation algorithms under investigation (ISSM, FSS, and mTOPS), the average RMSE is calculated over 100 trials when changing the SNR using fixed array configuration. CS is applied to the three wideband DOA estimation techniques using Chaotic Chebyshev sensing matrix of size $9\times 16$ to reduce the measurement vector length to be 9 instead of 16. Figure 10 illustrates the average RMSE against the input SNR extending from 4 to 22 dB for DOA estimation of closed two wideband signals received at angles of 20° and 20.5° for CACIS configuration using 16 antenna array elements with N = 11, M = 6, and $C$ = 2. It can be noted that for the three wideband DOA estimation techniques, the average RMSE decreases with the SNR increase for the whole range of input SNR. The Cramér-Rao bound (CRB) [38] is another important statistical metric for assessing the effectiveness of the three DOA estimation techniques, by providing a lower bound on the variance of unbiased DOA estimation results. Calculating the CRB versus SNR, as shown in Fig. 10, it is found that the ISSM technique has the lowest RMSE curve and becomes closest to the CRB.

Fig. 10

RMSE and CRB versus SNR for ISSM, FSS and mTOPS techniques combined with CS using CACIS configuration

Results reveal that when using generalized coprime antenna array with sufficient aperture, the three techniques combined with the proposed CS technique can estimate accurately the DOAs of the two closely spaced wideband sources with relatively small RMSE values, which demonstrates the robustness of the introduced CS in acquiring precise DOA estimation with reduced computational time. Despite the accurate resolution of the three techniques when combined with CS, the ISSM technique outperforms both FSS and mTOPS algorithms in terms of achieving the lowest RMSE over the whole range of input SNR, followed by mTOPS algorithm, and lastly FSS algorithm. The same performance is also obtained when comparing the three techniques combined with CS using CADiS configuration.

Recent studies investigated new CS techniques for enhancing the performance of DOA estimation [39,40,41]. In [27], CS was employed for narrowband DOA estimation using random gaussian sensing matrices. In [39], a CS framework was proposed for two-dimensional (2D) DOA and polarization estimation in mmWave polarized massive MIMO systems. In the current study, deterministic sensing matrices are employed because they are easier to generate and store than random sensing matrices. In [41], we investigated the applicability of CS using chaotic sensing matrices to the wideband DOA estimation problems by combining the ISSM algorithm with CS using the traditional ULA configuration, and the results revealed remarkable reduction in the computational complexity while keeping nearly the same estimation resolution. The initial results presented in [41] provides the motivation for developing the current comprehensive study of applying the introduced CS to the three state-of-the-art wideband DOA estimation techniques (ISSM, FSS, and mTOPS) using generalized coprime array configurations (CACIS, and CADiS). Results reveal that the introduced approach achieves high DOA estimation resolution resulted from using generalized coprime array configuration (CACIS or CADiS), while minimizing the computational complexity. Results also reveal that the ISSM technique combined with CS provides the best accuracy for DOA estimation using CADiS configuration while achieving significant reduction in the computational complexity.

Note that the low computational complexity of the proposed approach is achieved utilizing CS with deterministic chaotic Chebyshev sensing matrices that allow reducing the measurement vector dimension, while the high-resolution DOA estimation is acquired utilizing generalized coprime array configuration. The DOA estimation results of the CACIS and CADiS configurations are compared with ULA configuration using the same number of antenna array elements, and the results reveals the superior resolution of CACIS and CADiS configurations. The introduced CS approach is employed to reduce the dimension of the measurement vector, and hence decrease the computational burden with a negligible reduction in the DOA estimation accuracy. All results reveal comparable RMSE values when using the compressed and the actual measurement vectors over the whole range of the input SNR values or the range of the number of antenna array elements, which demonstrates the successful combining of the wideband DOA estimation algorithms with CS without deteriorating the DOA estimation accuracy.

3.5 Computational Complexity

It is not easy to compute the exact computational cost of the three wideband DOA estimation techniques under investigation [21]. The FSS algorithm requires the least computational cost because the focusing process includes calculating the MUSIC spatial spectrum once for the focused general covariance matrix by means of focusing matrices, regardless of the number of frequency bins. This means that $O(2{P}^{3})$ computations are required for each focusing matrix [20]. On contrast, the spatial spectrum of the ISSM technique is calculated for each angle sample and repeated for all frequency bins. Note that the MUSIC spatial spectrum construction for a single frequency bin requires number of computations $O\left({P}^{2}{\theta }_{T}\right)$, where ${\theta }_{T}$ is total number of angle samples. The mTOPS algorithm requires the highest computational cost because all its processes, including transformation, projection, construction of the ${{\varvec{D}}}_{{\varvec{m}}}$ matrix which needs number of computations $O\left(RP\left(P-R\right)\left(I-1\right)\right)$, and spatial spectrum calculation are obtained for each hypothesized angle.

The effectiveness of the introduced CS method in minimizing the processing time needed to estimate the DOAs of the wideband sources is examined by comparing the computational efficiency of the three wideband DOA estimation techniques under investigation (ISSM, FSS, and mTOPS) with and without CS. The proposed CS is employed to limit the measurement vector length to be 8. The ISSM, FSS, and mTOPS techniques are employed with and without CS to estimate DOAs of two closely spaced wideband sources arrived at angles − 0.5° and 0.5°with SNR = 20 dB using CADiS configuration because of its superior performance over both CACIS and ULA configurations as explained previously. Table 4 summarizes the consumed time in sec of ISSM, FSS, and mTOPS techniques with and without applying the CS when changing the number of antenna elements. The computational time of each approach is measured on a personal laptop (Intel core i5-450M CPU, 2.40 GHz, 4 GB RAM, and 64-bit windows 10 operating system) using MATLAB software. For consistency, the computational time is calculated by averaging 100 rounds for each case of number of elements. It can be noted that for all cases, the processing time needed for the DOA estimation process grows with enhancing the number of elements that increases the dimension of measurement vector. However, the increase rate of the consumed time using the compressed measurement vector is much lower than the case of utilizing the original measurement vector for the three techniques (ISSM, FSS, and mTOPS).

Table 4 The consumed time in sec of ISSM, FSS and mTOPS techniques with and without CS

Table 4 demonstrates that for any number of elements, the use of CS significantly reduces the processing time needed to estimate the DOAs using the three wideband DOA estimation techniques under investigation. The computational time reduction with the use of CS comes from the reduced size of measurement vector and the covariance matrix. Results show that with and without CS, mTOPS algorithm has the highest execution time, followed by ISSM, and lastly FSS has the lowest consumed time. This reveals that ISSM algorithm combined with CS provides the best accuracy for DOA estimation while achieving reasonable reduction in the computational complexity. Results reveal that the introduced CS technique allows preserving the DOA estimation resolution which relies on the number of the antenna array elements, while significantly reducing the computational burden. This elucidates the low computational complexity of three wideband DOA estimation algorithms when combined with the proposed CS technique without affecting the resolution accuracy.

The computational cost of the proposed CS technique is also examined when changing the number of angle samples within the angle search interval for the three wideband DOA estimation techniques (ISSM, FSS, and mTOPS) with and without CS. Table 5 summarizes the computational time in sec of ISSM, FSS, and mTOPS techniques with and without applying the CS when changing the number of angle samples from 361 and 36,001. The results shown in Table 5 are calculated using the same parameter setting used in Table 4 with fixed number of 40 antenna elements. It can be noted that for all cases, the consumed time increases with increasing the number of angle samples. However, the application of the introduced CS method to all the three techniques provides significant reduction in the execution time needed for the DOA estimation procedure. This elucidates the effectiveness of the introduced CS method in significantly minimizing the computational burden even when increasing the number of angle samples for wideband DOA estimation.

Table 5 The consumed time in sec of DOA estimation when varying number of angle samples using ISSM, FSS and mTOPS techniques with and without CS

4 Conclusion

This study introduces a new computationally efficient approach for wideband DOA estimation with high resolution. The proposed approach reduces the computational burden by applying CS with chaotic Chebyshev sensing matrix as a compression method to reduce the measurement vector dimension, while the high-resolution is obtained by generalized coprime array configuration with high aperture. To examine the effectiveness of the proposed approach, three state-of-the-art wideband DOA estimation algorithms, namely ISSM, FSS, and mTOPS, are investigated with and without applying the proposed CS technique using ULA, CACIS, and CADiS antenna array layouts. Various simulation scenarios are carried out to assess the DOA estimation accuracy of closely spaced wideband sources and investigate the accompanied computational cost. The robustness of the introduced approach is assessed using several evaluation metrics, including spatial spectrum, the RMSE when varying the SNR and the number of elements, and the consumed time when changing the number of elements and number of angle samples. Results reveal that the proposed CS technique allows preserving the high DOA estimation resolution resulted from using generalized coprime array configuration (CACIS or CADiS), while significantly minimizing the computational complexity of the three wideband DOA estimation techniques under investigation. Results also demonstrate that the ISSM algorithm combined with CS provides the best accuracy for DOA estimation using CADiS configuration while achieving remarkable reduction in the computational complexity. Further insight requires investigating the fabrication process for the proposed approach using realistic antenna elements instead of the omnidirectional elements under various sets of parameter regimes.