1 Introduction

Multi-band and small-size antenna arrays become an active field of research in modern wireless communications [1, 2]. Applications of multi-band antenna arrays include, but are not limited to, cellular mobile communications, satellite communications, Synthetic Aperture Radar (SAR), and automotive applications [3, 4]. The multi-band operation can be obtained by self-scalable fractal array, where an iterative algorithm is employed to replicate an initial geometry, called generator, several times over a variety of scale sizes to grow into the resultant fractal geometry [5, 6]. This approach facilitates the design of various fractal array configurations with different free aspects. Unlike ordinary antenna arrays which are band-limited, fractal arrays can work at distinct operating frequencies based on the fractal geometry and how the elements are produced at distinct expansion factors [5].

Fractal antenna arrays are like ordinary ones in the sense that they may be classified into three categories: linear, planar, and conformal arrays. One of the commonly used techniques for generating linear and planar fractal arrays is the concentric circular ring subarray generator [7, 8]. There are several types of fractal array designs based on this subarray generator, including linear Cantor, Sierpinski carpet, hexagonal, and pentagonal arrays [9,10,11,12,13]. Several recent designs of fractal antenna arrays have been developed for various wireless communication systems [14, 15]. In [16], a fractal array design of 18 transmit and 24 receive antennas was developed for a Multiple-Input Multiple-Output (MIMO) radar system. In this design, antenna array topologies based on space filling fractals are employed to approximate a circular shaped antenna array on a hexagonal grid and to reduce the Side-Lobe Level (SLL). In [17], a new circular fractal antenna array design of eight elements was developed for multi-band operation in various wireless standards, including Wi-Max (3.5–3.8 GHz), C-band applications (3.8–4.4 and 4.8–5.4 GHz), and WLAN (5.15–5.85 GHz). The size of this fractal array design is lower than ordinary circular antenna array by 6%, which reveals the compact size of fractal array designs.

Array pattern synthesis has drawn great attention in wireless communications during the past few decades [18,19,20]. It requires steering the peak of the radiation main lobe towards the Direction of Arrival (DOA) of a desired signal, while forming nulls in the radiation pattern towards the DOA of every undesired signal, and thus, providing a larger signal to interference plus noise ratio (SINR). Adaptive beamforming techniques should be used to compute the optimum excitation weights for antenna elements that achieve the required radiation pattern characteristics [21]. Several studies investigated the adaptive beamforming capability for different ordinary antenna arrays [22, 23]. To date, there are many optimization methods that were employed in adaptive beamforming for ordinary antenna arrays [24,25,26,27]. These optimization techniques are used to optimize the steering of the radiation main lobe, as well as the nulls, and consequently enhance the SINR. The performance of these techniques in finding the optimum combination weights is still insufficient due the problem of premature convergence [24].

Traditional adaptive beamforming techniques such as the Least Mean Squares (LMS) and the Recursive Least Squares (RLS) were investigated in several studies for ordinary antenna arrays [28]. Recently, several enhanced signal processing techniques based on LMS algorithm have been proposed for adaptive beamforming [29,30,31]. In [32], an L0-norm constrained normalized LMS (L0-CNLMS) adaptive beamforming algorithm was proposed for controllable sparse ordinary antenna arrays. Note that LMS-based techniques provide better beamforming performance than RLS-based algorithms. However, RLS method is not easily affected by changes in the eigenvalue prevalence of the correlation matrix of the input vector, and it provides faster convergence rate than LMS method [33, 34]. Recently, new techniques based on combining both LMS and RLS were investigated, and the results showed better performance and convergence rate than the standalone LMS or RLS [35, 36].

The estimation capabilities of Kalman filter can be exploited in blind adaptive beamforming with high rate of convergence and low misadjustment [37]. In [38] and [39], the extended Kalman filter was used for the adaptive beamforming of narrowband linear antenna array. This approach was proven to be robust against the possible mismatch that may occur between the required signal steering vector and the real steering vector. In [40], the unscented Kalman filter was investigated for blind beamforming of ordinary antenna arrays without using any constrained optimization techniques. This approach achieved superior performance over the RLS in terms of the convergence speed and output SINR.

All the previous studies suggested efficient and robust adaptive beamforming techniques for ordinary antenna arrays. On contrast, very few studies have investigated fractal array designs with adaptive beamforming capability [41,42,43]. In [41], the LMS algorithm was employed for the adaptive beamforming design of linear Cantor and Sierpinski carpet fractal antenna array. In [42], new designs of adaptive thinned hexagonal and pentagonal fractal arrays were proposed. In this design, the Ant Colony Optimization (ACO) method was employed for reducing the number of elements with SLL reduction, while the LMS algorithm was used for adaptive beamforming. In [43], a new rapid beamforming algorithm for fractal antenna array was investigated using the assignment of usage time and location tag algorithm.

The aim of this work is to propose a new adaptive beamforming method based on discrete Kalman filter for fractal antenna arrays in wireless environment with strong-jamming power. The remaining parts of this paper are organized as follows. In Sect. 2, the design of linear Cantor fractal array is introduced, then the theory of LMS, RLS, and discrete Kalman filter is presented. Section 3 discusses the simulation results of the suggested Kalman-based adaptive beamforming technique for linear Cantor fractal array, followed by comparing the beamforming results of Kalman filter with LMS and RLS techniques for different Signal to Interference (SIR) ratio in terms of beamforming stability, Half-Power Beam Width (HPBW), maximum SLL, nulls depth, and convergence rate. Afterwards, the performance of the proposed fractal array design is compared with the corresponding ordinary linear antenna array. The conclusions are provided in Sect. 4.

2 Methodology

2.1 Cantor Fractal Antenna Arrays

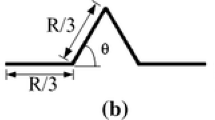
To obtain a final structure of fractal antenna array, a generating subarray, small array at a scale factor p = 1, is applied repeatedly. When repeatedly applied, it forms a larger array at a larger scaling factor (i.e., p > 1). One of the commonly used techniques for fractal array design is the linear Cantor array. It can be constructed through the repetitive application of a three-element generating sub-array [12]. This generating subarray comprises of three uniformly spaced elements, with turning off the central element, i.e., 101. At each stage of growth, 1 is replaced by 101 and 0 by 000 to form the array recursively. This makes the array pattern 101 000 101 at the second stage of growth (p = 2) and 101,000,101,000,000,000,101,000,101 at p = 3 and so on (see Fig. 1).

Fig. 1
figure 1

The first four growth stages of linear Cantor fractal array

Full size image
Fig. 2
figure 2

Structure of the proposed Kalman filter algorithm for adaptive beamforming

Full size image

The array factor of a subarray made of three elements with the representation 101 is

$$GA(\psi )=2\cos(\psi )$$
(1)

where \(\psi =k\mathrm{d}\cos\left(\theta \right)+\beta \), \(\theta \) is the angle between the propagation direction and the array axis, \(\mathrm{d}\) and \(\beta \) are the spacing and the progressive phase-shift of the generator array, respectively, \(k=\frac{2\pi }{\lambda }\) is the wavenumber, and \(\lambda \) is the wavelength.

Under the condition of an expansion factor equals three (\(\delta =3\)), the equation representing the array factor will be:

$${AF}_{p}\left(\psi \right)=\prod_{p=1}^{P}COS({3}^{p-1}\psi )$$
(2)

where p is the stage of growth.

2.2 Adaptive Beamforming

A novel adaptive beamforming approach based on discrete Kalman filter is proposed for pattern synthesis of fractal antenna array. This approach is employed by estimating the best weights of the array elements that decrease the error between the array output and the desired signal. The proposed Kalman filter-based beamformer is compared with the traditional LMS and RLS adaptive beamforming techniques [28, 44,45,46]. The algorithms of LMS, RLS, and Kalman filter are discussed in the following subsections (Fig. 2).

2.2.1 Least Mean Square (LMS) Algorithm

In LMS method, the weights of array element are computed and updated recursively using the steepest-descent technique [18]. The instantaneous gradient vector \(\nabla \mathrm{ J}(\mathrm{i})\) is used to update the weights of array elements as follows:

$$w\left(i+1\right)=w\left(i\right)+\frac{1}{2}\mu \left[-\widehat{ \nabla } J(i)\right]$$
(3)

where \(w\left(i\right)\) is the weight of array element at iteration \(i\) and \(\mu \) is a contrloing parmeter of the convergence rate. The instantaneous gradient vector \(\widehat{\nabla } J(i)\) can be expressed as:

$$\widehat{\nabla } J\left(i\right)=-2\widehat{P}\left(i\right)+2\widehat{R}\left(i\right)w\left(i\right)$$
(4)

where \(\widehat{R}\left(i\right)=\mathrm{x}\left(i\right){x}^{T}\left(i\right)\) is the correlation matrix of the array inputs\(x\left(i\right)\), and \(\widehat{P}\left(i\right)=x\left(i\right)d\left(i\right)\) is the cross-correlation vector between \(x\left(i\right)\) and the desired signal \(d\left(i\right).\) The element weights can be obtained by substituting \(\widehat{\nabla } J\left(i\right)\) from Eq. (4) into (3) as follows:

$$w\left(i+1\right)=w\left(i\right)+\mu \left[\widehat{P}\left(i\right)-\widehat{R}\left(i\right)w(i)\right]=w\left(i\right)+\mu \left[d\left(i\right)-{x}^{T}\left(i\right)w (i)\right]x\left(i\right)=w\left(i\right)+\mu e\left(i\right)x(i)$$
(5)

where \(e\left(i\right)\) is the estimated error. The step size is selected to be within the extent 0< \(\mu \)  < 1/ λmax, where λmax is the largest eigen value of correlation matrix \(\widehat{R}\) [44]. In this study, a step size of 0.05 is found to be the optimum value for achieving high performance.

2.2.2 Recursive Least Squares (RLS) Algorithm

The RLS technique overcomes the main disadvantage of LMS technique of having slow adaptation. Note that both LMS and RLS algorithms depend on error correction learning. However, the LMS follows the path of diminishing the instantaneous value of the squared estimation error for every iteration \(i, \mathrm{while}\) the RLS reduces the sum of squared estimation errors up to the current iteration \(i\) [45, 46].

In the RLS method, the intermediate vector \(r\left(i\right)\) and the gain vector \(k\left(i\right)\) are calculated at each iteration i = 1, 2, 3 … as follows:

$$r\left(i\right)=1+{\beta }^{-1} {x}^{T}\left(i\right)P\left(i-1\right) x\left(i\right)$$
(6)
$$k\left(i\right)={\beta }^{-1} P\left(i-1\right) x\left(i\right) / r(i)$$
(7)

where \(x\left(i\right)\) is the regressor input and \(P(i)\) is the inverse of the matrix of data autocorrelation. The initial value of \(P(i)\) is set to be \(P(0)={\lambda }^{-1}I\), where \(\lambda \) is a small positive constant and I is the identity matrix. \(\beta \) is a positive parameter, denoted by the forgetting factor, and it lies in the range 0 < < \(\beta \)  ≤ 1 to ensure exponential distribution for the weight, in which high weight is given to recent data, and less weight is assigned to past data. In this study, \(\beta \) = 0.999 is found to be the optimum value for achieving high performance.

The a priori estimation error is given by

$$e\left(i\right)=d\left(i\right)- {x}^{T}\left(i\right) w\left(i-1\right)$$
(8)

In order to obtain the updated weights \(w\left(i\right)\), the gain vector \(k\left(i\right)\) is multiplied by \(e\left(i\right)\) and added to the weight vector \(w\left(i-1\right)\) as follows:

$$w\left(i\right)=w(i-1)+k(i)e(i)$$
(9)

The inverse correlation matrix is recalculated with new input values using the updated weights as follows

$$P\left(i\right)=[{\beta }^{-1}P\left(i-1\right)-k\left(i\right){k}^{T}\left(i\right)r\left(i\right)]$$
(10)

The RLS algorithm outperforms the LMS in the convergence stability.

2.2.3 The Proposed Kalman Filter Algorithm

In this work, a linear discrete Kalman filter is used to obtain the required adaptive weights for array elements to steer the main lobe and the nulls in presence of noise towards the desired and interferer directions, respectively.

For N-element linear narrowband array, the array output is \(y\left(i\right)={w}^{T}\left(i\right)x(i)\), where \(x(i)\) is the input signal and \(w\left(i\right)\) is the weight vector at sample time \(i\). For wideband array, a tapped delay line filter should be included in each channel of the array using the same mathematical formulation of narrowband case, in which vectors \(w(i)\) and \(x(i)\) are used to represent tap weights and delayed signals, respectively. Let the state equation of optimal array weights be expressed as [37, 48]\(:\)

$${w}_{opt}\left(i+1\right)=\upphi \left(i+1,i\right) {w}_{opt}\left(i\right)$$
$${w}_{opt}\left(0\right)={w}_{0}$$
(11)

where \(\upphi \left(i+1,i\right)\) is a state transition matrix, and the index \((i+1,i)\) indicates the state value at sample time \(i+1\) based on measurements through \(i\). Note that for stationary environment, the array optimal weights will remain constant and \(\upphi \left(i+1,i\right)\) becomes the identity matrix. If the array signal environment is time-varying, a more sophisticated model should be developed for \(\upphi \left(i+1,i\right)\) to estimate the optimum array weights adaptively based on the changing environment.

Assume that the system measurements can be expressed by a noise contaminated version of the optimal array output as follows:

$$d\left(i\right)={x}^{T}\left(i\right){w}_{opt}\left(i\right)+\upsilon (i)$$
(12)

where \(d\left(i\right)\) is the reference signal, and \(\upsilon (i)\) is a Gaussian random variable with zero mean and variance \({\sigma }^{2}\left(i\right)\), representing the measurement noise. It can be deduced that the optimum estimate of the array weight vector \({\widehat{w}}_{opt}\left(i\right)\) is given by [48]:

$${\widehat{w}}_{opt}\left(i,i\right)=\upphi \left(i,i-1\right){\widehat{w}}_{opt}\left(i-1,i-1\right)+K\left(i\right)[d\left(i\right)-{x}^{T}\left(i\right)\upphi \left(i,i-1\right){\widehat{w}}_{opt}\left(i-1,i-1\right)]$$
(13)

where the index \((i,i-1)\) indicates a predicted quantity at sample time \(i\) based on measurements through \(i-1\), and \(K\left(i\right)\) is the Kalman gain vector. Note that the quantity between brackets in Eq. (13) represents the difference between the desired reference signal and the actual array output.

For stationary environment, the Kalman gain vector \(K\left(i\right)\) is given by

$$K\left(i\right)=P\left(i,i-1\right)x\left(i\right){[{x}^{T}\left(i\right)P\left(i,i-1\right) x\left(i\right)+{\sigma }^{2}\left(i\right)]}^{-1} $$
(14)

where \(P\left(i\right)\) is the covariance matrix of predicted error and it can be expressed as

$$P\left(i,i-1\right)=\upphi \left(i,i-1\right)P\left(i-1,i-1\right){\upphi }^{T}\left(i,i-1\right)$$
(15)

Substituting from Eq. (14) into Eq. (15), \(P\left(i,i\right)\) can be obtained as follows

$$P\left(i,i\right)= P\left(i,i-1\right)-\frac{P\left(i,i-1\right) x(i){x}^{T}\left(i\right)P\left(i,i-1\right)}{[{\sigma }^{2}\left(i\right)+ {x}^{T}\left(i\right)P\left(i,i-1\right) x\left(i\right)]}$$
(16)

The performance of KF depends on the precise estimate of the process noise variance and the measurement noise variance. In this work, a stationary environment is assumed, i.e., the optimal weight vector does not vary with time and, hence, the variance of process noise is set to be zero. The measurement noise variance \({\sigma }^{2}\left(i\right)\) can be obtained from the interpretation described in Eq. (12) of the output signal for the optimum array weight. With \(d\left(i\right)\) an approximation for the actual desired signal \(s\left(i\right)\), Eq. (12) can be expressed as follows [47, 48]

$$d\left(i\right)={x}^{T}\left(i\right){w}_{opt}\left(i\right)+\upsilon \left(i\right)=s\left(i\right)+\xi (i)$$
(17)

where \(\xi (i)\) is the error between the actual desired signal \(s\left(i\right)\) and the reference signal \(d\left(i\right)\). Consequently, the measurement noise \(\upsilon \left(i\right)\) can be written as

$$\upsilon \left(i\right)=s\left(i\right)+\xi \left(i\right)-{x}^{T}\left(i\right){w}_{opt}\left(i\right)$$
(18)

Assuming zero mean processes for \(\upsilon \left(i\right)\), \(s\left(i\right)\), and \(\xi \left(i\right)\), the measurement noise has zero mean \(E\left\{\nu \left(i\right)\right\}=0\), and consequently the variance of measurement noise \({\sigma }^{2}\left(i\right)\) is given by

$${\sigma }^{2}\left(i\right)=E\left\{\nu \left(i\right)\nu \left(i\right)\right\}- {E\left\{\nu \left(i\right)\right\}}^{2}= E\left\{\nu \left(i\right)\nu \left(i\right)\right\}$$
(19)

If \(\xi \left(i\right)\) does not correlate with \(s\left(i\right)\) and \(x\left(i\right)\), \({\sigma }^{2}\left(i\right)\) can be written as [47]

$${\sigma }^{2}\left(i\right)={{w}_{opt }^{T}\left(i\right)R}_{xx}(i){W}_{opt}(\mathrm{i})-2{W}_{opt }^{T}(\mathrm{i}) {r}_{xs}(\mathrm{i})+E\left\{{s(i)}^{2}\right\}+E\left\{{\xi (i)}^{2}\right\}=MMSE+E\left\{{\xi }^{2}\right\}$$
(20)

where \({R}_{xx}(\mathrm{i})\) is the average estimate of the received signal autocorrelation matrix, \({r}_{xs}(\mathrm{i})\) is the cross-correlation between \(x\left(i\right)\) and \(s\left(i\right)\), and MMSE is the minimum mean square error estimate for the array weights. An estimate for the noise variance \({\sigma }^{2}\left(i\right)\) can be obtained based on the MMSE estimate for optimum array weights. In this work, \({\sigma }^{2}\left(i\right)\) is first estimated using the MSSE and then tuned around that estimate to determine the value that maximizes the efficiency.

3 Results

The effectiveness of the proposed Kalman filter-based beamformer for pattern synthesis of linear Cantor fractal antenna array is investigated through MATLAB simulations using the following parameters: number of antenna elements N = 16, element spacing d = λ/4, and expansion factor \(\delta \) = 3. The effect of interfering Additive White Gaussian Noise (AWGN) is considered by carrying out the simulations at fixed value of SNR = 30 dB. Simulations are carried out on various array configurations, and the average of 100 simulation runs are computed at different values of Signal to Interference Ratio (SIR). The proposed technique is compared with LMS and RLS techniques in terms of beamforming stability, HPBW, maximum SLL, null depth at the DOA of interference signals, and convergence rate at different growth stages for different SIR values.

The array factor patterns of linear Cantor array at growth stage p = 3, f = 27 GHz, and SNR = 30 dB are shown in Fig. 3, assuming that the DOAs of the desired and the undesired signals are 30° and 60°, respectively. The results are obtained using LMS, RLS, and the proposed Kalman filter for different values of SIR. Figure 3a demonstrates that LMS, RLS, and Kalman algorithms provide adaptation of the radiation pattern for very low jamming power (SIR = 5 dB). Figure 3b reveals the poor performance of LMS technique for low to moderate jamming power (SIR =—10 dB) as it fails to form nulls in the radiation pattern towards the DOA of the interference signal at 60°. For a high SIR of -15 dB as shown in Fig. 3c, both RLS and LMS techniques failed to steer the peak of the radiation main lobe towards the DOA of the desired signal at 30°, revealing poor performance for high jamming power. On contrast, the proposed Kalman-beamformer achieved perfect adaptation of the radiation pattern synthesis at high jamming power (SIR values up to -20 dB). Moreover, the proposed approach identifies the exact locations of the nulls which decreases the interference from adjoining radiating systems.

Fig. 3
figure 3

The array factor patterns of linear Cantor array at growth stage p = 3, f = 27 GHz, and SNR = 30 dB using LMS, RLS, and the proposed Kalman filter for (a) SIR = 5 dB, (b) SIR = -10 dB, and (c) SIR = -15 dB

Full size image

The array factor patterns of linear Cantor array for different cases of angle difference between the desired and interference signals are shown in Fig. 4 using LMS, RLS, and Kalman algorithms at fixed SIR of 0 dB. Figure 4a shows the array factor patterns obtained for an angle difference of 30° between the DOAs of desired and the interfering signals, while Fig. 4b shows the same array factor patterns obtained for an angle difference of 5°. It can be noted that both LMS and RLS techniques provide unsatisfactory beamforming performance when the difference between the arrival angles of the desired signal and the interferer is small, even with low jamming power. The reason for this behavior is that both LMS and RLS techniques rely on the eigen prevalence of the signal correlation matrix. On contrast, the proposed Kalman filter-based beamformer achieves superior adaptation of the radiation pattern synthesis for both low and high jamming power scenarios. This shows that the Kalman algorithm maintains the same performance when undesired users become close to the main user, and hence not affecting the signal fidelity of the main user. This reveals the effectiveness of the proposed approach in real-time beamforming applications.

Fig. 4
figure 4

The array factor patterns of linear Cantor array at growth stage p = 2, f = 27 GHz, SNR = 30 dB, and SIR = 0 dB using LMS, RLS, and the proposed Kalman filter. The DOA of the desired and the undesired signal are (30°, 60°) for (a) and (30°, 35°) for (b), respectively

Full size image

A critical comparison between the proposed Kalman filter-based beamformer, RLS, and LMS techniques is made for linear Cantor array using different evaluation metrics, including the maximum SLL, HPBW, convergence rate, and the null depth at the DOA of interference signal. Table 1 shows those metrics at growth stages p = 2, 3, and 4 for different levels of SIR at fixed value of SNR = 30 dB. It can be noted that with the use of Kalman filter, the required radiation pattern is nearly the same at all growth stages (p = 2, 3, and 4). As shown in Table 1, the proposed Kalman beamformer provides deeper null towards the DOA of the undesired signal than the LMS and RLS techniques, especially at higher growth stages and higher SIR values. Also, the proposed approach achieves lower SLL than the LMS and RLS techniques. Moreover, the convergence speed of the proposed Kalman method outperforms those of other algorithms under comparison. It can be seen from Table 1 that for all techniques, as the growth stage is increased, the SLL value slowly decreases, while the HPBW is signficantly reduced. The results shown in Table 1 reveal that for wide range of jamming power (different SIR values), the proposed Kalman filter-based beamformer can maintain nearly the same steering of the radiation main lobe and nulls, maximum SLL, and HPBW. This demonstrates the effective implementation of proposed approach in high interference environment.

Table 1 The max SLL, HPBW, convergence rate, and the null depth at the DOA of interference signal at p = 2, 3, and 4 for linear Cantor array using LMS, RLS, and Kalman filter-based beamforming techniques
Full size table

Figure 5 demonstrates the convergence rate of LMS, RLS, and Kalman filter at growth stage p = 2 for SIR = -5 dB and SNR = 30 dB. It can be noted that the proposed Kalman method has the fastest convergence rate of 2 iterations, while the weights of LMS and RLS techniques converge to their best values in 10 and 3 iterations, respectively. Using the same operating conditions, the stability convergence of the Kalman algorithm is better than LMS and RLS methods. For rapid signal variations caused by high mobility rate of the user, the proposed Kalman filter beamformer can accurately steer the peak of the radiation main lobe towards the DOA of the desired signal and form deep null in the radiation pattern towards the DOA of the undesired signal as its convergence rate is very high. On contrast, LMS and RLS adaptive beamforming algorithms may fail to track the signal in such scenarios due to their slow convergence rate. This reveals the superior performance of the proposed adaptive beamforming technique in enhancing the capacity of mobile communication systems.

Fig. 5
figure 5

The convergence rate of LMS, RLS, and Kalman filter-based beamforming techniques at growth stage p = 2 for SIR = -5 dB and SNR = 30 dB

Full size image

Figure 6 illustrates the variations of Mean Square Error (MSE) with different levels of SIR using LMS, RLS, and Kalman filter. As shown in Fig. 6, the MSE amplitude decreases with SIR increase as we are moving from LMS to RLS algorithm, then to the Kalman algorithm. It can be noted that the LMS approach failed to provide adaptation of the radiation pattern for high jamming power (SIR < -5 dB), while the RLS produces poor adaptive beamforming performance for SIR < -10 dB and good performance for SIR > -5 dB. On the other hand, the proposed Kalman filter-based beamformer achieves superior adaptation of the radiation pattern synthesis even with very strong-jamming power up to SIR = − 20 dB. As shown in Fig. 6, the MSE of Kalman filter is lower than the RLS by around 20 dB for high SIR values (-10 dB < SIR < -20 dB), revealing its superior performance.

Fig. 6
figure 6

Variations of the MSE with different levels of SIR at growth stage p = 2, f = 27 GHz, and SNR = 30 dB using LMS, RLS, and Kalman adaptive beamforming techniques

Full size image

The proposed Kalman filter-based beamformer achieves multi-band operation for fractal antenna array, in which the radiation pattern characteristics, including the main lobe peak, nulls, and SLL are kept the same at distinct operating frequencies scaled by the expansion factor \(\delta \). Figure 7 shows the array factor patterns of linear Cantor array at growth stage p = 3 and SIR = -20 dB for three operating frequencies using the proposed Kalman filter. Note that the operating frequency of fractal arrays can be decreased by a factor of \({\delta }_{n}\) from the specified design frequency, where n = 1, 2,···, p − 1. Assuming that the fixed design frequency is 27 GHz, the array patterns shown in Fig. 7 are obtained for \(\delta \) =3 and n = 1, 2, 3, resulting in available operating frequencies of 3, 9, and 27 GHz. Figure 7 reveals that the array patterns of the proposed Kalman filter keep the same main lobe peak, nulls, and SLL at the three operating frequencies.

Fig. 7
figure 7

The array factor patterns of linear Cantor array at growth stage p = 3 and SIR = − 20 dB for three different operating frequencies using the proposed Kalman filter-based beamformer. The DOA of the desired and the undesired signal are (30°, 60°)

Full size image

Table 2 demonstrates the Kalman beamformer results of SLL, HPBW, and convergence rate of the linear Cantor array for three distinct operating frequencies at p = 3. It can be noted from Table 2 that the SLL is nearly the same at the three operating frequencies, while the HPBW is decreasing with the frequency increase. Also, the results show constant and fast convergence rate at the three operating frequencies. Table 2 reveals that the array weights of the proposed Kalman filter converge to their best values in only 3 iterations with a similar behaviour for all the three operating frequencies, revealing the superior performance of the proposed approach in multi-band operation. Figure 7 and Table 2 demonstrate that with the proposed Kalman filter-based beamformer, the designer can efficiently provide good adaptation of the radiation pattern synthesis at strong-jamming power, while maintaining the same SLL at different operating frequencies with fast convergence rate.

Table 2 The SLL, HPBW, and convergence rate of linear Cantor fractal array at three different operating frequencies using the proposed Kalman filter-based beamformer
Full size table

To validate the implementation of the proposed Kalman method in fractal antenna arrays, other fractal array configurations such as Sierpinski carpet, hexagonal, and pentagonal arrays have been investigated. The results show consistent performance in terms of beamforming accuracy and multi-band radiation pattern characteristics. Although the linear Kalman filter was employed in previous studies to acquire the adaptive weights for several adaptive signal processing applications, to the authors’ knowledge, it is the first time to investigate the Kalman filter as an adaptive beamforming technique in the synthesis of fractal antenna arrays. It represents a new efficient radiation pattern synthesis for fractal antenna array that can achieve the following characteristics: (a) multi-band operation, (b) adaptive beamforming capability in strong-jamming environment, (c) optimized gain, and (d) reduced array size. Note that the proposed adaptive fractal antenna array design can be employed in several wireless applications, including satellite communications, 4G/5G wireless mobile communications, aerial vehicles, automotive radar applications, and microwave communications. In [49], a fractal antenna array design for antenna gain improvement was developed for automotive radar systems operating at 24 GHz. A design of Sierpinski gasket equilateral triangular fractal antenna array was fabricated and tested for portable 4G/5G MIMO communication systems [50]. The multi-band behaviour of different fractal array configurations is experimentally validated in the patents of [51, 52].

3.1 Performance Analysis

The performance of the proposed fractal Cantor array design is compared with the corresponding ordinary linear antenna array. Figure 8. demonstrates the array factor patterns of Cantor array and ordinary linear array at high jamming power of SIR = -15 dB using the proposed Kalman filter for different number of antenna elements (N = 16, 32, and 64). Results show that discrete Kalman filter achieves good adaptive beamforming performance for both fractal and ordinary arrays at strong-jamming power. However, the main difference is that the Kalman filter-based beamformer can achieve multi-band operation for fractal array (see Figs. 8a, b, and c), in which the radiation pattern characteristics are kept the same at distinct operating frequencies (f = 3, 9, and 27 GHz) scaled by the expansion factor $$\boldsymbol{\delta }=$$ 3. For ordinary antenna arrays, the proposed Kalman filter-based beamformer provides good adaptation of the radiation pattern synthesis at only the specified design frequency of 27 GHz (see Fig. 8.d). This reveals that the linear Kalman filter not only achieves comparable high adaptive beamforming performance for both fractal and ordinary arrays at strong-jamming power but also provides multi-band operation for fractal antenna arrays.

Fig. 8
figure 8

The array factor patterns of fractal Cantor array (a, b, and c) and ordinary linear array (d) for different number of antenna elements at SNR = 30 dB and SIR = -15 dB using the proposed Kalman filter. The DOA of the desired and the undesired signal are (30°, 60°) at different operating frequencies (a) f = 27 GHz, (b) f = 9 GHz, and (c) f = 3 GHz for fractal Cantor array, and at fixed frequency (d) f = 27 GHz for ordinary linear array

Full size image

Table 3 shows the maximum SLL, HPBW, and the null depth at the DOA of interference signal using the proposed Kalman filter-based beamforming technique for fractal Cantor and ordinary linear arrays. The radiation pattern of the fractal Cantor array achieves lower HPBW and higher directivity than ordinary linear antenna array. It can be seen that the SLL of Cantor fractal arrays is higher than ordinary linear arrays. However, it can be reduced using several optimization methods. Results show that fractal Cantor array can achieve multi-band operation because distinct parts of the array are like each other at various scales, while ordinary linear array is band-limited because its operating frequency relies on the element spacing within the array. Figure 8 demonstrates that fractal Cantor array preserves its radiation pattern features at multiple operating frequencies, while ordinary linear array loses its beam focusing capability as the frequency varies from the specified design frequency. This reveals the superior performance of fractal Cantor array over ordinary linear array in terms of array size and multi-band operation [5].

Table 3 The maximum SLL, HPBW, and the null depth at the DOA of interference signal using the proposed Kalman filter-based beamforming technique for fractal Cantor array and ordinary linear array
Full size table

One of the main advantages of the fractal Cantor array is its computational efficiency in calculating the array factor compared to ordinary linear arrays. For ordinary linear array with odd number of antenna elements (N = 2 M + 1), M cosine functions should be computed, and M additions should be executed for each angle. On the other hand, for fractal Cantor array with the same number of antenna elements, p cosine function evaluations and p− 1 multiplications are required. This means that for the case of 81-element ordinary linear array, 40 cosine function evaluations and 40 additions should be performed, while for the case of fractal Cantor array with the same number of elements, 4 cosine function evaluations and 3 multiplications should be executed. This shows that the fractal array factor is at least M/p = 40/4 = 10 times faster than ordinary array factor, revealing the low computational cost of fractal Cantor array design.

A main challenge in the development of fractal array is the excessive number of antenna elements at higher expansion levels. However, optimization techniques can be employed to reduce the count of elements at higher growth stages and to improve the array factor properties. Note that fractal arrays are thinned arrays, due to their recursive geometric nature [12, 53]. Thinning of an antenna array implies turning off some antenna elements to obtain the required radiation features with the lowest possible count of antenna elements. However, the thinning process of fractal array may lead to high SLL which can be solved using optimization techniques. In [54], evolutionary optimization techniques were employed to develop a thinned rhombic fractal antenna array, achieving above 25% of thinning with better array factor features than the completely populated array. In [55], an iterative feed matrix method is employed in a Haferman carpet fractal antenna array to simplify the array factor computation. This allows the application of evolutionary optimization methods in decreasing the count of antenna elements and keeping the SLL as low as possible at different growth stages. In [56], the same iterative matrix approach was employed in the design of Sierpinski carpet fractal array, and differential evolution optimization algorithm was employed for reducing the number of elements and minimizing the SLL. In the future, different optimization techniques such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) will be investigated for optimizing several performance metrics of the proposed fractal antenna array design.

4 Conclusion

In this work, a novel technique of radiation pattern synthesis is proposed to merge the unique characteristics of fractal arrays with the adaptive beamforming capability in strong-jamming environment. The Kalman filter algorithm is investigated, for the first time, as an adaptive beamformer in the Cantor fractal array synthesis. The proposed Kalman filter-based beamformer is utilized to obtain the best weights of array elements in order to steer the main lobe peak and nulls of the radiation pattern toward the DOA of desired and interference signals, respectively, at distinct levels of jamming power. The effectiveness of the proposed approach is investigated by comparing its performance with the LMS and RLS techniques using several evaluation metrics, including the maximum SLL, HPBW, convergence rate, and the null depth at the DOA of interference signal. The proposed Kalman filter-based beamformer achieves superior performance over LMS and RLS techniques on various array configurations and for different SIR values. Simulation results demonstrate that the suggested approach manages not only to provide superior adaptation of the radiation pattern synthesis over a wide range of jamming power, but also to keep the same SLL at different operating frequencies with fast convergence rate. Morevere, the proposed technique has superior performance in tracking the desired user and eliminating the undesired signals, even when undesired users are close to the desired user, showing its ability to improve the capacity of various wireless systems. This elucidates that the suggested design can be effectively utilized in real-time and multi-band beamforming wireless applications for strong-jamming environment.