1 Introduction

Ever-increasing demands for achieving the fifth generation (5G) and beyond wireless network scenarios such as massive machine-type communications, ultra-reliable and low latency communications and enhanced mobile broadband [1,2,3,4] have made it inevitable to develop new waveforms as an alternative to the conventional orthogonal frequency division multiplexing (OFDM) [5, 6], which has some limitations reducing its chance to be employed in the future wireless systems. Even though the long-term evolution (LTE)/4G systems employ the OFDM waveform, there is no guarantee that it will not be replaced by another waveform in the future due to its deficiencies like the requirement of strict frequency synchronization process, having limited spectral efficiency with large amount of out-of-band emission and the need for using cyclic prefix, which reduces the data transmission rate. Filter bank multicarrier/offset quadrate amplitude modulation (FBMC/OQAM) [7,8,9,10] is one of the prominent waveform candidates which have the potential to replace the conventional OFDM in the next generation wireless systems. FBMC/OQAM stands out with its unique features eliminating the shortcomings of OFDM. The main advantages of FBMC/OQAM over the conventional OFDM can be summarized as follows [7,8,9,10]: First of all, the lower side lobes achieved by the usage of filter banks lead to almost negligible inter-symbol interference (ISI) in the FBMC/OQAM system, while having the high-level side lobes, which causes a significant ISI, is one of the main drawbacks of the OFDM system. Besides, there is no need to use cyclic prefix in the FBMC/OQAM. For this reason, it becomes possible to achieve higher data rates compared to the OFDM system. Apart from this, well localized pulse shape in both frequency and time makes the FBMC/OQAM a more suitable scheme for mobile environment. Moreover, FBMC/OQAM is fully compatible with the cognitive radio applications thanks to a very low adjacent channel leakage ratio of its transmission signal. Besides all these advantages, it is possible to utilize multiple-input multiple-output (MIMO) technology in the FBMC/OQAM system [11,12,13,14]. Employing a multi-antenna structure in the FBMC/OQAM transceiver not only makes the system more robust against the channel fading effects, but also leads to a significant capacity enhancement. In consequence of this, while the bit error rate (BER) of the system is reduced owing to the alleviation of multipath fading effects, the communication is carried out at higher data rates due to the aforementioned capacity increase [11,12,13,14].

1.1 Problem statement

In order to be able to coherently recover the transmitted symbols, symbol detection is an indispensable process to be carried out at the receiver side of any transmission scheme in wireless communication. Zero forcing (ZF) and maximum likelihood (ML) are the two popular algorithms widely utilized for symbol detection in various transmission systems [15,16,17]. However, although both of the aforementioned algorithms have some advantages, they also have significant drawbacks making them far from being an ideal symbol detector. For example, ZF algorithm is known with its low complexity and easy implementation. These are noteworthy features that an ideal symbol detector should have. But the related algorithm is also known with being vulnerable to severe channel conditions, which cause its performance to reduce considerably. Furthermore, the efficiency of the ZF algorithm is negatively affected by the increase of antenna number in MIMO systems [15]. Unlike the ZF algorithm, ML algorithm has the capability of delivering a flawless symbol detection performance in all circumstances. However, because of the exhaustive search procedure used for detecting the optimal symbols, its computational complexity can reach extremely high levels depending on the system parameters. In the ML algorithm, it is tried to find the optimal symbol vector, the size of which is equal to the number of antennas, via exhaustive search. To this end, the Euclidean distance of the received symbol vector to each of the possible symbol combinations likely to be transmitted to the receiver is calculated. Later on, the symbol combination that has the minimum Euclidean distance to the received symbol vector, which is distorted by the channel, is determined as the optimal symbol vector by the ML detector [16, 17]. Searching for the optimal symbol vector by trying all of the possible symbol combinations causes ML algorithm to have extremely high computational complexity. Moreover, since the increase in the number of antennas and modulation order leads to an exponential growth in the search space, the complexity of ML algorithm becomes even higher with the enhancement of these parameter values.

1.2 Motivation

On the other hand, there is the possibility of achieving near-ML performance with significantly lower computational complexity by integrating an optimization algorithm to the ML scheme in place of its exhaustive search procedure. To put it another way, instead of trying each symbol combination available in the discrete search space, it is possible to reach near-optimal solution with substantially smaller processing load by optimizing the symbol vectors via an efficient optimization algorithm. Metaheuristic optimization algorithms widely utilized in numerous engineering problems especially in recent years can also be considered for the optimization of symbol vectors. For example, after converting the quadrate amplitude modulation (QAM) symbol vectors from the combination of complex numbers to the binary bit sequences, it will be possible to carry out the optimization process directly in discrete space. To this end, discrete versions of the metaheuristic optimization algorithms are needed. Motivated by the possibility of reaching near-ML performance with considerably lower computational cost via an efficient symbol optimizer that has the capability of optimizing the symbol vectors directly in discrete space, we have developed a novel and quite efficient discrete version of harmony search (HS) algorithm [18] called disHS in this paper and integrated it to the ML algorithm to obtain an efficient symbol detector named disHS-ML, which has not only considerably lower computational complexity, but also near-optimal performance. The newly developed disHS-ML symbol detector was then applied to the MIMO-FBMC/OQAM system to make it more suitable to be employed in the forthcoming wireless technologies. The performance and complexity of the proposed disHS-ML strategy in MIMO-FBMC/OQAM system were compared with not only those of the classical symbol detectors like ZF and ML, but also the heuristic-based detectors such as BPSO-ML, disABC-ML and DBHS-ML, which were developed by integrating the binary particle swarm optimization [19], discrete artificial bee colony [20] and discrete binary harmony search [21] algorithms to the conventional ML scheme, respectively.

Another motivating factor to carry out this work is the lack of symbol detection study in which a metaheuristic-based ML strategy is developed for the MIMO-FBMC/OQAM system. This paper will make a significant contribution to fill the related gap existing in the literature. Apart from this, the absence of any HS-based symbol detection study in the literature, which can be considered as a significant motivation factor, played an important role in our decision to study on this subject.

1.3 Related works

As far as we know, no study has been performed yet regarding the symbol detection using metaheuristic-based ML strategies in the MIMO-FBMC/OQAM system. However, some studies in which the heuristic approaches were utilized for symbol detection in different transmission schemes can be found in the literature [22,23,24,25,26,27,28]. In [22], genetic algorithm (GA) was utilized in the ML strategy to obtain more accurate and computationally efficient symbol detector for the pulse amplitude modulation (PAM) system. In [23], both the standard and binary versions of the PSO algorithm were applied to the ML method to acquire near-ML detection performance with reduced complexity in MIMO communication systems. In [24], differential evolution (DE)-based ML detector was proposed for the MIMO-OFDM system. In [25], a symbol detector named MBER-BLAST, in which the PSO algorithm is employed for finding the detector weights, was proposed for the OFDM combined with space division multiple access (OFDM-SDMA) system. In [26], the authors benefited from the ABC algorithm to achieve a satisfying performance close to that of ML detector while reducing its computational complexity in massive MIMO system. In [27], a novel optimization method, which was generated by hybridizing the PSO and ant colony optimization (ACO) algorithms, was suggested to solve the problem of symbol detection in large MIMO systems. In [28], in order to efficiently reduce the complexity of ML detector and obtain a sufficiently good bit error rate (BER) results in MIMO-non orthogonal multiple access (MIMO-NOMA) systems, the authors proposed the backtracking search algorithm (BSA) to be used as a symbol vector optimizer in the ML scheme. While there is no study related to symbol detection based on HS algorithm in the literature, it is possible to come across numerous studies, in which the HS or one of its modified versions was successfully applied to diversified telecommunication problems such as pilot tones design, peak-to-average power ratio (PAPR) reduction, routing, data dissemination, etc. [29,30,31,32,33,34,35,36].

1.4 Contributions

The main contributions of the paper can be listed as follows:

  1. (1)

    A new and quite efficient version of the conventional HS algorithm has been developed in this paper to solve the problem of symbol detection encountered in MIMO-FBMC/OQAM system.

  2. (2)

    The novel discrete HS variant called disHS has been integrated to the classical ML scheme. After this integration, an advanced symbol detector named disHS-ML has been developed. Thanks to the usage of newly developed disHS algorithm as a symbol optimizer in the ML scheme, a great deal of complexity gain has been achieved.

  3. (3)

    An extensive analysis on the convergence and BER performances of the considered symbol detectors was carried out. In addition to this, quite comprehensive complexity analysis with detailed mathematical expressions and numerical comparisons was made. According to these analyses, the proposed disHS-ML strategy leaves behind the BPSO-ML, disABC-ML and DBHS-ML, which are the other metaheuristic-based symbol detectors considered for comparison in this paper, with regard to not only BER and convergence performance, but also the computational complexity.

The remainder of the paper is organized as follows: In Sect. 2, MIMO-FBMC/OQAM system is described. In Sect. 3, after giving the matrix representation of the FBMC/OQAM and its block frequency spreading approach, the symbol detection problem is formulated for the MIMO-FBMC/OQAM system. In Sect. 4, after introducing the conventional HS and the newly developed disHS algorithms respectively, the proposed disHS-ML symbol detector is explained. In Sect. 5, a quite comprehensive analysis on the experimental results and computational complexities of the considered symbol detectors is carried out. Finally in Sect. 6, the paper is concluded.

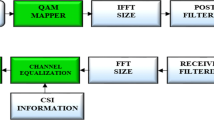
2 MIMO-FBMC/OQAM system description

Adopting the MIMO technology to the FBMC/OQAM system, which already has the capability of solving many chronic problems in wireless communication, is very important to make the related system more robust against the fading effects of the multipath channels. Apart from this, it becomes possible for the FBMC/OQAM system to provide communication at higher data rates in the case that it is combined with MIMO technology. In this section, it is aimed to explain the MIMO-FBMC/OQAM transmission procedure in a simple and understandable way [11,12,13].

In the case of transmitting the real valued symbol \(a_{m,n}\) by using a single antenna in the FBMC/OQAM system, the demodulated signal at the receiver side can be defined as follows:

$$y_{m,n} \approx h_{m,n} \cdot \left( {a_{m,n} + j \cdot u_{m,n} } \right) + n_{m,n}$$
(1)

where \(h_{m,n}\) represents the channel coefficients, \(u_{m,n}\) denotes the intrinsic interference and \(n_{m,n}\) indicates the noise part of the demodulated signal symbolized by \(y_{m,n}\). The reason for multiplying the intrinsic interference by j is that the interference part symbolized by \(u_{m,n}\) is pure imaginary while \(a_{m,n}\) symbols are real valued [11,12,13]. The subscripts m and n signify the subcarrier and time indices, respectively. On the other hand, when using \(N_{t}\) antennas at the transmitter and \(N_{r}\) antennas at the receiver to provide transmission over multiple antennas in the FBMC/OQAM system, the demodulated \(y_{m,n}^{(j)}\) signal at the jth antenna of the receiver is expressed in the following way:

$$y_{m,n}^{(j)} = \sum\limits_{i = 1}^{{N_{t} }} {h_{m,n}^{(ji)} } \cdot \left( {a_{m,n}^{(i)} + j \cdot u_{m,n}^{(i)} } \right) + n_{m,n}^{(j)}$$
(2)

where the subscripts i and j are the indices of transmit and receive antennas, respectively. For example, while the symbol \(a_{m,n}^{(i)}\) specifies the real valued symbol at the ith transmit antenna, \(h_{m,n}^{(ji)}\) corresponds to the channel coefficient between the ith transmit antenna and jth receive antenna. The Eq. (2) can also be expressed in matrix form as follows:

$$\underbrace {{\left[ {\begin{array}{*{20}c} {y_{m,n}^{(1)} } \\ \vdots \\ {y_{m,n}^{{(N_{r} )}} } \\ \end{array} } \right]}}_{{{\mathbf{y}}_{m,n} }} = \underbrace {{\left[ {\begin{array}{*{20}c} {h_{m,n}^{(11)} } & \cdots & {h_{m,n}^{{(1N_{t} )}} } \\ \vdots & \ddots & \vdots \\ {h_{m,n}^{{(N_{r} 1)}} } & \cdots & {h_{m,n}^{{(N_{r} N_{t} )}} } \\ \end{array} } \right]}}_{{{\mathbf{H}}_{m,n} }}\underbrace {{\left[ {\begin{array}{*{20}c} {a_{m,n}^{(1)} + j \cdot u_{m,n}^{(1)} } \\ \vdots \\ {a_{m,n}^{{(N_{t} )}} + j \cdot u_{m,n}^{{(N_{t} )}} } \\ \end{array} } \right]}}_{{{\mathbf{a}}_{m,n} + j \cdot {\mathbf{u}}_{m,n} }} + \underbrace {{\left[ {\begin{array}{*{20}c} {n_{m,n}^{(1)} } \\ \vdots \\ {n_{m,n}^{{(N_{r} )}} } \\ \end{array} } \right]}}_{{{\mathbf{n}}_{m,n} }}$$
(3)
$${\mathbf{y}}_{m,n} = {\mathbf{H}}_{m,n} \cdot \left( {{\mathbf{a}}_{m,n} + j \cdot {\mathbf{u}}_{m,n} } \right) + {\mathbf{n}}_{m,n}$$
(4)

where the channel coefficients are represented by the Nr × Nt sized \({\mathbf{H}}_{m,n}\) matrix.

3 Problem formulation

3.1 Representation of FBMC/OQAM in matrix form

In order to simplify the problem formulation, FBMC/OQAM system was represented in matrix form as in [9, 14]. The prototype filter at the transmitter of FBMC/OQAM system can be defined by a transmit matrix G as follows:

$${\mathbf{G}} = \left[ {{\mathbf{g}}_{1,1} \,\,\,{\mathbf{g}}_{2,1} \,\,\,.\,\,\,.\,\,\,.\,\,\,{\mathbf{g}}_{M,1} \,\,\,{\mathbf{g}}_{1,2} \,\,\,.\,\,\,.\,\,\,.\,\,\,{\mathbf{g}}_{M,N} } \right]\,\, = \left[ {\begin{array}{*{20}c} {g_{1,1}^{(1)} } & {g_{2,1}^{(1)} } & \cdots & {g_{M,1}^{(1)} } & {g_{1,2}^{(1)} } & \cdots & {g_{M,N}^{(1)} } \\ {g_{1,1}^{(2)} } & {g_{2,1}^{(2)} } & \cdots & {g_{M,1}^{(2)} } & {g_{1,2}^{(2)} } & \cdots & {g_{M,N}^{(2)} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {g_{1,1}^{(D)} } & {g_{2,1}^{(D)} } & \cdots & {g_{M,1}^{(D)} } & {g_{1,2}^{(D)} } & \cdots & {g_{M,N}^{(D)} } \\ \end{array} } \right]$$
(5)

The transmit matrix \({\mathbf{G}} \in {\mathbb{C}}^{D \times MN}\) consists of the transmit vectors \({\mathbf{g}}_{m,n} \in {\mathbb{C}}^{D \times 1}\) where the symbol D represents the total number of samples in time. In the above equation, M and N denote the number of subcarriers and the number of time-symbols, respectively. The transmit vector \({\mathbf{g}}_{m,n} \in {\mathbb{C}}^{D \times 1}\) represents the sampled version of the basis pulse that is obtained by shifting the prototype filter of the FBMC/OQAM scheme in time and frequency domains [14]. Namely, \({\mathbf{g}}_{m,n}\) is the discrete time representation of the basis pulse with D time-samples. On the other hand, it is possible to define the transmission symbols in the following form:

$${\mathbf{a}} = vec\left\{ {\left[ {\begin{array}{*{20}c} {a_{1,1} } & \cdots & {a_{1,N} } \\ \vdots & \ddots & \vdots \\ {a_{M,1} } & \cdots & {a_{M,N} } \\ \end{array} } \right]} \right\} = \left[ {a_{1,1} \,\,\,a_{2,1} \,\,\,.\,\,\,.\,\,\,.\,\,\,a_{M,1} \,\,\,a_{1,2} \,\,\,.\,\,\,.\,\,\,.\,\,\,a_{M,N} } \right]^{{\text{T}}}$$
(6)

where \({\mathbf{a}} \in {\mathbb{C}}^{MN \times 1}\). The transmission signal represented by \({\mathbf{s}} \in {\mathbb{C}}^{D \times 1}\) can then be written as follows:

$${\mathbf{s}} = {\mathbf{Ga}}$$
(7)

If the multipath channel is modeled by a time-variant convolution matrix \({\mathbf{H}} \in {\mathbb{C}}^{D \times D}\), the signal that has reached the receiver is expressed as:

$${\mathbf{r}} = {\mathbf{Hs}} + {\mathbf{n}} = {\mathbf{HGa}} + {\mathbf{n}}$$
(8)

where \({\mathbf{r}} \in {\mathbb{C}}^{D \times 1}\) denotes the signal at the receiver input and \({\mathbf{n}} \sim CN\left( {0,\,\,P_{n} \,{\mathbf{I}}_{D} } \right)\) represents the Gaussian noise in which the \(P_{n}\) and \({\mathbf{I}}_{D}\) correspond to the power of white Gaussian noise and D × D identity matrix, respectively. Finally, the formulation of the received symbols can be carried out in the following way:

$${\mathbf{y}} = {\mathbf{G}}^{{\text{H}}} {\mathbf{r}} = {\mathbf{G}}^{{\text{H}}} {\mathbf{HGa}} + {\mathbf{G}}^{{\text{H}}} {\mathbf{n}}$$
(9)

3.2 Block frequency spreading approach for FBMC/OQAM

The intrinsic interference caused by the constraint of orthogonality in FBMC/OQAM system prevents the straightforward implementation of MIMO methods, which can be easily applied to OFDM. On the other hand, it is possible to make the FBMC/OQAM system compatible with all MIMO methods used in OFDM by restoring its complex orthogonality with the help of block frequency spreading approach [14]. In this paper, in order to apply the MIMO detection methods to the MIMO-FBMC/OQAM, straightforwardly as in the classical MIMO-OFDM system, block frequency spreading approach was utilized in the FBMC/OQAM scheme in the following manner [14]:

At the transmitter side, the real valued symbols \({\mathbf{a}} \in {\mathbb{C}}^{MN \times 1}\) are acquired by spreading the QAM modulated data symbols \({\mathbf{x}} \in {\mathbb{C}}^{{\frac{MN}{2} \times 1}}\) via a precoding matrix \({\mathbf{C}} \in {\mathbb{C}}^{{MN \times \frac{MN}{2}}}\) as follows:

$${\mathbf{a}} = {\mathbf{Cx}}$$
(10)

At the receiver side, the de-spreading operation is carried out on the received symbols by multiplying them with \({\mathbf{C}}^{{\text{H}}}\) as expressed below:

$$\widetilde{{\mathbf{y}}} = {\mathbf{C}}^{{\text{H}}} {\mathbf{y}}$$
(11)

If the above equation is written in a more expanded form, the following expression is obtained:

$$\widetilde{{\mathbf{y}}} = {\mathbf{C}}^{{\text{H}}} {\mathbf{G}}^{{\text{H}}} {\mathbf{HGCx}} + {\mathbf{C}}^{{\text{H}}} {\mathbf{G}}^{{\text{H}}} {\mathbf{n}}$$
(12)

3.3 Formulation of symbol detection

In the FBMC/OQAM system based on block frequency spreading approach, the QAM modulated data symbols to be transmitted are defined by a matrix \({\mathbf{x}} \in {\mathbb{C}}^{{\frac{MN}{2} \times 1}}\), which has \(\frac{MN}{2}\) components. When it comes to MIMO transmission, each component symbolized by \(x_{m,n}\) becomes an Nt × 1 symbol vector as \(x_{m,n} = \left[ {x_{m,n}^{(1)} \,\,,\,\,x_{m,n}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,x_{m,n}^{{(N_{t} )}} } \right]^{{\text{T}}}\) where m and n are the subcarrier and symbol indices, respectively. Likewise, the received version of the \(x_{m,n}\) symbol vector at the receiver side can be defined as \(\widetilde{y}_{m,n} = \left[ {\widetilde{y}_{m,n}^{(1)} \,\,,\,\,\widetilde{y}_{m,n}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,\widetilde{y}_{m,n}^{{(N_{r} )}} } \right]^{{\text{T}}}\). As can be realized from the related vectors, while the number of transmitted symbols is equal to the number of transmit antennas, the number of received symbols is equal to the number of receive antennas. The task of ML-based symbol detection is to determine the symbol vector most likely to be transmitted by utilizing the received symbols. Let’s symbolize the QAM modulation order by Z. Since each symbol in the vector \(x_{m,n}\) can take Z different values (i.e., 4 different values for 4-QAM), the ML algorithm has to find the optimal symbol vector among \(Z^{{N_{t} }}\) alternatives, each of which has the possibility of being transmitted. To this end, each alternative is tested by the ML algorithm via the following equation:

$$x_{m,n}^{*} = \arg \,\,\,\mathop {\min }\limits_{{x_{m,n} }} \left\{ {\left\| {\widetilde{y}_{m,n} - H_{m,n} \cdot x_{m,n} } \right\|^{2} } \right\}$$
(13)

where \(H_{m,n}\) is the Nr × Nt channel coefficient matrix affecting the \(x_{m,n}\) symbol vector. In the equation above, the optimal symbol combination making the Euclidean distance in the parenthesis minimum is found by testing \(Z^{{N_{t} }}\) alternatives one by one. For this reason, the increase of modulation order Z and the number of transmit antennas Nt will result in an exponential growth in the computational complexity of ML algorithm. In order to achieve near-ML performance with considerably lower computational complexity, we have converted the symbol detection problem to a combinatorial optimization problem and utilized the newly developed disHS algorithm for optimizing the Nt—length QAM symbol vectors. By doing so, it has become possible to reach near-optimal solution iteratively without causing too much processing load.

In the formulation of ML symbol detection given in Eq. (13), it is assumed that the receiver has the knowledge of perfect channel coefficients \(H_{m,n}\). However, in practical systems, it is impossible to estimate the real channel coefficients without estimation errors. Therefore, we have modeled our MIMO-FBMC/OQAM system by taking into account the imperfect channel estimation. By doing so, the definition of ML detection becomes as follows:

$$x_{m,n}^{*} = \arg \,\,\,\mathop {\min }\limits_{{x_{m,n} }} \left\{ {\left\| {\widetilde{y}_{m,n} - \Psi_{m,n} \cdot x_{m,n} } \right\|^{2} } \right\}$$
(14)

In the equation above, the channel coefficients estimated imperfectly are represented by \(\Psi_{m,n}\) which can be expressed in the following way [37]:

$$\Psi_{m,n} = H_{m,n} + e \cdot \theta$$
(15)

where \(H_{m,n}\) corresponds to the actual channel coefficients and \(e \cdot \theta\) indicates the estimation error, in which \(\theta\) is the zero mean and unit variance complex Gaussian variable and e specifies the accuracy of channel estimation.

4 Methodology

4.1 Harmony search algorithm

Not long after its introduction to the science community by Zong Woo Geem and his friends in 2001 [18], harmony search (HS) algorithm has rapidly increased its popularity among the researchers due to its successful implementations in wide variety of optimization problems encountered in different fields. As can be realized from its name, HS algorithm was developed by imitating the procedure that the musicians comply with while searching for the perfect harmony. It is possible to idealize the related searching process carried out by the musicians to achieve the best harmony in the following way [18, 38,39,40]:

  1. (i)

    Any of the popular pitches is played from the memory.

  2. (ii)

    A new pitch is produced via the modification of any familiar pitch.

  3. (iii)

    A new pitch is generated in a completely random manner.

The equivalents of the above operations in the HS algorithm can be listed as follows:

  1. (i)

    Any value existing in the harmony memory (HM) is selected.

  2. (ii)

    A new value that is close to one of the existing ones in HM is produced.

  3. (iii)

    A new value is generated, randomly in a predefined range.

In the HS algorithm, while the implementation of the first operation depends on the value of harmony memory consideration rate (HMCR) parameter, the activation of the second operation is controlled by the parameter of pitch adjusting rate (PAR). The HMCR parameter cannot take any value out of the range [0, 1]. In order to effectively utilize the solutions existing in the HM, the value of HMCR should not be determined too close to the lower limit of the aforementioned range. Otherwise, it becomes impossible to take the advantage of good solutions that already exist in the HM. Similarly, choosing higher values close to the upper limit of the range [0, 1] for the HMCR parameter will not be the right approach either. Because, in case of determining the value of HMCR very close to 1, the algorithm will overuse the HM and the generated solutions will become quite similar to each other. Depending on this, the exploration capability of the HS algorithm will be affected, negatively. Hereby, it is crucial to determine a reasonable HMCR value for the optimal performance.

The operation of pitch adjustment, which is controlled by the parameter PAR, is performed by using the following equation:

$$x_{new} = x_{old} + bw \cdot \varepsilon$$
(16)

where \(x_{old}\) is an old solution existing in the HM while \(x_{new}\) is a new solution produced in the neighborhood of \(x_{old}\). In the equation above, bw denotes the bandwidth of the pitch and \(\varepsilon\) corresponds to a random number that takes the values in the range [− 1, 1].

The parameter PAR, which can take any value in the range [0, 1], determines whether or not the pitch adjustment operation will be carried out. How the HS algorithm operates can be explained in four steps as follows [18, 38,39,40]:

Step 1

A certain number of initial solutions are generated in a random way. These initial solutions named as harmonies in the HS algorithm are then assigned to a harmony memory, which can be expressed by n × D matrix in the following manner:

$${\mathbf{HM}} = \left[ {\begin{array}{*{20}c} {x_{1}^{(1)} } & {x_{1}^{(2)} } & \cdots & {x_{1}^{(D)} } \\ {x_{2}^{(1)} } & {x_{2}^{(2)} } & \cdots & {x_{2}^{(D)} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{n}^{(1)} } & {x_{n}^{(2)} } & \cdots & {x_{n}^{(D)} } \\ \end{array} } \right]$$
(17)

where n signifies the number of harmonies and D represents the dimension of each harmony in the HM matrix.

Step 2

  1. 2.1

    A random number represented by r1 is generated in the range [0, 1].

  2. 2.2

    if r1 ≤ HMCR.

  • One of the elements existing in the first column of the HM matrix is selected, randomly.

  • For the selected component, another random number symbolized by r2 is generated in the range [0, 1].

  • If r2 < PAR, pitch adjustment operation expressed in the Eq. (16) is applied to the selected element. By doing so, a new value adjacent to the related element is produced. The new value produced from the selected element is then assigned to the first dimension of the candidate solution represented by a 1 × D vector.

  • If r2 > PAR, pitch adjusting process is not put into practice and the selected component is directly assigned to the first dimension of the candidate solution vector.

  1. 2.3.

    if r1 > HMCR

  • Without considering the HM, a totally random value in a predefined range is generated to form the first dimension of the candidate solution vector.

Step 3

  1. 3.1

    The operations of Step 2 are reiterated for each of the remaining dimensions to complete the generation process of the candidate solution, which can be expressed as follows:

    $$candidate\,\,solution = \left[ {x_{i}^{(1)} \,\,,\,\,x_{i}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,x_{i}^{(D)} } \right]$$
    (18)
  2. 3.2

    Fitness calculation is carried out for the candidate solution by using the fitness function of the corresponding optimization problem to which the HS algorithm is applied. If the fitness value of the newly generated solution is better than that of the population member having the worst fitness quality in the HM matrix, the related worst member is replaced by the generated new solution. Otherwise, HM matrix is kept without any change for the next iteration.

  1. Step 4

    The operations carried out from Step 2 to Step 3 are repeated up to the moment that the stopping criterion is provided.

4.2 The proposed discrete harmony search (disHS) algorithm

The classical harmony search is one of the most powerful and commonly used population-based metaheuristic algorithms. However, it was originally developed for the continuous optimization problems. Since the optimization of QAM symbol vectors in the ML detector is a type of combinatorial optimization problem to be solved in discrete space, we have developed an exclusive and unique discrete version of the conventional HS algorithm called disHS in this paper. Thanks to this novel discretized HS variant, it has become possible to optimize the symbol vectors directly and efficiently in discrete space. The population members corresponding to harmonies to be optimized in the disHS algorithm are defined as follows:

$$h_{p}^{(d)} = \left[ {h_{p}^{(1)} \,\,,\,\,h_{p}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,h_{p}^{(D)} } \right]\,\,\,\,\,p = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,P$$
(19)

where \(h_{p}^{(d)} \in \left\{ {0,\,\,1} \right\}\), which means that each dimension of the solution vector can take the value of either 0 or 1. In the equation given above, P indicates the total number of harmonies existing in the harmony memory. The operations carried out step by step in the proposed disHS algorithm are given below:

  1. Step 1

    The initial population is constituted by generating P harmonies in a random way. These randomly generated first solutions, each of which corresponds to a harmony in the disHS algorithm, are then placed to the P × D HM matrix as follows:

    $${\mathbf{HM}} = \left[ {\begin{array}{*{20}c} {h_{1}^{(1)} } & {h_{1}^{(2)} } & \cdots & {h_{1}^{(D)} } \\ {h_{2}^{(1)} } & {h_{2}^{(2)} } & \cdots & {h_{2}^{(D)} } \\ \vdots & \vdots & \ddots & \vdots \\ {h_{P}^{(1)} } & {h_{P}^{(2)} } & \cdots & {h_{P}^{(D)} } \\ \end{array} } \right]$$
    (20)
  2. Step 2

    Fitness calculation is carried out for the initial population members. In order to save the fitness value of each harmony, an additional dimension is defined in the HM matrix. Apart from this, one more dimension is defined in the HM matrix to make each solution vector compatible with the process of cyclic bit flipping [41], which will be utilized to produce new adjacent solutions in the following step. In this extra dimension, the flipping index of each population member will be kept. So, the expanded version of the HM matrix can be expressed as follows:

    $${\mathbf{HM}} = \left[ {\begin{array}{*{20}c} {h_{1}^{(1)} } & {h_{1}^{(2)} } & \cdots & {h_{1}^{(D)} } & {fit\left( {h_{1}^{(d)} } \right)} & {\alpha_{1} } \\ {h_{2}^{(1)} } & {h_{2}^{(2)} } & \cdots & {h_{2}^{(D)} } & {fit\left( {h_{2}^{(d)} } \right)} & {\alpha_{2} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {h_{P}^{(1)} } & {h_{P}^{(2)} } & \cdots & {h_{P}^{(D)} } & {fit\left( {h_{P}^{(d)} } \right)} & {\alpha_{P} } \\ \end{array} } \right]\,\,\,\,\,,\,\,\,\,\,\begin{array}{*{20}c} {d = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,D} \\ {p = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,P} \\ \end{array}$$
    (21)

where \(\alpha_{P}\) symbolizes the flipping index of the Pth population member. The flipping index \(\alpha\) defined at the last dimensions of the solution vectors existing in the HM matrix is the key parameter of the cyclic bit flipping procedure used for generating new solutions in the proposed disHS algorithm. This parameter is used to determine which dimension of the solution vector, that is selected randomly from the HM matrix to generate a new solution, will be flipped by the flipping operator given in the Eq. (23).

Step 3

  1. 3.1

    The first random number denoted by \(r_{1} \in \left[ {0,\,\,1} \right]\) is generated.

  2. 3.2

    if r1 ≤ HMCR

  • One of the existing solutions is selected from the HM matrix in a random way. The randomly selected solution is defined as follows:

    $$S_{r}^{(d)} = \left[ {h_{r}^{(1)} \,\,,\,\,h_{r}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,h_{r}^{(D)} \,\,,\,\,fit\left( {h_{r}^{(d)} } \right)\,\,,\,\,\alpha_{r} } \right]\,\,\,\,\,,\,\,\,\,\,d = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,D$$
    (22)

    where r is a random integer generated in the range [1, P].

  • One adjacent solution is produced from \(S_{r}^{(d)}\) by utilizing the cyclic bit flipping procedure [41]. To this end, in the first instance, the following bit flipping operation is applied to the selected solution:

    $$S_{r}^{(d),new} = flip\left( {S_{r}^{(d)} } \right)_{{\alpha_{r} }}$$
    (23)

where the αrth component of the vector \(S_{r}^{(d)}\) is flipped from 1 to 0 or vice versa. Note that the elements of \(h_{r}^{(d)}\) in the vector \(S_{r}^{(d)}\) consist of ones and zeros, and the initial flipping index values are assigned as \(\alpha_{p} = \left[ {\alpha_{1} \,\,,\,\,\alpha_{2} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,\alpha_{P} } \right] = \left[ {1\,\,,\,\,1\,\,,\,\,.\,\,.\,\,.\,\,,\,\,1} \right]\). Therefore, the first value of αr, which corresponds to the flipping index of the randomly selected solution vector existing in the P × D HM matrix, will be equal to 1 as well.

Right after the operation of bit flipping, the value of αr is updated as follows:

$$\alpha_{r} = \alpha_{r} + 1$$
(24)

By doing so, it is provided that the flipping operation continues from the next bit in the case that the new solution is selected again for the generation of neighbor solution in the following iterations. For instance, let’s assume that the fifth population member represented by \(S_{5}^{(d)}\) is chosen from the HM matrix for the flipping operation in a random way and its current flipping index value is equal to 10 (\(\alpha_{5} = 10\)). In the flipping operation carried out by the Eq. (23), 10th element of the related vector would be flipped from 1 to 0 or vice versa. After that, the current flipping index of the related solution vector would be made equal to 11 via the Eq. (24) to keep going the flipping operation from the next element in the case that the related vector is selected again in the upcoming iterations.

In order to make certain that the flipping operation moves in a cyclic manner, the following operation is needed on the flipping index parameter subsequent to its increment by one:

$$\alpha_{r} = \bmod \left( {\alpha_{r} - 1\,,\,\,D} \right) + 1$$
(25)

where the value of αr is controlled by the modulo operation. Each time the αr exceeds the value of D, its value is returned back to 1. For example, when the value of αr becomes equal to D + 1, the Eq. (25) becomes as \(\alpha_{r} = \bmod \left( {D\,,\,\,D} \right) + 1\). In this case, since mod (D, D), which gives the remainder of dividing D by D, is equal to 0, the value of αr returns back to its initial value, which was determined as 1. In this way, as the iterations progress, the bit flipping operation is carried on, cyclically. Equations (24) and (25) are the two indispensable parts of the proposed disHS algorithm. It is impossible to integrate the cyclic bit flipping procedure to the disHS algorithm without these two equations. For example, in the absence of Eq. (24), the bit flipping operation would be performed on just the first dimension at each time since the initial flipping index values of the population members are appointed as \(\alpha_{p} = \left[ {\alpha_{1} \,\,,\,\,\alpha_{2} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,\alpha_{P} } \right] = \left[ {1\,\,,\,\,1\,\,,\,\,.\,\,.\,\,.\,\,,\,\,1} \right]\). In this case, the other dimensions of the solution vectors would remain unchanged throughout the optimization process and in consequence of this, there would be no improvement in the solution vectors. Similarly, if the Eq. (25) was not used in the disHS algorithm, the flipping index \(\alpha_{r}\), which is increased by 1 via the Eq. (24) subsequent to each flipping operation, could not be prevented from exceeding D and as a result of this, the bit flipping process could not be kept moving in cyclic fashion from the beginning to the end of the optimization process.

The reason of using cyclic bit flipping procedure for the generation of new solutions in the proposed disHS algorithm is to carry out a more systematic and efficient search in discrete space. Thanks to the integration of cyclic bit flipping procedure to the disHS algorithm, the possibility of leaving an unvisited position around the neighborhood of the existing solution vectors is minimized.

  • Fitness value of the new solution is calculated.

  • If the fitness of \(S_{r}^{(d),new}\) is better than that of the population member having the worst fitness quality in the HM matrix, \(S_{r}^{(d),new}\) is replaced by the related worst population member. Otherwise, no changes are made to the HM matrix.

3.3 if r1 > HMCR

The best solution is selected from the HM matrix. The related best solution having the best fitness value is defined as follows:

$$S_{best}^{(d)} = \left[ {h_{best}^{(1)} \,\,,\,\,h_{best}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,h_{best}^{(D)} \,\,,\,\,fit\left( {h_{best}^{(d)} } \right)\,\,,\,\,\alpha_{best} } \right]$$
(26)

The selected best solution is then subjected to the mutation operation in the following way: For each dimension of \(S_{best}^{(d)}\) in the range 1 ≤ d ≤ D, a random number \(r_{2} \in \left[ {0,\,\,1} \right]\) is generated. If r2 ≤ PAR, the related dimension is changed from 1 to 0 or vice versa. If r2 > PAR, the related dimension is not changed. The mutated version of the \(S_{best}^{(d)}\) solution can be expressed as follows:

$$S_{{{\text{mutant}}}}^{(d)} = \left[ {h_{{{\text{mutant}}}}^{(1)} \,\,,\,\,h_{{{\text{mutant}}}}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,h_{{{\text{mutant}}}}^{(D)} \,\,,\,\,fit\left( {h_{{{\text{mutant}}}}^{(d)} } \right)\,\,,\,\,\alpha_{{{\text{mutant}}}} } \right]$$
(27)

where αmutant is initialized from the value of 1.

After the implementation of mutation operation, while the best solution \(S_{best}^{(d)}\) is kept without any change, its mutated version represented by \(S_{{{\text{mutant}}}}^{(d)}\) replaces the worst solution in the HM matrix.

Step 4 The operations of Step 3 are repeated until the termination criterion is provided.

Step 5 The population member having the best fitness quality is selected as the optimal solution.

The pseudocode of the proposed disHS algorithm is given in Fig. 1.

Fig. 1
figure 1

The pseudocode of disHS algorithm

Full size image

4.3 Discrete harmony search-based ML strategy

As it is clear from the Sect. 4.2, the proposed disHS algorithm was designed for the combinatorial optimization problems that can be solved in binary search space. However, the QAM symbol vectors to be optimized in symbol detection problem consist of complex valued QAM symbol sequences, which is defined by \(x_{m,n} = \left[ {x_{m,n}^{(1)} \,\,,\,\,x_{m,n}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,x_{m,n}^{{(N_{t} )}} } \right]^{{\text{T}}}\) in Sect. 3.3. On the other hand, it is possible to convert the related complex valued symbol vectors to binary bit sequences. In the QAM modulation technique, each QAM symbol carries a certain bit sequence, the length of which is determined by the modulation order symbolized by Z. For example, since the number of bits per QAM symbol is calculated by \(\log_{2}^{Z} = k\), the number of bits carried by each symbol in 4-QAM modulation will be equal to \(\log_{2}^{4} = 2\). So, it is possible to represent each complex valued QAM symbol by its corresponding binary number. By doing so, the QAM symbol vectors can be transformed from the sequences of complex numbers to binary bit sequences. Therefore, the optimization process can be performed directly in binary search space by using the proposed disHS algorithm. In the disHS-based ML strategy called disHS-ML in this paper, the complex valued symbol vectors and their binary equivalents to be optimized are expressed as harmony vectors in the Eqs. (28) and (29), respectively:

$$x_{p}^{(i)} = \left[ {x_{p}^{(1)} \,\,,\,\,x_{p}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,x_{p}^{{(N_{t} )}} } \right]\,\,\,\,\,,\,\,\,\,\,p = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,P$$
(28)
$$b_{p}^{(j)} = \left[ {b_{p}^{(1)} \,\,,\,\,b_{p}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,b_{p}^{{(k \cdot N_{t} )}} } \right]\,\,\,\,\,,\,\,\,\,\,p = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,P$$
(29)

Since each symbol in the \(x_{p}^{(i)}\) vector carries k bits, the length of its binary equivalent given in Eq. (29) is equal to k ∙ Nt. Step by step explanation of applying the disHS algorithm to the ML detector for the optimization of QAM symbol vectors is given below:

Step 1 In the first place, random initial symbol vectors are generated directly in binary search space as expressed in the Eq. (29). Subsequently, P initial binary solutions with the length of k ∙ Nt are placed to the P × (k ∙ Nt) sized HM matrix as follows:

$${\mathbf{HM}} = \left[ {\begin{array}{*{20}c} {b_{1}^{(1)} } & {b_{1}^{(2)} } & \cdots & {b_{1}^{{(k \cdot N_{t} )}} } \\ {b_{2}^{(1)} } & {b_{2}^{(2)} } & \cdots & {b_{2}^{{(k \cdot N_{t} )}} } \\ \vdots & \vdots & \ddots & \vdots \\ {b_{P}^{(1)} } & {b_{P}^{(2)} } & \cdots & {b_{P}^{{(k \cdot N_{t} )}} } \\ \end{array} } \right]$$
(30)

Step 2 Two more dimensions are defined in the HM matrix to keep the fitness values and flipping indices of the population members, respectively as shown below:

$${\mathbf{HM}} = \left[ {\begin{array}{*{20}c} {b_{1}^{(1)} } & {b_{1}^{(2)} } & \cdots & {b_{1}^{{(k \cdot N_{t} )}} } & {f_{1} } & {\alpha_{1} } \\ {b_{2}^{(1)} } & {b_{2}^{(2)} } & \cdots & {b_{2}^{{(k \cdot N_{t} )}} } & {f_{2} } & {\alpha_{2} } \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {b_{P}^{(1)} } & {b_{P}^{(2)} } & \cdots & {b_{P}^{{(k \cdot N_{t} )}} } & {f_{P} } & {\alpha_{P} } \\ \end{array} } \right]$$
(31)

Later on, the fitness evaluation is carried out for the initial population members. Prior to each fitness calculation, the related binary bit sequence is converted to its equivalent complex valued sequence of QAM symbols to be used as an input parameter in the following fitness function:

$$f_{p} = fit\left( {x_{p}^{(i)} } \right) = \left\| {\widetilde{y}_{m,n} - \Psi_{m,n} \cdot x_{p}^{(i)} } \right\|^{2} \,\,\,\,\,,\,\,\,\,\,p = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,P\,\,;\,\,\,\,\,i = 1\,\,,\,\,2\,\,,\,\,.\,\,.\,\,.\,\,,\,\,N_{t}$$
(32)

where \(x_{p}^{(i)}\) is the complex valued equivalent of \(b_{p}^{(j)}\). As the last operation of Step 2, the flipping index of each solution is given the value of 1.

Step 3

3.1 A random number \(r_{1} \in \left[ {0,\,\,1} \right]\) is generated.

3.2 if r1 ≤ HMCR

One of the solution vectors, each of which corresponds to a single row in the HM matrix, is chosen in a random way. The randomly selected solution vector existing in the rth row of the HM matrix is expressed as follows:

$$S_{r}^{(j)} = \left[ {b_{r}^{(1)} \,\,,\,\,b_{r}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,b_{r}^{{(k \cdot N_{t} )}} \,\,,\,\,f_{r} \,\,,\,\,\alpha_{r} } \right]$$
(33)

Bit flipping operation is carried out on \(S_{r}^{(j)}\) to produce a neighbor solution via the following operator:

$$S_{r}^{(j),new} = flip\left( {S_{r}^{(j)} } \right)_{{\alpha_{r} }}$$
(34)

Subsequently, the following operations are performed to keep the operation of bit flipping running, cyclically:

$$\alpha_{r} = \alpha_{r} + 1$$
(35)
$$\alpha_{r} = \bmod \left( {\alpha_{r} - 1\,,\,\,k \cdot N_{t} } \right) + 1$$
(36)

The fitness quality of the new solution \(S_{r}^{(j),new}\) is evaluated. To this end, the binary bit sequence existing in the vector of \(S_{r}^{(j),new}\) is converted from \(b_{r}^{(j)} = \left[ {b_{r}^{(1)} \,\,,\,\,b_{r}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,b_{r}^{{(k \cdot N_{t} )}} } \right]\) to its equivalent complex QAM symbol sequence expressed as \(x_{r}^{(i)} = \left[ {x_{r}^{(1)} \,\,,\,\,x_{r}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,x_{r}^{{(N_{t} )}} } \right]\). The fitness value of \(S_{r}^{(j),new}\) is then calculated by using the resulted QAM symbol vector \(x_{r}^{(i)}\) in the fitness function as follows:

$$f_{r} = fit\left( {x_{r}^{(i)} } \right) = \left\| {\widetilde{y}_{m,n} - \Psi_{m,n} \cdot x_{r}^{(i)} } \right\|^{2}$$
(37)

In the case that the new solution \(S_{r}^{(j),new}\) has a better fitness quality compared to the worst population member existing in the HM matrix, \(S_{r}^{(j),new}\) is located in place of the related worst member. Otherwise, the HM matrix is left unaltered.

3.3. if r1 > HMCR

The solution having the best fitness quality in the HM matrix is selected and then subjected to the mutation operation. The probability of mutating any dimension of the binary bit sequence belonging to the selected best solution is determined by the parameter PAR as explained elaborately in Sect. 4.2. The related best solution and its mutated version can be expressed in the following way:

$$S_{best}^{(j)} = \left[ {b_{best}^{(1)} \,\,,\,\,b_{best}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,b_{best}^{{(k \cdot N_{t} )}} \,\,,\,\,f_{best} \,\,,\,\,\alpha_{best} } \right]$$
(38)
$$S_{{{\text{mutant}}}}^{(j)} = \left[ {b_{{{\text{mutant}}}}^{(1)} \,\,,\,\,b_{{{\text{mutant}}}}^{(2)} \,\,,\,\,.\,\,.\,\,.\,\,,\,\,b_{{{\text{mutant}}}}^{{(k \cdot N_{t} )}} \,\,,\,\,f_{{{\text{mutant}}}} \,\,,\,\,\alpha_{{{\text{mutant}}}} } \right]$$
(39)

Note that the initial value of \(\alpha_{{{\text{mutant}}}}\) is made equal to 1.

\(S_{{{\text{mutant}}}}^{(j)}\) produced from the \(S_{best}^{(j)}\) takes the place of worst solution in the HM matrix while \(S_{best}^{(j)}\) is preserved without any change for the next iterations.

Step 4 The operations carried out in the Step 3 are reiterated up to the stopping criterion is met.

Step 5 The binary bit sequence belonging to the population member that has the best fitness quality in the HM matrix is selected as the optimal bit sequence and then converted to its equivalent QAM symbol vector to fulfill the symbol detection process.

The flow diagram of the disHS-based ML strategy is given in Fig. 2.

Fig. 2
figure 2

Flow diagram of the disHS-ML strategy

Full size image

5 Results and analysis

In this section, the performance evaluation of the proposed disHS-ML symbol detector was carried out by comparing its BER achievements with those of the other symbol detectors considered in this paper for 4 × 4, 6 × 6 and 8 × 8 MIMO structures in the FBMC/OQAM system. In addition to the BER comparisons, convergence analyses of the newly developed disHS and the other considered optimization algorithms integrated to the ML symbol detector were made for each of the relevant antenna structures. Furthermore, the considered symbol detectors were extensively analyzed with regard to their complexities. For the aforementioned experimental analyses and system design, MATLAB 2018a simulation tool was used in this study. In the simulations, “Cost 207 Hilly Terrain” channel model with [0, − 2, − 4, − 7, − 6, − 12] dB power paths and [200, 400, 600, 15,000, 17200] ns relative delays was used. The reason for choosing one of the most challenging standard channel models called “Cost 207 Hilly Terrain” for the simulations is to make the performance comparisons of the considered symbol detectors in a more realistic environment. The other parameters determined for the MIMO-FBMC/OQAM system is given in Table 1.

Table 1 MIMO-FBMC/OQAM system parameters
Full size table

5.1 Search complexity analysis

In Table 2, the search complexities of both the conventional ML strategy and its intelligent optimization-based improved variants were obtained for 4 × 4, 6 × 6 and 8 × 8 antenna configurations, respectively. Overall computational complexities of the ML-based symbol detectors are directly determined by their search complexities. In other words, the search complexity is the main factor that makes the difference between the computational complexities of the aforementioned symbol detectors, each of which will also be obtained in Sect. 5.3. So, it is crucial to define the search complexities before making the computational complexity analysis. The search complexity of any ML-based strategy is defined by considering the number of Euclidean distance calculations performed throughout the search for the optimal QAM symbol vector. Note that the calculation of Euclidean distance between the received signal and the candidate QAM symbol vector multiplied by the channel coefficients is carried out via the expression in the parenthesis of arg min { ∙} operator given in the Eq. (13).

Table 2 Search complexities of the considered symbol detectors based on ML strategy
Full size table

In the classical ML technique, for the purpose of finding the optimal QAM symbol sequence, which provides the minimum Euclidean distance with the received signal, one Euclidean calculation is made for each symbol combination. According to this, the number of Euclidean calculations carried out during the symbol detection process in the ML technique will be directly equal to the number of possible QAM symbol combinations, which can be determined by the expression of \(Z^{{N_{t} }}\). Hereby, the search complexity of ML strategy can be expressed as \(SC = Z^{{N_{t} }}\), where Z is the modulation order and Nt is the number of transmit antennas.

In the improved ML strategies based on the metaheuristic optimization algorithms, the search complexity will be directly equal to the total number of fitness calculations, in which the QAM symbol vectors to be optimized are evaluated in point of their Euclidean distances to the received signal. Since all of the population members are subjected to the fitness evaluation process at each iteration or cycle of BPSO-ML and disABC-ML techniques, the number of population members is multiplied by the maximum number of iterations or cycles to determine the total number of fitness calculations and accordingly the search complexities of the related techniques as shown in the Table 2. On the other hand, in both the DBHS-ML and disHS-ML strategies, regardless of the harmony number or population size, one fitness evaluation is carried out for each search or iteration. For this reason, the total number of fitness calculations, which corresponds to the search complexity, will be directly equal to the maximum number of searches or iterations in the related strategies.

Since the growing number of antennas leads to an enhancement in the search space, which corresponds to the number of possible QAM symbol combinations calculated by \(Z^{{N_{t} }}\), higher number of searches and population members are needed for larger antenna configurations as demonstrated in Table 2. For example, for 4 × 4, 6 × 6 and 8 × 8 antenna configurations, while the population sizes of the proposed disHS-ML strategy were selected as 20, 25 and 30, those of the other considered strategies were determined as 20, 30 and 40, respectively. Likewise, while the search complexities of disHS-ML strategy were adjusted to 160, 400 and 900 for the related antenna configurations, those of the other benchmark techniques were equalized to the values of 200, 750 and 1800. As it is clear from the Table 2, the proposed disHS-ML symbol detector outperforms the other intelligent optimization-based symbol detectors by reaching lower bit error rate for each antenna configuration with much less search complexity and population size. Note that 160, 400 and 900 are the numbers of fitness evaluations determined for 4 × 4, 6 × 6 and 8 × 8 antenna configurations by considering the trade-off between the search complexity and BER performance of the proposed disHS-ML strategy. In order to reveal the power of disHS-ML technique, the search complexities of the other benchmark methods were set to much higher values in their favor. In spite of being put in a disadvantageous position by giving its opponents more research opportunity, the proposed symbol detector clearly leaves them behind by reaching much better solutions in less number of searches. The other parameter values belonging to the intelligent optimization-based ML detectors are given in Table 3.

Table 3 Simulation parameters of the metaheuristic-based ML detectors
Full size table

5.2 Convergence and BER analysis

In Fig. 3, the convergence analysis of the considered symbol detectors based on metaheuristic algorithms was carried out for 4 × 4 MIMO-FBMC/OQAM system at 12 dB SNR value. The related convergence curves were obtained as follows: Each of the metaheuristic-based symbol detectors was operated for 10 times at each fitness evaluation. By doing so, 10 different BER values were acquired for each fitness evaluation. These BER values were then averaged to achieve the related convergence curves given in Fig. 3. The line given at the bottom of the convergence curves shows the lowest BER level reached by the ML symbol detector by performing an exhaustive search. Since the ML detector always reaches the best solution by trying all of the possible symbol combinations, the BER level achieved by the ML is considered as the best BER level to be reached by a symbol detector. So, for any intelligent optimization-based symbol detector, the goal should be to converge this level by performing as little fitness calculation as possible. As can be clearly seen from the Fig. 3, the proposed disHS-ML symbol detector converges very quickly to the optimal solution, while the other ones can’t even get close after 200 fitness evaluations. For instance, 0.06047, 0.04792 and 0.03237 BER values that BPSO-ML, disABC-ML and DBHS-ML reach after 200 fitness evaluations can be achieved by the proposed disHS-ML strategy with only 79, 90 and 112 fitness evaluations, respectively. As mentioned before, the number of fitness evaluations should be determined by considering the trade-off between the BER performance and search complexity. As can be seen from the Fig. 3, the convergence behavior of the proposed disHS-ML strategy is almost completed at 160 fitness evaluations. For this reason, taking into account the aforementioned trade-off, the search complexity of disHS-ML was set to the value of 160 while those of the other techniques considered for comparison were equalized to 200 for 4 × 4 MIMO configuration as stated in Table 2.

Fig. 3
figure 3

Convergence analysis of the symbol detectors based on heuristic approaches for 4 × 4 MIMO-FBMC/OQAM system

Full size image

In Fig. 4, the BER performance of the proposed disHS-ML symbol detector was compared with not only the classical symbol detectors like ZF and ML, but also the improved ML variants based on intelligent optimization algorithms such as BPSO, disABC and DBHS. The related performance comparison was carried out in the 4 × 4 MIMO-FBMC/OQAM system. As it is evident in the Fig. 4, while the ZF technique falls far behind the other strategies in terms of BER performance, the ML scheme becomes the best performing symbol detection strategy as expected due to its exhaustive search procedure, which causes an excessive increase in the system complexity. When it comes to the improved ML strategies based on metaheuristic algorithms, the proposed disHS-ML detector shows near-ML performance by clearly leaving behind the other ones. Over and above, the disHS-ML shows the aforementioned superior performance by carrying out considerably lower number of fitness calculations compared to the other metaheuristic-based ML symbol detectors. For instance, if 10 dB SNR value is taken as a reference point, the BER values reached by the ZF, BPSO-ML, disABC-ML, DBHS-ML, disHS-ML and the conventional ML symbol detectors are equal to 1.43 × 10−1, 6.77 × 10−2, 5.48 × 10−2, 4.11 × 10−2, 3.23 × 10−2 and 2.82 × 10−2, respectively. As can be realized from these values, the proposed disHS-ML strategy gets very close to the optimal result, which is achieved by the ML detector, by making 0.88 × 10−2 BER difference to its closest competitor named DBHS-ML.

Fig. 4
figure 4

BER performance of the symbol detectors for 4 × 4 MIMO-FBMC/OQAM system

Full size image

In Fig. 5, the convergence curves of the intelligent optimization-based ML strategies were obtained for 6 × 6 MIMO configuration of the FBMC/OQAM system at 12 dB SNR value. With the increase in the MIMO configuration from 4 × 4 to 6 × 6, each strategy needs more fitness evaluations to converge the optimal solution as can be noticed by comparing the Figs. 3 and 5 due to the fact that the search space becomes larger with the related increment in the antenna configuration. As it is evident in the Fig. 5, the convergence performance of the proposed disHS-ML strategy is significantly better than those of the other benchmark strategies. It is capable of reaching a better BER level by performing lower fitness calculations compared to the other three symbol detectors based on heuristic approaches. From a different point of view, it is possible through the disHS-ML strategy to reach the same BER level with the other considered symbol detectors by carrying out much smaller number of fitness evaluations. For instance, BPSO-ML, disABC-ML and DBHS-ML need 750 fitness evaluations to reach 0.05013, 0.02831 and 0.01701 BER levels while 213, 261 and 314 fitness evaluations are sufficient for the disHS-ML to reach the aforementioned BER values, respectively. For an efficient symbol detection performance with considerably low search complexity, the number of fitness evaluations was determined as 400 for the disHS-ML strategy since its convergence is almost completed at the related point.

Fig. 5
figure 5

Convergence analysis of the symbol detectors based on heuristic approaches for 6 × 6 MIMO-FBMC/OQAM system

Full size image

In Fig. 6, the considered symbol detectors were compared with regard to their BER performance in the 6 × 6 MIMO-FBMC/OQAM system. In case of comparing the Fig. 6 with the Fig. 4, it will be seen that the BER performance of each technique improves with the expansion of antenna configuration from 4 × 4 to 6 × 6 except the ZF which is a type of linear symbol detector that is affected negatively by the increase in the number of antennas. As in the 4 × 4 MIMO-FBMC/OQAM system, the proposed disHS-ML symbol detector takes the lead among the metaheuristic-based ML strategies by showing the closest BER performance to that of the ML symbol detector. For instance, while the BER of the ML detector at 10 dB SNR is equal to 1.68 × 10−2, those of the disHS-ML, DBHS-ML, disABC-ML and BPSO-ML are equal to 1.96 × 10−2, 2.33 × 10−2, 3.24 × 10−2 and 4.98 × 10−2, respectively for the same SNR value.

Fig. 6
figure 6

BER performance of the symbol detectors for 6 × 6 MIMO-FBMC/OQAM system

Full size image

In Fig. 7, the convergence performance of the considered strategies were compared for 8 × 8 antenna structure at 12 dB SNR value. As can be understood from the convergence curves, disHS-ML symbol detector converges to the near-optimal solution approximately at 900 number of fitness evaluations. For this reason, the search complexity of the proposed scheme was set to 900. On the other hand, even 1800 fitness evaluations are not enough for the other three benchmark strategies to approach the BER result that is achieved by the proposed disHS-ML symbol detector with just 900 fitness evaluations. At the same time, substantially less number of fitness evaluations will be sufficient for the disHS-ML strategy to reach the BER values obtained by the other considered methods at the end of 1800 fitness evaluations. For instance, in order for the BPSO-ML, disABC-ML and DBHS-ML to reach 0.04900, 0.02347 and 0.01579 BER levels, 1800 number of fitness evaluations are required while the same BER levels can be achieved by the proposed scheme with 396, 506 and 574 fitness evaluations, respectively.

Fig. 7
figure 7

Convergence analysis of the symbol detectors based on heuristic approaches for 8 × 8 MIMO-FBMC/OQAM system

Full size image

In Fig. 8, the BER achievements of the considered symbol detectors in 8 × 8 MIMO-FBMC/OQAM system were compared. Since the antenna configuration used in this SNR (dB)-BER analysis is the largest one, the BER values achieved for each SNR value by the ML-based symbol detectors in the Fig. 8 are the lowest ones due to the fact that the increase of antenna configuration leads to the alleviation of channel fading effects and accordingly the improvement of BER performance in these symbol detectors excluding the ZF detector whose performance degrades with the enlargement of antenna structure as mentioned before. The expansion of search space by increasing the number of antennas doesn’t prevent the proposed disHS-ML strategy from leaving behind the other metaheuristic-based symbol detectors considered in this paper in point of BER performance. For instance, while the classical ML needs 8.05 dB SNR to reach 2 × 10−2  BER value, its three closest competitors disHS-ML, DBHS-ML and disABC-ML need 8.53, 9.83 and 11.74 dB SNRs to reach the same BER level. As can be inferred from these results, the proposed disHS-ML strategy provides 1.30 and 3.21 dB SNR gains over the DBHS-ML and disABC-ML symbol detectors by needing only 0.48 dB more SNR value compared to the ML detector, which has an extremely high complexity to be used in any system.

Fig. 8
figure 8

BER performance of the symbol detectors for 8 × 8 MIMO-FBMC/OQAM system

Full size image

In Fig. 9, in order to test the robustness and consistency of the proposed disHS-ML strategy, its BER performance was compared with the other considered intelligent optimization-based ML detectors in more severe conditions. To this end, the estimation error symbolized by e was increased from 25 to 40%. As can be realized from the Fig. 9, 15% enhancement in the estimation error doesn’t prevent the disHS-ML from outperforming the other advanced symbol detectors based on metaheuristic algorithms. While the increase of e from 25 to 40% causes a certain performance loss in each symbol detector, the proposed disHS-ML strategy maintains its performance superiority by making a significant difference to each of the benchmark strategies even in 40% channel frequency response mismatch. For instance, when the conditions are made more severe by increasing the value of e to 40%, the BER values of the BPSO-ML, disABC-ML, DBHS-ML and disHS-ML at 12 dB SNR become equal to 5.67 × 10−2, 2.76 × 10−2, 2.28 × 10−2 and 1.57 × 10−2, respectively.

Fig. 9
figure 9

BER performance of the metaheuristic-based ML detectors for two different e values in 8 × 8 MIMO-FBMC/OQAM system

Full size image

5.3 Computational complexity analysis

In this section, the computational complexities of the considered symbol detectors were obtained in terms of the number of complex multiplications [23]. After that, the complexity gains achieved by the proposed disHS-ML scheme over the conventional ML and the other considered metaheuristic-based ML strategies were calculated. Note that ZF symbol detector has the least computational complexity among the existing symbol detection methods. However, it is the most primitive method having the poorest symbol detection performance as well.

In the ZF symbol detector, \(4N_{t}^{3} + 2N_{t}^{2} N_{r}\) multiplications are required due to the calculation of pseudo-inverse matrix [23]. For this reason, the computational complexity of ZF detector can be expressed as follows:

$$C_{ZF} = 4N_{t}^{3} + 2N_{t}^{2} N_{r}$$
(40)

In the ML symbol detector, while the matrix multiplications lead to \(Z^{{N_{t} }} \cdot \left( {N_{r} \cdot N_{t} } \right)\) multiplications, the square operations cause \(Z^{{N_{t} }} \cdot N_{r}\) additional multiplications. Hereby, the total number of multiplications needed by the ML symbol detector will give its eventual computational complexity as follows:

$$C_{ML} = Z^{{N_{t} }} \cdot \left( {N_{r} \cdot N_{t} } \right) + Z^{{N_{t} }} \cdot N_{r} = Z^{{N_{t} }} \cdot \left( {1 + N_{t} } \right) \cdot N_{r}$$
(41)

where \(Z^{{N_{t} }}\) is the search complexity of ML, which was given in Table 2. The Eq. (41) can also be expressed as follows:

$$C_{ML} = SC \cdot \left( {1 + N_{t} } \right) \cdot N_{r}$$
(42)

where SC represents the search complexity of ML, which is equal to \(Z^{{N_{t} }}\). When it comes to the metaheuristic algorithm-based ML symbol detectors, the number of multiplications required for each fitness evaluation becomes equal to \(\left( {N_{t} \cdot N_{r} + \mu } \right)\), where μ corresponds to the additional multiplications required per fitness evaluation due to the parameter updating operations in the metaheuristic algorithms. It is known from the Table 2 that the search complexity of any metaheuristic-based strategy is actually equal to the number of fitness evaluations performed throughout the optimization process of the metaheuristic algorithm employed in the related strategy. For this reason, the multiplication of \(\left( {N_{t} \cdot N_{r} + \mu } \right)\) by the search complexity SC will give the total number of multiplications needed by the metaheuristic-based ML strategies throughout the symbol detection process. Herewith, the computational complexities of the symbol detectors based on metaheuristic algorithms can be determined by using the following expression:

$$C_{Heuristics} = SC \cdot \left( {N_{t} \cdot N_{r} + \mu } \right)$$
(43)

After writing the search complexities of the metaheuristic-based symbol detectors in place of the parameter SC in the Eq. (43), the computational complexities of the related detectors are obtained as follows:

$$C_{BPSO - ML} = NP \cdot MaxIter \cdot \left( {N_{t} \cdot N_{r} + \mu } \right)$$
(44)
$$C_{disABC - ML} = CS \cdot MaxCycle \cdot \left( {N_{t} \cdot N_{r} + \mu } \right)$$
(45)
$$C_{DBHS - ML} = MaxSearch \cdot \left( {N_{t} \cdot N_{r} + \mu } \right)$$
(46)
$$C_{disHS - ML} = MNI \cdot \left( {N_{t} \cdot N_{r} + \mu } \right)$$
(47)

In Fig. 10, the effect of antenna increment on the computational complexity of the proposed disHS-ML strategy for various MNI values was tested and compared with those of the ML and ZF detectors, respectively. As can be clearly seen from the Fig. 10, while the increase in the number of antennas leads to a relatively small increment in the computational complexity of the proposed strategy for each MNI value, the same cannot be said for the ML detector. As can be easily understood from the steepness of its complexity curve, a slightest increase in the number of antennas results in a huge enhancement in the computational complexity of ML symbol detector. ZF has been the least affected symbol detector by the related antenna increase as expected. However, even though the ZF is the method with the least computational complexity, having the poor symbol detection performance prevents it from being employed in any system.

Fig. 10
figure 10

The number of antennas versus computational complexity curves of the considered symbol detectors

Full size image

The complexity gains achieved by the disHS-ML strategy over the other considered methods can be computed by using the following equation:

$$Complexity\,\,Gain\,\,\left( \% \right) = \frac{{C_{x} - C_{disHS - ML} }}{{C_{x} }} \times 100$$
(48)

where \(C_{x}\) symbolizes the computational complexity of the corresponding method.

In Table 4, after obtaining the numerical values of the computational complexities for both the classical ML and disHS-ML symbol detectors by using their complexity expressions given in the Eqs. (41) and (47), respectively, the complexity gains achieved by the proposed strategy over the ML detector were calculated for 4 × 4, 6 × 6 and 8 × 8 antenna configurations. As it is evident from the Table 4, each increase of antenna configuration leads to an excessive enhancement in the computational complexity of classical ML detector. On the other hand, the related increments in the number of antennas cause significantly smaller enhancements in the complexity of the proposed disHS-ML strategy compared to the conventional ML detector. For this reason, the complexity gains achieved by the disHS-ML over the classical ML become greater with the increase of antenna configuration. For instance, while at least 43% complexity gain is achieved for 4 × 4 MIMO-FBMC/OQAM system, the related complexity gain reaches to more than 98% in case of increasing the antenna structure from 4 × 4 to 8 × 8.

Table 4 The complexity gains provided by the disHS-ML strategy over the ML symbol detector for varied antenna structures
Full size table

It is possible to analyze the disHS-ML strategy with regard to its complexity improvements over the other considered metaheuristic-based ML detectors. To this end, in the first place, the numbers of fitness evaluations (the search complexity (SC) values) sufficient for disHS-ML to reach the average BER values obtained by each of the considered methods for SC = 200, SC = 750 and SC = 1800 were determined by the simulation study. After that, the computational costs of the benchmark strategies for SC = 200, 750, 1800 and those of the disHS-ML scheme for the determined SC values sufficient for the proposed strategy to reach the maximum performances of the related benchmark strategies were computed via the Eqs. (44–47). Finally, the complexity gains achieved by the disHS-ML strategy over the other considered methods were calculated by using the Eq. (48).

In Table 5, which was created by completing the aforementioned operations, the proposed disHS-ML strategy is compared with the other symbol detectors one by one for 4 × 4, 6 × 6 and 8 × 8 MIMO configurations. In the first three rows, disHS-ML is compared to the BPSO-ML with regard to computational complexity for 4 × 4, 6 × 6 and 8 × 8 antenna structures while in the second and last three rows, it is compared to disABC-ML and DBHS-ML strategies, respectively for the related antenna configurations. As obviously seen from the Table 5, quite high complexity gains are achieved by the disHS-ML strategy over each of the other considered symbol detectors. With the increase in the number of antennas, the complexity gains become greater. For instance, while disHS-ML achieves 44% complexity gain over its closest competitor DBHS-ML for 4 × 4 MIMO structure, the related complexity gain goes up to at least 68% in the case that antenna configuration is made 8 × 8.

Table 5 The complexity gains achieved by disHS-ML over the other metaheuristic-based ML detectors
Full size table

6 Conclusion

In this study, in the first stage, a novel discrete HS variant called disHS was developed. After that, the newly developed disHS algorithm was integrated to the classical ML to create an advanced symbol detector named disHS-ML, which has the capability of reaching the near-ML performance with considerably lower computational complexity. The proposed disHS-ML strategy was then applied to the MIMO-FBMC/OQAM system and its BER performance in the related system was compared with not only the well-known classical symbol detectors like ZF and ML, but also the modern metaheuristic-based ML strategies such as BPSO-ML, disABC-ML and DBHS-ML for 4 × 4, 6 × 6 and 8 × 8 MIMO configurations. According to the simulation results, the proposed disHS-ML strategy leaves behind both the ZF and the other considered modern symbol detectors based on intelligent optimization algorithms by showing the closest BER performance to the ML scheme, which is a very complex and impractical symbol detector to be employed in any system. Apart from its successful BER performance, the complexity gain achieved by the proposed strategy over the conventional ML reaches to more than 98% for 8 × 8 antenna configuration. Moreover, it achieves at least 68% complexity gain over its closest competitor named DBHS-ML, which is a type of modern symbol detector as the proposed strategy. All these results show that the proposed disHS-ML strategy can be an efficient solution to the problem of symbol detection in the MIMO-FBMC/OQAM system.