Flow Rate Dependency of Steady-State Two-Phase Flows in Pore Networks: Universal, Relative Permeability Scaling Function and System-Characteristic Invariants

Abstract

The phenomenology of steady-state two-phase flow in porous media is conventionally recorded by the relative permeability diagrams in terms of saturation. Yet, theoretical, numerical and laboratory studies of flow in artificial pore network models and natural porous media have revealed a significant dependency on the flow rates—especially when the flow regime is capillary to capillary/viscous and part of the disconnected non-wetting phase remains mobile. These studies suggest that relative permeability models should incorporate the functional dependence on flow intensities. In the present work, a systematic dependence of the pressure gradient and the relative permeabilities on flow rate intensity is revealed. It is based on extensive simulations of steady-state, fully developed, two-phase flows within a typical 3D model pore network, implementing the DeProF mechanistic–stochastic model algorithm. Simulations were performed across flow conditions spanning 5 orders of magnitude, both in the capillary number, Ca, and the flow rate ratio, r, and for different favorable /unfavorable viscosity ratio fluid systems. The systematic, flow rate dependency of the relative permeabilities can be described analytically by a universal scaling function along the entire domain of the independent variables of the process, Ca and r. This universal scaling comprises a kernel function of the capillary number, Ca, that describes the asymmetric effects of capillarity across the entire flow regime—from capillarity-dominated to mixed capillarity/viscosity- to viscosity-dominated flows. It is shown that the kernel function, as well as the locus of the cross-over relative permeability values, are single-variable functions of the capillary number; they are both identified as viscosity ratio invariants of the system. Both invariants can be correlated with the structure of the pore network, through a function of Ca. Consequently, the correlation is associated with the wettability characteristics of the system. Among the potential applications, the proposed, universal, flow rate dependency scaling laws are the improvement of core analysis and dynamic rock-typing protocols, as well as integration into field-scale simulators or associated machine learning interventions for improved specificity/accuracy.

1 Introduction

Τwo-phase flow in porous media is a physical process whereby two phases flow simultaneously within a porous medium. A porous medium (PM) comprises a complex network of interconnected pores of sizes in the range of microns-to-millimeters. When the flow is immiscible, i.e., the two phases do not mix, one of the phases is wetting the interstitial surface of the pore network against the other, non-wetting phase.

Applications of two-phase flow in porous media are numerous within the industry, energy and environment sectors, e.g., enhanced oil recovery, CO₂ sequestration and geothermal harvesting, groundwater and soil contamination and subsurface remediation, the operation of multiphase trickle-bed reactors, the operation of proton exchange membrane fuel cells.

The size and time scales of the process span across many orders of magnitude. At the pore scale, the characteristic size is such that the flow takes place at the continuum scale (Stokes flow). Critical flow mechanisms occur within size domains spanning micro-to-millimeter scales. An intrinsic characteristic of immiscible two-phase flow in porous media is the disconnection of the non-wetting phase. Fluid immiscibility, wettability and the complex pore network structure (tortuosity, genus, dimensionality, micro-roughness, surface chemistry, etc.) result in the disconnection of the non-wetting phase into fluidic elements, namely ganglia and droplets, of correspondingly larger or smaller size when compared to the average pore size. Pore scale hydraulic instabilities-instigated by Haines jumps and the corresponding, propagating pressure pulses-trigger detachment of the non-wetting phase, break-up and pinch-off (Payatakes 1982; Berg et al. 2013) and lead to intermittent flows of the fluidic elements of the disconnected non-wetting phase (Reynolds et al. 2017; Spurin et al. 2019) as well as pressure waves and flow instabilities (Hönig et al. 2013; Rücker et al. 2021; Karadimitriou et al. 2023). These mechanisms have their share on increasing the incessant power dissipation in the incoherent motion of fluidic elements. The Young–Laplace forces acting across the N/W menisci separating the fluidic elements of the non-wetting phase from the surrounding wetting phase within the network capillaries are comparable to the Stokes flow, viscosity-induced resistances. As a result, an average pressure gradient builds-up along the flow direction. Averaging is considered over time and space in terms of appropriately sized, representative time periods and volume elements. The contribution of these effects on the macroscopic pressure gradient(s) depends on the interstitial structure of the flow and the interaction, through momentum exchange, between the two fluids and the solid matrix. Viscosity- and capillarity-induced forces have key roles in the momentum exchange.

Depending on the flow conditions, different flow regimes establish. These have been identified both in model pore networks (Avraam and Payatakes 1995; Tsakiroglou et al. 2007) and in natural porous media (Armstrong et al. 2017). In those regimes, a part of the disconnected elements of the non-wetting phase in the form of ganglia and droplets (Payatakes 1982; Tallakstad et al. 2009; Georgiadis et al. 2013; Yiotis et al. 2013; Armstrong et al. 2016) eventually organize to form larger structures at the high-end of the size spectrum, namely connected pathways of the non-wetting phase (Rucker et al. 2015). Similarly, at the low-end of the size spectrum, populations of very small droplets of the non-wetting phase (Datta et al. 2014; Pak et al. 2015) may become so small and form emulsions with the wetting phase (Guillen et al. 2012; Unsal et al. 2016; Rucker et al. 2017; Arab et al 2018). Moving-up from the scale of a few thousands pores into the realm of cm and m (pore-to-core-to-formation), porous medium heterogeneities and discontinuities appear, e.g., cracks, fractures, layering, etc. The collective behavior of the interaction between the two phases and the structure of the pore network has adverse effects on the meter-to-the-hundreds-of-meters-size domain. Two-phase flow in natural porous media then becomes a complex system and relevant issues on complexity, emergence, self-organization, etc., need to be considered (Cushman 1997; Faybishenko et al. 2015). So, long as the process may be observed and described at different size scales, it is essential to describe the flow at the representative elementary volume (REV) over the scale associated with the problem of interest. The REV is associated with averaging or up-scaling all interacting flow phenomena occurring within any statistically adequate volume and time frame and, in statistical mechanics terms, it must represent all possible fluidic microstates (Valavanides and Daras 2016; Bedeaux and Kjelstrup 2022).

The industry standard for the analysis and modeling of immiscible, two-phase flows in porous media is built around the concept of relative permeabilities. These have been contrived to extend the classic Darcy's law for one-phase (saturated) flow in porous media, into its fractional form version. Relative permeabilities are calculated from laboratory measurements, either with steady- or unsteady-state methods. In steady-state methods, the two phases are simultaneously injected at a fixed ratio into a core. When the system reaches steady-state conditions, the differential pressures are measured and the relative permeabilities are calculated. The resulting description is phenomenologic. In practice, e.g., in Special Core Analysis (SCAL), an appropriate number of specially selected cores at the size of centi-to-deci-meters are collected from the porous medium formation and then used as a model—or reference—medium to record the effects of simultaneous flow of model fluids (American Petroleum Institute 1998; McPhee et al. 2015). The core is placed tightly in a core holder and fluids are co-injected through the core at controlled flow rates. Measured values of flow rates versus pressure drops are then used to calculate the corresponding values of the relative permeabilities, so as to satisfy the Darcy fractional flow equations [see Eqs. (1), Sect. 2.1]. This is repeated for different flow conditions (e.g., by imposing different flow rates) in order to derive look-up tables or diagrams that describe the behavior of the examined flow system under immiscible twο-phase flow conditions. In recent research efforts, sophisticated micro-tomographic technologies (Georgiadis et al. 2013; Wildenschild and Sheppard 2013; Fusseis et al. 2014) have been implemented to scan the pore network structure, reveal the saturation profile and the interstitial flow structure along the core (Youssef et al. 2014, 2017), or even to capture micro-events occurring at high resolution domains in terms of time and size scales, e.g., Haines jumps (Berg et al. 2013) or in-situ dynamic alterations of contact angles (Andrew et al. 2015; Singh et al. 2016). Obviously, such improved SCAL techniques require more elaborate interventions and support equipment and are limited to relatively smaller core sizes. The output of SCAL measurements is a core-scale REV model (phenomenologic); the behavior of the core REV model is then incorporated into field-scale flow simulators.

Research efforts have dealt with the problem of correlating relative permeability values to values of saturation, assuming a priori that relative permeabilities are saturation-dependent. The assumption of saturation dependency has been established from the early years of oil extraction, and still is the standard approach in the industry until today. The objective is to deliver functional forms for fitting laboratory measured saturation and relative permeability data charts, with scope to incorporate these, together with saturation charts of capillary pressure, into field-scale simulators. Established approaches on fitting relative permeability vs saturation data sets are based on interpolating relative permeability against saturation values, using power law relationships (Corey 1954; Brooks and Corey 1964; Chierici 1984; Honarpour et al. 1986; Lomeland et al. 2005; Lomeland and Ebeltoft 2008; Lomeland 2018). These models attempt to provide appropriate functional expressions for fitting relative permeability values against saturation over the broadest domain possible in flow conditions. The Brooks–Corey and LET (Lomeland–Ebeltoft–Thomas) approaches are most commonly used in fitting data collected during core analysis. Their performance in adequately describing the phenomenology revealed by core analysis, as well as issues associated with sensitivity and uncertainty analysis of relative permeability parameterization, is examined and discussed in a recent publication by Berg et al. (2021). Albeit saturation dependency of relative permeabilities is established in industry, there is skepticism on whether it is the most efficient approach in describing the process. As saturation describes a volumetric state of the system but not a transport state, it brings no definite input to the momentum balance; therefore, it is questionable if it can provide any information on the kinetics of the macroscopic flow. In that context, it is questionable if saturation can be used as an independent variable per se (Valavanides 2018b). The long standing practice in defining the process state through combined relative permeability-capillary pressure–saturation charts does not improve things. The conventional capillary pressure–saturation data sets are obtained under static conditions; even so, they are not unique, as—due to hysteresis—they depend on the direction of the displacement, e.g., drainage or imbibition (Schluter et al. 2016; McClure et al. 2018).

The flow rate dependency of relative permeabilities has been identified as early as the first attempts to reveal the phenomenology of two-phase flow in porous media by Wyckoff and Botset (1936). Nevertheless, a systematic laboratory study across different flow regimes was never followed upon, possibly because of cost and time issues in deploying such an extensive, multi-parametric study and because, at the early days of the oil era, conditions were in consistency—to a certain degree—with saturation dependency. The last 2 decades, the issue of flow dependency is reconsidered, as models based on saturation dependency alone proved to be inefficient in describing the flow at intermediate flow conditions, i.e., when capillarity-induced resistances are comparable to viscous resistances. Theoretical, numerical, and laboratory studies of flow in artificial pore network models and natural porous media (Wildenschild et al. 2001; Nguyen et al. 2006; Aursjo et al. 2014; Sinha et al. 2017; Tsakiroglou et al. 2015; Krause and Benson 2015; Valavanides 2018a; Gao et al. 2020; Yiotis et al. 2019, 2021; Zhang et al. 2021) have identified flow rate dependency to be an underlying, inherent process characteristic, revealing a significant dependency of relative permeabilities on flow rates.

In parallel, research efforts to characterize a porous medium, implementing laboratory measurements under dynamic conditions (flow), namely dynamic rock typing, are currently in development (Mirzaei-Paiaman and Ghanbarian 2021). Studies have also shown the need to establish a comprehensive understanding of the degree and extent of how pertinent system characteristics and process parameters (interfacial tension, wettability, pressure, temperature, etc.) affect the relative permeabilities (Esmaeili et al 2019, 2020; Kumar et al. 2020; Arab et al. 2018, 2020, 2021). Yet, extracting the flow rate dependency characteristics from physical experiments in the laboratory is not an easy task, so long as the number of essential parameters, e.g., the viscosities of the two fluids, interfacial tension, wettability, do not scale similarly with flow intensity and pore network geometry. That increases significantly the number of independent variables and overloads the protocol of a systematic laboratory study. Moreover, because of end-effects in SCAL methods, there are issues associated with biasing of measurements. Virtual experiments are an alternative approach in dealing with the problem of scaling-up transport properties within a porous medium. Dynamic pore network simulators are an option; nevertheless, the computational time increases exponentially with network size—directly associated with the minimum size of the REV—as well as the degree of disconnection of the non-wetting phase.

Ιn the present work, we attempt to tackle the problem of flow rate dependency. We will see how a generic form of scaling function can be derived in order to describe the dependence of the reduced pressure gradient, x, or, equivalently, the relative permeabilities, on the local flow rate intensities of the wetting and the non-wetting phases. The latter is expressed in reduced form as the capillary number, Ca, and the N/W flow rate ratio, r.

The proposed universal scaling, Eq. (18), integrates the contributions of the two main sources of flow resistance, the capillary resistances and the viscous resistances, in decoupled, appropriately reduced format. In particular, the contribution of viscous resistances is accounted by a linear term of the flow rate ratio, r, with coefficient of linear increase the viscosity ratio of the fluid system. Τhe contribution of capillary resistances is accounted by a strongly decreasing function of the capillary number, Ca. This function provides an integrated description of the effects of capillarity related phenomena occurring during the interaction of the interstitial flows within the pore network. It is conceptually identified as the Intrinsic Dynamic Capillary Pressure (IDCP) function of the flow system. The IDCP function can be used as an identity of the fluid system. It is invariant to viscosity ratio. Another characteristic property is the locus of flow conditions whereby equal permeabilities are attained, namely the locus of cross-over relative permeabilities, also invariant to viscosity ratio. Both can be extracted from laboratory or virtual, steady-state co-injection experiments on any given flow system, implementing conventional SCAL techniques. Here, we will use the extensive data output produced from previous, systematic simulations, based on the DeProF model for steady-state, fully developed, two-phase flow in pore networks, Valavanides (2018a).

The novelty of the proposed scaling relays into improvements on the Darcy-scale description of steady-state, fully developed, two-phase flow in pore networks. The current work is complementary to a previous work, implementing an energy efficiency analysis, Valavanides (2018b), for two-phase flow in porous media. In that work, we proved the existence of the locus of critical flow conditions (CFCs), whereby maximum utilization of the input hydraulic power is achieved, as well as the collapsing of all the loci pertaining to different viscosity ratios into a universal locus, pertaining to equal viscosities. Each locus of CFCs is unique; therefore, it can also provide the identity of the flow system, comprising the two fluids and the porous medium, using a different norm (energy efficiency). In the current work, we have implemented fractional flow analysis and derived a scaling expression—a new phenomenologic law, Eq. (18), for the flow rate dependency of relative permeabilities. Fractional flow analysis is complementary to energy efficiency analysis. The scope is to provide a clearer image of the combined effects of viscosity, interfacial tension, wettability, pore network geometry, flow intensity, etc., on the structure of interstitial flows and relative permeabilities. The practical implementations relay to the use of a true-to-mechanism phenomenological law for two-phase flow in porous media. Potential applications could be integration in field-scale simulators or machine learning interventions to improve specificity/accuracy/training; also to improve existing SCAL protocols and associated workload in flow system- or rock-typing applications.

The paper is organized in 6 sections, including this introductory section. Section 2 provides a basic analysis of steady-state, two-phase flow in porous media, and a discussion on the concept of fully developed flow conditions. Section 3 presents the results of extended simulations with the DeProF model algorithm. Reduced pressure gradient values, x, are presented in plane (2D) diagrams; inherent trends are revealed and identified. Section 4, the core section of this work, presents how indicative, generic functional forms of Ca and r, describing the flow rate dependency of the relative permeabilities, are extracted from available data. The concept of intrinsic dynamic capillary pressure is also introduced here. Section 5 derives the corresponding functional form of the energy utilization index, f_EU, and the associated locus of critical flow conditions; characteristic invariant properties of the process are also revealed. Discussion, conclusions and suggestions for future research are presented in Sect. 6.

2 Analysis of Steady-State Two-Phase Flow in Porous Media

2.1 Basic Considerations

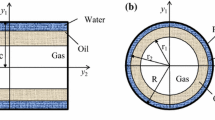
Consider the simultaneous, one-dimensional concurrent flow of a non-wetting phase and a wetting phase, at flow rates equal to ${\widetilde{q}}_{\mathrm{n}}$ and ${\widetilde{q}}_{\mathrm{w}}$, respectively, through a stream tube of fixed cross-section within a porous medium, Fig. 1. The cross-section of the cylindrical control volume may have any arbitrary shape, so long as, it is large enough to be considered homogeneous and side boundaries have no significant effect on the flow structure.

Fig. 1

A REV element of one-dimensional flow within a cylindrical, infinitely long, porous medium tube (top). The schematic drawings are successive scale-down depictions of the mixture of the wetting phase (WP, blue) and the non-wetting phase (NWP, red) within the interstitial flow (inset, top), the disconnection of the non-wetting phase (bottom) and the associated hysteresis due to the different contact angles, advancing, bottom left, and receding, bottom right. (The inset is a snapshot from the Avraam and Payatakes (1995) flow experiments in model pore networks, courtesy of D.G. Avraam.)

As a result of the externally imposed flow rates, corresponding pressure gradients, $\left( {\Delta \tilde{p}/\Delta \tilde{z}} \right)_{i}$, i = n, w, are induced upon the two phases. This type of concurrent immiscible flow is conventionally described by the set of phenomenological fractional flow Darcy relations,

$$\frac{{\tilde{q}_{{\text{n}}} }}{{\tilde{A}}} \equiv \tilde{U}_{{\text{n}}} = \frac{{\tilde{k}}}{{\tilde{\mu }_{{\text{n}}} }}k_{{{\text{rn}}}} \left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{n}}} \quad {\text{and}}\quad \frac{{\tilde{q}_{{\text{w}}} }}{{\tilde{A}}} \equiv \tilde{U}_{{\text{w}}} = \frac{{\tilde{k}}}{{\tilde{\mu }_{{\text{w}}} }}k_{{{\text{rw}}}} \left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{w}}}$$

(1)

where indices i = n, w indicate the wetting phase (w) and the non-wetting phase (n), both incompressible, $\tilde{q}_{i}$ are the corresponding flowrates across a porous medium surface of area $\tilde{A}$, perpendicular to the direction of macroscopic flow, $\tilde{U}_{i}$ are the corresponding superficial velocities, or flow rate intensities, $\left( {\Delta \tilde{p}/\Delta \tilde{z}} \right)_{i}$ the corresponding pressure differences over any length along the macroscopic flow direction, or pressure gradients along the stream tube, $\tilde{k}$ is the absolute permeability of the pore network and, $\mu_{i}$ are the dynamic viscosities of the two fluids.

Because of bulk viscosity and capillary hysteresis resistances, energy dissipation is manifested as pressure drop along the flow direction. A relative measure of the viscous forces over the capillary forces is provided by the capillary number. Here, we will use the conventional expression for evaluating the capillary number, Ca, as

$${Ca} = \frac{{\tilde{\mu }_{{\text{w}}} \tilde{U}_{{\text{w}}} }}{{\tilde{\gamma }_{{{\text{nw}}}} }}$$

(2)

where $\tilde{\gamma }_{{{\text{nw}}}}$ is the interfacial tension between the two phases.

Please note that the expression, Eq. (2), is conventional. It does not take into account the contribution of the viscous forces induced by the flow of both phases, neither those induced by capillarity and wettability, associated with the contact angles of the menisci. The latter, together with the asymmetries and micro heterogeneity in pore geometry, and other intrinsic, hysteresis effects associated with fluctuation dissipation, are the main sources of what is referenced as “capillary resistances”. These contributions have a significant impact on the resulting macroscopic pressure gradient(s). In that context, Oughanem et al. (2015) have extended the definition of the capillary number to take into account the effect of wettability. Valavanides (2018b) has proposed to include implicitly the relative magnitude of viscous to capillary forces by considering an effective, appropriately scaled, definition of the capillary number. Yet, that requires an assessment of the flow system over a broad domain of flow conditions.

The flow rate ratio, r, is defined as

$$r = \tilde{q}_{{\text{n}}} /\tilde{q}_{{\text{w}}} = \tilde{U}_{{\text{n}}} /\tilde{U}_{{\text{w}}}$$

(3)

and is essentially a kinematic property of the flow.

Ca and r are considered as the operational or flow parameters of the process.

The set of flow parameters is complemented by the set of system parameters, namely the absolute permeability of the pore network, $\tilde{k}$, the bulk viscosity ratio, $\kappa$, defined as

$$\kappa = \tilde{\mu }_{{\text{n}}} /\tilde{\mu }_{{\text{w}}}$$

(4)

the physicochemical characteristics of the two phases, e.g., the interfacial tension, $\tilde{\gamma }_{{{\text{nw}}}}$, the dynamic, receding and advancing contact angles of the menisci, $\theta_{{\text{R}}}$ and $\theta_{{\text{A}}}$, and relevant wettability properties, as well as other geometrical, topological and structural characteristics of the pore network.

So long as the process is regulated by imposing a set of flow rate values, $\tilde{q}_{{\text{n}}} , \tilde{q}_{{\text{w}}}$, across a porous medium surface, $\tilde{A}$, the superficial velocities, $\tilde{U}_{{\text{n}}} ,\tilde{U}_{{\text{w}}}$, can be considered to be the independent variables of the process. Therefore, without any loss of generality, Ca and r, from Eqs. (2) and (3), can be considered as the independent variables in the set of the phenomenological (cause-effect) fractional flow Darcy relations that describe the steady-state process. In that context, the pressure gradients, $\left( {\Delta \tilde{p}/\Delta \tilde{z}} \right)_{i} , \;i = {\text{n}},{\text{w}}$, are the dependent variables. The absolute permeability of the porous medium and the fluid viscosities are considered to be fixed; therefore, the relative permeabilities need to be determined for different flow conditions to form a definite set of cause-effect Darcy fractional flow relations. In the reservoir engineering domain, the applicable standard is to use one of the fractional flows, be it the non-wetting phase, f_n, or the wetting phase, f_w, correspondingly defined as

$$f_{{\text{n}}} = \frac{{\tilde{q}_{{\text{n}}} }}{{\tilde{q}_{{\text{n}}} + \tilde{q}_{{\text{w}}} }} = \frac{r}{r + 1}\quad {\text{and}}\quad f_{{\text{w}}} = \frac{{\tilde{q}_{{\text{w}}} }}{{\tilde{q}_{{\text{n}}} + \tilde{q}_{{\text{w}}} }} = \frac{1}{r + 1}$$

(5)

In the present work, we use as independent variable, the flow rate ratio, r, instead of the fractional flow, because it has the advantage of a more convenient description of the sought physical process, especially in detecting the critical flow conditions of maximum energy efficiency (see Sect. 5 and Valavanides et al. 2016). Switching between flowrate ratio and fractional flow is directly applicable from Eqs. (5).

The mobility ratio, $\lambda$, is defined as the ratio of the mobilities,

$$\lambda = \frac{{\tilde{\lambda }_{{\text{n}}} }}{{\tilde{\lambda }_{{\text{w}}} }} = \frac{{\frac{{k_{{{\text{rn}}}} }}{{\tilde{\mu }_{{\text{n}}} }}\left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{n}}} }}{{\frac{{k_{{{\text{rw}}}} }}{{\tilde{\mu }_{{\text{w}}} }}\left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{w}}} }} = \frac{1}{\kappa }\frac{{k_{{{\text{rn}}}} }}{{k_{{{\text{rw}}}} }} \frac{{\left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{n}}} }}{{\left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{w}}} }}$$

(6)

and is essentially a kinetic property of the flow as it relays to the pressure gradients, $\left( {\Delta \tilde{p}/\Delta \tilde{z}} \right)_{i} ,\; i = {\text{n}},{\text{w}}$.

When steady-state, fully developed flow conditions are established (see Appendix I), the pressure gradient is common in both fluids and the phenomenological (cause-effect) fractional flow Darcy relations become,

$${\text{fully developed flow }} \to \tilde{U}_{i} = \frac{{\tilde{q}_{i} }}{{\tilde{A}}} = \frac{{\tilde{k}}}{{\tilde{\mu }_{i} }}k_{ri} \frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}},\quad i = {\text{n}},{\text{w}}$$

(7)

Consequently, from Eq. (6), it turns out that a basic flow characteristic of steady-state fully developed flow is that the flow rate ratio becomes equal to the mobility ratio,

$${\text{fully developed flow}} \to r = \frac{{\tilde{q}_{{\text{n}}} }}{{\tilde{q}_{{\text{w}}} }} \equiv \frac{1}{\kappa }\frac{{k_{{{\text{rn}}}} }}{{k_{{{\text{rw}}}} }} = \frac{{\tilde{\lambda }_{{\text{n}}} }}{{\tilde{\lambda }_{{\text{w}}} }} = \lambda$$

(8)

The equivalence between flow rate ratio and mobility ratio in steady-state fully developed flow conditions is a critical characteristic property for the analysis of two-phase flows in pore networks. The assumption in Eq. (8) was referenced in earlier works (Avraam and Payatakes 1999; Valavanides and Payatakes 2001). Equality of pressure gradients is a trustworthy assumption, provided the flow is fully developed, and saturation gradients are negligible along any REV stream tube. This is equivalent to negligible end-effects if core-scale measurements are referred. On the same line, Standnes et al. (2017) have proposed a mechanistic model for estimating generalized relative permeabilities, whereby they have considered that equal pressure gradients settle in both phases within the representative volume element, neglecting end-effects. The kinematic-kinetic equivalence described by the expression in Eq. (8) can also be used in practice as a criterion on whether a specimen of pore network or porous medium can be considered as REV or not, and if fully developed flow conditions are established and to what degree, especially when end-effects are expected to be critical (Karadimitriou et al. 2023).

2.2 The Reduced Pressure Gradient for Fully Developed Two-Phase Flows in Porous Media

The conventional fractional Darcy description of immiscible, fully developed, two-phase flow in porous media is provided by Eqs. (7). We may recast these equations in a dimensionless form as follows.

We introduce the normative pressure gradient of an equivalent one-phase (saturated) flow of the wetting phase, $\left( {\Delta \tilde{p}/\Delta \tilde{z}} \right)^{1\Phi } ,$ at superficial velocity equal to $\tilde{U}_{{\text{w}}}$,

$$\tilde{U}_{{\text{w}}} = \frac{{\tilde{k}}}{{\tilde{\mu }_{{\text{w}}} }}\left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)^{1\Phi } \mathop \Rightarrow \limits^{{{\text{eqn }} \left( 2 \right)}} \left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)^{1\Phi } = \frac{{\tilde{\gamma }_{{{\text{nw}}}} {\text{Ca}}}}{k}$$

(9)

We may then use this pressure gradient to normalize the pressure gradient, induced during fully developed two-phase flow in a porous medium, into the reduced (dimensionless) macroscopic pressure gradient, $x$, given by

$$x = \frac{{\Delta \tilde{p}/\Delta \tilde{z}}}{{\left( {\Delta \tilde{p}/\Delta \tilde{z}} \right)^{1\Phi } }} = \frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}\frac{{\tilde{k}}}{{\tilde{\mu }_{{\text{w}}} \tilde{U}_{{\text{w}}} }} = \frac{{\Delta \tilde{p}/\Delta \tilde{z}}}{{\tilde{\gamma }_{{{\text{nw}}}} {Ca}/k}}$$

(10)

From the equivalence between flow rate ratio and mobility ratio, Eq. (8), at fully developed flow conditions, relative permeability values can be computed directly from the reduced pressure gradient, x, as

$$k_{{{\text{rw}}}} = \frac{1}{x}\quad {\text{and}}\quad k_{{{\text{rn}}}} = \kappa rk_{{{\text{rw}}}} = \kappa r\frac{1}{x}\quad {\text{or}}\quad \frac{{k_{{{\text{rn}}}} }}{{k_{{{\text{rw}}}} }} = \kappa r$$

(11)

The above relations comprise the essential definitions of relative permeabilities. When fully saturated flow conditions are met, $x = k_{{{\text{rw}}}} = 1$.

Using the reduced pressure gradient, two-phase flow in porous media may be described by a generalized functional form,

$$x = x\left( {{\text{Ca}}, \, r, \, \kappa ,\theta_{{\text{A}}} ,\theta_{{\text{R}}} ,\,{\varvec{x}}_{{{\text{pm}}}} } \right)$$

(12)

where $\theta_{{\text{A}}} ,\theta_{{\text{R}}}$, represent the dynamic advancing (A) and receding (R) contact angles of the o/w interface on the pore walls, and x_pm is a (sub-) set of (all) the dimensionless geometrical and topological parameters of the pore network that affect the flow (e.g., porosity, genus, coordination number, normalized chamber and throat size distributions, chamber-to-throat size correlation factors).

The set of physical variables in the parenthesis comprise the set of independent variables. These are classified into two groups. The group of the flow parameters $\left( {{\text{Ca}},r} \right)$ can be regulated during the process, and the group of the system parameters $\left( {\kappa ,\theta_{{\text{A}}} ,\theta_{{\text{R}}} ,{\varvec{x}}_{{{\text{pm}}}} } \right)$ are considered to have fixed values per flow system. The two groups are separated in Eq. (12) by a semicolon. The benefit of describing the sought process at fully developed flow conditions in the general form of Eq. (12) is the reduction in redundancies associated with the many physicochemical parameters of the flow system, without compromising the consistency of the underlying, true-to-mechanism, flow model.

The functional form in Eq. (12) is unknown. The objective of the present work is to extract a generalized, universal expression that can describe the physics of the flow consistently and that can be appropriately adjusted to match the behavior of different flow systems. In the next sections, we will see how an explicit function of the generalized, reduced pressure gradient, Eq. (12), has been revealed by matching extensive, systematic simulations, implementing a hybrid mechanistic-stochastic model (the DeProF model), over a broad domain $\left( {Ca,r} \right)$ of fully developed flow conditions for a set of physicochemical flow system parameters $\left( {\kappa ,\theta_{{\text{A}}} ,\theta_{{\text{R}}} ,{\varvec{x}}_{{{\text{pm}}}} } \right)$. Implementing a similar methodology, this functional form can be adapted to describe flows in different two-fluid/porous medium systems.

3 Prediction of Relative Permeabilities for Steady-State, Fully Developed, Two-Phase Flow in Model Pore Networks

3.1 DeProF Model for Two-Phase Flow in Pore Networks

The DeProF model is a hybrid mechanistic-stochastic model developed to describe immiscible, steady-state two-phase flow in pore networks (Valavanides 2018a). The model is based on the concept of decomposition of the macroscopic flow into prototype flows, hence the acronym DeProF. It takes into account the pore scale mechanisms and the sources of nonlinearity caused by the motion of interfaces, as well as other complex, network-wide cooperative effects, to estimate the conductivity of different classes of model pore unit cells. The different classes of unit cells are partitioned not only on geometric configurations but also on flow configurations, e.g., conducting/non-conducting, fully or partly saturated and containing one or several n/w menisci. Some critical characteristics of the DeProF model comprise:

• (a) Decomposition of the total flow into three constituent flows, namely Drop Traffic Flow, Ganglion Dynamics and Connected Pathway Flow, each with distinctive sizing of the disconnected fluidic elements of the non-wetting phase. All three comprise an ensemble of interacting fractional flows wandering within a phase space of constituent flows, see points (e) and (f).

• (b) Dynamic contact angles for the receding and advancing interfaces associated with drainage and imbibition events within pore unit cells.

• (c) Intermittent flow of fluidic elements is taken into account as a process stochastic property, based on calculated stranding and mobilization probabilities.

• (d) Scaling-up implemented by applying effective medium theory with appropriate expressions for pore-to-macro-scale consistency for mass and momentum balances over the wetting and non-wetting phases, result in an implicit expression in the form of Eq. (12).

• (e) Determination of the ensemble of physically admissible interstitial flow configurations or system flow microstates, consistent with the externally imposed flow conditions, satisfying Eq. (12).

• (f) Implementation of ergodicity to calculate the expected macroscopic, average reduced pressure gradient, from the ensemble of physically admissible flow microstates, see (e), for different steady-state, fully developed flow conditions and flow systems.

Using the DeProF model, we may obtain a semi-analytical solution to the problem of steady-state, fully developed, two-phase flow in pore networks in the form of Eq. (12). The model also predicts key physical quantities that describe the interstitial, bulk and interface structure of the flow: ganglion size and ganglion velocity distribution, fractions of mobilized/stranded populations, specific (per unit volume of porous medium) surface area, velocity and volume fractions of mobilized and stranded interfaces, degree of fragmentation of the non-wetting phase. If the geometry of the pore unit cells is explicitly provided in analytic expressions, the DeProF algorithm is relatively fast, with typical times between 10 and 60 min per (Ca, r)-run on a desktop computer, depending on the user-selected flow system properties and flow conditions.

3.2 DeProF Model Simulations

Extensive simulations implementing the DeProF algorithm have been carried out over a model pore network with characteristic properties similar to a typical Berea sandstone. Output data were used to derive maps describing the dependence of the flow structure on the independent flow variables, namely the capillary number, Ca, and the flow rate ratio, r (Valavanides 2018a). The simulations span 5 orders of magnitude in Ca $\left( { - 9 \le \log {\text{Ca}} \le - 4} \right)$ and in r $\left( { - 2 \le \log r \le 2} \right)$. Fluid systems with various—favorable and unfavorable—viscosity ratios, $\kappa = \tilde{\mu }_{{\text{n}}} /\tilde{\mu }_{{\text{w}}} \in \left\{ {0.2, 0.33, 0.67, 1.0, 1.5, 3.0, 9.0, 20} \right\}$, have been examined. The model flow systems differ only on the value of the viscosity ratio. Properties pertaining to capillarity, i.e., the interfacial tension, wettability, expressed by the dynamic advancing and receding contact angles, as well as the model pore network geometric/topologic characteristics, were kept fixed. The afore mentioned domain of flow conditions has been scanned in 41 steps over Ca, i.e., for values ${Ca}_{mj} = m \times 10^{j} , \;m \in \left\{ {1, 2, \ldots , 10} \right\}, \;j \in \left\{ { - 8, \ldots , - 5} \right\}$, and 21 steps over logr, i.e., for values $\log r_{i} = - 2 + 2i/10, \;i \in \left\{ {0, 1, 2, \ldots , 20} \right\}$.

Typical predictions of the reduced pressure gradient, x, for different values of Ca and r, and for different N/W viscosity ratio values, $\kappa$, are presented in Fig. 2. Diagrams are shaped into two classes, “iso-Ca” iso-capillary (left) and “iso-r” iso-flow rate ratio (right).

Fig. 2

Paired diagrams of predicted reduced pressure gradient values, x, for different values of capillary number, Ca, and flow rate ratio, r. Each pair corresponds to a n/w viscosity ratio value, $\kappa \in \left\{ {0.33, 1.0, 1.5, 20} \right\}$. Small markers depict raw values predicted by DeProF simulations (Valavanides 2018a). Markers are connected by straight line segments in groups of iso-Ca values (left parts of diagrams) and iso-r values (right parts of diagrams). In every diagram, the thick dashed line depicts an asymptote, the large blue circle and the red cross indicate characteristic values (see text)

In the following, we will identify and reveal some invariant characteristic properties of the process.

3.3 DeProF Model Simulations: Deciphering the Results

In single-phase flows in pore networks, the macroscale pressure gradient scales linearly with the superficial fluid velocity—as long as the flow is maintained below the Forscheimer regime. Flow linearity is also observed for certain two-phase flow conditions, especially so when the momentum and/or energy exchange between the two phases and through n/w interfaces (menisci) is minimum. Such conditions are met when disconnected fluidic elements of the non-wetting phase are stranded and flow of the non-wetting phase is through continuous pathways (fingers), and/or any capillary interactions are negligible when compared to the viscous resistances of the bulk phase flows.

This type of linear behavior is also predicted in the DeProF model simulations for certain flow conditions. In particular, we may note on the $\left\{ {x_{i} ,\log r_{i} } \right\}$ iso-Ca diagrams in Fig. 2 that, at the high-end of the flow rate ratio domain, all curves pertaining to constant-Ca values tend to converge asymptotically to an inclined straight dashed line; its functional form is given by the expression

$${\text{for}}\;r \to \infty ,\quad \log x = \log \kappa + \log r \Leftrightarrow x = \kappa r \Leftrightarrow r = \frac{1}{\kappa }x$$

(13)

Equation (13) states that at sufficiently large values of the flow rate ratio, $r \to \infty ,{ }$ the reduced pressure gradient, x, becomes a linear function of r, by a linearity constant equal to the viscosity ratio. Essentially, Eq. (13) describes the decoupling between the wetting and non-wetting phase flows. It can be recovered analytically by writing the definition of the reduced pressure gradient, x, as the ratio of the pressure gradient of the two-phase flow normalized with the pressure gradient that would have been built considering the flow of the wetting phase with superficial velocity equal to the superficial velocity during the two-phase flow, Eq. (10).

Now, considering the cases of very large values of the flow rate ratio, $r \to \infty$, the (common) pressure gradient (at steady-state fully developed flow conditions) approaches the following limit (of virtually saturated Darcy flow of the non-wetting phase),

$$\mathop {\lim }\limits_{r \to \infty } \frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}} = \frac{{\tilde{\mu }_{{\text{n}}} }}{{\tilde{k}}}\tilde{U}_{{\text{n}}}$$

(14)

Then, at this limit, simply by inserting Eq. (14) into the definition of the reduced pressure gradient, Eq. (10), we can recover a linear relation between the reduced pressure gradient, x, and the flow rate ratio, r,

$$x = \frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}\frac{{\tilde{k}}}{{\tilde{\mu }_{{\text{w}}} \tilde{U}_{{\text{w}}} }}\mathop{\longrightarrow}\limits^{r \to \infty }\frac{{\tilde{\mu }_{{\text{n}}} }}{{\tilde{k}}}\tilde{U}_{{\text{n}}} \frac{{\tilde{k}}}{{\tilde{\mu }_{{\text{w}}} \tilde{U}_{{\text{w}}} }} = \frac{{\tilde{\mu }_{{\text{n}}} }}{{\tilde{\mu }_{{\text{w}}} }}\frac{{\tilde{U}_{{\text{n}}} }}{{\tilde{U}_{{\text{w}}} }} = \kappa r \Rightarrow x\mathop{\longrightarrow}\limits^{r \to \infty }\kappa r$$

(15)

The higher the values of the capillary number, the earlier (in terms of flowrate ratio values) the approach to that decoupled-flow behavior, and the earlier Eq. (15) is recovered. Moreover, the logarithmic relation in Eq. (13) indicates that the gradient of the asymptote in the $\left( {\log x,\log {\text{Ca}}} \right)$ diagrams in Fig. 2 should be 1:1, irrespective of the system properties. This can be verified by observation across all the $\left\{ {x_{i} ,\log r_{i} } \right\}$ iso-Ca diagrams, irrespective of the value of the viscosity ratio.

Considering the $\left\{ {x_{i} ,\log {Ca}_{i} } \right\}$ iso-r diagrams, aligned on the right columns in Fig. 2, we observe a similarly interesting trend. At the low-end of the capillary number domain, all iso-r curves tend to converge asymptotically to a straight line, illustrated by the dashed thick line with (negative) inclination. The inclination of the asymptote is $- 1:1$, across all the $\left\{ {x_{i} ,\log {Ca}_{i} } \right\}$ iso-r diagrams, irrespective of the value of the viscosity ratio, $\kappa$. Again, decoupling between the flows of the wetting and non-wetting phases occurs at very low-Ca values. The lower the value of flowrate ratio, this asymptotic behavior is observed from higher Ca values. Moreover, we may verify by direct measurements that, in all diagrams, irrespective of the value of $\kappa$, the low-Ca asymptote crosses the $x = 1$ line (pertaining to “virtually saturated flow”) at the same value of the capillary number, $\log {Ca}_{{{\text{pm}}}} = - 4.75$. That is indicated by a large red cross (). In that context, the functional form of the low-Ca asymptote is given by

$${\text{For}}\;\;\log {Ca} \ll 0,\;\log x = \log {Ca}_{{{\text{pm}}}} - \log {Ca} \Leftrightarrow x = \frac{{{Ca}_{{{\text{pm}}}} }}{{{Ca}}}$$

(16)

Also note, in Eq. (16), that the value of the constant, ${Ca}_{{{\text{pm}}}}$, across all the fluid systems examined, is

$$\log {Ca}_{{{\text{pm}}}} = - 4.749 \Leftrightarrow {Ca}_{{{\text{pm}}}} = 1.782 \times 10^{ - 5}$$

(17)

Therefore, this value of ${Ca}_{{{\text{pm}}}}$ is considered to be a characteristic value (a property) of the fluid system. It depends on capillarity related characteristics, i.e., the tripartite interaction between interfacial tension, wettability (dynamic advancing and receding contact angles) and the pore network geometry. Should we have had the simulations rerun, with either a different wettability or different pore network geometry, that value would had changed. The open question is how sensitive the behavior of the fluid system/process would be to such changes, not only in simulations of virtual systems but also in applications in natural systems.

We see that, at the extremities of the flow conditions, the conventional assumption of saturation dependency of relative permeabilities is recovered. Yet, this is only a small part of the entire domain of flow conditions. For the rest of the flow domain, the broad, central region of moderate Ca values, where viscosity-induced resistances compete with capillarity-induced resistances, relative permeabilities are strongly nonlinear functions of the flow intensities of the wetting and non-wetting phases. In the following section, we will see how a universal functional form, $x\left( {Ca,r} \right)$, can be derived to fit the data, $x_{ij} \left( {{Ca}_{i} ,r_{j} } \right)$, predicted from the DeProF model simulations.

4 The Scaling Function for the Flow Rate-Dependent, Reduced Pressure Gradient

4.1 Introduction of the Scaling Function Model

We will continue with deriving a functional form for the reduced pressure gradient, $x\left( {Ca,r} \right)$, in order to best fit the data, $x_{ij} \left( {{Ca}_{i} ,r_{j} } \right)$, produced from the DeProF model simulations for 7 different systems of n/w viscosity ratio values, $\kappa \in \left\{ {0.33, 0.67, 1.0, 1.5, 3.0, 9.0, 20} \right\}$. The diagrams in Fig. 2 are representative data sets $x_{ij}$, for various viscosity ratio values.

We may start by examining the self-similar structure of the $x_{ij}$ values on the iso-Ca, diagrams stacked on the left column diagrams, in Fig. 2. In parallel we will observe the inherent asymptotic trends described by Eqs. (15) and (16).

We may observe a systematic trend, repeating for every fixed value of Ca. As $\log r$ is progressively increased, x starts from a constant value and then it progressively increases—following a power law trend—toward attaining a linear dependence on r. This trend can be described with the following functional form

$$x\left( {Ca,r} \right) = A\left( {\log {Ca}} \right) + \kappa r$$

(18)

In Eq. (18), the constant value at the low-r regime, when $\kappa r \to 0$, is represented by the term A, while the linear trend toward the asymptote line at the high-r regime, by $\kappa r$. We may also observe on the left column diagrams in Fig. 2 that, the constant value of $x$ attained at the low-r regime decreases with increasing Ca. Therefore A is correctly considered to be a function of the capillary number, $A = A\left( {\log {Ca}} \right)$. Moreover, all the iso-Ca lines converge asymptotically as $r \to 0$, at the same line, $x = \kappa r$. At those conditions, any capillarity effects, expressed by $A\left( {\log {Ca}} \right)$, should decrease with increasing Ca. This indicates that $A\left( {\log {Ca}} \right)$ should be a strongly decreasing function of Ca. The same self-similarity repeats consistently for different viscosity ratio values, $\kappa$. Focusing now on the right-column diagrams in Fig. 2, we may observe the trend of the iso-r lines into converging asymptotically, as ${Ca} \to \infty$, to the horizontal axis at value $x = 1$, indicating reduced pressure gradient values pertaining to saturated flow conditions. That is consistent with the definition of the reduced pressure gradient, Eq. (10), and gives an asymptotic behavior described by,

$$x\left( {Ca,r} \right)\mathop{\longrightarrow}\limits^{{{Ca} \to \infty }}1 + \kappa r,\quad A\left( {\log {Ca}} \right)\mathop{\longrightarrow}\limits^{{{Ca} \to \infty }}1$$

(19)

When flow conditions shift from intermediate to relatively high-Ca values, the interstitial flow progressively mutates from prevailing ganglion dynamics to a flow mixture rich in drop traffic flow and connected pathway flow. With further increase in Ca the non-wetting phase flow becomes bimodal, comprising connected pathways and drop traffic flow, whereby the relatively large drops of the non-wetting phase shutter into smaller droplets. The latter progressively loose contact with the pore walls, and the disconnected flow mutates to an emulsion-type flow mode. Consequently, in Eq. (19), the effects of menisci and capillary resistances fade away, $A \to 1$, and viscosity becomes the regulating factor, $\kappa r$. Details on the interstitial flow structure mutations as flow conditions intensify can be found in Valavanides (2018a).

The functional form, $A\left( {\log {Ca}} \right)$, describing the effect of the n/w menisci at different Ca values is revealed in the following paragraph by simple, least squares fitting.

4.2 Recovery of the Kernel Function $A\left( {\log {Ca}} \right)$

We will see how the kernel function $A\left( {\log {Ca}} \right)$ in Eq. (18) can be recovered for the particular flow system we examined. In principle, we need to have a sufficient amount of relative permeability values extending across a broad domain of flow conditions Ca and r. In the present paradigm, we will tap on the extensive DeProF model simulations (virtual experimens), covering a broad domain of flow conditions, $\log {Ca}$ and $\log r$, and for a variety of viscosity ratio values. Wettability and pore network geometry remained fixed across all simulations.

The reader who is not interested in following the technicalities of the fitting methodology may skip the details and directly refer to the result expressed in Eq. (26).

The functional form of the kernel function, $A\left( {\log {Ca}} \right)$, depends on the particular fluid system examined. Similar paradigms, in extracting $A\left( {\log {Ca}} \right)$ from laboratory experiments, are provided in Valavanides et al. (2020) and Karadimitriou et al. (2023).

4.3 Extraction of the Kernel Function, $A\left( {\log {Ca}} \right)$, by Fitting

We will implement least squares fitting to recover the $A\left( {\log {Ca}} \right)$ kernel function in Eq. (18). For any data set pertaining to a fixed-Ca simulation, $\log {Ca}_{i}$, we detect the value $A_{i} = A\left( {\log {Ca}_{i} } \right)$, that minimizes the sum of the squares of the fitting errors in each of the iso-Ca data sets (each set depicted with connected line in the diagrams exhibited on the left columns in Fig. 2). This is expressed as

$$\begin{aligned} & \min_{{A_{i} }} \left( {\mathop \sum \limits_{j = 1}^{{N_{i} }} \left[ {x\left( {\log {Ca}_{i} ,\log r_{j} } \right) - x_{ij} } \right]^{2} } \right) \mathop \Rightarrow \limits^{{ {\text{Eq. }} \left( {18} \right)}} \frac{{\text{d}}}{{{\text{d}}A_{i} }}\mathop \sum \limits_{j = 1}^{{N_{i} }} \left[ {A_{i} + \kappa r_{j} - x_{ij} } \right]^{2} = 0 \\ & \quad \Rightarrow A_{i} = \frac{1}{{N_{i} }}\left( {\mathop \sum \limits_{j = 1}^{{N_{i} }} x_{ij} - \kappa \mathop \sum \limits_{j = 1}^{{N_{i} }} r_{j} } \right),\quad 1 \le i \le 41,\quad j = 1, 2, \ldots ,N_{i} \le 21, \\ \end{aligned}$$

(20)

where N_i is the number of detected points (x_ij) pertaining to the constant capillary number value, ${Ca} = {Ca}_{i}$, for N_i different flowrate ratio values, r_j, ($j = 1, 2, \ldots ,N_{i} \le 21$). Please note that the last expression for $A_{i}$ in Eq. (20) is the average

$$A_{i} = \left\langle {A_{ij} } \right\rangle_{j} ,\quad 1 \le i \le 41,\quad 1 \le j \le N_{i} \le 21$$

(21)

We recall here that each set $A_{i} = A\left( {\log {Ca}_{i} } \right),\;{ }1 \le i \le 41$ pertains to a particular value of the n/w viscosity ratio, $\kappa$. So, for each examined value of the viscosity ratio, we get a different set comprising 41 pairs of values, $\left\{ {A_{i} ,\log {Ca}_{i} } \right\}, \;1 \le i \le 41$.

We repeat the procedure for each of the 7 viscosity ratio values, $\kappa \in \left\{ {0.33, 0.67, 1.0, 1.5, 3.0, 9.0, 20} \right\}$ that we have examined in the DeProF model simulations. These values are plotted in the diagram Fig. 3a. The 7 sets of coefficient values, $A_{i} ,\;1 \le i \le 41$, are depicted using 7 types of markers. Each type of marker indicates 41 data values $A_{i} , \;1 \le i \le 41$, pertaining to the data fitting, Eq. (20), for the corresponding constant-Ca_i runs. It is obvious that the 7 sets of $\left\{ {A_{i} ,\log {Ca}_{i} } \right\},\; 1 \le i \le 41$ points are lined-up on a tight formation. We may assess how the “tightness” is distributed over the 41 $\log {Ca}_{i}$ values by calculating the corresponding variances.

Fig. 3

a Values of the coefficients $A_{i} , 1 \le i \le 41$, used in Eq. (23) for the 41 constant-Ca runs. Each type of marker indicates a set of 41 data values $\left\{ {{Ca}_{i} , A_{i} } \right\}$ and pertains to a system with different viscosity ratio values, $\kappa = \tilde{\mu }_{{\text{n}}} /\tilde{\mu }_{{\text{w}}}$. b Blow-up detail of the calculated variance in each of the 41 log $\log A_{i}$ values over the 7 viscosity ratios in (a). (c) The corresponding 41 $\kappa$-averaged values, $\left\langle A \right\rangle_{i}$, indicated by red dot markers ( ). These are fitted by a function $A\left( {\log {Ca}} \right)$ (black, dash-dot curve), of the form Eq. (26)

The 41 ${Ca}_{i}$ variances over the 7 viscosity ratios are evaluated by

$$\sigma_{i}^{2} = \frac{1}{7}\mathop \sum \limits_{m = 1}^{7} \left( {\log A_{i} - \frac{1}{7}\mathop \sum \limits_{m = 1}^{7} \log A_{m} } \right)^{2} ,\quad 1 \le i \le 41$$

(22)

The 41 variances per ${Ca}_{i}$ of each set of $\log A$ values, pertaining to the 7 different viscosity ratios, are presented in the diagram, Fig. 3b. Variances pertaining to the capillarity dominated regimes, $\log {Ca} < - 6,$ are a bit higher than those in the capillary/viscous flow regimes, $- 6 < \log {Ca}$. Nevertheless, as the variances are quite small, we may calculate the average over the viscosity ratio values, $\left\langle {A_{i} } \right\rangle_{m}$, as

$$\left\langle {A_{i} } \right\rangle_{m} = \frac{1}{7}\mathop \sum \limits_{m = 1}^{7} A_{i,m} 1 \le i \le 41, \quad \kappa_{m} \in \left\{ {0.33, 0.67, 1.0, 1.5, 3.0, 9.0, 20} \right\}$$

(23)

The 41 averages calculated from Eq. (23) are plotted on the diagram Fig. 3c with 41 red dot markers ().

On the diagrams Fig. 3a and b, we may observe two distinct regions along the $\log {Ca}$ domain. At the low-Ca regime, the markers are almost aligned on a straight line with negative inclination, to be calculated by fitting. As the capillary number is increased, the markers tend to progressively attain the lowest physically admissible value $\left( {\log A \to 0} \right)$, and in doing so, they align asymptotically to the horizontal direction.

Focusing on the diagram Fig. 3c, each of the $1 \le i \le 41$ red dot markers () indicates the corresponding average $\left\langle {A_{i} } \right\rangle_{m}$ over the $1 \le m \le 7$ viscosity ratios, calculated from Eq. (23). The red dot markers () align along the inclined continuous line in black; the latter meets the horizontal axis at an obtuse angle at point C, at abscissa $\log {Ca}_{0}$.

We may then fit these markers by a bilinear function of the form

$$\log {Ca} = \log {Ca}_{0} + \frac{{C_{0} }}{{\left( {\log A} \right)^{2} }} - C_{3} \log A$$

(24)

where C₀ is a measure of the approach to the two asymptotes (the higher this value, the greater the distance from the asymptotes); $\left( { - 1/C_{3} } \right)$ is the gradient of the inclined asymptote; $\log {Ca}_{0}$ is the abscissa of the intersection of the two asymptotes (at point C).

Best fitting of the ensemble of $\log A$ values, for the entire set of viscosity ratios examined in the simulations, with Eq. (24), gives the values of the coefficients presented in Table 1. The curve fitting is plotted by the black dash-dot line in Fig. 3c.

Table 1 Estimated values of the $A\left( {\log {Ca}} \right)$ function coefficients, Eq. (24)

The red dashed line, pivoted at $\log {Ca}_{{{\text{pm}}}} = - 4.75$, () with negative gradient 1:1, see Eq. (17), is the asymptote delineated in the right column diagrams in Fig. 2. That is an indication of the self-similarity properties of the kernel function $A\left( {\log {Ca}} \right)$.

Returning to Eq. (24), $\log A$ is an implicit function of $\log {Ca}$. We need to solve the corresponding cubic equation in terms of $\log A$,

$$\left( {\log A} \right)^{3} C_{3} + \left( {\log A} \right)^{2} \log \frac{{{Ca}}}{{{Ca}_{0} }} - C_{0} = 0$$

(25)

The solution to the previous cubic equation is derived in “Appendix II” and is given by the following expression,

$$\log A\left( {\log {Ca}} \right) = \left\{ {\begin{array}{*{20}l} { - \frac{D}{{3C_{3} }}\left[ {1 + 2\cosh \left( {\frac{1}{3}\arccos h\left[ {1 - 2\frac{{B^{3} }}{{D^{3} }}} \right]} \right)} \right],} \hfill & {\quad D < 1} \hfill \\ {\sqrt[3]{{C_{0} /C_{3} }}} \hfill & {\quad D = 1} \hfill \\ { - \frac{D}{{3C_{3} }}\left[ {1 - 2\cosh \left( {\frac{1}{3}\arccos h\left[ {2\frac{{B^{3} }}{{D^{3} }} - 1} \right]} \right)} \right]} \hfill & {\quad 1 < D < B} \hfill \\ { - \frac{D}{{3C_{3} }}\left[ {1 - 2\cos \left( {\frac{1}{3}\arccos \left[ {2\frac{{B^{3} }}{{D^{3} }} - 1} \right]} \right)} \right]} \hfill & {\quad B \le D} \hfill \\ \end{array} } \right.$$

(26)

where

$$B = \sqrt[3]{{\frac{27}{4}C_{0} C_{3}^{2} }}\quad {\text{and}}\quad D = \log \frac{{{Ca}}}{{{Ca}_{0} }}$$

(27)

One may select to choose between the implicit or explicit expressions for $\log A\left( {\log {Ca}} \right)$, Eqs. (24) and (26), respectively. Note, the expression provided in Eq. (26) pertains to the particular fluid model system examined in the simulations and has no universal application. Evidently, each flow system, comprising the two fluids and the porous medium, has its own “finger-print” expression for $\log A\left( {\log {Ca}} \right)$. Similar paradigms in extracting $A\left( {\log {Ca}} \right)$ from laboratory measurements of different flow systems can be found in the literature (Valavanides et al. 2020; Karadimitriou et al. 2023). In the next section, we will interpret the physics underlying the $A\left( {\log {Ca}} \right)$ curve.

4.4 Physical Interpretation of the Kernel, $A\left( {\log {Ca}} \right)$: The Intrinsic Dynamic Capillary Pressure Function

As described in the previous paragraph, by fitting the data obtained from the simulations, Fig. 3, we get the functional form of $A\left( {\log {Ca}} \right)$. Obviously the values of the constants, Ca₀, C₀ and C₃, do not change with the viscosity ratio, at least not substantially and to the extent that algorithmic deficiencies of the DeProF model are unavoidable. Therefore, simulations indicate that $A\left( {\log {Ca}} \right)$ is invariant to changes in viscosity ratio.

Now, rearranging Eq. (18), we get

$$A\left( {\log {Ca}} \right) = x\left( {{Ca}, r} \right) - \kappa r$$

(28)

In that format, the function $A\left( {\log {Ca}} \right)$ is describing the effect of the n/w menisci on the transport configuration of the flow system at different flow conditions, i.e., at different flow intensities, or different Ca and r values. In Eq. (28), by subtracting the effects of flow resistances due to bulk viscosities, $\kappa r$, from the reduced pressure gradient, x, we get the relative contribution of the dynamic capillary resistances to the flow. Therefore, the values of the constants, Ca₀, C₀, and C₃, in Eq. (18) are expected to change with wettability (dynamic advancing and receding contact angles) and/or pore network geometry.

The dimensionless function, $A\left( {\log {Ca}} \right)$, may be given the name Intrinsic Dynamic Capillary Pressure—IDCP function. As such, the IDCP function is a characteristic property of the flow system, comprising the two fluids and the porous medium. It depends on capillarity related characteristics, i.e., the tripartite interaction between interfacial tension, wettability (dynamic advancing and receding contact angles) and the pore network geometry. The term dynamic in IDCP is used to indicate that capillary pressure is evaluated at different flow conditions, not in static equilibrium.

The IDCP curve plotted in the diagram in Fig. 3c (black dash-dot curve) represents the particular fluid system examined in the simulations (Eqs. (26), (27) and Table 1). Should we have had the simulations rerun—with either different wettability properties or different pore network geometry—its functional form, Eq. (28), would have changed. Any changes would be due to changes in the constituent physical variables of Eq. (28) and, most critically, to changes in the structure of the response of the system, $x\left( {Ca, r} \right)$. That would be the case if, the absolute permeability of the network in saturated flow conditions remains fixed, and changes would only pertain to wettability aspects. Albeit the IDCP curve is revealed from REV—virtually ex-core—measurements, it contains the essential information on the interaction between the structure of the network (associated with capillarity) and the motion of the n/w menisci. In that context, the IDCP curve surfaces-up, to a superficial, ex-core observer, the latent information associated with the ensemble of flow mechanisms at the pore scale, and the corresponding interstitial flow structures.

In the current paradigm of the IDCP curve in diagram Fig. 3c, we may identify 3 distinct regions. Starting from the capillary flow domain at relatively low-Ca values $\left( {\log {Ca} < - 5} \right)$, the IDCP curve is decreasing in an almost linear fashion, indicating a progressive mobilization of stranded fluidic elements, mainly the larger size ganglia. Then, there is a transition region of mixed capillary-viscous flow at moderate-Ca values $\left( { - 5 < \log {Ca} < - 4} \right)$, where the IDCP curve gradient progressively decreases. This is because the remaining stranded ganglia of smaller size has a smaller probability of mobilization. Then, moving to the viscous dominated flow regime of high-Ca values $\left( { - 4 < \log {Ca}} \right)$, the transitory behavior of the flow system turns into a smooth asymptotic behavior toward saturated flow $\left( {A \to 1} \right)$, as explained in the paragraph following Eq. (19).

4.5 Maps of Reduced Pressure Gradient and Relative Permeabilities

Using the scaling function Eqs. (18) and (26) with coefficient values from Table 1, we may reconstruct 2D, iso-Ca and iso-r diagrams, similar to those presented in Fig. 2. The diagrams in Fig. 4 provide an indicative direct comparison between plots of the source data (from DeProF model simulations) with plots of the scaling function derived in the previous section. The diagrams are paired. Diagrams of values predicted from DeProF model simulations are aligned on columns (a) and (c), Fig. 4. Plots of the analytical expression that fits the corresponding source data are aligned on columns (b) and (d). The fitting is quite consistent and accurate.

Fig. 4

Reduced pressure gradient values, x, for different values of capillary number, Ca, and flow rate ratio, r, and for various n/w viscosity ratio values, $\kappa \in \left\{ {0.33, 1.0, 1.5, 20} \right\}$. Diagrams in columns (a) and (c) plot the simulation results, Fig. 2. Diagrams in columns (b) and (d) show plots of $x\left( {Ca, r} \right)$ calculated analytically from the scaling function, Eqs. (18) and (26) with parameter values from Table 1. The fitting is quite consistent and accurate, both qualitatively and quantitatively

Diagrams of $x\left( {Ca, r} \right)$ and combined diagrams of $k_{{{\text{rn}}}} \left( {Ca, r} \right)$ and $k_{{{\text{rw}}}} \left( {Ca,r} \right)$ for different fluids with viscosity ratio values, $\kappa \in \left\{ {0.33, 0.67, 1.0, 1.5, 3.0, 9.0, 20} \right\}$, are presented in Figs. 5 and 6, respectively. The diagrams in Fig. 4, columns (b) and (d), are formed by intersections of the $x\left( {Ca, r} \right)$ 3D surface with iso-Ca and iso-r planes, perpendicular to the $\log {Ca}$ and the $\log r$ axes, respectively. These are merged to draw the 3D diagrams in Fig. 5. The combined relative permeability diagrams of $k_{{{\text{rn}}}}$ and $k_{{{\text{rw}}}}$ in Fig. 6 are drawn using Eq. (11).

Fig. 5

3D plots of the reduced pressure gradient, x, as a function of the capillary number, Ca, and of the flow rate ratio, r, based on Eqs. (18) and (26) with parameter values from Table 1, and for and for various n/w viscosity ratio values, $\kappa \in \left\{ {0.33, 1.0, 1.5, 20} \right\}$

Fig. 6

3D plots of the relative permeability for the wetting and non-wetting phase, k_rw (blue) and k_rn (light red), as a function of the flow rate ratio, r, and the capillary number, Ca, based on Eqs. (11), (18) and (26), with parameter values from Table 1, and for pairs of fluids with different n/w viscosity ratio values, $\kappa \in \left\{ {0.33, 1.0, 1.5, 20} \right\}$. The plane, S-shaped curve, formed by the intersection of the two relative permeability surfaces, the locus of cross-over relative permeabilities is invariant to viscosity ratio changes

We may focus on the intersection of the relative permeability surfaces, forming an S-type plane curve, the locus of cross-over relative permeability values, $k_{{{\text{r}}x}} = k_{{{\text{rn}}}} = k_{{{\text{rw}}}}$. We may observe its projections on the 3 mutually orthogonal planes of reference, $k_{{{\text{rn}}}} = k_{{{\text{rw}}}} = 0$, $\log {Ca} = - 8$ and $\log r = - 2$. The two projections on the planes $k_{{{\text{rn}}}} = k_{{{\text{rw}}}} = 0$ and $\log {Ca} = - 8$ are aligned on the two straight lines, $r = r_{x} = \kappa^{ - 1}$, perpendicular to each other. That is a consequence of the equivalence between the flow rate ratio and the mobility ratio, Eq. (8), in fully developed flow: At the cross-over relative permeability flow conditions, the flow rate ratio and the mobility ratio become reciprocal to the viscosity ratio,

$$\forall r = r_{x} : k_{{{\text{rn}}}} \left( {{Ca},r_{x} } \right) = k_{{{\text{rw}}}} \left( {{Ca},r_{x} } \right) \mathop \Rightarrow \limits^{{{\text{Eq. }}\left( 8 \right)}} r_{x} = 1/\kappa$$

(29)

The projection of the cross-over relative permeability curve on any fixed-Ca plane is invariant to viscosity ratio changes, so long as both wettability and pore network geometry remain fixed. Therefore, cross-over relative permeability conditions, $k_{{{\text{rn}}}} = k_{{{\text{rw}}}} = k_{{{\text{r}}x}}$ at $r_{x} = 1/\kappa$, will remain unaffected when flow systems with different viscosity ratio but with the same wettability and pore network geometry are examined.

This latent (or less-expected) characteristic property, comes as a direct consequence of the invariance of the IDCP curve, $A\left( {{Ca}} \right)$, to viscosity ratio changes (see Fig. 3a), and altogether may lead to the conjecture that the functional dependence of the cross-over relative permeability on Ca is a pure capillarity dominated system characteristic. As such, it could be used as an effective, pore network structure identity. Because of its potential implications in improving SCAL technology, this conjecture, merits systematic laboratory verification.

5 Energy Efficiency and Critical Flow Conditions

The energy efficiency or energy utilization index, f_EU, provides a reduced measure of the energy efficiency of the process. It is defined as the flow rate of the non-wetting phase per unit of the total hydraulic power spent, or equivalently, provided externally to the flow system by the driving/injection pumps to maintain two-phase flow at set flow conditions, Ca and r (Valavanides et al. 2016). It is used as a flow analysis and system characterization variable. The energy efficiency index may be evaluated in terms of macroscopic (REV) measurements,

$$f_{{{\text{EU}}}} = \frac{{k_{{{\text{rn}}}} }}{{\kappa \left( {r + 1} \right)}} = \frac{{rk_{{{\text{rw}}}} }}{r + 1} = \frac{r}{{x\left( {r + 1} \right)}} = \frac{{f_{{\text{n}}} }}{x}$$

(30)

The energy efficiency index has an important characteristic. For every fixed value of the capillary number, Ca, there exists a single value of the flow rate ratio, r*, for which the energy efficiency index, $f_{{{\text{EU}}}}^{*}$, attains a maximum value. This maximum is local; changing Ca to Ca′, the new maximum is met at another unique value $r^{*\prime }$. Therefore, for every flow system, comprising the two fluids and the porous medium, a unique locus of energy efficiency maxima is formed, $r^{*} \left( {{Ca}} \right)$. Flow conditions matching the $r^{*} \left( {{Ca}} \right)$ locus are called critical flow conditions (CFC) (Valavanides 2018b). Critical flow conditions can be revealed by special core analysis (Valavanides et al. 2016; 2020; Karadimitriou et al. 2023) provided that measurements are taken over an extended range of fully developed flow conditions.

Given the scaling function for the reduced pressure gradient, $x\left( {Ca, r} \right)$, Eq. (18), we may obtain, through Eq. (30), the analytic expression for the energy efficiency index, $f_{{{\text{EU}}}} \left( {Ca, r} \right)$. We may also derive the analytic expression for the locus of CFC by its conceptual definition,

$$\left. {\frac{{\partial f_{{{\text{EU}}}} }}{\partial r}} \right|_{r = r*} = 0 \Leftrightarrow \frac{\partial }{\partial r}\left( {\frac{{rk_{{{\text{rw}}}} }}{r + 1}} \right) = \frac{\partial }{\partial r}\left( {\frac{r}{r + 1} \frac{1}{{x\left( {Ca,r} \right)}}} \right) = 0$$

(31)

whereby importing the expression for the $x\left( {Ca,r} \right)$ scaling, Eq. (18), we get the CFC locus.

$$\frac{{\text{d}}}{{{\text{d}}r}}\frac{r}{{\left( {r + 1} \right)\left( {A + \kappa r} \right)}} = 0 \Rightarrow A - r^{*2} \kappa = 0 \Rightarrow r^{*} \left( {Ca} \right) = \sqrt {\frac{{A\left( {{Ca}} \right)}}{\kappa }}$$

(32)

The locus of critical flow conditions is configured by two separate factors, the viscosity ratio, $\kappa$, incorporating the bulk viscosity effects, and the IDCP function, $A\left( {{Ca}} \right)$, incorporating the capillarity effects. That is something expected as $f_{{{\text{EU}}}}^{*} \left( {Ca,r } \right)$ is essentially the minimum energy partitioning between viscosity- and capillarity-induced dissipation.

Plots of the energy efficiency index and critical flow conditions as a function of Ca and r, Eqs. (30), (18) and (26), for various viscosity ratio systems, are presented in Fig. 7. In every diagram, the 3D surface with the iso-$f_{{{\text{EU}}}}$ contour lines indicates the dependence of the energy efficiency index on $\log {Ca}$ and $\log r$. The thick red line indicates the trajectory of maximum energy efficiency values, $f_{{{\text{EU}}}}^{*} \left( {Ca,r } \right) = f_{{{\text{EU}}}} \left( {r^{*} \left( {Ca} \right)} \right)$, based on Eq. (32). On that trajectory, magenta colored ball markers are used to pinpoint the trajectory of $f_{{{\text{EU}}}}^{*} \left( {Ca,r } \right)$ over order of magnitude shifts in Ca, [$\log {Ca} \in \left\{ { - 4, - 5, - 6, - 7, - 8} \right\}$].

Fig. 7

Energy efficiency maps, $f_{{{\text{EU}}}} \left( {Ca, r} \right)$, based on Eqs. (30), for fluids with various n/w viscosity ratio values, $\kappa$. The maximum energy efficiency, $f_{{{\text{EU}}}}^{*} \left( {Ca,r^{*} } \right)$, as well as its horizontal projection, $r^{*} \left( {{Ca}} \right)$, are depicted by the red, thick curves. The curtain of drop lines maps the locus of critical flow conditions, $r^{*} \left( {{Ca}} \right)$; it is suspended from a horizontal plane at a height equal to the nominal value of the maximum attainable energy efficiency for each two-fluid system (ceiling of efficiency), $f_{{{\text{EU}}\infty }}^{*}$. Thinner red curves are projections of $f_{{{\text{EU}}}}^{*} \left( {Ca,r^{*} } \right)$ on the vertical planes. Ball markers are used to pinpoint order of magnitude changes in Ca

The projection of the trajectory of maximum energy efficiency, $f_{{{\text{EU}}}}^{*} \left( {Ca,r } \right)$, showing the locus of critical flow conditions, $r^{*} \left( {Ca} \right)$, on the $\log {Ca} \times \log r$ plain, lays—barely visible—under the $f_{{{\text{EU}}}} \left( {Ca, r} \right)$ surface. To show the locus clearly, the $f_{{{\text{EU}}}}^{*} \left( {Ca,r } \right)$ curve is re-projected, on a horizontal plane $\left( {{Ca} \times r } \right)$ located just above the 3D surface. Very thin red lines connecting the $f_{{{\text{EU}}}} \left( {Ca, r} \right)$ surface ridge to its new projection appear as a cylindrical curtain. The new projection depicted by a red dash–dotted curve lays at a height equal to the nominal value of the maximum attainable energy efficiency—the “ceiling of efficiency”—for the particular fluid system—better, for the particular value of the viscosity ratio (Valavanides 2018b). That value corresponds to the critical flow rate ratio, specifically, $r_{\infty }^{*} = 1/\sqrt \kappa$, and is theoretically estimated as

$$f_{{{\text{EU}}}} \left( {r^{*} \left( {{Ca}} \right)} \right) \mathop{\longrightarrow}\limits^{{{Ca} \to \infty }} f_{{{\text{EU}}\infty }}^{*} = 1/\left( {1 + \sqrt \kappa } \right)^{2}$$

(33)

The straight line asymptote, $r = r_{\infty }^{*} = 1/\sqrt \kappa$, is depicted with dashed red line and lays, barely visible, under the $f_{{{\text{EU}}}} \left( {{Ca}, r} \right)$ surface. Both of the aforementioned nominal values, $r^{*}$ and $f_{{{\text{EU}}\infty }}^{*}$, are estimated by considering the asymptotic limit at the high-end of the capillary number domain, whereby the flow resistance due to the effects of the n/w menisci and phenomena associated with capillarity, become negligible when compared to bulk viscosity flow resistances (Valavanides 2018b, Appendix).

Please note that Eq. (33) is recovered directly from Eq. (32) as ${Ca} \to \infty$ and $\log {Ca} \to 0 \Rightarrow A\left( {{Ca}} \right) \to 1$. In particular, Eq. (32) was derived from the DeProF simulations, whereas Eq. (33) from energy analysis at viscosity-dominated flow conditions (Valavanides 2018b, Appendix).

The shapes of the energy efficiency surface ridge, $f_{{{\text{EU}}}} \left( {r^{*} \left( {Ca} \right)} \right)$ and of the locus of critical flow conditions, $r^{*} \left( {{Ca}} \right)$, become more clear if we observe their projections on the three reference planes, Fig. 7. In particular, the projection of the maximum energy efficiency on the $\log r = - 2$ plane attains an S-shaped curve, confined asymptotically between the two horizontal lines, $f_{{{\text{EU}}}} = 0$ and $f_{{{\text{EU}}}} = f_{{{\text{EU}}\infty }}^{*} = 1/\left( {1 + \sqrt \kappa } \right)^{2}$. Similarly, the projection on the $\log {Ca} = - 8$ plane attains a smooth, half-U shaped, bilinear curve, delimited by two mutually perpendicular asymptotes, $f_{{{\text{EU}}}} = 0$ and $\log r = \log r_{\infty }^{*} = - 0.5\log \kappa$. Α set of three or four parameters may be used to describe, at an adequate level of approximation the particular S-shape projection. Furthermore, we may normalize the S-shape expression—associated with any particular two-fluid system—with the corresponding value of the maximum attainable efficiency (a n/w fluid system property) and, in doing so, we may also scale the Ca values, conventionally defined by Eq. (2), to a universal, system-reduced capillary number, defined as ${Ca}_{{\text{R}}} = \left( {\frac{{{Ca}}}{C}} \right)^{1/z}$, with parameters C and z infusing the combined effects of wettability and viscosity ratio of the two fluid/porous medium system (see Valavanides 2018b, Eq. (54)).

In such case, all the S-shape curves, pertaining to the same porous medium but with different viscosity ratios, are expected to collapse into a single, normalized S-shape, identical to the S-shape pertaining to the system with equal viscosities, $\kappa = 1$, as described in the same paper. This way the combined effect of the two bulk viscosities (normalized by the effect of the viscosity ratio) is decoupled from the combined effects of wettability and pore network geometry. The resulting normalized expression of the S-shape function could serve as the “phenotype” of the pore network for a particular wettability.

Τhe previous diagrams may be integrated into a universal relative permeability and energy efficiency diagram for fully developed flow in pore networks. Two diagrams, pertaining to indicative cases, with viscosity ratio values, $\kappa = 0.67$ and $\kappa = 1.5$, are presented in Fig. 8. The diagrams cover a domain of flow conditions for $- 8 \le \log {Ca} \le - 3.6$ and $- 2 \le \log r \le 2$. Note, the diagrams are drawn from analytical expressions derived in the previous sections.

Fig. 8

Universal, energy efficiency maps describing steady-state fully developed two-phase flow in pore networks for two values of n/w viscosity ratio, $\kappa = 0.67$ (top) and $\kappa = 1.5$ (bottom). The insert is the first impression of a universal diagram (adapted from Valavanides 2018b)

Plots of the relative permeability values as a function of $\log r$ are presented as trajectory curves for 5 fixed-Ca values, $\log {a}_{i} \in \left\{ { - 8, - 7, - 6, - 5, - 4} \right\}$. These trajectories are the intersections of the 5 fixed-Ca planes with the relative permeability surfaces, $k_{{{\text{rn}}}} \left( {Ca,r} \right)$ and $k_{{{\text{rw}}}} \left( {Ca,r} \right)$, plotted in Fig. 6. The relative permeability plots for the non-wetting phase are drawn in red color and those drawn for the wetting phase in blue color, in consistency with the coloring of the parent surfaces. Markers of different shape/size have been assigned to each fixed-Ca pair of relative permeability curves. The five cross-over relative permeability values at the crossings of the corresponding five pairs of relative permeability curves, are indicated with larger balls (in gray color), while the entire set of cross-over relative permeability values, is depicted by the black dashed, S-shape plane curve. All cross-over points correspond to the same flow rate ratio value, r_x; this is why the S-shape curve lays on the $r = r_{x} = 1/\kappa$ plane. For the indicative n/w viscosity ratio values, the fixed-r planes correspond to $\log r_{x} = - \log 0.67 = 0.1739$ on the top diagram $\left( {\kappa = 0.67} \right)$ and to $\log r_{x} = - \log 1.5 = - 0.1760$ on the bottom diagram $\left( {\kappa = 1.5} \right)$. The projections of the cross-over relative permeability surfaces on the two reference planes are depicted with gray, dashed lines; in particular, with a straight, thin gray line on the $\log {Ca} = - 8$ plane and an S-shape, dash gray line on the $\log r = 2$ plane.

Plot of the energy efficiency as a function of the flow conditions, $f_{{{\text{EU}}}} \left( {Ca, r} \right)$, Eq. (30), is shown by the gray color scale 3D surface. Contour lines and mesh lines correspond to the scaling and grid lines on the reference planes. The ridge of the energy efficiency surface, indicating the local maxima attained at critical flow conditions, is delineated by the continuous, thick red curve. The intersections with the fixed-Ca planes, $\log {Ca}_{i} \in \left\{ { - 8, - 7, - 6, - 5, - 4} \right\}$, are marked with violet ball markers. The projection on the $z = 0$ reference plane delineates with the red curve the critical flow conditions, $r^{*} \left( {Ca} \right)$; it is partly visible as it is obscured by the f_EU surface.

Projections on the $\log {Ca} = - 8$ and $\log r = 2$ reference planes are also plotted to depict the inherent configuration characteristics of the maximum energy efficiency curve. The projection on the $z = f_{{{\text{EU}}\infty }}^{*} = 1/\left( {1 + \sqrt \kappa } \right)^{2}$ plane, depicted by the red, dash–dotted plane curve provides a clearer layout of the locus of critical flow conditions. Again, as in the diagrams in Fig. 7, the drop lines form a cylindrical curtain, starting from the ridge of the $f_{{{\text{EU}}}} = \left( {Ca,r} \right)$ surface up to the ‘ceiling of efficiency’ (at the maximum level of attainable efficiency). The corresponding nominal values are: $f_{{{\text{EU}}\infty }}^{*} = 1/\left( {1 + \sqrt {0.67} } \right)^{2} = 0.3024$ on the top diagram, and $f_{{{\text{EU}}\infty }}^{*} = 1/\left( {1 + 1.5} \right)^{2} = 0.160$ on the bottom diagram. These limits are asymptotically reached at the corresponding nominal asymptotic values, $r_{\infty }^{*}$, of the critical flow rate ratio at very high-capillary number (fully viscous flow, ${Ca} \to \infty$), given by $\log r_{\infty }^{*} = \log \left( {1/\sqrt \kappa } \right)$, i.e., $\log r_{\infty }^{*} = - 0.5 \times \log 0.67 = 0.0870$ and $\log r_{\infty }^{*} = - 0.5 \times \log 1.5 = - 0.0880$, for the top and bottom diagram, respectively.

The energy efficiency map of any two-fluids /porous medium flow system in Fig. 7 or Fig. 8, provides a normative framework for assessing /evaluating the viscous/capillary character of any flow within that system, based on the imposed values of capillary number and flow rate ratio.

This type of diagram is an improved version of the classical phase diagram, proposed by Lenormand et al. (1988) and Lenormand (1990), coarsely depicting the flow structure map in terms of the capillary number and the viscosity ratio, as well as its 3D extension proposed by Ewing and Berkowitz (2001) to account for gravity effects.

6 Conclusions and Discussion

A generic form of flow rate dependency of the relative permeabilities for steady-state, fully developed two-phase flow in porous media is proposed. The functional form is the result of a two-stage derivation, i.e., systematic simulations and data fitting, extending over a broad range of flow conditions. The latter is expressed in terms of the capillary number, Ca, and the flow rate ratio, r. A variety of two-fluid viscosity ratio systems, $\kappa$, are examined.

In the first stage, virtual experiments of steady-state, fully developed, concurrent flow of two immiscible fluids within a homogeneous model pore network were performed implementing the DeProF model algorithm. The model pore network corresponded to a virtual core of infinite length in the absence of any end-effects. The systematic simulations examined an extended range of flow conditions, spanning 5 orders of magnitude over the capillary number, Ca, and the flow rate ratio, r, and for a variety of viscosity ratio systems, $\kappa$. The main product of the simulations was a dense matrix of reduced pressure gradient values for different values ${Ca}_{i}$ and $r_{j}$, $x_{ij} \left( {{Ca}_{i} ,r_{j} } \right)$. The reduced pressure gradient measures the relative increase in the pressure gradient of the mixed flow against that of a saturated flow of the non-wetting phase at the same flow rate (superficial velocity). By definition, in fully developed flow conditions, the reduced pressure gradient is equal to the inverse of the relative permeability of the non-wetting phase. The system properties associated with interface/capillary phenomena, i.e., interfacial tension, wettability (dynamic advancing and receding contact angles) and pore network structure, were kept fixed. In that context, it was possible to observe the effects of viscosity, independently from the effects of capillarity. Apart from reduced pressure gradient charts, the systematic simulations produced a complete description of the interstitial flow structure.

In the second stage, combining the essential physics underlying the process with data fitting on the charts produced by the simulations, we derived a universal functional form to describe the dependence of the reduced pressure gradient, x, in terms of the capillary number, Ca, and the flowrate ratio, r. The proposed functional form extends over orders of magnitude in Ca and r, and it is expressed as

$$x\left( {Ca,r} \right) = A\left( {\log {Ca}} \right) + \kappa r$$

(34)

whereby the effects of capillarity and viscosity are partitioned in two decoupled terms. The linear term describes the fractional contribution of the bulk viscosities through the N/W viscosity ratio, $\kappa$. The nonlinear term, $A\left( {\log {Ca}} \right)$, accounts the contribution of capillarity at different flow conditions. That nonlinear term is described as the Intrinsic Dynamic Capillary Pressure function. The relative contributions of those two terms depend on the flow conditions. The flow conditions that minimize the total energy dissipation per unit of non-wetting phase flow rate are called critical flow conditions.

The functional form of the flow dependency of relative permeabilities is recovered analytically from the reduced pressure gradient function, by implementing the conventional formulation of the phenomenological fractional Darcy law for fully developed flow, Eqs. (11). The functional form of the energy efficiency and the locus of critical flow conditions can also be derived analytically.

The Intrinsic Dynamic Capillary Pressure curve, formed by the ensemble of reduced, dynamic capillary pressure values at different flow conditions, accounted by $A\left( {\log {Ca}} \right)$ in Eq. (34), describes the transition of the capillarity effects on the average flow, between the extremities of the domain of flow conditions, i.e. from capillarity-dominated flows to viscous flows. The IDCP curve is unique for every flow system, and, in that context, it can be used as the identity of the system. Moreover, the IDCP curve is directly related to the physicochemical properties of the two-fluid system and its affinity to the pore network characteristics associated with dynamic capillary phenomena (geometry, topology, wettability).

One of the potential applications of the proposed scaling is in SCAL. That needs to be considered on the basis of established fully developed flow conditions and end-effects. The DeProF model is built around the equality of pressure gradients in both phases. That condition is attained when fully developed flow is in place. That is not a condition always attained in SCAL measurements, as evolution of the interstitial flow depends on the structure of the pore network, the wettability of the fluid system and the flow conditions (the intensity of the co-injection). In general, end-effects are pronounced when the role and effects of capillarity-associated phenomena are not suppressed by viscous resistances. The proposed methodology can be applied in SCAL but the results will be conditionally biased by end-effects. Yet, implementing a few checks, some of these simple, e.g., on the equality between imposed flow rate ratio and measured mobility ratio, and some a bit more complicated, e.g., energy efficiency vs flow conditions, we may detect the presence of end-effects. We have seen that capability in on-going research (Valavanides et al. 2020; Karadimitriou et al. 2023), whereby the effective IDCP functional form has been recovered implementing a similar methodology in fitting the ex-core measurements. Yet, the missing part(s) of the puzzle is on evaluating the extent/severity of end-effects and/or being able to cope with end-effects in un-biasing the ex-core measurements to get a concise and accurate (trustworthy) relative permeability map.

Another interesting application of the proposed approach is in revealing the structure of the interstitial flow. A convincing paradigm on how the IDCP curve may be used as a forensic tool in revealing the structure of the interstitial flow is the systematic SCAL study performed on a core of natural Clasach sandstone (Valavanides et al. 2020). An analysis of the measured relative permeabilities, similar to that described in Sect. 4.3 revealed a sharply decreasing intrinsic dynamic capillary pressure function, $A\left( {\log {Ca}} \right)$, over moderate- to/high-Ca flow conditions. That seemed to be contradicting the smooth, asymptotic transition to zero $\left( {\log A \to 0} \right)$ depicted in Fig. 3a. The sharp decrease in A at moderate/high-Ca flow conditions can be associated with a sharp reduction in capillary resistances. This could be attributed on progressive eradication of n/w menisci contacting the pore walls. And this could only happen if the small disconnected fluidic elements of the non-wetting phase (ganglia and large drops) break-up into tiny droplets and the immiscible flow of larger drops mutates into some kind of emulsion flow. Reviewing the conditions of the experiments, it turned out that the suspected emulsification was in fact the result of adding surfactant to suppress the interfacial tension in order to impose flow conditions at very high-Ca values. The particular structure of the intrinsic dynamic capillary pressure curve, revealed the onset of emulsification at high-Ca flowrates, an intrinsic flow characteristic, from ex-core measurements. The paradigm indicates the forensic capabilities of the IDCP curve.

Overall, the presented flow analysis is based on a set of appropriately reduced variables, eliminating redundancies, yet without compromising the specificity associated with the description of the process and/or the flow system. The derived analytical expressions of flow rate dependency fit surprising well the predicted values from systematic simulations with the DeProF model. They also provide an additional proof of consistency with respect to the existence of the universal relative permeability and energy efficiency map proposed by Valavanides (2018b), based on an energy analysis of the flow process, from first principles, phenomenological observations and independently of modeling assumptions.

In addition, generalized specific characteristic invariants, pertaining to the two-fluid and porous medium flow system, were revealed: the locus of Critical Flow Conditions, the locus of cross-over relative permeability conditions, as well as the Intrinsic Dynamic Capillary Pressure curve. All of these can be used as flow system identities at different degrees of specificity, i.e., as “genotype” of the two-fluid/porous medium flow system or “phenotype” of the porous medium. This could be a strong tool in developing flow system- or rock-typing methodologies and techniques.

Moreover, the ability to handle a functional form of the relative permeabilities, accounting for a mechanistic, flow rate dependency, may improve the specificity of field-scale simulators, or increase the efficiency in machine learning interventions.

Future research should address how capillarity-related system characteristics, in particular dynamic wettability or network geometry, may affect the loci of Critical Flow Conditions and cross-over relative permeabilities or the Intrinsic Dynamic Capillary Pressure curve. In that context, sensitivity analysis needs to be run on virtual systems, model pore networks or natural cores. Another potential application is in assessing the extent of end-effects in core analysis from ex-core measurements.

Appendix

1.1 I. Non-fully Developed Versus Fully Developed Flow Conditions

Returning to the conventional Darcy formulation for fractional flows, Eq. (1), apart from the flowrates and relative permeabilities, the pressure gradients are also indexed to account for different values along the wetting and non-wetting phases. In general, pressure differences build-up across interfaces separating disconnected fluidic elements of the non-wetting phase from the surrounding, connected wetting phase. The sum of the pressure discontinuities across an ensemble of menisci is expressed as the effective (measured) local capillary pressure between the two phases.

When pressure averages are considered over representative elementary volumes (REVs) for the wetting phase, $\tilde{p}_{{\text{w}}}$, and the non-wetting phase, $\tilde{p}_{{\text{n}}}$, at any cross-section perpendicular to the flow, we may write the definition of the average capillary pressure, $\tilde{p}_{{\text{c}}}$,

$$\tilde{p}_{{\text{c}}} \left( {\tilde{z}} \right) \equiv \tilde{p}_{{\text{n}}} \left( {\tilde{z}} \right) - \tilde{p}_{{\text{w}}} \left( {\tilde{z}} \right)$$

(35)

If the values of the REV flow variables do not change along the stream tube, then fully developed flow has been established. REV flow variables comprise integral or locally averaged values, e.g., superficial velocities, saturation, as well as constituent variables describing the flow structure, e.g., volumetric fractions of the so-called constituent flows; these comprise connected pathway flow, ganglion dynamics flow and emulsion-type flows, or, size distributions (moments) of fluidic elements (ganglia and droplets). An indicative example of the mixing of constituent flows is depicted by the inset snapshot in Fig. 1, taken from the Avraam and Payatakes experiments (1995) in 2D model pore networks. In general, fully developed flow conditions are established when steady-state two-phase flow is maintained along a REV stream tube within a homogeneous pore network. Τhe stream tube should be long enough to allow for an “entry length” for the flow structure to develop under dynamic equilibrium to a fully developed structure. Exhibits of flow transition from non-fully developed to fully developed structures can be found in Aursjo et al. (2014) (Fig. 7), whereby two-phase flows within long Hele-Shaw bead packs have been studied. A similar trend is observed in ganglion dynamics simulations, whereby the evolution of different ganglion size distributions downstream entry ports resulted in the same fully developed distribution (Fig. 14 in Valavanides et al. 1998).

When the flow is fully developed, the disparity between the pressure values in the two phases, the capillary pressure, Eq. (35), remains constant along the flow direction,

$$\frac{{\Delta \tilde{p}_{{\text{c}}} }}{{\Delta \tilde{z}}} = 0$$

(36)

and both phases share the same macroscopic pressure gradient, i.e.,

$$\left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{n}}} = \left( {\frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}} \right)_{{\text{w}}} = \frac{{\Delta \tilde{p}}}{{\Delta \tilde{z}}}$$

(37)

and consequently a common macroscopic pressure gradient, $\left( {{\Delta }\tilde{p}/{\Delta }\tilde{z}} \right)$, is established.

Establishment of fully developed flow is a critical problem in special core analysis (SCAL) as the measured values of the physical quantities (pressure gradients, saturation and flowrates), that are necessary to evaluate the true phenomenological relation at the REV scale, should not be biased by the, so called, “end-effects”. The latter may be substantial or not, depending on the extent of the non-fully developed entry-flow zone, that, on its turn, depends on the physicochemical properties of the two-fluid and porous medium flow system and the imposed flow conditions. In a nutshell, end-effects—if substantial—distort the equivalence between the laboratory examined core flow and the flow within a REV in-situ the formation. In that context, end-effects distort—to a degree—the trueness of the REV constitutive relations, and the specificity of any associated simulations. The effect tends to be significantly reduced, or even negligible, when relatively higher flowrates are imposed, as the non-fully developed length is significantly reduced. In that sense, at higher flow rates, saturation gradients along the core are significantly reduced and saturation attains some uniform value along the core.

1.2 II Determination of the Roots of the Cubic Eq. (25)

We will derive the roots of the cubic Eq. (25). Without any loss of generality we transform $\log {Ca} = x$ and $\log r = y$, to get a simpler form as

$$C_{3} y^{3} + \left( {x - x_{0} } \right)y^{2} - C_{0} = 0$$

(38)

where $C_{3} ,C_{0} > 0, x_{0} < 0$,

The discriminant of the cubic equation,

$$D = 4C_{0} \left( {x - x_{0} } \right)^{3} - 27C_{0}^{2} C_{3}^{2}$$

(39)

is positive when

$$D > 0 \Rightarrow x > x_{0} + \frac{3}{{\sqrt[3]{4}}}\sqrt[3]{{C_{0} C_{3}^{2} }}$$

(40)

and there are 3 distinct real roots (irreducible case). Therefore, we must avoid Cardano’s formulae since, in this case, we cannot express the roots in terms of real radicals.

For $= x_{0}$, we get

$$y\left( {x_{0} } \right) = \sqrt[3]{{C_{0} /C_{3} }}$$

(41)

For $x \ne x_{0}$, we implement the transformation,

$$y = t - \frac{{x - x_{0} }}{{3C_{3} }}$$

(42)

to obtain the cubic equation in reduced form,

$$t^{3} + pt + q = 0$$

(43)

where

$$p = - \frac{1}{3}\left( {\frac{{x - x_{0} }}{{C_{3} }}} \right)^{2} < 0$$

(44)

and

$$q = - \frac{{C_{0} }}{{C_{3} }} + \frac{2}{27}\left( {\frac{{x - x_{0} }}{{C_{3} }}} \right)^{3}$$

(45)

Since $< 0$, we can follow Vieta’s method (1591) to solve Eq. (12) for $x \ne x_{0}$.

In general, if we set

$$t = 2\cos \theta \sqrt { - p/3}$$

(46)

we obtain three real roots,

$$t_{k} = 2\sqrt {\frac{ - p}{3}} \cos \left[ {\frac{1}{3}\arccos \left( {\frac{3q}{{2p}}\sqrt {\frac{3}{ - p}} } \right) - \frac{2k\pi }{3}} \right],\quad k = 0,1,2$$

(47)

provided that

$$4p^{3} + 27q^{2} \le 0$$

(48)

On the other hand, if

$$4p^{3} + 27q^{2} > 0$$

(49)

and

$$p < 0$$

(50)

then, the reduced cubic equation has a single root, given by

$$t_{0} = - 2\frac{\left| q \right|}{q}\sqrt {\frac{ - p}{3}} \cosh \left[ {\frac{1}{3}\arccos h\left( {\frac{3\left| q \right|}{{ - 2p}}\sqrt {\frac{3}{ - p}} } \right)} \right]$$

(51)

Straightforward calculations lead to the following general expression,

$$y\left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{x_{0} - x}}{{3C_{3} }}\left[ {1 + 2\cosh \left( {\frac{1}{3}\arccos h\left( A \right)} \right)} \right],} \hfill & {\quad x - x_{0} < 0} \hfill \\ {\sqrt[3]{{\frac{{C_{0} }}{{C_{3} }}}},} \hfill & {\quad x - x_{0} = 0} \hfill \\ {\frac{{x_{0} - x}}{{3C_{3} }}\left[ {1 - 2\cosh \left( {\frac{1}{3}\arccos h\left( { - A} \right)} \right)} \right],} \hfill & {\quad 0 < x - x_{0} < B} \hfill \\ {\frac{{x_{0} - x}}{{3C_{3} }}\left[ {1 - 2\cos \left( {\frac{1}{3}\arccos h\left( { - A} \right)} \right)} \right],} \hfill & {\quad B \le x - x_{0} } \hfill \\ \end{array} } \right.$$

(52)

or

$$y\left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{x_{0} - x}}{{3C_{3} }}\left[ {1 + 2\cosh \left( {\frac{1}{3}\arccos h\left( A \right)} \right)} \right],} \hfill & {\quad \frac{x}{{x_{0} }} < 1} \hfill \\ {\sqrt[3]{{\frac{{C_{0} }}{{C_{3} }}}},} \hfill & {\quad \frac{x}{{x_{0} }} = 1} \hfill \\ {\frac{{x_{0} - x}}{{3C_{3} }}\left[ {1 - 2\cosh \left( {\frac{1}{3}\arccos h\left( { - A} \right)} \right)} \right],} \hfill & {\quad 1 < \frac{x}{{x_{0} }} < 1 + B} \hfill \\ {\frac{{x_{0} - x}}{{3C_{3} }}\left[ {1 - 2\cos \left( {\frac{1}{3}\arccos h\left( { - A} \right)} \right)} \right],} \hfill & {\quad 1 + B \le \frac{x}{{x_{0} }}} \hfill \\ \end{array} } \right.$$

(53)

where

$$A = A\left( x \right) = \frac{27}{2}\frac{{C_{0} C_{3}^{2} }}{{\left( {x_{0} - x} \right)^{3} }} + 1$$

(54)

and

$$B = 3\sqrt[3]{{\frac{{C_{0} C_{3}^{2} }}{4}}}$$

(55)

Now we may recover the solution to the original Eq. (25) by reverting $x = \log {Ca}$ and $y = \log r$, to get the expression of Eq. (26)