Sensitivity-based Parameter Calibration of Single- and Dual-continuum Coreflooding Simulation Models

Abstract

Our study is keyed to the development of a viable framework for the stochastic characterization of coreflooding simulation models under two- and three-phase flow conditions taking place within a core sample in the presence of preferential flow of the kind that can be associated with the presence of a system of fractures. We do so considering various modeling strategies based on (spatially homogeneous or heterogeneous) single- and dual-continuum formulations of black-oil computational models and relying on a global sensitivity-driven stochastic parameter calibration. The latter is constrained through a set of data collected under a water alternating gas scenario implemented in laboratory-scale coreflooding experiments. We set up a collection of Monte Carlo (MC) numerical simulations while considering uncertainty encompassing (a) rock attributes (i.e., porosity and absolute permeability), as well as (b) fluid–fluid/ fluid–solid interactions, as reflected through characteristic parameters of relative permeability and capillary pressure formulations. Modern moment-based global sensitivity indices are evaluated on the basis of the MC model responses, with the aim of (i) quantifying sensitivity of the coreflooding simulation results to variations of the input uncertain model parameters and (ii) assessing the possibility of reducing the dimensionality of model parameter spaces. We then rest on a stochastic inverse modeling approach grounded on the acceptance–rejection sampling (ARS) algorithm to obtain probability distributions of the key model parameters (as identified through our global sensitivity analyses) conditional to the available experimental observations. The relative skill of the various candidate models to represent the system behavior is quantified upon relying on the deviance information criterion. Our findings reveal that amongst all tested models, a dual-continuum formulation provides the best performance considering the experimental observations available. Only a few of the parameters embedded in the dual-continuum formulation are identified as major elements significantly affecting the prediction (and associated uncertainty) of model outputs, petrophysical attributes and relative permeability model parameters having a stronger effect than parameters related to capillary pressure.

1 Introduction

Multiphase flow in porous/fractured media is associated with a broad range of applications in the context of a variety of engineering sectors. These include oil/gas production, geologic storage of CO₂ or hydrogen, design of deep and shallow geothermal energy exploitation practices, assessment of the status of groundwater bodies and associated remediation approaches. In the current scenario related to natural geo-resources, decarbonization goals are increasingly pushing the industrial and research sectors towards promoting investments aiming at taking advantage of enhanced oil and gas recovery practices rather than targeting exploration for the discovery of new hydrocarbon reservoirs. In this context, decision making about the proper enhanced oil recovery strategy is typically grounded on results and interpretations of laboratory-scale coreflooding experiments. Thus, insights stemming from an appropriate integration of state-of-the-art coreflooding experiments and stochastic inverse modeling approaches yield critical information to enhance our ability to constrain predictions of multiphase flows taking place across natural geomaterials in the presence of multiple sources of uncertainty (Ranaee et al. 2019; Valdez et al. 2020; Berg et al. 2021a, b; Kuo and Benson 2021).

Water alternating gas (WAG) injection is a major enhanced oil recovery technology. It incorporates advantages and merits of waterflooding and gas injection techniques. WAG injection contributes to enhancing sweep efficiencies to stabilize injected fluid fronts and thus increasing oil recovery, as compared against the sole use of waterflooding or gas injection techniques (Afzali et al. 2018).

It is estimated that about half of the conventional hydrocarbon resources worldwide are stored in naturally fractured reservoirs (NFRs) (e.g., March et al. 2018; Burchette 2012). Quantification of multi-phase flow processes taking place in NFRs is then remarkably relevant to assist production from hydrocarbon-bearing geologic formations (Chen et al. 2010).

Responses of a reservoir to the implementation of a WAG injection practice may vary depending on elements associated with (i) petrophysical rock attributes (i.e., permeability and/or porosity) and their spatial heterogeneity as well as (ii) fluid–fluid and fluid–solid interactions in the system (as expresses through, e.g., relative permeability or capillary pressure curves). Previous works suggest that documented instances of failure of WAG projects have been typically attributed to incomplete characterization of spatial heterogeneity of reservoir attributes (e.g., Christensen et al. 2001; Afzali et al. 2018). Nygård and Andersen (2020) recently performed numerical simulations of immiscible WAG injections in a stratified reservoir model. These authors suggest the importance of investigating the interplay between various elements (e.g., heterogeneity and gravity) on the performance of WAG scenarios, as their individual effects differ from their synergic combination.

Laboratory scale studies associated with WAG injection in fractured media are still scarce. These are typically performed to gain insights on phenomenological aspects and on the way to possibly embed these into a mathematical model. Chakravarthy et al. (2004) perform a collection of coreflooding experiments in fractured cores. These authors find that WAG injection in such media yields a remarkable delay of the breakthrough time as compared to a continuous gas injection, thus leading to an enhanced oil recovery. Darvish et al. (2006) experimentally show that tertiary CO₂ injection can be considered as an effective enhanced oil recovery method in fractured reservoirs for targeting the residual oil after water injection. Agada and Geiger (2014) rely on a high-resolution numerical model to investigate the effects of non-wetting phase trapping under WAG injection in a naturally fractured heterogeneous carbonate reservoir. These authors show that the nature of the fractured system has a significant impact on the WAG recovery, especially in low-intensity fractured domains, where only a few isolated fractures can govern the overall system behavior. Otherwise, the main traits of the system of fractures in a high-intensity fractured reservoir tend to become less significant in the recovery process.

Approaches aiming at simulating flow in fractured rock systems are typically classified into two families. The first group includes methodologies that explicitly represent fractures as geometrical features in a numerical model (e.g., Geiger et al. 2009; Moinfar et al. 2014; Schmid and Geiger 2013; Fumagalli et al. 2016). Discrete fracture models (DFMs) account explicitly for the effect of individual fractures on fluid flow. Some studies (Cipolla and Wallace 2014; Wu and Olson 2016; Atsushi et al. 2018) suggest that some important underlying physics might be masked in DFMs due to a somehow over-simplification of the simulation model, especially in the presence of complex fracture geometries. Embedded discrete fracture models (EDFMs) can circumvent such issues (Moinfar et al. 2014; Cavalcante Filho et al. 2015; Shakiba and Sepehrnoori 2015; Yu et al. 2017). Compared to DFMs, that rely on complex unstructured grids to match the fracture geometry, EDFMs only adopt a set of fixed structured rectangular grids, fractures being explicitly described (see, e.g., Matthai et al. 2005; Hajibeygi et al. 2011; Sandve et al. 2012; Xu et al. 2017; Zhang et al. 2018). Tene et al. (2017) point out that EDFMs are not suitable to cope with situations in which fracture permeability is lower than matrix permeability and propose a projection-based embedded discrete fracture model (pEDFM) to overcome this issue. Du et al. (2022) present a three-dimensional pEDFM framework to cope with complex fracture networks in hydraulically fractured models. A key challenge of explicitly characterizing fractures in numerical models (e.g., DFMs, EDFMs, or pEDFMs) is that one must be able to adequately identify location and orientation of the discrete fractures across the system. Jiang et al. (2021) show that complex geological conditions can impose significantly high difficulties on the accurate evaluation of fracture locations.

The second group of approaches, denoted as dual porosity and/or dual permeability model, rests on a conceptual picture according to which the system can be viewed as formed by a collection of continua characterized by differing properties and coexisting in space. In this context, fractures are considered as a continuum system overlapped to a less permeable porous medium (e.g., Samimi et al. 2012; Geiger et al. 2013; Maier and Geiger 2013; Tecklenburg et al. 2016; Hui et al. 2018). These mathematical models rely on transfer functions to evaluate exchange rates between the two continua, i.e., the porous matrix and the fractures (e.g., Al-Kobaisi et al. 2009; Ramirez et al. 2009). These techniques can be beneficial in scenarios where (i) the system is characterized by densely spaced fractures (possibly distributed on multiple scales, including the presence of microfractures), and/or (ii) adequate information about fracture location/geometry is lacking. Elfeel et al. (2016) rely on a dual-continuum formulation to study the interplay between gravity and capillary forces during WAG practices. These authors suggest that evaluation of the block geometry, matrix permeability, as well as an appropriate use of relative permeability and capillary pressure correlations can significantly affect the evaluation of the flow transfer between the two continua. Ceriotti et al. (2019) focus on the formulation, calibration, and validation of a dual-continuum model for solute transport in porous media. In this context, the authors suggest that relying on sensitivity analysis techniques to diagnose the behavior of a given simulation model can be an efficient tool to design ad-hoc metrics for model calibration. It can also circumvent the use of weakly sensitive objective functions for parameter estimation.

Sensitivity analysis is a convenient framework to diagnose the behavior of a given model in response to uncertainty associated with its parameters. Here, we rely on Global Sensitivity Analysis (GSA) approaches (e.g., Saltelli et al. 2008) to assist understanding of the behavior of various modeling strategies aiming at rendering flow taking place across a fractured laboratory-scale core sample subject to two- and three-phase dynamics mimicking WAG practices. Quantifying the way uncertainty associated with parameters embedded in a given interpretive model drives variability of model outputs of interest can aid to address issues such as the identification of the most influential model parameters with respect to given model response(s) (Muleta and Nicklow 2005; Pappenberger et al. 2008; Wagener et al. 2009; Ruano et al. 2012; Hill et al. 2016); or the possibility to set some parameter(s) (which are deemed as uninfluential) at prescribed value(s) without significantly affecting model results (Degenring et al. 2004; van Griensven et al. 2006; Chu et al. 2015; Punzo et al. 2015; Nossent et al. 2011). In this broad framework, classical approaches to GSA rely on the variance of the population of a model output as a metric to fully characterize uncertainty (e.g., Sobol 1993, 2001; Sudret 2008; Fajraoui et al. 2011; Sochala and Le Maître 2013; Valdez et al. 2020; Landa-Marbán et al. 2020). Considering that the latter can yield at best an incomplete picture of the response of the system to uncertainty of model parameters, we rest here on the study of Dell’Oca et al. (2017). These authors propose a moment-based GSA approach to enable one to quantify the influence of uncertain model parameters on various (statistical) moments of a target model output. In this sense, these authors define sensitivity in terms of the average variation of key statistical moments of the probability density function of an output due to model parameter variability and propose synthetic sensitivity indices to quantify the concept. While these types of analyses and sensitivity metrics have been applied on selected flow and transport scenarios in porous media (e.g., Bianchi Janetti et al. 2019), to the best of our knowledge they have not yet been performed to unravel the complexities associated with modeling of WAG injection in dual-continuum media through comparison against diverse conceptual/mathematical modeling approaches.

Challenges associated with a proper sensitivity analysis are exacerbated by the complexity of the conceptual/mathematical model considered, in terms of model formulation and associated parametrization. Since GSA requires performing multiple runs of a given mathematical model, one typically resorts to a streamlined version of the model analyzed. The latter is obtained through the formulation of reduced-complexity surrogate models.

The polynomial chaos expansions (PCE) approach is a computationally efficient tool that has been successfully employed in a variety of engineering and Earth science applications to circumvent difficulties related to heavy computational costs (Sudret 2008; Fajraoui et al. 2011; Laloy et al. 2013; Sochala and Le Maître 2013; Formaggia et al. 2013; Porta et al. 2014; Zhao and Li 2019; Meng and Li 2019; Shen et al. 2020). Formaggia et al. (2013) introduce a model-driven uncertainty quantification workflow based on sparse grid sampling techniques in the context of a PCE approximation of a basin-scale geochemical evolution scenario. These authors perform GSA of selected system states (i.e., porosity, temperature, pressure, and fluxes) in the presence of uncertain mechanical and geochemical model parameters as well as boundary conditions. Porta et al. (2014) illustrate an inverse modeling procedure for the estimation of model parameters of sedimentary basins subject to compaction driven by mechanical and geochemical processes. The authors rely on the approximation of the system behavior through PCE which is then employed in the context of model calibration.

The main objective of our study is the introduction of a general framework for stochastic inverse modeling of multiphase flow in randomly heterogeneous fractured media characterized through continuum scale models under various sources of uncertainty. Our stochastic inverse modeling approach embeds the possibility of considering multiple conceptual/mathematical models, each associated with uncertain parameters, within the context of modern global sensitivity and uncertainty quantification frameworks. Here, we focus on two- and three-phase coreflooding scenarios. We provide an appraisal of the joint role of petrophysical rock attributes as well as parameters driving given relative permeability and capillary pressure formulations on system responses associated with diverse modeling strategies. We do so by constructing and calibrating, in a rigorous probabilistic framework, candidate models with differing mathematical formulations and parametrizations. We evaluate within a sensitivity-based calibration framework their ability to reproduce a set of collected data monitored during laboratory-scale investigations of multiphase flow on a Portland core sample.

Three alternative modeling strategies are employed to describe the system behavior. Two of these are based on homogeneous/heterogeneous single porosity/permeability black-oil simulation models and the third one is a dual porosity formulation of black-oil modeling scenarios. Each mathematical model is characterized by a set of uncertain parameters. We start from the premise that a deterministic model calibration is not informative of the uncertainties associated with the system behavior. Thus, we rest on a stochastic model calibration strategy. The latter yields multiple possible solutions of the inverse problem, each constrained through the set of available data. This approach enables one to provide predictions under uncertainty (see also, e.g., Ranaee et al. 2017; Valdez et al. 2020; Berg et al. 2021a, b; Kuo and Benson 2021). The latter is here quantified in terms of the posterior distribution of model parameters, i.e., the probability distribution of parameters conditional to available experimental observations. To this end, we rely on an acceptance–rejection sampling (ARS) approach. The latter is an unbiased sampler allowing generation of multiple independent realizations of the output of a given model upon sampling from the posterior parameter distribution. ARS has been recently employed by Russian et al. (2019) for the stochastic characterization of equivalent fracture apertures conditional to data acquired in quasi real time while drilling a well in a NFR.

Finally, we propose to employ formal model selection criteria to evaluate the performance of the calibrated sets of models. To this end, we consider the deviance information criterion (Spiegelhalter et al. 2002), which enables us to quantify and rank (in relative terms) the skill of the considered models to interpret the available data.

Our work is organized as follows. Section 2 introduces the methodological workflow, experimental results upon which our study leverages together with key theoretical elements underpinning the selected modeling approaches as well as their stochastic calibration and the application of model information criteria. Implementation of the workflow and the ensuing results are discussed in Sect. 3. Concluding remarks are presented in Sect. 4.

2 Materials and Methods

We consider the collection of two- and three-phase coreflooding experiments performed by Moghadasi et al. (2019) on a Portland limestone core sample. Our study is focused on the methodological workflow for the probabilistic assessment/calibration of single- and dual-continuum formulations of the black-oil mathematical models illustrate in Sect. 2.2.

We analyze the following set of model outputs as quantities of interest: (a) core-scale saturation, $S_{\alpha }$, with α = {w, o, g} denoting water, oil, and gas, respectively; and (b) pressure drop across the core sample, $\Delta P$. Each of these quantities depend on a set of N_P controlling parameters. The latter are collected in vector ${\varvec{\theta}}$ (whose entries are denoted as $\theta_{{\text{i}}}$, with i = 1, …, N_P; note that N_P depends on the mathematical formulation of the considered models).

The influence of the entries of model parameter vector ${\varvec{\theta}}$ on $S_{\alpha }$ and $\Delta P$ is assessed through a GSA framework. The latter is implemented upon random sampling the parameter space of variability ${{\varvec{\Gamma}}} = {\Gamma }_{{\theta_{1} }} \times \ldots \times {\Gamma }_{{\theta_{{{\text{N}}_{{\text{P}}} }} }}$, ${\Gamma }_{{\theta_{{\text{i}}} }}$ being the support (range of variability) of $\theta_{{\text{i}}}$. In such a model diagnosis approach we consider model parameters as independent random quantities.

To circumvent bottlenecks arising from the high computational costs (see Sect. 3) linked to the numerical models analyzed, we leverage on a surrogate modeling approach based on a PCE approximation (see Appendix A for details). The latter is then employed in the GSA and stochastic model calibration context. It enables us to perform multiple evaluations (i.e., of the order of 10⁶; see Sect. 3.2 and 3.3) of the outputs of the analyzed system, thus yielding statistically stable results at affordable computational costs.

Stochastic model calibration yields probability distributions of model parameters conditional on available datasets. Finally, the use of model selection criteria enables us to evaluate the relative skill of the selected candidate models to assist interpretation of the coreflooding experiments. Additional details about stochastic model calibration and model selection criteria are included in Sects. 2.3 and 2.4, respectively.

The general layout of the analysis workflow is depicted in Fig. 1, its key steps being:

• 1) Setup a suite of candidate mathematical models with differing degrees of complexity;

• 2) Evaluate of the range of variability (typically considering available literature studies) associated with uncertain model parameters;

• 3) Construct PCE-based surrogate models;

• 4) Select controlling parameters on the basis of a GSA;

• 5) Perform stochastic calibration of the candidate models by making use of laboratory coreflooding data;

• 6) Rank the candidate models on the basis of their skill to interpret available observations, as assessed through the evaluation of model selection criteria.

Fig. 1

Flowchart of the analysis framework

2.1 Coreflooding Experiments

Moghadasi et al. (2019) perform a sequence of steady state coreflooding experiments. These include a two-phase water–oil (WO) primary drainage experiment (i.e., injection of oil, D1), followed by imbibition (i.e., injection of water, I), secondary drainage (D2) and gas injection (to mimic a WAG scenario) on a limestone core sample. Table 1 lists the main attributes of the core sample and fluid properties from laboratory experiments.

Table 1 Main attributes of the Portland core-sample and fluid properties related to the laboratory experiments (Moghadasi et al. 2019)

While detailed information regarding crude oil composition and interfacial tension is not available, in line with previous work (see Hemmati-Sarapardeh et al. 2016 and references therein) we consider nitrogen as immiscible in the presence of crude oil.

Figure 2 depicts the temporal evolution of volumetric flow rates of water, $q_{{\text{w}}}^{*}$, oil, $q_{{\text{o}}}^{*}$, and gas, $q_{{\text{g}}}^{*}$, monitored after the primary drainage phase D1. The experimental campaign was structured across 42 days (i.e., 14 days for I, 11 days for D2, and 17 days for WAG) upon setting the combinations of $q_{{\text{w}}}^{*}$, $q_{{\text{o}}}^{*}$, and $q_{{\text{g}}}^{*}$ depicted in Fig. 2. Symbols in Fig. 2 represent 19 measured rates corresponding to 6, 5, and 8 measurements collected under I, D2 and WAG phases, respectively. According to Moghadasi et al. (2019), a total number of pore volumes PV = 1096, 861, and 1331 is injected during 14 days of I, 11 days of D2, and 17 days of WAG experiments, respectively, the total injection rate (i.e., 3.26 [PV/hr]) being constant across the experiment window.

Fig. 2

Temporal evolution of the volumetric flow rate of water, ${q}_{\mathrm{w}}^{*}$, oil, ${q}_{\mathrm{o}}^{*}$, and gas, ${q}_{\mathrm{g}}^{*}$, collected under I, D2 and WAG experiments

Quantities monitored during the experiments are listed in Table 2. These include temporal evolutions of volumetric flow rates, $q_{{\upalpha }}^{*}$, pressure drop, $\Delta P^{*}$, and (core-averaged) phase saturations, $S_{{\upalpha }}^{*}$. Note that here and in the following experimental observations are marked with the superscript “*”. Moghadasi et al. (2019) evaluate relative permeabilities of phase $\alpha$ in the two-phase (i.e., phase $\alpha$-phase i), $k_{{r\alpha i}}^{* X}$ (with X = I and D for imbibition and drainage, respectively) and in the three-phase system, ${k}^{*}_{{\text{r}_{{\alpha}}}}$, through the application of Darcy’s law across the core to calculate absolute oil, water, and gas permeabilities (see their Eq. (1)) and expressing these with respect to absolute water permeability. No detailed information is available on measurement accuracy, this element being further discussed in Sect. 2.3 with reference to the application of our stochastic inverse modeling approach. It can then be noted that some factors that could affect the accuracy of the data collected by Moghadasi et al. (2019) include, e.g., (i) core heterogeneity that may be responsible for incomplete fluid displacement and/or (ii) capillary end effects that are not properly accounted for (Andersen 2021; 2022; Berg et al. 2021a; Nazari Moghaddam and Jamiolahmady 2019; Kuo and Benson 2021; Li et al. 2021). As an example, in this context Andersen (2021; 2022) provide analytical solutions for the assessment of relative permeabilities for a core at steady state in the presence of capillary end effects.

Table 2 Data collected through laboratory coreflooding experiments: core-scale phase saturation, $S_{{\upalpha }}^{*}$., pressure drop, $\Delta P^{*}$, and injection rates $q_{{\upalpha }}^{*}$. Relative permeabilities under two-phase (WO) and three-phase conditions are evaluated through Darcy’s formulation

While some degree of fracturing was reported to be visible along the core during packing, location and geometry of the fractures was not monitored. Given the nature of the rock sample (i.e., a carbonate rock), the presence of preferential pathways possibly related to microfractures across the system can also be expected. In this context, we choose to rely on various continuum-scale formulations, with differing degree of complexity, to render the conceptual picture of the system behavior under the experimental conditions considered. We describe in Sect. 2.2 the details of the collection of mathematical models we employ.

2.2 Governing Mathematical Formulations

Three continuum-scale models are assessed to account for the spatial distribution of porosity and absolute permeability in the numerical simulation of the coreflooding experiments described in Sect. 2.1. These models are characterized by differing degrees of complexity and correspond to a homogeneous (Scenario H₀) and heterogeneous single-continuum (Scenario H₁) as well as a dual-continuum system (Scenario H₂).

Simulation strategies based on compositional formulations have been used in the literature to cope with EOR scenarios, such as, e.g., chemical flooding (Yu et al. 2014). As noted in Sect. 2.1, solubility and miscibility effects are not considered here. Thus, for simplicity we rely on a black-oil formulation. We remark that our general theoretical framework of stochastic inverse modeling is otherwise compatible with compositional formulations, which can be considered in future studies.

2.2.1 Homogeneous Single-Continuum Field (Scenario H ₀ )

Three-phase immiscible fluid flow in a black-oil modeling setting under isothermal conditions is formulated through (e.g., Lie 2019):

$$ \frac{\partial }{{\partial t}}\left( {\phi \rho _{\alpha } S_{\alpha } } \right) + \nabla \cdot \rho _{\alpha } \user2{u}_{\alpha } = 0\quad {\text{with }}\alpha = \left\{ {w,o,g} \right\} $$

(1)

Here, we recall that subscripts w, o, and g denote water, oil, and gas phases, respectively; $\phi$ is porosity; $t$ is time; ${S}_{\alpha }$, ${\rho }_{\alpha }$ and ${{\varvec{u}}}_{\alpha }$ denote saturation, density and Darcy velocity of phase α, respectively. Note also that hydrocarbon mass is not conserved within each phase (because of hydrocarbon mass interchange between the oil and gas phases), the total mass (across phases) of each component being otherwise conserved.

Darcy velocity, ${{\varvec{u}}}_{\alpha }$, is related to the gradient of the phase pressure, $p_{\alpha }$, as:

$$ {\varvec{u}}_{\alpha } = - \frac{{{\varvec{K}}{{k}}_{\text{r}{\alpha }} }}{{\mu_{\alpha } }}\left( {\nabla p_{\alpha } - \rho_{\alpha } {\mathbf{g}}} \right) $$

(2)

Here, $k_{\text{r}{\alpha }}$ and $\mu_{\alpha }$ are relative permeability and viscosity of phase α, respectively; g is gravity vector; and ${\varvec{K}}$ is the absolute permeability tensor, which we consider as diagonal and isotropic, i.e., ${\varvec{K}} \equiv K{\varvec{I}}$, ${\varvec{I}}$ being the identity matrix.

Solution of the system of Eqs. (1)–(2) is subject to (a) the constraint $S_{{\text{w}}} + S_{{\text{o}}} + S_{{\text{g}}} = 1$, (b) suitable expressions for water–oil, $p_{{{\text{cw}}}}$, and oil–gas, $p_{{{\text{cg}}}}$, capillary pressures, (c) initial and boundary conditions, as well as (d) a set of mathematical formulations conducive to evaluating relative permeabilities.

In this work, we consider that, in a water–oil system, $p_{{\text{w}}}$ and $p_{{\text{o}}}$ are related by a capillary pressure function that depends on saturation of water:

$$ p_{{\text{o}}} = p_{{\text{w}}} - p_{{{\text{cw}}}}^{X} \left( {S_{{\text{w}}} } \right) $$

(3)

Similarly, in a gas-oil system, $p_{{\text{g}}}$ and $p_{{\text{o}}}$ are related by a capillary pressure function that depends on saturation of gas:

$$ p_{{\text{g}}} = p_{{\text{o}}} - p_{{{\text{cg}}}}^{X} \left( {S_{{\text{g}}} } \right) $$

(4)

where X refers to the saturation paths of two-phase drainage (X = D) and imbibition (X = I). The capillary pressure–saturation relationship is described through the Brooks–Corey (Brooks and Corey 1964) formulation.

In case of primary drainage (i.e., D = D1), the Brooks–Corey formulation for WO and GO is:

$$ p_{{{\text{cw}}}}^{D1} = p_{{{\text{ew}}}} \left( {\frac{{1 - S_{{{\text{rwo}}}}^{D1} }}{{S_{{\text{w}}} - S_{{{\text{rwo}}}}^{D1} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{{{\text{pw}}}}^{D1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{{{\text{pw}}}}^{D1} }$}}}} \quad p_{{{\text{cg}}}}^{D1} = p_{{{\text{eg}}}} \left( {\frac{{1 - S_{{{\text{rog}}}}^{D1} }}{{1 - S_{{\text{g}}} - S_{{{\text{rog}}}}^{D1} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{{{\text{pg}}}}^{D1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{{{\text{pg}}}}^{D1} }$}}}} $$

(5)

Here, quantities $p_{{{\text{ew}}}}$ and $p_{{{\text{eg}}}}$ in Eqs. (3) are the entry capillary pressure in WO and GO primary drainage systems, respectively (Li 2010); $S_{{{\text{rwo}}}}^{D1}$ and $S_{{{\text{rgo}}}}^{D1}$ are the saturation endpoints of water and gas for drainage paths of WO and GO, respectively (Pini and Benson 2017); and $n_{{{\text{pw}}}}^{D1}$ and $n_{{{\text{pg}}}}^{D1}$ are model parameters.

For the remaining saturation paths (i.e., secondary drainage or imbibition), capillary pressure–saturation relationships are described through a modified version of the Brooks–Corey formulations (see, e.g., Pini and Benson 2017) for WO and GO as:

$$ p_{{{\text{cw}}}}^{Z} = p_{{{\text{ew}}}} \left[ {\left( {\frac{{1 - S_{{{\text{rwo}}}}^{Z} }}{{S_{{\text{w}}} - S_{{{\text{rwo}}}}^{Z} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{{{\text{pw}}}}^{Z} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{{{\text{pw}}}}^{Z} }$}}}} - 1} \right]\quad p_{{{\text{cg}}}}^{Z} = p_{{{\text{eg}}}} \left[ {\left( {\frac{{1 - S_{{{\text{rog}}}}^{Z} }}{{1 - S_{{\text{g}}} - S_{{{\text{rog}}}}^{Z} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{{{\text{pg}}}}^{Z} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{{{\text{pg}}}}^{Z} }$}}}} - 1} \right] $$

(6)

where quantities $n_{{{\text{pw}}}}^{Z}$ and $n_{{{\text{pg}}}}^{Z}$ are model parameters and saturation path Z refers to either secondary drainage (D2) or imbibition (I).

Note that the values of saturation endpoints can change from drainage to imbibition conditions, while they are the same under primary (D1) and secondary (D2) drainage conditions. The value of the exponents $n_{{{\text{pw}}}}^{Z}$ and $n_{{{\text{pg}}}}^{Z}$ depend on the saturation path (i.e., I, D1, or D2), thus embedding the effects of changing saturation paths on the characterization of capillary pressure.

We use the following Corey-type power-law equations to characterize two-phase relative permeabilities (Corey and Rathjens 1956), considering dependency on the saturation path cycle X:

$$ k_{{{\text{r}{\alpha}{i}}}}^{X} = k_{{{\text{r}{\alpha}{i}}}}^{M} \left( {\frac{{S_{{\alpha}} - S_{{{\text{r}{\alpha}{i}}}}^{X} }}{{1 - S_{{{\text{rwo}}}}^{X} - S_{{{\text{row}}}}^{X} }}} \right)^{{n_{{\alpha}{i}} }} \quad {\text{with}}\,\alpha = o,w $$

(7)

$$ k_{{{\text{r}{\alpha}{i}}}}^{X} = k_{{{\text{r}{\alpha}{i}}}}^{M} \left( {\frac{{S_{{\alpha}} - S_{{{\text{r}{\alpha}{i}}}}^{X} }}{{1 - S_{{{\text{rwo}}}}^{X} - S_{{{\text{rog}}}}^{X} - S_{{{\text{rgo}}}}^{X} }}} \right)^{{n_{{\alpha}{i}} }} \quad {\text{with}}\,\alpha = o,g $$

(8)

where $k_{{{\text{r}{\alpha}{i}}}}^{M}$ is the largest value of relative permeability of phase α in a two phase (α-i) system for X saturation path and $n_{{\alpha}{\text{i}}}$ is an empirical coefficient. Note Eq. (8) also includes residual water saturation, since the experimental observations in the OG condition are taken in the presence of connate water.

Similar to prior studies, we neglect hysteresis effects on two- and three-phase relative permeability of (a) water (as wetting phase) (e.g., Spiteri and Juanes 2006; Moghadasi et al. 2016, Ranaee et al. 2015; 2016) and (b) gas, under drainage conditions (e.g., Land, 1971; Jerauld, 1997; Killough 1976; Larsen and Skauge 1998; Blunt 2000; Agada and Geiger 2014). Values of three-phase oil relative permeability at a given oil saturation, $S_{{\text{o}}}$, are evaluated as (Baker 1988):

$$ k_{{{\text{ro}}}} = \frac{{\left( {S_{{\text{w}}} - S_{{{\text{rwo}}}}^{I} } \right)k_{{{\text{row}}}}^{I} + S_{{\text{g}}} k_{{{\text{rog}}}}^{D2} }}{{S_{{\text{w}}} - S_{{{\text{rwo}}}}^{I} + S_{{\text{g}}} }} $$

(9)

In summary, solution of Eqs. (1)–(9) in the context of the experimental setting described in Sect. 2.1 requires knowledge of 26 parameters. Considering the experimental saturation paths, we set $S_{{{\text{row}}}}^{D2} = S_{{{\text{rgo}}}}^{D2} = 0$, $S_{{{\text{rwo}}}}^{I} = S_{{{\text{rwo}}}}^{D2}$ and $S_{{{\text{rog}}}}^{I} = S_{{{\text{rog}}}}^{D2}$ ( Schlumberger Geo-Quest 2010), resulting in a set of 22 unknown (uncertain) model parameters (listed in Table 3). These imbue the effects of (a) porosity, (b) absolute permeability, (c) relative permeability and (d) capillary pressure (as expressed through a Corey-type modeling strategy) on the evaluation of multi-phase fluid flow.

Table 3 List of the uncertain model parameters for scenario H₀. Each uncertain parameter $\theta_{i}$ is characterized by a uniform distribution with support$[{U}_{{\ddot{\uptheta }}_{\mathrm{i}}}^{-}, {U}_{{\ddot{\uptheta }}_{\mathrm{i}}}^{+}]$

For the purpose of our analyses, we consider model parameters as independent and identically distributed random variables. Each uncertain parameter is characterized by a uniform distribution within a given support. Prior information on the extent of the latter is consistent with previous findings (e.g., Guédon et al. 2019) and are listed in Table 3. Note that the choice of uniform distributions enables one to assign equal weight to each of the values of a given model parameter within its support. To assess the impact of the selected distribution, we also consider the effect of characterizing model parameters through Gaussian distributions with the same mean and variance of their uniform counterparts and found no significant difference in the key results of our analyses (details not shown).

2.2.2 Randomly Heterogeneous Well-Connected Fields (Scenario H ₁ )

As described in Sect. 2.2.1, homogeneous fields are characterized by uniform values of system attributes across the entire simulation domain. Here, we consider the impact of representing the simulation domain as a randomly heterogeneous system with the presence of well-connected pathways (i.e., highly conductive paths).

We generate synthetic spatially heterogeneous three-dimensional permeability and porosity fields by leveraging on the approach proposed by (Hyman and Winter 2014). In this framework, a realization of a correlated Gaussian field is produced by convolving a prescribed kernel with an initial field of independent, identically distributed random variables. The kernel is defined as:

$$ {\text{g}}\left( {x,y,z,{\upzeta }} \right) = \frac{1}{{\left( {2\pi } \right)^{3/2} \cdot {\upzeta }^{3} }}\exp \left( { - \frac{{x^{2} + y^{2} + z^{2} }}{{2{\upzeta }^{2} }}} \right) $$

(10)

the intrinsic length scale, $\upzeta$, characterizing the strength of the spatial correlation of the field. Domains where high values of porosity/permeability are well-connected are obtained upon modifying the fields generated as described above through the approach suggested by Zinn and Harvey (2003) (to which we refer for additional details). The collection of random realizations of the well-connected heterogeneous fields is then employed in our numerical Monte Carlo simulation scheme (Sect. 3).

To ensure a consistent comparison with scenario H₀, we set the (ensemble) mean and standard deviation of the randomly heterogeneous permeability and porosity fields to the values associated with the supports of the uniform distributions listed in Table 3. Otherwise, we consider the intrinsic length scale, ${\upzeta }$, employed for the generation of the spatially heterogeneous collection of realizations of porosity and absolute permeability as an uncertain model parameter to be comprised in vector ${\varvec{\theta}}$. For simplicity, and given the target of our study, we consider the porosity and absolute permeability random fields to be mutually uncorrelated. We also consider these to be characterized by the same (uncertain) value of ${\upzeta }$. The latter is described through a uniform distribution within the support [0.5, 2.5] × 10^–2 m, thus encompassing a broad range of correlation degrees associated with the investigated domains. Parameters $\theta_{3}$–$\theta_{22}$ are described as illustrated in Sect. 2.2.1 and in Table 3. As such, scenario H₁ is characterized by a total of 21 uncertain model parameters.

2.2.3 Dual-continuum Field Formulation (Scenario H ₂ )

We consider here a dual-continuum formulation to simulate the coreflooding experiments illustrated in Sect. 2.1 while mimicking the occurrence of preferential pathways related to the action of highly connected zones (possibly including, e.g., fractures) within the system. Each grid block comprises two regions, respectively corresponding to: (i) a fractured/highly conducive space (with high permeability) embedded in (ii) a rock matrix.

The Dual Porosity formulation we rely upon is (e.g., Lie and Møyner 2021; Chen et al. 2006):

$$ \frac{\partial }{\partial t}\left( {\phi_\text{f} \rho_{\alpha } S_{{{\alpha}\text{f}}} } \right) + \nabla .\rho_{\alpha } {\varvec{u}}_{{{\alpha}\text{f}}} = - T_{\alpha } $$

(11)

$$ \frac{\partial }{\partial t}\left( {\phi \rho_{\alpha } S_{\alpha } } \right) = T_{\alpha } $$

(12)

where subscript $\mathrm{f}$ in Eq. (11) identifies quantities associated with the (highly permeable) fractures while Eq. (12) is related to the matrix. Term $T_{\alpha }$ is the matrix-fracture transfer rate for fluid phase $\alpha$, expressed as:

$$ T_{\alpha } = F_\text{s} \rho _{\alpha } \frac{{\user2{K}k_{{{\text{r}\alpha }}} }}{{\mu _{\alpha } }}\left( {\text{P} _{{\alpha} \text{f}} - \text{P} _{\alpha } } \right) $$

(13)

$F_{{\text{s}}}$ being a shape factor; $p_{{\alpha}{\text{f}}}$ and $p_{\alpha }$ refer to pressure in the fracture and rock matrix space, respectively.

While Eq. (13) is extensively used in industrial operational workflows and applications (e.g., Schlumberger Geo-Quest, 2010), we note that various formulations, which are not always mutually consistent, are provided in the literature for the evaluation of the shape factor (Barenblatt et al. 1960; Warren and Root 1963; Kazemi et al. 1976; Litvak 1985; Sonier et al. 1988; Gilman and Kazemi 1988). As a consequence, values of $F_{{\text{s}}}$ resulting from diverse formulations can range across orders of magnitude (Lu et al. 2008). Here, we follow Rangel-German and Kovscek (2003) and conceptualize $F_{{\text{s}}}$ as an uncertain model parameter whose value can be estimated through available flow data in an inverse modeling context. For a rock sample of characteristic length of the order of centimeters, we consider $F_{{\text{s}}}$ to vary across a support range of 0.5–50 [m⁻²] (see Table 4). We consider model parameter values for H₂ to be homogeneous across the system. Darcy velocity ${\varvec{u}}_{{\alpha}{\text{f}}}$ in the continuum associated with the fracture system is related to the gradient of $p_{{\alpha}{\text{f}}}$ via an equation similar to (2) and through the absolute permeability of the fracture continuum, $K_{{\text{f}}}$, and a set of equations (similar to Eqs. 7–8) to evaluate the associated relative permeabilities. Therefore, the model parameter vector, ${\varvec{\theta}}$, employed in H₂ includes the parameters listed in Table 3 (for the matrix) as well as an additional set of parameters (for the fracture/highly conducive continuum) listed in Table 4 (for a total of 45 parameters). Similar to the scenario considered in Sect. 2.2.1, model parameters are treated as independent and identically distributed random quantities. Values of all parameters are uniformly distributed within the corresponding supports listed in Tables 3 and 4.

Table 4 List of the model parameters considered for scenario H₂ related to the continuum corresponding to the fracture system. Uncertain parameter values are uniformly distributed within the support $[{U}_{\ddot{\uptheta }\mathrm{f}}^{-}, {U}_{\ddot{\uptheta }\mathrm{f}}^{+}]$

2.3 Surrogate Model, GSA, and Stochastic Model Calibration

We perform stochastic model calibration upon relying on the ARS approach. To reduce computational costs, we rely on a surrogate modeling strategy. Such a surrogate system model is constructed through the PCE approach, as discussed in the introduction and briefly illustrated in Appendix A. In the context of our study, the formulation of a surrogate model is key to obtain a large number of model realizations (of the order of 10⁶, as detailed in the following), which are required for moment-based GSA (see Appendix B) and for stochastic model calibration through ARS.

We remark that we perform GSA before calibration of the simulation models on the basis of experimental observations. As such, GSA is keyed to (i) improving our understanding of the importance of each model parameter on target model outputs, and hence (ii) identifying quantities which might be of limited influence in the context of a subsequent model calibration (e.g., Dell’Oca et al. 2017; Valdez et al. 2021; Ranaee et al. 2019; 2021).

Consider a vector ${\varvec{Y}}^{\user2{*}}$ whose entries are N experimental observations (here pressure drop, $\Delta P^{*}$, and (core-averaged) fluid phase saturations associated with available observation times, as seen in Sect. 2.1 and Table 2) of otherwise true values. Stochastic model calibration through ARS relies on drawing random samples from the posterior probability density function (pdf) of the parameter vector ${\varvec{\theta}}$, $f_{{{\varvec{\theta}}\left| {{\varvec{Y}}^{\user2{*}} } \right.}}$, given the vector of observed values, ${\varvec{Y}}^{\user2{*}}$. Here, we (i) follow Bayes’ theorem, (ii) take the prior pdf $f_{{\varvec{\theta}}}$ as uniform (see Sect. 2.2), and (iii) consider the likelihood $f_{{{\varvec{Y}}^{\user2{*}} \left| {\varvec{\theta}} \right.}}$ as multi-Gaussian, i.e.,:

$$ f_{{{\varvec{Y}}^{\user2{*}} \left| {\varvec{\theta}} \right.}} = \left( {2\pi \sigma_{\varvec{Y}}^{2} } \right)^{ - N/2} {\text{exp}}\left\{ { - \frac{{\left[ {{\varvec{Y}}^{\user2{*}} - {\varvec{Y}}} \right]^{T} \left[ {{\varvec{Y}}^{\user2{*}} - {\varvec{Y}}} \right]}}{{2\sigma_{{\varvec{Y}}}^{2} }}} \right\} $$

(14)

where $\sigma_{{\varvec{Y}}}$ is the standard deviation associated with measurement (or prior) errors. Note that while the theory illustrated below is developed in terms of measurement errors, true values are typically unknown so that they are replaced by model outputs ${\varvec{Y}} = {\varvec{Y}}\left( {\varvec{\theta}} \right)$ in Eq. (14), the term (${\varvec{Y}}^{\user2{*}}$ − Y) being usually denoted as residual. Random samples are drawn from $f_{{{\varvec{\theta}}\left| {{\varvec{Y}}^{\user2{*}} } \right.}}$ according to the following iterative steps:

• 1) Sample $\widetilde{\varvec{\theta}}$ from the support of ${\varvec{{\theta}}}$ and evaluate the temporal evolution (i.e., at the observation times corresponding to the available data; see also Table 2) of $\user2{Y}\left( \widetilde{\varvec{\theta}} \right)$ through the model considered (i.e., the PCE surrogate models of H₀, H₁, or H₂);

• 2) Evaluate the acceptance probability,$\gamma$, of $\widetilde{\varvec{\theta}}$ according to:

  $$ \gamma = {\text{exp}}\left\{ { - \frac{{\left[ {{\varvec{Y}}^{\user2{*}} - {\varvec{Y}}\left( \widetilde{\varvec{{\theta}}} \right)} \right]^{T} \left[ {{\varvec{Y}}^{\user2{*}} - {\varvec{Y}}\left( \widetilde{\varvec{{\theta}}} \right)} \right]}}{{2\sigma_{{\varvec{Y}}}^{2} }}} \right\} $$

  (15)

• 3) Draw a random value $u$ from a uniform distribution in the interval [0, 1];

• 4) Accept current realization of $\widetilde{\varvec{{\theta}}}$ if ${\text{ln}}u < {\text{ln}}\gamma$; otherwise reject $\widetilde{\varvec{{\theta}}}$ and return to Step 1.

Steps (1)-(4) are repeated until stable results for the distribution of $f_{{{\varvec{\theta}}\left| {{\varvec{Y}}^{*} } \right.}}$ are obtained. It is noted that the acceptance rate associated with random draws/realizations of model parameters depends on the strength of measurement errors through Eq. (14). Very high values of $\sigma_{{\varvec{Y}}}^{2}$ lead to accept a high number of realizations, all of these being virtually equally likely. Otherwise, very low values of $\sigma_{{\varvec{Y}}}^{2}$ results in a very low acceptance rate. In the absence of prior information about measurement errors, as in our setting, one typically selects $\sigma_{{\varvec{Y}}}^{2}$ to yield an acceptable compromise between acceptance rate and loss of data quality (see also Sect. 3.3).

2.4 Model Selection Criteria

Model selection criteria are employed to evaluate the relative skill of a candidate model (as compared against other models analyzed) to interpret available observations. We rely here on formal model selection criteria to evaluate (in a relative sense) the ability of each of the models we consider to interpret the available coreflooding data. Among the various model selection criteria proposed in the literature to discriminate amongst models (see, e.g., Riva et al. 2011; Hoge et al. 2018), we rest here on the deviance information criterion, DIC (Meyer 2014; Spiegelhalter et al. 2002; 2014), which is a generalization of the Akaike Information Criterion, AIC (Akaike 1974; Hurvich and Tsai 1989). Considering the posterior pdf of ${\varvec{\theta}}$, $f_{{{\varvec{\theta}}\left| {{\varvec{Y}}^{\user2{*}} } \right.}}$, evaluated via the ARS stochastic model calibration framework, the deviance $D\left( {\varvec{\theta}} \right)$ is defined as $D\left( {\varvec{\theta}} \right) = - 2{\text{log}}\left( {f_{{{\varvec{\theta}}\left| {{\varvec{Y}}^{\user2{*}}}\right.}} } \!\right)$ and the value of DIC is computed at the posterior parameter mean $\varvec{\overline{\theta }}$ as:

$$ \text{DIC}=D\left(\overline{\varvec{\theta}}\right)+2N_{\text{e}}$$

(16)

where $N_{{\text{e}}}$ is here taken as a metric of model complexity and does not necessarily coincide with $N_{{\text{P}}}$. Evaluation of $N_{{\text{e}}}$ relies on the observation that if the $f_{{\theta | \user2{Y}^{ * } }}$ is multivariate Gaussian, then $D\left( \theta \right)$ follows a ${\upchi }^{2}$ distribution (see Hoge et al. 2018) whose number of degrees of freedom, i.e.,

$$ N_{{\text{e}}} = \overline{{D\left(\varvec{\theta} \right)}} - D\left( \varvec{\bar{\theta }} \right) $$

(17)

is taken as a metric to evaluate $N_{{\text{e}}}$ (Spiegelhalter et al. 2014). Here, $\overline{{D\left(\varvec{\theta} \right)}}$ is the mean deviance, which is evaluated across the collection of accepted parameter realizations. We further note that, given its meaning, $N_{{\text{e}}}$ can (in principle) be larger than $N_{{\text{p}}}$ and that negative values for $N_{{\text{e}}}$ could arise under some circumstances, e.g., in the presence of a poor model fit (Celeux et al. 2006; Spiegelhalter et al. 2014).

Model discrimination criteria can then be employed to evaluate the posterior model probability, $p\left( {M_{\beta } {|}{\mathbf{Y}}^{*} } \right)$, of candidate model $M_{\beta }$ (among a suite of $N_{{\text{M}}}$ models) as (see Ye et al. 2008; Ranaee et al. 2017 and references therein):

$$ p\left( {M_{\beta } {|}{\mathbf{Y}}^{*} } \right) = \frac{{{\text{exp}}\left( { - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\Delta {\text{DIC}}_{\beta } } \right)p\left( {M_{\beta } } \right)}}{{\mathop \sum \nolimits_{l = 1}^{{N_{M} }} {\text{exp}}\left( { - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\Delta {\text{DIC}}_{{{l}}} } \right)p\left( {M_{{{l}}} } \right)}} $$

(18)

Here, $\Delta {\text{DIC}}_{\beta } = {\text{DIC}}_{\beta } - {\text{DIC}}_{{{\text{min}}}}$, ${\text{DIC}}_{\beta }$ being the value of the model selection criterion evaluated through Eq. (16) for model $M_{\beta }$; ${\text{DIC}}_{min}$ is the minimum value of ${\text{DIC}}_{\beta }$ across the $N_{{\text{M}}}$ candidate models; and $p\left( {M_{\beta } } \right)$ is the prior probability of model $M_{\beta }$. In our study we assign the same prior probability to each model $M_{\beta }$. We then rank each model according to the associated posterior probability, $p\left( {M_{\beta } {|}{\mathbf{Y}}^{*} } \right)$.

3 Results

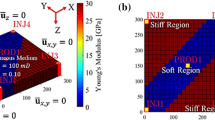
The three-dimensional cylindrical domain within which the modeling strategies illustrated in Sect. 2.2 are implemented is patterned after the coreflooding experiments of Sect. 2.1 in terms of geometry and initial/boundary condition. Consistent with the experimental procedure, the simulation of a primary drainage is considered for the initialization of the numerical domain. All simulations are performed with the MRST open-source toolkit (Lie 2019). An unstructured numerical grid comprising 11 and 201 cells in the longitudinal direction and across the transverse area of the system, respectively (for a total of 2211 computational grid cells), is used. This configuration is obtained after a grid sensitivity analysis and corresponds to a tradeoff between accuracy and computational time (details not shown). Some details about the three-dimensional numerical model set-up are illustrated in Appendix C, for completeness. The selected grid corresponds to an average CPU time of 21, 35, and 47.5 [min] for each forward model simulation associated with H₀, H₁, and H₂, respectively, with processor Inter(R) Xeon(R) CPU E5-2650 v3 @ 2.30 GHz with 128 GB RAM.

3.1 Characterization of the PCE Surrogate Models

Construction of a PCE surrogate model for a given quantity of interest entails performing forward simulations of the complete model for several combinations of the uncertain parameters. Here, we build and validate PCE surrogate models upon relying on a sample of 5000 Monte Carlo (MC) realizations of uncertain parameter values associated with each of the models considered. Classical MC sampling techniques across the random parameter space is characterized by modest efficiency (McKay et al. 1979; Kucherenko et al. 2015). Here, we rely on a Quasi-Monte Carlo approach (e.g., Caflisch 1998; Niederreiter 1992; Feil 2009; Maina et al. 2021) to sample model parameter values within the corresponding supports illustrated in Sect. 2.2.

Figure 3 depicts exemplary results of the temporal evolution of pressure drop and fluid saturations obtained through the numerical solution (via MRST) of the full system models analyzed.

Fig. 3

Temporal evolution of pressure drop (ΔP) and saturation of oil, water and gas computed via MRST for all scenarios. Thin gray curves correspond to MC realizations outcomes; bold solid and dashed curves respectively denote MC-based mean values and uncertainty intervals of width equal to ± twice the standard deviation around the corresponding mean

Visual inspection of these results reveals that uncertainty of model parameters propagates to the outputs in a way that makes it difficult to clearly discriminate the model conducive to some of the realizations obtained. In the case of the temporal histories of saturation, a significant difference amongst the modeling approaches is somehow visible only at late times and with reference to gas saturation. As such, at least from a qualitative standpoint, all three modeling approaches can be considered as plausible candidates to interpret the available data set.

We then construct a set of PCE surrogate models upon relying on 4000 (among the total of 5000) randomly selected MC results. A PCE approximation for ΔP and, given the relationship between fluid saturations, for (i) S_w for a two-phase system and (ii) S_w and S_g for a three-phase system (and consequently obtain also the surrogate model for S_o) is constructed for each of the observation times listed in Table 2.

The accuracy of the PCE approximations is then assessed by comparison against full model results obtained at the 19 observation times collected in Table 2 and corresponding to the collection of 1000 MC simulations that are excluded from the set of realizations used for the construction of the PCE. We note that the number of PCE coefficients to be estimated dramatically increases with the number of model parameters and the degree considered for the PCEs. In our case, PCEs requires the evaluation of 23, 22, or 46 (for PCEs of first order) and 276, 253, or 1081 (for PCEs of second order) coefficients for scenarios H₀, H₁, and H₂, respectively.

Figure 4 depicts scatterplots of S_w, S_o, S_g, and ΔP evaluated through each of the full computational models considered (for the collection of 1000 realizations forming the validation set) and their PCE-based counterparts. The appraisal of the quality of the surrogate model is completed through the results included in Table 5. The latter lists values of mean absolute percentage error, MAPE, between outputs from (i) the set of 4000 MC realizations employed to construct the PCEs (calibration set) or (ii) the validation set of 1000 MC realizations and their PCE-based counterparts. Our results suggest that second-order PCEs generally yield better approximations than their first-order counterparts, the latter providing results of slightly higher quality only with reference to ΔP values associated with MC simulations performed for H₁. As an additional remark, it can be noted that PCE approximations for H₀ and H₁ are of higher overall quality than those evaluated for H₂. This is possibly related to the observation that the number of uncertain parameters for H₂ is almost twice as much as that associated with H₀ and H₁ and PCEs of higher orders (or possibly a diverse surrogate modeling approach) could lead to enhanced quality approximations. This observation is particularly critical for the estimate of the pressure drop. We note that constructing PCEs of order 3 for H₂ would require performing 17,296 MC runs (corresponding to 570.5 [day] CPU time with the full system model). As such, we ground our further developments on the orders of approximation associated with the results embedded in Table 5, which we consider as a reasonable compromise between computational accuracy and time requirements, requiring approximately 8, 13, and 36 [hr] of CPU time (for PCEs of order 1) and 4, 6, and 37 [day] of CPU time (for PCEs of order 2) for H₀, H₁, and H₂, respectively. PCEs are then selected for each simulation scenario to estimate coreflooding responses according to the lowest MAPE values listed in Table 5. We further note that the analysis workflow we rely upon is fully compatible with other reduced-order modeling strategies and sampling strategies of model parameter space, whose suitability in this context can be subject to future studies.

Fig. 4

Scatter plots of full model outputs based on 1000 MC simulations (here termed as validation set) vs their counterparts evaluated through PCEs of order 1 and 2. Results are depicted for models a-d H₀, e–h H₁, and i-l H₂

Table 5 Performance of PCEs of order 1 and 2 to approximate the MC collection of full model outputs (i.e., fluid saturations, S_α, and pressure drop, ΔP)

3.2 Global Sensitivity Analysis

Consistent with the approach outlined in Sect. 2 and Appendix B, we quantify sensitivity of model outputs of interest to each uncertain model parameter $\theta_{{\text{i}}}$ through evaluation of the moment-based ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$ indices (see Eqs. (B.1)–(B.2)), respectively, quantifying the influence $\theta_{{\text{i}}}$ on mean and variance of Y, with Y = ΔP, S_w, S_o and S_g. As we recall in Sect. 2, GSA enables us to identify the uncertain input parameters which are most relevant for the subsequent step involving stochastic model calibration. In this context, GSA yields the overall relative importance of a given parameter on model responses across a given temporal window. On these bases, we retain for stochastic model calibration only parameters (collected in a vector ${\varvec{\theta}}_{{\text{R}}}$) which are deemed as influential to model outputs through the joint analysis of the ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$ metrics.

Table 6 lists the set of most influential parameters for each of the three mathematical models analyzed, as a result of the GSA. Note that, for the purpose of our demonstration, the most important parameters are here selected upon considering solely parameters associated with values of AMA indices (i.e., ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$) larger than half the largest AMA value evaluated considering the whole set of model parameters.

Table 6 GSA-based selected controlling parameters for models $H_{0}$, $H_{1}$, and $H_{2}$ collected in ${\varvec{\theta}}_{{\text{R}}}$

Notably, parameters such as the saturation endpoints as well as the exponents of the Corey-type power law equations describing relative two-phase permeabilities have been identified as most influential parameters for all scenarios. Comparing the single- and the dual-continuum fields, we note that, while in the former the system permeability is controlling the outputs of interest, in the latter this role is played by the permeability of the fracture continuum and by the shape factor, which regulates the flux transfer between the two overlapping continua.

An exemplary depiction of the results (in terms of values of ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$) obtained for a few selected controlling parameters for $H_{2}$ is offered in Fig. 5. The latter reveals that the largest values of ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$, quantifying the impact of $\theta_{i}$ on the mean of Y, correspond to (i) Y = S_w and $\theta_{{\text{i}}} = S_{{{\text{rwo}}}}^{D2} , \phi_{{\text{f}}}$ at the beginning of I (imbibition) and around the last stages of D2 (drainage) paths; and to (ii) Y = S_o at the final stages of (a) I for $\theta_{{\text{i}}} = S_{{{\text{row}}}}^{I}$ and, to a lesser extent, of (b) the three-phase WAG paths for $\theta_{{\text{i}}} = \phi_{{\text{f}}}$. We recall that values of ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$ for S_w (Fig. 5e) and S_o (Fig. 5f) coincide under two-phase conditions (associated with I, and D2), as S_w + S_o = 1. Variability of S_w (and hence S_o) is mainly affected by $S_{{{\text{row}}}}^{I}$ at the beginning of D2, while the impact of $S_{{{\text{rwo}}}}^{D2}$, and $\phi_\text{f}$ is significant under three-phase conditions. Otherwise, S_g (in terms of both ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$ indices) is strongly and persistently influenced by $n_{{{\text{go}}}}$, which drives the shape of gas relative permeability. Changes of mean values of $\Delta P$. are almost equally affected by $n_{{{\text{wo}}}}$, $n_{{{\text{ow}}}}$, $\phi_{{\text{f}}}$, and $F_{{\text{s}}}$, its variance being otherwise mostly sensitive to $K_{{\text{f}}}$, which exerts its influence across all of the experimental steps considered.

Fig. 5

Results for a-d ${\mathrm{AMAE}}_{{\theta}_{\mathrm{i}}}^{Y}$ and e–h ${\mathrm{AMAV}}_{{\theta }_{\mathrm{i}}}^{Y}$ global sensitivity indices obtained for ${{H}}_{2}$ and corresponding to few selected most influential controlling parameters (see Table 7). The shaded area corresponds to values of indices which are less than half the largest values documented for the indices across the observation window

3.3 Stochastic Model Calibration and Model Selection Criteria

Here, we discuss the results of the stochastic calibration of the surrogate models (based on the PCEs) associated with $H_{0}$, $H_{1}$, and $H_{2}$ yielding posterior pdfs of uncertain model parameters. Note that we rely on the GSA results and consider the most influential model parameters ${\varvec{\theta}}_{{\text{R}}}$ listed in Table 6 in the stochastic model calibration procedure, while setting the remaining parameters to the mean value associated with the corresponding supports listed in Tables 3 and 4. As an additional element of comparison, we also perform stochastic calibration of the aforementioned surrogate models upon considering the complete set of model parameters, ${\varvec{\theta}}$.

For the purpose of our analysis, we set the standard deviation of the ${\varvec{Y}}^{*}$ measurement errors to a constant value $\sigma_{{\text{Y}}} = 0.1$ (units are consistent with the type of data analyzed) as nonformation on this aspect is available (see Sect. 2.1). The selected value yields a generally reasonable compromise between a good acceptance rate and the loss of the quality of the data. We rely on 10⁶ realizations of the surrogate models, the overall acceptance rate being approximately 0.01% when considering the GSA-based selected influential parameters and 0.1% when considering all parameters, as detailed in the following.

Table 7 lists the key results of the ARS-based stochastic model calibration and of the model selection approach based on the deviance information criterion (described in Sects. 2.3 and 2.4, respectively) obtained upon considering only ${\varvec{\theta}}_{{\text{R}}}$ (i.e., the model parameters deemed as influential on the basis of GSA) or the complete collection of model parameters included in ${\varvec{\theta}}$.

Table 7 Main results of the ARS-based stochastic model calibration obtained upon considering ${\varvec{\theta}}_{{\text{R}}}$ or ${\varvec{\theta}}$. Results include: (a) the information metric, ${\text{DIC}}$, the effective number of model parameters, $N_{{\text{e}}}$, and the posterior model weights together with the number of model parameters subject to ARS. Smaller values of DIC (denoted in bold) correspond to a higher ability of the calibrated model to interpret available information

Table 7 shows that performance of the surrogate model associated with a dual-continuum system representation (i.e., scenario $H_{2}$) markedly improves (in terms of minimum value of DIC) when model complexity (in terms of the number of effective model parameters retained) is reduced by including results of GSA in our stochastic model calibration workflow. These results identify such a model as the most skillful in the model set, with (i) the lowest value of DIC and (ii) the highest value (about 99.9%) of posterior weight. Otherwise, they indicate than neither of the other modeling strategies assessed can be considered as a reliable alternative to H₂ to interpret the available experimental observations. Note that negative values for $N_{{\text{e}}}$ associated with model $H_{1}$ could be due to a poor model fit, as seen in Sect. 2.4 (Spiegelhalter et al. 2014). Otherwise, the results listed in Table 7 suggest that performing GSA is beneficial to assist decreasing complexity of simulation models H₀ and H₂.

The picture is complemented in Fig. 6 where we show posterior pdfs of the most influential model parameters associated with scenario $H_{2}$ (as obtained through GSA-assisted ARS) together with the adopted priors. We rely on the Kullback–Leibler divergence (KLD) (Kullback and Leibler 1951) to quantify the degree of similarity between posterior sample pdfs obtained by the GSA-assisted ARS and the corresponding posterior distributions obtained through ARS performed upon retaining all model parameters. We recall that KLD is a metric quantifying the amount of information lost when a given distribution is used to approximate another one, small values of KLD being thus associated with reduced loss of information. Here, we obtain very low values of KLD, these ranging from 10^–5 and 10^–2 depending on the parameter (see Fig. 6). For completeness, KLD values are also assessed to quantify similarities between prior (i.e., uniform; see Fig. 6) and posterior distributions of model parameters. The ensuing KLD values are of the order of 10^–1 (not shown), the highest value being equal to 0.54 and related to $K_{{\text{f}}}$, whose posterior exhibits a marked positive skewness across the support. These elements provide additional support to the robustness and reliability of our GSA-assisted stochastic inversion approach.

Fig. 6

Sample prior (solid blue line) and posterior pdfs of ARS (white bars) and GSA-assisted ARS (pink bars) for scenario H₂. KLD values between posterior pdfs obtained by ARS performed considering the full set of uncertain model parameters and GSA-assisted ARS are included

While there are (in general) no stark differences between the prior and posterior parameter distributions in Fig. 6, these results enable one to grasp the extent of the feedback between the influential model parameters and the available information content and are consistent with the indications of the GSA. The somehow moderate differences documented through prior and posterior parameter distributions can be related to the integral nature of the available experimental observations.

The probabilistic results obtained above yield an assessment of the way uncertainty associated with model parameters is propagated onto the target model outputs. Figure 7 depicts the temporal evolution of the 5th, 50th, and 95th percentiles of fluid saturations and total pressure drop obtained evaluating the full simulation model for scenario $H_{2}$ upon sampling the prior and posterior pdfs of model parameters. Experimental data are also included. One can note that prediction uncertainty only slightly decreases after stochastic model calibration, with respect to the corresponding uncertainty associated with the prior parameter pdfs. This result is in line with the observation that (a) only a sub-set of model parameters is found to be influential to the model results, (b) the amount and type of available data does not contain a sufficient level of information to strongly constrain the uncertainty propagated through the model to its outputs, and/or (c) the conceptual/mathematical models or the considered range of parameter values are not fully appropriate to represent the experimental evidences. While the amount of observations employed in our analysis is considered as typical of core-scale experimental procedures, our results suggest that integral data of the type available in the considered experiment should be complemented by additional local information, such as, e.g., fluid saturations along the core, to effectively constrain model characterization.

Fig. 7

Temporal evolution of the 5th, 50th, and 95th percentiles of fluid saturations and total pressure drop across the domain obtained for scenario ${H}_{2}$ upon sampling the prior and posterior pdfs of model parameters. Available experimental data are also included

Referring to Fig. 7, estimates of observed water saturations are of acceptable quality across the entire temporal window analyzed, while estimates of oil saturations are of acceptable quality only under two-phase conditions (up to 25 days). Otherwise, simulation results underestimate gas saturation and overestimate oil saturation during three-phase flow. This can be related to the observation that three-phase hysteresis effects are neglected for the characterization of three-phase oil relative permeability (see Eq. 9). Blunt (2000) shows that part of two-phase (oil–water) residual oil saturation can be displaced across the system under a layer drainage mechanism. This can lead to some gas trapping under three-phase conditions. To analyze this issue, Fig. 8 illustrates the three-phase saturation path across the ternary saturation diagram as associated with the 50th percentile values of fluid saturations obtained after ARS calibration of scenario H₂. The width of the envelopes associated with the 5th and 95th percentiles is also depicted (red curves) together with the experimental observations.

Fig. 8

Saturation path associated with values of fluid saturations obtained corresponding to the 50th percentile of the distribution obtained after ARS calibration of model H₂. The width of the envelopes associated with the 5th and 95th percentiles is also depicted (red curves) together with the experimental observations

High values of residual water saturation (i.e., 50%) can be noted for the experiment. Sharp switches of the saturation path are evidenced for the last observation point obtained during gas injection (corresponding to recording step 19 in Table 2 and highlighted with a star symbol in Fig. 8). Such a behavior is consistent with a conceptual picture according to which an inter-connected system of fractures possibly existing in the core sample can favor rapid fluid flow and is in line with the adopted modeling strategy. Thus, the injected nonwetting phase (i.e., gas under the explored WAG scenario) can migrate through such highly conductive features, while its transfer to the rock matrix continuum takes place across a much longer timescale.

We then evaluate relative permeabilities ensuing ARS calibration of model H₂ and considering the associated collection of saturation and pressure drop values. Figure 9 depicts the resulting 5th, 50th, and 95th percentiles of two-phase relative permeabilities of the matrix and fracture continua. These results suggest that estimates of OW relative permeabilities during (i) drainage and imbibition of the matrix and (ii) drainage inside the fractures are characterized by the highest levels of uncertainty.

Fig. 9

5th, 50th, and 95th percentiles of two-phase relative permeabilities of the matrix and fracture continua resulting from ARS calibration of model H₂

Finally, Fig. 10 depicts WO and OG mean capillary pressure of the matrix/fracture continuum versus fluid saturation. We recall that our GSA results (Sect. 3.2, Table 6) identify solely $S_{{{\text{rwo}}}}^{D2}$ of the parameters of the Corey-type capillary pressure model Eqs. (5)–(6) as influential to the model outcomes (according to the metrics employed). Our analysis (details not included) shows that uncertainty in $S_{{{\text{rwo}}}}^{D2}$ has a negligible effect on variation of capillary pressure curves. While additional studies are required to sustain these findings, our results suggest that it would be possible to neglect considering capillary pressures of the fracture system in the context of a dual-continuum model formulation for multiphase flow.

Fig. 10

Median (50th percentile) of two-phase capillary pressure associated with the matrix (solid lines) and fracture (dashed lines) continua resulting from ARS calibration of model H₂ for a, WO and b OG conditions

4 Conclusions

We illustrate a procedure to characterize, within in a stochastic framework, a collection of (competitive) models of coreflooding simulations under two- and/or three-phase flow conditions, with special concerns about the heterogeneity of rock properties and the occurrence of preferential pathways (of the kind associated with a fractured system) along the core sample. Three continuum-scale conceptual/modeling scenarios are assessed. These account for spatial distributions of porosity and absolute permeability with differing degrees of complexity and correspond to (i) homogeneous; (ii) heterogeneous; and (iii) fractured fields, as conceptualized through a dual-continuum approach. Stochastic model calibration (based on acceptance–rejection sampling, ARS) assisted by global sensitivity analysis (GSA-assisted ARS) is performed on a set of parameters that we have shown to be influential to key outcomes of the coreflooding simulations. We illustrate our approach on the set of two- and three-phase laboratory-scale steady-state coreflooding experiments performed by Moghadasi et al. (2019) on a Portland limestone core sample.

Our work leads to the following key conclusions:

• The results of our analysis clearly show that assisting stochastic inverse modeling through global sensitivity analysis and the application model reduction techniques can considerably contribute to (a) the reduction of the dimensionality of the uncertain model parameter space and (b) the ensuing identification of the most skillful model to represent two- and three-phase flow associated with laboratory-scale coreflooding scenarios constrained through experimental observations. We find out that, amongst the tested continuum-scale models, a dual-continuum formulation provides the best performance in the context of the experimental observations considered. Such model is associated with the highest posterior probability value (as evaluated through the deviance information criterion Eqs. (16)–(18)). Otherwise, typical system representations related to either a homogeneous or a heterogeneous domain, even in the presence of highly connected preferential pathways, are considered to be less skillful to interpret the experimentally observed system behavior.

• Only 8 of the 45 parameters embedded in the dual-continuum formulation are recognized as key sources of uncertainties significantly affecting the values (and associated uncertainty) of model outputs (fluids pressure and core-averaged saturations). These include (i) fracture porosity, $\phi_{{\text{f}}}$, and absolute permeability, $K_{{\text{f}}}$, (ii) the saturation endpoints (i.e., connate water and residual oil) within the matrix in WO systems, (iii) three empirical parameters describing the degree of convexity of the relative permeability curves of oil, water (in a WO system), and gas (in a OG system) within the matrix continuum (reflecting wettability conditions), and (iv) a shape factor representing the degree of mass transfer between the two continua (corresponding to the fracture and the porous matrix). Simulation results are virtually insensitive to the values of (i) characteristic parameters of the relative permeability and capillary pressure formulations adopted for the matrix continuum, and (ii) saturation endpoints and parameters of the adopted formulation for relative permeability or capillary pressure in the fracture continuum. Note that these specific results may differ for other experimental setups and/or when considering different formulations to represent relative permeability and capillary pressure embedded in the selected conceptual system models. We recall that the width of the support of the uncertain model parameters analyzed has been selected to be as large as possible on the basis of information available in the literature and past experience. As we show in a previous study (Ceriotti et al. 2018), the relative importance of a given model parameter in driving the uncertainty of the model output of interest can vary across the parameter space. A detailed assessment of this aspect would require the joint use of local and global sensitivity analysis approaches, which we defer to a future study.

• Recalling that we do not pursue a deterministic inverse modeling approach, we note that the quality of our stochastic model calibration results can suffer from a series of elements. These include, e.g., (i) the assumption of neglecting hysteresis effects for the characterization of three-phase relative permeabilities, (ii) the possibility that other mathematical formulations or modeling approaches can be employed to interpret the system behavior. We also note that while the amount of information employed in the stochastic model calibration is considered as typical of core-scale experimental procedures (including observations of pressure drop across the sample as well as two- and three-phase fluid saturations of the rock sample and flow), our results suggest that these types of integral data should be complemented by local (along the core) information to effectively constrain model characterization.

Our study provides a comprehensive analysis of the dynamics of multiphase flow in fractured/porous media and can form a robust basis to effectively assist (a) interpretation of data associated with coreflooding practices, (b) further design of laboratory coreflooding experiments, and (c) evaluation of the performance of the field-scale production scenarios.

Appendices

Appendix A: Polynomial Chaos Expansion

The polynomial chaos expansion (PCE) approximation allows evaluating a model output, $Y\left( {\varvec{\theta}} \right)$ (which belongs to the space of square integrable functions) at a reduced computational cost through:

$$ Y\left( {\varvec{\theta}} \right) = \mathop \sum \limits_{{{\upeta } \in {\mathbb{N}}^{{N_{{\text{p}}} }} }} {\varvec{\delta}}_{{\upeta }} {\varvec{\psi}}_{{\upeta }} \left( {\varvec{\theta}} \right) = \delta_{0} \psi_{0} + \mathop \sum \limits_{i = 1}^{{N_{{\text{p}}} }} \delta_{i} \psi_{1} \left( {\theta_{i} } \right) + \mathop \sum \limits_{j \ge i}^{{N_{{\text{p}}} }} \delta_{{{\text{ij}}}} \psi_{2} \left( {\theta_{{\text{i}}} ,\theta_{j} } \right) + \mathop \sum \limits_{k \ge j}^{{N_{{\text{p}}} }} \delta_{{{\text{ijk}}}} \psi_{3} \left( {\theta_{{\text{i}}} ,\theta_{{\text{j}}} ,\theta_{{\text{k}}} } \right) + \ldots \quad {\text{with}}\,{\varvec{\delta}}_{{\upeta }} = \mathop \smallint \nolimits_{{\Gamma}}^{{}} Y\left( {\varvec{\theta}} \right){\varvec{\psi}}_{{\upeta }} \left( {\varvec{\theta}} \right){\text{pdf}}\left( {\varvec{\theta}} \right){\text{d}}{\varvec{\theta}} $$

(A.1)

where $Y\left( {\varvec{\theta}} \right)$ is approximated by a linear combination of multivariate orthonormal polynomials, ${\varvec{\psi}}_{{\upeta }}$ (${\upeta }$ representing the order of the polynmial), and ${\varvec{\delta}}_{{\upeta }}$ are polynomial coefficients.

The family of polynomials to be used depends on the probability density function (pdf) characterizing the entries $\theta_{i}$ of ${\varvec{\theta}}.$ Since each $\theta_{i}$ is here considered to be uniformly distributed, we adopt Legendre polynomials. Evaluation of ${\varvec{\delta}}_{{\upeta }}$ requires solving the full model for multiple combinations the model parameters. Equation (A.1) can be rendered workable upon truncation of the summation to a set of polynomials with total degree $\omega$. Accuracy of Eq. (A.1) generally increases with $\omega$, requiring the evaluation of $N_{{\upomega }} = \left( {N_{{\text{P}}} + \omega } \right)!/\left( {N_{{\text{P}}} !\omega !} \right)$ coefficients.

As stated in Sect. 3.1, we build and validate PCE surrogate models upon relying on a sample of 5000 Monte Carlo (MC) realizations of uncertain parameter values associated with each of the models considered. We construct a set of 3 m surrogate models (comprising PCEs of the kind expressed through Eq. (A.1)) to represent values of ΔP, $S_{{\text{w}}}$, and $S_{{\text{g}}}$ (oil saturation being constrained by considering that fluid saturations sum up to unity) at each of the m = 19 temporal recording steps where data are observed (see also Table 2). We then calibrate these through least squares regression (see details in Tamellini and Nobile, 2022) against a sub-set of the above mentioned MC realizations of the full model, while using the remaining ones for validation (see details in Sect. 3.1). The PCE surrogate models are then employed to perform (i) global sensitivity analysis of the system behavior (Sect. 3.2) and (ii) stochastic inverse modeling (Sect. 3.3). We do so since attaining stable results for each of these approaches requires having at our disposal a number of Monte Carlo realizations of the order of 10⁶. Performing such a high number of simulations of the full model would be prohibitive, due to the markedly high computational costs involved (see Sect. 3).

Appendix B: Moment-based Sensitivity Indices

Dell’Oca et al. (2017) introduce a set of global sensitivity metrics, denoted as AMA indices (termed after the authors’ initials). Here, we focus on the following two AMA indices:

$$ {\text{AMAE}}_{{\theta_{{\text{i}}} }}^{y} = \left\{ {\begin{array}{*{20}c} {\frac{1}{{\left| {E\left[ y \right]} \right|}}\mathop \smallint \limits_{{{\Gamma }_{{\theta_{{\text{i}}} }} }}^{ } \left[ {\left| {E\left[ y \right] - E\left[ {y|\theta_{{\text{i}}} } \right]} \right|} \right] {{\rho} _{{\theta_{{\text{i}}} }}} {\text{d}}\theta_{{\text{i}}} = \frac{1}{{\left| {E\left[ y \right]} \right|}}E\left[ {\left| {E\left[ y \right] - E\left[ {y|\theta_{{\text{i}}} } \right]} \right|} \right] {\text{ if }} E\left[ y \right] \ne 0} \\ {\mathop \smallint \limits_{{{\Gamma }_{{\theta_{{\text{i}}} }} }}^{ } \left[ {\left| {E\left[ y \right] - E\left[ {y|\theta_{{\text{i}}} } \right]} \right|} \right] {{\rho} _{{\theta_{{\text{i}}} }}} {\text{d}}\theta_{{\text{i}}} = E\left[ {\left| {E\left[ {y|\theta_{{\text{i}}} } \right]} \right|} \right] {\text{ if }} E\left[ y \right] = 0} \\ \end{array} } \right. $$

(B.1)

$$ {\text{AMAV}}_{{\theta _{{\text{i}}} }}^{y} = \frac{1}{{V\left[ y \right]}}\int\limits_{{\Gamma _{{\theta _{{\text{i}}} }} }}^{{}} {\left[ {\left| {V\left[ y \right] - V\left[ {y|\theta _{i} } \right]} \right|} \right] {{\rho} _{{\theta_{{\text{i}}} }}} {\text{d}}\theta _{{\text{i}}} = \frac{{E\left[ {\left| {V\left[ y \right] - V\left[ {y|\theta _{{\text{i}}} } \right]} \right|} \right]}}{{V\left[ y \right]} }}$$

(B.2)

where ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{y}$ represent the sensitivity indices associated with the mean and variance of a given model output $y\left( {\varvec{\theta}} \right)$, respectively, as linked to variability of $\theta_{{\text{i}}}$; $E\left( \bullet \right){ }$ denotes expected value and $V\left( \bullet \right)$ denotes variance; $E\left[ y \right]$ and $V\left[ y \right]$ are the unconditional expectation and variance of $y$, respectively; $E\left[ {y|\theta_{{\text{i}}} } \right]$ and $V\left[ {y|\theta_{{\text{i}}} } \right]$ are the expected value and variance of $y$, respectively, conditional to a given value of parameter $\theta_{{\text{i}}}$ sampled across its support ${\Gamma }_{{\theta_{i} }}$; and $\rho_{{\theta_{i} }}$ is the marginal probability density of ${\rho} _{{\theta_{i} }}$ (here considered as uniform in our GSA). Note that indices ${\text{AMAE}}_{{\theta_{{\text{i}}} }}^{Y}$ and ${\text{AMAV}}_{{\theta_{{\text{i}}} }}^{Y}$ quantify the expected change of mean and variance of $Y$ due to variations of $\theta_{{\text{i}}}$, respectively. These indices take into account possible interactions between parameter $\theta_{{\text{i}}}$ and the remaining parameters in given model, even as they do not allow quantitative characterization of the strength and nature of possible parameter interactions as in the case, e.g., of the classical variance-based Sobol indices (see also Dell’Oca et al. 2017; Bianchi Janetti et al. 2019). We refer to Dell’Oca et al. (2017) for additional details about these moment-based global sensitivity indices.

Appendix C: Numerical Model

We set up a three-dimensional numerical simulation model with the same geometry and initial/boundary condition of the coreflooding experiments presented by Moghadasi et al. (2019) and described in Sect. 2.1. The cylindrical domain (of radius r and length L) is discretized into a set of 2211 unstructured elements. Note that mesh gridding (along core sample) is selected to be finer near the inlet and outlet section of the core simulation model (to adequately simulate effects of boundary conditions, BC). A coarser grid is selected for the rest of the simulation domain (to reduce computational costs associated with forward solutions of the full model employed for the construction of the PCE-based surrogate model) as depicted in Fig. 

Fig. 11

Key geometrical features of the three-dimensional numerical simulation model mimicking the core sample employed in the laboratory experiments described in Sect. 2.1: a mesh gridding and global view, and b boundary conditions, BC

11.

Rock compressibility is assumed to be negligible under the experimental conditions analyzed. Compressibility of water, oil, and gas are set to 10^–8, 10^–8, and 10^–4 [MPa⁻¹], respectively. This can result in a pressure dependency of the density ($\rho_{\alpha }$) of fluid phase $\alpha$. This is modeled as $\rho_{\alpha } \left( p \right) = \left[ {b_{\alpha } \left( {p_{0} } \right) \times {\text{exp}}\left( {p - p_{0} } \right) \times c_{\alpha } } \right] \times \rho_{\alpha } \left( {p_{0} } \right)$, where $b_{\alpha } \left( p \right)$ is the inverse formation volume factor (Lie 2019) and $c_{\alpha }$ is compressibility of fluid phase $\alpha$.

Numerical simulations are time dependent. For each Monte Carlo realization of the uncertain model parameters, the numerical domain is initialized with constant saturations of oil and connate water while pressure is at atmospheric value across the system.

Boundary conditions correspond to (i) the temporal evolution of the volumetric flow rate of water, oil, and gas depicted in Fig. 2; (ii) given pressure (corresponding to atmospheric value) at the outlet section; and (iii) no-flow along the lateral surface.

The time integration method is based on the fully implicit scheme available in the MRST toolbox. We set a timestep equal to 7.5 $\times$ 10^–10 [days] at the beginning of each path (I, D2, WAG). We then increase it geometrically until it reaches the target value of 0.0125 [day]. The latter is selected to ensure stability of the numerical simulations.