1 Introduction

The topic of the flow of a Bingham fluid when it is not saturating a porous matrix is a well-established field of study, and the literature is now quite mature. Efforts continue to develop different numerical methods which will allow an accurate computation of such flows, the chief difficulty being the presence of a yield surface which needs to be computed as part of the overall problem. In some simplified cases, the analysis can proceed analytically (such as for plane-Poiseuille and Hagen–Poiseuille flows), but in other one dimensional problems the analysis has to be completed by using a simple Newton–Raphson iteration equation on a transcendental equation which then allows the positions of the yield surfaces to be found. Examples of such works include those by Yang and Yeh (1965) and Bayazitoglu et al. (2007) who studied steady free convection in a vertical channel which is heated from the side. Steady convection will only ensue once the Rayleigh number is sufficiently large that the yield stress is overcome by the buoyancy force. For this free convection problem, there are two moving zero-shear regions (i.e. ones which act like solids) and three fluid regions undergoing shear. By contrast, Patel and Ingham (1994) considered mixed convection with the combination of buoyancy and a driving pressure gradient, while Barletta and Magyari (2008) studied a free convection version of vertical Couette flow. In both cases the number, the size and the locations of the plug-flow regions are dependent on further nondimensional parameters. One paper whose topic is closer to that of the present is that of Kleppe and Marner (1972) who considered a sudden change in the temperature of one the sidewalls and who then determined the evolution with time of the resulting velocity profile.

When a Bingham fluid saturates a porous medium there are some changes to the modelling of the equations of motion which are caused by the presence of the porous matrix. Just as the Navier–Stokes equations, which apply for a clear Newtonian fluid, are replaced by Darcy’s law, which applies in a porous medium, so it is that the usual yield-stress form of the Navier–Stokes equations, which gives zero shear when stresses are less than the yield stress, needs to be replaced by a Darcy–Bingham law. The first papers which presented such a law were those by Pascal (1979, 1981). This law appears later, see Eq. (1), but it provides a piecewise-linear dependence of the flux velocity on the applied pressure gradient; thus, there is a yield pressure gradient. When the pressure gradient (or, equivalently, body forces) is less than a threshold value then there is no flow. Further realism is obtained by considering the porous medium as an assembly of identical channels or pores, which gives the well-known Buckingham–Reiner law (1921). In this case the initial rise in the flow is quadratic immediately post-threshold, as opposed to linear in Pascal’s model. We also note that more sedate transitions to flow were found by Nash and Rees (2017) who considered distributions of channels/pores. In the present paper, we will adopt Pascal’s piecewise-linear form.

In this short paper, we will consider the flow of a Bingham fluid in a vertical circular cylinder which is filled with a porous medium. The flow is induced by means of applying a sudden heating to the outer surface, and therefore the paper may be categorised in the same way as the works of Kleppe and Marner (1972) and of Rees and Bassom (2015, 2016). The present paper extends the analyses of Rees and Bassom (2015, 2016) into a cylindrical domain, and therefore the work presented has been made as concise as possible. Therefore, the heating considered here takes two forms: (1) a new temperature and (2) a nonzero heat flux. Using Pascal’s piecewise-linear Darcy–Bingham law, the analysis proceeds analytically and again, a Newton–Raphson scheme has to be used in order to locate both the yield surfaces and, given that the flow domain is finite horizontally, the corresponding change to the initial hydrostatic pressure gradient.

2 Governing Equations

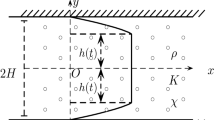
The present paper is concerned with a vertical cylindrical configuration and the subsequent evolution of the velocity and temperature fields once its bounding surface has its temperature raised from the reference temperature. The configuration we use is sketched in Fig. 1. In Case 1 the initial temperature is \(T_0\) and at the time \(t=0\) the temperature of the outer boundary is raised suddenly to \(T_1\), while, by way of contrast, Case 2 considers a sudden change in the boundary heat flux.

Fig. 1
figure 1

Definition sketch of the configuration being studied. Also shown are typical instantaneous temperature and vertical velocity profiles which are radially symmetric

Full size image

For the isothermal and unidirectional flow of a Bingham fluid saturating a homogeneous and isotropic porous medium, we may follow Pascal (1981) and write the equation,

$$\begin{aligned} {{\overline{w}}}= {\left\{ \begin{array}{ll} -{\displaystyle \frac{K}{\mu }} \Bigl [1-{\displaystyle \frac{G}{|{{\overline{p}}}_{{\overline{z}}}|}}\Bigr ]{{\overline{p}}}_{{\overline{z}}}&{}\quad \text {when } |{{\overline{p}}}_{{\overline{z}}}|>G,\\ 0 &{}\quad \text {otherwise}, \end{array}\right. } \end{aligned}$$
(1)

where G is used to denote the threshold pressure gradient above which the fluid is able to flow. Other terms in Eq. (1) are the common ones used for flows in porous media and they are given in the Nomenclature. In the present paper, we shall considering a free convective flow, and therefore buoyancy forces may also to be included in such an equation and we obtain,

$$\begin{aligned} { {{\overline{w}}}= {\left\{ \begin{array}{ll} -{\displaystyle \frac{K}{\mu }} \left[ 1-{\displaystyle \frac{G}{|{{\overline{p}}}_{{\overline{z}}}-\rho g \beta (T-T_0)|}}\right] \Bigl ({{\overline{p}}}_{{\overline{z}}}-\rho g \beta (T-T_0)\Bigr ) &{}\quad \text { when } |{{\overline{p}}}_{{\overline{z}}}-\rho g \beta (T-T_0)|>G,\\ 0 &{} \quad \text { otherwise}. \end{array}\right. }} \end{aligned}$$
(2)

We have taken \({{\overline{w}}}\) to be the vertical velocity here and have also assumed that the Boussinesq approximation applies. The reference temperature is \(T_0\).

The cases which we consider are regarded as being of infinite length in the vertical direction, although practically a long finite cylinder or annulus is highly likely to be essentially equivalent. This means that the thermal boundary layer which arises initially and its subsequent evolution will be unidirectional with the temperature and the vertical velocity being functions solely of the radius and time. In such cases, the equation of continuity is satisfied.

The governing equation for the heat transport is,

$$\begin{aligned} { \varsigma \frac{\partial T}{\partial {{\overline{t}}}} = \alpha \left( \frac{\partial ^2 T}{\partial {{{\overline{r}}}}^2} + \frac{1}{{{\overline{r}}}}{\displaystyle \frac{\partial T}{\partial {{\overline{r}}}}} \right) , } \end{aligned}$$
(3)

where \({{\overline{r}}}\) is the radial coordinate. Here \(\varsigma \) is the heat capacity ratio between the porous medium and the saturating fluid, and \(\alpha \) is the thermal diffusivity of the porous medium.

The governing equations, namely Eqs. (2) and (3), may be nondimensionalised using the following scalings,

$$\begin{aligned}&({{\overline{r}}},{{\overline{z}}})= R(r,z), \quad {{\overline{w}}}= {\displaystyle \frac{\alpha }{R}}w, \quad {{\overline{p}}}= \frac{\alpha \mu }{K}p, \quad T= T_0 + (T_1-T_0)\theta , \quad {{\overline{t}}}= \frac{\varsigma R^2}{\alpha } t,\nonumber \\&\quad G= \frac{\alpha \mu }{KR}\mathrm{Rb}, \end{aligned}$$
(4)

where \(T_1\) is the temperature of the hot surface and R is a chosen radius, and we obtain,

$$\begin{aligned} { w = {\left\{ \begin{array}{ll} \mathrm{Ra}\,\theta -{\displaystyle \frac{\partial p}{\partial z}} - \mathrm{Rb}, &{} \,\quad \mathrm{Rb}<\mathrm{Ra}\,\theta -{\displaystyle \frac{\partial p}{\partial z}},\\ &{}\\ 0, &{} \quad -\,\mathrm{Rb}<\mathrm{Ra}\,\theta -{\displaystyle \frac{\partial p}{\partial z}}<\mathrm{Rb},\\ &{}\\ \mathrm{Ra}\,\theta -{\displaystyle \frac{\partial p}{\partial z}} + \mathrm{Rb}, &{} \,\,\quad \mathrm{Ra}\,\theta -{\displaystyle \frac{\partial p}{\partial z}}<-\mathrm{Rb}, \end{array}\right. } } \end{aligned}$$
(5)

and

$$\begin{aligned} { {\displaystyle \frac{\partial \theta }{\partial t}} = \frac{\partial ^2 \theta }{\partial {r}^2}+\frac{1}{r}{\displaystyle \frac{\partial \theta }{\partial r}}. } \end{aligned}$$
(6)

In the above equations, the Darcy–Rayleigh number is given by

$$\begin{aligned} { \mathrm{Ra}= \frac{\rho g \beta (T_1-T_0) KR}{\mu \alpha },} \end{aligned}$$
(7)

and the Rees–Bingham number is,

$$\begin{aligned} { \mathrm{Rb}= \frac{\textit{KR}}{\mu \alpha } G. } \end{aligned}$$
(8)

This latter parameter is clearly a scaled version of the yield pressure gradient, G, and, given the presence of K and \(\alpha \), it could also be described as a porous convective Bingham number.

The initial condition in nondimensional form is simply that \(\theta =0\) at \(t=0\). The two cases which we consider now correspond to the following:

$$\begin{aligned} { \begin{array}{lll} \hbox {Case 1:} &{}\quad 0\le r \le 1 &{}\quad \theta =1 \quad \hbox {at}\quad r=1, \\ \hbox {Case 2:} &{}\quad 0\le r \le 1 &{}\quad \partial \theta /\partial r =-1 \quad \hbox {at}\quad r=1. \\ \end{array} } \end{aligned}$$
(9)

Case 1 is considered in the following section, but when Case 2 is considered in Sect. 4, then the modified boundary condition at \(r=1\) requires minor changes in the scaling for T and for the definition of \(\mathrm{Ra}\); these will be introduced in the appropriate place in the text.

3 Case 1: Constant Temperature

We consider the development of the temperature field within a vertical porous cylinder the initial temperature of which is \(\theta =0\) and where the temperature of the boundary at \(r=1\) is raised suddenly to \(\theta =1\). The evolution of the temperature field is governed solely by conduction and is unaffected by the induced flow.

We may solve Eq. (6) using separation of variables; in this way it is a standard textbook exercise to show that the final solution is

$$\begin{aligned} { \theta = 1 - \sum _{n=1}^\infty A_n J_0(\lambda _n r)e^{-\lambda _n^2 t} \quad \hbox {where} \qquad A_n = {\displaystyle \frac{\displaystyle \int _0^1 J_0(\lambda r) r\, \mathrm{d}r }{\displaystyle \int _0^1 J^2_0(\lambda r) r\, \mathrm{d}r}}, } \end{aligned}$$
(10)

and where the \(\lambda _n\) values are the positive zeros of the zeroth order Bessel function of the first kind, \(J_0\). Using standard results involving Bessel functions, this solution may be written in a simpler form:

$$\begin{aligned} { \theta = 1 - \sum _{n=1}^\infty {\displaystyle \frac{2}{\lambda _n J_1(\lambda _n)}} J_0(\lambda _n r) e^{-\lambda _n^2 t}.} \end{aligned}$$
(11)

Figures 2 and 3 are concerned with the temperature field. Although such curves are well known and appear in many textbooks and lecture notes, they nevertheless set the context for the resulting flow and are included for that reason. Figure 2 shows the temperature profile at a selected set of times. Clearly a very distinct boundary layer forms at very early times, and, when \(t\ll 1\), it may be shown to be given by the equivalent Cartesian solution, \(\mathrm{erfc}\,[(1-r)/2\sqrt{t}]\), until curvature effects become significant.

Fig. 2
figure 2

The evolution of the temperature profiles with time. The continuous curves correspond to \(t=10^{-4}\), \(10^{-3}\), \(10^{-2}\), \(10^{-1}\) and 1. The dotted curves are intermediate values; for example, the uppermost two correspond to \(t=0.2\) and \(t=0.5\). The other curves correspond to the analogous values of t

Full size image
Fig. 3
figure 3

The variation in time of the temperature at the centre of the cylinder

Full size image

The temperature at the origin will also be important in what follows, and therefore Fig. 3 shows this as a function of time. The origin remains at the original temperature until \(t\simeq 0.03\) after which the temperature rises towards 1. By the time \(t=1\) the temperature at the origin is \(\theta =0.9951\). At this point in time, the temperature of the cylinder is almost uniform and therefore there are no buoyancy forces available to drive a flow. That this should be so is evident if the present model problem forms the central portion of a very tall closed cylindrical cavity where the mean flow up the layer be zero. If we consider Eq. (5) in its Newtonian form, i.e. with \(w=\mathrm{Ra}\,\theta -p_z\), then the initial state, \(\theta =w=0\), means that \(p_z=0\). However, once the cylinder has heated up completely to \(\theta =1\), then the velocity field must again be zero, and therefore \(p_z\) has now risen to the value given by \(\mathrm{Ra}\). This simply corresponds to an adjustment in the hydrostatic pressure gradient because the new uniform temperature is different from the reference value. Therefore, the variation of \(p_z\) with time will also need to be computed as part of the solution procedure for w; this idea was also used in Rees and Bassom (2015, 2016).

The velocity field is given by solving Eq. (5). The chief difficulty is the determination of the location of the two yield surfaces between which the fluid is stationary. If the inner and outer yield surfaces are defined to be \(r=r_1\) and \(r=r_2\), respectively, then Eq. (5) tells us that

$$\begin{aligned} { \mathrm{Ra}\, \theta (r_1,t) - p_z + \mathrm{Rb}= 0,} \end{aligned}$$
(12)

and

$$\begin{aligned} { \mathrm{Ra}\, \theta (r_2,t) - p_z - \mathrm{Rb}= 0,} \end{aligned}$$
(13)

at all times. The third condition which needs to be satisfied is that the overall vertical flow is zero. This means that

$$\begin{aligned} { \int _0^{r_1} w\,r\,\mathrm{d}r + \int _{r_2}^1 w \, r\, \mathrm{d}r =0 } \end{aligned}$$
(14)

must be satisfied. After some lengthy manipulations, this condition may be written in the form,

$$\begin{aligned}&{\displaystyle \frac{\mathrm{Rb}}{\mathrm{Ra}}}\Bigl ( 1-r_1^2-r_2^2\Bigr ) +\Bigl [{\displaystyle \frac{p_z}{\mathrm{Ra}}}-1\Bigr ] \Bigl ( 1 + r_1^2 - r_2^2 \Bigr )\nonumber \\&\quad +\,4\sum _{n=1}^\infty {\displaystyle \frac{J_1(\lambda _n)+r_1J_1(\lambda _nr_1)-r_2J_1(\lambda _nr_2)}{\lambda _n^2J_1(\lambda _n)}}e^{-\lambda _n^2t} = 0. \end{aligned}$$
(15)

Equations (12), (13) and (15) form three nonlinear equations for the three unknowns, \(r_1\), \(r_2\) and \(p_z\) as functions of t. As with our previous papers Rees and Bassom (2015, 2016), the solutions were obtained using a multi-dimensional Newton–Raphson scheme which utilises numerical differentiation to obtain the iteration matrix.

Fig. 4
figure 4

Showing temperature and velocity profiles for \(\mathrm{Rb}/\mathrm{Ra}=0.1\) and for \(t=0.001\), 0.01, 0.1 and 0.3. Dotted curves correspond to temperature profiles and continuous curves to velocity profiles

Full size image

Figure 4 shows some example velocity profiles for the case, \(\mathrm{Rb}/\mathrm{Ra}=0.1\). When \(t=0.001\) the temperature field, which is also shown in Fig. 4, has penetrated only a small distance from \(r=1\). The resulting velocity profile consists of a narrow region of upward flow near the other surface, another narrow region of stagnant medium, and a very wide region of low amplitude negative velocity which includes the origin. The closer one gets to \(t=0\), the weaker the downflow is and the narrower are the regions of upflow and stagnation, as shall be seen in Fig. 5.

Fig. 5
figure 5

The variation in time of the location of the yield surfaces, \(r=r_1\) (lower) and \(r=r_2\) (upper). The curves correspond to \(\mathrm{Rb}/\mathrm{Ra}=0.01\), 0.1, 0.2, 0.3, 0.4, 0.45, 0.48 and 0.49

Full size image

Once time has reached \(t=0.01\) both the upflow and stagnant regions have widened substantially, and the magnitude of downflow in the centre of the cylinder has also increased. As t increases further the magnitude of the downflow and the width of the upflow region both reach a maximum and then decrease once more. The primary reason for this is the heating up of the centre of the cylinder which brings about a decrease in the available buoyancy force. Just before the fluid becomes completely stagnant, the upflow and downflow have both become weak and the regions they occupy have become narrow. At a point in time which depends on the value of \(\mathrm{Rb}/\mathrm{Ra}\) (see below, and Fig. 6) the fluid stops moving.

Fig. 6
figure 6

The variation with \(\mathrm{Rb}/\mathrm{Ra}\) of the time at which convection ceases

Full size image

In Fig. 5, we give a summary of how the yield surfaces vary in time for different values of \(\mathrm{Rb}/\mathrm{Ra}\). For each value of \(\mathrm{Rb}/\mathrm{Ra}\) two curves are presented and the fluid is stagnant in the region between those curves. Our previous comment about the narrowness of the stagnant region and its proximity to \(r=1\) at early times is clearly evident in that Figure. In addition, we also see that the width of the stagnant region increases as \(\mathrm{Rb}/\mathrm{Ra}\) increases; that this should be so is because of the reduced effective buoyancy when \(\mathrm{Rb}\) is large. We also see how, in all cases, the stagnant region eventually expands to fill the cylinder, but stagnation happens earlier for larger values of \(\mathrm{Rb}\).

Figure 6 shows what might be called the stagnation time as a function of \(\mathrm{Rb}/\mathrm{Ra}\). This is computed easily by first substituting \(r_1=0\), \(r_2=1\) into Eqs. (12) and (13) to obtain,

$$\begin{aligned} 1-\theta (0,t)=2\mathrm{Rb}/\mathrm{Ra}, \end{aligned}$$
(16)

and by solving for t in terms of \(\mathrm{Rb}/\mathrm{Ra}\) using a single-unknown Newton–Raphson scheme. Figure 6, however, is created easily by finding \(\mathrm{Rb}/\mathrm{Ra}\) as a function t. Given the form of Eqs. (12) and (13), it is clear that it is impossible to have any flow at any time should , and therefore flow cannot be initiated. On the other hand, the behaviour of the curve shown in Fig. 6 as \(\mathrm{Rb}\rightarrow 0\) may be found using Eq. (11). If we assume that \(\mathrm{Rb}/\mathrm{Ra}\) is small and that t is large, then it is sufficient to retain one term in the summation in (11) and therefore, when \(r=0\), Eq. (16) may be manipulated to give,

$$\begin{aligned} { t = -{\displaystyle \frac{1}{\lambda _1^2}} \ln \left( \lambda _1 J_1(\lambda _1) {\displaystyle \frac{\mathrm{Rb}}{\mathrm{Ra}}}\right) .} \end{aligned}$$
(17)

For example, if we were to have a very weak yield threshold, one for which \(\mathrm{Rb}/\mathrm{Ra}=10^{-6}\), then Eq. (17) gives a stagnation time of \(t=2.351\). This time increases to 4.739 when \(\mathrm{Rb}/\mathrm{Ra}=10^{-12}\).

Fig. 7
figure 7

The variation in time of the hydrostatic pressure gradient adjustment, \(\mathrm{d}p/\mathrm{d}z\), for \(\mathrm{Rb}/\mathrm{Ra}=0.01\), 0.1, 0.2, 0.3, 0.4, 0.45, 0.48 and 0.49

Full size image

Finally, Fig. 7 shows that the hydrostatic pressure gradient always increases in time from a value which is identical to \(\mathrm{Rb}\) (i.e. \(p_z/\mathrm{Ra}\) increases from \(\mathrm{Rb}/\mathrm{Ra}\)). It is only in the case of a Newtonian fluid that \(p_z/\mathrm{Ra}\) rises to a unit value.

4 Case 2: Constant Heat Flux

In this section we shall change the boundary condition on the outside of the cylinder from one with a constant temperature to one with a constant heat flux. Therefore, we consider the development of the temperature field where the initial temperature is \(\theta =0\), where the boundary condition at \(r=1\) is changed suddenly to \(\partial \theta /\partial {r}=-1\). In dimensional terms, this means that we shall apply

$$\begin{aligned} { k{\displaystyle \frac{\partial T}{\partial r}}=-q \quad \hbox {at} \quad r=R, } \end{aligned}$$
(18)

and that the Darcy–Rayleigh number, previously defined in Eq. (7) for Case 1, is now defined as,

$$\begin{aligned} { \mathrm{Ra}= {\displaystyle \frac{\rho g \beta q K R^2}{k\mu \alpha }}.} \end{aligned}$$
(19)

All other quantities and definitions are unchanged.

Once more, we may solve Eq. (6) using separation of variables, and standard techniques may be used to show that the final solution is

$$\begin{aligned} { \theta = 2t +{\textstyle \frac{1}{2}}r^2-{\textstyle \frac{1}{4}} - 2 \sum _{n=1}^\infty {\displaystyle \frac{J_0(\sigma _n r)}{\sigma _n^2J_0(\sigma _n)}}e^{-\sigma _n^2 t}, } \end{aligned}$$
(20)

where the \(\sigma _n\) values are the positive zeros of \(J'_0\), or, equivalently, the positive zeros of \(J_1\).

Fig. 8
figure 8

The evolution of the temperature profiles with time for the constant heat flux case. The continuous curves correspond to \(t=10^{-4}\), \(10^{-3}\), \(10^{-2}\) and \(10^{-1}\). The dashed curves correspond to \(t=0.2\), 0.3, 0.4 and 0.5 (uppermost). The dotted curves are the intermediate values, \(t=0.0002\) (lowest), 0.0005, 0.002, 0.005, 0.02 and 0.05

Full size image

Figure 8 shows how the temperature field evolves with time. Once more a thin boundary layer develops at early times, and it may easily be shown that \(\theta \sim 2t^{1/2} \mathrm{ierfc}[(1-r)/2\sqrt{t}]\); see Rees and Bassom (2016). Therefore, we expect the outer surface temperature to rise initially as \(2(t/\pi )^{1/2}\) before curvature effects become significant. But without the knowledge of the solution given in Eq. (20), it is clear that when there is uniform heat flux into the cylinder, then the overall heat content must rise linearly with time. Like Fig. 2, this Figure shows the presence of a narrow thermal boundary layer at small times which thickens until the origin is reached, but unlike in Fig. 2, the maximum temperature continues to rise. The evolution with time of both the boundary and central temperatures is shown in Fig. 9, together with the large-t asymptotic states, namely

$$\begin{aligned} { \theta (r=0) \sim 2t -{\textstyle \frac{1}{4}}, \quad \theta (r=1) \sim 2t + {\textstyle \frac{1}{4}}. } \end{aligned}$$
(21)

The exact solution and the large-t asymptotic solutions cannot be resolved visually once t is as large as 0.4. At this time, the asymptotic solution for the mid-point temperature is in error by roughly 0.001, while that for the circumference is in error by roughly 0.0004. At \(t=0.5\), the respective errors are smaller by a factor of 5.

Fig. 9
figure 9

The variation in time of the temperature at the centre (lower) and the edge (upper) of the cylinder. Continuous curves denote the exact solutions, while the dotted curves denote the large-t asymptotic solutions

Full size image
Fig. 10
figure 10

Showing temperature and velocity profiles for \(\mathrm{Rb}/\mathrm{Ra}=0.05\) and 0.2 for the indicated times (constant heat flux case). Dotted curves correspond to temperature profiles and continuous curves to velocity profiles. Larger magnitudes of velocity correspond to later times

Full size image

Figure 10 shows a selection of velocity profiles for \(\mathrm{Rb}/\mathrm{Ra}=0.05\) and 0.2. As for the constant temperature case, the yield locations and the hydrostatic pressure adjustment were computed first by solving Eqs. (12)–(14) using Eq. (20) as the temperature profile. Equation (14), the zero mean velocity condition, is found to be equivalent to

$$\begin{aligned}&{\displaystyle \frac{\mathrm{Rb}}{\mathrm{Ra}}}\Bigl ( 1-r_1^2-r_2^2\Bigr ) +\Bigl [{\displaystyle \frac{p_z}{\mathrm{Ra}}}-2t\Bigr ] \Bigl ( 1 + r_1^2 - r_2^2 \Bigr ) +{\textstyle \frac{1}{4}}\Bigl [(r_1^2-r_1^4)-(r_2^2-r_2^4)\Bigr ] \nonumber \\&\quad +\,4\sum _{n=1}^\infty {\displaystyle \frac{r_1J_1(\sigma _nr_1)-r_2J_1(\sigma _nr_2)}{\sigma _n^3J_0(\sigma _n)}}e^{-\sigma _n^2t} = 0. \end{aligned}$$
(22)

The value, \(\mathrm{Rb}/\mathrm{Ra}=0.05\), represents a weak yield threshold, and therefore the induced velocities are strong relative to when \(\mathrm{Rb}/\mathrm{Ra}\) is larger, and the region over which there is no flow is quite small. We also see that the flow strengthens as time progresses, although it eventually tends towards a steady state. When \(\mathrm{Rb}/\mathrm{Ra}=0.2\), which is just below the critical value above which flow is not possible, then the induced flow is weaker and the region of stagnation is much larger.

Given that the buoyancy force which is available to induce fluid motion is proportional to the temperature difference across the cylinder, it is clear that, for any chosen value of \(\mathrm{Rb}\), there must be an interval of time before that force overcomes the yield threshold and flow is induced. Therefore, there will an initiation time for flow. Figure 11 shows how the locations of the yield surfaces vary with time for a selected set of values of \(\mathrm{Rb}/\mathrm{Ra}\) and this confirms the presence of an initiation time. For example, when \(\mathrm{Rb}/\mathrm{Ra}=0.1\), the yield surfaces are at \(r=0\) and 1 when \(t=0.0269225\). At earlier times there is no flow, but at later times the region of stagnation decreases in width until it becomes fixed in time and centred close to \(r=0.6\). It is clear from this Figure that the initiation time increases with increasing \(\mathrm{Rb}/\mathrm{Ra}\), and this is seen in detail in Fig. 12 where it may also be seen that the initiation time tends to infinity as \(\mathrm{Rb}/\mathrm{Ra}\rightarrow {\textstyle \frac{1}{4}}\). That this is the maximum value for \(\mathrm{Rb}/\mathrm{Ra}\) may be shown easily by noting first that the maximum temperature difference within the cylinder varies from zero at \(t=0\) to 0.5 [see Eq. (22); Fig. 9]. Then, the equivalent of Eq. (16) is

$$\begin{aligned} { 2\mathrm{Rb}/\mathrm{Ra}= \theta (1,t)-\theta (0,t) \le 0.5, } \end{aligned}$$
(23)

for convection to arise, and hence the largest value of \(\mathrm{Rb}\) for which convection arises is \(\mathrm{Rb}=\mathrm{Ra}/4\).

Fig. 11
figure 11

The variation in time of the location of the yield surfaces, \(r=r_1\) (continuous) and \(r=r_2\) (dotted) for the constant heat flux case. The curves correspond to \(\mathrm{Rb}/\mathrm{Ra}=0.01\), 0.02, 0.03, 0.04, 0.05 0.1, 0.15 0.2, 0.21, 0.22, 0.23 and 0.24

Full size image
Fig. 12
figure 12

The variation with \(\mathrm{Rb}/\mathrm{Ra}\) of the time at which convection is initiated for the constant heat flux case. There is no flow when \(\mathrm{Rb}/\mathrm{Ra}>0.25\)

Full size image
Fig. 13
figure 13

The variation in time of the hydrostatic pressure gradient adjustment, \(\mathrm{Ra}^{-1}\mathrm{d}p/\mathrm{d}z\), (upper) and of \(\mathrm{Ra}^{-1}\mathrm{d}p/\mathrm{d}z-2t\) (lower) for the values of \(\mathrm{Rb}/\mathrm{Ra}\) given in the caption to Fig. 10 (constant heat flux case)

Full size image

Figure 13 shows the variation with time of the hydrostatic pressure gradient adjustment which is required in order to maintain a zero mean velocity, and which accounts for the change in the density of the fluid due to increasing mean temperature. Little detail may be seen when plotting the variation of \(p_z\) with time due to the magnitude of the 2t term in the expression for \(\theta \) in (20), and therefore the second frame in Fig. 13 shows how \(\mathrm{Ra}^{-1}p_z -2t\) varies with time. The beginning point of each curve represents the initiation time for convection. In all cases, this modified hydrostatic pressure gradient adjustment tends to zero as time progresses, suggesting that \(p_z\sim 2\mathrm{Ra}\,t\) for large times. Therefore, it is worth determining if there are any useful mathematical results which may be obtained for large times. A large-time analysis is facilitated by the fact that all of the Bessel function terms in Eqs. (20) and (22) tend exponentially to zero as t increases. It is then quite a short analysis to show that

$$\begin{aligned} { p_z = 2\mathrm{Ra}\,t, \qquad r_1=\sqrt{{\displaystyle \frac{1}{2}}-{\displaystyle \frac{2\mathrm{Rb}}{\mathrm{Ra}}}}, \qquad \hbox {and}\qquad r_2=\sqrt{{\displaystyle \frac{1}{2}}+{\displaystyle \frac{2\mathrm{Rb}}{\mathrm{Ra}}}}, } \end{aligned}$$
(24)

precisely when exponentially terms are neglected. The given locations of the yield surfaces agree to more than eight significant figures with our numerical work when \(t=1\).

5 Conclusions

In this paper, we have considered where the outer impermeable surface of a porous circular cylinder is subject either to a sudden change in the surface temperature or in the applied heat flux. The porous medium within the cylinder is saturated with a Bingham fluid. In both cases a thin thermal boundary layer is initiated at the outer surface which conducts inwards. When a constant temperature is applied, flow is initiated immediately when \(\mathrm{Rb}/\mathrm{Ra}<{\textstyle \frac{1}{2}}\), but this flow eventually ceases as the fluid at the centre of the cylinder heats up, thereby providing a buoyancy force which is too small to overcome the yield threshold of the Bingham fluid. On the other hand, when the surface is subject to a constant heat flux, there is no flow at early times, again due to have too small a buoyancy force. However, flow eventually initiates if \(\mathrm{Rb}/\mathrm{Ra}<{\textstyle \frac{1}{4}}\), and the flowfield tends towards a steady state. In undertaking this analysis, we have assumed that the flow and temperature fields are independent of z, the vertical coordinate, and this is the situation which is likely to pertain when the cylinder is very tall compared with its radius; such a tall but finite height means that the overall flow must satisfy a zero vertical mean value.

The present analysis may now be extended to flows which arise outside a heated cylinder which is embedded within a porous medium, or to cases of vertical annuli where the porous medium is confined between the two surfaces, or even to cases where a volumetric heating is initiated suddenly. We believe that it is extremely unlikely that these flows will undergo a convective instability because the Newtonian counterpart has already been shown to be unconditionally stable in various separate analyses; see Gill (1969), Rees (1988, 2011), Straughan (1988), Lewis et al. (1995) and Scott and Straughan (2013). The effect of the threshold pressure gradient is to reduce the strength of the basic fluid flow, which generally means that flows are less susceptible to unstable disturbances. We note, however, that such channels will admit instability, but only when quite substantial alterations have been made from the configuration considered by Gill (1969). Thus Barletta (2015) found that instability can arise when the impermeable surfaces are replaced by constant pressure surfaces. Shankar and Shivakumara (2017) allowed the porous medium to be saturated by an Oldroyd-B fluid, thereby extending the work of Rees (1988), and found that this situation may also be subject to instabilities. It may be argued that these two respective changes to the Gill’s configuration allow the fluid more freedom to be destabilised, whereas the present configuration represents less freedom.