Capillary Heterogeneity Trapping and Crossflow in Layered Porous Media

Abstract

We examine the effect of capillary and viscous forces on the displacement of one fluid by a second, immiscible fluid across and along parallel layers of contrasting porosity, and relative permeability, as well as previously explored contrasts in absolute permeability and capillary pressure. We consider displacements with wetting, intermediate-wetting and non-wetting injected phases. Flow is characterized using six independent dimensionless numbers and a dimensionless storage efficiency, which is numerically equivalent to the recovery efficiency. Results are directly applicable to geologic carbon storage and hydrocarbon production. We predict how the capillary–viscous force balance influences storage efficiency as a function of a small number of key dimensionless parameters, and provide a framework to support mechanistic interpretations of complex field or experimental data, and numerical model predictions, through the use of simple dimensionless models. When flow is directed across layers, we find that capillary heterogeneity traps the non-wetting phase, regardless of whether it is the injected or displaced phase. However, minimal trapping occurs when the injected phase is intermediate-wetting or when high-permeability layers contain a smaller moveable volume of fluid than low-permeability layers. A dimensionless capillary-to-viscous number defined using the layer thickness rather than the more commonly used system length is most relevant to predict capillary heterogeneity trapping. When flow is directed along layers, we show that, regardless of wettability, increasing capillary crossflow reduces the distance between the leading edges of the injected phase in each layer and increases storage efficiency. This may be counter-intuitive when the injected phase is non-wetting. Crossflow has a significant impact on storage efficiency only when high-permeability layers contain a smaller moveable volume of fluid than low-permeability layers. In that case, capillary heterogeneity traps the wetting phase, regardless of whether it is the injected or displaced phase.

1 Introduction

Geologic heterogeneity exerts a major influence on multiphase flow in the subsurface over many length scales, from the kilometre scale down to the micron scale. This is of great importance in many industrial and environmental contexts, such as geologic CO${}_2$ storage, contaminant remediation and hydrocarbon recovery. The most common and characteristic structure in porous sedimentary rocks is layering, i.e. the alternation of parallel, continuous layers of different lithologic and physical properties. Layers are observed at many different length scales, including lamination (millimetre-thick layers), bedding (centimetre- to metre-thick layers) and laterally extensive genetic and stratigraphic units that may correspond to flow zones in groundwater aquifers and hydrocarbon reservoirs (typically several metres to tens of metres in thickness) (e.g. Campbell 1967; Koltermann and Gorelick 1996; De Marsily et al. 1998; Jackson et al. 2003; Deveugle et al. 2011, 2014; Legler et al. 2013). Examination of multiphase flow in layered porous media is therefore essential to better understand how geologic heterogeneity controls flow in the subsurface.

In this paper, we examine immiscible, two-phase flow across and along homogeneous and parallel layers of contrasting petrophysical properties such as porosity, permeability and capillary pressure. The displacement of one phase by another may be controlled by any combination of the viscous, capillary and gravitational forces which drive multiphase flow. This work focuses on flow driven by capillary and viscous forces, noting that gravitational forces may have a significant impact on flow, especially when fluid density differences are significant or the system height is large (e.g. Hesse and Woods 2010; Li and Benson 2015). We do not attempt to predict exactly the behaviour of a given geologic reservoir or multiphase flow, but rather aim to (i) predict how the capillary–viscous force balance influences storage efficiency of the injected phase (fraction of the moveable pore volume occupied by the injected phase) as a function of a small number of key dimensionless parameters and (ii) provide a framework to support mechanistic interpretations of complex field or experimental data, and numerical model predictions, through the use of simple dimensionless models. Quantifying flow using storage efficiency makes results directly applicable to geologic CO${}_2$ storage, but also to hydrocarbon recovery using the numerically equivalent recovery efficiency (fraction of the moveable pore volume initially in place recovered).

The displacement of one fluid phase by another, across and along layers of contrasting permeability and capillary pressure, has been previously investigated in the context of hydrocarbon recovery (e.g. Dawe et al. 1992; Huang et al. 1995; Cinar et al. 2006; Alhamdan et al. 2012), and geologic CO${}_2$ storage (e.g. Krevor et al. 2011; Datta and Weitz 2013). When flow is oriented across layers, the non-wetting phase becomes trapped in rock layers with lower capillary pressure between layers with higher capillary pressure (Chang and Yortsos 1992; Ringrose et al. 1993; Krevor et al. 2011). This trapping mechanism, commonly referred to as capillary heterogeneity trapping, enhances the storage of non-wetting CO${}_2$ in geologic formations, improves hydrocarbon recovery from oil-wet reservoirs, but also hinders hydrocarbon recovery from water-wet reservoirs. When flow is oriented along layers, the injected phase tends to progress more rapidly through layers of higher permeability and/or containing lower moveable pore volumes (Debbabi et al. 2017). Crossflow due to transverse fluid mobility contrasts, termed viscous crossflow, typically occurs when layers are not separated by impermeable flow barriers, and has been shown to be controlled by the mobility ratios estimated across the leading edge of the injected phase in each layer (Debbabi et al. 2017). As the magnitude of capillary forces is increased, transverse capillary pressure gradients may also cause capillary crossflow. Earlier studies found capillary crossflow reduces the distance between the leading edges of the injected phase in the different layers when the injected phase is wetting (Yokoyama and Lake 1981). Regardless of the orientation of the layering, capillary forces may also introduce end effects that perturb flow into an open domain such as a borehole or a mixing zone at the downstream end of a core holder (Osoba et al. 1951; Lake 1989). Capillary end effects are caused by a capillary pressure discontinuity that exists at the outlet boundary of the system. These effects may influence the measurements of relative permeability or the predicted storage/recovery efficiency.

Most previous studies have expressed results in dimensional terms, thereby (i) making the results difficult to extrapolate across scales, or (ii) inadvertently exploring the same parameter space in different studies (compare results obtained by Corbett et al. 1992 and Ringrose et al. 1993 when expressed in terms of a dimensionless capillary-to-viscous number in Fig. 1). Previous studies also ignored the impact of rock wettability and contrasts in porosity and relative permeability on predicted storage/recovery efficiency.

Fig. 1

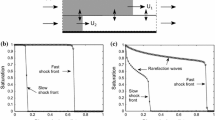
Results of separate numerical experiments by Corbett et al. (1992) and Ringrose et al. (1993), which report storage efficiency at 1 pore volume injected (PVI) as a function of flow rate and layer thickness for flow a across and b along layers. The results collapse into single curves when plotted against the local and transverse capillary numbers $N_{\mathrm{cv,l}}$ and $N_{\mathrm{cv,T}}$ defined later in this work (Table 1)

Here we report a treatment of multiphase flow through layered porous media using six independent dimensionless parameters obtained from inspectional analysis of the flow equations. We consider layers of contrasting porosity and relative permeability, in addition to the contrasts in absolute permeability and capillary pressure examined previously. Moreover, we examine displacements using intermediate-wetting injectants, in addition to the wetting and non-wetting cases examined previously. An outline of the paper is as follows. After first presenting the mathematical model (Sect. 2), we then present in Sect. 3 a set of six independent dimensionless numbers characterizing immiscible, two-phase flow in layered porous media. We examine in Sects. 4.1 and 4.2 the saturation profiles obtained when flow is directed, respectively, across and along layers. We report in Sect. 4.3 the sensitivity of storage efficiency to the governing dimensionless numbers. The implications of this analysis are discussed in Sect. 5, and finally, in Sect. 6, we gather the main conclusions of this investigation.

2 Mathematical Model

We investigate two-phase, immiscible, incompressible and isothermal flow through layered porous media in which the layers have contrasting petrophysical properties (Fig. 2). Layers are orientated perpendicular (Fig. 2a) or parallel (Fig. 2b) to the bulk flow direction.

Fig. 2

Schematic of the a 1D layer-perpendicular and b 2D layer-parallel flow models used in this work

Assuming gravity effects are negligible, flow is described by the continuity equations (Lake 1989)

$$\begin{aligned} \phi {\Delta }S\frac{\partial s}{\partial t}+\nabla \cdot \mathbf {q_i}= & {} 0 \end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot \mathbf {q_T} = \nabla \cdot \left[ \mathbf {q_i}+\mathbf {q_d}\right]= & {} 0 \end{aligned}$$

(2)

and the multiphase Darcy’s law

$$\begin{aligned} \mathbf {q_i}= & {} -\frac{k_{\mathrm{r,i}}\left( s\right) }{{\mu }_{\mathrm{i}}}\,\overline{\overline{k}}\cdot \mathbf {\nabla P_i} \end{aligned}$$

(3)

$$\begin{aligned} \mathbf {q_d}= & {} -\frac{k_{\mathrm{r,d}}\left( s\right) }{{\mu }_{\mathrm{d}}}\,\overline{\overline{k}}\cdot \mathbf {\nabla P_d}, \end{aligned}$$

(4)

where

$$\begin{aligned} s=\frac{S_{\mathrm{i}}-S_{\mathrm{i,r}}}{1-S_{\mathrm{i,r}}-S_{\mathrm{d,r}}} \end{aligned}$$

(5)

is the normalized injected-phase saturation, which varies between 0 and 1, $S_{\mathrm{i}}$ is the injected-phase saturation, $S_{\mathrm{i,r}}$ and $S_{\mathrm{d,r}}$ are the injected- and displaced-phase residual saturations, $\Delta S=1-S_{\mathrm{i,r}}-S_{\mathrm{d,r}}$ is the moveable saturation, $\phi$ is the porosity, $\mathbf {q_i}$ and $\mathbf {q_d}$ are the injected- and displaced-phase volumetric fluxes per unit area, $\mathbf {q_T}=\mathbf {q_i}+\mathbf {q_d}$ is the total volumetric fluid flux per unit area, $k_{\mathrm{r,i}}(s$) and $k_{\mathrm{r,d}}\left( s\right)$ are the relative permeabilities of the injected and displaced phases, ${\mu }_{\mathrm{i}}$ and ${\mu }_{\mathrm{d}}$ are the viscosities of the injected and displaced phase, $\overline{\overline{k}}$ the absolute permeability tensor (assumed diagonal here), and $P_{\mathrm{i}}$ and $P_{\mathrm{d}}$ the injected- and displaced-phase fluid pressures. We further define the injected- and displaced-phase fluid mobilities as

$$\begin{aligned} {\lambda }_{\mathrm{i}}=\frac{k_{\mathrm{r,i}}}{{\mu }_{\mathrm{i}}}, \end{aligned}$$

(6)

and

$$\begin{aligned} {\lambda }_{\mathrm{d}}=\frac{k_{\mathrm{r,d}}}{{\mu }_{\mathrm{d}}}, \end{aligned}$$

(7)

respectively, and the total fluid mobility as

$$\begin{aligned} {\lambda }_{\mathrm{T}}=\frac{k_{\mathrm{r,i}}}{{\mu }_{\mathrm{i}}}+\frac{k_{\mathrm{r,d}}}{{\mu }_{\mathrm{d}}}. \end{aligned}$$

(8)

The relative permeability curves are represented as functions of the normalized saturation s by the parametric forms

$$\begin{aligned}&\displaystyle k_{\mathrm{r,i}}(s)=k^{\mathrm{e}}_{\mathrm{r,i}}s^{n_{\mathrm{i}}}, \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle k_{\mathrm{r,d}}(s)=k^{\mathrm{e}}_{\mathrm{r,d}}{\left( 1-s\right) }^{n_{\mathrm{d}}}, \end{aligned}$$

(10)

where $k^{\mathrm{e}}_{\mathrm{r,i}}$ and $k^{\mathrm{e}}_{\mathrm{r,d}}$ are the end-point relative permeabilities, and $n_{\mathrm{i}}$ and $n_{\mathrm{d}}$ the Corey exponents of the injected and displaced phases, respectively. The capillary pressure $P_{\mathrm{c}}=P_{\mathrm{d}}-P_{\mathrm{i}}$ is represented as a function of the normalized saturation and of the normalized permeability using a Leverett-type relationship (Leverett 1941),

$$\begin{aligned} P_{\mathrm{c}}(s)=P^{\mathrm{e}}_{\mathrm{c}}\sqrt{\frac{\overline{k_xk^{\mathrm{e}}_{\mathrm{r,d}}}}{k_xk^{\mathrm{e}}_{\mathrm{r,d}}}}J(s), \end{aligned}$$

(11)

where $P^{\mathrm{e}}_{\mathrm{c}}$ is a constant characteristic capillary pressure, $\overline{k_xk^{\mathrm{e}}_{\mathrm{r,d}}}$ is the average displaced-phase longitudinal permeability at the injected-phase residual saturation (chosen as a harmonic average for flow across layers and as an arithmetic average for flow along layers), and J is a Leverett-type function. Here we focus on capillary pressure contrasts caused by permeability variations rather than wettability variations, so we choose the Leverett J-function identically throughout the model. The shape of the Leverett J-function is chosen to represent a given rock wettability (Fig. 3). The characteristic capillary pressure $P^{\mathrm{e}}_{\mathrm{c}}$ is chosen identically irrespective of wettability throughout the model.

Fig. 3

Leverett J-functions used for wetting, intermediate-wetting, and non-wetting injectants

Each layer is internally homogeneous, with identical thickness H for layer-perpendicular flow and H / 2 for layer-parallel flow. The total model length is denoted L for both layer-perpendicular and layer-parallel flow models. Here the layers may differ in longitudinal absolute permeability $k_x$ (with $k^1_x>k^2_x$), end-point relative permeabilities $k^{\mathrm{e}}_{\mathrm{r,i}}$ and $k^{\mathrm{e}}_{\mathrm{r,d}}$, porosity $\phi$ and moveable saturation ${\Delta }S$. However, the Corey exponents $n_{\mathrm{i}}$ and $n_{\mathrm{d}}$ are chosen to be the same in both layers, and the end-point relative permeabilities $k^{\mathrm{e}}_{\mathrm{r,i}}$ and $k^{\mathrm{e}}_{\mathrm{r,d}}$ are constrained to obtain identical fractional flow curves in both layers in the viscous limit (see “Appendix 1”). The impact of contrasts in these fractional flow curves on flow along parallel layers has been previously examined in a companion paper (Debbabi et al. 2017). For layer-parallel flow models, we also assume the layers have identical transverse permeability $k_z$ such that $k^1_z= k^2_z\le k^{min}_x$ where $k^1_z$ and $k^2_z$ are the transverse permeabilities of layers 1 and 2, respectively, and $k^{min}_x$ is the lowest longitudinal permeability of the two layers. Numerical experiments, not reported here, show that relaxing this constraint, to allow $k^1_z\ne k^2_z$, but enforcing $k_z\le k_x$ in each layer as typically observed in geologic systems, has negligible impact on the results because crossflow is dominantly controlled by the lowest transverse permeability of the two layers.

We use boundary conditions similar to those reported by Debbabi et al. (2017), but additionally account for capillary pressure differences between the two phases. Initially ($t=0$), the displaced-phase pressure is uniform ($P_{\mathrm{d}}=P_0)$ and the normalized saturation is zero throughout the domain ($s=0$). At the inlet face, the boundary conditions are a constant average volumetric influx per unit area ${\overline{q}}_{\mathrm{in}}$, distributed to maintain uniform injected-phase pressure ($P_{\mathrm{i}}=P_{\mathrm{in}}(t)$). The other boundary conditions are a fixed pressure equal to the initial pressure $P_0$ (for both the injected and displaced phases) on the outlet (opposing) face, and no flow across the other faces. This choice of boundary conditions is consistent with conventional and physically reasonable core-flooding and borehole boundary conditions used in groundwater and oil reservoir models (Richardson et al. 1952; Aziz and Settari 1979; Wu 2000).

Solutions of the multiphase flow equations (1)–(4) were obtained using a commercial code that implements a finite-volume–finite-difference approach to discretize the governing equations (Eclipse 100). Further details are reported in “Appendix 2”.

3 Scaling Analysis

We scale the flow equations (1)–(4) following the inspectional analysis reported by Debbabi et al. (2017), but additionally account for capillary effects. The dimensionless independent variables used include the dimensionless distances $\hat{x}=x/L$ and $\hat{z}=z/H$ (for layer-parallel flow only), and the dimensionless time $\hat{t}=t\ {\overline{q}}_{\mathrm{in}}/\overline{\phi \mathrm {\Delta }S}L$ (which is equivalent to the number of moveable pore volumes of displacing phase injected). We obtain eight dimensionless numbers, six of which are independent, to describe immiscible, two-phase flow across and along layered porous media (see “Appendix 1”). The dimensionless numbers, their interpretation and the ranges of values explored here are summarized in Table 1.

Table 1 Governing dimensionless numbers and range of values explored

The longitudinal capillary number $N_{\mathrm{cv,L}}$, which is applicable to both layer-perpendicular and layer-parallel flow, has previously been used to quantify the importance of capillary diffusion (Lake 1989) and capillary end effects (Huang and Honarpour 1998). Our definition differs from similar numbers previously used (e.g. Yokoyama and Lake 1981; Chang and Yortsos 1992) as we account here for contrasts in the relative permeability end points between layers, and preserve a general capillary pressure scaling $P^{\mathrm{e}}_{\mathrm{c}}$. Taking a flow rate of 1 m.day${}^{-1}$, which is typical for oilfield displacements and an upper bound for geologic CO$_2$ storage (Singh et al. 2010; Ringrose 2014), an average permeability of 500 mD, a characteristic capillary pressure of 1500 Pa and a fluid viscosity of 5 cP yields values of $N_{\mathrm{cv,L}}$ ranging from ${\sim }10^{-5}$ at the kilometre scale to ${\sim }1$ at the centimetre scale. Our numerical experiments (introduced in “Appendix 2”) confirmed earlier work indicating that longitudinal capillary numbers $N_{\mathrm{cv,L}}<0.1$ are required to eliminate end effects (see “Appendix 3”). This ensures our results are independent of the particular model implementation, but also prevents capillary diffusion effects from being significant.

The local capillary number $N_{\mathrm{cv,l}}$, which is new to this work, is applicable to flow directed across layers. We demonstrate in Sect. 4.3 that $N_{\mathrm{cv,l}}$ quantifies the importance of capillary heterogeneity trapping. The local capillary number is similar to the longitudinal capillary number, except we use the layer thickness H rather than the total system length L as the characteristic length scale. Layer thickness may range from less than one millimetre to several hundreds of metres (Koltermann and Gorelick 1996). Using the characteristic values suggested above, the local capillary number $N_{\mathrm{cv,l}}$ ranges from ${\sim }10^{-4}$ up to ${\sim }10^{2}$. We also characterize permeability heterogeneity using the number of layers directed perpendicular to the flow direction ($f_{\mathrm{L}}$) and explore values ranging from 10 to 1000 to determine representative behaviours. Note that the ratio of $N_{\mathrm{cv,l}}$ to $f_{\mathrm{L}}$ yields the longitudinal capillary number $N_{\mathrm{cv,L}}$. Combinations of their values are constrained here to eliminate end effects ($N_{\mathrm{cv,L}}<0.1$). Data from laboratory flooding experiments and mini-models confirm that possible values of the local and longitudinal capillary numbers span at least two or three orders of magnitude (Fig. 4).

Fig. 4

Possible combinations of the local and longitudinal capillary numbers computed using data from laboratory flooding experiments (Graue 1994; Honarpour et al. 1995; Krevor et al. 2011) and mini-models (Kortekaas 1985; Chang and Yortsos 1992; Ringrose et al. 1993)

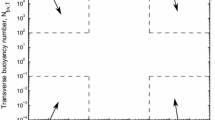
For flow along layers, we introduce the effective aspect ratio $R_{\mathrm{L}}$, which quantifies the amounts of viscous crossflow, and the transverse capillary number $N_{\mathrm{cv,T}}$, which quantifies the amounts of capillary crossflow. Their definitions again differ from previously used numbers (e.g. Zapata and Lake 1981; Yokoyama and Lake 1981) as we account here for contrasts in the relative permeability end points between layers, and preserve a general capillary pressure scaling $P^{\mathrm{e}}_{\mathrm{c}}$. The effective aspect ratio $R_{\mathrm{L}}$ typically varies over the range 0.01–100 in layered sedimentary systems (L / H is typically large, of order 10–100, while $k_z/k_x$ is typically small, of order 10${}^{-6}- 1$). Using the characteristic values suggested above, the transverse capillary number may vary between 0 and 1000. It is, however, sufficient to vary $N_{\mathrm{cv,T}}$ from 0 to 100 to observe representative flow behaviours (Yokoyama and Lake 1981). Note that the ratio of $N_{\mathrm{cv,T}}$ and $R^2_{\mathrm{L}}$ yields the longitudinal capillary number $N_{\mathrm{cv,L}}$. Combinations of their values are constrained here to eliminate end effects ($N_{\mathrm{cv,L}}<0.1$). Data from core-flooding experiments, mini-models and oilfield case studies confirm that possible values of the effective aspect ratio and transverse capillary numbers span at least two or three orders of magnitude (Fig. 5).

Fig. 5

Possible combinations of the effective aspect ratio and transverse capillary number computed using data from laboratory flooding experiments (blue data points; Dawe et al. 1992; Cinar et al. 2006; Reynolds and Krevor 2015), mini-models (dark data points; Ringrose et al. 1993) and oilfield case studies (red data points; Cronquist 1968; Reitzel and Callow 1977; George and Stiles 1978). These computed data confirm capillary crossflow can be significant across many length scales, ranging from the core scale to the field scale (e.g. Little Creek Field)

For flow across and along layers, the longitudinal permeability ratio ${\sigma }_x$ quantifies permeability heterogeneity; this is identical to the expression suggested by Debbabi et al. (2017). The storage ratio $R_{\mathrm{s}}$ is the ratio of the moveable fluid volumes in each layer. The ratio is identical to the storage ratio introduced by Debbabi et al. (2017) except we ignore here contrasts in the viscous-limit fractional flow curves (see definition in “Appendix 1”) between layers. A suite of core-plug measurements taken along a single well from a North Sea field (Tjølsen et al. 1991) shows that plausible combinations of the permeability and storage ratios span one or two orders of magnitude (see Fig. 3 in Debbabi et al. 2017). Here, for the sake of generality, we do not restrict the combinations of permeability ratio and storage ratio investigated, varying the permeability ratio over the range 1–100 and the storage ratio over the range 0.1–10.

The shock-front mobility ratio $M_{\mathrm{f}}$ describes the ratio of the total mobility across the shock front, i.e. calculated at the upper and lower saturation values $s_{\mathrm{f}}$ and $s_{\infty }$ that, in the viscous limit, bound the discontinuity that defines the shock. There is a consistent change in viscous crossflow behaviour at a shock-front mobility ratio $M_{\mathrm{f}}=1$ (see Debbabi et al. 2017). Unless mentioned otherwise, we further choose $M_{\mathrm{f}}=0.5$. Numerical experiments with $M_{\mathrm{f}}=1.2$, not reported here, confirm this has no influence on the findings presented in this work.

In the immiscible two-phase flow studied here, the dimensionless numbers allow exact scaling of results from one system to another if the systems have relative permeability and J-Leverett curves with identical shapes (Rapoport 1955). These two key properties reflect the rock wettability and pore geometry. We demonstrated in a companion paper (Debbabi et al. 2017) that the shapes of the relative permeability curves, which can be approximately scaled by the shock-front mobility ratio, define viscous crossflow behaviour. We show in this paper that the shape of the J-Leverett curve defines capillary heterogeneity trapping and capillary crossflow behaviours. We consider the three J-Leverett curves reported in Fig. 3 as a means to explore the generic cases of wetting, intermediate-wetting and non-wetting injectants.

Following Debbabi et al. (2017), we quantify the impact of the dimensionless numbers on flow in terms of a dimensionless storage efficiency, defined as

$$\begin{aligned} E_{\mathrm{s}}=\frac{\mathop {\iint }{s\phi {\Delta }S\ \mathrm {d}x\mathrm {d}z}}{\mathop {\iint }{\ \phi {\Delta }S\ \mathrm {d}x\mathrm {d}z}}. \end{aligned}$$

(12)

The storage efficiency measures the fraction of the injected phase that is retained within the model, and is relevant when characterizing the geologic storage of carbon in subsurface reservoirs and the location of NAPLs in contaminated aquifers. The storage efficiency is also numerically equivalent to the recovery efficiency, which measures the fraction of the displaced phase that is removed from the model and is relevant to hydrocarbon production. Quantifying the effect of the dimensionless numbers in terms of the storage/recovery efficiency (henceforth termed the storage efficiency) therefore yields results of broad interest.

4 Results

4.1 Saturation Distribution with Layer-Perpendicular Flow

We begin by examining saturation profiles along an alternation of ten high- and low-permeability layers of contrasting capillary pressure curves when the injectant is wetting, intermediate-wetting and non-wetting (Fig. 6). We consider a moderate capillary effect ($N_{\mathrm{cv,l}}=0.5$) with indicative, moderate-permeability contrast (${\sigma }_x=5$) but no storage contrast ($R_{\mathrm{s}}=1$). The numerical results show that capillary pressure contrasts between layers cause accumulation of fluid trapped upstream of capillary barriers and the formation of saturation discontinuities at layer boundaries to maintain capillary pressure continuity. High-permeability layers act as capillary barriers to the wetting phase, and low-permeability layers to the non-wetting phase. This is consistent with earlier work (e.g. Kortekaas 1985; Chang and Yortsos 1992; Krevor et al. 2011). However, the behaviour is more complex when the injectant is intermediate-wetting. The low-permeability capillary barriers alternately trap the displaced phase when saturation is less than 0.5, but trap the injected phase at larger saturation values (Fig. 6b). We show in Sect. 4.3 that this change in trapping behaviour makes trapping negligible for the overall system. Numerical experiments, not reported here, show that contrasts in storage capacity between layers, i.e. the ratio of moveable fluid volumes in each layer ($R_{\mathrm{s}}$), do not change the saturation patterns reported in Fig. 6. However, we will show in Sect. 4.3. that storage contrasts ($R_{\mathrm{s}}\ne 1$) may have a significant impact on storage efficiency.

Fig. 6

Characteristic saturation profiles across an alternation of high- and low-permeability layers for different wettability states

4.2 Saturation Distribution with Layer-Parallel Flow

We now consider two-layered models oriented parallel to the bulk flow direction. We examine saturation distribution as a function of the amounts of viscous ($R_{\mathrm{L}}$) and capillary crossflow ($N_{\mathrm{cv,T}}$) for different wettability states. Combinations of values of $R_{\mathrm{L}}$ and $N_{\mathrm{cv,T}}$ explored are reported in Fig. 7b. These are constrained to eliminate end effects ($N_{\mathrm{cv,L}}<0.1$; see excluded area in grey in Fig. 7b). With small values of $R_{\mathrm{L}}$ and $N_{\mathrm{cv,T}}$, no crossflow occurs between layers (Fig. 7c; no crossflow). With large values of $R_{\mathrm{L}}$ but small values of $N_{\mathrm{cv,T}}$, viscous crossflow occurs (Fig. 7d; viscous crossflow equilibrium) and is controlled by the shock-front mobility ratio $M_{\mathrm{f}}$ (Debbabi et al. 2017). With large values of $R_{\mathrm{L}}$ and $N_{\mathrm{cv,T}}$, capillary crossflow dampens transverse capillary pressure gradients and is more significant than viscous crossflow (Fig. 7a; capillary crossflow equilibrium). Boundaries of these different flow domains, which are separated by transition regions, are suggested in Fig. 7b as dashed lines. Although changing other dimensionless parameters such as the shock-front mobility ratio or the storage ratio moves the boundaries of the domains, their general shape remains unchanged. We find that increasing capillary crossflow reduces the distance between the leading edges of the injected phase in the two layers, regardless of wettability. The capillary crossflow equilibrium regime has been previously reported for wetting injectants when $N_{\mathrm{cv,T}}>50$ (e.g. Yokoyama and Lake 1981) but not for non-wetting injectants. The crossflow behaviour may be counter-intuitive when the injected phase is non-wetting. In this case, the injected phase is expected to remain within the high-permeability layers. Yet, a non-negligible fraction of the injected phase crossflows towards the low-permeability layer, while the displaced phase crossflows in the opposite direction. This result is not a numerical artefact. The exchange of phases between layers is required to dampen transverse gradients in capillary pressure that forms as saturation increases rapidly within the high-permeability layer (see Fig. 12).

Fig. 7

Characteristic saturation distribution during flow along layers as a function of the amounts of viscous ($R_{\mathrm{L}}$) and capillary crossflow ($N_{\mathrm{cv,T}}$). Without capillary effects (b, c), identical saturation distributions were obtained for both wettability states. White arrows indicate crossflow direction if any

4.3 Storage/Recovery Efficiency as Function of the Dimensionless Numbers

We continue our analysis by exploring the storage/recovery efficiency as a function of the local and transverse capillary numbers $N_{\mathrm{cv,l}}$ and $N_{\mathrm{cv,T}}$, the permeability ratio ${\sigma }_x$ and the storage ratio $R_{\mathrm{s}}$. The correlations reported here provide a useful basis for the interpretation of core-flooding experiments and more complex numerical models used to quantitatively predict storage or recovery efficiency.

4.3.1 Layer-Perpendicular Flow

Variations in $N_{\mathrm{cv,l}}$ and $f_{\mathrm{L}}$. We begin by examining storage efficiency as a function of the local capillary number $N_{\mathrm{cv,l}}$ and the number of layers $f_{\mathrm{L}}$. We choose moderate-permeability contrasts (${\sigma }_x=5$) but no storage contrasts ($R_{\mathrm{s}}=1$). The numerical results show that capillary heterogeneity trapping of the non-wetting phase increases with $N_{\mathrm{cv,l}}$ regardless of whether the non-wetting phase is injected or displaced (Fig. 8). Minimal trapping occurs when the injectant is intermediate-wetting. Regardless of the number of layers and wettability, capillary heterogeneity trapping only becomes significant when $N_{\mathrm{cv,l}}>0.1$. The results also indicate a weak dependency on the number of layers $f_{\mathrm{L}}$ (Fig. 8). This shows that the longitudinal capillary number $N_{\mathrm{cv,L}}=N_{\mathrm{cv,l}}/f_{\mathrm{L}}$ has little influence on storage efficiency when it is varied but $N_{\mathrm{cv,l}}$ is maintained fixed. We conclude that the local capillary number is the relevant dimensionless parameter to quantify capillary heterogeneity trapping.

Fig. 8

Change in storage efficiency at 1 MPVI (relative to the capillary-free case $N_{\mathrm{cv,l}}=0$) with the local capillary-to-viscous force balance ($N_{\mathrm{cv,l}}$) and the number of layers ($f_{\mathrm{L}}$) when flow is directed across layers. Circles denote cases using a wetting injectant, crosses a intermediate-wetting injectant and squares a non-wetting injectant

Variations in ${\sigma }_x$ and $R_{\mathrm{s}}$. We now examine changes in storage efficiency (relative to a homogeneous medium, ${\sigma }_x=R_{\mathrm{s}}=1$) as we vary the permeability ratio ${\sigma }_x$ from 1 to 100, and the storage ratio $R_{\mathrm{s}}$ from 1 to 10 (Fig. 9). We consider a system of 10 layers with an indicative value of $N_{\mathrm{cv,l}}=0.5$ that yields moderate capillary heterogeneity trapping. We use wetting, intermediate-wetting and non-wetting injectants. The results show that the volume of non-wetting phase trapped in the system, whether it is injected or displaced, increases with the permeability ratio ${\sigma }_x$ and the storage ratio $R_{\mathrm{s}}$ (Fig. 9). However, trapping is minimal when the injected phase is intermediate-wetting regardless of ${\sigma }_x$ and $R_{\mathrm{s}}$. Trapping is also minimal for small $R_{\mathrm{s}}$. Because the volume of non-wetting phase trapped in high-permeability layers is in this case similar to the volume of wetting phase trapped in low-permeability layers, there is no noticeable trapping effect at the overall system scale.

Fig. 9

Change in storage efficiency at 1 MPVI (relative to a reference homogeneous model) as the rock property contrasts ($\sigma _x$ and $R_{\mathrm{s}}$) are varied in the presence of capillary effects ($N_{\mathrm{cv,l}}=0.5$) when flow is directed across layers. Circles denote cases using a wetting injectant, crosses a intermediate-wetting injectant and squares a non-wetting injectant

4.3.2 Layer-Parallel Flow

Variations in $N_{\mathrm{cv,T}}$. We examine changes in storage efficiency (relative to an equivalent, capillary-free case, $N_{\mathrm{cv,T}}=0$) as we vary the amount of capillary crossflow ($N_{\mathrm{cv,T}}$) for various storage contrasts ($R_{\mathrm{s}}$) (Fig. 10). We choose $R_{\mathrm{L}}=100$ to observe a wide range of capillary crossflow amounts without having results influenced by end effects (Fig. 7). We consider a fixed and indicative permeability contrast ${\sigma }_x=5$, and use both wetting and non-wetting injectants. The results show that storage efficiency increases with the amount of capillary crossflow ($N_{\mathrm{cv,T}}$) regardless of wettability and of the other dimensionless parameters. In general, capillary crossflow only influences storage efficiency when $N_{\mathrm{cv,T}}>0.1$; the exact threshold also depends on the storage ratio $R_{\mathrm{s}}$. Similar results have been previously obtained for wetting injectants (Yokoyama and Lake 1981) but not for non-wetting injectants. However, crossflow only has a significant impact on storage efficiency when the high-permeability layer has comparable or lower storage capacity than the low-permeability layer ($R_{\mathrm{s}}\le 1$). In the opposite case (e.g. $R_{\mathrm{s}}=10$), the additional bulk rock volume contacted by the crossflowing injectant represents a small fraction of the overall moveable pore volume. Crossflow then has little influence on storage efficiency.

Fig. 10

Change in storage efficiency at 1 MPVI (relative to the capillary-free case $N_{\mathrm{cv,T}}=0$) as the amount of capillary crossflow ($N_{\mathrm{cv,T}}$) is varied with various storage contrasts ($R_{\mathrm{s}}$) when flow is directed along layers. Circles denote cases using a wetting injectant and squares a non-wetting injectant. Note that the wettability state does not influence the trends

Variations in ${\sigma }_x$ and $R_{\mathrm{s}}$. We now examine changes in storage efficiency (relative to a homogeneous medium, $\sigma _x=R_{\mathrm{s}}=1$) as we vary the permeability ratio $\sigma _x$ from 1 to 100, and the storage ratio $R_{\mathrm{s}}$ from 0.1 to 10 (Fig. 11). We use both wetting and non-wetting injectants, and choose $N_{\mathrm{cv,T}}=50$ and $R_{\mathrm{L}}=100$ to examine storage efficiency sensitivity in the “capillary crossflow equilibrium” regime (Fig. 7). Scenarios without capillary crossflow have been previously explored in Debbabi et al. (2017). Here, results show that the volume of wetting phase trapped in the system, whether it is injected or displaced, increases with the permeability ratio $\sigma _x$ but decreases with the storage ratio $R_{\mathrm{s}}$. However, further numerical experiments, not reported here, show trapping reaches a minimum as the injectant wettability is varied between the strongly wetting and non-wetting end members. Trapping is also minimal when the storage ratio $R_{\mathrm{s}}$ is large. In that case, capillary crossflow has little influence on the overall fraction of the moveable pore volume contacted.

Fig. 11

Change in storage efficiency at 1 MPVI (relative to a reference homogeneous model) with permeability contrasts ($\sigma _x$) and storage contrasts ($R_{\mathrm{s}}$) when flow is directed along layers. Circles denote cases using a wetting injectant and squares a non-wetting injectant

5 Discussion

The results reported here are applicable to immiscible, incompressible flow in layered porous media irrespective of material property contrasts, fluid property contrasts and length scale, so long as buoyancy effects are negligible. Example applications for our models include plug-scale experiments in the laboratory (10 cm scale), waterflooding of hydrocarbon reservoirs (100 m scale) and CO${}_2$ storage in regional aquifers (km scale). The results provide a framework to support mechanistic interpretations of complex field or experimental data, and numerical model predictions, through the use of simple dimensionless models.

This study shows that knowledge of the local and transverse capillary numbers, and permeability contrasts, is not sufficient to evaluate the impact of capillary heterogeneity trapping and capillary crossflow on storage efficiency. The storage ratio $R_{\mathrm{s}}$, which accounts for contrasts in porosity and end-point saturation between layers, also determines whether these mechanisms have a significant impact on storage efficiency. In most geologic settings, high-permeability layers tend to have larger porosities and lower initial water saturation than low-permeability layers, so the storage ratio is greater than 1 ($R_{\mathrm{s}}>1$; Timur 1968; Ahmed et al. 1991; Tjølsen et al. 1991; Nelson 1994). In this case, our results indicate that capillary heterogeneity trapping is likely to be significant when flow is directed across layers, unless the injected phase is intermediate-wetting. However, capillary crossflow, when flow is directed along layers, is not likely to be significant.

Our dimensionless results can be used to identify heterogeneity length scales which have significant influence on multiphase flow in the subsurface. When flow is directed across layers, we can use the local capillary number to predict the critical layer thickness below which capillary trapping is significant, i.e. when $N_{\mathrm{cv,l}}>0.1$. Using characteristic values from Sect. 3, we find that layers as thick as ${\sim }10$ cm may cause significant trapping. It is well known that millimetre-thick laminas and decimetre-thick beds are ubiquitous in clastic reservoirs (Campbell 1967; Van Wagoner et al. 1990). Capillary heterogeneity trapping is therefore very likely unless the reservoir is intermediate-wetting or flow rates are several orders of magnitude larger than typical reservoir conditions. Grid blocks used in typical reservoir models are generally much larger than these critical layering scales—dimensions are of order $\sim$100 m in the horizontal direction and $\sim$5 m in the vertical direction—and are therefore unable to directly capture capillary heterogeneity trapping. Scale-dependent, dynamic corrections on relative permeability curves are therefore essential to resolve the subgrid response of multiphase flow to heterogeneity. Likewise, when flow is directed along layers, the transverse capillary number can be used to predict layer thickness below which capillary crossflow damps the effects of heterogeneity, i.e. when $N_{\mathrm{cv,T}}>0.1$. At the inter-well scale ($L \sim 1000\,\hbox {m}$), using a vertical-to-horizontal permeability ratio of $\sim$0.1 and characteristic values taken from Sect. 3, we find that capillary crossflow eliminate the effects of heterogeneity in well-communicating flow units thinner than $\sim$3 m. Typical vertical grid block dimensions are therefore sufficient to capture accurately horizontal flow.

The dimensionless results can also be applied to guide relative permeability measurements in layered core plugs. Core-flooding experiments are often performed at conditions where the capillary-to-viscous force balance which control flow can significantly change with parameters such as the flow rate or the fluid properties (Honarpour et al. 1995; Reynolds and Krevor 2015; Krause and Benson 2015). It is important to perform experiments at various flow conditions to quantify how scales influence the results and extrapolate the results in a consistent manner (Huang et al. 1995). Our results indicate that relative permeability should be measured over a range of local and transverse capillary numbers $N_{\mathrm{cv,l}}$ and $N_{\mathrm{cv,T}}$ that are larger than 0.1, to vary significantly the capillary-to-viscous force balance and its impact on measurements, but that enforce $N_{\mathrm{cv,L}}<0.1$ to avoid capillary end effects which artificially perturb measurements.

6 Conclusions

We examined the impact of capillary and viscous forces on flow across and along layers of contrasting porosity and relative permeability, in addition to previously examined contrasts in absolute permeability and capillary pressure curves. We considered displacements using intermediate-wetting injectants, in addition to the wetting and non-wetting cases examined previously. We have characterized the two-phase flow using six independent dimensionless parameters obtained from inspectional analysis of the flow equations (Table 1). The impact of the dimensionless numbers on flow was quantified in terms of a dimensionless storage efficiency, so results are directly applicable, regardless of scale, to geologic CO${}_{2}$ storage, but can also be applied to hydrocarbon production using the numerically equivalent recovery efficiency.

When flow is directed across layers, capillary heterogeneity traps the non-wetting phase, whether it is the injected or displaced phase. However, minimal trapping occurs when the injected phase is intermediate-wetting or in the unlikely case that high-permeability layers contain less volumes of moveable fluids than low-permeability layers ($R_{\mathrm{s}}<1$). We find that the local capillary number $N_{\mathrm{cv,l}}$ rather than the more common longitudinal capillary number $N_{\mathrm{cv,L}}$ predicts when capillary heterogeneity trapping is significant ($N_{\mathrm{cv,l}}>0.1$). Trapping of the non-wetting phase increases with increased permeability contrasts (${\sigma }_x$) and storage contrasts ($R_{\mathrm{s}})$.

When flow is directed along layers, we show that, regardless of wettability, increasing capillary crossflow, quantified by the transverse capillary number $N_{\mathrm{cv,T}}$, reduces the distance between the leading edges of the injected phase in the two layers and increases storage efficiency. This may be counter-intuitive when the injected phase is non-wetting. In general, capillary crossflow is significant when $N_{\mathrm{cv,T}}>0.1$. However, crossflow has a significant impact on storage efficiency only in the unlikely case that the high-permeability layers contain less volumes of moveable fluids than the low-permeability layers ($R_{\mathrm{s}}<1$). In that case, capillary heterogeneity traps the wetting phase, regardless of whether it is the injected or displaced phase.

The dimensionless results reported provide a framework to support mechanistic interpretations of complex field or experimental data, and numerical model predictions, through the use of simple dimensionless models.

Appendices

Appendix 1: Derivation of Governing Dimensionless Numbers

We follow here the methodology described by Debbabi et al. (2017) and additionally account for capillary effects to obtain the set of dimensionless scaling groups presented in Table 1. The methodology is similar to the commonly termed “inspectional analysis”, which has been previously applied to homogeneous (Shook et al. 1992) and simple layered porous media (Zhou et al. 1997).

Inspectional analysis of the flow equations. Before non-dimensionalizing the flow equations, we first expand Eq. (1) to identify the distinct contributions of viscous and capillary effects to saturation changes. This requires the injected-phase volumetric flux per unit area to be expressed as a function of the total flux, i.e.

$$\begin{aligned} \mathbf {q_i}=f_{\mathrm{i}}\, \mathbf {q_T} + \frac{{\lambda }_{\mathrm{i}}{\lambda }_{\mathrm{d}}}{{\lambda }_{\mathrm{T}}}\ \overline{\overline{k}}\cdot \mathbf {\nabla P_c}, \end{aligned}$$

(13)

where $f_{\mathrm{i}}$ denotes the dimensionless ratio of the injected to the total fluid mobility $f_{\mathrm{i}}={\lambda }_{\mathrm{i}}/{\lambda }_{\mathrm{T}}$, which corresponds to the injected-phase fractional flow in the viscous limit, and controls the efficiency with which the injected phase displaces the phase initially in place (see Debbabi et al. 2017). Re-injecting the latter expression into the continuity equation (1) yields the following (dimensional) formulation of the governing flow equations

$$\begin{aligned}&\displaystyle \phi {\Delta }S\frac{\partial s}{\partial t}+\mathbf {q_T}\cdot \mathbf {\nabla f_i} + \left[ \frac{{\lambda }_{\mathrm{i}}{\lambda }_{\mathrm{d}}}{{\lambda }_{\mathrm{T}}}\ \overline{\overline{k}}\cdot \mathbf {\nabla P_c}\right] =0, \end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf {q_T}= \nabla \cdot \left[ -{\lambda }_{\mathrm{T}}\, \overline{\overline{k}}\cdot \mathbf {\nabla P_d} + \lambda _{\mathrm{i}}\, \overline{\overline{k}} \cdot \mathbf {\nabla P_c} \right] =0. \end{aligned}$$

(15)

Normalizing the flow equations using the dimensionless quantities $\hat{x}=x/L$, $\hat{z}=z/H$ (for layer-parallel flow only), $\hat{t}=t\ {\overline{q}}_{\mathrm{in}}/\overline{\phi {\Delta }S}L$, ${\hat{q}}_x=q_x/{\overline{q}}_{\mathrm{in}}$, ${\hat{q}}_z=q_z L\overline{k_zk^{\mathrm{e}}_{\mathrm{r,d}}}/{\overline{q}}_{\mathrm{in}} H \overline{k_xk^{\mathrm{e}}_{\mathrm{r,d}}}$, ${\widehat{\lambda }}^j_{\mathrm{T}}={\lambda }^j_{\mathrm{T}}/(k^{e,j}_{\mathrm{r,d}}/{\mu }_{\mathrm{d}})$, ${\widehat{\lambda }}^j_{\mathrm{i}}={\lambda }^j_{\mathrm{i}}/(k^{e,j}_{\mathrm{r,d}}/{\mu }_{\mathrm{d}})$ and ${\widehat{\lambda }}^j_{\mathrm{d}}={\lambda }^j_{\mathrm{d}}/(k^{e,j}_{\mathrm{r,d}}/{\mu }_{\mathrm{d}})$ for $j=1,\ 2$, $\hat{P}=\overline{k_xk^{\mathrm{e}}_{\mathrm{r,d}}} (P_{\mathrm{d}}-P_0)/L {\overline{q}}_{\mathrm{in}}{\mu }_{\mathrm{d}}$, ${\hat{P}}_{\mathrm{c}}=P_{\mathrm{c}}/P^{\mathrm{e}}_{\mathrm{c}}$, ${\hat{k}}_{x,d}=k_xk^{\mathrm{e}}_{\mathrm{r,d}}/\overline{k_xk^{\mathrm{e}}_{\mathrm{r,d}}}$, ${\hat{k}}_{z,d}=k_zk^{\mathrm{e}}_{\mathrm{r,d}}/\overline{k_zk^{\mathrm{e}}_{\mathrm{r,d}}}$ and ${\hat{C}}_{\mathrm{s}}=\phi {\Delta }S/\overline{\phi \mathrm {\Delta }S}$, we obtain the following dimensionless form governing flow equations

$$\begin{aligned}&{\hat{C}}_{\mathrm{s}}\frac{\partial s}{\partial \hat{t}}+{\hat{q}}_{T,x}\frac{\partial f_{\mathrm{i}}}{\partial \hat{x}}+R^2_{\mathrm{L}}{\hat{q}}_{T,z}\frac{\partial f_{\mathrm{i}}}{\partial z}+N_{\mathrm{cv,L}}\frac{\partial }{\partial \hat{x}}\left[ {\hat{k}}_{x,d}\ f_{\mathrm{i}}\ {\widehat{\lambda }}_{\mathrm{d}}\ \frac{\partial {\hat{P}}_{\mathrm{c}}}{\partial \hat{x}}\right] \nonumber \\&\qquad + N_{\mathrm{cv,T}}\frac{\partial }{\partial \hat{z}}\left[ {\hat{k}}_{z,d}\ f_{\mathrm{i}}\ {\widehat{\lambda }}_{\mathrm{d}}\ \frac{\partial {\hat{P}}_{\mathrm{c}}}{\partial \hat{z}}\right] =0, \end{aligned}$$

(16)

$$\begin{aligned}&\frac{\partial {\hat{q}}_{T,x}}{\partial \hat{x}}+R^2_{\mathrm{L}}\frac{\partial {\hat{q}}_{T,z}}{\partial \hat{z}}=\frac{\partial }{\partial \hat{x}}\left[ -{\hat{k}}_{x,d}{\widehat{\lambda }}_{\mathrm{T}}\frac{\partial \hat{P}}{\partial \hat{x}}+ N_{\mathrm{cv,L}}\ {\hat{k}}_{x,d}\ {\widehat{\lambda }}_{\mathrm{i}}\frac{\partial {\hat{P}}_{\mathrm{c}}}{\partial \hat{x}}\right] \end{aligned}$$

(17)

$$\begin{aligned}&\qquad +R^2_{\mathrm{L}}\frac{\partial }{\partial \hat{z}}\left[ -{\hat{k}}_{z,d}{\widehat{\lambda }}_{\mathrm{T}} \frac{\partial \hat{P}}{\partial \hat{z}}+N_{\mathrm{cv,L}}{\hat{k}}_{z,d}\ {\widehat{\lambda }}_{\mathrm{i}}\frac{\partial {\hat{P}}_{\mathrm{c}}}{\partial \hat{z}}\right] =0. \end{aligned}$$

(18)

From these dimensionless flow equations, we identify the governing dimensionless numbers reported in Table 1 as constant coefficients appearing in the partial differential equations or constant coefficients controlling functionals appearing in the differential equations. The effective aspect ratio $R_{\mathrm{L}},$ the longitudinal capillary number $N_{\mathrm{cv,L}}$ and the transverse capillary number $N_{\mathrm{cv,T}}$ directly appear as constant coefficients within the coupled partial differential equations. The end-point mobility ratios $M_{\mathrm{e}}=k^{\mathrm{e}}_{\mathrm{r,i}}{\mu }_{\mathrm{d}}/k^{\mathrm{e}}_{\mathrm{r,d}}{\mu }_{\mathrm{i}}$, which is chosen identically in all layers and later replaced by the shock-front mobility ratio $M_{\mathrm{f}}$ as explained further in this section, and the Corey exponents $n_{\mathrm{i}}$ and $n_{\mathrm{d}}$, are identified as a consequence of our relative permeability parameterization from

$$\begin{aligned}&\displaystyle f_{\mathrm{i}}(s)=\frac{M_{\mathrm{e}}s^{n_{\mathrm{i}}}}{M_{\mathrm{e}}s^{n_{\mathrm{i}}}+{\left( 1-s\right) }^{n_{\mathrm{d}}}}, \end{aligned}$$

(19)

$$\begin{aligned}&\displaystyle {\widehat{\lambda }}_{\mathrm{T}}(s)={\widehat{\lambda }}_{\mathrm{i}}(s)+{\widehat{\lambda }}_{\mathrm{d}}(s)=M_{\mathrm{e}}s^{n_{\mathrm{i}}}+{\left( 1-s\right) }^{n_{\mathrm{d}}}. \end{aligned}$$

(20)

The spatially dependent functionals ${\hat{k}}_{x,d}$, ${\hat{k}}_{z,d}$ and ${\hat{C}}_{\mathrm{s}}$ are parameterized by the longitudinal and transverse permeability ratios, ${\sigma }_x={\left( k_xk^{\mathrm{e}}_{\mathrm{r,d}}\right) }_1/{\left( k_xk^{\mathrm{e}}_{\mathrm{r,d}}\right) }_2$ and ${{\sigma }_z=\left( k_zk^{\mathrm{e}}_{\mathrm{r,d}}\right) }_1/{\left( k_zk^{\mathrm{e}}_{\mathrm{r,d}}\right) }_2$, the storage ratio of moveable pore volumes in each layer, ${R_{\mathrm{s}}=\left( \phi {\Delta }S\right) }_1/{\left( \phi {\Delta }S\right) }_2$, and for layer-perpendicular flow, the number of layers, $f_{\mathrm{L}}=L/H$. While the transverse permeability ratio is formally required to scale the displacement, numerical experiments not reported here showed the ratio has no influence on normalized saturation distributions. We therefore omit the transverse permeability ratio from further mention in this text.

Table 2 Dimensional parameters used to perform the numerical experiments reported in Figs. 6 and 7

Dimensionless number selection. Previous work showed that the impact of relative permeability curves on leading-order viscous crossflow behaviour can be captured using the mobility ratios evaluated across the shock fronts (Debbabi et al. 2017). We therefore choose to replace the end-point mobility ratio $M_{\mathrm{e}}$ by the shock-front mobility ratio $M_{\mathrm{f}}$ (Table 1). This does not affect the consistency of the set of dimensionless numbers used. When flow is oriented across layers, we also choose to use the local capillary number $N_{\mathrm{cv,l}}=N_{\mathrm{cv,L}}f_{\mathrm{L}}$, which we show in this work, quantifies capillary heterogeneity trapping, instead of the longitudinal capillary number $N_{\mathrm{cv,L}}$.

Appendix 2: Validation of the Numerical Method

Solutions of the multiphase flow equations (1)–(4) were obtained using a commercial code that implements a finite-volume–finite-difference approach to discretize the governing equations (Eclipse 100). Flow was simulated using Cartesian grids. Time stepping was fully implicit. We used resolutions ranging from 1000 $\times$ 1 up to 10,000 $\times$ 1 cells for layer-perpendicular flow, and from 200 $\times$ 200 up to 800 $\times$ 800 cells for layer-parallel flow, to demonstrate that the solutions were converged. Storage efficiency measured at 1 MPVI varied by less than 0.5 % over the range of grid resolutions explored for the cases reported in Figs. 6 and 7. The selected Corey exponents are $n_{\mathrm{i}}=n_{\mathrm{d}}=2$ in both layers; these values are typical for geologic porous media. Dimensional values used to perform the numerical experiments reported in Figs. 6 and 7 are shown in Table 2.

We also verified that the numerical scheme captures accurately capillary heterogeneity effects on flow solutions. When flow is directed across layers, we confirmed that saturations in the high- and low-permeability layers at boundaries, which are reported in Fig. 6, maintain capillary pressure continuous across the layers (see Fig. 12a; saturation combinations obtained analytically following Kortekaas (1985) are represented as dashed lines). When flow is directed along layers, we examined transverse saturation discontinuities reported in Fig. 7 with large amounts of capillary crossflow ($N_{\mathrm{cv,T}}=50$). We find that almost all saturation combinations measured (except a few combinations measured near the leading edge of the injected phase) maintain capillary pressure uniform in the transverse direction. As $N_{\mathrm{cv,T}}$ is further increased to 500, all saturation values along the layer boundary converge towards combinations maintaining capillary pressure continuous. This is expected with large amounts of capillary crossflow (Yokoyama and Lake 1981).

Fig. 12

Cross-plots of saturation in high- and low-permeability layers at layer boundaries for a the layer-perpendicular flow solutions reported in Fig. 6 and b the layer-parallel flow solutions reported in Fig. 7 with large amounts of capillary crossflow ($N_{\mathrm{cv,T}}=50$) and further increased ($N_{\mathrm{cv,T}}=500$)

Appendix 3: Quantification of Capillary End Effects

Capillary end effects are caused by a capillary pressure discontinuity that exists at the outlet boundary of the system (Osoba et al. 1951; Lake 1989). This causes the formation of saturation gradients near the outlet end (see Fig. 13) that can influence the measurements of relative permeability or the predicted storage/recovery efficiency.

Fig. 13

Typical post-breakthrough saturation profile in a homogeneous water-wet model as a function of the longitudinal capillary number $N_{\mathrm{cv,L}}$. Capillary pressure is set to zero in the outlet cell of the model

Fig. 14

Changes in storage efficiency with the longitudinal capillary number $N_{\mathrm{cv,L}}$ for various buffer permeabilities and layer ordering with a wetting and b non-wetting injectants. Buffer permeability is successively chosen as the harmonic permeability average of the layered system, the lowest permeability value and as an infinitely large value. Layer ordering H/L (high/low permeability) is also swapped to L/H to verify conclusions are maintained

We examined conditions under which storage efficiency remains independent of capillary end effects. This is important to ensure results do not depend on the model implementation, but also to identify conditions for which core-plug measurements of layered samples and mini-models numerical experiments are not influenced by capillary end effects. This is achieved here for the layer-perpendicular model without loss of generality. We examine the sensitivity of storage efficiency to the permeability of a buffer added at the downstream end of the model as a function of the longitudinal capillary number $N_{\mathrm{cv,L}}$ (Fig. 14). We consider a moderately heterogeneous layered model (${\sigma }_x=5$ and $f_{\mathrm{L}}=10$), with indicative values of $M_{\mathrm{f}}=0.5$ and $R_{\mathrm{s}}=1$. The buffer permeability is successively chosen as the lowest of the two layer permeability values, the harmonic average, and as 100,000 times the harmonic average (to describe a porous-free outlet). We also change the layer ordering from high/low permeability (H/L) to low/high permeability (L/H), as well as the wettability. For all cases considered, storage efficiency remains independent of capillary end effects for $N_{\mathrm{cv,L}}<0.1$. The results of numerical experiments not reported here yield the same criterion for $f_{\mathrm{L}}=100$ and 1000 layers. A similar bound was obtained by Lake (1989) and Huang and Honarpour (1998) for homogeneous systems. We further impose $N_{\mathrm{cv,L}}<0.1$ in the rest of this work.