$H^{*}$ Peusner’s Form of the Kedem–Katchalsky Equations for Non-homogenous Non-electrolyte Binary Solutions

Abstract

The paper presents a hybrid matrix form of Kedem–Katchalsky equations that contains Peusner’s coefficients $H_{ij}^{*}\;(i, j = 1, 2)$ for the conditions of concentration polarization and $H_{ij}$ for homogeneous solutions. The aqueous glucose solutions were analyzed in Nephrophan membrane system with membrane in horizontal plane. The calculations of coefficients $H_{ij}^{*}$ were made for the A and B configurations of the membrane system. In the A configuration glucose solution with higher concentration was located below and the solution with lower concentration above the membrane. In configuration B locations of the solutions were reversed. Non-diagonal coefficients of matrix $[H^{*}]$ (concentration polarization conditions) were shown to be linearly dependent on average concentration of glucose solution in the membrane. $H_{12}^{*}$ in A configuration was lower than in B configuration. Non-diagonal coefficients of matrix $[H^{*}]$ were lower than appropriate coefficients of matrix [H] (homogeneous solutions). For diagonal coefficients of matrix $[H^{*}]$ coefficient $H_{11}^{*}$ is constant and equal to $H_{11}$, whereas $H_{22}^{*}$ and $H_{22}$ are nonlinearly dependent on average concentration of glucose solution in the membrane. Value of $H_{22}^{*}$ in A was lower than in B configuration of the membrane system. Additionally, $H_{22}^{*}$ were lower than $H_{22}$. For both A and B configurations and concentration polarization conditions, the coefficients $H_{12}^{*}$ and $H_{22}^{*}$ of matrix $[H^{*}]$ are different for average solution concentrations ${>}5.41\,\hbox {mol}\,\hbox {m}^{-3}$ due to convective mixing of solutions in B configuration.

1 Introduction

Peusner’s Network Thermodynamics (Peusner’s NT) is one of the methods used to describe transport in membrane systems that enables symmetrical and/or hybrid transformation of classical Kedem–Katchalsky equations to network forms (Peusner 1970, 1983, 1985, 1986). For homogeneous binary non-electrolyte solutions there are two symmetrical and two hybrid forms of network K–K equations. The symmetrical forms of these equations contain Peusner’s coefficients $R_{ij}$ or $L_{ij}$ and hybrid forms—Peusner’s coefficients $P_{ij}$ and $H_{ij}$ (Peusner 1983, 1986; Batko et al. 2013). These coefficients appear in matrix form of the phenomenological equations. The coefficients $L_{ij}$ and $R_{ij}$ derive directly from the Onsager’s phenomenological equation. The introduction of the coefficients $P_{ij}$ and $H_{ij}$ is a consequence of application of network thermodynamics techniques.

The assumption of homogeneity of the solutions separated by a membrane is satisfied only when solutions of different concentrations separated by a membrane are homogeneous (thoroughly mixed by mechanical stirring) (Katchalsky and Curran 1965; Ślęzak 1989). If these solutions are not mechanically stirred, the concentration boundary layers (CBL) are formed on both sides of artificial and/or biological membranes. The formation of CBL is an important process that occurs in the technical and biological systems (Barry and Diamond 1984; Shachar-Hill and Hill 1993; Larchet et al. 2008; Pappenheimer 2001; Grzegorczyn et al. 2008; Mishchuk 2010; Nikonenko et al. 2010; Grzegorczyn and Ślęzak 2012; Wang et al. 2014). These layers change the concentration gradient through the membrane and serve as additional kinetic barriers to the fast permeating substances and, in result, reduce the values of the volume and solute fluxes (Abu-Rjal et al. 2014; Barry and Diamond 1984; Ślęzak 1989; Dworecki 1995; Dworecki et al. 2003, 2005; Kargol 2000; Ślęzak et al. 1985, 2010). The processes of creation and destruction of CBLs may be visualized by optical methods (Dworecki 1995; Fernández-Sempere et al. 2009; Salcedo-Diaz et al. 2014).

In our previous papers (Ślęzak et al. 2012a, b; Batko et al. 2014a, b, 2015) network forms of the Kedem–Katchalsky equations were applied to interpret the transport of binary non-electrolyte solutions through horizontally mounted membrane in concentration polarization conditions. The coefficients $L_{ij}^{*}, R_{ij}^{*}$ and $P_{ij}^{*} (i, j \in \{1, 2\})$ were calculated for aqueous solutions of glucose and polymer membrane. Additionally, the values of coefficients $L_{ij}^{*}, R_{ij}^{*}$ and $P_{ij}^{*}$ were compared to the values of coefficients $L_{ij}, R_{ij}$ and $P_{ij}$ calculated for conditions of solution homogeneity for the same values $\bar{{C}}$ and two configurations of membrane system. There was a threshold value of concentration $(\bar{{C}}_\mathrm{{cr}})$ and only for $\bar{{C}} > \bar{{C}}_\mathrm{{cr}}$ the coefficients $L_{ij}^{*}, R_{ij}^{*}$ and $P_{ij}^{*}$ were dependant on the membrane system configuration. It was also shown that for $\bar{{C}} > \bar{{C}}_\mathrm{{cr}}$ coefficients relations $L_{ij}^{*}/L_{ij}, R_{ij}^{*}/R_{ij}$ and $P_{ij}^{*}/P_{ij}$ depended on a membrane system configuration.

In the present paper, Kedem–Katchalsky equations were transformed into hybrid matrix form and applied to interpret the membrane transport of non-electrolyte solutions in conditions of concentration polarization. We assessed the influence of the concentration polarization on the value of Peusner’s coefficients $H_{ij}^{*}$, for aqueous solutions of glucose and a Nephrophan hemodialysis membrane. The values of these coefficients were compared to the values of coefficients $H_{ij}$ calculated for the same concentrations of homogeneous solutions and different configurations of the membrane. To find new coefficients better describing the membrane transport in concentration polarization conditions for both configurations of the membrane system, we analyzed other combinations of coefficients of matrixes $[H^{*}]$ and [H] for A and B configurations.

2 Theory

Similar to the previous papers (Ślęzak et al. 2012a, b; Batko et al. 2014a, b, 2015), let us consider a single-membrane system schematically presented in Fig. 1, in which an electroneutral, selective polymer membrane (M) separates two non-homogeneous (mechanically unstirred) binary non-electrolyte solutions with concentrations $C_{l}$ and $C_{h} (C_{l}< C_{h})$ at the initial moment ($t = 0$). The membrane transport processes are isothermal and stationary, and no chemical reaction occurs in the solutions separated by membrane. According to the Kedem and Katchalsky formalism, the membrane is characterized by the hydraulic permeability ($L_{p}$), reflection ($\sigma$) and solute permeability ($\omega$) coefficients (Kedem and Katchalsky 1958). The values of these coefficients do not depend on the configuration of the membrane system (Ślęzak 1989).

Fig. 1

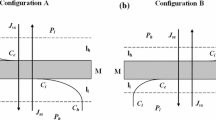
Configurations A and B of a single-membrane system: M—membrane; $l_{l}$ and $l_{h}$—the concentration boundary layers (CBLs), $P_{h}$ and $P_{l}$—mechanical pressures; $C_{l}$ and $C_{h}$—concentrations of solutions outside the boundaries; $C_{e}$ and $C_{i}$—the concentrations of solutions at boundaries $\hbox {l}_{l}/M$ and $M/l_{h}$; $J_{vm}$—the volume fluxes through membrane M; $J_{vs}$—the volume fluxes through complex $l_{l}/M/l_{h} J_{sl}, J_{sh}$ and $J_{sm}$—the solute fluxes through layers $l_{l}$, $l_{h}$ and membrane, respectively; $J_{ss}$—the solute fluxes through complex $l_{l}/M/l_{h}$ (Ślęzak et al. 2012a, b).

As shown in Fig. 1, for a single-membrane system with a horizontally oriented membrane, configurations A and B may be distinguished (Ślęzak 1989; Batko et al. 2014a, b). In this system, water and dissolved substance that diffuse through the membrane form the concentration boundary layers (CBL) $l_{l}$ and $l_{h}$ on both sides of the membrane. The layers $l_{l}$ and $l_{h}$ are treated as pseudomembranes, and their thicknesses are denoted by $\delta _{l}$ and $\delta _{h}$ (Ślęzak et al. 1985, 2005, 2010). In configuration A, solutions with concentration $C_{l}$ and $C_{h}$ are located in the compartments above and below the membrane, respectively, and their thicknesses are denoted by $\delta _{l} = \delta _{h} = \delta _{A }= \delta _{d}$. In this configuration the layers of higher density are under layers with lower density (Ślęzak et al. 1985; Ślęzak 1989). The structure of layers $l_{l}$ and $l_{h}$ is gravitationally stable, since the density gradient in CBLs is parallel to the vector of gravity ($\vec {g})$ (Ślęzak et al. 1985; Dworecki et al. 2005). Thus in configuration A only diffusive transport occurs and the diffusion process is characterized by diffusion coefficient $D_{l} = D_{h}=D_{A} = D_{d}$ (Ślęzak et al. 1985; Dworecki et al. 2005).

In the configuration B, solutions with concentrations $C_{l}$ and $C_{h}$ are placed inversely relative to the membrane mounted horizontally and the density gradient in CBL is anti-parallel to the vector of gravity. In this configuration the CBL of higher density are above CBL with lower density. Although the density gradient is antiparallel to $\vec {g}$, a layer system in this configuration is stable, since the viscous forces prevent vertical movement of the solutions. This means that at small difference of concentrations the viscosity prevails, the solution remains in a stable state, and the substance is transported by diffusion. In this steady state all concentration fluctuations, the same as the liquid density fluctuations, are suppressed. The transition from stable to unstable state occurs when the buoyant forces are larger than the viscous forces. In this moment, convective transport occurs in addition to diffusion. In convective state, liquid non-active state is unstable relative to any small disturbance. This process is a membrane version of the Rayleigh–Benard–Taylor phenomenon (Ślęzak et al. 1985; Dworecki et al. 2005; Grzegorczyn and Ślęzak 2012). In this configuration, both diffusive and diffusive–convective conditions may occur. This indicates that the membrane transport process is characterized by diffusion coefficient ($D_{d})$ and convective diffusion coefficient ($D_{dk})$. In general, for configurations A and B we assume that $D_{r }=D_{d }+D_{dk}$ ($r = A$ or B). In configuration A and B (for $\bar{{C}} < \bar{{C}}_\mathrm{{cr}} ), D_{A }= D_{B }=D_{d }$ and $D_{dk }$= 0 and in configuration B for $\bar{{C}}\ge \bar{{C}}_\mathrm{{crit.}} , D_{B }=D_{d }+D_{dk}$ and $D_{dk }> D_{d}$. Additionally $\delta _{B }= \delta _{dk}$ and $\delta _{dk }< \delta _{d}$.

For concentration polarization conditions we denote the concentrations of solutions at boundaries $l_{l}/M$ and $M/l_{h}$ by $C_{e}$ and $C_{i}$ ($C_{e} < C_{i}, C_{e} > C_{l}, C_{i} < C_{h})$, respectively. We assume that the mass density $(\rho )$ of the solutions of concentrations $C_{l}, C_{e}, C_{i}$ and $C_{h}$ fulfills the condition $\rho _{l} <\rho _{e} < \rho _{i} <\rho _{h}$. The thickness $(\delta )$ is a basic parameter of CBL (Schlichting and Gersten 2000) that can be evaluated by the optical (Dworecki 1995; Nikonenko et al. 2010) and the volume or solute fluxes methods (Barry and Diamond 1984; Ślęzak et al. 2010; Jasik-Ślęzak et al. 2011). In certain hydrodynamic conditions CBLs can be partially destroyed by natural convection (Dworecki et al. 2005; Nield and Bejan 2006). This process limits the growth of thickness $\delta _{l}$ and $\delta _{h}$ of the layers $l_{l}$ and $l_{h}$ to critical values ($\delta _{l})_\mathrm{{cr}}$ and ($\delta _{h})_\mathrm{{cr}}$ and accelerates diffusion of substances outside the layers (Ślęzak et al. 1985; Dworecki et al. 2005). The transport parameters of layers $l_{l}$ and $l_{h}$ are characterized by the solute permeability coefficients: $\omega _{l}=D_{l} (RT\delta _{l})^{-1}$ and $\omega _{h}=D_{h} (RT\delta _{h})^{-1}$, where $D_{l}$ and $D_{h}$ are the diffusion coefficients in layers $l_{l}$ and $l_{h}$, respectively (Katchalsky and Curran 1965). The solute permeability coefficient of complex $l_{l}/M/l_{h}$ is denoted by $\omega _{s}$. The following relation between coefficients $D_{l}$, $\omega$, $D_{h}$, $\delta _{l}$, $\delta _{h}$ and $\omega _{s}$ is fulfilled $\omega ^{-1} + RT(\delta _{l}D_{h }+ \delta _{h}D_{l})D_{l}^{-1}D_{h}^{-1} = \omega _{s}^{-1}$ (Katchalsky and Curran 1965; Demirel 2007).

The development of natural convection process is controlled by a concentration Rayleigh number $(R_{C})$ that characterizes loss of stability (Ślęzak et al. 1985; Dworecki et al. 2005). Hydrodynamic stability of CBL in membrane systems is controlled by the concentration Rayleigh number $(R_{C})$, which may be written in the following form (Dworecki et al. 2005)

$$\begin{aligned} R_C =\frac{gRT\omega \delta ^{4}\alpha _C (C_h -C_l )}{\nu D(D+2RT\omega \delta )}=\frac{gRT\omega \delta ^{4}\alpha _C \bar{{C}}\ln (C_h C_l ^{-1})}{\nu D(D+2RT\omega \delta )} \end{aligned}$$

(1)

where g—the gravitational acceleration, $\delta$—thickness of the CBL, $\alpha _{C }= (\partial \rho /\partial C)/\rho$—variation of density with the concentration, $\rho$—mass density, D—diffusion coefficient of the solute and $\nu$—the kinematic viscosity of the fluid. The value of $R_{C}$ depends on the gravity acceleration, concentration, viscosity and density of the transported solutions (Dworecki et al. 2005; Jasik-Ślęzak et al. 2011; Ślęzak et al. 2010). For configuration B, when the value of $R_{C}$ reaches a critical value $(R_{C})_\mathrm{{cr}}$, transition from non-convective (stable) to the convective (unstable) state is observed. $(R_{C})_\mathrm{{cr}}$ is reached at the bifurcation point. In the previous paper (Ślęzak et al. 2010) it was shown that the critical value of concentration Rayleigh number $(R_{C})_\mathrm{{cr}} = 1709.3$ was reached for $\bar{{C}}_\mathrm{{cr}} = 5.41\,\hbox {mol}\,\hbox {m}^{-3}$. $(R_{C})_\mathrm{{cr}}$ is the limit of the stability of membrane system relative to any concentration (density) disturbance (Landau and Lifshitz 1987).

For the $R_{C} > (R_{C})_\mathrm{{ct}}$ the hydrodynamic instability leads to the natural convection which reduces the thickness of CBL and increases the value of concentration gradient of the membrane and consequently volume and solute fluxes (Ślęzak et al. 2010). The existence of such regulatory mechanism at the presence of a gravitational field justifies amplification and rectification of the volume and solute fluxes (Kargol 1992; Ślęzak 1989; Jasik-Ślęzak et al. 2011; Ślęzak et al. 2012a, b). These effects occur in single- and double-membrane systems containing binary or ternary solutions in conditions of concentration polarization when the density gradient in CBL formed in surroundings of horizontally mounted membrane is anti-parallel to the vector of gravity (Kargol 1992; Ślęzak 1989; Ślęzak et al. 2012a, b). In these conditions, the process of turbulent natural convection develops until the dendric-type structure called “plum structure” is formed (Puthenveettil and Arakeri 2008; Puthenveettil et al. 2011; Ramareddy and Puthenveettil 2011). Compactness of “plum structure” increases with increasing value of the $R_{C}$ number (Puthenveettil and Arakeri 2008).

Noteworthy, the formation of the spatial structure of liquid instability phenomenon known as Rayleigh–Benard phenomenon has several versions. The earliest known version discovered by Bernard is caused by thermoconvection between a heated and a not non-heated plate (Normand et al. 1977). Later different version of the spatial structure of the liquid caused by electroconvection was observed due to electric field applied between the horizontally mounted electrodes (Baranowski and Kawczyński 1972; Baranowski 1980; Ward and Le Blanc 1984; Han and Grier 2005, 2006, 2012). Recently, studies focus mainly on electroconvection between the horizontally mounted electrodes separated by an ion exchange membrane (Larchet et al. 2008; Rubinstein and Zaltzman 2000; Moya and Horno 2004; Nikonenko et al. 2010; Serna et al. 2014).

The Bernard phenomenon and its electrochemical and membrane counterparts occur in similar circumstances: Despite increase in the value of the control parameter in conditions that are close to the position of the equilibrium, the membrane system is stable, since in these conditions stable state corresponds to the minimum entropy production. The system loses stability after reaching the critical value at the bifurcation point, and it may lead to conditions sufficient to initiate all irreversible processes that may occur in the system (Kondepudi and Prigogine 1981; Prigogine 1997). In addition to the bifurcation point, a class of phenomena appears that is classified as dissipative structures. This means that the matter gains new properties, in which the main role is played by fluctuations and instabilities, since entropy production generally increases in systems far from equilibrium (Prigogine 1997; Kondepudi 2008).

A hybrid equation is a source of coefficients $H_{ij}^{*}$ under the conditions of concentration polarization, for a bi-directional two-port of Peusner’s NT with single input force $X_{1}$ and conjugate flux $J_{1}^{*}$ and a single output flux $J_{2}^{*}$ and force $X_{2}$

$$\begin{aligned} \left[ {{\begin{array}{c} {X_1 } \\ {J_2 ^{*}} \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {H_{11} ^{*}}&{} {H_{12} ^{*}} \\ {H_{21} ^{*}}&{} {H_{22} ^{*}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_1 ^{*}} \\ {X_2 } \\ \end{array} }} \right] =[H^{*}] \left[ {{\begin{array}{c} {J_1 ^{*}} \\ {X_2 } \\ \end{array} }} \right] \end{aligned}$$

(2)

For the conditions of homogeneity of solutions separated by the membrane, the above equation can be rewritten as (Peusner 1983, 1985, 1986)

$$\begin{aligned} \left[ {{\begin{array}{c} {X_1 } \\ {J_2 } \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {H_{11} }&{} {H_{12} } \\ {H_{21} }&{} {H_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_1 } \\ {X_2 } \\ \end{array} }} \right] =[H] \left[ {{\begin{array}{c} {J_1 } \\ {X_2 } \\ \end{array} }} \right] \end{aligned}$$

(3)

For the conditions of concentration polarization, the K–K equations can be written as (Ślęzak et al. 2010)

$$\begin{aligned} \left[ {{\begin{array}{c} {J_{vs} } \\ {J_{ss} } \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {\zeta _p L_p }&{}\;\; {-\zeta _p L_p \zeta _v \sigma } \\ {\zeta _p L_p (1-\zeta _a \sigma )\bar{{C}}}&{}\;\; {\zeta _s \omega -\zeta _p L_p \zeta _v \sigma (1-\zeta _a \sigma )} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\Delta P} \\ {\Delta \pi } \\ \end{array} }} \right] \end{aligned}$$

(4)

where $J_{vs}$ is a volume and $J_{ss}$ is a solute flux under the conditions of concentration polarization; $\zeta _{p}$, $\zeta _{v}$, $\zeta _{a}$ and $\zeta _{s}$ are hydraulic, osmotic, advective and diffusive Katchalsky’s coefficients, respectively; $L_{p}$, $\sigma$ and $\omega$ are the coefficients of hydraulic permeability, reflection and solute permeability for membrane, respectively; $\Delta P =P_{h}-P_{l}$ is the hydrostatic pressure difference ($P_{h}, P_{l}$ are the higher and lower value of hydrostatic pressure; if pressure $P_{h}$ is applied to the chamber with higher concentration $(C_{h})$, then $\Delta P > 0$); $\Delta \pi = RT(C_{h }- C_{l})$ is the osmotic pressure difference (RT is the product of the gas constant and absolute temperature, $C_{h}$ and $C_{l}$ ($C_{h}>C_{l})$ are the solution concentrations; $\bar{{C}}=(C_{h}-C_{l})[\ln (C_{h}C_{l}^{-1})]^{-1}$ is the average solutions concentration in the membrane.

By transforming Eqs. (2) and (4) for suitable forces $X_{1 }= \Delta P - \Delta \pi , X_{2 }= \Delta \pi / \bar{{C}}$ and fluxes $J_{1}^{*}=J_{vs}$ and $J_{2}^{*}= J_{ss}$ for the system $l_{l}/M/l_{h}$ we obtain

$$\begin{aligned} \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {J_{ss} } \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {\frac{1}{\zeta _p L_p }}&{} {-(1-\zeta _v \sigma )\bar{{C}}} \\ {(1-\zeta _a \sigma )\bar{{C}}}&{} {\bar{{C}}\zeta _s \omega } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_{vs} } \\ {\frac{\Delta \pi }{\bar{{C}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {H_{11} ^{*}}&{} {H_{12} ^{*}} \\ {H_{21} ^{*}}&{} {H_{22} ^{*}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_{vs} } \\ {\frac{\Delta \pi }{\bar{{C}}}} \\ \end{array} }} \right] \end{aligned}$$

(5)

From Eq. (5) for selective membrane $(0 <\sigma < 1)$ it can be obtained $H_{11}^{*} = \zeta _{p}^{-1}L_{p}^{-1}, H_{12}^{*} = -(1 - \zeta _{v} \sigma )\bar{{C}} \ne H_{21}^{*}=\bar{{C}}(1 - \zeta _{a} \sigma )$ and $H_{22}^{*}=\bar{{C}}\zeta _{s}\omega$. This means that in the Eq. (6), the symmetry relation $H_{12}^{*}=H_{21}^{*}$ is not fulfilled. For unselective membrane we can write $H_{11}^{*}= (\zeta _{p}L_{p})^{-1}, H_{12}^{*} =H_{12}^{*}=\bar{{C}}$ and $H_{22}^{*} =\bar{{C}}\zeta _{s}\omega$. In this case for semipermeable membrane $H_{11}^{*}= \zeta _{p}^{-1}L_{p}^{-1}, H_{12}^{*}=H_{21}^{*}=H_{22}^{*}= 0$. The determinant of matrix $[H^{*}]$ is equal

$$\begin{aligned} \det [H^{*}]=\bar{{C}}\left[ {\frac{\zeta _s \omega }{\zeta _p L_p }+\bar{{C}}(1-\zeta _v \sigma )(1-\zeta _a \sigma )} \right] \end{aligned}$$

(6)

In the homogeneity conditions of solution separated by selective membrane, i.e., when the condition $\zeta _{p} = \zeta _{v} = \zeta _{a} = \zeta _{s} = 1$ is fulfilled, Eq. (5) can be expressed as

$$\begin{aligned} \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {J_s } \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {\frac{1}{L_p }}&{} {-(1-\sigma )\bar{{C}}} \\ {(1-\sigma )\bar{{C}}}&{} {\bar{{C}}\omega } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_v } \\ {\frac{\Delta \pi }{\bar{{C}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{cc} {H_{11} }&{} {H_{12} } \\ {H_{21} }&{} {H_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_v } \\ {\frac{\Delta \pi }{\bar{{C}}}} \\ \end{array} }} \right] \end{aligned}$$

(7)

The determinant of matrix [H] can be rewritten as

$$\begin{aligned} \det [H]=\bar{{C}}\left[ {\frac{\omega }{L_p }+\bar{{C}}(1-\sigma )^{2}} \right] \end{aligned}$$

(8)

By comparing Eqs. (3) and (7) for selective membrane ($L_{p }> 0, 0 < \sigma < 1$ and $\omega > 0$), we obtain $H_{11}=L_{p}^{-1}, H_{12 }= -(1 - \sigma )\bar{{C}} \ne H_{21}=\bar{{C}}(1 - \sigma )$ and $H_{22}=\bar{{C}}\omega$. This means that in the Eq. (7), the symmetry relation $H_{12}=H_{21}$ is not fulfilled. For unselective membrane ($\sigma = 0$) we can write $H_{11 }$= ($L_{p})^{-1}$ and $H_{12 }=\bar{{C}}, H_{22 }=\bar{{C}}\omega$. Additionally, for unselective membrane, the Eq. (7) can be written in a following form det $[H] = \bar{{C}}\omega (L_{p})^{-1}$. The transport properties of semipermeable membrane are characterized by $L_{p }> 0, \sigma = 1$ and $\omega = 0$. In that case for this membrane $H_{12}=H_{21}=H_{22 }= 0$ and det $[H] = 0$.

The results of experimental studies for a Nephrophan membrane and aqueous solutions of glucose presented in the previous paper (Ślęzak et al. 2010) suggest that $(\zeta _{p})_{r} = (\zeta _{a})_{r} = 1$ and $(\zeta _{v})_{r} = (\zeta _{s})_{r} = \zeta _{r}$. In the paper (Ślęzak et al. 2005) it was shown that $\zeta _{r}$ coefficient can be presented in the form

$$\begin{aligned} \zeta _r =D_r (D_r +2RT\omega \delta _r )^{-1} \end{aligned}$$

(9)

where $D_{r}$—diffusion coefficient, RT—product of the gas constant and the thermodynamic temperature $\delta _{r}$—thickness of the concentration boundary layers, $r = A$ or B. Diffusive–convective conditions occur when the concentration exceeds the critical value $\bar{{C}}_\mathrm{{cr}}$ (Ślęzak et al. 2010).

When we divide suitable coefficients of matrixes $[H^{*}]$ and [H] for diffusive $(r =A)$ or convective states $(r =B)$ we obtain

$$\begin{aligned}&\displaystyle \frac{\left( H_{11} ^{*}\right) _r }{H_{11} }=\frac{\left( H_{21} ^{*}\right) _r}{H_{21} }=1 \end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \frac{\left( H_{12} ^{*}\right) _r }{H_{12} }=\frac{1-\zeta _r \sigma }{1-\sigma }=\frac{2RT\omega \delta _r +D_r (1-\sigma )}{(1-\sigma )(D_r +2RT\omega \delta _r )} \end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle \frac{\left( H_{22} ^{*}\right) _r }{H_{22} }=\zeta _r =\frac{D_r }{D_r +2RT\omega \delta _r } \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \frac{\det [H^{*}]_r }{\det [H]}=\det \left( {\frac{[H^{*}]_r }{[H]}} \right) =\frac{\zeta _r \omega +\bar{{C}}L_p (1-\zeta _r \sigma )(1-\sigma )}{\omega +\bar{{C}}L_p (1-\sigma )^{2}} \end{aligned}$$

(13)

Considering the Eq. (9) in Eq. (13) we obtain

$$\begin{aligned} \frac{\det [H^{*}]_r }{\det [H]}=\frac{D_r \omega +\bar{{C}}L_p (1-\sigma )[D_r (1-\sigma )+2RT\omega \delta _r ]}{(D_r +2RT\omega \delta _r )[\omega +\bar{{C}}L_p (1-\sigma )^{2}]} \end{aligned}$$

(13a)

The above expressions illustrate the dependence of concentration polarization for diffusive conditions $(r =A)$ and a diffusive–convective conditions $(r=B)$ on a value of $(H_{12}^{*})_{r}/H_{12}$ and $(H_{22}^{*})_{r}/H_{22}$, and det $[H^{*}]_{r}$/det [H]. Based on Eqs. (10)–(13), we can write

$$\begin{aligned}&\displaystyle \frac{\left( H_{12} ^{*}\right) _r }{H_{12} }=\frac{1}{1-\sigma }\left( {1-\sigma \frac{\left( H_{22} ^{*}\right) _r }{H_{22} }} \right) \end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \frac{\det [H^{*}]}{\det [H]}=\alpha _1 \left( {\alpha _2 +\alpha _3 \frac{\left( H_{22} ^{*}\right) _r }{H_{22} }} \right) \end{aligned}$$

(15)

where $\alpha _{1} = [\omega + \bar{{C}}\,L_{p} \sigma (1- \sigma )^{2}]^{-1}, \alpha _{2}=\bar{{C}}\,L_{p}(1- \sigma ), \alpha _{3} = \omega - \bar{{C}}\,L_{p} \sigma (1- \sigma )$.

It can be assumed that a value of diffusion coefficient $(D_{A})$ under diffusive conditions is constant and independent of $\bar{{C}}$. The thickness of concentration boundary layer under diffusive conditions ($\delta _{A}$ and $\delta _{B}$ for $\bar{{C}} < \bar{{C}}_\mathrm{{cr}} )$ is different than under diffusive–convective conditions ($\delta _{B}$ for $\bar{{C}}\ge \bar{{C}}_\mathrm{{cr}} )$ and is dependent on $\bar{{C}}$ (Ślęzak et al. 2010).

The diffusion coefficient for the convection–diffusion conditions ($D_{B})$ is dependent on the concentration of the solutions (Ślęzak et al. 2010). In order to calculate coefficient $D_{B}$ we transform Eq. (14) into

$$\begin{aligned} D_B ^{2}+a_1 D_B +a_2 =0 \end{aligned}$$

(16)

where $a_{1 }= 2 RT \omega \delta _{B}, a_{2 }= - gRT \omega \delta _{B}^{4}\alpha _{C}(C_{h }- C_{l})(R_{C} \nu )^{-1}$.

3 Results and Discussion

In our previous papers (Ślęzak et al. 2012a, b; Batko et al. 2014a, b, 2015) we used the coefficients of concentration polarization ($\zeta _{p}, \zeta _{v}, \zeta _{s}$ and $\zeta _{a})$ and membrane transport parameters ($L_{p}$, $\sigma$, $\omega$) to calculate the matrices [$R^{*}$], [$L^{*}$] and [$P^{*}$]. The coefficients of concentration polarization and membrane transport parameters are contained in the Kedem–Katchalsky formalism. The procedure used to determine the coefficients $\zeta _{p}, \zeta _{v}, \zeta _{s}$ and $\zeta _{a }$ was also described in the previous paper (Ślęzak et al. 2010). In the present paper we used these coefficients and parameters to calculate the coefficients $H_{11}^{*}, H_{12}^{*}, H_{21}^{*}$ and $H_{22}^{*}$ in the matrix $[H^{*}]$. In the previous paper (Ślęzak et al. 2010) we showed that only coefficients $(\zeta _{v})_{r }$ and $(\zeta _{s})_{r} (r =A, B)$ depended on the concentration of solutions and membrane system configuration. The value of $\zeta _{p }= \zeta _{a} = 1$ both for solution homogeneity and for concentration polarization, regardless of solution concentration and membrane system configurations (Ślęzak et al. 2010). To calculate $H_{12}^{*}$ and $H_{22}^{*}$, ratios $H_{12}^{*}/H_{12}$ and $H_{22}^{*}/H_{22}$, determinants det $[H^{*}]_{r}$, det [H] and ratio of the determinants det $[H^{*}]_{r}$/det [H], we used the following data (Ślęzak 1989): $L_{p }= (4.9 \pm 0.1) \times 10^{-12}\, \hbox {m}^{3}\,\hbox {N}^{-1}\,\hbox {s}^{-1}$, $\sigma = (6.8 \pm 0.1) \times 10^{-2}, \omega = (8.0 \pm 0.3) \times 10^{-10}\, \hbox {mol}\, \hbox {N}^{-1}\,\hbox {s}^{-1}, D_{A}=D_{d} = 0.69 \times 10^{-9}\, \hbox {m}^{2}\hbox {s}^{-1}$, $(T = 295 \pm 0.2)$ K, $R = 8.31\, \hbox {J}\, \hbox {mol}^{-1}\,\hbox {K}^{-1}$ and values of dependencies $\delta _{r }=f(\bar{{C}})$ and $\zeta _{r }=f(\bar{{C}})\;(r =A, B)$ presented in Table 1. To calculate the coefficient $D_{B}$, we used dependence $\delta _{B }= f(\bar{{C}})$ presented in Table 1 and $g = 9.81\, \hbox {m} \,\hbox {s}^{-2}, \alpha _{C} = 6.01 \times 10^{-5}\, \hbox {m}^{3}\, \hbox {mol}^{-1},\nu = 1.012 \times 10^{-6}\, \hbox {m}^{2}\,\hbox {s}^{-1}$.

Table 1 Values of the concentration polarization coefficient ($\zeta _{i})$ and thicknesses of concentration boundary layers ($\delta _{i})$ in configurations A ($\zeta _{A}$, $\delta _{A})$ and B ($\zeta _{B}$, $\delta _{B})$ for mean concentrations of glucose ($\bar{{C}})$ (Ślęzak et al. 2010)

Calculations based on Eqs. (5) and (7) show that $H_{11}^{*}=H_{11 }= 2 \times 10^{11}\, \hbox {Ns} \,\hbox {m}^{-3}$ are independent of both concentration of solutions and the configuration of the membrane system. Therefore, the values of these coefficients are identical, in condition of both homogeneity and concentration polarization of solutions separated by the membrane $(H_{11}^{*} / H_{11} = 1$).

Dependencies of coefficients $(H_{12}^{*})_{r}=f(\bar{{C}})$, $(H_{21}^{*})_{r}=f(\bar{{C}})$ and $(H_{22}^{*})_{r}=f(\bar{{C}})$ on the average concentration $\bar{{C}}$ and configuration of the membrane system are shown in Figs. 2, 3 and 4. Figure 2 shows that values of coefficients $H_{12}$, $(H_{12}^{*})_{A}$ and $(H_{12}^{*})_{B}$ decrease almost linearly with the increase in average concentration $\bar{{C}}$ and these coefficients fulfill the following condition $H_{12 }> (H_{12}^{*})_{B}> (H_{12}^{*})_{A }< 0$. Only for $\bar{{C}}\le 5.41\, \hbox {mol} \,\hbox {m}^{-3 }(H_{12}^{*})_{B }= (H_{12}^{*})_{A}$. For coefficient $(H_{12}^{*})_{r}$ and $\bar{{C}} > 5.41 \,\hbox {mol}\, \hbox {m}^{-3}$, the difference $\Delta H_{12 }= (H_{12}^{*})_{B }- (H_{12}^{*})_{A} < 0$ is a measure of natural convection effect. This expression can also be written as $\Delta H_{12}^{*}=\bar{{C}}\sigma (\zeta _{B }$- $\zeta _{A})$. Figure 3 shows that values of coefficients $H_{21 }$ and $(H_{21}^{*})_{r}$ increase linearly with increase of $\bar{{C}}$ and that $H_{21 }= (H_{21}^{*})_{r}> 0$. This indicates that the values of these coefficients are independent of the membrane system configuration or conditions under which they were appointed, i.e., $(H_{21}^{*})_{r}/ H_{21} = 1$.

Fig. 2

Graphic illustration of dependences $H_{12}=f(\bar{{C}})$ (graph 1), $(H_{12}^{*})_{A}=f(\bar{{C}})$ (graph 2) and $(H_{12}^{*})_{B}=f(\bar{{C}})$ (graph 3) calculated based on Eq. (5) for aqueous glucose solutions in an homogeneity solution conditions (graph 1), diffusive condition (graph 2) and diffusive–convective condition (graph 3). Line 4 represents the dependence $\Delta H_{12}^{*} =(H_{12}^{*})_{B}-(H_{12}^{*})_{A}=f(\bar{{C}})$ for convection effect

Fig. 3

Graphic illustration of dependence $(H_{21}^{*})_{r (r=A, B)}=H_{21 }=f(\bar{{C}})$ calculated based on Eq. (5) for aqueous glucose solutions in concentration polarization conditions and homogeneity solution conditions

Fig. 4

Graphic illustration of dependence $H_{22}=f(\bar{{C}})$ (line 1), $(H_{22}^{*})_{A}=f(\bar{{C}})$ (curve 2), $(H_{22}^{*})_{B}=f(\bar{{C}})$ (curve 3) calculated based on Eq. (5) for aqueous glucose solutions in a homogeneity solution conditions (line 1), diffusive condition (curve 2) and diffusive–convective condition (curve 3). Curve 4 represents the dependence $\Delta H_{22}^{*} =(H_{22}^{*})_{B}-(H_{22}^{*})_{A}=f(\bar{{C}})$ for convection effect

Graph 1 in Fig. 4 shows that dependence $(H_{22}^{*})_{r }=f(\bar{{C}})$ obtained for the conditions of homogeneity of solutions separated by the membrane is linear. Dependence $(H_{22}^{*})_{A}=f(\bar{{C}})$ obtained for diffusive conditions (curve 2) and dependence $(H_{22}^{*})_{B}=f(\bar{{C}})$ obtained for diffusive–convective conditions (curve 3) show that the coefficients $(H_{22}^{*})_{A}$ and $(H_{22}^{*})_{B}$ are nonlinearly dependent on the average concentration $\bar{{C}}$ and fulfill the condition $(H_{22}^{*})_{A} < (H_{22}^{*})_{B} < H_{22}$. For $\bar{{C}}\le 5.41\, \hbox {mol} \,\hbox {m}^{-3}$, $(H_{22}^{*})_{A }= (H_{22}^{*})_{B}$ and for $\bar{{C}} > 5.41 \,\hbox {mol} \,\hbox {m}^{-3}$, $(H_{22}^{*})_{B} > (H_{22}^{*})_{A}$. The difference $\Delta H_{22}^{*}= (H_{22}^{*})_{B }- (H_{22}^{*})_{A}$ is a measure of natural convection effect for coefficient $H_{22}^{*}$. For graph 4 presented in Fig. 4 we obtain: $\Delta H_{22}^{*}= 0$ (for $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3})$ and $\Delta H_{22}^{*}> 0$ (for $\bar{{C}} > 5.41 \,\hbox {mol} \,\hbox {m}^{-3})$. The expression for $\Delta H_{22}^{*}$ can also be written in the following form $\Delta H_{22}^{*}=\bar{{C}}\omega (\zeta _{B }- \zeta _{A})$.

In Fig. 5 different versions of dependence det $[H^{*}]_{r}=f(\bar{{C}})$ are presented. For the solution homogeneity conditions, this dependence can be described as det $[H] = f(\bar{{C}})$ illustrated in graph 1. Graph 2 obtained for diffusive conditions illustrates the dependence det $[H^{*}]_{A}=f(\bar{{C}})$, and graph 3 obtained for the diffusive–convective conditions illustrates dependence det $[H^{*}]_{B }=f(\bar{{C}})$. Comparison of graphs 2 and 3 results in det $[H^{*}]_{B} = \hbox {det} [H^{*}]_{A}$ (for $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3})$ and det $[H^{*}]_{B} > \hbox {det} [H^{*}]_{A}$ (for $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3})$. Furthermore, the difference $\Delta$(det $[H^{*}]) = \hbox {det} [H^{*}]_{B} - \hbox {det} [H^{*}]_{A}=\bar{{C}}(\zeta _{B }- \zeta _{A})[ \omega L_{p}^{-1} - \bar{{C}}\sigma (1- \sigma )]$ defines the natural convection effect for det $[H_{22}^{*}]_{r}$ (curve 4).

Fig. 5

Graphic illustration of dependence det $[H] = f(\bar{{C}})$ (line 1), det $[H^{*}]_{A}=f(\bar{{C}})$ (curve 2) and det $[H^{*}]_{B}=f(\bar{{C}})$ (curve 3) calculated based on Eq. (6) for aqueous glucose solutions in homogeneity solution conditions (line 1) and concentration polarization conditions: diffusive condition (curve 2) and diffusive–convective condition (curve 3). Curve 4 represents the dependence $\Delta$(det $[H^{*}]) =\hbox {det} [H^{*}]_{B}- \hbox {det} [H^{*}]_{A}=f(\bar{{C}})$ for convection effect

Figure 6 shows a dependence $D_{B }=f(\bar{{C}})$ obtained from solution of Eq. (16). From the curve shown in this figure it results that for $6.57 \,\hbox {mol} \,\hbox {m}^{-3} < \bar{{C}}\le 9.32 \,\hbox {mol} \,\hbox {m}^{-3}$, the value $D_{B }< D_{A}$ and that for $\bar{{C}}> 9.32 \,\hbox {mol} \,\hbox {m}^{-3} D_{B}$ increases linearly with the increase of $\bar{{C}}$. In configuration B for $\bar{{C}}\ge \bar{{C}}_\mathrm{{cr}} , D_{B }=D_{d }+D_{dk}$ and $D_{dk }> D_{d}$. Therefore, $D_{dk}/D_{d }=D_{B}/D_{A}- 1$. It can be shown that for $\bar{{C}}> 9.32 \,\hbox {mol} \,\hbox {m}^{-3} D_{dk}/D_{d }> 0$ and increases with the increase of $\bar{{C}}$ and for $\bar{{C}}= 21.67$, $D_{dk}/D_{d} = 2.84$.

Fig. 6

Graphic illustration of dependence $D_{B}=f(\bar{{C}})$ calculated based on Eq. (15) for aqueous glucose solutions in configuration B of a single-membrane system (diffusive–convective condition)

Figure 7 is a graphical illustration of dependence $(H_{12}^{*})_{r}/H_{12 }= f(\bar{{C}})$ for the conditions of diffusion (curves 1 and $1'$) and a diffusion–convection (curves 2 and $2'$). Curve 1 presents the solution of Eq. (11), and the curve $1'$ presents solution of Eq. (11) considering the Eq. (9). The curves 2 and $2'$ illustrate the results of calculations carried out based on Eq. (11) considering the Eq. (9) and results of calculations $D_{B }=f(\bar{{C}})$ performed based on Eq. (16). The course of the curves presented in the Fig. 7 shows that for $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3 }(H_{12}^{*})_{A}/H_{12} = (H_{12}^{*})_{B}/H_{12} = 1.06$ and for the $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3 }(H_{12}^{*})_{A}/H_{12} > (H_{12}^{*})_{B}/H_{12}$.

Fig. 7

Graphic illustration of dependence $(H_{12}^{*})_{A}/H_{12}=f(\bar{{C}})$ (curves 1, 1 $'$) (curves 1 and 1 $'$) and $(H_{12}^{*})_{B}/H_{12}=f(\bar{{C}})$ (curves 2 and 2 $'$) for the configuration A and B of the membrane system, respectively. Curves 1 and 2 were calculated based on Eq. (11), whereas curves 1 $'$ and 2 $'$ based on Eqs. 11) and (15). The courses of curves 2 and 2 $'$ are located within 0.2 % error range

Figure 8 is a graphical illustration of dependence $(H_{22}^{*})_{r}/H_{22 }= f(\bar{{C}})$ for the conditions of diffusion (curves 1 and $1'$) and a diffusion–convection (curves 2 and $2'$). Curve 1 shows the results of calculations performed based on Eq. (13) and the curve $1'$ based on Eq. (13) considering the Eq. (9). Curves 2 and $2'$ illustrate the results of calculations performed based on Eqs. (13) and (9) considering the results of calculations $D_{B}=f(\bar{{C}})$ performed based on Eq. (16). The course of the curves presented in Fig. 8 indicates that for $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3 }(H_{22}^{*})_{A}/H_{22} = (H_{22}^{*})_{B}/H_{22} = 0.21$ and for $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3 }(H_{22}^{*})_{B}/H_{22} > (H_{22}^{*})_{A}/H_{22}$.

Fig. 8

Graphic illustration of dependence $(H_{22}^{*})_{A}/H_{22}=f(\bar{{C}})$ (graph 1 and 1 $'$) and $(H_{22}^{*})_{B}/H_{22}=f(\bar{{C}})$ (graph 2 and 2 $'$) for the configuration A and B of the membrane system, respectively. Curves 1 and 2 were calculated based on Eq. (13), whereas curves 1 $'$ and 2 $'$ based on Eqs. (13) and (15). The courses of curves 2 and 2 $'$ are located within the 5 % error range

Figure 9 shows graphical dependencies det $[H^{*}]_{r}$/det $[H]= f(\bar{{C}})$ for the diffusive conditions (curves 1 and $1'$) and the diffusive–convective conditions (curves 2 and $2'$). Curve 1 and curve $1'$ represent the results of calculations performed based on Eqs. (13) and (13a), respectively. The curves 2 and $2'$ illustrate the results of calculations performed based on Eqs. (13) and (13a), considering the results of calculations $D_{B }=f(\bar{{C}})$ that were based on Eq. (16). The courses of the curves presented in the figure show that for $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3 }$det $[H^{*}]_{A}$/det $[H] = \hbox {det} [H^{*}]_{B}/\hbox {det} [H] = 0.23$ and for the $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3}\;\hbox {det} [H^{*}]_{B}/\hbox {det} [H] > \det [H^{*}]_{A}/\det [H]$.

Fig. 9

Graphic illustration of dependences det $\{[H^{*}]_{A}/[H]\} = f(\bar{{C}})$ (curves 1 and $1'$) and det $\{[H^{*}]_{B}/[H]\}$ (curves 2 and $2'$) for the configuration A and B of the membrane system, respectively. Curves 1 and 2 were calculated based on Eq. (14), whereas curves $1'$ and $2'$ based on Eqs. (14) and (15). The courses of curves 2 and $2'$ are located within the 5 % error range

Similar to pairs of coefficients $L_{ij}$ and $L_{ij}^{*}, R_{ij}$ and $R_{ij}^{*}, P_{ij}$ and $P_{ij}^{*}$, ($i, j \in \{1, 2\})$ with the same indices, for pair of Peusner’s coefficients $H_{ij}$ and $H_{ij}^{*}$, units are the same and values are different. Comparing diagonal and non-diagonal coefficients of matrix $[H^{*}]$ with different indices, units are different and values differ by over tenfold. Similarly to $L_{ij}^{*}/L_{ij}, R_{ij}^{*}/R_{ij}$ and $P_{ij}^{*}/P_{ij}$ ratios, $H_{ij}^{*}/H_{ij}$, ratio is dimensionless and its values have the same order of magnitude at least for a Nephrophan membrane and water glucose solutions. This facilitates analysis of the results obtained under conditions of concentration polarization or homogeneity of solutions. Calculation of det $[\hbox {H}^{*}]/[H]$ allows to reduce the number of Peusner’s coefficients needed to characterize transport properties of the membrane.

Considering the Eqs. (10)–(13) and the results obtained in previous papers (Ślęzak et al. 2012a, b; Batko et al. 2014a, b, 2015) we can write

$$\begin{aligned}&\displaystyle \frac{\left( H_{11} ^{*}\right) _r }{H_{11} }=\frac{\left( L_{11} ^{*}\right) _r }{L_{11} }=\frac{\left( H_{21} ^{*}\right) _r }{H_{21} }=\frac{\left( L_{21} ^{*}\right) _r }{L_{21} }=1 \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \frac{\left( H_{12} ^{*}\right) _r }{H_{12} }=\frac{\left( L_{12} ^{*}\right) _r }{L_{12} }=\zeta _r \frac{\left( R_{12} ^{*}\right) _r }{R_{12} }=\frac{[\zeta _r \omega +\beta _1 (1-\zeta _r \sigma )]}{L_p \beta _2 }\frac{\left( P_{12} ^{*}\right) _r }{P_{12} } \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle \frac{\left( H_{22} ^{*}\right) _r }{H_{22} }=\frac{R_{22} }{\left( R_{22} ^{*}\right) _r }=\beta _3 \left( {\beta _2 \frac{\left( L_{22} ^{*}\right) _r }{L_{22} }-\beta _1 } \right) =\beta _3 \left( {\beta _2 \frac{P_{22} }{\left( P_{22} ^{*}\right) _r }-\beta _1 } \right) \end{aligned}$$

(19)

$$\begin{aligned}&\displaystyle \det \left( {\frac{[H^{*}]}{[H]}} \right) =\det \left( {\frac{[P]}{[P^{*}]}} \right) =\beta _2 \left[ {\beta _1 +\beta _3 \det \left( {\frac{[L^{*}]}{[L]}} \right) } \right] =\beta _2 \left[ {\beta _1 +\beta _3 \det \left( {\frac{[R^{*}]}{[R]}} \right) } \right] \nonumber \\ \end{aligned}$$

(20)

where $\beta _{1}=\bar{{C}}L_{p}(1- \sigma$), $\beta _{2} = \omega$ + $\bar{{C}}L_{p}(1- \sigma )^{2},\beta _{3} = [\omega - \bar{{C}}L_{p} \sigma (1- \sigma )]^{-1}$.

To show the dependence between the configurations B and A of the membrane system we calculate the respective quotients of coefficients $H_{11}^{*}$,$H_{12}^{*}, H_{21}^{*}, H_{22}^{*}$ and det $[H^{*}]$ for configurations B and A of the membrane system following the expressions written below:

$$\begin{aligned}&\displaystyle \kappa _{ij} =\frac{\left( H_{ij} ^{*}\right) _B }{\left( H_{ij} ^{*}\right) _A }, \quad i, j = 1, 2 \end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle \kappa _{\det } =\frac{\det [H^{*}]_B }{\det [H^{*}]_A } \end{aligned}$$

(22)

Considering above equations, Eqs. (5) and (9) with the use of relatively simple algebraic operation, we obtain

$$\begin{aligned} \kappa _{12}&=\frac{\left( H_{12} ^{*}\right) _B }{\left( H_{12} ^{*}\right) _A }=\frac{1-\zeta _B (\bar{{C}})}{1-\zeta _A (\bar{{C}})} \end{aligned}$$

(23)

$$\begin{aligned} \kappa _{22}= & {} \frac{\left( H_{22} ^{*}\right) _B }{\left( H_{22} ^{*}\right) _A }=\frac{\zeta _B (\bar{{C}})}{\zeta _A (\bar{{C}})}=\frac{1-\kappa _{12} [1-\zeta _A (\bar{{C}})]}{\zeta _A (\bar{{C}})} \end{aligned}$$

(24)

$$\begin{aligned} \kappa _{\det }= & {} \frac{\zeta _B (\bar{{C}})\omega +\bar{{C}}L_p [1-\zeta _B (\bar{{C}})\sigma ](1-\sigma )}{\zeta _A (\bar{{C}})\omega +\bar{{C}}L_p [(1-\zeta _A (\bar{{C}})\sigma ](1-\sigma )} \end{aligned}$$

(25)

where $\zeta _{B}(\bar{{C}})=D_{B}(\bar{{C}})[D_{B}(\bar{{C}})+2 RT \omega \delta _{B}(\bar{{C}})]^{-1}$, $\zeta _{A}(\bar{{C}})=D_{A}(\bar{{C}})[D_{A}(\bar{{C}})+2 RT \omega \delta _{A}(\bar{{C}})]^{-1}$.

Calculations show that $\kappa _{11 }= \kappa _{12} = 1$. In Fig. 10 curves 1, $1'$, 2, $2'$, 3 and $3'$ illustrate the dependence $\kappa _{12 }=f(\bar{{C}})$, $\kappa _{22 }=f(\bar{{C}})$ and $\kappa _{\mathrm{det} }=f(\bar{{C}})$ calculated on the basis of Eqs. (23)–(25), considering the dependence $D_{B}=f(\bar{{C}})$ shown in Fig. 6 and $\delta _{A }= f(\bar{{C}})$ and $\delta _{B }= f(\bar{{C}})$ shown in Table 1.

Fig. 10

Graphic illustration of dependencies $\kappa _{12 }=(H_{12}^{*})_{B}/(H_{12}^{*})_{A}= f(\bar{{C}})$ (curves 1, 1 $'$), $\kappa _{22 }=(H_{22}^{*})_{B}/(H_{22}^{*})_{A}= f(\bar{{C}})$ (curves 2, 2 $'$) and $\kappa _{\mathrm{det} }$= det $[H^{*}]_{B}$/det [$H_{ij}^{*}]_{A}$ (curves 3 and 3 $'$), respectively. Curves 1 and 2 were calculated based on Eq. (17), curve 3 based on Eq. (18) and curves 1 $'$–3 $'$ based on Eqs. (19)–(21), respectively

From the Fig. 10 it results that coefficients $\kappa _{12}$, $\kappa _{22}$ and $\kappa _{\mathrm{det }}$ do not depend on the concentration of solutions separated by a membrane and membrane system configurations $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3}$. For this range of concentration their values are $\kappa _{12 }= \kappa _{22 }= \kappa _{\mathrm{det }}= 1$, similar to a value of the last common point of the curves 1, 2, 3 and 4. Similarly to the curves shown in the previous figures, the last common point with coordinates $\bar{{C}} =5.41\,\hbox {mol} \,\hbox {m}^{-3}$ and $\kappa _{12 }= \kappa _{22 }= \kappa _{\mathrm{det} }= 1$ may be considered as a bifurcation point. Only for $\bar{{C}} > 5.41\,\hbox {mol} \,\hbox {m}^{-3}, \kappa _{12}$ values are independent of the concentration of solutions separated by a membrane with accuracy to the second significant digit. A comparison of these characteristics shows that for the same value of $\bar{{C}}$ condition $\kappa _{22} > \kappa _{\mathrm{det}} >\kappa _{12}$ is satisfied.

To show the dependence between the states of diffusion–convection, diffusion and homogeneity, we define the coefficients $\chi _{12}$, $\chi _{22}$ and $\chi _{\mathrm{det}}$

$$\begin{aligned}&\displaystyle \chi _{12} =\frac{\left( H_{12} ^{*}\right) _B -\left( H_{12} ^{*}\right) _A }{H_{12} }=-\frac{\sigma }{1-\sigma }[\zeta _B (\bar{{C}})-\zeta _A (\bar{{C}})] \end{aligned}$$

(26)

$$\begin{aligned}&\displaystyle \chi _{22} =\frac{\left( H_{22} ^{*}\right) _B -\left( H_{22} ^{*}\right) _A }{H_{22} }=\zeta _B (\bar{{C}})-\zeta _A (\bar{{C}}) \end{aligned}$$

(27)

$$\begin{aligned}&\displaystyle \chi _{\det } =\frac{\det [H^{*}]_B -\det [H^{*}]_A }{\det [H]}=\frac{[\zeta _B (\bar{{C}})-\zeta _A (\bar{{C}})][\omega -\bar{{C}}L_p \sigma (1-\sigma )]}{\omega +\bar{{C}}L_p (1-\sigma )^{2}} \end{aligned}$$

(28)

where $\zeta _{B}(\bar{{C}})=D_{B}(\bar{{C}})[D_{B}(\bar{{C}}) + 2 RT\omega \delta _{B}(\bar{{C}})]^{-1}$, $\zeta _{A}(\bar{{C}})=D_{A}(\bar{{C}})[D_{A}(\bar{{C}}) + 2 RT \omega \delta _{A}(\bar{{C}})]^{-1}$.

Fig. 11

Graphic illustration of dependences $\chi _{12 }=\{(H_{12}^{*})_{B} - (H_{12}^{*})_{A}\}/H_{12 }= f(\bar{{C}})$ (curve 1, 1 $'$), $\chi _{22 }=\{(H_{22}^{*})_{B} - (H_{22}^{*})_{A}\}/H_{22 }= f(\bar{{C}})$ (curve 2, 2 $'$) and $\chi _{\mathrm{det}}=\{\hbox {det} [H^{*}]_{B} - \hbox {det} [H^{*}]_{A}\}/\hbox {det} [H]= f(\bar{{C}})$ (curve 3, 3 $'$). Curves 1–3 and 1 $'$–3 $'$ were calculated based on Eqs. (22)–(24), respectively

In Fig. 11, curves 1, $1'$, 2, $2'$, 3 and $3'$ illustrate the dependence $\chi _{12 }=f(\bar{{C}})$, $\chi _{22 }=f(\bar{{C}})$ and $\chi _{\mathrm{det} }=f(\bar{{C}})$ calculated based on Eqs. (26)–(28) considering dependences $D_{B}=f(\bar{{C}})$ shown in Fig. 6 and dependence $\delta _{A }=f(\bar{{C}})$ and $\delta _{B }=f(\bar{{C}})$ shown in Table 1. The results of calculations are shown in Figs. 2, 3, 4 and 5. The courses of the curves presented in this figure show that for $\bar{{C}} \le 5.41\,\hbox {mol} \,\hbox {m}^{-3 }$ the relation $\chi _{12} = \chi _{22 }= \chi _{\mathrm{det}} = 0$ is satisfied. For $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3 }$ dependences $\chi _{22} >\chi _{\mathrm{det}} >\chi _{12}$, $\chi _{12} < 0, 0 < \chi _{22} < 0.5$ and $0 < \chi _{\mathrm{det}} < 0.5$ are fulfilled. Moreover, this figure shows that curves 1 and $1'$ nearly overlap and the curves 2 and $2'$ and 3 and $3'$ are located within the 5 % error range. Moreover, curves 2, $2'$, 3 and $3'$ are located within the 15 % error range. Comparing Eqs. (26)–(28) it may be noticed that

$$\begin{aligned} \chi _{12}= & {} -\frac{\sigma }{1-\sigma }\chi _{22} \end{aligned}$$

(29)

$$\begin{aligned} \chi _{\det }= & {} \frac{\omega -\bar{{C}}L_p \sigma (1-\sigma )}{\omega +\bar{{C}}L_p (1-\sigma )^{2}}\chi _{22} \end{aligned}$$

(30)

The values of $(H_{ij}^{*})_{r}$ ($r = A$ or B) were compared to the values of coefficients $H_{ij}$ (for homogeneity solution conditions). Calculations show that $H_{11 }=H_{11}^{*}$ = const. For $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3 }$ condition $(H_{12}^{*})_{\mathrm{A}} <(H_{12}^{*})_{\mathrm{B}} < H_{12}< 0$ is fulfilled and the coefficients $(H_{12}^{*})_{\mathrm{B}}$, $(H_{12}^{*})_{\mathrm{A}}$, and $H_{12}$ are approximately linearly dependent on $\bar{{C}}$. Values of the coefficient $H_{21 }=H_{21}^{*}$ are positive and linearly dependent on $\bar{{C}}$. For $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3}$ condition $(H_{22}^{*})_{\mathrm{A}} < (H_{22}^{*})_{\mathrm{B}}< H_{22 }> 0$ is fulfilled and the coefficients $(H_{22}^{*})_{\mathrm{A}}, (H_{22}^{*})_{\mathrm{B}}, H_{22}$, and $H_{12}$ are nonlinearly dependent on $\bar{{C}}$ and dependent on the membrane system configuration. In addition, coefficients that facilitate interpretation of the calculations results are defined using various differences and ratios of coefficients $(H_{ij}^{*})_{\mathrm{r}}$ and $H_{ij}$, with the same indicators for the A and B configurations of the membrane system. It is also shown that there is a threshold value of $\bar{{C}}$, above which the ratios $(H_{12}^{*})_{\mathrm{r}}/H_{12}$ and $(H_{22}^{*})_{\mathrm{r}}/H_{22}$ are dependent both on $\bar{{C}}$ and the configuration of the membrane system.

The evolution of thermodynamic systems can be described using dependences $\varphi = f(\lambda )$, where $\varphi$ is the order parameter and $\lambda$ is the critical parameter (Kondepudi 2008). In the case investigated in the paper, the concentration $\bar{{C}}$ may be a control parameter that may be used to determine distance of the system from equilibrium. If $\bar{{C}}$ increases, the system recedes from equilibrium and in the point where $\bar{{C}}=\bar{{C}}_\mathrm{{cr}}$ reaches the threshold of thermodynamic branch stability at the bifurcation point. At or near the equilibrium state ($\bar{{C}} = 0$) (in the configuration A and in configuration B for $\bar{{C}} < \bar{{C}}_\mathrm{{cr}} )$ steady state is gravitationally stable, since the influence of the gravitational field on the membrane transport is negligible. Starting at this point, the thermodynamic branch becomes unstable due to concentration (density) fluctuations and the increasing difference in concentrations causes a stationary non-equilibrium state, to which the system heads spontaneously. This state may be more complex than the corresponding equilibrium state. Dworecki et al. (1995, 2005), used laser interferometry to show that interference fringes are regular and its curvature is present only in the CBL areas in this condition. If we gradually increase value $\bar{{C}}$ for $\bar{{C}} > \bar{{C}}_\mathrm{{cr}}$, then in the non-equilibrium state the layer system loses stability as evidenced by convection flows. Therefore, interference fringes are irregular (Dworecki et al. 2005). This means that in the absence of the gravitational field ($g = 0$) or under conditions where the two solutions separated by a membrane are homogeneous solutions (thoroughly mixed by mechanical stirrers serve as idealization of this state) configurations A and B of membrane system are equivalent. In contrast, the CBL system is not sensitive to change in the direction of constant gravitational field after changing from A to B configuration (in concentration range $\bar{{C}} < \bar{{C}}_\mathrm{{cr}})$, and then the CBL system is equally probable. Consideration of the influence of the gravitational field ($g \ne$ 0) changes the bifurcation diagram from symmetrical to asymmetrical (Kondepudi and Prigogine 1981). From interferometric research it results that in the concentrations range $\bar{{C}} > \bar{{C}}_\mathrm{{cr}}$, CBL system in configuration B is sensitive to the influence of constant gravitational field. In conditions that are distant from equilibrium and for membrane with regular, square pores, solutions located above and below the membrane form dendritic spatial structure called “plum structure” for the concentration Rayleigh number that is in the following range $(10^{10 }\le R_{C }\le 10^{11})$ (Puthenveettil and Arakeri 2008). This “plum structure” can be considered as a dissipative structure, since it is formed under conditions far from equilibrium. This suggests that the role of the order parameter could be played by coefficients $\kappa _{12}, \kappa _{22}, \kappa _{\mathrm{det}}, \chi _{12}, \chi _{22 }$ and $\chi _{\mathrm{det}}$.

Peusner’s Network Thermodynamics (PNT) allows transformation of a symmetric or hybrid membrane transport equations for homogeneous and non-homogeneous binary non-electrolyte solutions. Peusner’s procedure enables the transformation of classical Kedem–Katchalsky equations to alternative forms L, R, P or H (for homogeneous solutions), and $L^{*}, R^{*}, P^{*}$ or $H^{*}$ (for non-homogeneous solutions) of Kedem–Katchalsky equations, by replacing $\Delta P$ on $\Delta P-\Delta \pi$ and $\Delta \pi$ on $\Delta \pi /\bar{{C}}$ =RT ln ($C_{h}/C_{l})$.

For L, R, P and H Kedem–Katchalsky equations, these transformations provide network forms of these equations with new types of coefficients: $L_{ij}$,$R_{ij}, P_{ij}$ or $H_{ij}$ ($i, j \in \{1, 2\}$). Each coefficient can be a combination of practical coefficients, i.e., the hydraulic permeability ($L_{p})$, the solute permeability ($\omega$) and the reflection ($\sigma$) coefficients, and average concentration ($\bar{{C}})$, occurring in the classical Kedem–Katchalsky equations. For Nephrophan membrane it can be assumed that coefficients $L_{p}$, $\sigma$ and $\omega$ are constant (Ślęzak 1989).

Similarly, for $L^{*}, R^{*}, P^{*}$ and $H^{*}$ Kedem–Katchalsky equations, these transformations provide network forms of these equations with new types of coefficients: $L_{ij}^{*}, R_{ij}^{*}, P_{ij}^{*}$ or $H_{ij}^{*}$ ($i, j \in \{1, 2\}$). Each coefficient can be a combination of practical coefficients, i.e., the hydraulic permeability ($L_{p})$, the solute permeability ($\omega$) and the reflection ($\sigma$) coefficients, average concentration ($\bar{{C}})$ and Katchalsky’s coefficients: hydraulic ($\zeta _{p})$, osmotic ($\zeta _{v})$, advective ($\zeta _{a})$ and diffusive ($\zeta _{s})$ occurring in the classical Kedem–Katchalsky equations . The coefficients $L_{ij}^{*},R_{ij}^{*}, P_{ij}^{*}$ or $H_{ij}^{*}$ ($i, j \in \{1, 2\}$) may be calculated based on the experimentally determined coefficients $L_{p}$, $\sigma$, $\omega$, $\zeta _{p}$, $\zeta _{v}$, $\zeta _{a}$ and $\zeta _{s}$. The results of calculations presented in current and previous papers (Ślęzak et al. 2012a, b; Batko et al. 2014a, b, 2015) show that the values of coefficients $R_{ij}^{*}, L_{ij}^{*}, P_{ij}^{*}$ and $H_{ij}^{*}$ ($i, j \in \{1, 2\}$) are sensitive to the concentration of the solutions separated by a membrane and the order of arrangement of solutions relative to the direction of gravity acceleration. The network forms of K–K equations containing Peusner’s coefficients $R_{ij}^{*}, L_{ij}^{*}, P_{ij}^{*}$ and $H_{ij}^{*}$ ($i, j \in \{1, 2\}$) may be used as a new tool to study membrane transport.

4 Conclusions

• 1. The paper presents a hybrid matrix form of Kedem–Katchalsky equations that contain coefficients $H_{ij}^{*}$ (i, j = 1, 2) for the conditions of concentration polarization. The obtained equations were applied to the interpretation of transport of the aqueous glucose solutions with concentrations $C_{h}$ and $C_{l}$ ($C_{h} > C_{l})$ through the Nephrophan membrane that was oriented in the horizontal plane. The calculations of coefficients $H_{ij}^{*}$ were made for the A and B configurations of the membrane system. In the A configuration glucose solution with concentration $C_{h}$ was located below the membrane and the solution with concentration $C_{l}$ above the membrane. In configuration B locations of the solutions were reversed. The values of $(H_{ij}^{*})_{r}$ ($r = A$ or B) were compared to the values of coefficients $H_{ij}$ (for homogeneity solution conditions). Calculations show that $H_{11 }=H_{11}^{*}$ = const.

• 2. Based on the presented study, we can conclude that PNT is an alternative manner of description of membrane transport both for homogeneity of solutions separated by a membrane and in conditions of concentration polarization.

• 3. There is a threshold value of concentration $\bar{{C}}$, above which the values of coefficients $H_{12}^{*}$and $H_{22}^{*}$ are dependent on the configuration of the membrane system and the values of these coefficients in the convective state are greater than their values in non-convective state.

• 4. Coefficient $H_{11}^{*}$ has constant values, i.e., independent of the concentration of solutions separated by a membrane and the membrane system configurations. The coefficients $H_{12}^{*}, H_{21}^{*}$ and $H_{22}^{*}$ are linearly $(H_{21}^{*})$ or nonlinearly $(H_{12}^{*}, H_{22}^{*})$ dependent on the solution concentration. For $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3 }$ condition $(H_{12}^{*})_{B} < (H_{12}^{*})_{\mathrm{A}} < H_{12}< 0$ is fulfilled and the coefficients $(H_{12}^{*})_{\mathrm{B}}, (H_{12}^{*})_{\mathrm{A}}$, and $H_{12}$ are approximately linearly dependent on $\bar{{C}}$. Values of the coefficient $H_{21 }=H_{21}^{*}$ are positive and linearly dependent on $\bar{{C}}$. For $\bar{{C}} >5.41\,\hbox {mol} \,\hbox {m}^{-3}$ condition $(H_{22}^{*})_{\mathrm{A}} < (H_{22}^{*})_{\mathrm{B} }< H_{22 }> 0$ is fulfilled and the coefficients $(H_{22}^{*})_{\mathrm{A}}$, $(H_{22}^{*})_{\mathrm{B}}, H_{22}$, and $H_{12}$ are nonlinearly dependent on $\bar{{C}}$ and dependent on the membrane system configuration.

• 5. Nonlinearity of characteristics $H_{12}^{*}=f(\bar{{C}})$ and $H_{22}^{*}=f(\bar{{C}})$ is a result of competition between spontaneously occurring processes of diffusion and natural convection.