Closed paths in graphs vs. voting theory

Abstract

Features of graphs that hinder finding closed paths with particular properties, as represented by the Traveling Salesperson Problem—TSP, are identified for three classes of graphs. Removing these terms leads to a companion graph with identical closed path properties that is easier to analyze. A surprise is that these troubling graph factors are precisely what is needed to analyze certain voting methods, while the companion graph’s terms are what cause voting theory complexities as manifested by Arrow’s Theorem. This means that the seemingly separate goals of analyzing closed paths in graphs and analyzing voting methods are complementary: components of data terms that assist in one of these areas are the source of troubles in the other. Consequences for standard decision methods are in Sects. 2.5, 3.7 and the companion paper (Saari in Theory Decis 91(3):377–402, 2021). The emphasis here is on paths in graphs; incomplete graphs are similarly handled.

1 Introduction

Two challenging decision theory concerns in the social sciences are to find optimal paths in a weighted graph and to understand difficulties that arise with methods dependent on majority voting. Of surprise is how the approach developed here addresses both issues in a similar but complementary manner. The method is to identify and remove those aspects of the data that cause difficulties. What remains for graph theory, for instance, is a simpler, more easily analyzed companion graph (the sharpest possible) that retains all of the original graph’s closed path properties. These two themes are connected in that the theory for majority voting over pairs is complementary to finding the companion graphs. That is, the data portions that assist advances in one of these areas create problems in the other. Readers primarily interested in voting theory can treat the graph discussion as describing the structure of terms that complicate voting and decision theory, while those primarily interested in graph theory would have the opposite priority.

Beyond simplifying the analysis of these topics, eliminating the superfluous data components exposes what information a decision process actually uses; this introduces new tools to understand their many different applications. As a pairwise voting example, removing the unnecessary data parts reveals a new type of transitivity that uncovers mysteries from related topics and applications, and it can quickly identify weaknesses of several widely used decision techniques. In the same spirit knowing what data features are actually used to find paths in graphs partly explains the difficulties experienced by some path-finding algorithms. As currently being done with certain topics that rely on voting and path procedures, knowing what information truly is relevant for an application provides fresh insights about it.

Fig. 1

A graph and its companion

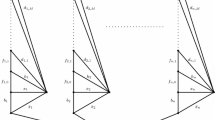
To illustrate the companion graph comment, associated with the undirected symmetric graph Fig. 1a is its companion (Fig. 1c) and a factor (Fig. 1b) of 66. The connection (Sect. 3) is that the length of any Fig. 1a Hamiltonian circuit (a connected closed path that passes through each vertex once) is the circuit’s Fig. 1c length plus 66. The simplicity of Fig. 1c makes it much easier to analyze; e.g., while it is not immediately obvious which Fig. 1a Hamiltonian path is the shortest, the greedy algorithm (GA; it selects the locally optimal available choice at each step) shows that Fig. 1c’s shortest Hamiltonian path is $V_1 {\mathop {\longrightarrow }\limits ^{-4}} V_2 {\mathop {\longrightarrow }\limits ^{-2}} V_4 {\mathop {\longrightarrow }\limits ^{0}} V_6 {\mathop {\longrightarrow }\limits ^{-4}} V_3 {\mathop {\longrightarrow }\limits ^{-2}} V_5 {\mathop {\longrightarrow }\limits ^{0}} V_1$ of length $-12$. This path, then, also is the shortest Fig. 1a Hamiltonian circuit but with length $66-12=54.$ The companion graphs are developed and explained in this paper. Decision and voting theory consequences of this structure are in Sects. 2.5, 3.7 and the associated paper (Saari, 2021).

Searching for optimal paths (e.g., shortest or longest) underscores the complexity of a graph’s path dependent structures. But the graph’s path-independent structure is what causes difficulties. This assertion is proved by decomposing a relevant space of graphs into a subspace where all paths are independent and its orthogonal complement where all paths are dependent. One class of graphs, for instance, is identified with the space of asymmetric paired comparisons. A “decision theory” decomposition (Saari, 2021) divides this space into a linear subspace¹ with a sufficiently strong form of transitivity to ensure path-independence and its normal bundle defined by a specific type of cycles.

Voting and decision methods seek transitive outcomes, so the cyclic components introduce complexities as manifested by Arrow’s Impossibility Theorem (Arrow, 1963; Saari, 2019). Projecting the data to the transitive subspace eliminates these difficulties and simplifies analyzing voting methods (Saari, 2021, Sect. 2.5). But cycles, not linear orders, are central for closed paths, so the path-independent components hinder the analysis. Orthogonally projecting the data to the cyclic subspace lowers the degrees of freedom (the number of relevant variables), removes trouble-causing terms, reveals what variables truly are responsible for a stated issue, uncovers the system’s inherent symmetries, and simplifies finding optimal paths. This decomposition resembles (and is motivated by) one for game theory (Jessie & Saari, 2019) where one component of a game has all (and only) information needed to find all pure and mixed Nash strategic properties, and another one has the information to capture coordination, cooperation, etc.

Three classes of graphs are examined. The first uses the differences from the average cost between vertices. The second and third are, respectively, the standard undirected symmetric and the directed asymmetric cost settings. Symmetry structures for these classes differ; e.g., the symmetries for the first type of graphs (Sect. 2.1, Theorem 2) are three-cycles where a A, B, C cycle’s costs of going from A to B, B to C, and C to A are identical. Symmetries for the standard symmetric case (Sect. 3) are a form of four-cycles. Symmetries for the asymmetric setting (Sect. 4) are the more complicated product of three and four cycles. Some sample features are derived to illustrate how these symmetries simplify finding and analyzing path properties. Most proofs are in Sect. 6.

2 Asymmetric excess costs

Reimbursing a salesperson for the average cost of traveling between cities creates an incentive for the salesperson to select routes with below average costs. For notation, it takes 30 min to walk from home, H, to campus, C; returning uphill requires 40 min, so the average is 35. The “excess cost function” registers differences from the average where $C {\mathop {\longrightarrow }\limits ^{5}} H \text { also denotes } H {\mathop {\longrightarrow }\limits ^{-5}} C.$ To connect this notation with N voter pairwise voting, let $C {\mathop {\longrightarrow }\limits ^{5}} H$ be where candidate C beats H with five votes above the average of $\frac{N}{2}$, while H loses to C with five votes below $\frac{N}{2}$.

Graphs in the space of asymmetric weighted, n-vertex graphs (no loops) that are considered in this section, $\mathbb {G}^n_A$, are complete (i.e., each pair of vertices is connected with paths) and

$$\begin{aligned} V_j {\mathop {\longrightarrow }\limits ^{x}} V_k \text { represents both } V_j {\mathop {\longrightarrow }\limits ^{x}} V_k \text { and }V_k {\mathop {\longrightarrow }\limits ^{-x}} V_j.\end{aligned}$$

(1)

Only an arc’s positive cost direction (in voting, this is who wins and by how much) need be represented because moving counter to an arrow identifies a “below average” cost (Eq. 1). So $V_2$ in Fig. 2a is a “source” (in voting theory, a Condorcet winner) because all positive value directions point away; it is a “sink” with the negative value directions. Conversely, $V_4$ is a sink (Condorcet loser) with positive value directions and a source for negative value directions. Subscripts A and S indicate, respectively, asymmetric and symmetric cases.

Fig. 2

Cyclic component; $\mathcal {G}^5_{A, cyclic}$

Figure 2 depicts the approach; graph $\mathcal {G}^5_A$ is uniquely decomposed into a “closed path independent” component $\mathcal {G}^5_{A, cpi}$ (Definition 1), which is central for analyzing voting methods, and a cyclic component $\mathcal {G}^5_{A, cyclic}$, which is $\mathcal {G}^5_A$’s simpler companion graph, to define $\mathcal {G}^5_A= \mathcal {G}^5_{A, cpi} + \mathcal {G}^5_{A, cyclic}.$ The goal is to decompose any n-vertex $\mathcal {G}^n_A \in \mathbb {G}^n_A$ into its path-independent and dependent terms

$$\begin{aligned} \mathcal {G}^n_A = \mathcal {G}^n_{A, cpi} + \mathcal {G}^n_{A, cyclic}.\end{aligned}$$

(2)

Definition 1

For $n\ge 3$, $\mathcal {G}^n_{A, cpi} \in \mathbb {G}^n_A$ is “closed path independent” (cpi) iff all closed paths have length zero. A graph is “strongly transitive” iff the path lengths of any triplet $\{V_i, V_j, V_k\}$ satisfy

$$\begin{aligned} V_i {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{y}} V_k = V_i {\mathop {\longrightarrow }\limits ^{z=x+y}} V_k.\end{aligned}$$

(3)

Both Eq. (3) paths start at $V_i$ and end at $V_k$, so the equality designates equal path lengths. “Strong transitivity” comes from voting and decision theory (Saari, 2021).

Theorem 1

A graph is strongly transitive iff it is cpi. Strongly transitive graphs (equivalently, cpi graphs) with n vertices define a $(n-1)$-dimensional linear subspace $\mathbb{S}\mathbb{T}_A^n \subset \mathbb {G}^n_A$.

To check that Fig. 2b is strongly transitive, select any triplet, say $\{V_1, V_3, V_5\},$ and determine whether this triangle’s leg lengths, $V_1 {\mathop {\longrightarrow }\limits ^{5}} V_3 {\mathop {\longrightarrow }\limits ^{3}} V_5$ and $V_1 {\mathop {\longrightarrow }\limits ^{8}} V_5$, satisfy the Eq. (3) triangle equality, which they do. This property ensures (Sect. 1) that the arc directions define the desired linear ordering for voting theory. For instance, identifying positive arc directions with “$\succ$” in Fig. 2b defines the transitive $V_1\succ V_2\succ V_3 \succ V_5\succ V_4$ ranking. To equate strong transitivity with cpi, reversing $V_1 {\mathop {\longrightarrow }\limits ^{8}} V_5$ defines the closed path $V_1 {\mathop {\longrightarrow }\limits ^{5}} V_3 {\mathop {\longrightarrow }\limits ^{3}} V_5 {\mathop {\longrightarrow }\limits ^{-8}} V_1$ with zero length.

While the proof of Theorem 1 is in Sect. 6, proving that $\mathbb{S}\mathbb{T}_A^n$ is a linear subspace is an exercise. For the dimensionality assertion,² strong transitivity ensures that the $V_i \rightarrow V_j$ arc length equals that of $V_i {\mathop {\longrightarrow }\limits ^{x}} V_1 {\mathop {\longrightarrow }\limits ^{y}} V_j$ where $V_i \rightarrow V_j$ is rerouted to pass through $V_1$. As all arc lengths for $\mathcal {G}^n_{A, cpi}\in \mathbb{S}\mathbb{T}^n_A$ are determined by the $\{V_1\rightarrow V_k\}_{k=2}^n$ lengths, $\mathbb{S}\mathbb{T}_A^n$ has dimension $(n-1)$.

As asserted next, $\mathcal {G}^n_{A, cpi}$ is $\mathcal {G}^n_A$’s path-independent component described in the Sect. 1.

Corollary 1

For $\mathcal {G}^n_{A, cpi} \in \mathbb{S}\mathbb{T}_A^n$, all paths starting at $V_i$ and ending at $V_j$ have length equal to the $V_i\rightarrow V_j$ arc that connects the endpoints.

A Fig. 2b example of Corollary 1 is that the 4 length of $V_2 {\mathop {\longrightarrow }\limits ^{7}} V_5 {\mathop {\longrightarrow }\limits ^{3}} V_4 {\mathop {\longrightarrow }\limits ^{-10}} V_2 {\mathop {\longrightarrow }\limits ^{10}} V_6 {\mathop {\longrightarrow }\limits ^{-6}} V_3$, where paths can revisit vertices, equals the arc length connecting the endpoints $V_2 {\mathop {\longrightarrow }\limits ^{4}} V_3$. With majority voting over pairs, this expression is where the sum of differences of tallies from $\frac{N}{2}$ over a sequence of pairs of candidates always equals this tally difference between the first and last listed candidates.

2.1 Cyclic normal bundle

As Theorem 3 (below) asserts, the $\mathcal {G}^n_{A, cpi}$ linear orderings conceal $\mathcal {G}^n_A$’s closed path properties (Eq. 2). This means that all closed path properties are embedded in the normal bundle of $\mathbb{S}\mathbb{T}_A^n$. The $\mathbb {G}^n_A$ and $\mathbb{S}\mathbb{T}^n_A$ dimensions are $n\atopwithdelims ()2$ and $(n-1)$, so $\mathbb{S}\mathbb{T}^n_A$’s normal subspace, $\mathbb {C}^n_A$, has dimension ${{n-1}\atopwithdelims ()2}$. As described next, $\mathbb {C}^n_A$ is determined by three-cycles.

Theorem 2

(Saari, 2021) For $n\ge 3$, the linear subspace orthogonal to $\mathbb{S}\mathbb{T}_A^n$, $\mathbb {C}_A^n$, has dimension ${{n-1}\atopwithdelims ()2}$. A basis for $\mathbb {C}^n_A$, which consists of three-cycles with equal costs between successive vertices, is

$$\begin{aligned} \{V_1 {\mathop {\longrightarrow }\limits ^{1}} V_j {\mathop {\longrightarrow }\limits ^{1}} V_k {\mathop {\longrightarrow }\limits ^{1}} V_1\}_{1<j<k\le n}. \end{aligned}$$

(4)

More generally, if $\mathcal{C}\mathcal{B}^n_A$ is a set of ${n-1}\atopwithdelims ()2$ three-cycles, where each arc in a three-cycle has length 1 and each three-cycle has one arc that is not in any other $\mathcal{C}\mathcal{B}^n_A$ three-cycle, then $\mathcal{C}\mathcal{B}^n_A$ is a $\mathbb {C}^n_A$ basis.

According to Theorem 2, the $\mathcal {G}^n_{A, cyclic} \in \mathbb {C}^n_A$ structure is governed by three-cycles. To motivate their Eq. (4) form, strong transitivity requires $V_1 {\mathop {\longrightarrow }\limits ^{x}}V_j {\mathop {\longrightarrow }\limits ^{y}} V_k = V_1 {\mathop {\longrightarrow }\limits ^{z}} V_k$, which defines the equation $x+y-z=0$. The path form of the gradient of this equation, $(1,1, -1)$, is the Eq. (4) three-cycle $V_1 {\mathop {\longrightarrow }\limits ^{1}} V_j {\mathop {\longrightarrow }\limits ^{1}} V_k {\mathop {\longrightarrow }\limits ^{1}} V_1$. Of importance is that all Hamiltonian and closed paths in $\mathcal {G}^n_{A, cpi}$ have the same length of zero. This means that these $\mathcal {G}^n_{A, cpi}$ paths provide minimal to no information that can distinguish between paths. Instead the information that can differentiate between paths comes from the three-cycles. These cycles, which measure how a triplet’s $\mathcal {G}^n_A$ data deviates from its cpi “zero length,” are the only parts of $\mathcal {G}^n_A$ that reflect path properties. That is, $\mathcal {G}^n_{A, cyclic}$ identifies all of the intrinsic relevant parts of $\mathcal {G}^n_{A}$ needed to determine closed path properties.

This discussion motivates and leads to a central result asserting that the goal expressed in the Sect. 1 and Eq. (2) has been realized (Eq. 5). The theorem’s concluding statement is crucial for what follows.

Theorem 3

Space $\mathbb {G}^n_A$ is divided into a linear subspace $\mathbb{S}\mathbb{T}^n_A$ and its orthogonal complement $\mathbb {C}^n_A$. For $\mathcal {G}_A^n \in \mathbb {G}^n_A$, there are unique $\mathcal {G}^n_{A, cpi} \in \mathbb{S}\mathbb{T}^n_A$ and $\mathcal {G}^n_{A, cyclic} \in \mathbb {C}^n_A$ so that

$$\begin{aligned} \mathcal {G}_A^n = \mathcal {G}^n_{A, cpi} + \mathcal {G}^n_{A, cyclic};\end{aligned}$$

(5)

$\mathcal {G}^n_{A, cpi}$ and $\mathcal {G}^n_{A, cyclic}$ are, respectively, the orthogonal projections of $\mathcal {G}^n_A$ to $\mathbb{S}\mathbb{T}_A^n$ and to $\mathbb {C}^n_A$.

The length of a closed path in $\mathcal {G}_A^n$ equals its length in $\mathcal {G}^n_{A, cyclic}$.

The critical last statement (identifying $\mathcal {G}^n_{A, cyclic}$ as $\mathcal {G}^n_A$’s companion graph) essentially repeats the observation that all closed paths in $\mathcal {G}^n_{A, cpi}$ have the same length, so $\mathcal {G}^n_{A, cpi}$ offers no relevant information about closed path properties. This assertion follows from the linearity of Eq. (5), which requires the length of a path in $\mathcal {G}_A^n$ to equal the sum of its lengths in $\mathcal {G}^n_{A, cpi}$ and $\mathcal {G}^n_{A, cyclic}.$ By design, a closed path’s length in $\mathcal {G}^n_{A, cpi}$ is zero, so a path’s length in $\mathcal {G}_A^n$ and in $\mathcal {G}^n_{A, cyclic}$ must agree. As $\mathcal {G}^n_{A, cpi}$ consists of those portions of $\mathcal {G}^n_A$ entries that contribute nothing substantive to closed path lengths, it can be dropped. Thus, all relevant closed path information for $\mathcal {G}^n_A$ is encoded in the three-cycles of $\mathcal {G}^n_{A, cyclic}$. Stated differently, closed paths of $\mathcal {G}^n_A\in \mathbb {G}^n_A$ reflect $\mathcal {G}^n_{A, cyclic}$’s three-cycle structure while $\mathcal {G}^n_{A, cpi}$ can camouflage this information. Removing $\mathcal {G}^n_{A, cpi}$ (i.e., dropping the obscuring terms) makes it easier to find closed paths or optimal Hamiltonian circuits by analyzing the simpler $\mathcal {G}^n_{A, cyclic}$ (e.g,, Fig. 2c) rather than $\mathcal {G}^n_A$ (e.g., Fig. 2a).

Fig. 3

Interpreting $\mathcal {G}^n_{A, cyclic}$

To expand on the comment that the $\mathcal {G}^n_{A, cpi}$ entries contribute nothing substantive about closed path lengths, computing the $V_1 {\mathop {\longrightarrow }\limits ^{8}} V_2 {\mathop {\longrightarrow }\limits ^{10}} V_3 {\mathop {\longrightarrow }\limits ^{-12}} V_1$ length of 6 in Fig. 3a involves a subtraction. To analyze this structure, let the unknown optimal values of the cancelled terms be u, v, and w from, respectively, arcs $\widehat{V_1V_2}$, $\widehat{V_2V_3}$, and $\widehat{V_3V_1}$. That is, $(8-u)+(10-v)+(-12-w)=6, \text { where the canceled terms } u+v+w= 0$ define a zero-length closed path. This cancellation applies to all triplets for $n\ge 3$, so the extracted values define a $\mathbb{S}\mathbb{T}_A^n$ graph. Thus, when computing path lengths, treat the subtractions as removing $\mathcal {G}^n_A$ terms that define a linear order.

The optimal way to eliminate all $\mathcal {G}^n_A$ terms creating a linear order is to select the $\mathbb{S}\mathbb{T}_A^n$ graph that most closely resembles $\mathcal {G}^n_A$. This is its orthogonal projection $\mathcal {G}^n_{A, cpi}$ (Theorem 3). With Fig. 3b, the $\mathcal {G}^3_{A, cpi}$ component extracts $u+v+w= 6+8-14=0$. These entries make no substantive contribution to closed path properties, so the remaining arc portions, which define $\mathcal {G}^3_{A, cyclic}$, become the operative values that determine path lengths and properties. Using $\mathcal {G}^3_{A, cyclic}$ rather than $\mathcal {G}^3_A$ to find properties, it follows immediately that the path length of Fig. 3c’s cycle $V_1 {\mathop {\longrightarrow }\limits ^{2}} V_2 {\mathop {\longrightarrow }\limits ^{2}} V_3 {\mathop {\longrightarrow }\limits ^{2}} V_1$ is 6.

This behavior holds in general; e.g., each Fig. 2b triplet identifies the optimal cancellation when computing $\mathcal {G}^5_A$ path lengths. By removing all linear ordering effects, the remaining $\mathcal {G}^n_{A,cyclic}$ terms become the operative intrinsic path components. For instance, the simplest closed path is a triplet; if it is an isolated cycle, then Eq. (4) provides all of its properties and arc lengths. If it is not isolated, its properties come from the algebra of these fundamental cycles. (For instance, $V_2 {\mathop {\longrightarrow }\limits ^{2}} V_1$ in Fig. 2c is the sum of this arc’s length in two cycles.) Removing the $\mathcal {G}^n_{A, cpi}$ clutter leaves the more tractable $\mathcal {G}^n_{A, cyclic}$.

Slightly modifying Theorem 3 yields a simple expression for the length of any connected path. But, if the path is not closed, information from $\mathcal {G}^n_{A, cpi}$ is needed.

Corollary 2

The length of a path in $\mathcal {G}^n_A$ that connects $V_j$ with $V_k$ is the length of this path in $\mathcal {G}^n_{A, cyclic}$ plus the length of the $V_j\rightarrow V_k$ arc in $\mathcal {G}^n_{A, cpi}$.

Proof

The length of a path in $\mathcal {G}^n_A$ equals the sum of its lengths in $\mathcal {G}^n_{A, cpi}$ and $\mathcal {G}^n_{A, cyclic}$. According to Corollary 1, the length of a connected path in $\mathcal {G}^n_{A, cpi}$ starting at $V_j$ and ending at $V_k$ equals the length of the $V_j\rightarrow V_k$ arc connecting the endpoints. So the length of the path in the two components equals its $\mathcal {G}^n_{A, cyclic}$ length plus the length of the $V_j\rightarrow V_k$ arc to complete the proof. $\square$

To illustrate, the path length of 15 for $V_1 {\mathop {\longrightarrow }\limits ^{14}} V_4 {\mathop {\longrightarrow }\limits ^{-6}} V_3 {\mathop {\longrightarrow }\limits ^{-4}} V_1 {\mathop {\longrightarrow }\limits ^{8}} V_5 {\mathop {\longrightarrow }\limits ^{3}} V_4$ in $\mathcal {G}^5_A$ (Fig. 2a), which can meet vertices multiple times, equals the easier computed length of 4 for $V_1 {\mathop {\longrightarrow }\limits ^{3}} V_4 {\mathop {\longrightarrow }\limits ^{0}} V_3 {\mathop {\longrightarrow }\limits ^{1}} V_1 {\mathop {\longrightarrow }\limits ^{0}} V_5 {\mathop {\longrightarrow }\limits ^{0}} V_4$ in $\mathcal {G}^5_{A, cyclic}$ plus 11 from the $\mathcal {G}^5_{A, cpi}$ arc $V_1{\mathop {\longrightarrow }\limits ^{11}} V_4$. For majority voting, this expression shows that adding the “difference from average” tallies for a sequence of paired comparisons equals adding the cyclic portion of these values to the strictly transitive portion of the tally between the first and last listed candidate. The Fig. 3a arc length of 18 for $V_1 {\mathop {\longrightarrow }\limits ^{8}} V_2\ {\mathop {\longrightarrow }\limits ^{10}} V_3$ equals this path’s length of four in Fig. 3c plus the $V_1 {\mathop {\longrightarrow }\limits ^{14}} V_3$ length of 14 in Fig. 3b.

To show that the $\mathcal {G}^n_{A, cyclic}$ structures determine path properties, notice that a closed path can be shorter than the path that stops at the penultimate step. The reason is that a closed curve cancels all $\mathcal {G}^n_{A, cpi}$ terms, but $\mathcal {G}^n_{A, cpi}$ values remain if a path stops prematurely (Corollary 2). For instance, the Fig. 2a path $V_1 {\mathop {\longrightarrow }\limits ^{-1}} V_2\ {\mathop {\longrightarrow }\limits ^{3}} V_3 {\mathop {\longrightarrow }\limits ^{6}} V_4 {\mathop {\longrightarrow }\limits ^{-3}} V_5 {\mathop {\longrightarrow }\limits ^{-8}} V_1$ has length $-3$, but if the path ends at $V_5$, its length is 5.

As another example, it is stated in the Sect. 1 that knowing what portions of a graph contribute, or do not, to the path lengths introduces a way to understand difficulties of numerical approaches developed to find optimal outcomes. While there are many of these path finding methods (e.g., see Cook, 2012), because of simplicity of the greedy algorithm (GA), only it is used here. Using GA shows that $V_1 {\mathop {\longrightarrow }\limits ^{3}} V_4 {\mathop {\longrightarrow }\limits ^{3}} V_2 {\mathop {\longrightarrow }\limits ^{2}} V_5 {\mathop {\longrightarrow }\limits ^{2}} V_3 {\mathop {\longrightarrow }\limits ^{1}} V_1$ of length 11 is the longest $\mathcal {G}^5_{A, cyclic}$ (Fig. 2c) Hamiltonian path. (According to Eq. 1, its reversal of length -11 is the shortest.) But when GA is applied to $\mathcal {G}^5_A$, it fails to find this path. The source of this failure is that the $\mathcal {G}^5_{A, cpi}$ values divert the GA algorithm. To support this assertion, applying GA to $\mathcal {G}^5_A$ to find its longest Hamiltonian path yields the incorrect

$$\begin{aligned} V_1 {\mathop {\longrightarrow }\limits ^{14}} V_4 {\mathop {\longrightarrow }\limits ^{-3}} V_5 {\mathop {\longrightarrow }\limits ^{-1}} V_3 {\mathop {\longrightarrow }\limits ^{-3}} V_2 {\mathop {\longrightarrow }\limits ^{1}} V_1.\end{aligned}$$

(6)

To explain this error, apply GA to the path-independent terms of $\mathcal {G}^5_{A, cpi}$. The fact that it generates the same Eq. (6) path verifies that $\mathcal {G}^5_{A, cpi}$ is the sole cause of this particular GA problem.

The above uses the fact (Eq. 1) that finding the longest and shortest $\mathcal {G}^n_{A, cyclic}$ Hamiltonian paths (which also are those of $\mathcal {G}^n_A$) coincide. This is stated formally.

Corollary 3

If the length of a path in $\mathcal {G}^n_{A, cyclic}$ is x, the length of its reversal is $-x$.

2.2 Decomposition

We now know that $\mathcal {G}^n_{A, cpi}\in \mathbb{S}\mathbb{T}^n_A$ causes difficulties, so we need to discover how to find it. As $\mathcal {G}^n_{A, cpi}$ is the orthogonal projection of $\mathcal {G}^n_A$, this is a linear algebra exercise (Saari, 2021) with computations of the order $O(n^2)$.

To associate graphs with vectors, let $\textbf{d}_A^n\in \mathbb {R}_A^{n\atopwithdelims ()2}$ be

$$\begin{aligned} \textbf{d}_A^n=(d_{1, 2}, d_{1, 3}, \dots , d_{1, n}; d_{2, 3}, \dots , d_{2, n}; d_{3, 4}, \dots ; d_{n-1, n}), \text { where } d_{i, j} = -d_{j, i};\end{aligned}$$

(7)

the semicolons designate where the first subscript changes. To identify $\mathbb {G}^n_A$ with $\mathbb {R}_A^{n\atopwithdelims ()2}$, let $d_{i, j}$ be the arc length $V_i {\mathop {\longrightarrow }\limits ^{d_{i, j}}} V_j.$ As $V_i {\mathop {\longrightarrow }\limits ^{d_{i, j}}} V_j$ defines $V_j {\mathop {\longrightarrow }\limits ^{-d_{i, j}}} V_i$, it follows that $d_{j, i}=-d_{i, j}$. Let $\mathbb{S}\mathbb{T}_A^n \subset \mathbb {G}^n_A$ also denote the $(n-1)$-dimensional (strongly transitive) subspace of $\mathbb {R}_A^{n\atopwithdelims ()2}$ where each triplet $\{i, j, k\}$ satisfies $d_{i, j} + d_{j, k} = d_{i, k}$. As such, $\mathbb {R}^{n\atopwithdelims ()2}_A$ and $\mathbb {G}^n_A$ are interchangeable.

Definition 2

For vertex $V_j$ of $\mathcal {G}_A^n \in \mathbb {G}^n_A$, let $\mathcal {S}_A(V_j)$ be the sum of the arc lengths leaving vertex $V_j$, $j=1, \dots , n.$

Theorem 4

(Saari, 2021) For $\mathcal {G}_A^n\in \mathbb {G}^n_A$, the $\mathcal {G}^n_{A, cpi}$ path length from $V_i$ to $V_j$ is $d_{i, j}=\frac{1}{n}[\mathcal {S}_A(V_i) - \mathcal {S}_A(V_j)]$, $i, j \in \{1, \dots , n\}$. Both $\mathcal {G}_A^n$ and $\mathcal {G}_{A, cpi}^n$ satisfy $\sum _{j=1}^n \mathcal {S}_A(V_j)=0$. Graph $\mathcal {G}^n_{A, cyclic}$ is given by $\mathcal {G}^n_{A, cyclic} =\mathcal {G}^n_A-\mathcal {G}^n_{A, cpi}$. All $\mathcal {G}^n_{A, cyclic}$ vertices satisfy the stronger $\mathcal {S}_A(V_j)=0.$ Conversely, if all vertices of $\mathcal {G}^n_A\in \mathbb {G}^n_A$ satisfy $\mathcal {S}_A(V_j)=0,$ then $\mathcal {G}^n_A = G^n_{A, cyclic} \in \mathbb {C}^n_A$

The concluding statement follows from Theorem 4’s first sentence. This is because $\mathcal {S}_A(V_j)=0$ for all vertices requires all $d_{i, j}$ legs of $\mathcal {G}^n_{A, cpi}$ to equal zero. As $\mathcal {G}^n_{A, cpi}=0$, $\mathcal {G}^n_A$ equals $\mathcal {G}^n_{A, cyclic}$.

Fig. 4

Decomposition of a $\mathcal {G}_A^6$

To illustrate Theorem 4 with $\mathcal {G}^6_{A}$ (Fig. 4a), the $S_A(V_j)$ values (called ‘Borda Values’ in Saari, 2021) are

$$\begin{aligned} \mathcal {S}_A(V_1) = (-1-5 -3+4 -1) =-6, \mathcal {S}_A(V_2) = 0, \mathcal {S}_A(V_3) = 12, \mathcal {S}_A(V_4)= -12, \mathcal {S}_A(V_5)=-18, \mathcal {S}_A(V_6) = 24.\end{aligned}$$

(8)

Thus (Theorem 4), the $\mathcal {G}^6_{A, cpi}$ values (Fig. 4b) are $d_{1, 2} = \frac{1}{6}[\mathcal {S}_A(V_1) - \mathcal {S}_A(V_2)] = -1, d_{1, 3} = 3, d_{1, 4} = 1, d_{1, 5} = 2, d_{1, 6}=-5, d_{2, 3} = -2, d_{2, 4} = 2, d_{2, 5} = 3, d_{2, 6} = -4, d_{3, 4} = 4, d_{3, 5}=5, d_{3, 6}= -2, d_{4, 5} = 1, d_{4, 6}=-6, d_{5, 6}= -7.$ The crucial graph $\mathcal {G}^6_{A, cyclic}$ (Fig. 4c) follows from $\mathcal {G}^6_{A, cyclic} = \mathcal {G}^6_A - \mathcal {G}^6_{A, cpi}$.

In Fig. 4, the redundant $\mathcal {G}^6_{A, cpi}$ (Fig. 4b) dominates $\mathcal {G}_A^6$’s structure even though the simpler $\mathcal {G}^6_{A, cyclic}$ (Fig. 4c) determines all of $\mathcal {G}_A^6$’s closed path properties. Namely, when analyzing $\mathcal {G}^6_A$ paths, the $\mathcal {G}^6_{A, cpi}$ terms only contribute to the complexity. As such, similarities between the graphs $\mathcal {G}^6_{A, cpi}$ and $\mathcal {G}^6_A$ signal that $\mathcal {G}^6_A$ computations of closed path lengths experience many cancellations. The actual $\mathcal {G}^6_A$ path properties are determined by $\mathcal {G}^6_{A, cyclic}$.

Fig. 5

Advantages of $\mathcal {G}_{A, cyclic}^n$

Figure 5 illustrates how seriously $\mathcal {G}^n_{A, cpi}$ can cloud a path analysis. Path properties are determined by the exceptionally simple $\mathcal {G}^6_{A, cyclic}$ (Fig. 5c), but this clarity is absent from $\mathcal {G}^6_A$ (Fig. 5a), which resembles the associated $\mathcal {G}^6_{A, cpi}$. As indicated with the help of Corollary 4, this is a general phenomenon.

Definition 3

Two graphs $\mathcal {G}^n_{A_1}, \mathcal {G}^n_{A_2} \in \mathbb {G}^n_A$ are “closed path equivalent” iff $\mathcal {G}^n_{A_1, cyclic} = \mathcal {G}^n_{A_2, cyclic}$.

Corollary 4

The “closed path equivalent” relationship is an equivalence relation. Two graphs are equivalent iff their difference is a graph in $\mathbb{S}\mathbb{T}_A^n$. Thus, an equivalence class of this relationship is the sum of a $\mathcal {G}^n_{A, cyclic}$ and the $(n-1)$-dimensional linear subspace $\mathbb{S}\mathbb{T}_A^n$.

Clearly, for a given $\mathcal {G}^n_{A, cyclic}$, most of the $\mathcal {G}^n_{A, cpi}$ choices from the vast offerings of the $(n-1)$-dimensional $\mathbb{S}\mathbb{T}_A^n$ dictate the form of $\mathcal {G}^n_A$ and obscure properties of the relevant $\mathcal {G}^n_{A, cyclic}$.

2.3 Structure of triplets

Closed path properties of $\mathcal {G}^n_A$ involve the algebraic structure of the $\mathcal {G}^n_{A, cyclic}$ cycles. This requires identifying $\mathcal {G}^n_{A, cyclic}$’s three-cycles, which is described next.

Theorem 5

For $\mathcal {G}^n_{A, cyclic}$, only one three-cycle of a Theorem 2basis has a $\widehat{V_jV_k}$ arc. The cycle’s multiple is the $V_j {\mathop {\longrightarrow }\limits ^{d_{j, k}}} V_k$ weight in $\mathcal {G}^n_{A, cyclic}$.

Proof

Arc $V_j {\mathop {\longrightarrow }\limits ^{d_{j, k}}} V_k$ in $\mathcal {G}^n_{A, cyclic}$ appears only in $V_s {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{x}} V_k {\mathop {\longrightarrow }\limits ^{x}} V_s$ of the $\mathcal{C}\mathcal{B}^n_A$ basis. As all weights in a three-cycle agree, this is the cycle’s multiple. $\square$

To illustrate, Fig. 2c has the three three-cycles $V_1 {\mathop {\longrightarrow }\limits ^{3}} V_4 {\mathop {\longrightarrow }\limits ^{3}} V_2 {\mathop {\longrightarrow }\limits ^{3}} V_1, \, V_1 {\mathop {\longrightarrow }\limits ^{1}} V_2 {\mathop {\longrightarrow }\limits ^{1}} V_3 {\mathop {\longrightarrow }\limits ^{1}} V_1$ and $V_2 {\mathop {\longrightarrow }\limits ^{2}} V_5 {\mathop {\longrightarrow }\limits ^{2}} V_3 {\mathop {\longrightarrow }\limits ^{2}} V_2$. Figure 4c has the four three-cycles $V_2 {\mathop {\longrightarrow }\limits ^{5}} V_4 {\mathop {\longrightarrow }\limits ^{5}} V_3 {\mathop {\longrightarrow }\limits ^{5}} V_2, V_1 {\mathop {\longrightarrow }\limits ^{4}} V_6 {\mathop {\longrightarrow }\limits ^{4}} V_4 {\mathop {\longrightarrow }\limits ^{4}} V_1, V_3 {\mathop {\longrightarrow }\limits ^{3}} V_4 {\mathop {\longrightarrow }\limits ^{3}} V_6 {\mathop {\longrightarrow }\limits ^{3}} V_3,$ and $V_1 {\mathop {\longrightarrow }\limits ^{2}} V_5 {\mathop {\longrightarrow }\limits ^{2}} V_3 {\mathop {\longrightarrow }\limits ^{2}} V_1.$ In a Hamiltonian path, at most two arcs of a three-cycle can be used; otherwise the path returns prematurely to a vertex. With this caveat, GA can succeed with $\mathcal {G}^n_{A, cyclic}$ but fail with $\mathcal {G}^n_A$. For instance, the GA delivers the longest Fig. 4c Hamiltonian path $V_3 {\mathop {\longrightarrow }\limits ^{5}} V_2 {\mathop {\longrightarrow }\limits ^{5}} V_4 {\mathop {\longrightarrow }\limits ^{4}} V_1 {\mathop {\longrightarrow }\limits ^{4}} V_6 {\mathop {\longrightarrow }\limits ^{0}} V_5 {\mathop {\longrightarrow }\limits ^{2}} V_3$ with length 20,  which equals its $\mathcal {G}^6_A$ (Fig. 4a) path length (Theorem 3). For $\mathcal {G}^n_A\in \mathbb {G}^n_A$, its shortest Hamiltonian route reverses the longest.

To further illustrate how path properties reflect those of the $\mathbb {C}^n_A$ basis, if a vertex is a source or sink, it imposes an obstacle in finding optimal paths; e.g., if $V_j$ is a sink for negative cost directions (as is $V_6$ in Fig. 4a), then all options to leave $V_j$ require selecting a positive cost direction. As Theorem 6 asserts, this $\mathcal {G}^n_A$ sink/source problem is inherited from $\mathcal {G}^n_{A, cpi}$. And $\mathcal {G}^n_{A, cpi}$ almost always has them! So, if $\mathcal {G}^n_A$ has a source and/or sink, expect that its structure is strongly influenced by $\mathcal {G}^n_{A, cpi}$.

Theorem 6

While $\mathcal {G}^n_A$ can have a sink and/or a source, this is impossible for a $\mathcal {G}^n_{A, cyclic}$. In contrast, if all $\mathcal {G}^n_{A, cpi}$ cost directions are non-zero, then both the positive and negative cost directions have a sink and a source. For either positive or negative costs, $\mathcal {G}^n_A$ has at most one source and one sink.

2.4 Incomplete graphs

Because the arc lengths of $\mathcal {G}^n_{A, cyclic}$ are the operative data portions, it follows that incomplete graphs inherit portions of these simpler companion graphs. An approach, then, is to complete an incomplete graph and use only the relevant potions of its cyclic components. To illustrate, $\mathcal {G}_A^6$ (Fig. 6a) excludes arcs $\widehat{V_1V_6}$, $\widehat{V_3V_4}$, $\widehat{V_3V_6}$, and $\widehat{V_4V_5}$, so complete $\mathcal {G}^6_A$ by replacing the gaps with arcs of arbitrarily lengths. (In Fig. 6a, zero length arcs are added.) Denote the completed graph by $\tilde{\mathcal {G}}_A^6$, and compute $\tilde{\mathcal {G}}^6_{A, cpi}$ (Fig. 6b) and $\tilde{\mathcal {G}}^6_{A, cyclic}$ (Fig. 6c). Theorem 7 asserts that the length of a closed path in $\mathcal {G}^6_A$ equals its length in $\tilde{\mathcal {G}}^6_{A, cyclic}$. (The Fig. 6b, c dashed arrows are forbidden arcs.) Thus the GA generated path $V_2 {\mathop {\longrightarrow }\limits ^{10}} V_4 {\mathop {\longrightarrow }\limits ^{3}} V_6. {\mathop {\longrightarrow }\limits ^{5}} V_5 {\mathop {\longrightarrow }\limits ^{7}} V_3 {\mathop {\longrightarrow }\limits ^{2}} V_1 {\mathop {\longrightarrow }\limits ^{-1}} V_2$ of length 26, which uses 7 of the 9 largest allowed $\tilde{\mathcal {G}}^6_{A, cyclic}$ leg lengths, is the longest $\mathcal {G}^6_A$ Hamiltonian path.

Fig. 6

An incomplete $\mathcal {G}_A^6$

Theorem 7

For an incomplete $\mathcal {G}_A^n$, replace all non-admissible arcs with arcs of arbitrary lengths to define $\tilde{\mathcal {G}}_A^n$; compute $\tilde{\mathcal {G}}_{A, cyclic}^n$. The length of a closed path in $\mathcal {G}_A^n$ equals its length in $\tilde{\mathcal {G}}_{A, cyclic}^n$.

The length of an admissible connected path starting at $V_j$ and ending at $V_k$ in the incomplete $\mathcal {G}^n_A$ is its length in $\tilde{\mathcal {G}}^n_{A, cyclic}$ plus the length of the $V_j\rightarrow V_k$ arc in $\tilde{\mathcal {G}}^n_{A, cpi}$.

The concluding Theorem 7 assertion allows the $V_j\rightarrow V_k$ arc in $\tilde{\mathcal {G}}^n_{A, cpi}$ to be a forbidden $\mathcal {G}^n_A$ choice. As a Fig. 6 example, the $\mathcal {G}^6_A$ path $V_6 {\mathop {\longrightarrow }\limits ^{12}} V_5 {\mathop {\longrightarrow }\limits ^{5}} V_3$ has length 17. In $\tilde{\mathcal {G}}^6_{A, cyclic}$ this path $V_6 {\mathop {\longrightarrow }\limits ^{5}} V_5 {\mathop {\longrightarrow }\limits ^{7}} V_3$ has length 12, which is added to the 5 length from the banned $V_6 {\mathop {\longrightarrow }\limits ^{5}} V_3$ arc in $\tilde{\mathcal {G}}^6_{A, cpi}$.

Proof

A closed path’s length in $\mathcal {G}_A^n$ is the same in $\tilde{\mathcal {G}}_A^n$ and (by Theorem 3) in $\tilde{\mathcal {G}}_{A, cyclic}^n$.

A connected path’s length in $\mathcal {G}^n_A$ is the same in $\tilde{\mathcal {G}}^n_A$, which equals the sum of its lengths in $\tilde{\mathcal {G}}^n_{A, cpi}$ and $\tilde{\mathcal {G}}^n_{A, cyclic}$. Its $\tilde{\mathcal {G}}^n_{A, cpi}$ length is that of its $V_j\rightarrow V_k$ arc, which completes the proof. $\square$

For a technical explanation of Theorem 7, according to Theorem 4, adding $V_i {\mathop {\longrightarrow }\limits ^{x}} V_j$ to $\mathcal {G}^n_A$ (perhaps to complete $\mathcal {G}^n_A$) adds arc $V_i {\mathop {\longrightarrow }\limits ^{\frac{2x}{n}}} V_j$ and the $(n-2)$ paths $\{V_i {\mathop {\longrightarrow }\limits ^{\frac{x}{n}}} V_k {\mathop {\longrightarrow }\limits ^{\frac{x}{n}}} V_j\}_{k\ne i, j}$ to $\tilde{\mathcal {G}}^n_{A, cpi}$, plus the $(n-2)$ cycles $\{V_i {\mathop {\longrightarrow }\limits ^{\frac{x}{n}}} V_j {\mathop {\longrightarrow }\limits ^{\frac{x}{n}}} V_k {\mathop {\longrightarrow }\limits ^{\frac{x}{n}}} V_i\}_{k\ne i, j}$ to $\tilde{\mathcal {G}}^n_{A, cyclic}$. If $x=0$, only the $V_i {\mathop {\longrightarrow }\limits ^{0}} V_j$ arc is involved. If $x\ne 0$, the new cycles change certain $\tilde{\mathcal {G}}^n_{A, cyclic}$ arc weights to reflect the algebra of overlapping cycles. But when computing the length of a closed path that does not include the $\widehat{V_iV_j}$ arc, the added terms cancel. This is because if, say, $V_i$ is a vertex of the closed path, one connecting arc with the added $\frac{x}{n}$ weight leaves $V_i$ while another connecting arc, with the added $-\frac{x}{n}$, enters.

2.5 Voting, statistics

It is unfortunate for standard voting and decision theory concerns that the set of transitive vectors is not a linear space. For instance, both $d^*_{1, 2} = d^*_{2, 3} = 3, \, d^*_{1, 3} = 1$ and $d^{\#}_{1, 2} = d^{\#}_{2, 3} = d^{\#}_{1, 3} = -2$ are transitive, but the sum is not. This weakness can be partly circumvented because (Theorem 3) a transitive vector is the unique sum of a strongly transitive and a cyclic vector. Not only do cyclic terms create difficulties when seeking a linear order, but as no alternative is favored in a $A {\mathop {\longrightarrow }\limits ^{x}}B, B {\mathop {\longrightarrow }\limits ^{x}}C, C {\mathop {\longrightarrow }\limits ^{x}}A$ cycle, it is arguable that cycles should not contribute to the outcome. Thus, a goal in voting or non-parametric statistics should be to replace data containing cycles with the closest strongly transitive choice—the orthogonal projection $\mathcal {G}^n_{A, cpi}$.

This projection corresponds to widely accepted methods. In voting, the Borda Count resembles the four-point grading system because a n-candidate ballot is tallied by assigning $n-j$ points to the $j^{th}$ ranked candidate, $j=1,\dots , n.$ As known, a candidate’s Borda tally agrees with the sum of points received in majority vote paired comparisons over all other candidates; e.g., if $d_{k, j}$ registers how candidate $V_k$’s tally differs from the $\frac{N}{2}$ average in a $\{V_k, V_j\}$ majority vote election with N voters, then $V_k$’s Borda tally (Definition 2) is $\sum _{j\ne k}\{d_{k, j} + \frac{N}{2}\} = S(V_k) + \frac{(n-1)N}{2}.$ Consequently the Borda and $\mathcal {G}^n_{A, cpi}$ rankings must agree. Similarly, Haunsperger (1992) proved that the ranking obtained by the Kruskal–Wallis test in non-parametric statistics (it converts data into paired comparisons) is equivalent to the Borda rule, so its outcomes also agree with the $\mathcal {G}^n_{A, cpi}$ ranking.

2.6 Lower degrees of freedom

As developed, the space $\mathbb {G}^n_A$ separates into components that affect paths in different ways. The first, $\mathbb{S}\mathbb{T}^n_A$, consists of terms that obscure analyzing paths and their properties as they define linear orders that add nothing of value for closed paths. This subspace, however, is central for resolving certain voting and statistical concerns. The second, $\mathbb {C}^n_{A}$, has all (and only) closed path information, which means that all remaining complexity problems about paths are consequences of the algebra of these cycles. This simplifies deriving closed path properties, computing lengths, designing algorithms with the (somewhat predictive) algebra of three-cycles and removing components that only add to the complexity of finding path properties. General path properties come from the $\mathbb {C}^n_{A}$ basis, which characterizes all $\mathcal {G}^n_{A, cyclic}$ choices. When seeking general closed path properties, $\mathbb {C}^n_A$ is a best possible refined component. This is because the simplest closed path is a triplet, so that three-cycle must be in $\mathbb {C}^n_A$.

3 Symmetric cost settings

Turn now to the important $\mathbb {G}^n_S$, which is the space of n-vertex complete symmetric weighted (no loops) graphs. Its wide array of practical applications explains the strong interest in finding the minimal length paths. As nicely described in Cook (2012, Chap. 3), these applications include the organization of data, the aiming of telescopes, lasers, and X-rays, the guiding of industrial machines, the mapping of genomes, and on and on.

The goal in this section is to identify and eliminate those terms that cause problems when searching for optimal paths. Mimicking what is developed for $\mathbb {G}^n_A$, a graph is replaced with a simpler companion graph. In the space $\mathbb {G}^n_S$, “symmetric” requires $d_{i, j}\equiv d_{j, i}$, where $d_{i, j}$ could be the distance between cities $V_i$ and $V_j$ that is the same in both directions. Or, consider a warehouse where all material is moved with pairs of machines; here $d_{i, j}$ could represent the combined weight of what is handled by the $\{V_i, V_j\}$ pair.

Following the lead of Eq. (2), a $\mathcal {G}^n_S\in \mathbb {G}^n_S$ is divided into

$$\begin{aligned} \mathcal {G}^n_S = \mathcal {G}^n_{S, cpi} + \mathcal {G}^n_{S, cyclic}, \end{aligned}$$

(9)

where $\mathcal {G}^n_{S, cpi}$ collects all path independent terms (hence all of these paths have the same length) that create difficulties. Similar to what was found in Sect. 2, all $\mathcal {G}^n_S$ closed path properties come from $\mathcal {G}^n_S$’s companion graph $\mathcal {G}^n_{S, cyclic}$, which measures deviations from “sameness.” Thus its arc lengths become the essential and operative values that determine all closed path properties of $\mathcal {G}_S^n \in \mathbb {G}^n_S$.

Fig. 7

Closed path independence for $\mathbb {G}^4_S$

The $\mathbb {G}^n_S$ cpi definition differs from that of $\mathbb {G}^n_A$; e.g., rectangles replace triangles. For instance, $\mathcal {G}_S^4 \in \mathbb {G}^4_S$ (Fig. 7a) is cpi iff all Hamiltonian paths have the same length. Of the six routes, three reverse the other three, so this condition requires the three Fig. 7b routes to have equal length. Cancellations force the sums of the vertical, the horizontal, and the diagonal lengths to agree, or

$$\begin{aligned} x_1+x_2=y_1+y_2 = z_1+z_2.\end{aligned}$$

(10)

Any Hamiltonian path for $\mathcal {G}_S^4\in \mathbb {G}^4_S$ consists of two of the pairs of diagonal, vertical, or horizontal edges. As such, the two smallest Eq. (10) sums for a given $\mathcal {G}_S^4$ define the shortest path with length equal to the sum of their sums. Illustrating with Fig. 7d, $x_1+x_2= 10, \, y_1+y_2= 11, \, z_1+z_2 = 9$, so the shortest Hamiltonian circuit uses the diagonal and horizontal edges to define the path $V_1 {\mathop {\longrightarrow }\limits ^{7}} V_3 {\mathop {\longrightarrow }\limits ^{9}} V_4 {\mathop {\longrightarrow }\limits ^{2}} V_2 {\mathop {\longrightarrow }\limits ^{1}} V_1$ of length 19. (Should three vertices define a triangle with the fourth in the interior, the three pairs are defined by the triangle’s three vertices. A pair is the arc from a vertex to the interior point coupled with the leg of triangle that is opposite the vertex.)

All cpi graphs in $\mathbb {G}^4_S$ satisfy two independent equations (Eq. 10) in six variables. One solution has zero leg lengths, so all solutions (i.e., all cpi graphs $\mathcal {G}^4_{S, cpi}$) are characterized by Eq. (10)’s four-dimensional kernel. A choice uses weights $\{\omega _j\}_{j=1}^4$ where the $\omega _j$ assigned to vertex $V_j$, $j=1, \dots , 4$ defines the $\widehat{V_jV_k}$ length of ${\omega _j+\omega _k}$ (Fig. 7c); values that satisfy Eq. (10). For $\mathbb {G}^4_S$, these are the ‘closed path independent’ graphs. The common path length depends on how often a vertex is visited; e.g., a $\mathcal {G}^4_{S, cpi}$ closed path that visits each of the three vertices $\{V_i\}_{i=1}^3$ twice has length $4\sum _{j=1}^3 \omega _j$; all Hamiltonian paths in $\mathcal {G}^4_{S, cpi}$ have length $T(\mathcal {G}_{S, cpi}^4) = 2\sum _{j=1}^4 \omega _j$. Everything extends to $n\ge 4.$

Definition 4

A graph $\mathcal {G}^n_S \in \mathbb {G}^n_S$ is ‘closed path independent’ iff for each set of vertices $\mathcal {D}$, all closed paths that pass once through each vertex of $\mathcal {D}$ have the same length.

Theorem 8

For $n\ge 4$, $\mathcal {G}^n_{S, cpi} \in \mathbb {G}^n_S$ is a cpi graph if, for each $j=1, \dots , n,$ a weight $\omega _j$ is assigned to vertex $V_j$ where the $\widehat{V_jV_k}$ length is ${\omega _j+\omega _k}$, $j\ne k$. A closed path passing once through the vertices $\{V_j\}_{j\in \mathcal {D}}$ has length $2\sum _{j\in \mathcal {D}} \omega _j$, thus all Hamiltonian path lengths in $\mathcal {G}^n_{S, cpi}$ are $2\sum _{j=1}^n \omega _j$.

A goal specified in the Sect. 1 is to find the path independent components of a $\mathcal {G}^n_S$. As the following verifies, it is $\mathcal {G}^n_{S, cpi}$, which is expected because all Hamiltonian circuits in $\mathcal {G}^n_{S, cpi}$ have the same length.

Corollary 5

For $\mathcal {G}^n_{S, cpi}$ and a set of vertices $\mathcal {D}$ that includes $\{V_j, V_k\}$, all paths starting at $V_j$ and ending at $V_k$ that pass once through each vertex of $\mathcal {D}$ have the same length.

Proof

This is the common length of closed paths in $\mathcal {D}$ (Definition 4) minus $\omega _j + \omega _k$. $\square$

To determine the structure of $\mathcal {G}^n_{S, cpi}$, identify $\mathbb {G}^n_S$ with $\mathbb {R}^{n\atopwithdelims ()2}_S$. Here, $\mathbb {R}^{n\atopwithdelims ()2}_S$ differs from $\mathbb {R}^{n\atopwithdelims ()2}_A$ (Eq. 7) because in $\mathbb {G}^n_A$ (Sect. 2.2), $d_{i, j}=-d_{j, i}$, but in $\mathbb {G}^n_S$, $d_{i, j}=d_{j, i}$. Thus,

$$\begin{aligned} \textbf{d}_S^n=(d_{1, 2}, d_{1, 3}, \dots , d_{1, n}; d_{2, 3}, \dots , d_{2, n}; d_{3, 4}, \dots ; d_{n-1, n}) \in \mathbb {R}^{n\atopwithdelims ()2}_S, \text { where } d_{i, j} = d_{j, i};\end{aligned}$$

(11)

Theorem 9

The space of $\mathcal {G}^n_{S, cpi}$ graphs, denoted by $\mathbb {CPI}_S^n$, is a n-dimensional linear subspace of $\mathbb {G}^n_S$, or, equivalently, of $\mathbb {R}^{n\atopwithdelims ()2}_S.$ Let $\textbf{B}^n_j \in \mathbb {R}_S^{n\atopwithdelims ()2}$ be where $d_{j, k} = 1$ for all $k\ne j, k=1, \dots , n$; all other $d_{u, v}=0$. A basis for $\mathbb {CPI}_S^n$ is $\{\textbf{B}^n_j\}_{j=1}^n$.

As $\mathcal {G}^n_{S, cpi}$ identifies the components of $\mathcal {G}_S^n$ entries with linear structures that cloud the analysis of closed paths, attention shifts to the companion graph $\mathcal {G}^n_{S, cyclic} = \mathcal {G}_S^n-\mathcal {G}^n_{S, cpi}$. The dimensions of $\mathbb {G}_S^n$ and $\mathbb {CPI}_S^n$ are $n\atopwithdelims ()2$ and n, so $\mathbb {CPI}_S^n$’s normal subspace, $\mathbb {C}^n_S$, has dimension $\frac{n(n-3)}{2}$. (For a comparison, the dimension of $\mathbb {C}^n_A$ is ${{n-1}\atopwithdelims ()2} = \frac{n(n-3)}{2} + 1$.) Space $\mathbb {C}^n_A$ has a four-cycle structure (Theorem 10), which identifies what symmetries define $\mathcal {G}^n_S$’s closed paths.

Theorem 10

Let vector $\textbf{c}^n_{i, j, k, s}$ be where $d_{i, j} = 1, d_{j, k}=-1, d_{k, s}=1, d_{s, i}=-1$; all other $d_{u, v}=0$. Space $\mathbb {C}^n_S$ is spanned by all $\{\textbf{c}^n_{i, j, k, s}\}$. It has dimension $\frac{n(n-3)}{2}$ and it is orthogonal to $\mathbb {CPI}_S^n$. One basis is

$$\begin{aligned} \mathcal {A}^n_{1, 2} \cup \mathcal {B}^n_{1, 2} \text { where }\mathcal {A}^n_{1,2} = \{\textbf{c}^n_{1, 2, j, k}\}_{2<j<k\le n}, \, \mathcal {B}^n_{1, 2} = \{\textbf{c}^n_{1, 2, j, 3}\}_{j=4}^n.\end{aligned}$$

(12)

To motivate the $\textbf{c}^n_{i, j, k, s}$ vectors, if the arc lengths of the route around the perimeter of Fig. 7a satisfy the Eq. (10) cpi requirement, then $x_1-y_2+x_2-y_1=0$. The path form of this equation’s gradient, $(x_1, y_2, x_2, y_1) = (1, -1, 1, -1)$, is $\textbf{c}^4_{1, 2, 3, 4}$. In general, $\textbf{c}^n_{i, j, k, s}$ defines the four-cycle

$$\begin{aligned} \textbf{c}^n_{i, j, k, s} = V_i {\mathop {\longrightarrow }\limits ^{1}} V_j {\mathop {\longrightarrow }\limits ^{-1}} V_k {\mathop {\longrightarrow }\limits ^{1}} V_s {\mathop {\longrightarrow }\limits ^{-1}} V_i \end{aligned}$$

(13)

where each vertex has one leg of length 1 and one of length $-1$. With Fig. 7a, the $\textbf{c}^4_{1, 2, 3, 4}$ and $\textbf{c}^4_{1, 4, 2, 3}$ multiples are, respectively, $\frac{1}{4}\{(x_1+x_2) -(y_1+y_2)\}$ and $\frac{1}{4}\{(y_1+y_2) - (z_1+z_2)\}$. Namely, $\textbf{c}^n_{i, j, k, s}$ measures how $\mathcal {G}^n_S$ data deviate from cpi sameness. In doing so, it identifies which data edges of a four-tuple form ridges or valleys, which is critical information about the data structure. Indeed, as all Hamiltonian circuits in $\mathcal {G}^n_{S, cpi}$ have identical lengths, the $\mathcal {G}^n_{S, cpi}$ component provides limited information about path structures. Instead, all valued particulars come from $\mathcal {G}^n_{S, cyclic}$.

Proof

That $\textbf{c}^n_{i, j, k, s}$ is orthogonal to each $\textbf{B}^n_t$ is immediate. If $t\ne i, j, k, s$, the scalar product is zero. If t is one of these indices, say $t=j$, then one component of $\textbf{c}^n_{i, j, k, s}$ with vertex $V_j$ is positive and the other component is negative, so the scalar product with $\textbf{B}^n_t$ is zero.

Establishing the linear independence of Eq. (12) follows a switching pattern. Iteratively, it will be shown that all coefficients of $\sum _{2<j<k\le n} \alpha _{j, k} \textbf{c}^n_{1, 2, j, k} = \textbf{0}$ must equal zero. For each of the ${n-3}\atopwithdelims ()2$ top vectors in $\mathcal {A}^n_{1, 2}$ (i.e., $j, k\ge 4$), only vector $\textbf{c}^n_{1, 2, j, k}$ has a non-zero $d_{j, k}$, so $\alpha _{j, k}=0.$ For all remaining vectors, either j or k equals 3. Of these, only the top $\mathcal {B}^n_{1, 2}$ vector of $\textbf{c}^n_{1, 2, n, 3}$ has a non-zero $d_{2, n}$, so $\alpha _{n, 3}=0$. The top remaining $\mathcal {A}^n_{1, 2}$ vector is $\textbf{c}^n_{1, 2, 3, n}$, where, with the removal of $\textbf{c}^n_{1, 2, n, 3}$, only $\textbf{c}^n_{1, 2, 3, n}$ has non-zero $d_{3, n}$, so $\alpha _{3, n}=0$. The obvious induction argument of switching between remaining $\mathcal {A}^n_{1, 2}$ and $\mathcal {B}^n_{1, 2}$ vectors continues. That is, if s is the upper bound of the remaining j, k values, then only $\textbf{c}^n_{1, 2, s, 3} \in \mathcal {B}^n_{1, 2}$ has a non-zero $d_{2, s}$ term, so $\alpha _{s, 3}=0$. The top remaining $\mathcal {A}^n_{1, 2}$ vector is $\textbf{c}^n_{1, 2, 3, s}$; as $\textbf{c}^n_{1, 2, s, 3}$ was removed, only $\textbf{c}^n_{1, 2, 3, s}$ of the remaining vectors has a non-zero $d_{3, s}$ term, so $\alpha _{3, s}=0$ and $s-1$ is the largest remaining j, k value. This completes the proof. $\square$

3.1 Decomposing $\mathbb {G}^n_S$

Theorem 11 summarizes the above; it is the $\mathbb {G}^n_S$ version of Theorem 3.

Theorem 11

For $n\ge 4$, $\mathbb {G}^n_S$ has an n-dimensional linear subspace $\mathbb {CPI}_S^n$ and an orthogonal $\frac{n(n-3)}{2}$ dimensional linear subspace $\mathbb {C}^n_S$. A $\mathcal {G}_S^n\in \mathbb {G}^n_S$ has a unique decomposition $\mathcal {G}_S^n = \mathcal {G}^n_{S, cpi} + \mathcal {G}^n_{S, cyclic}$ where $\mathcal {G}^n_{S, cpi}\in \mathbb {CPI}^n_S$ and $\mathcal {G}^n_{S, cyclic} \in \mathbb {C}^n_S$ are, respectively, the orthogonal projection of $\mathcal {G}^n_S$ to $\mathbb {CPI}^n_S$ and to $\mathbb {C}^n_S$.

Fig. 8

Interpreting $\mathcal {G}^n_{S, cyclic}$

Before computing $\mathcal {G}^n_{S, cpi}$ and the crucial $\mathcal {G}^n_{S, cyclic}$, Fig. 8 is used to explain their roles and to relate $\mathcal {G}^n_{S, cpi}$ and $\mathcal {G}^n_{A, cpi}.$ According to Theorem 11, $\mathcal {G}^n_{S, cpi}$ is the $\mathbb {CPI}_S^n$ graph that most closely resembles $\mathcal {G}^n_S$, which is apparent from Fig. 8a, b. A defining feature of $\mathcal {G}^n_{A, cpi} \in \mathbb{S}\mathbb{T}_A^n$ and $\mathcal {G}^n_{S, cpi} \in \mathbb {CPI}_S^n$ is that for both and any set of vertices, the length of all closed paths in the respective graph that meet each vertex once is the same. Without any difference in lengths, these details are redundant when selecting among paths. The decompositions of $\mathbb {G}^n_A$ and $\mathbb {G}^n_S$ remove these path independent values to focus on the companion graphs $\mathcal {G}^n_{A, cyclic}$ and $\mathcal {G}^n_{S, cyclic}$ with the relevant data from the original graph ($\mathcal {G}^n_A$ or $\mathcal {G}^n_S$).

The sum of the Fig. 8b vertical edges, horizontal edges, and diagonals each equals 30. Thus, all $\mathcal {G}^4_{S, cpi}$ (Fig. 8b) Hamiltonian paths have length 60. Three of the six Fig. 8a Hamiltonian circuits are $V_1 {\mathop {\longrightarrow }\limits ^{17}} V_2 {\mathop {\longrightarrow }\limits ^{17}} V_3 {\mathop {\longrightarrow }\limits ^{17}} V_4 {\mathop {\longrightarrow }\limits ^{13}} V_1$ with length 64, $V_1 {\mathop {\longrightarrow }\limits ^{17}} V_2 {\mathop {\longrightarrow }\limits ^{12}} V_4 {\mathop {\longrightarrow }\limits ^{17}} V_3 {\mathop {\longrightarrow }\limits ^{14}} V_1$ with length 60, and $V_1 {\mathop {\longrightarrow }\limits ^{14}} V_3 {\mathop {\longrightarrow }\limits ^{17}} V_2 {\mathop {\longrightarrow }\limits ^{12}} V_4 {\mathop {\longrightarrow }\limits ^{13}} V_1$ with length 56; the other three circuits are reversals. The average length of these paths is 60, which agrees with its Fig. 8b value. This comparison accurately suggests that, for any set of vertices used to define closed paths, what happens in $\mathcal {G}^n_{S, cpi}$ is the average of what happens in $\mathcal {G}^n_S.$ Thus, path lengths in the companion $\mathcal {G}^n_{S, cyclic}$ (e.g., Fig. 8c) measure differences from the average. Trivially, $V_1 {\mathop {\longrightarrow }\limits ^{-2}} V_3 {\mathop {\longrightarrow }\limits ^{0}} V_2 {\mathop {\longrightarrow }\limits ^{-2}} V_4 {\mathop {\longrightarrow }\limits ^{0}} V_1$ in Fig. 8c has the shortest length of $-4$; it is the shortest Fig. 8a path with length $-4$ from the average of 60, or 56.

3.2 Computing $\mathcal {G}^n_{S, cpi}$ and $\mathcal {G}^n_{S, cyclic}$

It remains to find and use $\mathcal {G}^n_{S, cyclic}$. The $O(n^2)$ computations needed to determine $\mathcal {G}^n_{S, cpi}$ and $\mathcal {G}^n_{S, cyclic}$ follow the lead of Sect. 2.2. This is because $\mathcal {G}^n_{S, cpi}$ is the orthogonal projection of $\mathcal {G}^n_S$ to $\mathbb {CPI}^n_S$ where a basis is known (Theorem 9). Entries for $\mathcal {G}^n_{S, cpi}$ and $\mathcal {G}^n_{S, cyclic}$ are based on the following.

Definition 5

For $V_j$ of $\mathcal {G}_S^n \in \mathbb {G}^n_S$, let $\mathcal {S}_S(V_j)$ be the sum of the arc lengths attached to vertex $V_j$, $j=1, \dots , n.$ Let $T(\mathcal {G}_{S}^n) = \frac{1}{n-1} \sum _{j=1}^n \mathcal {S}_S(V_j)$.

The average length of the $(n-1)$ arcs with $V_j$ as a vertex is $\frac{1}{n-1}S(V_j)$, so $T(\mathcal {G}_{S}^n)$ is the average $\mathcal {G}^n_S$ Hamiltonian path length. As $\mathcal {G}^n_{S, cyclic}$ consists of $\textbf{c}^n_{i, j, k, s}$ cycles, each $\textbf{c}^n_{i, j, k, s}$ arc entering a vertex has a leaving arc with the same weight but opposite sign (Eq. 13); thus $S_S(V_j)=0$. This equation means that all $S_S(V_j)$ values for $\mathcal {G}^n_{S}$ and $\mathcal {G}^n_{S, cpi}$ agree. As $T(\mathcal {G}^n_S)$ sums the $\frac{1}{n-1}S_S(V_j)$ values, the average Hamiltonian path lengths in $\mathcal {G}^n_{S}$ and in $\mathcal {G}^n_{S, cpi}$ agree, or (as suggested with Fig. 8)

$$\begin{aligned} T(\mathcal {G}^n_{S}) = T(\mathcal {G}^n_{S, cpi}) = 2\sum _{j=1}^n \omega _j.\end{aligned}$$

(14)

Fig. 9

Decomposition of a $\mathcal {G}_S^5 \in \mathbb {G}^5_S$

Agreement between $S_S(V_j)$ values in $\mathcal {G}_S$ and $\mathcal {G}^n_{S, cpi}$ provides equations to find the unknowns $\{\omega _j\}_{j=1}^n$. Illustrating with Fig. 9a, as $S_S(V_1) = 81$ for $\mathcal {G}^5_S$, the same value holds for $\mathcal {G}^5_{S, cpi}$, which means that $\sum _{j=2}^5( \omega _1+\omega _j)= 4\omega _1 + \sum _{j=2}^5\omega _j =81$. In general, the unknown $\{\omega _j\}_{j=1}^n$ satisfy

$$\begin{aligned} S_S(V_j) = \sum _{k\ne j} (\omega _j+\omega _k) = (n-1)\omega _j + \sum _{k\ne j} \omega _k = (n-2)\omega _j + \sum _{k=1}^n \omega _k = (n-2)\omega _j + \frac{1}{2}T(\mathcal {G}^n_{S, cpi}).\end{aligned}$$

(15)

Using $T(\mathcal {G}^n_S) = \mathcal {T}(\mathcal {G}^n_{S, cpi})$ (Eq. 14), the values of the $\mathcal {G}^n_{S, cpi}$ weights are

$$\begin{aligned} \omega _j = \frac{1}{n-2}[S_S(V_j) - \frac{1}{2}T(\mathcal {G}_{S}^n)], \, j=1, 2, \dots , n. \end{aligned}$$

(16)

These $\omega _j$ weights, which define $\mathcal {G}^n_{S, cpi}$ and $\mathcal {G}^n_{S, cyclic}$, lead to a central result about path lengths.

Theorem 12

For $\mathcal {G}^n_S\in \mathbb {G}^n_S$, Eq. (16) defines the weights of its $\mathcal {G}^n_{S, cpi}$ component. Let $\mathcal {G}^n_{S, cyclic} = \mathcal {G}^n_S-\mathcal {G}^n_{S, cpi}.$ The $\mathcal {G}_S^n$ length of a Hamiltonian circuit equals $T(\mathcal {G}_S^n)$ plus its $\mathcal {G}^n_{S, cyclic}$ path length.

Proof

A $\mathcal {G}^n_S$ path length is the sum of its $\mathcal {G}^n_{S, cpi}$ and $\mathcal {G}^n_{S, cpi}$ lengths. All $\mathcal {G}^n_{S, cpi}$ Hamiltonian paths have length $T(\mathcal {G}^n_{S, cpi}) = T(\mathcal {G}_S^n)$, so Theorem 12 follows. $\square$

To illustrate Theorem 12, the Fig. 9a computations from $\mathcal {G}_S^5$ are $S_S(V_1) = 81, S_S(V_2) = 60, S_S(V_3) = 42, S_S(V_4) = 90, S_S(V_5) = 63$, so $T(\mathcal {G}_S^5) = 84.$ Consequently (Eq. 16) $\omega _1 = \frac{1}{3}[81-42]= 13, \, \omega _2 = 6, \, \omega _3= 0, \, \omega _4= 16, \, \omega _5 = 7,$ from which $\mathcal {G}^5_{S, cpi}$ and the central $\mathcal {G}^5_{S, cyclic}$ of Fig. 9b, c follow.

The Fig. 1 values are $\omega _1=7, \omega _2=7, \omega _3=9, \omega _4=1, \omega _5=1, \omega _6=8,$ which yield the Fig. 1b value of 66. Similarly, for Fig. 10, the $\mathcal {G}^6_{S, cpi}$ weights are $\omega _1=6, \omega _2 = 3, \omega _3=5, \omega _4=9, \omega _5=14, \omega _6= 8.$ As required by Definition 4, for any rectangle in $\mathcal {G}^6_{S, cpi}$ (Fig. 10b), the sums of its horizontal edges, its vertical edges, and its diagonals agree. For any five vertices, the lengths of all $\mathcal {G}^6_{S, cpi}$ closed curves that meet all five vertices once are the same. As all $\mathcal {G}^6_{S, cpi}$ Hamiltonian paths have the same length, they have nothing that can be used to compare paths. As Fig. 10 shows (similar to Corollary 4), the $\mathcal {G}^n_{S, cpi}$ complexities can dominate the $\mathcal {G}^n_S$ structure.

Fig. 10

A $\mathcal {G}_S^6$

Turning to the critical $\mathcal {G}^n_{S, cyclic}$, negative arc values normally are avoided with symmetric costs to avoid cycling that can generate an arbitrarily small path length. This problem is sidestepped here because cycling increases the “average value,” which replaces $T(\mathcal {G}^n_{S, cpi})$ in Theorem 12 with a larger value; e.g., if each vertex is met twice, $T(\mathcal {G}^n_{S, cpi})$ is replaced with $2T(\mathcal {G}^n_{S, cpi})= 2(2\sum _{j=1}^n\omega _j)$. This means that $\mathcal {G}^n_{S, cyclic}$ entries identify how the arc lengths “differ from the average,” so following arcs with negative lengths corresponds to following “below average cost” arcs.

Again, GA may be successful with $\mathcal {G}^n_{S, cyclic}$ but fail with $\mathcal {G}^n_S$. This is because the $\mathcal {G}^n_{S, cpi}$ terms can divert GA. With Fig. 9c, GA identifies the shortest $\mathcal {G}^n_{S, cyclic}$ Hamiltonian circuit of $V_1 {\mathop {\longrightarrow }\limits ^{-16}} V_2 {\mathop {\longrightarrow }\limits ^{-1}} V_4 {\mathop {\longrightarrow }\limits ^{-14}} V_5 {\mathop {\longrightarrow }\limits ^{-4}} V_3 {\mathop {\longrightarrow }\limits ^{-1}} V_1$, which clearly is the shortest because it uses all five negative cost arcs to have length $-36$. Its $\mathcal {G}_S^5$ length (Theorem 12) is $T(\mathcal {G}_S^5) - 36 = 84-36 = 48.$ The $\mathcal {G}^5_{S, cpi}$ terms, however, throw GA off the track when it is applied to $\mathcal {G}^5_S$ (Fig. 9a).

Similarly, the GA identifies the shortest Fig. 10c Hamiltonian path $V_1 {\mathop {\longrightarrow }\limits ^{-3}} V_5 {\mathop {\longrightarrow }\limits ^{-2}} V_2 {\mathop {\longrightarrow }\limits ^{-3}} V_4 {\mathop {\longrightarrow }\limits ^{-1}} V_3 {\mathop {\longrightarrow }\limits ^{0}} V_6 {\mathop {\longrightarrow }\limits ^{-2}} V_1$ of $-11$. With the $\omega _j$ values for Fig. 10b, $T(\mathcal {G}^6_{S, cpi})= 90,$ so the shortest Hamiltonian path in Fig. 10a is 11 below this average, or $90-11=79.$ Again, GA fails for $\mathcal {G}^6_S$ only because the $\mathcal {G}^6_{S, cpi}$ entries divert it.

Fig. 11

Finding paths

3.3 Finding shortest paths

The $\mathcal {G}^n_{S, cyclic}$ arc lengths reflect “difference from the average,” which leads to an easily computed lower bound for Hamiltonian path lengths.

Corollary 6

For $\mathcal {G}^n_S$, let the adjustment $\mathcal {A}(\mathcal {G}^n_{S, cyclic})$ be the sum of the n smallest arc lengths in $\mathcal {G}^n_{S, cyclic}$. All $\mathcal {G}^n_S$ Hamiltonian path lengths are bounded below by $T(\mathcal {G}^n_S) + \mathcal {A}(\mathcal {G}^n_{S, cyclic})$. The shortest Hamiltonian graph is bounded above by $T(\mathcal {G}^n_S)$.

The last statement follows because $T(\mathcal {G}^n_S)$ is the average length of a Hamiltonian path. Thus some Hamiltonian path length equals or is smaller than $T(\mathcal {G}^n_S)$. For Fig. 9, $\mathcal {A}(\mathcal {G}^5_{S, cyclic})= -36$, so the lower bound is $84-36 =48$, which is the length of its shortest Hamiltonian path. With Fig. 10, $\mathcal {A}(\mathcal {G}^5_{S, cyclic}) = -12$ for the lower bound of $90-12=78$, but the shortest Hamiltonian path has the larger length of 79. The difference arises because the $-1$ length of $\widehat{V_2V_6}$ is not used in the path. As the example suggests, sharper Corollary 6 estimates follow from the four-cycle geometry.

Again, GA may find optimal paths when applied to $\mathcal {G}^n_{S, cyclic}$ and fail with $\mathcal {G}^n_S$. Figure 11, for instance, shows the GA paths for Figs. 9 and 10. To further illustrate, find the shortest closed path in Fig. 10, that passes once through each of the four vertices $\{V_1, V_2, V_4, V_5\}$. The six $\mathcal {G}^6_{S, cyclic}$ arc lengths of these vertices are $\{-3, -3, -2, 0, 3, 5\}$ where GA is not needed because the first four terms define the minimal closed path $V_2 {\mathop {\longrightarrow }\limits ^{-3}} V_4 {\mathop {\longrightarrow }\limits ^{0}} V_1 {\mathop {\longrightarrow }\limits ^{-3}} V_5 {\mathop {\longrightarrow }\limits ^{-2}} V_2$ of length $-8$. The T value for this set is $2(\omega _1+\omega _2+\omega _4+\omega _5),$ which, in $\mathcal {G}^6_{S, cpi}$, is the sum of the rectangle’s vertical and horizontal legs or 64. So the length of this shortest $\mathcal {G}^6_S$ closed path over these vertices in $\mathcal {G}^6_S$ is $64-8= 56.$

3.4 Four cycle structure

As all essential closed path properties of $\mathcal {G}^n_S$ reflect the four-cycle symmetries (Theorem 12), general properties characterizing paths and $\mathcal {G}^n_{S, cyclic}$ are useful.

Corollary 7

If $\mathcal {G}^n_S$ has the property that $S_S(V_j)=0$, $j=1, \dots , n$, then $\mathcal {G}^n_S\in \mathbb {C}^n_S$.

If a cycle in $\mathcal {G}^n_{S, cyclic}$ has the property that each vertex in the cycle has only two non-zero arcs connected to it, then the cycle has an even number of vertices and the arc lengths have the same magnitude where signs change in an alternating manner.

Proof

The condition of the first assertion requires $T(\mathcal {G}^n_S)=0$ (Definition 5) and $\omega _j=0$, $j=1, \dots , n$ (Eq. 16). As $\mathcal {G}^n_{S, cpi}= 0$, it follows that $\mathcal {G}^n_S = \mathcal {G}^n_{S, cyclic}$.

The second assertion follows from the $S_S(V_j)=0$ property. If a vertex has only two non-zero arcs, then one is the negative of the other. The path’s next vertex has one of these weights, so the magnitudes continue. As the negative value is every other arc, there must be an even number of vertices in order for the starting vertex to have the $S_S(V_j)=0$ property. $\square$

According to Corollary 7, the $\mathcal {G}^n_{S, cyclic}$ symmetries restrict the form of certain cycles. Consider the partial cycle $V_1 {\mathop {\longrightarrow }\limits ^{1}} V_2 {\mathop {\longrightarrow }\limits ^{-1}} V_3 {\mathop {\longrightarrow }\limits ^{1}} V_4 {\mathop {\longrightarrow }\limits ^{-1}} V_5 {\mathop {\longrightarrow }\limits ^{1}} V_?.$ If the cycle had an odd number of vertices where $V_?=V_1$, then both non-zero arcs for $V_1$ have length 1, which violates $S_S(V_1)=0$. Therefore, another vertex is needed leading to the cycle’s end being “$\dots V_5 {\mathop {\longrightarrow }\limits ^{1}} V_6 {\mathop {\longrightarrow }\limits ^{-1}} V_1.$” This six-vertex cycle expressed with the basis is $\textbf{c}_{1, 2, 3, 4} + \textbf{c}_{1, 4, 5, 6}$ where the contributions of these vectors to the $\widehat{V_1V_4}$ arc length cancel.

What can complicate the $\mathcal {G}^n_{S, cyclic}$ algebra are overlapping four-cycles. This complexity can be handled with the switching, iterative approach used in the proof of Theorem 10.

Theorem 13

To express a $\mathcal {G}^n_{S, cycle} \in \mathbb {C}^n_S$ in terms of the basis in Eq. (12), for $4\le j<k$, the multiple of $\textbf{c}^n_{1, 2, j, k} \in \mathcal {A}^n_{1, 2}$ is $d_{j, k}$ from the $V_j {\mathop {\longrightarrow }\limits ^{d_{j, k}}} V_k$ arc in $\mathcal {G}^n_{S, cycle}$. (If the arc is not in the graph, its value is zero.) After determining the multiple of a basis vector, remove the associated four-cycle from the graph. In what remains, the multiple of the top $\textbf{c}^n_{1, 2, n, 3} \in \mathcal {B}^n_{1, 2}$ is the negative of the $d_{2, n}$ value in the of $V_2 {\mathop {\longrightarrow }\limits ^{d_{2, n}}} V_n$ arc in the reduced graph. After removing this four-cycle, the top remaining $\mathcal {A}^n_{1, 2}$ vector is $\textbf{c}^n_{1, 2, 3, n}$; its coefficient is the length in $V_3 {\mathop {\longrightarrow }\limits ^{d_{3, n}}} V_n$ in the reduced graph, which leaves $n-1$ as the largest remaining index in the reduced graph. In general, if the largest remaining index is s, the multiple of the top remaining $\mathcal {B}^n_{1, 2}$ vector, $\textbf{c}^n_{1, 2, s, 3}$, is the negative of $d_{2, s}$ from the reduced graph’s $V_2 {\mathop {\longrightarrow }\limits ^{d_{2, s}}} V_s$ arc. The top of the remaining $\mathcal {A}^n_{1, 2}$ vectors is $\textbf{c}^n_{1, 2, 3, s}$; its multiple is the $d_{3, s}$ value of the $V_3 {\mathop {\longrightarrow }\limits ^{d_{3, s}}} V_s$ arc in the reduced graph.

To explain one of the sign changes, the associated arc for $\textbf{c}^n_{1, 2, n, 3}$ is $V_1 {\mathop {\longrightarrow }\limits ^{1}} V_2 {\mathop {\longrightarrow }\limits ^{-1}} V_n {\mathop {\longrightarrow }\limits ^{1}} V_3 {\mathop {\longrightarrow }\limits ^{-1}} V_1$, so for $V_2 {\mathop {\longrightarrow }\limits ^{d_{2, n}}} V_n$ to hold, the coefficient for $\textbf{c}^n_{1, 2, n, 3}$ must be the negative of $d_{2, n}$.

Proof

The proof is essentially that of Theorem 10; removing basis vectors in the specified manner leaves, at each stage, a single $d_{u, v}$ value of a certain type. Because $\mathbb {C}^n_S$ is the sum of these four-cycles, the existence of this $d_{u, v}\ne 0$ requires the associated $\textbf{c}^n_{1, 2, k, s}$ to be in the decomposition; the form of this four-cycle requires $d_{u, v}$ to be the vector’s multiple. A difference is that if $d_{u, v}$ identifies a vector from $\mathcal {B}^n_{1, 2}$, the multiple is the negative of $d_{u, v}$, as required by the form of the associated four-cycle. If the vector is from $\mathcal {A}^n_{1, 2}$, then $d_{u, v}$ is the multiple. $\square$

Using this approach, the Fig. 9c four-cycles of $\mathcal {G}^5_{S, cyclic}$ are $-14\textbf{c}^5_{1, 2, {\textbf{4}, 5}}$, $-\textbf{c}^5_{1, \textbf{2, 5,} 3}$, $10\textbf{c}^5_{1, 2, \textbf{3, 5}}$, $-13\textbf{c}^5_{1, \textbf{2, 3,} 4}$ and $15\textbf{c}^5_{1, 2, 4, 3}$.

3.5 Related results

To illustrate that all closed path properties depend on the $\mathbb {C}^n_S$ basis, recall that if arc costs represent Euclidean distances in the planar problem and if the triangle inequality is satisfied, then minimal Hamiltonian paths cannot have a self intersection (Flood, 1956). Where else can this behavior arise? Here the answer involves $\mathcal {G}^n_{S, cpi}$.

Theorem 14

For $n\ge 3$, $\mathcal {G}^n_{S, cpi}$ satisfies the triangle inequality iff all weights $\omega _j$ are non-negative.

If $\omega _k<0$, then the associated $S_S(V_k)$ is bounded above by $\frac{1}{2}T(\mathcal {G}^n_S)$ (Eq. 16), so the average of arc lengths attached to $V_k$ is much smaller than the average over the graph.

Proof

The $\mathcal {G}^n_{S, cpi}$ arc length for $\widehat{V_iV_k}$ is $\omega _i + \omega _k$. For a triplet, the sum of the lengths of the arcs $\widehat{V_iV_j}$ and $\widehat{V_jV_k}$ is $\omega _i +2\omega _j +\omega _k$, which differs from the $\widehat{V_iV_k}$ length by $2\omega _j$. Thus, the triangle inequality is satisfied iff $\omega _j\ge 0$. This must hold for all legs of all triplets, so $\omega _j\ge 0$ for all j. $\square$

Fig. 12

Finding properties of $\mathcal {G}^n_{S, cyclic}$

Turning to $n=4$ and the $\mathbb {C}^4_S$ basis, the terms {$u\textbf{c}^4_{1, 4, 2, 3}+v\textbf{c}^4_{1, 2, 3, 4}$} (Fig. 12a) represent all possible $\mathcal {G}^4_{S, cyclic}$ structures, it characterizes all closed path properties and their lengths for $\mathcal {G}^4_S\in \mathbb {G}^4_s$. Assuming the rectangular Fig. 12a faithfully represents the modeled concern (e.g., using actual rather than Euclidean costs), the issue is to understand which (u, v) values (that is, which choices of $\mathcal {G}^4_{S, cyclic}$) require a shortest Hamiltonian path to avoid the crossing diagonals. The answer follows from Fig. 12a as this property requires the sum of the diagonal lengths to be greater than the sum of the vertical edges and of the horizontal edges, or $-u>v, \, -u> u-v$. These values are depicted by the open, unbounded, shaded Fig. 12b region, which displays a surprisingly large selection of $\mathcal {G}^4_{S, cyclic}$ (hence $\mathcal {G}^4_S$) graphs that satisfy this property.

To compare this wedge with what happens should $\mathcal {G}^4_S$ satisfy the triangle inequality, for any $\{V_i, V_k, V_j\}$ triangle in $\mathcal {G}^4_{S}$, the sum of the $\widehat{V_iV_k}$ and $\widehat{V_kV_j}$ leg lengths is an upper bound for the $\widehat{V_iV_j}$ leg length. To illustrate with i = 1, k=4, and j=3, the triangle inequality is

$$\{(u-v) + (\omega _1+\omega _4)\} + \{v + (\omega _4 +\omega _3)\} \ge -u + (\omega _1+\omega _3), \text { or } \omega _4 \ge -u.$$

Applying a similar calculation to the three triangles that have if $V_k$ is not on the triangle’s compared edge, then

$$\begin{aligned} \omega _k\ge -u, \quad \omega _k \ge v, \quad \omega _k \ge u-v.\end{aligned}$$

(17)

Theorem 15

For $\mathcal {G}^4_S$, if any $\omega _k<0$, then $\mathcal {G}^4_S$ does not satisfy the triangle inequality. Let $\omega =\min (\omega _1, \omega _2, \omega _3, \omega _4)$. The region where $\mathcal {G}^4_S$ satisfies the triangle inequality is defined by substituting $\omega$ for $\omega _k$ in Eq. (17); it is depicted by the closed, bounded, shaded triangle in Fig. 12c.

Proof

If $\omega _k<0$, then Eq. (17) cannot be satisfied. The remainder follows from the above. $\square$

If $\omega =0$, the triangle inequality is satisfied only for $u=v=0$, which requires $\mathcal {G}^4_{S, cyclic}=0$ so $\mathcal {G}^4_S=\mathcal {G}^4_{S, cpi}$. The triangle inequality and the non-crossing of the diagonals for the shortest Hamiltonian path hold in the intersection of the shaded portions of Fig. 12b, c; this is the Fig. 12b shaded triangle limited on the left by $u\ge -\omega$. What remains are regions (i.e., choices of $\mathcal {G}^4_{S, cyclic}$) where the triangle inequality is satisfied but the shortest Hamiltonian path includes the diagonals, and a sizable region (the shaded unbounded Fig. 12b region for $u<-\omega$) where the diagonals are not in the shortest Hamiltonian circuit and the triangle inequality is not satisfied.

The above indicates in a simple setting the kinds of results that are possible. Other conclusions for $\mathcal {G}^n_{S, cyclic}$ follow in a similar manner. A Fig. 12d basis, which captures all $\mathcal {G}^5_{S, cyclic}$ behaviors, is $\{v\textbf{c}^5_{1, 2, 3, 4} + w\textbf{c}^5_{2, 3, 4, 5} + x\textbf{c}^5_{3, 4, 5, 1} +$ $y\textbf{c}^5_{4, 5, 1, 2} + z\textbf{c}^5_{5, 1, 2, 3}\}$.

3.6 Extensions and incomplete graphs

With minor modifications, other Sect. 2 results for the asymmetric $\mathbb {G}^n_A$ transfer to the symmetric $\mathbb {G}^n_S$. For instance, Corollary 2 describes connected paths that start and stop at specified vertices; the following is a similar result for $\mathcal {G}^n_S$.

Theorem 16

Consider the class of paths starting at $V_j$ and ending at $V_k$, $j\ne k$, that pass once through each of the other $\mathcal {G}^n_S$ vertices. The length of such a path in $\mathcal {G}^n_S$ is its path length in $\mathcal {G}^n_{S, cyclic}$ plus $\{T(\mathcal {G}^n_S) -(\omega _j+\omega _k)\}$.

For an example, consider all Fig. 10 paths that start at $V_1$, end in $V_5$, and pass through each of $V_2, V_3, V_4, V_6$ once. Because $\omega _1+\omega _5$ is the weight of the $\widehat{V_1V_5}$ leg in $\mathcal {G}^6_{S, cpi}$, its value is 20. So any path with these conditions has the path’s length in $\mathcal {G}^6_{S, cyclic}$ plus $T(\mathcal {G}^6_S) - 20 = 70$. Using Fig. 10b, after removing the solid $\widehat{V_1V_5}$ arc, the shortest path is $V_1\rightarrow V_6 \rightarrow V_3 \rightarrow V_4 \rightarrow V_2 \rightarrow V_5$ of length $-8$, so this path in $\mathcal {G}^6_S$ (Fig. 10a) has length $70-8=62.$

Incomplete graphs are handled as in Sect. 2. Namely, complete the graph by adding arcs of any desired length to obtain $\tilde{\mathcal {G}}_S^n$, and compute $\tilde{\mathcal {G}}^n_{S, cpi}$ and $\tilde{\mathcal {G}}^n_{S, cyclic}$ For incomplete graphs, $\infty$ is typically assigned to inadmissible arcs; do so only with $\tilde{\mathcal {G}}^n_{S, cyclic}.$ (That any value can be assigned to the missing arcs underscores the intrinsic values of the $\tilde{\mathcal {G}}^n_{S, cyclic}$ arc lengths. An explanation for the impact of different values is similar to that following Theorem 7.)

Theorem 17

For an incomplete symmetric graph $\mathcal {G}^n_S$, let $\tilde{\mathcal {G}_S^n}$ include the missing $\mathcal {G}_S^n$ arcs where each has an arbitrary selected length. Compute $T(\tilde{\mathcal {G}_S^n})$ and $\tilde{\mathcal {G}}^n_{S, cyclic}.$ The length of a $\mathcal {G}_S^n$ Hamiltonian path is $T(\tilde{\mathcal {G}}_S^n)$ plus its $\tilde{\mathcal {G}}^n_{S, cyclic}$ length.

Adding arcs of zero length simplifies computations because the $S_S(V_j)$ values for $\mathcal {G}_S^n$ and $\tilde{\mathcal {G}_S^n}$ will agree, and $T(\mathcal {G}_S^n) = T(\tilde{\mathcal {G}_S^n}).$

Proof

A Hamiltonian path length in $\mathcal {G}_S^n$ is the same in $\tilde{\mathcal {G}_S^n}$, which equals $T(\tilde{\mathcal {G}_S^n})$ plus its length in $\tilde{\mathcal {G}^n}_{S, cyclic}.$ The result follows. $\square$

Fig. 13

An incomplete $\mathcal {G}_S^6$

As $\widehat{V_1V_4}$ and $\widehat{V_2V_5}$ are not admitted in Fig. 13, include them in Fig. 13a with zero lengths (the two dashed arcs in Fig. 13a). The $S_S(V_j)$ values of $\tilde{\mathcal {G}_S^n}$ are $S_S(V_1) = 27, S_S(V_2) = 27, S_S(V_3) = 39, S_S(V_4) = 23, S_S(V_5) = 23, S_S(V_6) = 51$. Thus $T(\tilde{\mathcal {G}_S^n}) = 38,$ $\omega _1=\frac{1}{4}[27-19]=2, \omega _2=2, \omega _3= 5, \omega _4= 1, \omega _5=1, \omega _6 = 8,$ and Fig. 13b, c follow. The two inadmissible Fig. 13c arcs (with length of $-3$) can be dropped or replaced with $\infty$ (Fig. 13c). With the simpler $\tilde{\mathcal {G}}^6_{S, cyclic}$, its shortest Hamiltonian path $V_1 {\mathop {\longrightarrow }\limits ^{-2}} V_3 {\mathop {\longrightarrow }\limits ^{0}} V_2 {\mathop {\longrightarrow }\limits ^{-1}} V_6 {\mathop {\longrightarrow }\limits ^{-2}} V_4 {\mathop {\longrightarrow }\limits ^{2}} V_5 {\mathop {\longrightarrow }\limits ^{0}} V_1$ of length $-3$ includes all allowed arcs with negative costs. This path in $\mathcal {G}_S^6$ has the “below average” length of $T(\mathcal {G}_S^6) - 3 = 35.$

3.7 Decisions; transitive rankings

An intent of the $\mathcal {G}^n_S$ data may be to rank the $\{V_j\}_{j=1}^n$ in the more complicated setting where the data describe joint contributions of pairs rather than their differences. If $d_{i,j}$ represents the driving distance between cities $V_i$ and $V_j$, for instance, which cities are, in general, farther from others? Should $d_{i, j}$ represent the sum of the weights handled by machines $V_i$ and $V_j$, the decision problem is to rank the effort expended by the different machines.

Answers for “linear ordering” questions follow from Eq. (16), which leads to

$$\begin{aligned} S_S(V_j) = (n-2)\omega _j + \frac{n-2}{2}T(\mathcal {G}_S^n), \quad j=1, 2, \dots , n. \end{aligned}$$

(18)

As $\frac{1}{n-1} S_S(V_j)$ is the average weight of the arcs attached to $V_j$, Eq. (18) shows that the $\omega _j$ weights reflect the average contribution of each $V_j$.³ As such, a natural ranking of the $\{V_j\}_{j=1}^n$ choices follows ordering the $\{\omega _j\}_{j=1}^n$ values. This selection most accurately represents the original data by being the orthogonal projection of $\mathcal {G}^n_S$ to $\mathbb {CPI}^n_S$. (This discussion mimics that of Sect. 2.5 for voting and non-parametric statistics.)

For instance, in Fig. 10b, the $\mathcal {G}^6_{S, cpi}$ weights are $\omega _1=6, \omega _2 = 3, \omega _3=5, \omega _4=9, \omega _5=14, \omega _6= 8.$ Because $\omega _5> \omega _4> \omega _6> \omega _1> \omega _3 > \omega _2,$ a natural ranking is $V_5> V_4> V_6> V_1> V_3 > V_2.$ As in Sect. 2, ranking concerns are addressed by projecting $\mathcal {G}^n_S$ to the path independent structures of $\mathbb {CPI}^n_S.$

4 Graphs with general asymmetric costs

Other systems can be similarly reduced. Graphs with a path independence property, where the lengths of all closed paths passing once through each vertex of a specified set are the same, identify components of $\mathcal {G}^n$ entries that provide very limited information but frustrate analyzing closed paths. The subspace’s normal bundle measures deviations from neutrality, so it is critical in determining closed path properties.

This analysis is not necessary for the standard space of graphs with asymmetric costs. The reason is that, for each pair, the arc lengths $V_j {\mathop {\longrightarrow }\limits ^{x}} V_k$ and $V_k {\mathop {\longrightarrow }\limits ^{y}} V_j$ can be represented as an {average cost, excess cost} pair; e.g., $\{a=\frac{x+y}{2}, V_j {\mathop {\longrightarrow }\limits ^{x-a}} V_k\}$. By applying the Sects. 2 and 3 approaches to each component, the above results about incomplete graphs, path lengths, etc., transfer.

Fig. 14

Decomposing an asymmetric $\mathcal {G}^5$

To illustrate with Fig. 14, representing the Fig. 14a costs as {average cost, excess cost} pairs converts the original graph into $\mathcal {G}^5 = \mathcal {G}^5_S +\mathcal {G}^5_A \in \mathbb {G}^5_S \times \mathbb {G}^5_A$, where $\widehat{V_jV_k}$’s length in $\mathcal {G}^5_S$ is the average cost of its arcs, and $\mathcal {G}^5_A$ represents how costs differ from the average. Thus, with $V_1 {\mathop {\longrightarrow }\limits ^{26}} V_3$ and $V_3 {\mathop {\longrightarrow }\limits ^{14}} V_1$ from Fig. 14a, $\widehat{V_1V_3}$’s length in $\mathcal {G}^5_S$ is 20 and $\mathcal {G}^5_A$ has $V_1 {\mathop {\longrightarrow }\limits ^{6}} V_3$.

Analyzing $\mathcal {G}^5_S + \mathcal {G}^5_A$ follows as above: find each graph’s cpi and cyclic components. Removing $\mathcal {G}^5_{S, cpi}$ and $\mathcal {G}^5_{A, cpi}$ leaves Fig. 14b, c. A $\mathcal {G}^5$ Hamiltonian path length (with $\mathcal {G}^5_{S, cpi}$ weights $\omega _1=10, \, \omega _2=10, \, \omega _3 = 8, \, \omega _4= 12, \, \omega _5= 6$) equals $T(\mathcal {G}^5_{S, cpi}) = 92$ plus the sum of its $\mathcal {G}^5_{S, cyclic}$ and $\mathcal {G}^5_{A, cyclic}$ lengths. Expressing $\mathcal {G}^5_{S, cyclic} + \mathcal {G}^5_{A, cyclic}$ in a standard Fig. 14d form, its shortest Hamiltonian path of $V_1 {\mathop {\longrightarrow }\limits ^{-5}} V_2 {\mathop {\longrightarrow }\limits ^{-1}} V_4 {\mathop {\longrightarrow }\limits ^{-4}} V_3 {\mathop {\longrightarrow }\limits ^{-3}} V_5 {\mathop {\longrightarrow }\limits ^{1}} V_1$ follows. Its $\mathcal {G}^5$ path length is $T(\mathcal {G}^5_{S, cpi}) -12 = 80$.

Notice for $\mathcal {G}^n_{S, cpi} + \mathcal {G}^n_{A, cpi}$ and any subset of vertices $\mathcal {D}$, all closed paths that passes through each vertex of $\mathcal {D}$ once has the same length. This value is the common length of these closed paths in $\mathcal {G}^n_{S, cpi}$ because the length of each such path in $\mathcal {G}^n_{A, cpi}$ is zero. A related decision problem is to rank the alternatives with data of the Fig. 14a form. The approach is to follow what is done above by using information from the $\mathcal {G}^5_{S, cpi}$ and $\mathcal {G}^5_{A, cpi}$ components. The outcome depends on the adopted criterion; e.g., ranking the vertices in terms of average weight of paths entering and leaving each vertex leads to the ranking of $\mathcal {G}^n_{S, coi}$.

5 Summary

Components of a graph’s entries that hamper finding closed path properties and contribute to the NP hard complexity are identified as the subspace of linear independent paths; this is where all Hamiltonian paths over any subset of vertices have the same length. But if all paths have the same length, this information cannot distinguish among them. Removing these entries reveals what part of the data generates differences between paths. In this manner, the graph’s essence is expressed in terms of a simpler companion graph with a smaller degree of freedom. In addition, as all closed graph properties can be expressed in terms of inherent symmetry structures, this means that all remaining complexities of finding optimal paths are caused by the algebra of these cycles (primarily with overlapping edges). The structure of these cycles can change with the kinds of graphs.

6 Proofs

Results not proved above or in Saari (2021) are proved here.

Proofs of Theorem 1, Corollary 1

For triplet $\{V_i, V_j, V_k\}$ in a cpi graph, the closed path $V_i {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{y}} V_k {\mathop {\longrightarrow }\limits ^{z}} V_i$ has length zero, so $x+y = -z.$ Thus, $V_i {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{y}} V_k = V_i {\mathop {\longrightarrow }\limits ^{-z= x+y}} V_k$ satisfies Eq. (3). As all triplets satisfy Eq. (3), a cpi graph is strongly transitive.

A triplet $\{V_i, V_j, V_s\}$ in a strongly transitive graph satisfies $V_i {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{y}} V_s = V_i {\mathop {\longrightarrow }\limits ^{z}} V_s$ where $z=x+y$. Applying a fourth alternative $V_t$ to this relationship yields

$$(V_i {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{y}} V_s) {\mathop {\longrightarrow }\limits ^{u}} V_t = (V_i {\mathop {\longrightarrow }\limits ^{z}} V_s) {\mathop {\longrightarrow }\limits ^{u}} V_t = V_i {\mathop {\longrightarrow }\limits ^{w}} V_t,$$

where $w=z+u = x+y+u.$ With the obvious induction argument, it follows that any path from $V_i$ to $V_k$ has the same length as the direct path from $V_i$ to $V_k$. (This proves Corollary 1.) A closed path has $V_k=V_i$, so its length is that of $V_i$ to $V_i$, or zero. Hence, a strongly transitive graph is cpi.

To prove that the set of strongly transitive graphs forms a linear subspace, notice that a multiple $\mu$ of a strongly transitive graph in $\mathbb {G}^n_A$ changes all path lengths by this multiple; thus the new graph’s arcs remain strongly transitive. Therefore the multiple defines another $\mathbb {G}^n_A$ strongly transitive graph. (If $\mu <0$, then positive cost arcs in the original graph become negative cost arcs in the new graph.) Similarly, for two strongly transitive $\mathbb {G}^n_A$ graphs and any $\{V_i, V_j, V_k\}$ triplet, the first graph satisfies $V_i {\mathop {\longrightarrow }\limits ^{x}} V_j {\mathop {\longrightarrow }\limits ^{y}} V_k = V_i {\mathop {\longrightarrow }\limits ^{x+y}} V_k$ while the second satisfies $V_i {\mathop {\longrightarrow }\limits ^{\tilde{x}}} V_j {\mathop {\longrightarrow }\limits ^{\tilde{y}}} V_k = V_i {\mathop {\longrightarrow }\limits ^{\tilde{x}+\tilde{y}}} V_k.$ Combining these graphs leads to $V_i {\mathop {\longrightarrow }\limits ^{x+\tilde{x}}} V_j {\mathop {\longrightarrow }\limits ^{y + \tilde{y}}} V_k = V_i {\mathop {\longrightarrow }\limits ^{(x+y) + (\tilde{x} + \tilde{y})}} V_k$, which satisfies Eq. (3). Thus the set of strongly transitive graphs in $\mathbb {G}^n_A$, $\mathbb{S}\mathbb{T}_A^n$, is a linear subspace. $\square$

Proof of Theorem 2

With the Eq. (4) basis of $\{V_1 {\mathop {\longrightarrow }\limits ^{1}} V_j {\mathop {\longrightarrow }\limits ^{1}} V_k {\mathop {\longrightarrow }\limits ^{1}} V_1\}_{1<j<k\le n}$ only the three-cycle $V_1 {\mathop {\longrightarrow }\limits ^{1}} V_s {\mathop {\longrightarrow }\limits ^{1}} V_k {\mathop {\longrightarrow }\limits ^{1}} V_1$ has a $\widehat{V_sV_k}$ arc. For the independence of the arcs, if $\textbf{c}_{j,k}$ represents the only $\mathcal{C}\mathcal{B}^n_A$ cycle with a $\widehat{V_jV_k}$ arc, it must be shown that $\sum x_{j,k}\textbf{c}_{j,k} = \textbf{0}$ iff all $x_{j,k}=0.$ But as $\textbf{c}_{j,k}$ is the only vector with a non-zero j, k component, $x_{j,k}=0.$ That these cycles are in $\mathbb{S}\mathbb{T}_A^n$’s normal bundle is proved in Saari (2021). As this set consists of ${n-1}\atopwithdelims ()2$ linearly independent elements that are orthogonal to $\mathbb{S}\mathbb{T}^n_A$, it is a basis for the normal bundle. $\square$

Proof of Theorem 3

Equation (5) is an immediate consequence of the representation of $\mathbb {G}_A^n$ into the orthogonal subspaces $\mathbb{S}\mathbb{T}_A^n$ and $\mathbb {C}^n_A$. The last comment is proved above. $\square$

Proof of Corollary 4

That Definition 3 relationship defines an equivalence relationship (reflexive, symmetric, transitive) follows from the equality of the cyclic components. The difference between two $\mathbb {G}^n_A$ graphs is the difference between their cpi and cyclic components. As their cyclic components agree, the difference is between cpi components. As $\mathbb{S}\mathbb{T}_A^n$ is a linear subspace, this difference is in $\mathbb{S}\mathbb{T}_A^n$. $\square$

Proof of Theorem 6

That $\mathcal {G}^n_{A, cpi}$ normally has a sink and source for positive and negative directions follows from the strong transitivity of all triplets. Thus the n alternatives define a transitive ranking. As no leg has zero length, the transitive ranking has no ties, so there is a single top and a bottom ranked term. For positive directions, the top alternative is a source, the bottom one is a sink.

That $\mathcal {G}^n_{A, cyclic}$ cannot have a source or a sink follows from the fact that $S_A(V_j)=0$ for each vertex. (This statement follows from the property that each three-cycle attached to a vertex has one leg pointing in and one leg, of same magnitude, pointing out.) Thus, each $\mathcal {G}^n_{A, cyclic}$ vertex with non-zero arcs has at least one positive direction pointing in and at least one pointing out.

To show that $\mathcal {G}^n_A$ has a most one source, assume it has two at $V_j$ and $V_k$. That is, all arcs leaving $V_j$ and leaving $V_k$ have positive costs. But the arc connecting $V_j$ to $V_k$ with a positive cost contradicts the property for $V_k$. The proof for sinks is the same. $\square$

Proof of Theorem 8

As $\mathbb {CPI}^n_S$ is n-dimensional (Theorem 9) and as the n-independent values $\{\omega _j\}_{j=1}^n$ define an n-dimensional subspace of graphs in $\mathbb {G}^n_S$ with all specified properties (Definition 4), the theorem follows. $\square$

Proof of Theorem 9

Set $\{\textbf{B}^n_j\}_{j=1}^{n-1}$ is independent because only $\textbf{B}^n_j$ has a non-zero $d_{j, n}$ coordinate. If $\{\textbf{B}^n_j\}_{j=1}^{n}$ is not independent, there is a summation $\sum _{j=1}^{n-1} x_j\textbf{B}^n_j = \textbf{B}^n_n.$ In the sum, each $x_j=1$ to capture $\textbf{B}^n_n$’s $d_{j, n}=1$ component. But $\textbf{B}^n_1 + \textbf{B}^n_2$ has $d_{1, 2}=2$ rather than the required zero for $\textbf{B}^n_n$. Thus the linear subspace spanned by $\{\textbf{B}^n_j\}_{j=1}^{n}$ is n-dimensional. This space captures the structure of $\mathcal {G}^n_{S, cpi}$ graphs because the $d_{i, j}$ component of $\sum _{s=1}^n \omega _s \textbf{B}^n_s$ is the required $\omega _i+\omega _j$. $\square$

Proof of Theorem 16

A path’s length in $\mathcal {G}^n_S$ is the sum of its lengths in $\mathcal {G}^n_{S, cpi}$ and in $\mathcal {G}^n_{S, cyclic}$. $\square$