Skip to main content
SpringerLink
Log in

The premium as informational cue in insurance decision making

  • Published:
Theory and Decision Aims and scope Submit manuscript

Abstract

Often in insurance decision making, there are risk factors on which the insurer has an informational advantage over the consumer. But when the insurer sets and posts a premium for the consumer to consider, the consumer can potentially use the premium as an informational cue for the loss probability, and thereby to reduce the insurer’s informational advantage. We study, by means of a behavioral model, how consumers would use the premium as an informational cue in such contexts. The belief formation process in our model assumes that both prior knowledge and the premium (as a proportion of the compensation) might have an impact on the consumer’s estimate of the loss probability. Moreover, the premium impacts the estimate through an anchoring-and-adjustment process. The model potentially leads to violations of rational expectations, with which the consumer overestimates the loss probability beyond what could be inferred from the premium, given the premise that the insurer must seek to break even or earn an expected profit. Our model analysis moreover implies that the frequency of such violations is non-increasing as the premium increases. Last, the model implies a generally inverted-U relationship between insurance demand and the premium so that the demand is upward sloping at low premium levels and downward sloping at high premium levels. A pilot field study and a laboratory experiment provide robust evidence for our model implications and calibrations for its parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. An implicit assumption here is as follows: I always expects that there is some positive probability that C will accept his/her offer, whatever the premium (or, more rigorously, that C believes that I expects so). This is consistent with refinement ideas in the game theory literature, such as sequential equilibrium (Kreps and Wilson 1982), which assumes that players may tremble and thus there is always a positive probability for a player to play any available strategy, including out-of-equilibrium strategies (in which case the probability is infinitesimally small). On the other hand, if C considers that I may make “mistakes” in the form of a zero-mean random shock around what I might have intended to offer under the aim of expected utility maximization, then at least the expected value of q under C’s belief should not be higher than p, and the inequality must still hold.

  2. In the PLAY-LSR condition, participants are told that their payoffs from their guesses are $100π if there is a breakdown and $(100–100π), if there is no breakdown. In the PLAY-QSR condition, participants are told that their payoffs from their guesses are $(200π–100π2) if there is a breakdown and $(100–100π2), if there is no breakdown. In both of these conditions, participants are also told that only one of their ten guesses is randomly selected for payment. Participants are also told that their expected probability-payoff is maximized if they report probabilities truthfully.

References

  • Abdellaoui, M., Baillon, A., Placido, L., & Wakker, P. P. (2011). The rich domain of uncertainty: Source functions and their experimental implementation. The American Economic Review,101(2), 695–723.

    Google Scholar 

  • Andersen, S., Fountain, J., Harrison, G. W., & Rutström, E. E. (2014). Estimating subjective probabilities. Journal of Risk and Uncertainty,48, 207–229.

    Google Scholar 

  • Ball, S. B., Bazerman, M. H., & Carroll, J. S. (1991). An evaluation of learning in the bilateral winner’s curse. Organizational Behavior and Human Decision Processes,48(1), 1–22.

    Google Scholar 

  • Barseghyan, L., Molinari, F., O’Donoghue, T., & Teitelbaum, J. C. (2013). The nature of risk preferences: Evidence from insurance choices. The American Economic Review,103(6), 2499–2529.

    Google Scholar 

  • Chade, H., & Schlee, E. (2012). Optimal insurance with adverse selection. Theoretical Economics,7, 571–607.

    Google Scholar 

  • Charness, G., & Dufwenberg, M. (2006). Promises and partnership. Econometrica,74(6), 1579–1601.

    Google Scholar 

  • Charness, G., & Levin, D. (2009). The origin of the winner’s curse: a laboratory study. American Economic Journal: Microeconomics,1(1), 207–236.

    Google Scholar 

  • Chen, T., Kalra, A., & Sun, B. (2009). Why do consumers buy extended service contracts? Journal of Consumer Research,36(4), 611–623.

    Google Scholar 

  • Cutler, D. M., & Zeckhauser, R. (2004). Extending the theory to meet the practice of insurance. Brookings-Wharton Papers on Financial Services,2004(1), 1–53.

    Google Scholar 

  • Dufwenberg, M., Gächter, S., & Hennig-Schmidt, H. (2011). The framing of games and the psychology of play. Games and Economic Behavior,73(2), 459–478.

    Google Scholar 

  • Einhorn, H. J., & Hogarth, R. M. (1985). Ambiguity and uncertainty in probabilistic inference. Psychological Review,92(4), 433.

    Google Scholar 

  • Epley, N. (2004). A tale of tuned decks? Anchoring as accessibility and anchoring as adjustment. In D. J. Koehler & N. Harvey (Eds.), The Blackwell handbook of judgment and decision making (pp. 240–256). Malden: Blackwell Publishing.

    Google Scholar 

  • Epley, N., & Gilovich, T. (2010). Anchoring unbound. Journal of Consumer Psychology,20(1), 20–24.

    Google Scholar 

  • Eyster, E., & Rabin, M. (2005). Cursed equilibrium. Econometrica,73(5), 1623–1672.

    Google Scholar 

  • Faro, D., & Rottenstreich, Y. (2006). Affect, empathy, and regressive mispredictions of others’ preferences under risk. Management Science,52(4), 529–541.

    Google Scholar 

  • Hendren, N. (2013). Private information and insurance rejections. Econometrica,81, 1713–1762.

    Google Scholar 

  • Ho, T. H., Lim, N., & Camerer, C. F. (2006). Modeling the psychology of consumer and firm behavior with behavioral economics. Journal of Marketing Research,43(3), 307–331.

    Google Scholar 

  • Hogarth, R. M., & Kunreuther, H. (1989). Risk, ambiguity, and insurance. Journal of Risk and Uncertainty,2(1), 5–35.

    Google Scholar 

  • Hogarth, R. M., & Kunreuther, H. (1995). Decision making under ignorance: Arguing with yourself. Journal of Risk and Uncertainty,10(1), 15–36.

    Google Scholar 

  • Holt, C. A., & Sherman, R. (1994). The loser’s curse. The American Economic Review,84(3), 642–652.

    Google Scholar 

  • Hsee, C. K., & Weber, E. U. (1997). A fundamental prediction error: Self–others discrepancies in risk preference. Journal of Experimental Psychology: General,126(1), 45.

    Google Scholar 

  • Huysentruyt, M., & Read, D. (2010). How do people value extended warranties? Evidence from two field surveys. Journal of Risk and Uncertainty,40(3), 197–218.

    Google Scholar 

  • Jindal, P. (2015). Risk preferences and demand drivers of extended warranties. Marketing Science,34, 39–58.

    Google Scholar 

  • Kagel, J. H., & Levin, D. (1986). The winner’s curse and public information in common value auctions. The American Economic Review,76(5), 894–920.

    Google Scholar 

  • Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica,47(2), 263–291.

    Google Scholar 

  • Kilka, M., & Weber, M. (2001). What determines the shape of the probability weighting function under uncertainty? Management Science,47(12), 1712–1726.

    Google Scholar 

  • Kőszegi, B., & Rabin, M. (2006). A model of reference-dependent preferences. The Quarterly Journal of Economics,121, 1133–1165.

    Google Scholar 

  • Koufopoulos, K., & Kozhan, R. (2014). Welfare-improving ambiguity in insurance markets with asymmetric information. Journal of Economic Theory,151, 551–560.

    Google Scholar 

  • Kreps, D. M., & Wilson, R. (1982). Sequential equilibria. Econometrica,50(4), 863–894.

    Google Scholar 

  • Kubovy, M., Rapoport, A., & Tversky, A. (1971). Deterministic vs probabilistic strategies in detection. Attention, Perception and Psychophysics,9(5), 427–429.

    Google Scholar 

  • Kunreuther, H., Hogarth, R., & Meszaros, J. (1993). Insurer ambiguity and market failure. Journal of Risk and Uncertainty,7, 71–87.

    Google Scholar 

  • Kunreuther, H., Novemsky, N., & Kahneman, D. (2001). Making low probabilities useful. Journal of Risk and Uncertainty,23(2), 103–120.

    Google Scholar 

  • Kunreuther, H. C., Pauly, M. V., & McMorrow, S. (2013). Insurance and behavioral economics: Improving decisions in the most misunderstood industry. New York: Cambridge University Press.

    Google Scholar 

  • Lichtenstein, S., Slovic, P., Fischhoff, B., Layman, M., & Combs, B. (1978). Judged frequency of lethal events. Journal of Experimental Psychology: Human Learning and Memory,4(6), 551.

    Google Scholar 

  • Luce, D. R. (1959). Individual choice behavior: A theoretical analysis. New York: Wiley.

    Google Scholar 

  • McFadden, D. (1980). Econometric models for probabilistic choice among products. Journal of Business,53(3), S13–S29.

    Google Scholar 

  • Moore, E., & Eckel, C. (2003). Measuring ambiguity aversion. Unpublished manuscript, Department of Economics, Virginia Tech.

  • Nyarko, Y., & Schotter, A. (2002). An experimental study of belief learning using elicited beliefs. Econometrica,70(3), 971–1005.

    Google Scholar 

  • Offerman, T., Sonnemans, J., & Schram, A. (1996). Value orientations, expectations and voluntary contributions in public goods. The Economic Journal,106(437), 817–845.

    Google Scholar 

  • Rabin, M., & Thaler, R. H. (2001). Anomalies: risk aversion. The Journal of Economic Perspectives,15(1), 219–232.

    Google Scholar 

  • Raghubir, P., & Menon, G. (1998). AIDS and me, never the twain shall meet: The effects of information accessibility on judgments of risk and advertising effectiveness. Journal of Consumer Research,25(1), 52–63.

    Google Scholar 

  • Rothschild, M., & Stiglitz, J. (1976). Equilibrium in competitive insurance markets: An essay on the economics of imperfect information. Quarterly Journal of Economics,90(4), 629–649.

    Google Scholar 

  • Sherris, M. (2006). Solvency, capital allocation, and fair rate of return in insurance. Journal of Risk and Insurance,73, 71–96.

    Google Scholar 

  • Stiglitz, J. (1977). Monopoly, non-linear pricing and imperfect information: The insurance market. Review of Economic Studies,44, 407–430.

    Google Scholar 

  • Sunstein, C. R., & Zeckhauser, R. (2010). Dreadful possibilities, neglected probabilities. In E. Michel-Kerjan & P. Slovic (Eds.), The irrational economist: Making decisions in a dangerous world (pp. 173–185). New York: Public Affairs.

    Google Scholar 

  • Sydnor, J. (2010). (Over) insuring modest risks. American Economic Journal: Applied Economics,2(4), 177–199.

    Google Scholar 

  • Tversky, A., & Fox, C. R. (1995). Weighing risk and uncertainty. Psychological Review,102(2), 269.

    Google Scholar 

  • Tversky, A., & Kahneman, D. (1983). Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment. Psychological Review,90(4), 293.

    Google Scholar 

  • Tversky, A., & Wakker, P. (1995). Risk attitudes and decision weights. Econometrica,63(6), 1255–1280.

    Google Scholar 

Download references

Acknowledgements

This study was funded by University of Macau (Grant number SRG2016-00070-FBA).

Author information

Authors and Affiliations

  1. Faculty of Business Administration, University of Macau, Macau, China

    Robin Chark

  2. Cambridge Judge Business School, University of Cambridge, Trumpington Street, Cambridge, CB2 1AG, UK

    Vincent Mak

  3. Department of Marketing, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong, China

    A. V. Muthukrishnan

Authors
  1. Robin Chark
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vincent Mak
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. V. Muthukrishnan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Robin Chark.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A Equilibrium analysis of the insurance trading model

In this appendix, we offer a game-theoretic analysis of the insurance trading model in the main text with an additional assumption that the Bernoulli utility functions of the two players (insurer and consumer) are common knowledge among them. We also allow for a general prior distribution for the loss probability q, which we label as F(·), in our analysis; in the experiment in this study, F(·) was specifically the prior uniform distribution over 0, 0.01, 0.02, … 0.5. Our objective is to formulate how, in equilibrium, an expected utility maximizing insurer would set the premium as a function of q, and how the consumer would form rational updated beliefs based on the premium. We focus on pure-strategy equilibria in which the insurer’s offered premium is a single-valued function of the true loss probability q, and, upon observing an offered premium, the consumer accepts or rejects the offer with probability one. We also make the convenient tie breaking assumption that, if a consumer is indifferent between accepting and rejecting an offer, he/she will accept the offer.

In addition to the notations introduced in the main text, denote the insurer I’s Bernoulli utility function as UI(·). Without loss of generality and for reasons of expositional convenience, we adopt the normalization assumption that UI(0) = 0. Thus, if there is no trade, I’s utility is UI(0) = 0. If there is a trade with premium p, I’s expected utility from the trade is q UI(pc − c) + (1 − q)∙UI(pc); I should offer a contract with premium p only if this quantity is not less than UI(0) i.e., only if

$$ q \le U_{I} \left( {pc} \right)/\left[ {U_{I} \left( {pc} \right) \, {-}U_{I} \left( {pc - c} \right)} \right] = q_{I} \left( p \right) , $$
(1a)

qI(p) being a function of p (note that UI(pc − c) is negative because pc − c < 0 and also because of our normalization assumption that UI(0) = 0). In the special case of a risk-neutral I, qI(p) = p. We then introduce the following result:

Lemma A1

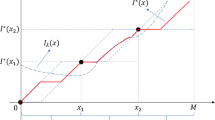
In equilibrium: (1) trade always occurs with the same premium, say p*, regardless of q; (2) if there is trade, the consumer’s updated belief of q upon observing offered premium p* is the prior distribution truncated over [0,\( q_{I} (p*) \)].

Proof

First note that \( q_{C} (p) \) strictly increases with p because UC(·) is strictly increasing in its argument. Next note that, given q, the higher the premium the higher the expected utility of the insurer in the event of a trade. If an insurer with q = q1 offers premium p in equilibrium in (rational) expectation of a trade (which would be realized in equilibrium), it must be because: (a) inequality (1) in the main text is satisfied at with q = q1, and (b) any higher p would lead to no trade because the consumer would reject the offer. Thus, any insurer with q < q1 also finds it optimal to offer premium p in expectation of a trade, since inequality (1) would still be satisfied. This implies that trade always occurs at the same premium, say p*, and must occur whenever inequality (1) is satisfied with premium p*, i.e., whenever q is less than or equal to \( q_{I} (p*) \); hence the lemma.

Lemma A1 captures the intuition that an insurer with a low loss probability would tend to mimic that of a higher loss probability as long as the consumer would accept the offer of the latter, because by pretending that the loss probability is higher than the true value, the insurer can potentially charge a higher premium than otherwise. This essentially leads to all insurers charging the same premium in the event of a trade, when the consumer could only infer that the true loss probability cannot be higher than some upper bound (i.e., \( q_{I} (p*) \)) because of inequality (1a), but nothing more. In that case, the consumer’s conditional expected value of q must be the expected value of the truncated distribution in Lemma A1, which is \( \int_{0}^{{q_{I} (p*)}} {qdF} /F(q_{I} (p*)) \).

Given an equilibrium, the consumer would have a well-defined willingness to pay, which is the highest premium at which the consumer would accept the offer. An expected utility maximizing insurer would, therefore, like to charge this willingness-to-pay as the premium as long as it satisfies inequality (1a), which then would lead to a trade. Therefore, the equilibrium premium with trade must be the maximum possible premium that satisfies Lemma A1 and inequality (1). This leads to the following:

Proposition A1

If \( p_{m} = \mathop {\hbox{max} }\limits_{{p \in (\underline{q} ,1)}} \left\{ {p:\int_{0}^{{q_{I} (p)}} {qdF} /F(q_{I} (p)) = q_{C} (p)} \right\} \) exists, then, in any equilibrium, the insurer presents an offer with premium p* = \( p_{m} \) < 1 whenever \( q \le q_{I} (p_{m} ) \), in which case the consumer accepts the offer. If \( p_{m} \) does not exist or if \( q > q_{I} (p_{m} ) \), there is no trade in equilibrium.

Proof

Any candidate p* that satisfies Lemma A1 and inequality (1) must satisfy \( \int_{0}^{{q_{I} \left( {p^{*} } \right)}} {qdF} /F\left( {q_{I} \left( {p^{*} } \right)} \right) \ge q_{C} \left( {p^{*} } \right) \). An expected utility maximizing insurer would choose to offer a premium p that is as high as possible if trade can result. The maximal value of p that satisfies \( \int_{0}^{{q_{I} (p)}} {qdF} /F\left( {q_{I} (p)} \right) \ge q_{C} (p) \) must be attained at either the upper bound of p’s domain, namely 1 or at the value \( p_{m} \) that solves \( \int_{0}^{{q_{I} \left( {p_{m} } \right)}} {qdF} /F\left( {q_{I} \left( {p_{m} } \right)} \right) = q_{C} \left( {p_{m} } \right) \). However, when p = 1, \( q_{I} (p) = 1 \), so that \( \int_{0}^{{q_{I} (p)}} {qdF} /F\left( {q_{I} (p)} \right) \) is simply the prior mean which must be less than \( q_{C} (p) = 1 \), and thus the equilibrium trade premium p* must be pm (if pm exists at all), and is offered by the insurer whenever \( q \le q_{I} (p_{m} ) \). If \( p_{m} \) does not exist or \( q > q_{I} (p_{m} ) \), there is no premium that can satisfy Lemma A1 and inequalities (1) and (1a) which leads to trade, and so there cannot be any trade. Note that the proposition is silent on out-of-equilibrium beliefs, such as what will be consumer’s belief had the insurer offered a premium p below p*—something that should occur with zero probability in equilibrium. On this issue, any updating that is consistent with Proposition A1 is admissible, a reasonable possibility being that q is always distributed according to the prior truncated over \( [0,q_{I} (p)] \), whatever p is.

Overall, Proposition A1 extends the intuition of Lemma A1 and highlights that the insurer would offer a premium that is the highest possible at which the consumer would (just) like to trade—at least as long as such a premium still incentivizes the insurer to trade. This should indeed lead to trade given the consumer’s equilibrium updating process, and the consistency requirement implies that the equilibrium premium with trade must be \( p_{m} \), if it exists. Hence, if \( p_{m} \) exists, the equilibrium has separating properties with which trade occurs whenever \( q \le q_{I} \left( {p_{m} } \right) \).

Finally, we note that while all equilibria under our consideration share the common characteristic of Proposition A1, they may differ in how insurers would charge if pm does not exist or when q > qI (pm). The only requirement in these cases is that the consumer would reject the offer in equilibrium. If pm does not exist, and the insurer assumes that the consumer always have some positive probability of accepting an offer (see footnote 1), the insurer will always present an offer in these cases with a premium p that satisfies q ≤ qI (p)—but which will be rejected by the consumer with probability one. That is, the equilibrium is a pooling one with no trade. If pm exists but q > qI (pm), Lemma A1 implies that the premium must be higher than pm for consumer’s updated belief as stated in the lemma to fulfill rational expectations. Again a premium p that satisfies q ≤ qI (p) would be appropriate.

Appendix B Sample instructions in the experiment

[All currencies are in Hong Kong dollars (US$1 ≈ HK$7.8).]

2.1 Instructions for the PLAY-AON condition

Welcome to our experiment. You will receive $70 for showing up, regardless of the results. In addition, ten of you will be chosen to receive a $100 endowment with some risk, i.e., the ones being selected may lose his/her endowment with some probability for the reason to be discussed below. You will make ten similar decisions and we will call them ten rounds.

2.1.1 The drivers

Imagine you have a car. The car may suffer from some type of mechanical failure or breakdown and needs to be repaired. You will choose between (1) taking a chance on the car breaking down and paying for a repair, which costs $100, and (2) purchasing insurance to insure yourself against having to pay for a repair. However, you do not know the exact probability of the breakdown. You only know the probability ranges from 0 to 50%. If you choose to purchase the insurance, you will pay the premium and keep the rest of your money. The risk is then transferred to the insurer.

2.1.2 The insurer

At the beginning of the experiment, one of you will be chosen randomly as the insurer. We have to determine the exact percentage chance out of the 0–50% range. Each of the percentage chances of the car needing a repair in the range is equally likely. The insurer will draw from a box a chip of 51 chips to determine the exact percentage chance of the car needing repair. (There are 51 numbers in the range of 0–50%: 0, 1, 2, 3, …, 49, 50.) Let us suppose the insurer draws a 9. Then the percentage chance of the car needing repair is 9%.

2.1.3 The premium

The probability will only be known to the insurer until the end of the experiment. After the insurer learns the percentage chance, he/she will set the price for the insurance (also known as the premium). Then the premium will be announced to all drivers.

2.1.4 The driver

As a driver, you are asked to make two decisions. First, the insurance decision is whether you accept the insurer’s offer and buy the insurance or not. Second, you are asked to guess the exact percentage chance drawn.

2.1.5 Driver’s payoff

After all of you have made all ten insurance decisions; for each round, one of the drivers will be chosen randomly to receive another $100 endowment. This driver will draw a chip from another box of 100 chips (1–100) to determine whether the car needs a repair or not. If the number is higher than the percentage chance, the car is fine. If the number the driver draws is equal to or smaller than the percentage chance of the car needing a repair, then the car has a breakdown. Following the above example where the drawn percentage chance is 9, if the driver draws a 10 or above, the car is fine. If the driver draws a 9 or smaller, the car breaks down. The cost of the repair is borne by either the driver or the insurer depending on the driver’s insurance decisions as discussed above. The cost of the repair simply goes back to the experimenter’s research fund.

2.1.6 Insurer’s payoff

Since there will be ten rounds, the maximum possible exposure for the insurer can be as much as $100 × 10 = $1000. Thus, only two out of ten rounds will be selected randomly to determine the insurer’s payoff. The insurer will receive (1) $70 for showing up, (2) an endowment of $200, and (3) the profit or loss from the two random rounds. For the remaining eight rounds, the insurer’s decisions are still effective but the counterparty becomes the experimenter, instead of the insurer.

2.1.7 The logistics

  1. 1.

    After all of you finished reading these instructions, we will randomly draw one of you to be the insurer.

  2. 2.

    In the beginning of each round, the insurer will draw from a box a chip numbered 0–50 to determine the exact percentage chance of failure. Thus, the percentage chances of failure vary from round to round. The percentage chances are private information to the insurer. You will only know these numbers after all ten rounds.

  3. 3.

    The insurer set the premium for the insurance.

  4. 4.

    The premium is announced.

  5. 5.

    Then you are asked to decide if you want to buy the insurance or not at the premium set by the insurer.

  6. 6.

    You are also asked to guess the percentage chance drawn by the insurer. You will get an extra $20 for each correct guess. Since there are ten rounds, you have ten chances.*Footnote 2

  7. 7.

    Your decisions will be collected. Please remember to fill out your name and student ID.

  8. 8.

    Since we have ten rounds, steps 2–7 are repeated ten times.

  9. 9.

    After we collect all your decisions, we will randomly draw one driver for each round. Since we have ten rounds, ten drivers will be randomly selected.

  10. 10.

    Each of the drivers will draw a number from 1 to 100 as described above to determine if his/her car needs a repair. These drivers’ payoff will depend on (1) their insurance decisions, (2) the number drawn by the insurer representing the percentage chance of failure, and (3) the number drawn by themselves determining if their cars need repair or not.

  11. 11.

    The 10% chances drawn by the insurer will be revealed to all of you. For all drivers (not limited to the 10 who are selected), if you guess correctly what the percentage chance the insurer drawn, for each correct guess an extra $20 will be added to your payoffs. The table below is for you to record your guesses.

  12. 12.

    We will pay you one by one and the experiment is over.

2.2 Note

  • At the end of the experiment, we will pay you individually and privately.

  • Do not communicate with any other participant during this experiment. Participants who do not abide by this rule will be excluded from the experiment and from all payments.

  • If you have questions concerning the experiment please raise your hand and I will come to you. In order not to influence other participants’ decisions, your questions will be addresses privately.

  • Thank you again for your participation in our research.

2.3 Instructions for the SPEC-AON condition

Welcome to our experiment. There are two parts in this experiment and you are participating in the part 2. Part 1 has already run previously. In this part, you will make ten similar decisions and we will call them ten rounds. The relationship between the outcomes of part 1 and your decisions and payoffs will be described below.

2.3.1 The game in part 1

This game was repeated ten times (rounds) and involved a number of players: one insurer and some drivers.

2.3.2 The drivers

Each driver has a car. The car may suffer from some type of mechanical failure or breakdown and needs to be repaired. He/she will choose between (1) taking a chance on the car breaking down and paying for a repair, which costs $100, and (2) purchasing insurance to insure himself/herself against having to pay for a repair. However, he/she does not know the exact probability of the breakdown. He/she only knows the probability ranges from 0 to 50%. If he/she chooses to purchase the insurance, he/she will pay the premium and keep the rest of his/her money. The risk is then transferred to the insurer.

2.3.3 The insurer

At the beginning of the experiment, one of the participants will be chosen randomly as the insurer. We have to determine the exact percentage chance out of the 0–50% range. Each of the percentage chances of the car needing a repair in the range is equally likely. The insurer will draw from a box a chip of 51 chips to determine the exact percentage chance of the car needing repair. (There are 51 numbers in the range of 0–50%: 0, 1, 2, 3, …, 49, 50.) Let us suppose the insurer draws a 9. Then the percentage chance of the car needing repair is 9%.

2.3.4 The premium

The probability will only be known to the insurer until the end of the experiment. After the insurer learns the percentage chance, he/she will set the price for the insurance (also known as the premium). Then the premium will be announced to all drivers.

2.3.5 The insurance decision

Seeing the premium set by the insurer, the drivers are asked to make insurance decisions on whether to accept the insurer’s offer and buy the insurance or not.

2.3.6 Driver’s payoff

After all of the drivers have made all ten insurance decisions, for each round, one of the drivers will be chosen randomly to draw a chip from another box of 100 chips (1–100) to determine whether the car needs a repair or not. If the number is higher than the percentage chance, the car is fine. If the number the driver draws is equal to or smaller than the percentage chance of the car needing a repair, then the car has a breakdown. Following the above example where the drawn percentage chance is 9, if the driver draws a 10 or above, the car is fine. If the driver draws a 9 or smaller, the car breaks down. The cost of the repair is borne by either the driver or the insurer depending on the driver’s insurance decisions as discussed above. The cost of the repair simply goes back to the experimenter’s research fund.

2.3.7 Insurer’s payoff

The insurer will receive the profit or loss from the insurance contracts on top of his/her show up fee.

2.4 Part 2

2.4.1 Your task

Observing the premium set by the insurer, you are asked to make ten guesses on the percentage chances drawn by the insurer in each round.

2.4.2 Your payoff

You are asked to make your estimation of the probabilities about the percentage chance in each round. You are asked to report these probabilities in percentages. You will get an extra $20 for each correct guess. Since there are ten rounds, you have ten chances. The 10% chances drawn by the insurer will be revealed to all of you at the end of this experiment.

2.4.3 The logistics

  1. 1.

    Part 1 has already run previously. The percentage chances and the premium set by the insurer in the ten rounds were recorded.

  2. 2.

    After all of you finished reading these instructions, the ten premium set by the insurer will be announced.

  3. 3.

    You are asked to guess the percentage chance (0–50%) drawn by the insurer.

  4. 4.

    This sheet will be collected. Please remember to fill out your name below. The amount will be determined later.

  5. 5.

    The actual outcomes of whether a breakdown occurred or not will be revealed to all of you. Remember the breakdown was jointly determined by the percentage chances (0–50%) drawn by the insurer and the drivers drawn from the 100 chips.

  6. 6.

    Your decisions will be collected. Your payoff will be calculated accordingly. You will be paid one by one and the experiment is over.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chark, R., Mak, V. & Muthukrishnan, A.V. The premium as informational cue in insurance decision making. Theory Decis 88, 369–404 (2020). https://doi.org/10.1007/s11238-019-09732-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11238-019-09732-5

Keywords

Search

Navigation