Abstract
In this paper, we provide a Bayesian analysis of the well-known surprise exam paradox. Central to our analysis is a probabilistic account of what it means for the student to accept the teacher’s announcement that he will receive a surprise exam. According to this account, the student can be said to have accepted the teacher’s announcement provided he adopts a subjective probability distribution relative to which he expects to receive the exam on a day on which he expects not to receive it. We show that as long as expectation is not equated with subjective certainty there will be contexts in which it is possible for the student to accept the teacher’s announcement, in this sense. In addition, we show how a Bayesian modeling of the scenario can yield plausible explanations of the following three intuitive claims: (1) the teacher’s announcement becomes easier to accept the more days there are in class; (2) a strict interpretation of the teacher’s announcement does not provide the student with any categorical information as to the date of the exam; and (3) the teacher’s announcement contains less information about the date of the exam the more days there are in class. To conclude, we show how the surprise exam paradox can be seen as one among the larger class of paradoxes of doxastic fallibilism, foremost among which is the paradox of the preface.



Similar content being viewed by others
Notes
Strictly speaking, the teacher’s announcement does not imply that the student will receive exactly one surprise exam during the term. In what follows, when we speak of “the surprise exam” (or “the exam”) this phrase may be understood as referring to the first surprise exam that the student will receive.
The paradox in its various forms has a long and well-documented history. While a similar scenario to the surprise exam paradox was described in O’Connor (1948), curiously, it seems to have only been first acknowledged that a surprise event could occur despite its having been announced in Scriven (1951). A detailed history of the paradox’s origins can be found in Sorensen (1988, Chap. 7). For a survey of the various approaches to the problem appearing in the literature prior to 1983, see Margalit and Bar-Hilel (1983). A more recent survey can be found in Chow (1998). The most recent online version of Chow’s paper (which can be found at arXiv:math/9903160v4 [math.LO]) contains a comprehensive bibliography listing all the papers that are relevant to the paradox published prior to June 2011.
This is essentially the solution proposed by Quine (1953) except that Quine describes the illicit assumption as the assumption that the student knows (rather than accepts) that he will receive a surprise exam prior to the last day of class. Quine rejects this assumption on the grounds that if the student is prepared to accept the teacher’s announcement as contradictory after following through with the fallacious line of reasoning, then he could not have known that he would receive a surprise exam on the basis of the teacher’s announcement. Kripke (2011) criticizes Quine’s response to the problem on the grounds that under normal conditions the student does, in fact, know that he will receive a surprise exam upon hearing the teacher’s announcement.
Admittedly, there is a plausible reading of surprise according to which a surprising event is one which is unexpected. But here “unexpected” has a meaning akin to that of the term “undesirable”, where to describe a certain state of affairs in this way is not merely to say that one lacks any desire that it should be so, but instead that one desires that it should not be so.
There are at least three limitations of this account that prevent it from serving as a satisfactory general definition of a surprising event. First, whereas a surprising event is here defined relative to the agent’s expectations at the time of that event’s occurrence, strictly speaking, a surprising event ought to be defined relative to the expectations of the agent at the time at which he learns of that event’s occurrence. Second, the proposed account ignores the possibility of an agent’s being surprised by an event the occurrence of which he has simply failed to consider. Thus, for example, John may be surprised to discover that there is a spaceship hovering in the sky outside his window despite the fact that, prior to looking out his window, he may not have explicitly formed any expectation of observing a spaceship-less sky. Third, to describe an event as surprising not only implies something about one’s epistemic state at the time at which one learned of its occurrence, but also says something about the phenomenology of the discovery itself. A surprising event is not just unexpected but is also, in some sense, startling or shocking. We will assume that for the purposes of analyzing the paradox such subtleties may be ignored.
Probabilistic approaches to the paradox are not new. In particular, Clark (1994a, b), Hall (1999), Borwein et al. (2000) and Schumacher and Westmoreland (2008) all adopt probabilistic approaches to the problem. The latter two, in particular, are worth mentioning. Borwein et al. (2000) proposes a fascinating analysis of the paradox in which no categorical criterion is proposed as to when an exam is to count as a surprise exam, but is instead framed entirely in terms of the degree to which an exam is surprising. The specific question that the paper asks is what probability distribution maximizes the student’s expected degree of surprisal, as measured by the negative log of the probability. Schumacher and Westmoreland (2008) proposes a very similar framework to that developed in this paper. However, their account of what it means to coherently accept the teacher’s announcement differs substantially from our own.
In what follows, we are not always careful to distinguish between conditionalization as a norm governing the static process of suppositional reasoning, and conditionalization as a norm governing the dynamic process of belief revision. While we often give weight to considerations of fluency or style over those of accuracy, in fact, it would be more true to our intention to think of conditions (1) and (2) as norms governing the student’s suppositional reasoning immediately following the teacher’s announcement, so that all that we are concerned with is the internal coherence of the student’s doxastic state at that particular time.
We adopt the usual convention that the conjunction of an empty set of events is the necessary event, \(\top \), and that the disjunction of an empty set of events is the impossible event, \(\bot \). In accordance with this convention, it follows from the above definition that \(\sigma _P(E_1)=P(\lnot E_1|\top )=P(\lnot E_1)\). The quantity \(\sigma _P(E_n)\) is only well defined if \(P(\lnot E_1\wedge \cdots \wedge \lnot E_{n-1})>0\). If this is not the case, we will stipulate that \(\sigma _P(E_n)=0\).
If, for example, John is told by Lev that he will be surprised by the ending of the book, then what must hold of the conclusion of the book in order for Lev’s statement to be true depends on how John responds to Lev’s remark. If, in response to Lev’s remark, John is led to expect that it was the Butler who committed the murder, then Lev has spoken truly just in case the Butler did not do it, for it is only in this case that John’s expectations will be confounded. If, on the other hand, John comes to believe on the basis of Lev’s remark that it was the Colonel who did it, then if it turns out that the true culprit was the Butler, Lev will have spoken truly. It may be noted, in contrast, that if John is told by Lev that he would have been surprised by the ending of the book, then what must hold of the conclusion of the book in order for Lev’s statement to be true, depends only on John’s doxastic state prior to Lev’s remark.
A similar pragmatic explanation can be given as to why it is wrong to assert of an arbitrarily chosen ticket in a fair lottery that one was surprised to discover that that ticket had won (despite the probability of its winning being extremely low). Since the lottery is fair, this assertion implies that the surprise index \(\alpha \) has been set at a value such that the claim “the outcome of the lottery was surprising” supplies no information about the actual outcome of the lottery.
In this more general framework, the student’s epistemic state is not modeled by a probability function, but instead by a sequence of modal operators \(A_1,\ldots ,A_N\), where \(A_n(E)\) means that the student accepts E just prior to the nth day of class. To say that acceptance is dogmatic is to say that \(A_n(E)\) implies \(A_n(A_m(E))\), for all \(1\le n\le m\le N\). If acceptance is dogmatic, then given only very modest assumptions about acceptance, it can be shown that the student cannot coherently accept that he will receive a surprise exam. In other words, it can be shown that the following two claims imply that the student’s acceptations at the time of the teacher’s announcement are contradictory.
-
1.
\(A_1(E_1\vee \cdots \vee E_N)\)
-
2.
\(A_1(E_n\rightarrow A_n(\lnot E_n))\), for \(n=1,\ldots ,N\).
For an analysis of the paradox along these lines, see Kripke (2011).
-
1.
This can be made precise as follows. We define a probabilistic model of the modal language described in fn. 11 as a pair \((E_n,P)\), where P is a probability function defined on the non-modal sentences of the language. We say that \((E_n,P)\) satisfies the proposition \(A_m(\varphi )\) if a Bayesian agent with prior probabilities P would assign a probability of 1 to \(\varphi \) conditional on what he would know just prior to the mth day of class were the exam to be administered on day n, i.e.:
$$\begin{aligned} (E_n,P)\models A_m(\varphi ) \text { iff } P\left( \bigvee \{E_i: (E_i,P)\models \varphi \}|\psi _{n,m}\right) =1 \end{aligned}$$where:
$$\begin{aligned} \psi _{n,m}=\left\{ \begin{array}{ll} \lnot E_1\wedge \cdots \wedge \lnot E_{m-1} &{}\quad \text {if }m\le n\\ E_n &{}\quad \text {if }n<m \end{array}\right. \end{aligned}$$It is easy to confirm that, relative to this semantics, acceptance is dogmatic, i.e., for any \(n\le m\), and any sentence \(\varphi \):
$$\begin{aligned} A_n(\varphi )\models A_n(A_m(\varphi )) \end{aligned}$$Strictly speaking, these examples do not imply that \(\beta \) depends on these contextual features, since, in both of these examples, the constraints only fix the lower-bound for the acceptance index. Scenarios in which precise (non-trivial) constraints are imposed on both the upper- and lower-bounds of \(\beta \) are not so easy to fabricate. A general (albeit vague) constraint that applies in almost all contexts of assertion is that the value of \(\beta \) be less than 1 since it is only in highly contrived settings that an assertion is understood as licensing a bet on the asserted claim at any odds whatsoever.
If
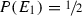 , then
, then 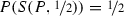 . This means that in the one-day case, the student can judge it to be as likely as not that he will receive the exam on a day on which he will judge it to be as likely as not that he will not receive the exam. This, however, is not a possible explication of the claim that the student expects to receive a surprise exam, since, in this case, the condition \(P(S(P,\alpha ))\ge \beta \) is only satisfied for
. This means that in the one-day case, the student can judge it to be as likely as not that he will receive the exam on a day on which he will judge it to be as likely as not that he will not receive the exam. This, however, is not a possible explication of the claim that the student expects to receive a surprise exam, since, in this case, the condition \(P(S(P,\alpha ))\ge \beta \) is only satisfied for 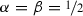 . Given, however, that the student could be said to expect to receive a surprise exam if the surprise and acceptance indices could both be raised by any (infinitesimal) amount, it may perhaps be more accurate to describe an acceptance of the teacher’s announcement in the one-day case as “borderline” incoherent.
. Given, however, that the student could be said to expect to receive a surprise exam if the surprise and acceptance indices could both be raised by any (infinitesimal) amount, it may perhaps be more accurate to describe an acceptance of the teacher’s announcement in the one-day case as “borderline” incoherent.Suppose, for example, that \(N=2\). Then, if the student’s probabilities are given by \(P(E_1)=0.45\); \(P(E_2)=0.1\); and \(P(E_3)=0.45\), then \(P(S(P,0.55))\ge 0.55\), and so the student can coherently be described as expecting to receive a surprise exam. The general claim that for all \(N\ge 2\) there exists a probability function satisfying \(P(S(P,\alpha ))\ge \beta \), for some
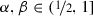 is a corollary of Theorem 5 below, the proof of which is given in Appendix 1.
is a corollary of Theorem 5 below, the proof of which is given in Appendix 1.Proof. Suppose for contradiction that
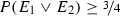 . It follows from the fact that
. It follows from the fact that 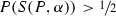 that
that 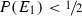 . But then \(P(E_2)>P(E_3)\), which means that
. But then \(P(E_2)>P(E_3)\), which means that 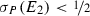 , and so, since
, and so, since 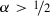 , \(S(P,\alpha )=E_1\). But this means that
, \(S(P,\alpha )=E_1\). But this means that  . Contradiction.
. Contradiction.Following the approach adopted in Kripke (2011), we may formulate such auxiliary assumptions by appeal to the notion of a “school rule”, where the function of such a rule is to provide the student with grounds for dogmatically accepting a given proposition independently of any additional information that he may receive. Thus, if we suppose that there is a school rule in place requiring that, in every class, an exam must be given (so that the effect of the teacher’s announcement is simply to inform the student of the fact that the exam that he is certain that he will receive, will also be a surprise) then, for the reasons outlined above, the student cannot coherently accept the teacher’s announcement if the class meets twice. Hence, an alternative way of formulating the above explanation of what is odd about the teacher’s announcement in the two-day case is that the announcement cannot be accepted in any context in which there is (in effect) a school rule in place requiring that the student be given an exam.
Not everyone thinks so. For example, Thalos (1997) provides a resolution to the puzzle that is explicit in its appeal to causal intuitions.
This is obvious, since to assign a probability of 1 to the event \(E_1\vee E_2\vee E_3\) has the effect of reducing the problem to the two-day case, and, as we have already seen, the student can expect to receive a surprise exam if the class meets only twice.
Kripke suggests that this approach can be generalized so as to apply to the case in which \(N>2\). He writes:
What if there are many days?\(\ldots \) Once again, we could invoke the “rule of the school” device. We can suppose that it is long-settled school policy that the exam must be given on a day when the students do not know that it will be given, even on the day before. And, of course, we also suppose that school policy demands an exam. Given these things, the supposition that the exam will be given on day \(N-1\) will lead to a contradiction of the appropriate premises. This type of idea could be iterated to exclude successive days from the list. The rule of the school will get successively more complicated and involve iterations of knowledge about knowledge, lack of knowledge, and the preservation of the situation. (Kripke 2011, p. 38)
This last sentence is vague, and it is unclear how exactly Kripke intends to complicate the school rules in a natural way so as to exclude successive days of class, one at a time. The rule that he appeals to in the three-day case is simply the rule requiring that the student be given, not only an exam, but a surprise exam. But this rule, in fact, makes the teacher’s announcement incoherent no matter how many days there are in class.
Sober (1998) offers an analysis of the surprise exam paradox that appeals to this type of adversarial relationship between the student and the teacher.
In Hall (1999), a similar rationale is offered in support of the claim that, in response to the teacher’s announcement, the student ought to conclude that the exam is unlikely to be given on the last day of class (in Hall’s example, the class meets five times, beginning on Monday and ending on Friday):
If the professor waits until Friday to give the exam, then she will have acted in such a way that the student can no longer justifiably believe that she has spoken truly. Worse: her announcement will come true precisely because she has waited so long that the student can no longer trust it, and so cannot take it as providing him with reason enough to believe that there will be an exam. That’s utterly sneaky—in contrast with, say, a Wednesday exam, which would warrant no such accusation. Furthermore, the professor is perfectly aware that a Friday exam will have this effect; so unless she wishes to be quite mischievously deceptive, she will not wait that long. The student knows all this—and has, moreover, no reason aside from the announcement to consider the professor deceptive in this way. So [the probability of a Friday exam] should \(\ldots \) be small \(\ldots \). (Hall 1999, p. 689)
Hall’s point, in this passage, is that the student ought to assign a low probability to receiving the exam on the last day of class, since were he to receive the exam that day, he would know that the teacher’s plan was to trick him, and presumably he has no reason to believe that the teacher is anything but honest.
If \(P(\lnot E_1\wedge \cdots \wedge \lnot E_{n-1})=0\), then \(P_n\) is not well defined. In this case, as before, we will simply stipulate that \(E_n\) is not included in \(S_1(P)\). This stipulation obviously has no effect on \(P(S_1(P))\).
This is a direct corollary of Theorem 5, the proof of which is given in Appendix 1.
For example, Williamson (2000) presents a version of the paradox where the school’s custodian has seen, from a distance, a date for a surprise exam marked on the calendar and has informed the students of what he has seen.
Consider, for example, a laboratory setting in which test tubes are used to store very small amounts of liquid. In such a setting, when one says that all the test tubes are full, this can be understood to mean that all the test tubes contain a small amount of liquid.
This is reflected in the fact that one glass is fuller than another, in any context, if the former is closer to a completely full glass (and farther from a completely empty one) than the latter. For a semantics of gradable adjectives that accounts for this fact about the use of such adjectives in comparative constructions, see Kennedy (2007)
It may be noted that this probability distribution is a simple Bernoulli distribution, i.e., it is that which the student would adopt were he to believe that prior to each class the teacher decides whether or not to give the student the exam that day by tossing a coin with bias \(\alpha \) in favor of heads, and administering the exam just in case the coin lands showing tails. This may strike the reader as odd since it may seem as if the student is somehow obtaining substantial information as to the nature of the chance mechanism by which the date of the exam is to be determined simply by interpreting the teacher’s announcement strictly. However, in the Bayesian framework, it is not assumed that an agent’s subjective probabilities reflect any judgment as to the objective chances with which various events will occur.
In the 5-day case, Hall considers the following probability distribution:
$$\begin{aligned} P(E_n)=\left\{ \begin{array}{ll} 0.31 &{}\quad n=1,2,3\\ 0.062 &{}\quad n=4\\ 0.007 &{}\quad n=5\\ 0.001 &{}\quad n=6\\ \end{array}\right. \end{aligned}$$He notes that, “\(\ldots \) it is not difficult to argue that [this distribution] describes a rationally appropriate response the student can have to the announcement – at least, on the assumption that the professor has heretofore given the student no reason to consider [the teacher] untruthful, deceptive, or devious.” (Hall 1999, p. 687) However, putting \(\beta =0.99\) (as Hall does), we can see that, in this case, the student not only expects (or to use Hall’s language, “knows”) that he will receive a surprise exam, but that he also expects (“knows”) that he will receive the exam prior to the last day of class.
Hall (1999) criticizes the analysis of the paradox given in Wright and Sudbury (1977), claiming that: “They are at pains to insist that an adequate account of the surprise exam paradox must show how the [teacher’s] announcement can be informative. But their account does nothing whatsoever to explain what is distinctively informative about [his] claim that the exam will come as a surprise.” (p. 684) While Hall is quite right to insist that an account of the paradox be able to explain what is informative about the claim that the exam will come as a surprise, a satisfactory account should further explain why the informativeness of this claim decreases with increasing N. Hall’s account cannot explain this fact.
The information entropy of a probability distribution P is given by:
$$\begin{aligned} H(P)= \sum _{n=1}^{N+1} P(E_n)\log P(E_n) \end{aligned}$$The higher the entropy of P, the less information it contains about when the exam will be given, with H taking its maximum value of \(\log (N+1)\) when P is the uniform distribution.
We acknowledge that “belief” is an ambiguous term that may refer to a variety of different cognitive states, not all of which stand in this particular relation to surprise. For example, the sense in which one may be said to have a “belief” in what is, at present, our best scientific account of the world, is one which seems compatible with an expectation that these accounts will ultimately turn out to be false. Consequently, the question of how to model scientific fallibilism (when it is grounded on a pessimistic meta-induction, for example) is not the same sort of question as how to model the student’s acceptance of the teacher’s announcement. Arló-Costa and Pedersen (2012) offers a brief survey of the types of qualitative beliefs that have been discussed in the literature. They consider full beliefs [c.f. Levi (1980)], plain beliefs [c.f. Spohn (2012)], and expectations [c.f. Gärdenfors (1994)] as distinct notions of qualitative belief. Finally, it is worth pointing out one consequence of considering beliefs that have the proposed inverse relation to surprise. Since one would not and should not be surprised to learn that an arbitrary ticket in a fair lottery had won (see fn. 10), then one neither would nor should believe (in the relevant sense) that each ticket will lose. In this sense, the lottery paradox is not analogous to the surprise exam paradox since the lottery paradox relies upon the intuition that it is rational to believe that any given ticket in a fair lottery will lose.
The standard presentations construe the preface paradox as resulting from two intuitions concerning rational belief. The first is the conjunction principle, which states that if it is rational to believe that P and rational to believe that Q, then it is rational to believe that P and Q. The second is the no-contradiction principle, which states that it is never rational to believe an explicit contradiction, e.g., that P and not-P. The problem then is to explain how, in light of these two intuitions, the author can both possess a rational belief in each of the claims that she makes in her book, and also a rational belief to the effect that at least one these claims is false, since the conjunction of all of these beliefs yields an explicit contradiction. The standard response, defended in Makinson (1965), Klein (1985), Kyburg (1997), and Foley (1993), is to reject the conjunction principle. Our intent in this section is not to discuss the preface paradox as it is traditionally presented, but rather to highlight the ways in which our resolution of the surprise exam paradox can be brought to bear on this particular problem.
An added benefit of viewing the author as expressing her fallibility in terms of surprise is that we avoid some hard to interpret expressions of fallibility that are used in most presentations of the preface paradox. See Kim (2015) for a detailed discussion.
The line of reasoning employed by the student to produce a paradoxical conclusion can also be employed by the author to the same effect. We simply have to situate the story in a thought experiment in which an omniscient oracle calls our historian and tells her that she will receive a call once a day and be told, starting with the first claim and ending with the last, whether or not that particular claim is true. The oracle then announces that the author will receive news of a surprising error. It is then straightforward to see that the student’s reasoning can be used, mutatis mutandis, by the author.
It is worth reminding the reader that in our treatment of the surprise exam paradox, we do not assume that there is only one surprise exam during the term (see fn. 1). Instead, we simply focus our discussion on the first surprise exam. Therefore, we can apply our resolution straightforwardly to the preface paradox so long as we make it clear that we are talking about the first surprising error. In doing so, we allow for the possibility that there is more than one error in the book.
There are some advantages to considering the surprise version of the preface paradox and adopting our proposed solution. First, the surprise version makes no assumptions about what is expressed by the author’s expression of fallibility. In this version, determining what is expressed becomes a crucial part of explaining how the author coherently accepts her own announcement of fallibility. In contrast, one problem facing many discussions of the preface paradox is that they are grounded in contentious assumptions about what is expressed by an author’s expression of fallibility. Furthermore, by leaving what can be expressed by the author’s prefatory remarks as an interpretative task, we are viewing the puzzle of accepting one’s own fallibility not as a purely epistemic puzzle. Rather, on our view of the puzzle, part of the difficulty in accepting an announcement of one’s fallibility is determining how strictly one can be speaking when expressing one’s fallibility. Our solution relies upon the idea that we can express varying degrees of fallibility and as a result, there are varying degrees to which one may accept one’s own fallibility.
References
Arló-Costa, H., & Pedersen, A. P. (2012). Belief and probability: A general theory of probability cores. International Journal of Approximate Reasoning, 53(3), 293–315.
Borwein, D., Borwein, J. M., & Marechal, P. (2000). Surprise maximization. The American Mathematical Monthly, 107(6), 517–527.
Chow, T. Y. (1998). The surprise examination or unexpected hanging paradox. American Mathematical Monthly, 105, 41–51.
Clark, D. (1994a). How expected is the unexpected hanging? Mathematics Magazine, 67(1), 55–58.
Clark, R. (1994b). Pragmatic paradox and rationality. Canadian journal of philosophy, 24(2), 229–242.
Foley, R. (1993). Working without a Net. Oxford: Oxford University Press.
Gärdenfors, P. (1994). The role of expectations in reasoning. Heidelberg: Springer.
Hall, N. (1999). How to set a surprise exam. Mind, 108(432), 647–703.
Kennedy, C. (2007). Vagueness and grammar: The semantics of relative and absolute gradable adjectives. Linguistics and Philosophy, 30(1), 1–45.
Kim, B. (2015). This paper surely contains some errors. Philosophical Studies, 172(4), 1013–1029.
Klein, P. (1985). The virtues of inconsistency. The Monist, 68(1), 105–135.
Kripke, S. (2011). On two paradoxes of knowledge. In Philosophical troubles: Collected papers (Vol. 1). New York: Oxford University Press.
Kyburg, J. H. E. (1997). The rule of adjunction and reasonable inference. Journal of Philosophy, 94(3), 109–125.
Levi, I. (1980). The enterprise of knowledge. Cambridge, MA: MIT Press.
Makinson, D. C. (1965). The paradox of the preface. Analysis, 25, 205–207.
Margalit, A., & Bar-Hilel, M. (1983). Expecting the Unexpected. Philosophia, 13(3–4), 263–288.
O’Connor, D. J. (1948). Pragmatic paradoxes. Mind, 57(227), 358–359.
Quine, W. V. (1953). On a so-called paradox. Mind, 62(245), 65–67.
Schumacher, B., & Westmoreland, M. (2008). Reverand Bayes takes the unexpected examination. Math Horizons, 16(1), 26–27.
Scriven, M. (1951). Paradoxical announcements. Mind, 60(239), 403–407.
Sober, E. (1998). To give a surprise exam, use game theory. Synthese, 115(3), 355–373.
Sorensen, R. A. (1988). Blindspots. Oxford: Oxford University Press.
Spohn, W. (2012). The laws of belief: Ranking Theory and its philosophical applications. Oxford: Oxford University Press.
Thalos, M. (1997). Conflict and co-ordination in the aftermath of oracular statements. The Philosophical Quarterly, 47(187), 212–226.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Wright, C., & Sudbury, A. (1977). The paradox of the unexpected examination. Australasian Journal of Philosophy, 55, 41–58.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
For a given probability P, let \(\sigma ^0_P=\sigma _P\) and let:

Given, the event \(S_{m-1}(P)\) (\(m\ge 1\)), put

and

In this appendix, we will prove the following result:
Theorem 5
For any \(m\ge 0\), there exists a probability function P satisfying:

for all \(i=0,\ldots ,m\), if and only if \(N>m+1\).
We first establish the following lemma:
Theorem 6
For any probability P and any \(m\ge 0\), \(S_{m+1}(P)\models S_m(P)\).
Proof
The proof will proceed by induction on m. Suppose, for contradiction, that \(E_n\models S_1(P)\) but \(E_n\not \models S_0(P)\). From the fact that \(E_n\models S_1(P)\), it follows that  . But since \(E_n\not \models S_0(P)\):
. But since \(E_n\not \models S_0(P)\):

Thus,  , and so, since
, and so, since  , \(E_n\models S_0(P_n)\). But since \(\sigma _P(E_n)=\sigma _{P_n}(E_n)\), this contradicts the assumption that \(E_n\not \models S_0(P)\). Hence, \(S_1(P)\models S_0(P)\).
, \(E_n\models S_0(P_n)\). But since \(\sigma _P(E_n)=\sigma _{P_n}(E_n)\), this contradicts the assumption that \(E_n\not \models S_0(P)\). Hence, \(S_1(P)\models S_0(P)\).
Now, assume that, for any probability P, \(S_m(P)\models S_{m-1}(P)\) (\(m\ge 1\)) and let \(E_n\models S_{m+1}(P)\). Then, \(P(\lnot E_1\wedge \cdots \wedge \lnot E_{n-1})>0\) and  . But since, by assumption, \(S_m(P)\models S_{m-1}(P)\) it follows that
. But since, by assumption, \(S_m(P)\models S_{m-1}(P)\) it follows that  , and so \(E_n\models S_m(P)\). Hence, \(S_{m+1}(P)\models S_m(P)\), which completes the induction. \(\square \)
, and so \(E_n\models S_m(P)\). Hence, \(S_{m+1}(P)\models S_m(P)\), which completes the induction. \(\square \)
We now proceed to the proof of Theorem 5. To prove the only-if direction of the claim, it suffices to show that for any probability P:

The proof proceeds by induction on N. If \(N=1\), then

for any probability P. Now let \(N>1\), and suppose that, for all \(i=1,\ldots ,N-1\), there is no probability P with \(P(E_1\vee \cdots \vee E_{N-i+1})=1\) satisfying

It follows that

for \(i=1,\ldots ,N-1\), for otherwise, the function defined by
would satisfy (5). But (6) implies that
for \(i=1,\ldots ,N-1\), and so, from Theorem 6, we have
for \(i=1,\ldots ,N-1\). Moreover, since \(E_{N+1}\not \models S_0(P)\), by Theorem 6, \(E_{N+1}\not \models S_{N-1}(P)\), and so we have \(S_{N-1}(P)\models E_1\). Now, suppose that  . Then
. Then  , which implies that \(E_1\not \models S_0(P)\). But then, by Theorem 6, \(E_1\models S_{N-1}(P)\), and so \(S_{N-1}(P)\equiv \bot \). Contradiction. Hence,
, which implies that \(E_1\not \models S_0(P)\). But then, by Theorem 6, \(E_1\models S_{N-1}(P)\), and so \(S_{N-1}(P)\equiv \bot \). Contradiction. Hence,  .
.
We now prove the if direction of Theorem 5. Suppose that \(m+1<N\). We will construct a probability P satisfying:

for \(i=0,1,\ldots ,m\).
Let c be any value in the open interval  , and for each \(n=1,\ldots ,N+1\), let
, and for each \(n=1,\ldots ,N+1\), let
Then P is a probability function. Moreover, for any k such that \(1\le k\le N+1\):
Since  , it follows that \(S_0(P_k)= E_k\vee \cdots \vee E_N\), and so:
, it follows that \(S_0(P_k)= E_k\vee \cdots \vee E_N\), and so:
But since c is in the interval  , it follows that
, it follows that
Now suppose that
for some \(1<i<m \). Then \(S_i(P_k)=E_k\vee \cdots \vee E_{N-i}\), and so
But since c is in the interval  , it follows that
, it follows that
Hence, by induction, (7) holds for all \(i=1,\ldots ,m\). This (together with the fact that \(S(P_0)= E_1\vee \cdots \vee E_N\)) implies that \(S_i(P)= E_1\vee \cdots \vee E_{N-i}\), for \(i=0,1,\ldots ,m\). But then, since \(m<N-1\):

for \(i=0,1\ldots ,m\).
Appendix 2
In this appendix, we will prove Theorems 3 and 4. Both propositions follow straightforwardly from the following lemma:
Theorem 7
For each  , let
, let
Then, \(P_\alpha (S(P_\alpha ,\alpha ))\ge P(S(P,\alpha ))\), for any probability P. Moreover, the inequality is strict unless \(P= P_\alpha \).
Proof
It is easy to verify that \(\sigma _{P_\alpha }(E_n)=\alpha \), for \(n=1,\ldots ,N\). Hence, \(S(P_\alpha ,\alpha )= E_1\vee \cdots \vee E_N\) and \(P_\alpha (S(P_\alpha ,\alpha ))=1-\alpha ^N\).
Fix  and let P be any probability. For \(n=1,\ldots ,N+1\), put
and let P be any probability. For \(n=1,\ldots ,N+1\), put
Then, for \(n=1,\ldots ,N\):
Thus, \(P(S(P,\alpha ))\) is equal to the probability of:
For each \(n=1,\ldots ,N\), let
(here we assume that \(0/0=1\)), and define \(q_n^*\) inductively as follows:
A simple induction confirms that, for \(n=1,\ldots ,N+1\), both (i) \(q_n^*\ge q_n\); and (ii) \(q_n^*\ge \alpha ^{n-1}\). Hence:
Note that the inequality is strict unless \(q_{n+1}= \alpha q_n\), for \(n=1,\ldots ,N\). But this is equivalent to the claim that \(P=P_\alpha \). \(\square \)
To prove Theorem 3, we first take note of the obvious fact that (for a given N) if \((\alpha ,\beta )\) is coherent, then \((\alpha ,\beta ')\) is coherent, for all \(\beta '\) such that  . In addition, we note that for any
. In addition, we note that for any  , it follows from Theorem 7 that \((\alpha ,1-\alpha ^N)\) is coherent, but that if \(\beta >1-\alpha ^N\), \((\alpha ,\beta )\) is incoherent. These two facts together entail Theorem 3.
, it follows from Theorem 7 that \((\alpha ,1-\alpha ^N)\) is coherent, but that if \(\beta >1-\alpha ^N\), \((\alpha ,\beta )\) is incoherent. These two facts together entail Theorem 3.
To prove Theorem 4, simply note that Theorem 3 implies that if \((\alpha ,\beta )\) satisfies the condition stated in the proposition, then \(\beta =1-\alpha ^N\). The result then follows from Theorem 7.
Rights and permissions
About this article
Cite this article
Kim, B., Vasudevan, A. How to expect a surprising exam. Synthese 194, 3101–3133 (2017). https://doi.org/10.1007/s11229-016-1096-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-016-1096-y





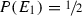 , then
, then 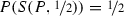 . This means that in the one-day case, the student can judge it to be as likely as not that he will receive the exam on a day on which he will judge it to be as likely as not that he will not receive the exam. This, however, is not a possible explication of the claim that the student expects to receive a surprise exam, since, in this case, the condition
. This means that in the one-day case, the student can judge it to be as likely as not that he will receive the exam on a day on which he will judge it to be as likely as not that he will not receive the exam. This, however, is not a possible explication of the claim that the student expects to receive a surprise exam, since, in this case, the condition 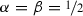 . Given, however, that the student could be said to expect to receive a surprise exam if the surprise and acceptance indices could both be raised by any (infinitesimal) amount, it may perhaps be more accurate to describe an acceptance of the teacher’s announcement in the one-day case as “borderline” incoherent.
. Given, however, that the student could be said to expect to receive a surprise exam if the surprise and acceptance indices could both be raised by any (infinitesimal) amount, it may perhaps be more accurate to describe an acceptance of the teacher’s announcement in the one-day case as “borderline” incoherent.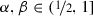 is a corollary of Theorem
is a corollary of Theorem 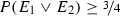 . It follows from the fact that
. It follows from the fact that 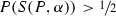 that
that 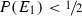 . But then
. But then 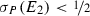 , and so, since
, and so, since 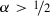 ,
,  . Contradiction.
. Contradiction.