1 Introduction

Presently, it is generally accepted that the solar atmosphere is highly inhomogeneous and this inhomogeneity is intrinsically related to the magnetic field. One of the main blocks of the solar-atmosphere structuring are coronal magnetic loops (see e.g. the review by Reale, 2014). The footpoints of coronal loops are attached to the solar chromosphere. The coronal magnetic loops are elongated in the magnetic-field direction. Their cross-section has the characteristic size of a few Mm, while their length can vary in a wide range and can be up to a few hundred Mm. The ratio of plasma densities inside the loop is higher than that outside. The ratio of these densities can vary in a very large range from values only slightly higher than unity to one hundred times or more.

Coronal magnetic loops are dynamic structures. In particular, transverse oscillations of coronal loops have been observed. The first observations were made by Transition Region and Coronal Explorer (TRACE) space craft in 1998. They were reported by Aschwanden et al. (1999) and Nakariakov et al. (1999), and interpreted as kink oscillations of magnetic tubes. After these first observations, kink oscillations of coronal magnetic loops have been routinely observed by space missions (e.g. Goddard et al., 2016; Abedini, 2018; Nechaeva et al., 2019).

The first observed coronal-loop kink oscillations were large-amplitude standing waves. Later, also low-amplitude propagating waves have been detected with the Coronal Multi-channel Polarimeter (CoMP). They have been observed propagating along overdense coronal structures like coronal loops and plumes (Tomczyk et al., 2008; Morton, Weberg, and McLaughlin, 2019; Morton et al., 2021; Yang et al., 2020; Li et al., 2023). Propagating kink oscillations have been also observed in solar prominences (Okamoto et al., 2007).

It was observed that the kink waves mainly propagate upwards with the amplitude of the upward-propagating perturbations being much higher than the amplitude of the downward-propagating perturbations (e.g. Tomczyk et al., 2007; Tomczyk and McIntosh, 2009) (see also the review by Banerjee et al., 2021). In the case of open waveguides, like spicules, this observation implies that the kink perturbations are driven in the lower part of the solar atmosphere. For closed waveguides this observation can be considered as evidence that there is very strong wave damping preventing the appearance of the reflected wave from the other end of the waveguide. However, this condition is not enough to eliminate the appearance of the reflected waves. The wavelengths of the observed propagating waves are of the order of the characteristic scale of inhomogeneity along the waveguides. In this case, the waves are described by the wave equation with variable phase speed. The solution to this equation is a superposition of two waves propagating in opposite directions. In general, even when a wave propagating in one direction is launched at one end of a waveguide, at some distance from this end, the amplitudes of the two waves are of the same order, which implies that there is strong wave reflection from the inhomogeneity. Hence, a question arises as to why the downward-propagating waves that should be created by the wave reflection are not observed. This problem was partly addressed by Ruderman et al. (2013) who showed that for a particular variation of the density and radius of the cross-section kink waves can propagate without reflection along an inhomogeneous waveguide. Petrukhin, Ruderman, and Pelinovsky (2015) showed that the same result is true for propagating pulses of kink waves.

The results obtained by Ruderman et al. (2013) and Petrukhin, Ruderman, and Pelinovsky (2015) are based on the reduction of the wave equation to the Klein–Gordon equation. For particular dependences of the phase speed on the spatial variable this equation has constant coefficients and thus can be solved analytically. The main result obtained by these authors is that the kink waves can propagate without reflection when the dependence of the phase speed of the kink waves on the distance along the waveguide is either linear or quadratic. In this article, we present another method of studying non-reflective wave propagation based on the reduction of the wave equation to the Euler–Poisson–Darboux equation. We will show that for a particular variation of the density and loop cross-section along the waveguide the reflected wave is absent, as this occurs in a homogeneous waveguide. The article is organised as follows: In the next section we formulate the problem and write down the governing equations. In Section 3 we briefly describe the reduction of the wave equation to the Euler–Poisson–Darboux equation and formulate the conditions when it describes the non-reflective wave propagation. In Section 4 we apply the general theory to the kink-wave propagation in coronal magnetic loops. Section 5 contains the summary of the results and our conclusions.

2 Problem Formulation

We consider kink-wave propagation along a straight magnetic tube in the cold-plasma approximation. The tube cross-section is assumed to be circular with the radius varying along the tube. The plasma density can also vary along the tube, but does not vary across the tube. In cylindrical coordinates \([r,\varphi ,z]\) with the \(z\)-axis coinciding with the tube axis, the plasma density is defined by

$$ \rho = \left \{ \textstyle\begin{array}{l@{\quad}l} \rho _{\mathrm{i}}(z), & r < R(z), \vspace*{1.5mm} \\ \rho _{\mathrm{e}}(z), & r > R(z), \end{array}\displaystyle \right . $$
(1)

where \(R(z)\) is the tube cross-sectional radius, and indices “i” and “e” refer to quantities inside and outside the tube, respectively. At \(r = R(z)\) there is a jump of the density, so \(\lim _{r \to R-0}\rho = \rho _{\mathrm{i}}(z)\) and \(\lim _{r \to R+0}\rho = \rho _{\mathrm{e}}(z)\). It is shown by Ruderman, Verth, and Erdélyi (2008) that in the thin-tube approximation plane-polarised kink waves are described by

$$ \frac{\partial ^{2} S}{\partial t^{2}} - C_{\mathrm{k}}^{2}(z) \frac{\partial ^{2} S}{\partial z^{2}} = 0, $$
(2)

where \(S = \eta /R\), \(\eta \) is the tube displacement, \(C_{\mathrm{k}}\) the kink speed defined by

$$ C_{\mathrm{k}}^{2}(z) = \frac{2B^{2}(z)}{\mu _{0}[\rho _{\mathrm{i}}(z) + \rho _{\mathrm{e}}(z)]}, $$
(3)

\(\mu _{0}\) the magnetic permeability of free space and \(B\) the magnetic-field magnitude related to the tube radius by

$$ B(z)R^{2}(z) = \text{const}. $$
(4)

Recently, Ruderman and Petrukhin (2023) studied kink waves in expanding and twisted magnetic tubes. They showed that even in this case kink waves are described by Equation 2. However, in this case \(S = (\eta /R)\,\exp (-{\mathrm{i}}amz/2)\), where \(a\) determines the shape of magnetic-field lines and \(m = \pm 1\). Namely, the magnetic-field lines are helices with the pitch \(4\pi /a\), while the sign of \(m\) determines if the helix is left or right handed. It is also worth noting that while in an untwisted tube there is only one propagating kink wave, in a twisted tube there are two propagating kink waves, accelerated with the phase speed exceeding the kink speed, and decelerated with the phase speed below the kink speed.

Equation 2 is used below to study non-reflective propagation of kink waves.

3 General Theory

Following Pelinovsky and Kaptsov (2022) we look for the solution to Equation 2 in the form

$$ S(z,t) = \Phi (\tau (z),t) . $$
(5)

Then, Equation 2 reduces to

$$ \frac{\partial ^{2}\Phi}{\partial t^{2}} - C_{\mathrm{k}}^{2}\left ( \frac{{\mathrm{d}}\tau}{\mathrm{d}z}\right )^{2} \frac{\partial ^{2}\Phi}{\partial \tau ^{2}} - C_{\mathrm{k}}^{2} \frac{{\mathrm{d}}^{2}\tau}{\mathrm{d}z^{2}} \frac{\partial \Phi}{\partial \tau} = 0. $$
(6)

Now, we impose the condition

$$ C_{\mathrm{k}}^{2}\left (\frac{{\mathrm{d}}\tau}{\mathrm{d}z}\right )^{2} = 1, \qquad C_{\mathrm{k}}^{2}\frac{{\mathrm{d}}^{2}\tau}{\mathrm{d}z^{2}} = \frac {k}{\tau}. $$
(7)

This is the system of equations for \(C_{\mathrm{k}}\) and \(\tau \). Using Equation 7 we reduce Equation 6 to the Euler–Poisson–Darboux equation (Von Mises, 1958):

$$ \frac{\partial ^{2}\Phi}{\partial t^{2}} - \frac{\partial ^{2}\Phi}{\partial \tau ^{2}} - \frac {k}{\tau} \frac{\partial \Phi}{\partial \tau} = 0. $$
(8)

Below, we only consider \(k = 2l\), where \(l\) is an integer number not equal to zero. When \(l = 1\), Equation 8 coincides with the equation describing spherically symmetric waves in three-dimensional space. We note that this is a typical situation in applied mathematics when two different problems are described by the same equations. In general, for \(l > 0\), Equation 8 describes spherically symmetric waves in space of dimension \(2l + 1\). Eliminating \(C_{\mathrm{k}}\) in Equation 7 yields

$$ \tau \frac{{\mathrm{d}}^{2}\tau}{{\mathrm{d}}z^{2}} = 2l\left ( \frac{{\mathrm{d}}\tau}{{\mathrm{d}}z}\right )^{2} . $$
(9)

To integrate this equation we write \({\mathrm{d}}\tau /{\mathrm{d}} z = q(\tau )\). Then, we obtain

$$ \tau \frac{{\mathrm{d}}q}{{\mathrm{d}}\tau} = 2lq. $$
(10)

The general solution to this equation is \(q = q_{0}\tau ^{2l}\), where \(q_{0}\) is a constant. Then, the equation for \(\tau \) is

$$ \frac{{\mathrm{d}}\tau}{{\mathrm{d}}z} = q_{0}\tau ^{2l}. $$
(11)

Integrating this equation we obtain

$$ \tau = \frac{\tau _{0}}{(1 + z/z_{0})^{1/(2l-1)}}, $$
(12)

where \(\tau _{0}\) and \(z_{0}\) are positive constants; \(q_{0}\) can be expressed in terms of \(\tau _{0}\) and \(z_{0}\), but we do not give this expression because it is not used below. Substituting Equation 12 into Equation 7 yields

$$ C_{\mathrm{k}} = C_{\mathrm{f}}(1 + z/z_{0})^{2l/(2l-1)}, $$
(13)

where \(C_{\mathrm{f}} = z_{0}(2l - 1)/\tau _{0}\) is the value of \(C_{\mathrm{k}}\) at \(z = 0\) corresponding to the base of the magnetic tube. We emphasise that \(z_{0}\) and \(\tau _{0}\) are free parameters. Taking \(l = 1\) we obtain a quadratic profile of \(C_{\mathrm{k}}\). Previously, Ruderman et al. (2013) also obtained that kink waves propagate without reflection in a magnetic tube with a quadratic profile of the kink speed. However, the expression for \(C_{\mathrm{k}}\) that they obtained is three-parametric, while the expression for \(C_{\mathrm{k}}\) given by Equation 13 contains only two free parameters. As a result, Ruderman et al. (2013) were able to obtain a profile of the kink speed that is symmetric with respect to the middle point of a magnetic tube with finite length. Obviously, it is not possible using \(C_{\mathrm{k}}\) given by Equations 13 because it is a monotonic function of \(z\).

When \(l < 0\) we put \(l = -n\) and transform Equations 12 and 13 to

$$ \tau = \tau _{0}(1 + z/z_{0})^{1/(2n+1)}, \quad C_{\mathrm{k}} = C_{\mathrm{f}}(1 + z/z_{0})^{2n/(2n+1)}. $$
(14)

When \(l > 0\) the general solution to Equation 8 with \(k = 2l\) is given by

$$ \Phi _{l} = \frac{1}{\tau ^{2l-1}}\sum _{j=0}^{l-1}a_{j}\tau ^{j} \frac{\partial ^{j} W}{\partial t^{j}}, $$
(15)

where

$$ W = \theta (t - \tau ) + \psi (t + \tau ), $$
(16)

\(\theta \) and \(\psi \) are arbitrary functions, and the coefficients \(a_{j}\) are defined by the substitution of Equation 15 into Equation 8. Below, we only consider waves propagating in the positive \(z\)-direction. Since \({\mathrm{d}}\tau /{\mathrm{d}}z < 0\) these wave are described by the function \(\psi \). In accordance with this we take \(\theta \equiv 0\). Then, for \(l = 1,2,3\) solutions to Equation 8 are given by

$$ \Phi _{1} = \frac{1}{\tau}\psi (t + \tau ), \quad \Phi _{2} = \frac{1}{\tau ^{3}}\psi (t + \tau ) - \frac{1}{\tau ^{2}} \frac{\partial \psi (t + \tau )}{\partial t}, $$
(17)
$$ \Phi _{3} = \frac{3}{\tau ^{5}}\psi (t + \tau ) - \frac{3}{\tau ^{4}} \frac{\partial \psi (t + \tau )}{\partial t} + \frac{1}{\tau ^{3}} \frac{\partial ^{2}\psi (t + \tau )}{\partial t^{2}}. $$
(18)

Now, we consider \(l < 0\), so that \(k = 2l = -2n\). To distinguish between the solutions to Equation 8 for \(k = 2l > 0\) and \(k = -2n < 0\) we denote the solution to Equation 8 in the latter case as \(\widetilde{\Phi}_{n}\). Substituting \(\widetilde{\Phi}_{n} = \tau ^{2n+1}\Psi \) into Equation 8 with \(k = -2n\) we obtain

$$ \frac{\partial ^{2}\Psi}{\partial t^{2}} - \frac{\partial ^{2}\Psi}{\partial \tau ^{2}} - \frac{2(n+1)}{\tau} \frac{\partial \Psi}{\partial \tau} = 0. $$
(19)

It follows from this result that \(\Psi = \Phi _{n+1}\) and, consequently, \(\widetilde{\Phi}_{n} = \tau ^{2n+1}\Phi _{n+1}\). Then, we obtain

$$ \widetilde{\Phi}_{n} = \sum _{j=0}^{l} a_{j}\tau ^{j} \frac{\partial ^{j} W}{\partial t^{j}}. $$
(20)

Again we consider waves propagating upwards. Now, \(\tau \) is a monotonically increasing function of \(z\), which implies that the upward-propagating waves are described by the function \(\theta \). In accordance with this, we now take \(\psi \equiv 0\). As before, \(W\) is defined by Equation 16, while the coefficients \(a_{j}\) are defined by substituting Equation 20 into Equation 8 with \(k = -2n\). In particular, we obtain

$$ \widetilde{\Phi}_{1} = \theta (t - \tau ) - \tau \frac{\partial \theta (t - \tau )}{\partial t}, \;\; \widetilde{\Phi}_{2} = 3\theta (t - \tau ) - 3\tau \frac{\partial \theta (t - \tau )}{\partial t} + \tau ^{2} \frac{\partial ^{2}\theta (t - \tau )}{\partial t^{2}}. $$
(21)

4 Application to Waves Propagating in Coronal Loops

In this section we apply the general theory to kink propagation along coronal loops. We use a popular model of a coronal loop with a half-circle shape immersed in an isothermal atmosphere. We assume that the plasma temperature inside and outside of the loop is the same. This implies that the ratio of densities inside the loop \(\rho _{\mathrm{i}}\) and outside the tube \(\rho _{\mathrm{e}}\) is constant, \(\rho _{\mathrm{i}}/\rho _{\mathrm{e}} = \zeta > 1\). The plasma density inside the loop is given by

$$ \rho _{\mathrm{i}} = \rho _{\mathrm{f}}\exp (-h/H), $$
(22)

where \(h\) is the height in the atmosphere, \(H\) is the atmospheric scale height and the subscript “f” indicates that a quantity is calculated at the loop footpoint. The relation between \(h\) and the length \(z\) along the loop is

$$ h = \frac {L}{\pi}\sin \frac{\pi z}{L} , $$
(23)

where \(L\) is the length of the loop. Substituting Equation 23 into Equation 22 yields

$$ \rho _{\mathrm{i}} = \rho _{\mathrm{f}}\exp \left (-\frac {L}{\pi H}\sin \frac{\pi z}{L}\right ). $$
(24)

Using this expression and Equation 4 we obtain from Equation 3

$$ C_{\mathrm{k}} = C_{\mathrm{f}}\left (\frac{R_{\mathrm{f}}}{R(z)}\right )^{2} \exp \left (\frac {L}{2\pi H}\sin \frac{\pi z}{L}\right ), \quad C_{\mathrm{f}} = B_{\mathrm{f}}\sqrt{\frac{2\zeta}{\mu _{0}\rho _{\mathrm{f}}(\zeta + 1)}}. $$
(25)

Comparing Equations 13 and 25 we obtain that the kink waves propagate along the coronal loop without reflection when the variation of the cross-sectional radius along the loop is defined by

$$ \lambda (z) = \frac{R(z)}{R_{\mathrm{f}}} = \left (1 + \frac {z}{z_{0}} \right )^{-l/(2l-1)} \exp \left (\frac {L}{4\pi H}\sin \frac{\pi z}{L}\right ), $$
(26)

where we now do not make a distinction between the positive and negative values of \(l\). Hence, \(l\) can be any integer number different from zero. As a result, we obtain two infinite sequences of the variation of the cross-sectional radius along the loop corresponding to non-reflecting propagation of kink waves along the loop. We obtain the fist sequence taking \(l = 1,2,\dots \), and the second sequence taking \(l = -1,-2,\dots \)

We now introduce the loop expansion factor \(\lambda _{0}\), which is the ratio of the loop cross-sectional radii at the loop apex and at the footpoint. It is given by

$$ \lambda _{0} = \left (1 + \frac {L}{2z_{0}}\right )^{-l/(2l-1)}\exp \left (\frac {L}{4\pi H}\right ). $$
(27)

It follows from Equation 27 that

$$ \frac {L}{z_{0}} = 2\lambda _{0}^{1/l-2}\exp \left ( \frac{(2l-1)L}{4\pi lH}\right ) - 2. $$
(28)

The left-hand side of Equation 28 is positive. It immediately follows from this condition that

$$ \lambda _{0} < \exp \left (\frac {L}{4\pi H}\right ). $$
(29)

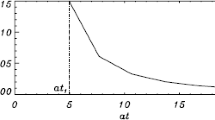
In particular, \(\lambda _{0} < 1.284\) for \(L = \pi H\), and \(\lambda _{0} < 1.649\) for \(L = 2\pi H\). We calculated the dependence of \(\lambda \) on \(z\) for \(L = \pi H\) and \(L = 2\pi H\). We found that for both values of \(L\) the difference between the two curves showing the dependence of \(\lambda \) on \(z\), one corresponds to \(l = 1\), and the other to any value of \(l \neq 0\), is extremely small and they are almost indistinguishable. Hence, we only plot curves corresponding to \(l = 1\). An important property of particular dependences of the loop radius on the length along the loop corresponding to the non-reflecting wave propagation that were obtained by Ruderman et al. (2013) is that \(\lambda _{0}\) must be higher than a definite value that depends on \(L = \pi H\). Hence, the results obtained here can be considered as complementary to those obtained by Ruderman et al. (2013).

The dependencies of \(\lambda \) on \(z\) for \(L = \pi H\) and \(L = 2\pi H\), and for \(l =1\) are shown in Figures 1 and 2 for various values of \(\lambda _{0}\). We note that although \(\lambda _{0}\) is called the expansion function, in fact the ratio of the maximum cross-sectional radius of the loop to that at \(z = 0\) is slightly higher than \(\lambda _{0}\) and it is taken at \(z\) slightly less than \(L/2\). We also see in Figures 1 and 2 that, after initial expansion, the magnetic-flux tube starts to contract and eventually its cross-section becomes substantially less than that at \(z = 0\). However, the exact behaviour of the loop cross-section beyond the loop apex is not very important because there the oscillation amplitude becomes exponentially small due to damping caused by resonant absorption.

Figure 1
figure 1

Dependence of \(\lambda \) on \(z\) for \(L = \pi H\). The solid, dashed and dash-dotted curves correspond to \(\lambda _{0} = 1.05,\;1.15\) and 1.25.

Full size image
Figure 2
figure 2

Dependence of \(\lambda \) on \(z\) for \(L = 2\pi H\). The solid, dashed and dash-dotted curves correspond to \(\lambda _{0} = 1.1,\;1.3\) and 1.5.

Full size image

Ruderman, Verth, and Erdélyi (2008) used a model of an expanding magnetic tube with a potential equilibrium magnetic field. The simplest method of determining the magnetic-field magnitude in the solar corona is the following. The magnetic field in the solar photosphere is determined using the Zeeman effect. Then, it is assumed that the magnetic field is potential and the Laplace equation for the magnetic-field potential is solved using the magnetic field in the solar photosphere as the boundary condition. In particular, it was obtained on the basis of this method that the loop expansion must be quite large with the ratio of the loop cross-sectional radii at the loop apex and the footpoint on the order of 5 or even higher. However, observations show that the ratio of the maximum cross-sectional radius to that at the loop footpoint almost never exceeds 2 (Golub et al., 1990; Klimchuk et al., 1992; Klimchuk, 2000; Watko and Klimchuk, 2000; López Fuentes, Klimchuk, and Démoulin, 2006; Brooks et al., 2007; Kucera et al., 2019).

One possible explanation for weak coronal-loop expansion is that the coronal magnetic loops are twisted, so that the equilibrium magnetic field is not potential but force-free with the non-zero azimuthal component. Recently, Li et al. (2020) reported the observation of an extra long (length about 130 Mm) coronal loop with very weak variation of the cross-sectional radius along the loop. To explain this phenomenon the authors presented a model of an expanding and twisted magnetic loop embedded in an isothermal atmosphere. This model is based on using the thin-tube approximation (e.g. Ferriz-Mas and Schüsler, 1989). In particular, in this approximation the vertical magnetic-field component times the tube cross-sectional area is a constant. At the tube boundary the total pressure inside the tube must be equal to the external pressure. As a result, in an untwisted tube the decrease of the external pressure with height results in the decrease of the magnetic-field magnitude. Since the radial component of the magnetic field is much less than the vertical component in the thin-tube approximation, it follows that the vertical component decreases and, as a result, the tube cross-sectional radius increases. Li et al. (2020) showed that the magnetic twist decreases the magnetic pressure at the tube boundary. This slows down the rate of decrease of the magnetic-field vertical component with the height and, as a result, the rate of increase of the cross-sectional radius. Li et al. (2020) considered a magnetic tube in a magnetic-free environment. However, it seems that their model can be generalised for a magnetic tube in a magnetic environment.

As we have already pointed out in Section 2, Ruderman and Petrukhin (2023) showed that the propagation of kink waves in a twisted magnetic tube is described by the same equation as in an untwisted magnetic tube. Hence, the results obtained in this section are valid for both untwisted and twisted coronal magnetic loops.

5 Summary and Conclusions

In this article, we study non-reflective propagation of kink waves in magnetic-flux tubes. The kink-wave propagation is described by the wave equation with the spatially dependent velocity. This equation reduces to the Euler–Poisson–Darboux equation. Then, we consider particular cases when the Euler–Poisson–Darboux has exact analytic solutions. We presented the expressions describing the spatial dependence of the phase speed corresponding to the non-reflective propagation of kink waves.

The general theory is applied to the kink-wave propagation in coronal magnetic loops. We use the model of a coronal loop with a half-circular shape embedded in an isothermal atmosphere. It is assumed that the plasma temperature is the same inside and outside of the tube. We presented two infinite sequences of the spatial dependences of variation of the cross-sectional tube radius corresponding to the non-reflective propagation of kink waves. Calculations show that all these dependences are practically the same and the curves showing these dependences are almost indistinguishable. The dependences of the loop cross-sectional radius on the distance along the loop are shown for two loop heights in Figures 1 and 2. We introduced the loop-expansion factor defined as the ratio of loop cross-sectional radii at the middle of the loop and at the footpoint. We found that loops with the cross-sectional radius variation along the loop corresponding to non-reflective wave propagation only exist when the loop-expansion factor is less than a critical value. The critical value is an increasing function of the loop height.