1 Introduction

Predictions of solar activity encompass multiple timescales. Long-term predictions include anticipating the amplitude of the next Solar Cycle before solar minimum. Short-term predictions would include the probability of solar flares or coronal mass ejections (CMEs) in the next 24 h. In between those limits are intermediate predictions of solar activity months to a few years in the future, such as the MSAFE model of Niehaus, Euler, and Vaughan (1996) or the Lincoln–McNish model on which MSAFE is based (McNish and Lincoln, 1949). Unlike the long-term predictions, which may give only the amplitude of the upcoming cycle and possibly the timing of the maximum, the latter two provide the time dependence of the sunspot number.

One aspect of solar-cycle prediction that is often overlooked is the use of current conditions to validate predictions. We will describe such a confirming prediction of the amplitude of Solar Cycle 25 (SC 25) using the time dependence of the sunspot number, derived from a method first proposed by Lantos (2000) using the maximum slope, or the slope at the inflection point, of the sunspot number during the ascending part of the solar cycle. Note that because of the length of the filters used in the analysis, a prediction of SC 25 using this method cannot be made until well after the inflection point.

This paper is organized with this Introduction, followed by Section 2, where we describe the data and methodology employed in the data analysis, from which a value of \(130.7 \pm 0.5\) for the amplitude of SC 25 is obtained. One possible explanation of the correlation using a shape function follows in Section 3. Section 4 compares this maximum-slope prediction variable with the Hilbert transform of the sunspot number. Finally, we conclude by comparing the current SC 25 amplitude prediction with polar-field precursor predictions of SC 25 made before and just after solar minimum, a comparison with a prediction using the maximum slope from numerical differencing, and other remarks.

2 Preparation and Analysis of the Data

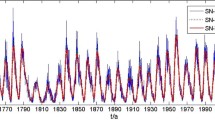
We will use the smoothed sunspot number starting in 1843 (Solar Cycle 9) for our analysis. The 13-month smoothed monthly total sunspot number (Version 2, which we will call \(S\) (Clette et al., 2014; Clette and Lefèvre, 2016)) was downloaded from the SILSO website.Footnote 1 The original data is plotted as the blue line in Figure 1.

Figure 1
figure 1

The time dependence of the S–G filtered \(S\) (in black) plotted as a function of time. The time derivative of \(S\) from that filter is shown in red, with red vertical dashed lines showing the maximum values used in the correlation fit. Also plotted under the filtered data is the monthly sampled \(S\) (in blue). The horizontal dotted line is the zero level of all curves.

Full size image

The Savitzky–Golay (S–G) filter implemented in idl as savgol was used to both smooth and calculate the derivative of \(S\). An S–G filter tends to preserve heights and widths of the peaks even when those peaks are relatively narrow. A fourth-degree fit was used in the filter and the width parameter was 81 points. This width removes most of the interannual variability in \(S\). However, the width parameter must be selected to provide a unique maximum in the slope of the rising phase. To address the ambiguity in this parameter, several width parameters were tested. Three fits (linear, linear with errors in both axes, and parabolic) to the amplitude and maximum-slope correlation points were evaluated at the current epoch and averaged. The width of 81 points produced the smallest variance among those fits and was used in the analysis. This means that 40 months have to pass before the maximum slope becomes insensitive to the length of the filter. During the data analysis \(S\) was available through June 2023 (2023.458) and the maximum slope was at 2021.873, a difference of only 20 months. That means the value of the slope may still change, but less so as time goes by.

The S–G smoothed data is shown as the black curve in Figure 1, along with the first derivative in red. All of the sunspot cycles in the plot have unique values of the maximum in the slope during the rising phase. This means that the predictive variable is measured at a definite time. That is not true of the declining phase, where at least six of the cycles have a more complicated time dependence of the slope. That would mean ambiguity in which peak is the predictor value. This uniqueness problem has been explored for geomagnetic solar-cycle predictions (Pesnell, 2014).

The maximum slopes were found by searching the derivative curve between solar minimum and maximum for the historical cycles and between solar minimum and the latest values in the current cycle. The times of solar minimum and maximum listed in Pesnell (2018) were used for the limits. The maximum values of the Savitzky–Golay smoothed data were found by searching between successive minima. Due to the additional smoothing, the peak values were smaller than those listed in Table 1 of Pesnell (2018) and the current maximum values were multiplied by 1.091 to correct for this. Those values are plotted in a slope–amplitude diagram (Figure 2). The correlation coefficient of the points was 0.987, which has a significance of essentially 1 for the 16 cycles considered here.

Figure 2
figure 2

Slope–amplitude diagram for 16 solar cycles. The diamonds in this graph have the maximum slope plotted as the independent variable vs. the upcoming maximum as the dependent variable. The linear correlation fit in Equation 1 is shown in a solid dark blue line, the fit allowing for errors in both variables (Equation 2) in a red chain dashed line, and the parabolic fit (Equation 3) in a green dashed line. The predicted amplitudes of SC 25, found by evaluating the fits at the maximum slope of 3.17 for the current cycle, are shown as an X, plus sign, and a diamond in the respective colors. The diamond labeled ‘9’ corresponds to the conditions of Solar Cycle 9, the most deviant point in the set.

Full size image

The SC 9 peak (the one furthest from the correlation line in Figure 1) is 38 months after solar minimum, noticeably longer than the average of 1.9 years for Solar Cycles 1 – 23. This may indicate SC 9 may need further understanding.

Three fits of \(S_{\mathrm{max}}\) vs. \(dS/dt|_{\mathrm{max}}\) were performed. A standard linear fit gave

$$ S_{\mathrm{max}} = 29.90 + 31.96 \, dS/dt|_{\mathrm{max}}. $$
(1)

A fit assuming errors in both variables (5 in \(S_{\mathrm{max}}\) and 0.2 in the slope) is

$$ S_{\mathrm{max}} = 27.26 \, (\pm 6.8) + 32.50 \, (\pm 1.3) \, dS/dt|_{ \mathrm{max}}. $$
(2)

A parabolic fit was also performed, which gave

$$ S_{\mathrm{max}} = 24.88 + 34.10 \, dS/dt|_{\mathrm{max}} - 0.2056 \, (dS/dt|_{ \mathrm{max}})^{2}. $$
(3)

Each fit was evaluated at the maximum slope for the current cycle of 3.17 (the rightmost maximum in the red curve of Figure 1). The average of those values is the reported prediction for the amplitude of SC 25 of \(S_{25} = 130.7 \pm 0.5\), using the standard deviation of the predictions as the uncertainty. This is an extremely small error for a solar-cycle amplitude prediction. Also, the correlation is 0.987 for 16 points, which is among the best in the field of solar-cycle predictions. This may be explained, in part, by the characteristics of the shape function. This will be explored in the next section.

3 A Theoretical Shape of the Sunspot Number

A prediction of the amplitude of \(S\) requires a shape function to illustrate the possible time dependence. Pesnell (2020) and Hathaway, Wilson, and Reichman (1994) used the functional form

$$ S(t) = A \frac{t^{3}}{e^{(t/b)^{2}} - c} = A b^{3} \frac{x^{3}}{e^{x^{2}} - c} \equiv A b^{3} f(x) $$
(4)

to represent the time dependence of the sunspot number. In this equation, \(A\) is related to the amplitude of the cycle, \(b\) is a time-scaling constant, \(t\) is the time elapsed since solar minimum (\(t_{\mathrm{min}}\)), and \(x \equiv t/b\) is a dimensionless time variable. All of the characteristics of a cycle are contained in \(A\) and \(b\) as the dependence on \(x\) is identical in every cycle.

Each solar cycle has unique values of \(A\) and \(b\) that can be calculated with a nonlinear least-squares fit of the shape function in Equation 4 to the sunspot number in each cycle (Pesnell, 2020). Those fitted values were used to derive correlation fits between \(A\) and \(b\) with \(S_{\mathrm{max}}\) that are used to display the time dependence of a prediction of \(S\).

The shape function of Equation 4 automatically provides several relationships. Setting \(c = 0.71\) and holding it constant means that the time from minimum to maximum is linearly related to \(b\)

$$ t_{\mathrm{max}} - t_{\mathrm{min}} = 1.081 b $$
(5)

and the maximum of \(S\) is the function evaluated at \(x_{\mathrm{max}} = 1.081\)

$$ S_{\mathrm{max}} = 0.504 A b^{3}. $$
(6)

We now show that the shape function of Equation 4 has a correlation between the maximum slope during the rising phase and the amplitude similar to that found in the data analysis of Section 2.

Changing to \(x\), the derivative (slope) of Equation 4 is

$$ \frac{dS}{dx} = \frac{S}{x} \left [ 3 - 2 x^{2} \frac{e^{x^{2}} }{e^{x^{2}} - c}\right ], $$
(7)

which has a maximum during the rising phase at \(x_{1} = t_{1}/b = 0.50989\). The variations of \(S\) and \(dS/dx\) are shown in Figure 3.

Figure 3
figure 3

The shape function \(S\) (dashed line) and its derivative (Equation 7) as functions of \(x\) for an entire cycle. The vertical lines show the maxima of each (labeled \(x_{1}\) for the derivative and \(x_{\mathrm{max}}\) for \(S\).) The minimum in the slope near \(x \sim 1.65\) is not useful as a predictor of the next cycle as it will have different values of \(A\) and \(b\).

Full size image

We then write that

$$ \left . \frac{dS}{dx} \right |_{\mathrm{max}} = S(x_{1}) g(x_{1}) = 1.851 S(x_{1}), $$
(8)

where \(g(x_{1})\) is a constant in the family of curves represented by Equation 4. Next, we write

$$ S(x) = \frac{S_{\mathrm{max}}}{0.504} \frac{x^{3}}{e^{x^{2}} - c}, $$
(9)

which, when evaluated at \(x_{1}\), is in the form of another constant in the family of curves

$$ S(x_{1}) = S_{\mathrm{max}} f(x_{1}) = 0.4481 S_{\mathrm{max}}. $$
(10)

Combining Equations 10 and 8 gives

$$ \left . \frac{dS}{dx} \right |_{\mathrm{max}} = S_{\mathrm{max}} f(x_{1}) g(x_{1}) = 0.4481 \times 1.851 S_{\mathrm{max}} = 0.830 S_{ \mathrm{max}}. $$
(11)

To compare with the data, we return to the time derivative

$$ \left . \frac{dS}{dt} \right |_{\mathrm{max}} \propto 0.830 \frac{S_{\mathrm{max}}}{b}, $$
(12)

showing that the maximum slope during the rising phase is proportional to the maximum value (or amplitude) and inversely proportional to the value of \(b\) for that cycle. A parabolic fit was used in Section 2 to see if any trends were induced by this \(b\) dependence, but none were found in the historical data. The \(b\) parameter does vary less than \(S_{\mathrm{max}}\) (see Figure 2 in Pesnell, 2020). This analysis supports the correlation functions found in Section 2 as viable confirming predictions of the amplitude of SC 25.

Although a similar analysis could be carried out for any point in time of the theoretical shape function, the values of \(b\) and \(x\) may be poorly estimated in the early phases of a sunspot cycle. Using the time of maximum slope provides an objective selection criterion for when to evaluate the prediction function in the data.

3.1 Timing Information

Using the shape function as a guide, the value of \(b\) for SC 25 (\(b_{25}\)) can be estimated from \(x_{1}\) as \(b_{25} = (2021.873- 2019.96) /0.50989 = 3.75\). This gives the date of solar maximum as either \(t_{\mathrm{max}} = 2019.96 + x_{\mathrm{max}} b_{25} \approx 2024.0\) (Equation 5) or \(t_{\mathrm{max}} = 2021.873 + (x_{\mathrm{max}} - x_{1} ) b_{25} \approx 2024.0\) (see the discussion following Equation 7), which are identical. The standard deviation of the rise times of Solar Cycles 1 – 24 is \(\pm 1\) yr (Pesnell, 2018), which we use as the uncertainty of the predicted peak. These estimates place solar maximum in 2023 or 2024, indicating that SC 25 is already reaching its peak level of activity. It is the uniqueness of the timing of the maximum slope that allows these estimates to be made.

4 The Slope via a Hilbert Transform

The Hilbert transform (ℋ) is well known in signal processing. They can be used to demodulate audio signals riding on a radio-frequency carrier. For a real-valued dataset the Hilbert transform returns the out-of-phase part of the signal needed for that demodulation. When applied to \(S\), \({\mathcal {H}}(S)\) produces a value remarkably similar to the first derivative from the Savitzky–Golay filter in Section 2 above. Figure 4 shows a correlation plot of the slope from the S–G analysis in Section 2 and \({\mathcal {H}}[ S(t) ]\), where the hilbert routine in idl was used to generate the transform. The correlation coefficient of 0.935 for 2154 points implies that a good correlation exists between the two quantities.

Figure 4
figure 4

The real part of the Hilbert transform of \(S\) (\({\mathcal {H}}[S]\)) as the \(x\) variable vs. the slope of \(S\) as the \(y\) variable since 1843. The sloped blue line is a linear fit of the form \(\mathrm{slope} = -3.5 + 0.042\, {\mathcal {H}}[S]\). This plot shows that the Hilbert transform can also be used as a confirming prediction of the amplitude (and possibly the timing) of the current sunspot cycle.

Full size image

This has a simple explanation. The Hilbert transform is a linear operator:

$$ {\mathcal {H}}[ f(t) + g(t) ] = {\mathcal {H}}[f(t)] + {\mathcal {H}}[g(t)]. $$
(13)

The sunspot number has a Fourier-series representation that is dominated by a peak at a period of approximately 10 years, with the next peak a factor of 3 or more smaller in amplitude. Thus, the Hilbert transform of \(S\) can be written as

$$ {\mathcal {H}}[ S(t) ] = {\mathcal {H}}[ A_{10} \sin (2 \pi t/10)] + { \mathcal {H}}[\mathrm{smaller\ terms}] = A_{10} \cos (2 \pi t/10) + { \mathcal {H}}[\mathrm{smaller\ terms}]. $$
(14)

This implies that \({\mathcal {H}}[ S(t) ] \approx \frac{dS}{dt} + \mathrm{corrections}\). However, the slope has a simpler physical interpretation.

5 Conclusions

A prediction of the amplitude of SC 25 using data during the rising phase of the cycle results in a predicted amplitude of \(130.7 \pm 0.5\). The predictive variable is the maximum of the slope of the smoothed sunspot number during the rising phase. The derivative is determined using a Savitzky–Golay filter with 81 points and a fourth-degree fit in the filter. The unnormalized coefficients were used in the analysis. An analysis of a shape factor used to model the time dependence of sunspot cycles shows that the correlation arises from the time dependence and that using the maximum slope is a way to select the correct time when analyzing the data.

The timing of the peak of SC 25 can now be estimated by the timing of the maximum in the slope during the rising phase. The latter fixes \(b\) and then two estimates of the timing of the maximum can be derived. Both estimates indicate that SC 25 will peak before the end of 2024.

Pesnell (2020) lists a predicted amplitude for SC 25 of \(S_{25} = 125 \pm 40\), peaking at \(2024.6 \pm 1.5\) yr. This was an update of the SODA polar magnetic-field precursor prediction (\(S_{25} = 135 \pm 25\), peaking at \(2025.2 \pm 1.5\)) described in Pesnell and Schatten (2018), to accommodate the actual solar-minimum date of 2019.96 and a small change in the polar field between 2017 and 2020. The current prediction agrees with those predictions in amplitude and the timing is consistent within uncertainties with the prediction of Pesnell (2020). The current prediction is inconsistent with a rapid increase in solar activity to levels well above that predicted by the SODA precursor.

Although this is an impressive correlation, there are caveats. The most deviant point in Figure 2 is for Solar Cycle 9, the first cycle considered and the one where the boundary conditions assumed for the S–G filter have the most influence. Due to its proximity to the end of the time range the maximum slope of the current cycle may be affected in a similar way. That means the correlation fit may be accurate but the current value of the maximum slope must be calculated well after it occurs.

The Hilbert transform was examined to see if it was less sensitive to the edge effects of looking close to the end of the time series. The excellent correlation with the slope derived from the Savitsky–Golay fit shows this may be true, but the edge effects are more difficult to assess as the Fourier transform used to calculate \({\mathcal {H}}(S)\) ranges over the entire time interval of the data.

As this paper was nearing completion, a similar analysis appeared in Aparicio, Carrasco, and Vaquero (2023), which includes a predicted amplitude for SC 25 of \(131 \pm 32\), in excellent agreement with the magnitude in this work but a somewhat larger error bar. This work used numerical differences for the derivative that were then smoothed using a 3-month running average. As a result their correlation plot (i.e., Figure 1 of Aparicio, Carrasco, and Vaquero, 2023) has more scatter than the corresponding Figure 2. Similar predictions using variations on the slope–amplitude correlation appeared in Efimenko and Lozitsky (2022, \(S_{25} = 185 \pm 18\)) and Du (2020, \(S_{25} = 135.5 \pm 33.2\)).

The use of confirming predictions may prove useful for refining our knowledge of the progression of solar cycles and possibly more accurate predictions from the curve-fitting techniques.