Can High-Mode Magnetohydrodynamic Waves Propagating in a Spinning Macrospicule Be Unstable Due to the Kelvin–Helmholtz Instability?

Abstract

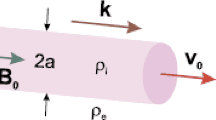
We investigate the conditions at which high-mode magnetohydrodynamic (MHD) waves propagating in a spinning solar macrospicule can become unstable with respect to the Kelvin–Helmholtz instability (KHI). We consider the macrospicule as a weakly twisted cylindrical magnetic flux tube moving along and rotating around its axis. Our study is based on the dispersion relation (in complex variables) of MHD waves obtained from the linearized MHD equations of an incompressible plasma for the macrospicule and cool ($\beta = 0$, with $\beta$ the plasma to the magnetic pressure) plasma for its environment. This dispersion equation is solved numerically using appropriate input parameters to find out an instability region or window that accommodates suitable unstable wavelengths on the order of the macrospicule width. It is established that an $m = 52$ MHD mode propagating in a macrospicule with width of 6 Mm, axial velocity of $75~\mbox{km}\,\mbox{s}^{-1}$, and rotating one of $40~\mbox{km}\,\mbox{s}^{-1}$ can become unstable against the KHI with growth times of 2.2 and 0.57 min at 3 and 5 Mm unstable wavelengths, respectively. These growth times are much shorter than the macrospicule lifetime, which lasts about 15 min. An increase or decease in the width of the jet would change the KHI growth times, which remain more or less of the same order when they are evaluated at wavelengths equal to the width or radius of the macrospicule. It is worth noting that the excited MHD modes are super-Alfvénic. A change in the background magnetic field can lead to another MHD mode number, $m$, that ensures the required instability window.

Appendix A: Derivation of the Wave Dispersion Relation

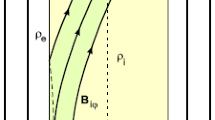
We recall that we modeled the spinning macrospicule as a rotating and axially moving twisted magnetic flux tube of radius $r = a$. In a cylindrical coordinate system, the magnetic and velocity fields inside the jet are assumed to be

$$\bigl( 0, B_{\mathrm{i}\phi }(r), B_{\mathrm{i}z} \bigr) \quad \mbox{and} \quad \bigl( 0, U_{\phi }(r), U_{z} \bigr), $$

respectively. Linearized ideal MHD equations, which govern the incompressible dynamics of perturbations in the rotating jet, are

$$\begin{aligned} &\frac{\partial }{\partial t}\boldsymbol{v} + (\boldsymbol{U}\cdot \nabla ) \boldsymbol{v} + (\boldsymbol{v}\cdot \nabla ) \boldsymbol{U} = - \frac{\nabla p_{\mathrm{tot}}}{\rho _{\mathrm{i}}} + \frac{ ( \boldsymbol{B}_{\mathrm{i}} \cdot \nabla )\boldsymbol{b}}{ \rho _{\mathrm{i}} \mu } + \frac{ ( \boldsymbol{b} \cdot \nabla ) \boldsymbol{B}_{\mathrm{i}}}{\rho _{\mathrm{i}} \mu }, \end{aligned}$$

(8)

$$\begin{aligned} & \frac{\partial }{\partial t}\boldsymbol{b} - \nabla \times ( \boldsymbol{v} \times \boldsymbol{B}_{\mathrm{i}} ) - \nabla \times ( \boldsymbol{U} \times \boldsymbol{b} ) = 0, \end{aligned}$$

(9)

$$\begin{aligned} & \nabla \cdot \boldsymbol{v} = 0, \end{aligned}$$

(10)

$$\begin{aligned} & \nabla \cdot \boldsymbol{b} = 0, \end{aligned}$$

(11)

where $\boldsymbol{v} = (v_{r}, v_{\phi }, v_{z})$ and $\boldsymbol{b} = (b_{r}, b_{\phi }, b_{z})$ are the perturbations of fluid velocity and magnetic field, respectively, and $p_{\mathrm{tot}}$ is the perturbation of the total pressure $p_{\mathrm{t}}$.

Assuming that all perturbations are proportional to $g(r)\exp [\mathrm{i} ( -\omega t + m \phi + k_{z} z ) ]$, with $g(r)$ being just a function of $r$, we obtain from the above set of equations the following ones:

$$\begin{aligned} & -\mathrm{i}\sigma v_{r} -2\frac{U_{\phi }}{r}v_{\phi }- \mathrm{i}\frac{f _{B}}{\mu \rho _{\mathrm{i}}}b_{r} + 2\frac{B_{\mathrm{i}\phi }}{ \mu \rho _{\mathrm{i}} r}b_{\phi }= -\mathrm{i}\frac{1}{\rho _{ \mathrm{i}}}\frac{\mathrm{d}p_{\mathrm{tot}}}{\mathrm{d}r}, \end{aligned}$$

(12)

$$\begin{aligned} & -\mathrm{i}\sigma v_{\phi }+ \frac{1}{r} \frac{\mathrm{d} ( r U _{\phi } )}{\mathrm{d}r}v_{r} - \mathrm{i}\frac{f_{B}}{\mu \rho _{\mathrm{i}}}b_{\phi }- \frac{1}{\mu \rho _{\mathrm{i}}} \frac{1}{r}\frac{\mathrm{d} ( r B_{\mathrm{i}\phi } )}{ \mathrm{d}r}b_{r} = - \mathrm{i} \frac{1}{\rho _{\mathrm{i}}} \frac{m}{r}p_{\mathrm{tot}}, \end{aligned}$$

(13)

$$\begin{aligned} & -\mathrm{i}\sigma v_{z} - \mathrm{i} \frac{f_{B}}{\mu \rho _{\mathrm{i}}}b_{z} = -\mathrm{i}\frac{1}{ \rho _{\mathrm{i}}}k_{z} p_{\mathrm{tot}}, \end{aligned}$$

(14)

$$\begin{aligned} & -\mathrm{i}\sigma b_{r} - \mathrm{i}f_{B} v_{r} = 0, \end{aligned}$$

(15)

$$\begin{aligned} & -\mathrm{i}\sigma b_{\phi }- r\frac{\mathrm{d}}{\mathrm{d}r} \biggl( \frac{U _{\phi }}{r} \biggr)b_{r} - \mathrm{i}f_{B} v_{\phi }+ r\frac{ \mathrm{d}}{\mathrm{d}r} \biggl( \frac{B_{\mathrm{i}\phi }}{r} \biggr)v _{r} = 0, \end{aligned}$$

(16)

$$\begin{aligned} & -\mathrm{i}\sigma b_{z} - \mathrm{i}f_{B} v_{z} = 0, \end{aligned}$$

(17)

$$\begin{aligned} & \biggl( \frac{\mathrm{d}}{\mathrm{d}r} + \frac{1}{r} \biggr)v_{r} + \mathrm{i}\frac{m}{r}v_{\phi }+ \mathrm{i}k_{z} v_{z} = 0, \end{aligned}$$

(18)

where

$$ \sigma = \omega - \frac{m}{r}U_{\phi }- k_{z} U_{z} $$

(19)

is the Doppler-shifted frequency and

$$ f_{B} = \frac{m}{r}B_{\mathrm{i}\phi } + k_{z} B_{\mathrm{i}z}. $$

(20)

It is now convenient to introduce the Lagrangian displacement, $\boldsymbol{\xi }$, and express it via the fluid velocity perturbation through the relation (Chandrasekhar, 1961)

$$\mathit{v}=\frac{\partial \mathit{\xi }}{\partial t}+(\mathit{U}\cdot \mathrm{\nabla })\mathit{\xi }-(\mathit{\xi }\cdot \mathrm{\nabla })\mathit{U},$$

which yields

$$ v_{r} = -\mathrm{i}\sigma \xi _{r}, \qquad v_{\phi }= -\mathrm{i}\sigma \xi _{\phi }- r\frac{\mathrm{d}}{ \mathrm{d}r} \biggl( \frac{U_{\phi }}{r} \biggr)\xi _{r}, \qquad v_{z} = - \mathrm{i}\sigma \xi _{z}. $$

(21)

In terms of $\boldsymbol{\xi }$, Equations 12 – 18 can be rewritten as

$$\begin{aligned} &\biggl[ \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} - r\frac{\mathrm{d}}{ \mathrm{d}r} \biggl( \frac{U_{\phi }^{2}}{r^{2}} \biggr) + \frac{1}{ \mu \rho _{\mathrm{i}}}r \frac{\mathrm{d}}{\mathrm{d}r} \biggl( \frac{B _{\mathrm{i}\phi }^{2}}{r^{2}} \biggr) \biggr]\xi _{r} - 2\mathrm{i} \biggl( \sigma \frac{U_{\phi }}{r} + \frac{1}{r} \frac{B_{\mathrm{i} \phi }f_{B}}{\mu \rho _{\mathrm{i}}} \biggr)\xi _{\phi } \\ &\quad = \frac{1}{ \rho _{\mathrm{i}}} \frac{\mathrm{d}p_{\mathrm{tot}}}{\mathrm{d}r}, \end{aligned}$$

(22)

$$\begin{aligned} & \bigl( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} \bigr)\xi _{\phi }+ 2 \mathrm{i} \biggl( \sigma \frac{U_{\phi }}{r} + \frac{1}{r}\frac{B_{ \mathrm{i}\phi }f_{B}}{\mu \rho _{\mathrm{i}}} \biggr)\xi _{r} = \mathrm{i} \frac{1}{\rho _{\mathrm{i}}}\frac{m}{r}p_{\mathrm{tot}}, \end{aligned}$$

(23)

$$\begin{aligned} & \bigl( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} \bigr)\xi _{z} = \mathrm{i} \frac{1}{\rho _{\mathrm{i}}}k_{z} p_{\mathrm{tot}}, \end{aligned}$$

(24)

$$\begin{aligned} & \biggl( \frac{\mathrm{d}}{\mathrm{d}r} + \frac{1}{r} \biggr)\xi _{r} + \mathrm{i}\frac{m}{r}\xi _{\phi }+ \mathrm{i}k_{z} \xi _{z} = 0, \end{aligned}$$

(25)

where

$$ \omega _{\mathrm{Ai}} = \frac{f_{B}}{\sqrt{\mu \rho _{\mathrm{i}}}} $$

(26)

is the local Alfvén frequency inside the jet.

Excluding $\xi _{\phi }$ and $\xi _{z}$ from these equations, we obtain

$$\begin{aligned} & \rho _{\mathrm{i}} \bigl( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} \bigr) \biggl( \frac{\mathrm{d}\xi _{r}}{\mathrm{d}r} + \frac{\xi _{r}}{r} \biggr) + 2\rho _{\mathrm{i}}d_{2} \frac{m}{r}\xi _{r} = \biggl( \frac{m ^{2}}{r^{2}} + k_{z}^{2} \biggr)p_{\mathrm{tot}}, \end{aligned}$$

(27)

$$\begin{aligned} & \rho _{\mathrm{i}}d_{1} \xi _{r} = \bigl( \sigma ^{2} - \omega _{ \mathrm{Ai}}^{2} \bigr) \frac{\mathrm{d}p_{\mathrm{tot}}}{\mathrm{d}r} - 2\frac{m}{r}d_{2} p _{\mathrm{tot}}, \end{aligned}$$

(28)

where

$$d_{1} = ( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} )^{2} - r ( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} ) [ \frac{ \mathrm{d}}{\mathrm{d}r} ( \frac{U_{\phi }^{2}}{r^{2}} ) - \frac{1}{\mu \rho _{\mathrm{i}}}\frac{\mathrm{d}}{\mathrm{d}r} ( \frac{B _{\mathrm{i}\phi }^{2}}{r^{2}} ) ] - 4d_{2}^{2}, \; d _{2} = \sigma \frac{U_{\phi }}{r} + \frac{B_{\mathrm{i}\phi } f_{B}}{ \mu \rho _{\mathrm{i}}r}. $$

By presenting $\xi _{r}$ from Equation 28 in terms of $p_{\mathrm{tot}}$ and inserting it into Equation 27, we obtain the following equation for the total pressure perturbation:

$$\begin{aligned} &\biggl[ \bigl( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} \bigr)\frac{ \mathrm{d}}{\mathrm{d}r} + \frac{\sigma ^{2} - \omega _{\mathrm{Ai}} ^{2} + 2m d_{2}}{r} \biggr] \\ &\quad {}\times \biggl[ \frac{\sigma ^{2} - \omega _{\mathrm{Ai}}^{2}}{d_{1}}\frac{ \mathrm{d}p_{\mathrm{tot}}}{\mathrm{d}r} - \frac{2md_{2}}{d_{1}} \frac{p _{\mathrm{tot}}}{r} \biggr] - \biggl( \frac{m^{2}}{r^{2}} + k_{z} ^{2} \biggr)p_{\mathrm{tot}} = 0. \end{aligned}$$

(29)

This equation can be significantly simplified by considering that the rotation and the magnetic twist of the jet are uniform, that is,

$$ U_{\phi }(r) = \Omega r \quad \mbox{and} \quad B_{\phi }(r) = A r, $$

(30)

where $\Omega$ and $A$ are constants. In this case, Equation 29 takes the form of the Bessel equation

$$ \frac{\mathrm{d}^{2}p_{\mathrm{tot}}}{\mathrm{d}r^{2}} + \frac{1}{r}\frac{ \mathrm{d}p_{\mathrm{tot}}}{\mathrm{d}r} - \biggl( \frac{m^{2}}{r^{2}} + \kappa _{\mathrm{i}}^{2} \biggr)p_{\mathrm{tot}} = 0, $$

(31)

where

$$ \kappa _{\mathrm{i}}^{2} = k_{z}^{2} \biggl[ 1 - 4 \biggl( \frac{\sigma \Omega + A\omega _{\mathrm{Ai}}/\!\sqrt{\mu \rho _{\mathrm{i}}}}{ \sigma ^{2} - \omega _{\mathrm{Ai}}^{2}} \biggr)^{2} \biggr]. $$

(32)

The equation governing plasma dynamics outside the jet (without twist and velocity field, i.e. $A = 0$, $\Omega = 0$, and $U_{z} = 0$) is the same Bessel equation, but $\kappa _{\mathrm{i}}$ is replaced by $k_{z}$.

Inside the jet, the solution to Equation 31 bounded on the jet axis is the modified Bessel function of the first kind,

$$ p_{\mathrm{tot}}(r \leqslant a) = \alpha _{\mathrm{i}}I_{m}( \kappa _{\mathrm{i}}r), $$

(33)

where $\alpha _{\mathrm{i}}$ is a constant.

Outside the jet, the solution bounded at infinity is the modified Bessel function of the second kind,

$$ p_{\mathrm{tot}}(r > a) = \alpha _{\mathrm{e}}K_{m}(k_{z} r), $$

(34)

where $\alpha _{\mathrm{e}}$ is a constant.

To obtain the dispersion equation governing the propagation of MHD modes along the jet, the solutions at the jet surface need to be merged through boundary conditions.

It is well known that for non-rotating and untwisted magnetic flux tubes, the boundary conditions are the continuity of the Lagrangian radial displacement and total pressure perturbation at the tube surface (Chandrasekhar, 1961), that is,

$$ \xi _{\mathrm{i}r}|_{r=a} = \xi _{\mathrm{e}r}|_{r=a} \quad \mbox{and} \quad p_{\mathrm{tot\,i}} \bigg| _{r=a} = p_{\mathrm{tot\,e}}|_{r=a}, $$

(35)

where total pressure perturbations $p_{\mathrm{tot\,i}}$ and $p_{\mathrm{tot\,e}}$ are given by Equations 33 and 34, respectively.

When the magnetic flux tube is twisted and still non-rotating and the twist has a discontinuity at the tube surface, then the Lagrangian total pressure perturbation is continuous and the boundary conditions are (see, e.g., Bennett, Roberts, and Narain, 1999; Zaqarashvili et al., 2010; Zaqarashvili, Vörös, and Zhelyazkov, 2014)

$$ \xi _{\mathrm{i}r}|_{r=a} = \xi _{\mathrm{e}r}|_{r=a} \quad \mbox{and} \quad p_{\mathrm{tot\,i}} - \frac{B_{\mathrm{ i}\phi }^{2}}{\mu a} \xi _{\mathrm{i}r} \bigg| _{r=a} = p_{\mathrm{tot\,e}}|_{r=a}. $$

(36)

The second term in the second boundary condition stands for the pressure from the magnetic tension force.

If a non-twisted, $B_{\mathrm{i}\phi } = 0$, tube rotates and the rotation has discontinuity at the tube surface, the boundary condition for the Lagrangian total pressure perturbation has a similar form as the second boundary condition in Equation 36,

$$ \xi _{\mathrm{i}r}|_{r=a} = \xi _{\mathrm{e}r}|_{r=a} \quad \mbox{and} \quad p_{\mathrm{tot\,i}} + \frac{\rho _{\mathrm{i}} U_{\phi }^{2}}{a}\xi _{\mathrm{i}r}\bigg| _{r=a} = p_{\mathrm{tot\,e}}|_{r=a}. $$

(37)

Here, the second term that describes the contribution of the centrifugal force to the pressure balance can be derived from Equation 28 for $B_{\mathrm{i}\phi } = 0$ by multiplying that equation by $\mathrm{d}r$, and considering the limit of $\mathrm{d}r \to 0$ through the boundary $r = a$, one obtains the relation $\mathrm{d} [ p_{\mathrm{tot}} + (\rho _{\mathrm{i}} U _{\phi }^{2}/a)\xi _{r} ] = 0$, or, equivalently, the second boundary condition in the above equation. Hence, the boundary condition for the Lagrangian total pressure perturbation in rotating and magnetically twisted flux tubes has the form

$$ p_{\mathrm{tot\,i}} + \biggl( \frac{\rho _{\mathrm{i}} U_{ \phi }^{2}}{a} - \frac{B_{\mathrm{i}\phi }^{2}}{\mu a} \biggr) \xi _{\mathrm{i}r} \bigg| _{r=a} = p_{\mathrm{tot\,e}}|_{r=a}. $$

(38)

In the case of uniform rotation and magnetic field twist, Equation 30, the boundary conditions for the Lagrangian radial displacement $\xi _{r}$ and the total pressure perturbation $p_{\mathrm{tot}}$ are

$$ \xi _{\mathrm{i}r}|_{r=a} = \xi _{\mathrm{e}r}|_{r=a} \quad \mbox{and} \quad p_{\mathrm{tot\,i}} + a \biggl( \rho _{\mathrm{i}} \Omega ^{2} - \frac{A^{2}}{\mu } \biggr)\xi _{\mathrm{i}r} \bigg| _{r=a} = p_{\mathrm{tot\,e}}|_{r=a}. $$

(39)

Using these boundary conditions, we obtain the dispersion equation of normal MHD modes propagating in rotating and axially moving twisted magnetic flux tubes (Zaqarashvili, Zhelyazkov, and Ofman, 2015)

$$\begin{aligned} & \frac{ ( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} )F_{m}( \kappa _{\mathrm{i}}a) - 2m ( \sigma \Omega + A\omega _{ \mathrm{Ai}}/\! \sqrt{\mu \rho _{\mathrm{i}}} )}{\rho _{ \mathrm{i}} ( \sigma ^{2} - \omega _{\mathrm{Ai}}^{2} )^{2} - 4\rho _{\mathrm{i}} ( \sigma \Omega + A\omega _{\mathrm{Ai}}/\! \sqrt{ \mu \rho _{\mathrm{i}}} )^{2}} \\ &\quad {}= \frac{P_{m}(k_{z} a)}{\rho _{\mathrm{e}} ( \sigma ^{2} - \omega _{\mathrm{Ae}}^{2} ) - ( \rho _{\mathrm{i}}\Omega ^{2} - A^{2}/\mu )P_{m}(k_{z} a)}, \end{aligned}$$

(40)

where

$$F_{m}(\kappa _{\mathrm{i}}a) = \frac{\kappa _{\mathrm{i}}aI_{m}^{\prime }(\kappa _{\mathrm{i}}a)}{I_{m}(\kappa _{\mathrm{i}}a)}, \qquad P_{m}(k _{z} a) = \frac{k_{z} aK_{m}^{\prime }(k_{z} a)}{K_{m}(k_{z} a)}, \qquad \omega _{\mathrm{Ae}} = \frac{k_{z} B_{\mathrm{e}}}{\sqrt{ \mu \rho _{\mathrm{e}}}}. $$

We note that in the case of a non-rotating twisted flux tube, $\Omega = 0$, the above Equation 40 recovers the well-known dispersion relation of normal MHD modes propagating in cylindrical twisted jets (see, e.g., Zhelyazkov and Zaqarashvili, 2012). If the environment medium is a cool plasma, as is the case of our macrospicule, where the thermal pressure $p_{\mathrm{e}} = 0$, the $k_{z} a$ in $P_{m}(k_{z} a)$ must be replaced by $k_{z} a[ 1 - ( \omega / \omega _{\mathrm{Ae}} )^{2} ]^{1/2}$, which yields the wave dispersion relation we used in Equation 3.