Uncovering Complexities in Horizontal Inequality: A Novel Decomposition of the Gini Index

Abstract

This study introduces an innovative tool to analyse how various inequality factors, including geography, race, and gender, contribute to overall inequality. Traditional approaches typically partition populations into groups based on a single factor and assess inequality by additively decomposing an inequality measure into within- and between-group components. After discussing the theoretical impossibility of additively decomposing the Gini index into within- and between-group components, in fact, we propose a Gini decomposition into two highly informative within- and between-components, with substantial improvement upon the usual assessment of horizontal inequality. This method represents a significant advancement over the traditional horizontal inequality assessment, which only compares group means and overlooks the complexities of differences between groups. Our approach accurately captures the nuances of group disparities, offering a robust measure of horizontal inequality. Through rigorous simulations and empirical analysis of the OECD Income Distribution Database, we validate the effectiveness of our method in evaluating and understanding inequality. This work enriches the toolkit available to researchers in the field by offering a framework for selecting the most suitable measure of horizontal inequality, along with the code for implementing the proposed decomposition.

1 Introduction

Evaluating population inequality necessitates an analysis of disparities among subgroups, particularly when examining populations distinguished by pronounced gender or territorial divides, or disparities linked to age, ethnicity, or religion. All these sources of horizontal inequality hamper well-being and development. Their negative impact is widely recognised, to the extent that their reduction is the focus of Sustainable Development Goals 5 and 10 of the United Nations Development Programme.

What are the principal factors-such as geography, ethnicity, gender, etc.-underpinning economic divides? Are these disparities narrowing over time? What interventions are most effective in bridging the gaps between population subgroups? Conventionally, addressing these policy questions involves decomposing inequality by factors to derive two components: one measuring within-group disparities and the other capturing between-group disparities, the latter of which significantly informs on horizontal inequality. This approach has been extensively used in the literature on horizontal inequality (see, e.g., Gachet et al., 2019; McDoom et al., 2019; Canelas & Gisselquist, 2019). Given the wide range of possible inequality measures and decompositions, Josa & Aguado (2020) offers a comprehensive review of the available methodologies and their implications, providing a practical framework for choosing the most appropriate measure.

This work introduces a further decomposition of the Gini index, which contributes to the existing literature because its between-component is well suited to measure horizontal inequality and addresses a critical issue that we term oversimplification. This distinguishes our decomposition from other methodologies prevalent among researchers. The methods for decomposing inequality indicators (see Deutsch & Silber, 1999 for a review) share a common approach, pursuing the additive decomposability property (Bourguignon, 1979; Shorrocks, 1980). An inequality measure is additively decomposable if it can be expressed as the sum of two components observing the following constraints: the within-group component has to be the average inequality within subgroups weighted by population size, while the between-group component has to depend explicitly on the distance between the group means and on the group sizes.

Ebert (2010) highlights how the conventional constraint on the between-group component can lead to oversimplification, especially when examining horizontal inequality between groups with similar means but different distributions, or when analyzing inequality dynamics. While some indicators based on means might suggest converging groups, the underlying distributions could be diverging. While this phenomenon is occasional, it is common for the distance between means to differ from the distance between distributions, or for the two distances to have different dynamics.

The Gini index, a commonly used measure of inequality, is not additively decomposable. Its conventional decompositions require an additional term if the within- and between-components observe the constraints of additive decomposability.

In this paper we show that, by relaxing these constraints, it is possible both to obtain a two-component decomposition of the Gini index and to solve oversimplification. This innovative approach features two components that quantify inequality within and between groups, the latter of which solves the issue of oversimplification by calculating the average inequality between individuals ranking in identical quantiles across different subgroups.

The paper unfolds as follows. Section 2 introduces the notation that we use throughout the paper; then it discusses the conventional subgroup decompositions of the Gini index and introduces a benchmark measure for horizontal inequality, before presenting the intuition leading to our decomposition. Section 3 formalises the new decomposition in the case of equal-sized groups and shows its properties. Section 4 extends the decomposition to the case of groups with different sizes. Section 5 presents the Monte Carlo experiment that studies the correlations between alternative measures, highlighting the informativeness of the proposed decomposition. Section 6 uses the OECD Income Distribution Database to analyse the income inequality of EU countries, providing striking evidence in favour of our between-component. Section 7 provides conclusive remarks and a vademecum for choosing the most appropriate measure of horizontal inequality.

2 The Gini Index and Horizontal Inequality

Consider a population of N units. We denote by $x_i$ the income of the generic individual $i=1,\dots ,N$, by $\mu =\sum _1^Nx_i/N$ the average income of the population, and by G its Gini index. When considering a partition of the population into K groups, denote the vector of their sizes with $\textbf{n}=\left( n_1,\dots n_K\right)$, where $\sum _{k=1}^Kn_k=N$. Let $x_{i}^{k}$ be the i-th element of the group $k=1,\dots ,K$ (non decreasing) vector of incomes $\textbf{x}^k=(x_{1}^{k},\dots ,x_{n_k}^{k})$. Furthermore, we denote by $\mu _k$ the mean of group k, and by $G_k$ its Gini index.

Among the many different formulations of the Gini index (see Giorgi et al., 2005; Giorgi, 2011; Ceriani & Verme, 2015 and Ceriani & Verme, 2012), we consider the following:

$$\begin{aligned} G=\frac{1}{2\mu N^2}\sum _{i=1}^{N}\sum _{j=1}^{N}|x_i-x_j |=\frac{g}{2\mu N^2} \end{aligned}$$

(1)

where the numerator g is the sum of all the pairwise absolute differences between individual income. It is normalised by the factor $(2\mu N^2)^{-1}$, so that G is scale invariant and $G\in \left[ 0,1\right]$ if all $x_i\ge 0$.

2.1 Subgroup Decomposition of the Gini Index

A wide variety of Gini index decompositions exist, originating from alternative formulations of the index and diverse methodological approaches.

We mainly focus on the most widespread and intuitive decomposition, whose between-component, often called GGini, is widely used to measure horizontal inequality. It was presented for the first time in Bhattacharya and Mahalanobis (1967). This decomposition consists of two components that measure inequality within and between groups, plus a third term, which by construction is the residual of the decomposition. We can express the general structure of the Bhattacharya and Mahalanobis decomposition as follows:

$$\begin{aligned}&G=G_w^{BM}{} +G_b^{BM}{} +R^{BM} \end{aligned}$$

(2)

The within component $G_w^{BM}$ measures the inequality within groups by a weighted average of the Gini index of each group. It reads:

$$\begin{aligned} G_w^{BM}=\sum _{k=1}^{K}\frac{\mu _k}{\mu } \frac{n_k^2}{N^2} G_k \end{aligned}$$

(3)

and each weight is the product between the income and population shares of the group k.

As for the between component in Eq. (2), it reads:

$$\begin{aligned} GGini=G_b^{BM}=\frac{1}{2\mu N^2} \sum _{k=1}^{K}\sum _{h=1}^{K}n_kn_h |\mu _k-\mu _h | \end{aligned}$$

(4)

A notable feature of the GGini is that the weight of each mean difference is the product of the sizes of the groups. This means the GGini quantifies between-group inequality by applying the Gini index to scenarios devoid of inequality within groups, i.e. when each observation has the average income of its group. It is the inequality between the weighted means. Unfortunately, due to oversimplification, this is not always fully representative of horizontal inequality. As a compelling example, $GGini=0$ when groups have the same mean but their distributions differ in terms of variability, skewness, or higher moments, indicating the presence of horizontal inequality. Oversimplification also arises when the averages are different, being not the predominant source of the differences between the distributions of the groups. Except in rare cases, this oversimplification manifests as an underestimation of horizontal inequality.

Equation 4 represents the reference for further decompositions of the Gini index proposed over time; a contribution that partially deviates from the approach of Bhattacharya and Mahalanobis is attributed to Yitzhaki and Lerman (1991). Its general structure is the same as Eq. (2). We identify the components of this decomposition by replacing the superscripts of the three components with YL. Regarding $G_w^{YL}$, it only differs from Eq. (3) in the structure of the weights, weighting each $G_k$ by the income share of group k:

$$\begin{aligned} G_w^{YL}=\sum _{k=1}^{K}\frac{\mu _k}{\mu } \frac{n_k}{N} G_k \end{aligned}$$

(5)

Given the structure of the weights, the correlation ${{\,\mathrm{\rho }\,}}(G_w^{BM},G_w^{YL})=1$ if the groups have the same size, but it decreases with the size variability.

Regarding $G_b^{YL}$, it reads:

$$\begin{aligned} G_b^{YL}=2cov(\mu _k,\bar{F}_k)/\mu \end{aligned}$$

(6)

where $\bar{F}_k$ is the average rank of the members of group k in the overall population. The two between-components in Eqs. (4)–(6) appear very different, but, like any between component of a subgroup decomposition of inequality, $G_b^{YL}$ is also based on the comparison of the means of the groups and suffers from oversimplification.

2.2 A Benchmark Measure of Horizontal Inequality

Having two vectors of m quantiles representing two income distributions, we consider the following as a measure of their diversity:

$$\begin{aligned} Eb_{kh}=\frac{1}{m}\sum _{j=1}^m|x_{j}^k-x_{j}^h | \end{aligned}$$

It is proposed by Ebert (1984) and is the simple average difference between quantiles. In his paper, Ebert proposes a more general class of measures based on a parameter r. $Eb_{kh}$ corresponds to $r=1$. A previous proposal by Dagum (1980) had already developed a measure of economic distance between two income distributions, but it has been criticised by Shorrocks (1982) due to its asymmetric nature. Ebert proposal, instead, presents all the properties of a distance and observes a general axiomatic approach. Furthermore, it perfectly reflects our idea that a measure of horizontal inequality between groups must compare their overall distributions. We generalise this measure to the case of K groups by using the same weighting structure of Eq. (4):

$$\begin{aligned} HI=\frac{1}{2\mu N^2}\sum _{k=1}^{K}\sum _{h=1}^{K}n_kn_hEb_{kh} \end{aligned}$$

so that HI is scale invariant and the weight of each $Eb_{kh}$ depends on the number of pairs between the two groups.

We provide an additional reason why HI is a suitable benchmark for horizontal inequality. We define the GGini for quantile j as

$$\begin{aligned} GGini_j=\frac{1}{2\mu _jN^2} \sum _{k=1}^{K}\sum _{h=1}^{K}n_kn_h |x_j^k-x_j^h | \end{aligned}$$

(7)

where $\mu _j=\sum _{k=1}^Kx_j^k/K$ is the average, across groups, of observations ranking in the $j-th$ position of their group. Using Eq. (7), we can rewrite HI as follows:

$$\begin{aligned} HI=\frac{1}{m}\sum _{j=1}^m\frac{1}{2\mu N^2}\sum _{k=1}^{K}\sum _{h=1}^{K}n_kn_h|x_{j}^k-x_{j}^h |=\sum _{j=1}^m\frac{\mu _j}{m\mu }GGini_j \end{aligned}$$

(8)

This benchmark evaluates the horizontal inequality of each quantile using the Gini index, then averages the results weighting each $GGini_j$ by the income share of quantile j. The advantage of HI over GGini in measuring horizontal inequality is twofold. First, HI allows us to consider the differences between groups that are not captured by the mean. Second, decomposing HI in its addenda by k and/or by j produces informative indicators that allow one to know which groups and which parts of their distributions struggle the most. One can study the contribution of the bottom quartile to horizontal inequality and discover that the poor in one group suffer relatively more inequality than the poor in the other group, or that even if the groups are not equal on average, the poor are similar in the two groups. Horizontal inequality between two groups has different implications if it originates at the top, middle, or bottom of the distribution. For example, knowing the sources of horizontal inequality could be crucial when relating it to conflicts. Horizontal inequality triggers the start of conflicts, while within-group inequality shapes their intensity (Cederman et al., 2011; Esteban & Ray, 2011; Huber & Mayoral, 2019). The inequality-conflict literature clearly states that the presence of poor people experiencing bad living conditions and rich people, who can finance the conflict, is an essential engine for civil war. Explicitly considering horizontal differences at the top, middle, or bottom of the distribution helps to study which aspects of group distributions and group differences shape the incentive to fight, allowing one to test refined hypotheses about the drivers of conflicts and their intensity.

To conclude this section, we describe the intuition to derive, from the Gini index, a measure with the peculiarities of HI and such that its complement to the Gini measures the inequality within groups.

2.3 A New Insight

Consider a population partitioned into K equal-sized groups and define n as their size. The numerator of the Gini index in Eq. (1) can be written as:

$$\begin{aligned} g=\sum _{i=1}^{N}\sum _{j=1}^{N}|x_{i}-x_{j} |=\sum _{k=1}^{K}\sum _{h=1}^{K}\sum _{i=1}^{n}\sum _{j=1}^{n}|x_{i}^{k}-x_{j}^{h} | \end{aligned}$$

(9)

Fig. 1

A two-group-two-individual illustration, with group $k=\{8,3\}$ and group $h=\{6,2\}$. The left panel highlights all the pairwise differences between units, considered twice so that their sum constitutes g. The vertical, horizontal, and black diagonal differences have intuitive decomposition. The right panel illustrates the decomposition of the grey diagonals

Figure 1 provides an innovative insight into the structure of the Gini index. It illustrates a two-group-two-individual situation, with group $k=\{8,3\}$ and group $h=\{6,2\}$. Figure 1a highlights all pairwise differences between units, considered twice so that their sum constitutes g.

As the scheme suggests, we can distinguish three kinds of difference: vertical, horizontal, and diagonal. Vertical differences involve same-group pairs. Horizontal differences involve same-rank (same-quantiles) pairs from different groups. Diagonal differences involve different-rank pairs from different groups. We assign vertical and horizontal differences to within and between components, respectively. Although diagonal differences involve pairs of different groups, they also reflect vertical (same-group) differences and are not entirely attributable to inequality between groups. For example, imagine replacing the values in the scheme so that the groups are identical: pose $x_1^h=x_1^k=8$ and $x_2^h=x_2^k=3$. The values of the diagonal differences - 5 - are equal to the vertical ones and should not contribute to the absent horizontal inequality.

At this stage, diagonal differences can be instinctively thought of as the addenda of a residual term arising from the decomposition, and it seems natural to associate their sum with the conventional residuals $R^{BM}$ and $R^{YL}$. These residuals - which are non-negative and disappear if the distributions of the groups do not overlap - are interpretable in terms of overlapping, stratification, and transvariation between the distributions of the groups (Yitzhaki & Lerman, 1991; Lambert & Aronson, 1993; Yitzhaki, 1994; Dagum, 1997 and Costa, 2021). This interpretation does not apply to the sum of diagonal differences, which is positive even when the groups do not overlap. The sum of diagonals is zero only if there is perfect equality, since the diagonals contain information on both within- and between-group inequality. Going back to Fig. 1, we propose a strategy to disentangle each diagonal difference in two informative contributions to within- and between-group inequality.

The two black diagonals in Fig. 1a are intuitively decomposable. For example, looking at the solid black diagonal line and moving along the legs of the solid black triangle, the difference between the richest member of group k and the poorest member of group h is 6 since the former is 5 points richer than the poorest individual in her group, who is 1 unit richer than her counterpart in group h ($6=5+1$). A similar argument holds from the opposite point of view, which is looking at the dashed black diagonal line, representing the difference between the poorest member of group h and the richest member of group k ($6=4+2$). The two black diagonal differences are predominantly due to and reflect the inequality within the two groups. Consequently, we suggest splitting their contribution to g ($6+6=12$) assigning $5+4=9$ to the within component and $1+2=3$ to the between one.

This strategy becomes inapplicable for grey diagonals, which are the focus of Fig. 1b. Here, the three values involved in the path along the grey legs do not increase or decrease monotonically as for the black lines, namely the product between the horizontal and the vertical signed differences is negative. In such cases, we should subtract the horizontal value from the vertical value to obtain the value of the diagonal difference. However, it would be paradoxical to decrease the between component by the horizontal value, i.e. by 1 in the case of the solid grey lines.¹

As Fig. 1b illustrates, we suggest splitting each diagonal difference proportionally to the vertical and horizontal ones and assigning these two (positive) values to the within and between components, respectively. Using the proportional scaling to decompose the diagonals ensures that adding all their contributions to the within and between components preserves the proportion between the sum of vertical and horizontal differences. This is the key for the informativeness of the final components.

We have just presented the intuition that underlies the decomposition. In the next section, we formalise the decomposition under the hypothesis of equal-sized groups, which is relaxed in Sect. 4.

3 The Decomposition Proposal

Starting from Eq. (9), we suggest the following decomposition for each non-zero difference²:

$$\begin{aligned} |x_{i}^k-x_{j}^h |&=|x_{i}^k-x_{j}^h | \frac{|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |}{|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |}\\&=|x_{i}^k-x_{j}^k |\frac{|x_{i}^k-x_{j}^h |}{|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |}+|x_{j}^k-x_{j}^h |\frac{|x_{i}^k-x_{j}^h |}{|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |}=\\&=|x_{i}^k-x_{j}^k |w_{ij}^{kh}+|x_{j}^k-x_{j}^h |w_{ij}^{kh}\end{aligned}$$

(10)

where the two addenda are, respectively, contributions to the within and between components, while $w_{ij}^{kh}=|x_{i}^k-x_{j}^h |/(|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |)$ is the scaling factor. The scaling factor $w_{ij}^{kh}$ equals 1 in cases of vertical differences (where $k=h$), horizontal differences (where $i=j$), and for specific differences like the black diagonals (where $k\ne h$, $i\ne j$ and $(x_{i}^k-x_{j}^k)\cdot (x_{j}^k-x_{j}^h)\ge 0$). This equality simplifies Eq. (10), which reduces to $|x_{i}^k-x_{j}^h |=|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |$ for these particular instances, reflecting the intuitive allocation of differences to the within and between components. Differences such as grey diagonals ($k\ne h$, $i\ne j$ and $(x_{i}^k-x_{j}^k)\cdot (x_{j}^k-x_{j}^h)<0$) are associated with $w_{ij}^{kh}\in [0,1)$. In this case, $w_{ij}^{kh}<1$ because $|x_{i}^k-x_{j}^h |<|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |$: the scaling factor reduces the vertical and horizontal differences so that the contributions to the within and between components add up to $|x_{i}^k-x_{j}^h |$.

The decomposition of the Gini index follows by substituting Eq. (10) into Eq. (9). Denoting $\sum _{h=1}^{K}w_{ij}^{kh}=w_{ij}^{k}$ and $\sum _{i=1}^{n}w_{ij}^{kh}=w_{j}^{kh}$, we obtain:

$$\begin{aligned} g=g_w+g_b=\sum _{k=1}^{K}\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}^{k}|x_{i}^k-x_{j}^k |+\sum _{k=1}^{K}\sum _{h=1}^{K}\sum _{j=1}^{n}w_{j}^{kh}|x_{j}^k-x_{j}^h | \end{aligned}$$

(11)

and we can write

$$\begin{aligned} G=G_w^A+G_b^A=\frac{g_w}{2\mu N^2}+\frac{g_b}{2\mu N^2} \end{aligned}$$

(12)

The Gini index consists of two terms. We interpret $G_w^A$ and $G_b^A$ as the within and between components of inequality because, respectively, they depend on the contributions from same-group and same-rank pairwise differences. Clearly, $G_b^A$ does not explicitly depend on the group means, therefore it does not observe the additive decomposability property. Pursuing a between-component that measures horizontal inequality while comparing the entire distributions of the groups inevitably leads to contrast with the definition of additive decomposability. However, while additive decomposability is desirable when the goal is to understand how resources are unequally distributed between groups, we believe that relaxing the constraint it imposes on the between component is essential to accurately capture horizontal inequality.

The within and between components involve, respectively, $w_{ij}^k$ and $w_j^{kh}$. These weights ensure that each same-group (same-rank) difference contributes to within (between) inequality according to how much it affects the diagonal ones. For example, if a vertical difference increases, thus enlarging some of the grey-like diagonal differences, then the related scaling factors consistently increase and inflate the weight $w_{ij}^k$. The structure of the weights follows from that of the scaling factors, which is not necessarily unique. In Eq. (10) we multiply $|x_{i}^k-x_{j}^h |$ by 1, expressed as the ratio of $|x_{i}^k-x_{j}^k |+|x_{j}^k-x_{j}^h |$ to itself. Alternatively, we might consider multiplying by the ratio of $f(x_{i}^k-x_{j}^k) + f(x_{j}^k-x_{j}^h)$ to itself, where $f(\cdot )$ represents any monotonic and continuous function. This adjustment introduces a broader class of decompositions, enabling a focus on either large or small differences based on the choice of $f(\cdot )$ (e.g., $f(x)=x^2$ or $f(x)=\sqrt{|x |}$ would put more emphasis on large or small differences, respectively). However, since we are decomposing a measure of inequality based on the linear distance (Mehran, 1976), we think that the natural choice is proportional scaling, which is the only one that preserves the linearity of the Gini index in the components of its decomposition.

The R package implementing the described decomposition technique is available on GitHub. To ensure the GiniDecA package can be installed from GitHub, first check if the devtools package is installed. If not, install devtools using the following command in R:

Afterward, install GiniDecA in the R environment

and use the GiniDec function as in the example below:

3.1 Properties of the Decomposition

Our decomposition enjoys relevant properties, both in the within- and the between-group components. Given $w_{ij}^{kk}=1$, $w_{jj}^{kh}=1$ and $w_{ij}^{kh}\ge 0$, we have $w_{ij}^{k}\ge 1$ and $w_{j}^{kh}\ge 1$. Therefore, the following properties hold:

$$G_{w}^{A} = 0 \Leftrightarrow \left| {x_{i}^{k} - x_{j}^{k} } \right| = 0\quad \forall i,j,k$$

(i)

$$G_{b}^{A} = 0 \Leftrightarrow \left| {x_{j}^{k} - x_{j}^{h} } \right| = 0\quad \forall j,k,h$$

(ii)

The first relation ensures that the within component is zero iff all the same-group differences are zero, i.e. there are no differences between groups. The second condition guarantees that the between-component is zero iff all the same-rank differences are zero, i.e. the groups have the same distribution.

Properties (i)-(ii) are conceptually analogous. All the most widespread decompositions of inequality have a within component that, like ours, observes property (i). As for property (ii), $G_b^{BM}$ and $G_b^{YL}$ satisfy its sufficiency—they are zero if the groups have the same distribution - while they do not satisfy its necessity - they are zero even if the groups have different distributions. Our between-component observes both the sufficiency and necessity of property (ii), being zero iff the groups have the same distribution.

Additional important properties concern the algebraic similarity of $G_w^{A}$ with Eqs. (3)–(5), and of $G_b^A$ with Eq. (8). Regarding $G_w^{A}$, we can rewrite it as

$$\begin{aligned} G_w^{A}&=\frac{1}{2\mu N^2}\sum _{k=1}^{K}\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}^{k}|x_{i}^k-x_{j}^k |\\&=\sum _{k=1}^{K}\frac{\mu _k}{\mu }\frac{n^2}{N^2}\cdot \frac{1}{2\mu _k n^2}\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}^{k}|x_{i}^k-x_{j}^k | \end{aligned}$$

(13)

The term $\sum _{i=1}^{n}\sum _{j=1}^{n}w_{ij}^{k}|x_{i}^k-x_{j}^k |/2\mu _k n^2$ would equal $G_k$ if all the weights $w_{ij}^k=1$, resulting in $G_w^{A}=G_w^{BM}$. This never happens but, as we discussed, each $w_{ij}^k$ preserves the information of the vertical differences that it multiplies. Therefore, the correlation between $G_w^A$ and $G_w^{BM}$ is naturally high. Being $n/N=1/K$, if all the weights are $w_{ij}^k=K$ then $G_w^{A}=G_w^{YL}$. Actually, $1\le w_{ij}^k\le K$, therefore the weighting structure of $G_w^{A}$ is the middle ground between those of $G_w^{BM}$ and $G_w^{YL}$. This is why $G_w^{A}$ is highly correlated with both $G_w^{BM}$ and $G_w^{YL}$.

A similar discussion holds by comparing $G_b^{A}$ with the horizontal inequality benchmark defined in Eq. (8). Our between component reads:

$$\begin{aligned} G_b^{A}&=\frac{1}{2\mu N^2}\sum _{k=1}^{K}\sum _{h=1}^{K}\sum _{j=1}^{n}|x_{j}^k-x_{j}^h |w_{j}^{kh}\\&=\sum _{j=1}^{n}\frac{\mu _j}{n\mu }\frac{1}{2\mu _jN^2}\sum _{k=1}^{K}\sum _{h=1}^{K}nw_{j}^{kh}|x_{j}^k-x_{j}^h |\end{aligned}$$

(14)

which has a comparable structure to Eq. (8). $G_b^A$ and HI would be equivalent if all the weights were $w_{j}^{kh}=n$. Again, it never happens and since $1\le w_{j}^{kh}\le n$ then $G_b^A$ is usually lower than HI. It is important to avoid confusing this relation with an underestimation of horizontal inequality. We argue that the weights $w_{j}^{kh}$ guarantee such a strong correlation between $G_b^A$ and HI that we can consider $G_b^A$ lower than HI simply due to a scaling transformation. We confirm the high correlation between $G_b^A$ and HI, and between $G_w^A$, $G_w^{BM}$ and $G_w^{YL}$, using a Monte Carlo simulation. We present the experiment and its results in Sect. 5.

Concluding this section, we observe that, as discussed for HI, isolating the addenda of $G_b^A$ by j and k provides indicators which allow one to understand which parts of the distributions differ the most between the groups, and which group differs the most from the others. We believe that these indicators are another tool from which several fields of the inequality literature can benefit.

4 The Different-Sized Groups Extension

This section shows that our methodology is robust even when groups are of different sizes, extending beyond the initial assumption of equal-sized groups. It was necessary to understand the decomposition arguments, but our decomposition approach can be flexibly adapted to scenarios where groups vary in size, ensuring broader applicability. In this case, Eq. (9) becomes:

$$\begin{aligned} g=\sum _{i=1}^{N}\sum _{j=1}^{N}|x_i-x_j |=\sum _{k=1}^{K}\sum _{h=1}^{K}\sum _{i=1}^{n_k}\sum _{j=1}^{n_h}|x_{i}^k-x_{j}^h | \end{aligned}$$

and a way to ensure the existence of the element $x_{j}^k$ is necessary for the implementation of our decomposition proposal. We propose two distinct solutions. The first evaluates the two components without approximation. However, this exact approach may require computational resources that are impractical for large datasets. The second solution drastically reduces computational requirements by paying the cost of a negligible approximation.

4.1 The Exact Approach

Consider a new common size $n=lcm\left( \textbf{n}\right)$ and the weights $p_{k}=n_k/n$, so to build the repopulated vectors $y^k=(y_{1}^k,\dots ,y_{n}^k)=(\underbrace{x_{1}^k\dots x_{1}^k}_{p_{k}^{-1}},\dots \underbrace{x_{n_k}^k\dots x_{n_k}^k}_{p_{k}^{-1}})$. We can show:

$$\begin{aligned} \sum _{i=1}^{n_k}\sum _{j=1}^{n_h}|x_{i}^k-x_{j}^h |=\sum _{i=1}^{n}\sum _{j=1}^{n}p_k p_h|y_{i}^k-y_{j}^h | \end{aligned}$$

(15)

Figure 2 provides the intuition of Eq. (15). Imagine two groups composed, respectively, of two and three individuals, as reported in the left rectangle. Replace them with those in the right rectangle. According to the principle of population, $\textbf{x}^k$ and $\textbf{y}^k$ (as well as $\textbf{x}^h$ and $\textbf{y}^h$) have the same within-group inequality. In addition, the cumulative distribution functions of the two groups are the same before and after the replacement, and hence the distance between the two groups is also unvaried. However, each difference between couples in the left scheme appears, in the right scheme, 9 times if the couple belongs to $\textbf{y}^k$, 4 times if it belongs to $\textbf{y}^h$ and 6 times if the two units belong to different groups. The $p_k$ and $p_h$ in Eq. (15) adjust by multiplying the differences, respectively, by 1/9, 1/4 and 1/6. In this way, equal-sized groups are obtained preserving the correspondence with the Gini index and with the original distributions of the groups.

Fig. 2

A two-group illustration of repopulation in the exact approach. The left panel represents two groups composed, respectively, of two and three individuals. The exact approach replace them with the equal-sized groups in the right rectangle and introduces the weights $p_k$ and $p_h$ in Eq. (15) to preserve the correspondence with the Gini index

We decompose the Gini index using a technique that is analogous to the one used to derive Eq. (11). The only difference is in the new weights $w_{ij}^{k}=\sum _{h=1}^Kp_kp_hw_{ij}^{kh}$ and $w_{j}^{kh}=\sum _{i=1}^np_kp_hw_{ij}^{kh}$, which incorporate the information needed to preserve the original importance of each couple.

Unfortunately, in most cases, this approach requires an unaffordable computational effort because of the potentially huge magnitude of the least common multiple. To reduce computational requirements, we present an alternative procedure, which we refer to as quantilisation.

4.2 Quantilisation

Differently from the exact approach, we propose to consider a lower value of n and to calculate differently each $\textbf{y}^k$: for each group, the vector $\textbf{y}^k$ contains the n quantiles from the income vector of the group. As for $p_k$, their calculation is the same employed in the exact approach, but now nothing constrains $n\ge n_k$, thus it can be $p_k>1$. The decomposition is the same, but G, $G_w$ and $G_b$ now incur in some approximation.

To employ this method, there are the definition of quantile and the value of n to be selected. For the former, we advise the Definition 7 reported in Hyndman and Fan (1996), which is the default definition adopted by the $quantile$ function in various statistical software. Given each vector ${\textbf {x}}^k$, accordingly to this definition and in order to minimise the approximation, we suggest first to interpolate linearly the $n_k$ vertices $\left( (i-1)/(n_k-1),x_{i}^k\right)$, and then to estimate the n quantiles by the values associated with the probabilities

$$\begin{aligned} prob_j=\frac{j-1}{n-1}\,\,\,\,j=1,\dots ,n \end{aligned}$$

(16)

on the resulting piecewise linear curve.

Regarding the value of n, we define $w_k=n_k/\sum _{k=1}^Kn_k$ and advise the value:

$$\begin{aligned} n=\sum _{k=1}^Kw_kn_k=\frac{\sum _{k=1}^Kn_k^2}{\sum _{k=1}^Kn_k} \end{aligned}$$

(17)

which determines n as the average of the $n_k$, each weighted by its own share of population $w_k$.

The decisions proposed for both the quantile definition and for the value of n are motivated in the appendix. Here, we only inform that, if they are employed, the approximation that the quantilisation procedure copes with is minimal and negligible. To obtain two estimates of the exact components, which are consistent and sum up to the Gini index of the original data, it is sufficient to multiply the shares of the components, obtained by quantilisation, by the value of the index evaluated on original data.

5 Monte Carlo Experiment: Comparison of Alternative Decompositions

This section details the Monte Carlo simulation developed to examine the correlations between alternative decomposition components and established benchmarks. In particular, the experiment studies the correlation of $G_w^A$ and $G_w^{BM}$ with $G_w^{YL}$; and the correlation of $G_b^A$, GGini and $G_b^{YL}$ with HI. The aim is to validate the effectiveness of our approach in capturing within-group and between-group inequality. We also carried out the experiment using $G_w^{BM}$ instead of $G_w^{YL}$ as the reference point for the inequality within the groups. This additional simulation confirms the discussion after Eq. (13), which stresses that the weighting structure of $G_w^A$ is the balancing between those of $G_w^{BM}$ and $G_w^{YL}$.

The experiment works with three predetermined parameters: the number of groups, the parameter(s) of the distribution of $\textbf{n}$ and the coefficient of variation between the averages of the groups ($CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$). The latter is an indirect parameter, which derives from imposing credible conditions on the parameters of the lognormal distribution that is used to sample incomes. More details about the income simulation procedure and its theoretical foundations can be found in the Appendix. Here, we only stress that the parameters of the lognormal distribution are micro-founded. Indeed, as detailed in the second part of the Appendix, they are chosen sampling from the parameters estimated in Bandourian et al. (2002) using real data along different countries and periods. This guarantees robust results with respect to real income distributions.

The procedure is schematised in Fig. 3 and can be summarised as follows:

Fig. 3

The Monte Carlo experiment in a scheme

Step I. Fixing K and (n, r), generate the vector $\textbf{n}$: each $n_k$ is drawn from a uniform $\left[ n, (1+r)\cdot n\right]$, where $100\cdot r$ is the maximum percentage deviation from the minimum n.

Step II. Fixing $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$, generate the income vectors from the lognormal distribution 50 times, each time evaluating all the statistics involved ($G_w^A$, $G_w^{BM}$, $G_w^{YL}$, $G_b^A$, $G_b^{BM}$(=GGini), $G_b^{YL}$ and HI). The 50 points allow us to estimate the following triples of correlation estimates:

$$\begin{aligned} \left[ \begin{array}{l} {{\,\mathrm{\rho }\,}}\left( {G_w^{A }},G_w^{YL}\right) \\ {{\,\mathrm{\rho }\,}}\left( {G_w^{BM}},G_w^{YL}\right) \\ {{\,\mathrm{\rho }\,}}\left( {G_w^{YL}},G_w^{YL}\right) \end{array}\right] , \;\; \left[ \begin{array}{l}{{\,\mathrm{\rho }\,}}\left( {G_b^{A}},HI\right) \\ {{\,\mathrm{\rho }\,}}\left( {G_b^{BM}},HI\right) \\ {{\,\mathrm{\rho }\,}}\left( {G_b^{YL}},HI\right) \end{array}\right] \end{aligned}$$

Step III. To evaluate the correlation while increasing the variability of the means of the groups, repeat Step II for eight values of $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$.

The simulation runs Step I-III 20 times and delivers, for each value of $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$, 20 replicates of the triples defined in Step II. For each position in the triple, we summarise its 20 replicates by their average and standard deviation. For each position in the triple, the eight pairs $\left( \mu ,sd\right)$ corresponding to the eight values of $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$ are averaged pairwise, determining four pairs $\left( \overline{\mu },\overline{sd}\right)$. They correspond to low, medium-low, medium-high, and high (L, M-L, M-H, H) $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$. The experiment evaluates multiple scenarios by also varying the number of groups K and the parameters (n, r).

Table 1 Correlations between the benchmarks and the components from three Gini index decompositions: A, BM, and YL in the third column identify the decomposition proposed in this work, in Bhattacharya & Mahalanobis (1967) and in Yitzhaki & Lerman (1991), respectively. The correlations are evaluated by the algorithm presented in Sect. 5 for different values of K, $\textbf{n}$ and $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$. In this table, the eight vectors of correlation replicates for each component are summarised by their average and standard deviation, which are averaged pairwise in four pairs $(\overline{\mu }$, $\overline{sd})$, corresponding to low, medium-low, medium-high and high (L, M-L, M-H, H) $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$

Results

We present in Table 1 the four pairs $(\overline{\mu }$, $\overline{sd})$ for representative parameters ($K=3,30$; $n=10,100$; $r=1,4$).

As for the within component, both ${{\,\mathrm{\rho }\,}}(G_w^{A},G_w^{YL})$ and ${{\,\mathrm{\rho }\,}}(G_w^{BM},G_w^{YL})$ are rarely below 0.9, with the first being generally higher and less volatile. The only exception occurs when the variability in $\textbf{n}$ is low (i.e. when r is low): in this case ${{\,\mathrm{\rho }\,}}(G_w^{BM},G_w^{YL})$ is sometime higher. This is because ${{\,\mathrm{\rho }\,}}(G_w^{BM},G_w^{YL})=1$ when the groups are equal-sized, decreasing with the variability of $\textbf{n}$.

The correlations depend marginally on the specification of the parameters. Higher values of K negatively influence ${{\,\mathrm{\rho }\,}}(G_w^{A},G_w^{YL})$, but increasing the values in $\textbf{n}$ absorbs this small effect; ${{\,\mathrm{\rho }\,}}(G_w^{A},G_w^{YL})$ also decreases for higher values of $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$, while its variability increases. In any case, all the $\overline{\mu }$ referred to our within component are never below 0.92 and the highest $\overline{sd}$ is $2.8\cdot 10^{-2}$.

When performing the Monte Carlo experiment using $G_w^{BM}$ as the reference instead of $G_w^{YL}$, we obtain results that substantially mirror those presented. As expected, thanks to its weighting structure, our within component is the middle ground between $G_w^{YL}$ and $G_w^{BM}$.

Regarding the comparison of $G_b^{A}$, $G_b^{BM}$ and $G_b^{YL}$ with HI, regardless of K and $\textbf{n}$, ${{\,\mathrm{\rho }\,}}(G_b^{A},HI)$ is always the highest ($\approx 1$) and least volatile, showing striking advantages in situations where the variability of the means is not large. It slightly decreases and shows higher $\overline{sd}$ when the variability in $\textbf{n}$ increases and the values in $\textbf{n}$ and K are small. When the variability of the means increases, explaining most of the differences between groups and reducing their overlap, ${{\,\mathrm{\rho }\,}}(G_b^{BM},HI)$ increases and narrows the gap with ${{\,\mathrm{\rho }\,}}(G_b^{A},HI)$; also ${{\,\mathrm{\rho }\,}}(G_b^{YL},HI)$ increases with the variability of the means, but remains much smaller and the most volatile. In conclusion, according to the Monte Carlo experiment, $G_b^A$ is the most suitable between-component to capture the complexity of horizontal inequality when the groups have similar means. It provides richer information than the conventional between-components unless the group averages are so far apart as to drastically reduce overlapping between the distributions and explain most of the difference between the groups.

6 Horizontal Inequality Between the EU Country Pairs

Fig. 4

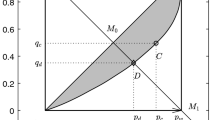
Horizontal inequality of the European Union country pairs in 2018, as measured by HI, GGini and $G_b^{A}$. Comparison of HI (x-axes) with the GGini and $G_b^A$ (y-axes). Oversimplification of the GGini takes the form of underestimation of horizontal inequality and is not rare when groups have similar mean. The scatter relating HI and $G_b^A$ has no outliers and confirms ${{\,\mathrm{\rho }\,}}(G_b^{A},HI)\approx 1$

This section underscores the importance of choosing an accurate measure for effectively assessing and tracking the evolution of horizontal inequality. Our analysis makes use of the OECD Income Distribution Database, which provides the average household income in each decile of all EU countries, adequately transformed into Purchasing Power Parity (PPP) from 2004 to 2018, to ensure comparability.

First, we measure the income inequality across all pairs of EU countries for the year 2018. For each country pair, we decompose the inequality between their income deciles by Eqs. (2) and (12). We also evaluate HI between the two countries. Finally, we compare the inequality between countries as measured by $G_b^A$, GGini and HI to study the differences between alternative measures of horizontal inequality. In Fig. 4, each point represents the horizontal inequality of a country pair in the space $(HI, G_b)$. Black and grey points relate HI, respectively, to GGini and $G_b^A$. Comparing GGini and HI highlights that they are perfectly correlated over several country pairs, especially the most dissimilar couples. However, there are couples of countries that significantly reduce ${{\,\mathrm{\rho }\,}}\left( {G_b^{BM}},HI\right)$. Indeed, when the inequality between two countries is medium to low, GGini often underestimates the inequality between countries, sometimes being significantly lower than the value we would expect based on HI. The oversimplification issue does not involve our between-group component. Comparing HI with $G_b^A$ highlights their strong correlation over all the country pairs, even those with similar means and different distributions.

To explore how horizontal inequality has evolved over time, we examine two contrasting pairs of countries: a pair over which the GGini and HI are correlated, and a pair having distributions leading to the GGini oversimplification.

The first case study, featuring Italy and Greece, is illustrated in Fig. 5a, showcasing their between-inequality dynamics as measured by $G_b^A$, GGini and HI. All three measures report the same evolution, as long as the correlation between HI and GGini is perfect and that between HI and $G_b^{A}$ is above 0.99. The inequality between the two countries decreases slightly from 2004 to 2009, while it more than doubles between 2009 and 2013. In order to investigate the reasons explaining the evolution of horizontal inequality, in Fig. 6a we focus on three peculiar years (2004, 2009, 2013) and plot the difference (as a fraction of the mean) between the income deciles of the two countries. The reduction of horizontal inequality between Italy and Greece from 2004 to 2009 is primarily due to the decrease in the gap in the richest decile. Between 2009 and 2013, all (positive) differences between deciles are at least double. Consequently, also the difference between the Italian and Greek means more than doubles, which explains the perfect correlation between GGini and HI in Fig. 5a.

Fig. 5

Horizontal inequality between Italy and Greece (left panel) and between the UK and Italy (right panel) from 2004 to 2018, as measured by HI, GGini and $G_b^A$. All three measures in the left panel depict the same evolution of horizontal inequality between Italy and Greece, while HI and $G_b^A$ strongly differ from GGini when comparing the United Kingdom and Italy (right panel)

Fig. 6

Differences between income deciles of Italy and Greece (top panel) and of the UK and Italy (bottom panel). The difference is reported as a fraction of the overall mean. The Italian deciles always dominate the Greek ones. Differently, there is stochastic dominance between income deciles of the UK and Italy only in the most recent years. This explains the conflicting trajectories of Fig. 5b

The comparison between the United Kingdom and Italy presents a starkly different scenario, as depicted in Figs. 5b and 6b. In this case, GGini evolves differently from HI - the correlation of the two series is 0.27. On the contrary, the correlation between $G_b^A$ and HI is still greater than 0.99. We use Fig. 6b to explain this contrasting evidence. We note that all the deciles of the two countries are quite similar in 2004, except for the last one. The distance between the deciles (but the first) increases considerably in 2009. Accordingly, both HI and $G_b^A$ reach their maximum in 2009, while GGini reaches its minimum. This happens because the $10^{th}$ decile is higher in the UK while the other deciles are higher in Italy; therefore, the differences between the deciles compensate and produce a small difference between the means. Considering the distributions to be closer in 2009 than in 2004 overlooks critical details, demonstrating a clear case of oversimplification. As further confirmation of our argument, the GGini massively increases between 2009 and 2014, despite no evidence of such a large increase in the distance between the two distributions. Again, the fast increase of the GGini is motivated by the sign of the differences between the deciles, rather than their magnitude. Going back to Fig. 4, all perfectly correlated black dots correspond to pairs of countries such that the income distribution of one country dominates the other over all quantiles (stochastic dominance), as in the case of Italy and Greece. When there is no stochastic dominance between distributions, it is our conviction that the ability of $G_b^A$ to measure horizontal inequality is considerably superior to that of the GGini.

7 Conclusions

This study introduces an innovative Gini index decomposition technique designed to overcome the limitations of traditional methods in evaluating horizontal inequality. The most widespread subgroup decompositions of inequality deliver within- and between-group components. The latter, which is based on the comparison of the means of the groups, is commonly used to assess horizontal inequality. Yet, a comprehensive assessment of horizontal inequality necessitates considering additional distributional characteristics beyond mere averages. Addressing this gap, our method introduces a between-group component that encompasses the full distributions of groups, offering a more detailed comparison than solely focusing on their means. This makes it particularly appropriate to measure horizontal inequality, as confirmed by a Monte Carlo experiment and empirical analysis, both assessing the strong correlation of our component with a benchmark measure of horizontal inequality.

Our decomposition has another advantage. Conventional decompositions of the Gini index present a residual term in addition to the within- and the between-components. This residual disappears only if the distributions of the groups do not overlap. Exploiting a new insight into the Gini index, we disentangle each addendum of the index into two informative contributions to within- and between-group inequality, obtaining a two-component decomposition without the need to include a residual term. Hence, in our decomposition, inequality within groups explains a share of the Gini index, while excess inequality only depends on inequality between groups.

Empirical analysis confirms the relevance of our decomposition to support both cross-sectional and longitudinal analysis of inequality. Studying the cross-sectional inequality between the European country pairs in 2018, we compare our between component ($G_b^A$), and that of the most widespread Gini decomposition (GGini), with the horizontal inequality benchmark (HI). While GGini and HI show strong correlation across numerous country pairs, GGini tends to underestimate horizontal inequality in cases where countries have similar means but different distributions. On the contrary, $G_b^A$ and HI have a strong correlation over all the country pairs. Studying inequality over time, our analysis spans between 2004 and 2018 and involves the Italy-Greece and the United Kingdom-Italy country pairs. The analysis reveals that unlike $G_b^A$ and HI, GGini occasionally falls short in capturing the intricate dynamics and evolution of differences between groups.

Our discussion points out that both GGini and $G_b^A$ accurately measure horizontal inequality when there is stochastic dominance between the distributions. In this case, the information provided by the two measures is the same of HI, and the advantage of our decomposition is to avoid the residual. This advantage disappears when the distributions of the groups do not overlap because the residual of the conventional decompositions of the Gini index vanishes. When, instead, there is no distribution that dominates the other over all quantiles, ${{\,\mathrm{\rho }\,}}(G_b^A,HI)$ remains high while GGini underestimates horizontal inequality and fails to assess its evolution. In such cases, we argue that our decomposition provides a more nuanced understanding of inequality between groups.

In sum, we firmly believe that the decomposition technique presented herein significantly broadens the usefulness of the Gini index for inequality research, paving the way for novel investigations into horizontal inequality and beyond.

Appendix

1.1 On the Quantilisation Procedure

This part of the appendix discusses the suggested value of n and of the definition of quantiles in the quantilisation procedure, explaining their optimality and quantifying the magnitude of the approximation incurred.

Defining $\textbf{w}=\left( w_1,\dots w_K\right)$ we can rewrite the suggested value of n as $n=\textbf{w} \textbf{n}^\intercal$.

Fig. 7

Approximation of the between component share for different choices of n (expressed in terms of the probability associated to n in the inverse distribution function of the vector $\textbf{n}$). The approximation is evaluated by comparing the 150 between-share obtained by the quantilisation procedure with the 150 obtained by the exact approach. The left panel summarises those differences by MSE$(S_b/S_b^r)$ (left scale) and MAE$(S_b/S_b^r)$ (right scale). Right panel shows the boxplots of the 150 relative differences for each choice of n

This expression determines n as the average of the $n_k$, each weighted by the share of population $w_k$. We study the performance of this value in Fig. 7, where we evaluate the approximation by looking at the relative discrepancy between the two shares $G_b/G$ from the exact approach and the quantilisation method. To be precise, we define $S_b=G_b/G$ as the between component share obtained by the quantilisation method and $S_b^r=G_b^r/G^r$ as the reference share obtained by the exact approach. The relative discrepancy is measured by the Mean and the Absolute Squared Error of $S_b/S_b^r$ w.r.t. $1=S_b^r/S_b^r$. They are calculated running 150 simulations and evaluating the empirical counterpart of MSE$(S_b/S_b^r)={{\,\mathrm{\mathbb {E}}\,}}[(S_b/S_b^r-1)^2]$ and MAE$(S_b/S_b^r)={{\,\mathrm{\mathbb {E}}\,}}[|S_b/S_b^r-1 |]$.

At each iteration, we draw lognormal income vectors with sizes $\textbf{n}$, as described in the second section of this Appendix. We compare the approximation with alternative choices of n, which are the minimum and the maximum of $\textbf{n}$, its deciles (expressed in the plot as probabilities of the inverse distribution function) and the value obtained by Eq. (17). Generating the vector $\textbf{n}$, we impose constraints on its elements to ensure affordable values for $lcm(\textbf{n})$. To be specific, the algorithm firstly specifies K ($=5$, 10 or 20). Then it builds a vector $\textbf{mul}$ composed by the divisors of $2^4 3^3 5$ that belong to an interval $\left[ min,max\right]$. The min ($=36$ or 72) and the max ($=360$ or 720) are both included in $\textbf{n}$. The other $K-2$ values are sampled with repetition from $\textbf{mul}$. With this choice the lcm cannot exceed the value 2160 and the computations are affordable. Figure 7 represents the results for $K=20$, $min=72$ and $max=720$.

As we show in Fig. 7a, the proposed value of n - represented by the solid indicators - minimizes (or reach a value very close to the minimum of) the approximation that this method copes with, both for the MSE (left scale) and the MAE (right scale). This result is achieved thanks to vanished distortion and variance reduction, as we show in Fig. 7b. We stress the irrelevance of the approximation when the suggested n is employed: according to the MAE, which is interpretable as average absolute percentage error, the error is 0.22%.

Table 2 Percentage approximation of the quantilisation procedure as measured by the MAE of the between component share, for different parameter specifications. The last column represents the average fraction of elements in the vector $\textbf{n}$ which are lower than the suggested n

The magnitude of the percentage approximation changes with the simulation parameters, as Table 2 points out. It reports the percentage MAE of the between component share for different choices of n, K and of the interval [min, max]. Results are really encouraging. The values of the MAE are below the percentage point in half of the parameter specifications, and they are always below $1\%$ when the suggested choice of n is employed.

For each choice of n, when the ratio $\nicefrac {max}{min}$ decreases, the approximation reduces, too. If that ratio stays constant, the MAE informs about better performance for higher min and max. Results are enhanced when n is selected by Eq. (17) and the number of groups is high. The described dependence of the MAE on the values of n, K and of the interval [min, max] proves the consistency of our procedure, and may ensure even lower approximation in many realistic scenarios where the parameters are presumably more conducive.

The suggested choice of n almost always guarantees a relevant reduction in the computational cost associated to $n=max(\textbf{n})$. This reduction is not negligible in our simulations: $\bar{p}$ is the average value, in the 150 simulations, associated to our choice of n in the inverse distribution function of $\textbf{n}$. It is reported in the last column of the table and range from 0.69 to 0.84.

As supported by the values in the third column of the table - which decrease when $min(\textbf{n})$ increases - it could be also acceptable to choose a value $n<<min(\textbf{n})$ if $min(\textbf{n})$ is high and a computational saving choice is required.

Fig. 8

Between component share approximation of the 9 quantile definitions presented in Hyndman & Fan (1996), for different choices of n (expressed in terms of the probability associated to n in the inverse distribution function of the vector $\textbf{n}$). Approximation is measured by MSE$(S_b/S_b^r)$, calculated by the same procedure generating Fig. 7. Using the software R, each quantile definition can be selected by the option type of the function quantile(). Here, $T_j$ stands for selecting the option type=j

All these results are associated to the quantile definition that we suggest. Our choice comes from the comparison of the approximation achieved using the nine different quantile definitions presented in Hyndman & Fan (1996) in the procedure which generates Fig. 7a. As we show in Fig. 8, the Definition 7 essentially presents the lowest MSE (and MAE) for each choice of n and it ensures computational advantages because the MSE approaches 0 for smaller n.

The outstanding performance of Definitions 1 and 2 when the probability is close to 1 are exceptions. Both the definitions rely on a stepwise cumulative probability function which selects the quantiles from the set of values in the starting vector. Thus, if $p=1$ and $max(\textbf{n})=lcm(\textbf{n})$, the vector of quantiles corresponds to the $\textbf{y}^k$ of the exact approach, and no approximation is encountered, with evident advantages starting from $p=0.8$. Nonetheless, in the vast majority of real applications, the vector $\textbf{n}$ is much more variable than the bounded vectors used in these simulations. Hence $lcm(\textbf{n})$ is generally far from $max(\textbf{n})$ and the Definition 7 from Hyndman & Fan (1996) is definitely recommended.

Actually, the optimal performance associated to the suggested quantiles selection strategy should not come as a surprise. Its outstanding results have a twofold explanation. First, the performance of the proposed choice of n directly derives from its consistency with the exact-approach weighting system. This choice assigns greater weights $w_k$ to the sizes of the most sized groups, which is desirable because these are the groups with the biggest $p_k$. It is reasonable to preserve their information by choosing a large n and by resampling the smallest groups. But if many small groups are present, n is attracted towards their small size. Here, the quantilisation of the biggest groups is preferred to resampling the many small groups. The second explanation for the optimal performance of the suggested strategy is the following. Eq. (16) selects the values $prob_j$ so as to partition the interval [0, 1] in $n-1$ equal parts, with 0 and 1 two of the n vertices of the partition. It is straightforward to verify that, with our suggestions, $min(\textbf{x}^k)$ and $max(\textbf{x}^k)$ are preserved for each n and k. Moreover, if $n_k=n$   $\forall$  k, then the vectors $\textbf{x}^k$ are entirely preserved, too. Both these properties, which ensure robustness w.r.t. outliers, hold at the same time only employing Definition 7 from Hyndman & Fan (1996) and the suggested choice of the values $prob_j$.

1.2 The Income Simulation Algorithm

A Monte Carlo algorithm is employed to evaluate the approximation of the quantilisation procedure and to estimate correlations. This section of the appendix provides with the theoretical foundations of the income simulation procedure feeding both these algorithms.

The distribution of $\textbf{n}$ is a K-variate uniform, where the number of groups K and the extremes of the distribution are determined ex-ante. A uniform distribution is also exploited to draw the expected average income of each group: ${{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \sim \textit{Unif}(m,M)$. The minimum m of this distribution is set to $10^4$. As for the maximum M, it is fixed to $5\cdot 10^4$ in the simulations described in the first part of this appendix. Differently, in the simulations presented in Sect. 5, M is varied to highlight how correlations depend on the variability of the means of the groups. This is possible because a modification of M directly affects $CV[{{\,\mathrm{\mathbb {E}}\,}}[\mu _k]]$. For the uniform distribution ${{\,\mathrm{\mathbb {E}}\,}}_u\left[ {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \right] =(M+m)/2$ and $\textrm{Var}_u\left[ {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \right] =(M-m)^2/12$, therefore the coefficient of variation of ${{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right]$ is

$$\begin{aligned} CV\left[ {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \right] =\frac{\sqrt{\mathbb {V}_u\left[ {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \right] }}{\mathbb {E}_u\left[ {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \right] }=\frac{1}{\sqrt{3}}\frac{(M-m)}{(M+m)}\in \left[ 0,\frac{1}{\sqrt{3}}\right] \end{aligned}$$

and, with m fixed, it only depends on the value of M.

The values of M are selected so that the coefficient of variation divides the interval into S equal parts. Denote by $M^{(s)}$, $s=1\dots S$ the different values required for this scope. The values $M^{(s)}$ satisfy:

$$\begin{aligned} \frac{M^{(s)}-m}{M^{(s)}+m}-\frac{M^{(s-1)}-m}{M^{(s-1)}+m}=c \end{aligned}$$

with $M^{(0)}=m$ and $c= 1/\left( \sqrt{3}S\right)$. With easy calculations, the following holds:

$$\begin{aligned} M^{(s)}=\frac{m(cM^{(s-1)}+cm+2M^{(s-1)})}{(2m-cM^{(s-1)}-cm)} \end{aligned}$$

and the $M^{(s)}$ can be calculated iteratively.

Once all the parameters are fixed, we draw the incomes of each group from a lognormal distribution with expected value ${{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \sim \textit{Unif}(m,M)$. The last requirement is to define a meaningful way to determine the two parameters $\eta$ and $\sigma ^2$ of the distribution. As it is well known, for a lognormal distribution the following holds:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] =e^{\eta _k+\frac{\sigma _k^2}{2}} \end{aligned}$$

(18)

This equation allows an effective way to determine the two elements $\eta _k$ e $\sigma _k$:

$$\begin{aligned}&\eta _k=\alpha _k \ln {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \end{aligned}$$

(19)

$$\begin{aligned}&\sigma _k^2=2\left( 1-\alpha _k\right) \ln {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] \end{aligned}$$

(20)

Their ratio is

$$\begin{aligned} c_k=\frac{\sigma _k^2}{\eta _k}=\frac{2\left( 1-\alpha _k\right) \ln {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] }{\alpha _k \ln {{\,\mathrm{\mathbb {E}}\,}}\left[ \mu _k\right] }=\frac{2(1-\alpha _k)}{\alpha _k} \end{aligned}$$

At this point, we consider the 82 couples of lognormal parameters estimated in Bandourian et al. (2002) using 82 real income distributions from 23 countries over several years (from the end of sixties to the end of nineties). We evaluate all the $c_i=\sigma _i^2/\eta _i$, $\,i=1,\dots ,82$.

Realistic values for $\alpha _k$ can be obtained sampling a value of i for each group and posing $c_k=c_i$, solving the following equation:

$$\begin{aligned} c_i=c_k=\frac{2(1-\alpha _k)}{\alpha _k}\, \Longrightarrow \, \alpha _k=\frac{2}{c_i+2} \end{aligned}$$

(21)

Therefore $\eta _k$ and $\sigma ^2_k$ are determined by Eqs. (19)–(21).

The appropriateness of the last step - i.e. sampling a value of i for each group and using the correspondent $c_i$ - is justified by the fact that the 82 values of $\alpha$ in Bandourian et al.(2002) are not influenced by the associated ${{\,\mathrm{\mathbb {E}}\,}}[\mu _k]$: a simple linear regression reports an approximately null coefficient ($5.6\cdot 10^{-4}$) and a large p-value (0.65) for the regressor ${{\,\mathrm{\mathbb {E}}\,}}[\mu _k]$. Consequently, there are 82 credible proportions to split ${{\,\mathrm{\mathbb {E}}\,}}[\mu _k]$ in $\eta _k$ and $\sigma _k^2/2$. We exploit them to simulate income.