Effortful Bayesian updating: A pupil-dilation study

Abstract

When confronted with new information, rational decision makers should update their beliefs through Bayes’ rule. In economics, however, new information often includes win-loss feedback (profits vs. losses, success vs. failure, upticks vs. downticks). Previous research using a well-established belief-updating paradigm shows that, in this case, reinforcement learning (focusing on past performance) creates high error rates, and increasing monetary incentives fails to elicit higher performance. But do incentives fail to increase effort, or rather does effort fail to increase performance? We use pupil dilation to show that higher incentives do result in increased cognitive effort, but the latter fails to translate into increased performance in this paradigm. The failure amounts to a “reinforcement paradox:” increasing incentives makes win-loss cues more salient, and hence effort is often misallocated in the form of an increased reliance on reinforcement processes. Our study also serves as an example of how pupil-dilation measurements can inform economics.

1 Introduction

Incentives are one of the most important drivers of economic behavior. Higher incentives should lead to better performance since larger outcomes offset the additional costs of “thinking harder.” However, the relation between incentives and performance is complex and far from straightforward (Jenkins et al., 1998; Camerer and Hogarth 1999; Gneezy et al., 2011). Known difficulties and paradoxes include ceiling effects (Kahneman et al., 1968; Samuelson and Bazerman 1985), choking under pressure (Baumeister 1984; Baumeister and Showers 1986; Ariely et al., 2009), and crowding out of intrinsic motivation through extrinsic incentives (Deci et al., 1999; Gneezy and Rustichini 2000). These and other phenomena, however, reflect problems at different steps in the assumed chain of implications connecting incentives to performance. The general assumption is that higher incentives increase effort, and increased effort results in higher performance. Thus, whenever performance fails to react to increased incentives, it is unclear which of the two links might have broken down. Did incentives fail to influence effort, or did effort fail to boost performance? Economic policies and interventions designed to improve performance will have to contend with different issues in each case.

While effort might be directly observable for tasks requiring physical labor, this is generally not the case for the type of cognitive and analytical, high-skill tasks typical of a knowledge-based economy. In those tasks, actual (cognitive) effort cannot be directly measured, and hence it becomes impossible to distinguish breakdowns of the link from incentives to effort from breakdowns of the link from effort to performance. In this work, we consider a simple, well-established belief-updating task which is representative of this category and has been shown to elicit a large number of errors and be relatively impervious to monetary incentives in the past (Charness and Levin 2005; Charness et al., 2007; Achtziger and Alós-Ferrer 2014; Achtziger et al., 2015; Hügelschäfer and Achtziger 2017; Alós-Ferrer et al., 2017; Li et al., 2019). This task is especially interesting because the information participants receive includes a win-loss component. This captures a characteristic of many economic applications. Projects fail or succeed, firms make profits or losses, and stocks go up or down. This win-loss feedback cues basic reinforcement behavior (“win-stay, lose-shift”) which would not make sense if the win-loss information was absent, and gives rise to well-known phenomena as outcome bias or the focus on past performance (e.g. Baron and Hershey 1988). In the task we focus on, it has been shown that the high error rates originate precisely on the activation of reinforcement behavior due to the win-loss feedback (Charnes and Levin 2005; Achtziger and Alós-Ferrer 2014; Achtziger et al., 2015). We are interested in understanding why incentives do not improve performance in this particular task. Thus, we set out to investigate the origin of this failure in this setting.

To solve the problem of the unobservability of cognitive effort in this task, we focus on a type of measurement which goes beyond the type of data usually employed in economics: pupil dilation. It is well-established (see, e.g., Beatty and Lucero-Wagoner 2000, for an overview) that the human eye’s pupil dilates reliably with the amount of mental effort exerted in a task. For instance, a number of early studies (Hess and Polt 1964; Kahneman and Beatty 1966; Kahneman et al., 1968; Kahneman and Peavler 1969) showed that pupil size correlated with the difficulty level in cognitive tasks as multiplication, number and word memorization, or mentally adding one to each digit in a previously-memorized sequence.

Eye tracking measurements are relatively common in psychology and neuroscience, but have only recently gained popularity in economics. However, most of those target gaze and fixations patterns to study search patterns or processes of information acquisition (e.g. Knoepfle et al., 2009; Reutskaja et al., 2011; Hu et al. 2013; Polonio et al., 2015; Devetag et al., 2016; Alós-Ferrer et al., 2021), and not pupil dilation. An exception is Wang et al. (2010), who (in addition to fixation patterns) examined pupil dilation in sender-receiver games and found larger pupil dilation when deceiving messages were sent.

Pupil dilation can be seen as a neural correlate of decision making, since pupil diameter correlates with activity in brain networks associated with the allocation of attention to motivationally-relevant tasks (Aston-Jones and Cohen 2005; Murphy et al., 2014). As such, our study contributes to the growing literature drawing on neuroscience methods to study behavior under risk and uncertainty. For example, recent research has used functional Magnetic Resonance Imaging (fMRI) to study how different kinds of risk are perceived (Ekins et al., 2014), or the differences between strategic and nonstrategic uncertainty (Chark and Chew 2015). More generally, this literature encompasses novel manipulations, measurements, and correlates of risky choice, thereby expanding the researcher’s toolbox. For example, Wang et al. (2013) used cognitive load to explore the limits of valuation anomalies in risky choice, and Burghart et al. (2013) studied the effect of blood alcohol concentration on risk preferences.

We conducted an experiment on the belief-updating task mentioned above, which we focused on precisely because previous research has shown that incentives fail to improve performance in this task. We varied incentives within subjects and measured pupil dilation. As we expected, we found larger pupil dilation for higher incentives, indicating an increase in effort, even though overall performance did not react to incentives. Previous research on this paradigm (Achtziger and Alós-Ferrer 2014; Achtziger et al., 2015) allows us to discard the possibility of ceiling effects and link errors to (fast, impulsive) reinforcement processes. Our analysis also allows us to exclude arousal as a possible alternative explanation for larger pupil dilation. Hence, we conclude that incentives do increase effort in the cognitive task we consider, but this effort might be misallocated to counterproductive processes. Indeed, in an EEG study, Achtziger et al. (2015) found that higher error rates under high incentives in this task were linked to larger amplitudes in (extremely early) brain potentials associated to reinforcement learning. In other words, our results suggest that, in this paradigm, one finds the paradoxical situation that increasing monetary rewards does increase effort, but since it also increases the salience of the win-loss cues on which reinforcement processes operate, the increase in effort is channeled through such processes, counteracting any positive effects of incentives in performance.

The paper is structured as follows. Section 2 discusses the belief-updating task and the related literature. Section 3 presents the experimental design in detail. Section 4 discusses the behavioral and pupillary results. Section 5 concludes.

2 The belief-updating task

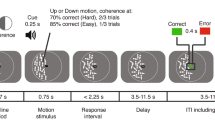
The decision task is as follows. There are two urns (left and right) containing 6 colored balls each (black or white). The urn compositions depend on an unknown state of the world (a or b; called “first” and “second” in the instructions). In state a, the left urn contains 4 black and 2 white balls, and the right urn contains 6 black balls. In state b, the left urn contains 2 black and 4 white balls, and the right urn contains 6 white balls (see Fig. 1 for a schematic representation). The prior probability of each state is $\frac 12$, known by participants, and the state is independently realized across trials.

Fig. 1

Schematic representation of the task. In each trial, the participant first selects an urn, from which a ball is extracted (first draw). A black ball is a win (resulting in payment), a white ball is a loss (no payment). The ball is replaced into the urn, and the participant selects an urn again. Error rates for the second draw are low if the first draw was from right, and very high if the first draw was from left, reflecting alignment or conflict between Bayesian updating and reinforcement, respectively

Each trial consists of two consecutive draws. In the first draw, the participant is asked to choose which urn a single ball should be extracted from (with replacement). She is paid if and only if the ball is of a pre-specified color (e.g. black).¹ In the second draw within the trial, the participant is asked to choose an urn a second time. A ball is then extracted again, and the participant is paid again if the ball is of the appropriate color. The trial ends after the second extraction, and the next trial starts with the state of the world being redrawn. The participant goes through a total of 128 trials, with three different starting conditions for the first draw (following the standard implementation of the task; Charness and Levin 2005, Achtziger and Alós-Ferrer 2014). In 64 of the trials, all is as described above, and in particular the participant freely decides the urn in both draws. In the other 64 trials, however, the participant is forced to make the first draw from a specific urn (half from the left, half from the right).² Forced trials are included to ensure enough observations where the first draw is made from the left urn.

The key manipulation in our study was the level of incentives, which was varied within participants. In 64 of the trials, a winning ball was worth 3 Eurocents (low incentives), and in the remaining trials it was worth 12 Eurocents; that is, incentives were quadrupled between conditions (in contrast, earlier studies as Achtziger and Alós-Ferrer 2014 and Achtziger et al., 2015 only doubled them). The different incentive levels were intermixed following pseudorandomized sequences. That is, for each trial, the actual level of incentives was announced at the beginning of the trial, and it was not possible for participants to predict it. This is crucial to be able to set a cue to time-lock the measurements of pupil dilation.

The analysis of choice data in this task is centered on the second draw; the first draw serves only the purpose to generate information allowing to update beliefs. If the first draw was from the right urn, the state of the world is fully revealed, and error rates for the second draw are typically low. This is because the right urn in both states of the world consists of 6 balls of the same color, which are different across states. Thus the color reveals the current state of the world (e.g., in Fig. 1, a black ball from the right urn reveals that the current state of the world is a). In this case, optimal behavior simply prescribes to repeat the first-draw choice if the participant won (a black ball was extracted), and switch otherwise. If the first draw was from the left urn, rational decision making prescribes updating the prior through Bayes’ rule. The urn compositions are calibrated in such a way that the ensuing rational prescription is to repeat the first-draw choice if the participant lost (a white ball was extracted), and switch otherwise. Charness and Levin (2005) found high and persistent error rates for this kind of decisions, and argued that the reason was that the prescription contradicts the intuitive tendency to repeat decisions which have “worked” in the past. Charness et al. (2007) relied on the same paradigm and showed again high error rates, but also demonstrated that interacting in groups improved performance.

Achtziger and Alós-Ferrer (2014) formulated a dual-process model (see also Alós-Ferrer 2018; Alós-Ferrer and Ritschel 2021) which, in this paradigm, reduces to decisions being codetermined by two different processes. One is a deliberative process implementing the optimal prescriptions given Bayesian updating of beliefs, while the other is a more intuitive, simple reinforcement heuristic, i.e. “win-stay, lose-shift.” After a first draw from the right urn, both processes are in alignment (make the same prescription) and error rates are low, after a first draw from the left urn they are in conflict (make different prescriptions) and error rates are high. The model makes specific predictions for the relative response times of errors and correct responses depending on alignment or conflict, which were confirmed in an experiment. This study also included treatments with different incentives (between subjects) and found that doubling the magnitude of monetary incentives did not reduce error rates. Although error rates in this paradigm are generally high, a ceiling effect can be excluded. The reason is that Charness and Levin (2005), Charness et al. (2007), and Achtziger and Alós-Ferrer (2014) included treatments that removed the win-loss cue on which reinforcement acts, which resulted in sizable performance increases. They did so by not remunerating the first-draw extraction and announcing which was the winning color only at the beginning of the second draw. That is, at the time of the first draw subjects did not know the winning color and reinforcement could not interfere with Bayesian updating due to the absence of win-loss cues. Hence, the high error rates do not arise from the intrinsic difficulty of the task, but rather from the interference of reinforcement processes.

Achtziger et al. (2015) carried out an electroencephalography (EEG) study with this task and analyzed neural correlates of reward processing for win/loss feedback during the belief-updating phase. The study also included treatments with doubled incentives (between subjects). Behavioral results again showed no performance increase across incentive conditions. Neural results showed that, for high incentives (but not for low), the amplitudes of an early event-related potential (the Feedback-Related Negativity; Holroyd and Coles 2002, Holroyd et al., 2003) closely related to reinforcement learning were consistently higher for participants who committed more errors under conflict (i.e., after a first draw from the left urn). Since that potential peaks far before the actual response (around 200 to 300 milliseconds after stimuli presentation), the interpretation is that, when incentives are high and hence more salient, participants who react more strongly to win-loss cues tend to rely more on reinforcement and hence make more mistakes.

The paradigm has also been used in a number of other studies. Hügelschäfer and Achtziger (2017) showed that certain non-monetary interventions (committing to goals or formulating implementation intentions; Gollwitzer 1999; Achtziger and Gollwitzer 2008) can sometimes reduce the reliance on reinforcement. Li et al. (2019) manipulated the subjects’ mindset (deliberative vs. implemental mindset; Gollwitzer 1990; Achtziger and Gollwitzer 2008) and showed performance improvements. Alós-Ferrer et al. (2017) added a win or loss frame to the task and found that a loss frame increases the tendency to shift away from an unsuccessful option. Alós-Ferrer et al. (2016) asked whether inertia could also play a role in this paradigm, and found that it had only minor effects compared to reinforcement, but that this role was magnified in a symmetric variant where reinforcement and Bayesian updating were always in alignment. Jung et al. (2019) followed up on Alós-Ferrer et al. (2016) and further studied motivational and cognitive explanations for decision inertia using the latter variant.

More generally, urn-based paradigms have a long history in economics as a device to study behavior under risk or uncertainty. Classical examples include, for instance, the work of Grether (1980, 1992) and El-Gamal and Grether (1995) to study heuristics and biases (see also Alós-Ferrer and Hügelschäfer 2012; Achtziger et al., 2014). Different urn-based implementations have been used to study Bayesian learning under risk (e.g., Poinas et al., 2012), (Knightian) uncertainty (e.g., Trautman and Zeckhauser 2013), or sequential learning under the risk of early termination (Viscusi and DeAngelis 2018). However, those studies typically differ from the paradigm we employ in that learning is based on sample information without a win-loss valence, and hence reinforcement is not usually a concern. In the cognitive neuroscience literature, Daw et al. (2011) used a two-stage paradigm (not urn-based), in which different Tibetan characters led to different states. However, in this paradigm subjects learned the transition probabilities from experience, as opposed to deriving them from an induced prior. This makes the analysis of individual decisions more difficult for our purposes. Further, only the second-stage outcome was paid, and hence the link to reinforcement is less clear.

3 Experimental design and procedures

Participants were measured individually in an isolation cubicle. The experiment was programmed in PsychoPy (Peirce 2007) and participants were recruited using ORSEE (Greiner 2015). A total of 60 subjects, recruited from the general student population of the University of Cologne (Germany), participated in the experiment. Two subjects failed to comply with the instructions and were dropped from the sample.³ The dataset hence consists of a total of N = 58 subjects (26 females, mean age 22.53 years, SD= 2.77). Each individual session lasted between 45 and 60 minutes, and subjects earned an average of 10.67 Euro (SD= 0.53), plus a 4 Euro show-up fee.

Figure 2 shows the sequence of events.⁴ Each trial started by displaying a fixation cross for 1000 ms. Then, the trial’s incentives (“3 Cents” or “12 Cents”) were displayed for 1500 ms in the same position as the fixation cross. During that time both urns were gray and could not be selected. These forced waiting intervals are important for pupillometry measurements as they allow the pupil to react. Then the urns turned blue as a signal that they could be selected. In trials with forced first draws, only the available urn turned blue. The participants chose an urn (without any time pressure) by pressing the “F” or “J” key for the left or right urn, respectively. After an urn was selected, feedback was shown in two steps. First, a random ball in the chosen urn changed its color to either black or white and at the same time, a larger ball of the same color was displayed underneath the selected urn. This screen was displayed for 500 ms. Then, both urns turned gray (but the larger ball underneath remained) and the participant had to wait for 2000 ms, allowing him or her to process the feedback. The procedure was then repeated for the second draw (where both urns were always available), with the difference that the (larger) ball reflecting the result of the first draw was kept on screen. After the second draw’s feedback was shown, the participant had to press the space bar to continue to the next trial, which started after 500 ms. During the inter-trial interval, the urns disappeared to reinforce that the state of the world was re-drawn and a new trial was starting.

Fig. 2

Sequence of events and decisions

Pupil size was measured using an SMI RED500 remote eye tracker. The participants’ head was supported by a chin-rest minimizing random movement. Participants were placed 55 cm in front of a 22” screen which showed the stimuli with a resolution of 1680 × 1050 pixels. Pupil size was recorded at 250 Hz using iView X software, version 2.8.43. The eye tracker was calibrated at the beginning of each individual session using a standard two-step procedure. The first step consisted of a 5-point calibration routine. In a second step, the participants saw a screen with numbered circles exactly at the positions in which information for the experiment was being presented. An experimenter asked the participants to fixate on each of those circles and verified whether the eye tracker registered the gaze at that position. Blinks were removed after data collection and before calculating average pupil sizes. For the analysis of pupil dilation, we constructed a z-score for each participant, standardizing pupil size by subtracting the mean pupil dilation over the whole experiment and dividing by the standard deviation. The data was then smoothed using a moving average with a 60 ms window. Finally, the z-score was used to calculate pupil dilation using the stimulus onset in each trial (first draw’s fixation cross for the reaction to incentives, 200 ms before the first draw’s feedback for the reaction to feedback) as the baseline for pupil size change.

4 Results

4.1 Behavioral results

We first examine the effect of incentives on performance. Previous studies (Achtziger and Alós-Ferrer 2014; Achtziger et al., 2015) found no effects of incentives, but their comparison was between subjects and incentives were doubled from one treatment to the other. In contrast, our comparison is within subjects and incentives were quadrupled. As a performance measure, we compare error rates (for the second draw) between low- and high-incentive trials, and we rely on non-parametric (two-tailed) Wilcoxon-Signed-Rank (WSR) tests.

Errors are defined as decisions contrary to the prescription of normative optimization following Bayesian updating of beliefs. Recall that, following previous work, decisions after a first draw from the right urn are in alignment and error rates are typically very low, while decisions after a first draw from the left urn are in conflict and error rates are typically very high (conflict and alignment refers to the two involved processes, namely Bayesian updating and reinforcement). High error rates under alignment are indicative of lack of attention. Two subjects exhibited extremely high error rates in alignment situations and were excluded from the analysis.⁵ For the resulting sample (N = 58), the overall error rate in alignment situations was, as expected, very low. Participants made an average of 2.52% of errors, which did not differ across incentive conditions (low incentives mean 2.56%, high incentives mean 2.52%; WSR, N = 58, z = 1.070, p = .2847).

The appropriate measure of performance, however, is the error rate in conflict situations. In that case, and since the normative prescription is of the form “win-shift, lose-stay,” we can distinguish two types of errors, namely win-stay and lose-shift errors. As illustrated in Fig. 3, error rates were not significantly different across incentive levels for any of the two types. The average win-stay error rate was 38.89% for low incentive trials and 37.82% for high incentive trials (WSR test, N = 58, z = 0.414, p = .6787). The average lose-shift error rate was 39.22% for low incentive trials and 41.75% for high incentive trials (WSR test, N = 58, z = − 0.810, p = .4181). That is, higher incentives did not increase performance, confirming earlier observations by Achtziger and Alós-Ferrer (2014) and Achtziger et al. (2015) even though our comparison is within subjects and high incentives quadrupled the monetary reward compared to low incentives.

Fig. 3

Error rates in conflict situations for both incentive conditions split by win-stay and lose-shift errors

Although our measure of performance refers to errors in the second draw, we can also analyze behavior in the first draw. Recall that in half the trials the participants were free to choose from which urn to extract the first ball. A straightforward computation shows that a fully rational, Bayesian decision maker should always start with the right urn, which reveals the state of the world (Charness and Levin 2005; Achtziger and Alós-Ferrer 2014). This is the reason that this task includes forced draws, to ensure a sufficient number of observations with left first draws, i.e. conflict situations. When free to choose for the first draw, participants chose the left urn on average 20.64% during low-incentive trials and 15.57% during high-incentive trials. The difference is not statistically significant according to a WSR test (N = 58, z = 1.340, p = .1803).

4.2 Pupillometry analysis

Figure 4 displays the grand average (across subjects) of pupil dilation (as z-score) over the whole trial, differentiating low- and high-incentive trials. The baseline for each trial is pupil size during the 1000 ms when the fixation cross was displayed. The first vertical line indicates stimulus onset (i.e., the announcement of the magnitude of incentives in the trial), and the second vertical line indicates the start of the first draw. The figure demonstrates a large difference in pupil dilation between low- and high-incentive trials. Pupil dilation across incentive levels starts to diverge shortly after the incentives are revealed and remains clearly different for the duration of the trial, suggesting higher cognitive effort for higher incentives. Dilation itself reaches a peak for both incentive conditions around 3000 ms, i.e. 1500 ms after the start of the first draw.

Fig. 4

Pupil dilation (z-score) averaged over all subjects and all trials for low and high incentives for the full duration of a trial (dilation relative to pupil size during the fixation cross). First vertical line indicates the stimulus onset of the incentive condition. Second vertical lines indicates the end of the incentive stimulus shown and the beginning of the first draw. Shaded areas represent the 95% CI

Since trial duration was not fixed, response times generally differ across trials and subjects, complicating the analysis. Thus, comparing pupil size averages would not be meaningful. Therefore, to substantiate the difference illustrated in Fig. 4, we computed peak pupil dilation during each trial. Since we have a clear, directional hypothesis, we present one-sided tests. A WSR test confirms that cognitive effort, as measured by peak dilation, was significantly higher in high incentive trials (peak dilation= 1.0990) compared to low incentive trials (peak dilation= 0.9922; N = 58, z = 4.549, p < 0.0001). We repeated the analysis above distinguishing cases of conflict (first draw from left) and alignment (first draw from right). This is illustrated in the top row of Fig. 5. We confirm the previous result for both types of situations. Peak pupil dilation was significantly higher in high-incentive compared to low-incentive conflict trials (peak dilation= 1.2311 vs. 1.0832; N = 58, z = 3.821, p < 0.0001), and also significantly higher in high-incentive compared to low-incentive alignment trials (peak dilation= 1.0474 vs. 0.9576; N = 58, z = 3.674, p = 0.0001).

Fig. 5

Pupil dilation (z-score) averaged over all subjects and trial types for low and high incentives for the full duration of a trial (dilation relative to pupil size during the fixation cross). Top-row panels show pupil dilation in conflict (first draw from left) and alignment (first draw from right) trials. Middle- and bottom-row panels show pupil dilation for conflict and alignment trials when the first trial was a forced or a free choice, respectively. First vertical line indicates the stimulus onset of the incentive condition. Second vertical lines indicates the end of the incentive stimulus shown and the beginning of the first draw. Shaded areas represent the 95% CI

We can further refine the whole-trial analysis by additionally distinguishing trials according to whether the first draw was free or forced.⁶ The panels in the middle and bottom rows on the left-hand side of Fig. 5 show pupil dilation in conflict situations when the first draw was forced and free, respectively. The result remains unchanged in both cases. Peak dilation was significantly higher in high-incentive compared to low-incentive conflict trials both for forced draws (peak dilation= 1.2252 vs. 1.0687; N = 58, z = 3.674, p = 0.0001) and for free draws (peak dilation 1.2482 vs. 1.1285; N = 31, z = 1.764, p = 0.0389).⁷ The panels in the middle and bottom rows on the right-hand side of Fig. 5 show pupil dilation in alignment situations when the first draw was forced and free, respectively. Again, the result remains unchanged in both cases. Peak dilation was significantly higher in high-incentive compared to low-incentive alignment trials both for forced draws (peak dilation= 0.9985 vs. 0.9380; N = 58, z = 1.916, p = 0.0277) and for free draws (peak dilation= 1.0875 vs. 1.0041; N = 58, z = 3.472, p = 0.0003).

A different way to look at pupil dilation as a measure of effort is to examine the period just before the second draw. After participants made the first-draw decision and feedback was shown, they had to wait for 2500 ms before they could decide for the second draw, as described in Section 3. In this time, participants already had the necessary feedback and could start processing it to make their next decision, e.g. by updating beliefs. Hence, pupil dilation in this interval is a measure of cognitive effort directly related to the processing of relevant information. Additionally, the interval’s length was fixed for all trials and all participants, allowing for a clear-cut comparison. We therefore used the mean pupil dilation in this interval to further analyze the effect of incentives on effort. To avoid spillover effects from previous pupil dilation differences between low- and high-incentive trials, we reset the baseline to the average pupil size in the 200 ms interval before the feedback was revealed.

Figure 6 displays the average pupil dilation starting with the first draw’s feedback and until the end of the second draw, again differentiating low- and high-incentive trials. Our main focus is the fixed-length 2500 ms interval on the left-hand side of the figure, which ends with the beginning of the second trial. After an initial increase in both incentive conditions, the pupil dilated clearly more under high incentives than under low incentives. The mean pupil dilation in the interval was accordingly larger under high incentives (average 0.2051) compared to low incentives (average 0.1722). The difference was significant according to a WSR test (N = 58, z = 2.830, p = .0023). This further suggests that participants exerted more effort in high- than in low-incentive trials when processing feedback to make the following decision. The right-hand side of Fig. 6 displays the pupil dilation until the end of the second draw, which obviously differs across participants and trials. The dotted line represent the inverse cumulative distribution function of response times (right axis) and hence indicates how many observations are used to compute the average pupil dilation at each point in time in this part of the graph. Around 75% of second-draw decisions were made within 700 ms, further suggesting that our decision to limit the analysis to the fixed feedback time interval was appropriate. The Appendix provides a more detailed discussion of response times.

Fig. 6

Pupil dilation (z-score) averaged over all subjects and all trials for low and high incentives during the feedback phase of the first draw (dilation relative to pupil size of 200 ms before the feedback was shown). First vertical line indicates the stimulus onset of the feedback of the first draw. Second vertical lines indicates the beginning of the second draw. The dotted line represents the inverse cumulative distribution function of response times (right axis). Shaded areas represent the 95% CI

Since feedback could correspond to either a winning or a losing ball, which might affect pupil dilation due to arousal, we repeat the analysis conditioning on the type of feedback (see also Section 4.3 for a discussion on cognitive effort and arousal). Figure 7 displays the average pupil dilation for low- and high-incentive trials in the 2500 ms of the feedback interval conditioning on loss (left) and win (right) feedback. We confirm the previous result in both cases. Mean pupil dilation was larger in high-incentive compared to low-incentive trials both after loss feedback (.1685 vs. .1310; WSR test, N = 58, z = 2.156, p = .0155) and after win feedback (.2429 vs. .2127; WSR test, N = 58, z = 1.955, p = .0253). Thus, we confirm higher cognitive effort in high-incentive compared to low-incentive trials independently of the type of feedback received.

Fig. 7

Pupil dilation (z-score) averaged over all subjects and trial types (loss vs. win feedback) for low and high incentives during the feedback phase of the first draw (dilation relative to pupil size of 200 ms before the feedback was shown). First vertical line indicates the stimulus onset of the feedback of the first draw. Second vertical lines indicates the beginning of the second draw. Shaded areas represent the 95% CI

To complement the nonparametric analysis, Table 1 presents simple, subject-level regression models. The dependent variable is the change in mean pupil dilation between the high- and low-incentive trials during the feedback interval after the first draw. Hence, the constant of the regression quantifies the positive change in pupil dilation from low to high incentive. Model 1 includes only this constant (and is hence equivalent to a t-test) and shows that the constant is positive and highly significant (p = .0098). Models 2 and 3 add the average error rate over low-incentive trials and a gender dummy (Female) as controls. The constant remains significantly positive (Model 2: p = .0103; Model 3: p = .0184), while the control variables themselves are not significant.⁸

Table 1 Regression table, change in mean pupil dilation

In summary, we found significantly more cognitive effort, as indicated by larger pupil dilation, in the high-incentive trials than in the low-incentive ones, while simultaneously observing no change in performance. This conclusion is supported by non-parametric and parametric tests and is observed both over the whole trial and in the interval which presumably captures the start of feedback processing.

4.3 Cognitive effort versus arousal

Pupil dilation also reacts to arousal (e.g., Hess and Polt 1960; Bradley et al. 2008), and hence one might raise the concern that pupil dilation could just reflect increased arousal due to feedback and higher incentives instead of cognitive effort. Our data allows us to test for (and discard) this alternative explanation. Consider the final feedback after the second draw. This feedback serves only to communicate the outcome, but, since the trial ends and the state will be redrawn in the next one, it is not immediately relevant for any subsequent decision. If pupil dilation reflected only arousal and not cognitive effort, pupil dilation after the second draw should be comparable to pupil dilation after the first one. On the contrary, if pupil dilation reflects cognitive effort, there should be no difference between low- and high-incentive trials after the second-draw feedback, but there should be clear differences between the first and the second draws.⁹

Figure 8 displays pupil dilation for both feedback intervals (both lasted 2500 ms). Solid lines correspond to the first draw, and dashed lines to the second draw. In both cases, we differentiate low- and high-incentive trials. The first observation is that there are very large differences in pupil dilation between the first and the second draws, for each incentive condition. These differences are highly significant according to WSR tests for mean pupil dilation (high incentives: first draw mean dilation 0.2051, second draw mean dilation 0.0165, N = 58, z = 4.967, p < .0001; low incentives: first draw mean dilation 0.1722, second draw mean dilation 0.0105, N = 58, z = 4.247, p < .0001). This suggests that participants exerted more effort after the first-draw feedback, when information had to be cognitively processed to make a subsequent decision, compared to the second-draw feedback.

Fig. 8

Difference in pupil dilation (z-score) between the first and second draw feedback averaged over all subjects and all trials for low and high incentives. The first and second vertical lines indicate the feedback stimulus onset and end, respectively. Shaded areas represent the 95% CI

Figure 8 also suggests that pupil dilation was not larger for high incentives compared to low incentives after the second-draw feedback. Indeed, a WSR test reveals no differences (N = 58, z = 0.399, p = .3450). That is, the difference in pupil dilation across incentive conditions found for first-draw feedback is absent after the second draw. The difference in mean pupil dilation across incentive conditions was 0.0329 for the first draw and only 0.0059 for the second draw feedback (WSR test for differences-in-differences in mean pupil dilation, N = 58, z = 1.483, p = .0691). This, together with the differences in pupil dilation between first and second draw, speaks against an interpretation of our data based on arousal and supports the conclusion that higher incentives successfully induced more effort.

4.4 Cognitive effort and performance

In the previous subsections, we have shown that higher incentives did not increase overall performance, but they induced larger pupil dilation. Further, the larger pupil dilation was not caused by arousal, suggesting that higher incentives induced higher cognitive effort, which however did not translate into better performance. In this subsection we examine the relation between changes in pupil dilation across incentive levels and changes in performance at the individual level.

For each subject, define Change in Accuracy as the average performance improvement between the high- and low-incentive trials. That is, we computed the difference in correct-response rates between the high- and low-incentive conflict trials (or, equivalently, the difference in error rates between the low- and the high-incentive conflict trials). Positive values show that a subject improved in the high incentive trials compared to the low incentive trials. We focus on conflict situations because error rates under alignment were very low. Analogously, define Change in Pupil Dilation as the average change in peak pupil dilation between high- and low-incentive conflict trials. Positive values hence indicate higher cognitive effort in the high- compared to the low-incentive trials.

If higher cognitive effort results in better performance, we would expect a positive, significant correlation between Change in Accuracy and Change in Pupil Dilation. The correlation, however, was not significant when considering the entire sample (N = 58, ρ = 0.089, p = .5079). To further explore the possible relation between cognitive effort and performance, we considered possible individual heterogeneity. Achtziger et al. (2015) found that participants with high error rates displayed stronger neural reactions related to reinforcement in response to the win/loss feedback during high incentive trials, suggesting that they relied more on reinforcement. We hence performed a median split, as in Achtziger et al. (2015), on the average error rates in conflict trials (averaged across high and low incentives). That is, we label subjects with high error rates Intuitive and subjects with low error rates Rational. We expected that rational subjects (in this sense), but not intuitive ones, would exhibit an improvement in performance for larger cognitive effort, as measured by changes in pupil dilation.

Figure 9 displays the Change in Pupil Dilation versus the Change in Accuracy while classifying subjects according to the median split on error rates. As expected, the correlation was significant and positive for rational participants (N = 29, ρ = 0.4933, p = .0065), but it was not significantly different from zero for intuitive participants (N = 29, ρ = − 0.173, p = .3685). This is in agreement with Achtziger et al. (2015), which suggested that intuitive subjects relied more heavily on reinforcement and hence their possible increase in cognitive effort failed to result in an improvement in performance.¹⁰

Fig. 9

Scatterplot of Change in Pupil Dilation in Conflict (high–low incentive trials) and Change in Accuracy (high–low incentive trials). Median split by average conflict error rates in conflict trials. Lines indicate a linear fit of the observations

To complement the nonparametric analysis, Table 2 presents simple, subject-level regression models. The dependent variable is the Change in Accuracy between high- and low-incentive trials. Model 1 includes only the constant, which is not significant. This reflects that there is no improvement in performance due to higher incentives. Model 2 includes the Change in Pupil Dilation coefficient as a dependent variable, which is also not statistically significant (p = .5062). Model 3 adds the “Intuitive” dummy, taking the value 1 when the participant was in the high-error-rates group, reflecting the heterogeneity discussed in Achtziger et al. (2015). This model also adds the interaction of the Intuitive dummy with the Change in Pupil Dilation coefficient. Thus, the Change in Pupil Dilation coefficient now captures the effect for rational subjects only (those with low error rates), i.e. those less prone to a strengthened reinforcement bias due to higher incentives. This coefficient is positive and highly significant (p = .0073), indicating that for rational subjects larger pupil dilation differences between high- and low-incentive trials did resulted in a performance improvement. The linear combination test at the bottom of the table shows that, in contrast, the effect of Change in Pupil Dilation for the intuitive subjects is not significant (p = .3046).

Table 2 Regression table, change in accuracy in conflict situations

In summary, we found that there is link between higher cognitive effort and an improvement in performance in this Bayesian Updating paradigm. However, this link is restricted to those participants less prone to the reinforcement bias, in agreement with the neural-level heterogeneity pointed out by Achtziger et al. (2015).

5 Discussion

The relation between incentives and performance is a nuanced one. In this study, we show that when performance in cognitive tasks involves updating beliefs, but the information to be used for this purpose includes win-loss feedback (profits vs. losses, success vs. failure, upticks vs. downticks), higher incentives might successfully induce higher cognitive effort, but nevertheless fail to elicit higher performance. By adding pupil-dilation evidence to previous studies on this task, which used choice data (Charness and Levin 2005; Charness et al., 2007), response times (Achtziger and Alós-Ferrer 2014), and brain activity (Achtziger et al., 2015), we obtain an overall picture of a “reinforcement paradox:” increasing incentives makes win-loss cues more salient, resulting (at least for some decision makers) in a higher reliance on reinforcement processes, which, by virtue of ignoring beliefs, can lead decision makers astray.

Our study also serves as an illustration of the value of pupil-dilation studies for economics. The link between incentives and performance is a fundamental one both for economic theory and economic policy, but when incentives fail to increase performance, it is important to know whether incentives have failed to elicit effort, or on the contrary they have successfully elicited effort but the latter has failed to translate into performance. For cognitive tasks, effort is often not directly or at least not easily observable. The measurement of pupil dilation in laboratory studies can be invaluable to provide a direct correlate of cognitive effort. As society moves a larger proportion of the labor force into cognitive tasks and away from routine or physical labor, the proportion of tasks and jobs where effort is not directly observable will increase, and hence it becomes important to be able to establish clear links between incentive schemes, as an economic policy instrument, and cognitive effort.

Appendix

Response times are important when discussing cognitive effort (see, e.g., Alós-Ferrer and Buckenmaier 2021). However, it needs to be pointed out that our experiment included fixed time intervals of 1500 ms after the announcement of incentives and of 2500 ms after the first-draw feedback in which the participants could not yet provide a response. Those intervals served the purpose to allow for pupil dilation, which is the main focus of our study. This aspect of the design clearly interferes with response times and one should be careful when drawing conclusions from the latter. Nevertheless, we report response times here for completeness (see Achtziger and Alós-Ferrer 2014, for a study of response times in this Bayesian updating paradigm).

Figure 10 displays histograms of response times for the first (left-hand side) and second draws (right-hand side), after the fixed time intervals mentioned above. All tests below are two-sided WSR tests with N = 58. For first draws, the average response time was 1048 ms (SD= 1227 ms, median= 729 ms). Individual average response times were shorter for forced first draws (mean= 916 ms, SD= 1187 ms, median= 664 ms) than for free first draws (mean= 1179 ms, SD= 1252 ms, median= 844 ms; z = − 5.214, p < 0.0001). Comparing across incentive levels, there was no significant difference for forced draws (high 907 ms, low 924 ms; z = − 0.662, p = 0.5080), but for free draws participants responded significantly faster in high (1135 ms) than low (1224 ms) incentive trials (z = − 2.358, p = 0.0184).

Fig. 10

Histograms of response times for the first (left-hand side) and second draw (right-hand side) after time intervals in which the participant could not respond. The first draw data split by forced and free draws and second draw data split by conflict and alignment situations. Observations 2 standard deviations away from the mean response time were not included in the graph (211 out of 7,424 in the first draw and 204 out of 7,424 in the second draw)

The average response time for the second draw was 756 ms (SD= 1173 ms, median= 460 ms). Unsurprisingly, response times were shorter for alignment situations, where both decision processes prescribe the same answer (mean= 589 ms, SD= 611 ms, median= 433 ms), than for conflict situations (mean= 1080 ms, SD= 1777 ms, median= 536 ms; z = − 6.461, p < 0.0001). Comparing across incentive levels, we found no significant differences neither in conflict (high 1070 ms, low 1241 ms; z = − 0.809, p = 0.4185) nor in alignment (high 575 ms, low 614 ms; z = − 0.600, p = 0.5485).