Introduction

Nowadays, the recycling of platinum group metals plays a very important role in the management of strategic resources. The number of primary sources of platinum is strictly limited. Therefore, the recycling of this metal is an important technological issue. Platinum is one of the most expensive metals among the platinum group metals (PGM). This is mainly due to its low production and its lack of substitutes in some areas. The main use of platinum is a widely understood to be in catalysis. Only in 2014, about 50.000 kg of platinum was recovered from automobile catalysts in the USA, while the world production of platinum is at the level of 160.000 kg per year. Also, a significant amount of platinum is used in jewels. However, the recycling in this area is not significant, mainly because of the long life of the products.

The life time of the platinum based catalysts is estimated to be less than 1 year in the example of nitric acid production [1]. In this application, catalyst replacement is required every 3–12 months [2]. Platinum is also often used in hydrogenation and dehydrogenation reactions [3]. However, in those reactions, the catalyst can be poisoned by compounds such as S, P, As, Zn, Hg, halides, Pb, NH3, C2H2 [2].

The recovery of PGM can be achieved using several different methods [4, 5]. The pyrometallurgical method is mainly limited to PGM pre-concentration [6]. In the case of waste materials based on carbon, the pyrometallurgical method can be used for catalyst carrier removal. The most frequently applied method is based on a hydrometallurgical process consisting of several different stages. In general, there are three approaches to hydrometallurgical PGM recovery [7]. The first one is based on selective dissolution of the support materials. After this stage, the PGM-rich phase can be obtained, and next subjected to further hydrometallurgical processing. The second approach is based on the selective dissolution of catalysts without the dissolution of the support. This method is preferred. However, it can be applied only in a few cases. The third method is related to the total dissolution, i.e. carrier as well as catalyst. The platinum dissolution process is often carried out in cyanate [8, 9] or chloride [10–12] containing media as complex forming ligands.

To remove platinum ions form aqueous solutions, several different methods can be used. One of the most promising method is based on ion exchange using different extractants, for example Cyanex 923 [13], Purolite S985, XUS 43600.00 and LewatitM + MP 600 [10], Cyanex 471x [14]. An electrochemical method can be also used for PGM recovery [15–17]. However, this method has several significant disadvantages. Among them is the lack of selectivity, and in the case of chloride ion containing media, chlorine gas evolution. A reduction method can also be applied for precious metal recovery. For example, vitamin C [18, 19], sodium borohydrate [20], DMAB [21–23], hydrazine [24], ethanol [25], and methanol [26] can be used as reductants. First of all, those methods are not selective, i.e. it is impossible to separate PGMs using those methods. Moreover, it is also very difficult to separate PGMs from solutions containing base metals at elevated concentrations.

Another very promising method for precious metal recovery is their adsorption on activated carbon (AC) and/or carbon based materials. Our previous studies were focused on the application of this method to gold [27, 28] and platinum [29] recovery using different types of activated carbons. Those studies were focused on the recovery of precious metals from acidic, chloride ion containing aqueous solutions. This topic was also investigated by others. Aktas and Morcali have shown that using AC, it is possible to remove 99% of Pt(IV) ions in time less than 1 h. [30]. It should also be noted that this method is efficient. It is possible to obtain a load of AC over 5% of PGM [31]. Chen et al. investigated the process of platinum ions adsorption on carbon fibers [32]. They have shown that the adsorption process is accompanied with the reduction of Pt(IV) to Pt(II) and next to Pt(0). It was demonstrated that about 25% of Pt exists in the metallic state on the surface of AC fibers (ACF). On the one hand, this effect is advantageous because the efficiency of the process is higher, but on the other hand, strong oxidants have to be used to recover platinum.

It seems that there is still too little work focused on platinum recovery from waste materials. This is mainly related to the fact that these studies are carried out by companies focused on precious metals recovery, which consider this knowledge as their confidential know-how.

In this paper, we would like to investigate the possibility of AC application to platinum recovery from dilute acidic aqueous solutions. This method might be used to reduce metal losses in commonly applied technologies of precious metal refining and separation.

Experimental

In all our experiments, commercially available AC (AC) purchased from Norit(ROX 0.8) was applied in non-modified form. The platinum(IV) chloride complex was obtained according to the methodology described in the previous paper [29].

The measurements of the rate of Pt(IV) chloride complex ion adsorption onto AC were carried out in the cyclic glass reactor kept in the thermostat at constant temperature. After the constant temperature in the system was reached, a suitable amount of AC was added to the reactor. The total volume of the solution was equal to 300 mL. The sample of about 0.5 or 3.5 mL of the solution was taken periodically and analyzed spectrophotometrically (Shimadzu, model PC 2501, Japan) to detect changes of Pt(IV) chloride ion concentration. The volume of the sample taken for analysis depends on the concentration of Pt(IV) in the solution. For high concentration, a quartz cuvette with the 2 mm path length was used, while for lower concentration, a quartz cuvette with the 10 mm path length was applied. After the analysis, the sample was returned to the cyclic reactor to maintain the constant volume of the reagents. The results were cross checked using microwave plasma atomic emission spectrometer (MP-AES, Agilent 4200). In this case, samples of 1 mL of the solution were taken periodically, then mixed with 1 mL of 0.1 M hydrochloric acid. Then the sample were analyzed. The solution was mixed by the glass stirrer dipped into the reactor at the c.a. 2 cm distance from its bottom. The glass stirrer was made of two pieces, where the first one is 22 mm length and the second one was welded in the middle of the first one and had 150 mm length. The glass cyclic reactor was shaped like a cylinder, with the diameter of 90 mm and the height of 93 mm. The rotor speed (Mr) was adjusted and controlled using CAT R-50D stirrer. All experimental conditions are gathered in Table 1.

Table 1 Conditions applied during kinetic measurements of adsorption process
Full size table

The pH of the solution was controlled by the addition of HClO4 (70%, Avantor, analytical grade) in the case of pH 0, 2 and 3. In the case of experiment performed at pH = 1, HCl was used (37%, Avantor, analytical grade). To keep a constant chloride ion concentration of 0.1 M, NaCl (Avantor, analytical grade) or HCl were used.

Results and discussion

It is well known that the Pt(IV) chloride complex absorbs light in the UV–VIS range. This in turn can be used to determine the concentration of platinum in the solution. The calibration curve is shown in Fig. 1.

Fig. 1
figure 1

a The influence of Pt(IV) of initial concentration on the absorbance level, b graphical determination absorption coefficient for Pt(IV) chloride complexes

Full size image

The spectrophotometric method gives an excellent sensitivity as well as high precision. Moreover, thanks to the application of this method, additional sources of error related to the sample dissolution can be eliminated.

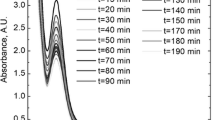
The evolution of UV–VIS spectra during the adsorption process was recorded (see Fig. 2a). Then, the absorbance was registered, and the kinetic curves were plotted. An example of such a curve is shown in Fig. 2b. It is well known that according to Beer’s law, the absorbance is a linear function of the concentration:

$$Abs = \varepsilon \cdot l \cdot [Pt(IV)]$$
(1)
Fig. 2
figure 2

a Evolution of UV–VIS spectra during the adsorption process, b registered kinetic curve. Experimental conditions: [Pt(IV)] = 1 × 10−4, [AC] = 1.67 g/L, pH = 1, T = 298 K, Mr = 1200 rpm

Full size image

Here Abs is the absorbance, ε is the molar absorption coefficient, l is the path length (thickness of analyzed liquid sample), [Pt(IV)] is the concentration of Pt(IV) chloride complex ions.

From Eq. 1, it is possible do determine the concentration of the light absorbing compound. In the case of the platinum(IV) chloride complex, the molar absorption coefficient is equal to 25200 mol L−1 cm−1 [29].

Initial rate method

The initial rate method was used to determine the order of the reaction. Taking into account our observations (see Fig. 2a, b), the following reaction model was initially assumed:

$$[Pt(IV)] + [AC]\mathop{\longrightarrow}\limits{k}[Pt(IV)]@[AC]$$
(2)

As long as the reaction product is not defined, the notation \([Pt(IV)]@[AC]\) will be used for the product of this reaction.

The rate law for reaction 2 can be given in the following form:

$$r_{0} = k \cdot [Pt(IV)]_{0}^{\alpha } \cdot [AC]_{0}^{\beta }$$
(3)

Here k is the reaction rate constant, \([Pt(IV)]_{0}\) is the initial concentration of the platinum(IV) chloride ion, \([AC]_{0}\) is the initial concentration of AC, r 0 is the initial reaction rate, α and β are the orders of the reaction with respect to platinum(IV) chloride ion and AC, respectively.

The initial rate of a reaction is the instantaneous rate at the beginning of the reaction (i.e., when t = 0). The initial rate is equal to the negative of the slope of the curve of Pt(IV) concentration versus time at t ~0. In this case, dt is equal to ~2 min and is graphically shown in Fig. 2b.

Bearing in mind that the AC is insoluble in water, its concentration can be treated as a constant. Under this assumption, Eq. 3 can be simplified and given in the following form:

$$r_{0} = k_{obs} \cdot [Pt(IV)]_{0}^{\alpha }$$
(4)

In this formula, kobs is called the observed rate coefficient and is defined as follows:

$$k_{obs} = k \cdot [AC]_{0}^{\beta }$$
(5)

Using the logarithmic form of Eq. 4, it is possible to determine the order of the reaction from the slope of obtained dependence:

$$\log \left( {r_{0} } \right) = \alpha \cdot \log \left( {[Pt(IV)]_{0} } \right) + \log \left( {k_{obs} } \right)$$
(6)

This is shown in Fig. 3.

Fig. 3
figure 3

Determination of reaction order using initial rate method experimental conditions: [AC] = 1.67 g/L, T = 323 K, pH = 1, Mr = 1200 rpm

Full size image

It can be seen that the determined reaction order is equal to 1.02 ± 0.02. Consequently, it can be assumed that it is equal to 1. The obtained result is in good agreement with the initially assumed reaction scheme (see Eq. 2).

Under isolated conditions, Eq. 2 can be used to derive the following differential equation:

$$r = \frac{d[Pt(IV)]}{dt} = - k_{obs} \cdot [Pt(IV)]$$
(7)

The solution is of the following form:

$$[Pt(IV)] = [Pt(IV)]_{0} \cdot e^{{ - k_{obs} t}}$$
(8)

Solution 8 was fitted to the obtained kinetic data (see Fig. 2a) to determine observed rate coefficient. It should be noted that the correctness of Eq. 5 can be checked by plotting kobs as a function of AC initial concentration. The obtained results are shown in Fig. 4.

Fig. 4
figure 4

Influence of AC initial concentration on the observed rate coefficient. Experimental conditions: [Pt(IV)] = 1 × 10−4 M, T = 323 K, pH = 1, Mr = 1200 rpm

Full size image

The fitted straight line passes through the origin of the coordinate system. This means that the effect of removal of platinum (IV) ions is directly related to the amount of AC and that the previously postulated assumption 5 is valid. The slope of the line is equal to 0.18 L g−1 min−1.

Influence of temperature on the process rate

To determine the activation energy, enthalpy and entropy of activation, Arrhenius as well as the Eyring equations were used, respectively.

The Arrhenius dependence can be given in the following form:

$$k = A \cdot e^{{ - \frac{{E_{a} }}{R \cdot T}}}$$
(9)

Here A is the pre-exponential factor (min−1), Ea is the activation energy (J/mol), T is the temperature (K) and R is the gas constant, 8.314 J mol−1 K−1.

The Eyring equation correlates rate constant with thermodynamic characteristics of the process:

$$k = \frac{{k_{B} \cdot T}}{h}e^{{\frac{{\Delta S^{\dag } }}{R}}} \cdot e^{{ - \frac{{\Delta H^{\dag } }}{RT}}}$$
(10)

Here k B is the Boltzmann constant, h is the Planck constant.

The logarithmic form of Eq. 10 is:

$$\ln \frac{k}{T} = - \frac{{\Delta H^{\dag } }}{RT} + \ln \frac{{k_{B} }}{h} + \frac{{\Delta S^{\dag } }}{R}$$
(11)

The plot in Fig. 5b can be used for the determination of the activation parameters such as enthalpy (∆H†) and entropy of activation (∆S †). The obtained results are summarized in Table 2.

Fig. 5
figure 5

Graphical method for activation energy (a) and enthalpy and entropy of activation (b) determination using Arrhenius and Eyring dependences. Experimental conditions: [Pt(IV)] = 5 × 10−4 M, [AC] = 1.67 g/L, pH = 1, Mr = 1200 rpm

Full size image
Table 2 The parameters of Arrhenius and Eyring equations
Full size table

Using the logarithmic forms of Arrhenius and Eyring equations, it is possible to determine the activation parameters from the slope and intercept of the fitted straight lines. The obtained results are shown in Fig. 5.

The calculated values of activated energy as well as enthalpy and entropy of activation are gathered in Table 2. Statistical analysis of the Eyring equation showed that the ∆H† and ∆S † standard errors are correlated. The standard error of entropy of activation was calculated according to the methodology described by Lente et al [33].

The enthalpy ∆H † is about 16 kJ/mol and is comparable to the activation energy calculated according to the Arrhenius equation. In turn, the entropy of activation has a negative value. It suggests that the number of degrees of freedom of the Pt(IV) chloride complex ions decreases. Such an effect was also observed for other ions [27, 34, 35] during the adsorption process. In the case of the Arrhenius equation, which is often used for activation energy determination, the pre-exponential factor is also called the frequency factor. It strongly depends on the reaction as well as the temperature [36]. For heterogeneous reactions, it generally has small values in the range from 0.78 [28, 29] to 98 min−1, while in homogenous aqueous phase, it is of the order of 109 s−1 [21].

Influence of mixing rate on the process rate

Fig. 6 shows the effect of the mixing rate on the observed rate constant. It is well known that in the case of heterogeneous reactions, the rate limiting step can be either the surface reaction or mass transfer from the solution to the surface. In general, in the studies of heterogeneous reactions, the rotating disc method is used. In this case, instead of the rotating disc, we assumed that the agitation rate is directly proportional to the rotation rate of the AC pellets suspended in the solution. From these experiments, it is possible to determine the limiting step of the process. When the reactant diffuses through the stagnant boundary layer surrounding the pellet, the rate constant (kc) is represented by the mass-transfer coefficient [37]:

Fig. 6
figure 6

The influence of mixing rate on the observed rate coefficient. Experimental conditions: [Pt(IV)] = 1 × 10−4 M, [AC] = 1.67 g/L, T = 323 K, pH = 1

Full size image
$$k_{c} = \frac{D}{\delta }$$
(12)

Here kc is the mass transfer coefficient, δ is thickness of the diffusion layer and D is the diffusion coefficient of reacting species.

Under appropriate conditions, Eq. 12 can be rearranged as follows [37]:

$$k_{c} \sim \frac{{D_{Pt(IV)}^{{\frac{2}{3}}} \cdot V^{{\frac{1}{2}}} \cdot \rho^{{\frac{1}{6}}} }}{{L_{p}^{{\frac{1}{2}}} \cdot \mu^{{\frac{1}{6}}} }}$$
(13)

Here L p is the length of the AC pellet, µ is the viscosity of the solution, ρ is the solution density,\(D_{Pt(IV)}\) is the diffusion coefficient of the Pt(IV) chloride complex, and V is the fluid velocity, which is directly proportional to the Mr according to following equation:

$$V = Mr \cdot r$$
(14)

Here r is the radius.

It can be expected that for the diffusion-limited reaction, the plot kobs v.s. \(V^{{\frac{1}{2}}}\) should be linear. However, an important assumption has to be taken: the mixing rate is proportional to fluid velocity. The obtained results are shown in Fig. 6, which demonstrates that the fitted line does not pass through the origin of kobs v.s \(\sqrt {Mr}\) coordinates.

This in turn suggests that the studied process is complex, and it runs under mixed control. In this situation, the diffusion and reaction rates seem to be comparable.

For the first order reaction and at the steady-state, the kinetics depends on the rate constant and concentration of Pt(IV). However, under mixed control, it also depends on mass the transfer coefficient. The relation between kobs and rate constant as well as mass the transfer coefficient can be expressed as follow [37]:

$$k_{obs} \sim \frac{{k_{c} \cdot k}}{{k_{c} + k}}$$
(15)

Here kc is the mass transfer coefficient.

It should be noted that for the mixing rate 1200 rpm, the obtained kobs also deviates from the trend line (Fig. 6), which, in turn, suggests that above this value process might to be controlled only by one factor i.e. reaction rate constant. Moreover, as it can be seen (Fig. 6), below 200 rpm, the process is clearly controlled by diffusion.

Influence of pH on the process rate

The influence of pH on the observed rate constants is shown in Fig. 7a. It can be seen that the rate of the adsorption decreases with a decrease of [H+] ion concentration. As it can be seen, the mechanism of the process is probably different depending on pH of the solution (see Fig. 7a). At the first stage, a fast absorbance decrease is observed. However, after ca. 10 min, the opposite effect is registered, and an almost constant level is reached finally.

Fig. 7
figure 7

The influence of pH on the observed rate constants, a (experimental conditions: [Pt(IV)] = 5 × 10−5 M, [AC] = 1.67 g/L, T = 323 K, Mr = 1200 rpm), b an exemplar of kinetic curve at pH = 0

Full size image

It should be noted that the solution containing Pt(IV) chloride ions was prepared about 1 h before the experiment. The effect of Pt(IV) aqueous complexes formation during the studies can be rather excluded. Taking into account the UV–VIS spectral analysis, the observed phenomenon can be discussed. For this purpose, a detailed analysis of UV–VIS spectrum evolution during the adsorption is required (see Fig. 8a).

Fig. 8
figure 8

Evolution of UV–Vis spectrum during the adsorption at pH equal to 0 (a), b 1st derivative of the chosen spectrum after t = 60 min. Experimental conditions: experimental conditions: [Pt(IV)] = 5 × 10−5 M, [AC] = 1.67 g/L, T = 323 K, Mr = 1200 rpm

Full size image

Two isosbestic points can be observed. The first one is located at the wavelength 220 nm and the second one at the wavelength 238 nm. After the derivation of the registered spectrum, the maximum of absorption bands can be determined (see Fig. 8b). Gammons [38] has attributed the peak located at the wavelength 233 to the Pt(II) chloride complex ion. It has to be noted that the first derivative of the UV–Vis spectrum of pure solutions is exhibits a peak at this wavelength. This suggest that the observed species must exist in the solution at the very beginning. Murray et al. [39] describe that the following equilibrium is observed in aqueous solution:

$$PtCl_{6}^{2 - } + H_{2} O\overset {\beta_{1} }\;\leftrightarrows\;PtCl_{5} H_{2} O^{ - } + Cl^{ - }$$
(16)

Moreover, they describe that the maximum absorption bend for [PtCl5(H2O)−] is located at 230 nm and 262 nm. This value in turn is very close to the maximum absorption bend of observed species.

It has to be noted that the molar absorption coefficient for [PtCl5(H2O)−] is equal to 11600 M−1 cm−1 [39], and is much lower in comparison with [PtCl6 2−]. This may explain the fast decrease of absorbance at the early stage of the process but does not explain the increase of absorbance after ca. 10 min. Therefore, additional experiments were performed. The obtained results are shown in Fig. 9.

Fig. 9
figure 9

Kinetic curves registered using AES and UV–VIS methodes, a chloride ion concentration controlled by addition 0.1 M NaCl, b chloride ion concentration controlled by additon 0.1 M HCl, C) chloride ion concentration controlled by addition 1 M NaCl. Experimental conditions: [Pt(IV)] = 5 × 10−5 M, [AC] = 1.67 g/L, T = 323 K, Mr = 1200 rpm

Full size image

All three experiments were performed at pH = 0, only the concentration and source of chloride ions was changed. In the case of Fig. 9a, 0.1 M NaCl and 1 M HClO4 were used, whereas in the case of Fig. 9b, 0.1 M HCl and 0.9 M HClO4 were used. In both cases, pseudo-oscillation is observed in the UV–VIS spectrum. This clearly confirms that the effect is not related to the presence of sodium ions but only to the chloride ions. The third experiment sheds light on the mechanism. In Fig. 9c, two kinetic curves are shown, where the first one was obtained using the AES method and the second one was obtained using the UV–VIS method (recorded at 262 nm). When the concentration of chloride ions is equal to 1 M, there is no pseudo-oscillation. Moreover, it seems that initial rates are the same in both cases. This in turn confirms that the studied process is complex and mast consist of several steps.

Capacity test

The capacity test was also performed. The aim of this experiment was to check if there is an influence of previously absorbed Pt(IV) on the rate of further adsorption processes. The obtained results are shown in Fig. 10. It can be seen that there is no change of adsorption rate for different samples pre-loaded with platinum. Moreover, the obtained results show that the capacity of AC is significantly higher in comparison with the initial concentration of Pt(IV) chloride complexes used in the studies.

Fig. 10
figure 10

Capacity test. Experimental conditions: [Pt(IV)] = 1 × 10−4 M, [AC] = 1.67 g/L, T = 296 K, pH = 1

Full size image

It should be noted that the mass of Pt per unit mass of AC was calculated assuming that the adsorption efficiency is 100%. Pre-loaded AC was obtained in previous experiments, in which the influence of initial Pt(IV) concentration on the observed rate constant was investigated.

It should also be noted that this experiment was carried out without mixing.

Norit ROX 0.8 was used by van Dam and van Bekkum [40] as the Pt base catalyst carrier. They have shown that the adsorption capacity of Pt by ROX 0.8 is up to 10%. In our experiments, we have obtained loading up to 7%. As it can be seen, there is no change in the process rate. This suggest that even more Pt can be absorbed by ROX 0.8.

XPS analysis of obtained deposit

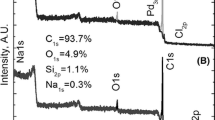
XPS analysis was performed on the sample after Pt(IV) adsorption. The XPS spectrum is shown in Fig. 11.

Fig. 11
figure 11

XPS analysis of the sample after adsorption of Pt(IV) at the experimental conditions: T = 348 K, [Pt(IV)] = 5 × 10−4 M, Mr = 1200 rpm, [AC] = 1.67 g/L, pH = 1

Full size image

It can be observed that a significant amount of oxygen is present on the surface of AC with only some traces of other elements. To determine the oxidation state of platinum on the surface of AC after the adsorption process, further analysis with high resolution XPS were performed. The obtained results are shown in Fig. 12.

Fig. 12
figure 12

High resolution XPS of the Pt 4f core excitation

Full size image

The explanation of the legend shown in Fig. 12 is given in Table 3, as well as the interpretation of acquired spectra.

Table 3 Analysis of high resolution XPS results
Full size table

The shape of the Pt4f core excitation envelope suggests presence of at least two doublet components in the spectrum. Therefore, the high resolution spectrum was deconvoluted on two doublets. The electron binding energy (BE) of Pt4f7/2 peaks allows the assignment of the electronic states to these peaks. Thus, spectrum component A at BE of 72.3 eV can be assigned to Pt2+ in PtO or Pt(OH)2 [41, 42]. Component B of the spectrum at 74.1 eV can be ascribed to Pt4+ bonded to oxygen like in PtO2 or Pt(OH)4 [41, 42]. The full width at half maximum of the fitted component profiles is around 2 eV, which suggests a lack of well-defined crystalline surrounding of the given platinum ions and rather number of possible types of chemical compounds/structures than the specific ones.

Taking into account the results obtained during the studies of the influence of pH on the rate of the process, it can be concluded that the adsorption process is associated with the chemisorption. It cannot be excluded that carbon and a complex of platinum(IV) chloride and platinum(II) forms a weak bond with functional groups (for example Π bond), which is broken after the change of pH. On the one hand, the obtained results are quite different from those obtained by Chen [32], who showed that the adsorption process is accompanied with the reduction of Pt(IV) to Pt(II) and Pt(0). On the other hand, van Dam and van Bekkum have shown that only two forms of Pt(II) and Pt(IV) are present at the surface after the impregnation of AC ROX 0.8 using chloroplatinic (IV) acid by 5 days at room temperature [40]. Moreover, van Dam and van Bekkum obtained a high load of Pt on AC, reaching level of Pt up to 10% of total mass. It is suggested that in case of the studied AC (ROX 0.8), the process of Pt stripping is possible [43].

Pt stripping test

To support our previous suggestions about the stripping of adsorbed platinum form the surface of AC, an additional test was performed. In this test, two samples of AC ROX 0.8 were used after the adsorption of Pt(IV). Those samples contain different amounts of preloaded Pt: 5.8 and 58 mg/g. The size of the samples is ca. 0.5 g. The stripping test was performed at the room temperature. As the stripping solution, 50 mL of 1 M HCl was applied. It is important to underline that at pH = 0, desorption was also observed during the kinetic studies (see “Influence of pH on the process rate” section. The obtained results are shown in Fig. 13.

Fig. 13
figure 13

Kinetic curve observed during desorption test

Full size image

It was calculated that in the case of the more concentrated sample, ca. 6.4% of Pt can be desorbed under these conditions. The stripping process requires to be optimized to find the best conditions. A higher concentration of chloride ions is probably required, or stronger ligands can be used to elute the Pt from AC.

Discussion

Taking into account all gathered information, we suggest that the studied process consists of at list 3 subsequent reactions:

$$PtCl_{6}^{2 - } + AC\mathop{\longrightarrow}\limits{{k_{1}}}\,\cdot\,PtCl_{4}^{2 - } + AC + 2Cl^{ - }$$
(17)
$$PtCl_{6}^{2 - } + AC\mathop{\longrightarrow}\limits{{k_{2}\,\cdot\,}}PtCl_{6}^{2 - } @AC$$
(18)
$$PtCl_{4}^{2 - } + H_{2} O\overset {K'}\,\leftrightarrows\,PtCl_{2} [H_{2} O]_{2} + 2Cl^{ - }$$
(19)
$$PtCl_{4}^{2 - } + AC\mathop{\longrightarrow}\limits{{k_{3}\,\cdot\,}}PtCl_{4}^{2 - } @AC$$
(20)

The first one is related to the reduction of Pt(IV) to Pt(II). This reaction is confirmed by the UV–VIS analysis as well as XPS. The strong effect of pH as well as chloride ion concentration was observed. Therefore, it is suggested that \(PtCl_{2} [H_{2} O]_{2}\) or other aqua complex is formed in the studied system. An increase of chloride ion concentration shifts the equilibrium (Eq. 19). Therefore, pseudo-oscillation in the system can be observed depending on the chloride ion concentration in the system.

The mixing rate has a great impact on the observed process rate. It was shown that the process is controlled by diffusion and reaction. The adsorption capacity tests showed that up to 7% concentration of Pt on AC can be obtained. This result is extremely promising especially taking into account that at least part of the Pt can be stripped using concentrated hydrochloric acid. However, the stripping conditions need to be investigated in detail to find optimal conditions.

Conclusions

Taking into account the obtained results, it can be postulated that the AC Norit ROX 0.8 exhibits an excellent ability of platinum(IV) chloride ion adsorption. This effect can be used for platinum recovery from diluted aqueous solutions.

The obtained results have also shown that the desorption of Pt(IV) is possible by changes of pH of the solution. Thanks to that, AC can be used as a simple and inexpensive extractant for Pt(IV) ions. However, the effectiveness of this process has to be investigated in detail to determine the best conditions for Pt(IV) stripping.

It was shown that after the adsorption process, platinum is present on the surface of AC in two oxidation states +4 and +2. The amount of those two species is about equal.

AC Norit ROX 0.8 exhibits an excellent absorption capability. Thanks to that, it is possible to recover and pre-concentrate a significant amount of platinum from diluted aqueous solutions containing chloride complexes of Pt(IV).

Unfortunately, the mechanism of Pt(IV) adsorption is not fully understood. H. Kasaini and R.K. Mbaya suggest [43] that the interaction between Pt(IV) and AC ROX 0.8 have physisorption nature, whereas Van Dam and Van Bekkum [40] suggest that there is chemisorption for the same AC. The proposed division of sorption phenomena to the chemisorption and physysorption is imprecise. For this reason, there are differences in the interpretation of identical results. In our opinion, an intermediate form of Pt(II) complex is formed at the surface of AC, so then the process can be called chemisorption. Moreover, the chemical properties of the surface e.g. amount and type of functional groups, have essential impact on the process rate and mechanism.