Asymptotic behavior of a system of two coupled queues when the content of one queue is very high

Abstract

We consider a system of two parallel discrete-time single-server queues, queue 1 and queue 2. The service time of any customer in either queue is equal to 1 time slot. Arrivals during consecutive slots occur independently from slot to slot. However, the arrival streams into both queues are possibly mutually interdependent, i.e., during any slot, the numbers of arrivals in queue 1 and queue 2 need not be statistically independent. Their joint probability generating function (pgf) A(x, y) fully characterizes the queueing model. As a consequence of the possible intra-slot correlation in the arrival process, the numbers of customers present (“system contents”) in queues 1 and 2, at any given slot boundary, are not necessarily independent either. In a previous paper, we have already discussed the mathematical difficulty of computing their steady-state joint pgf $U(z_1,z_2)$; explicit closed-form results can only be obtained for specific choices of A(x, y). In this paper, we therefore look at the problem from an other angle. Specifically, we study the (asymptotic) conditional steady-state behavior of the system under the condition that the content of queue 1 is (temporarily) very high (goes to infinity). For ease of terminology, we refer to the system as the “asymptotic system” in these circumstances. We prove that the asymptotic system is nearly identical to the original (unconditional) system, but with a modified joint arrival pgf $A^*(x,y)$ that can be computed explicitly from A(x, y). This fundamental result allows us to determine the stability condition of queue 2 in the asymptotic system, and explicitly compute the classical queueing performance metrics of queue 2, such as the pgf, the moments and the approximate tail distribution of its system content, when this condition is fulfilled. It also leads to accurate approximative closed-form expressions for the joint tail distribution of the system contents in both queues, in the original (unconditional) system. We extensively illustrate our methodology by means of various specific (popular) choices of A(x, y). In some examples, where an explicit solution for $U(z_1,z_2)$ or for the (approximative) joint tail distribution is known, we retrieve the known results easily. In other cases, new results are found for arrival pgfs A(x, y) for which no explicit results were known until now.

1 Introduction

The purpose of this paper is to contribute to a subdomain of queueing theory concerned with the joint analysis of multiple queues. Whereas a multitude of papers exists in which mathematical techniques are developed for the analysis of one single, isolated queue, analyses where several queues are considered simultaneously are rather scarce, unless, of course, these queues operate completely independently of each other. A joint analysis of multiple queues becomes (nearly) unavoidable as soon as these queues influence each other; such queues are sometimes referred to as “coupled queues”. There may be various reasons for the coupling between queues: the arrival streams into the queues may be mutually dependent, the queues may have to share the same service facilities, (part of) the input into one queue may be (part of) the output of other queues, etc. It is well-known that the joint analysis of coupled queues is, in general, quite hard, even when restricted to the situation where only two queues are at play.

Various mathematical techniques have been proposed to study the behavior of two coupled queues, where the purpose of the analysis basically comes down to an attempt to compute the steady-state joint distribution or joint probability generating function (pgf) of the numbers of customers present (the “system contents”) in these queues, or, at least, some (mixed) moments, tail approximations, etc. of the joint distribution. With no claim on completeness, we briefly summarize some of those techniques here.

In many cases, a kernel-type functional equation for the joint pgf of the two system contents pops up in the analysis of two coupled queues. A particularly well-known general principal method, from the field of complex analysis, to find exact solutions of such equations is the so-called “boundary-value approach”, which is described in great detail in the classical books by Cohen and Boxma [12] and by Fayolle et al. [17]. Although the boundary-value approach can deal with various kinds of kernel-type functional equations, it has the disadvantage that it involves singular integrals and conformal mappings, which may be very complicated, and also requires quite some additional numerical work. It does not usually lead to “simple”, easy-to-use formulas. The theory behind the boundary-value approach was developed several decades ago; yet the technique has been used frequently ever since; some examples of (relatively recent) applications are in the context of tandem queues (see, e.g., Resing and Ormeci [26], van Leeuwaarden and Resing [28]), polling systems (see, e.g., Saxena et al. [27]) and retrial queues (see, e.g., various papers by Dimitriou [14,15,16]), and there are many more.

Another method that has been used on various occasions to study the behavior of two coupled queues is the “compensation approach”, a rather versatile technique for the analysis of two-dimensional Markov chains satisfying certain conditions, without transforms (pgfs), initiated by Adan and various co-authors, and very well documented in the paper Adan et al. [4]. Basically, in this method, the desired unknown joint distribution is expressed as a sum of bivariate geometric product forms satisfying the inner balance equations of the Markov chain, and the coefficients of the individual terms in the sum are determined in a clever way. The compensation approach has been used in various applications and contexts; in particular, we mention the study of switching elements in communications networks (Boxma and van Houtum [6]) and the analysis of multiprogramming queues (Adan et al. [2]); a more general application of the compensation approach for random walks in the quarter plane is discussed in Adan, van Leeuwaarden and Raschel [3].

Other researchers have successfully applied the so-called “uniformization method”, a complex-function-based technique, for various models; see, e.g., Kingman [24] and Flatto and McKean [19] for the study of two parallel queues and Jaffe [22, 23] for the analysis of clocked switching elements. In the uniformization method, a parameter representation is introduced for the algebraic curve that represents the set of zero-tuples of the kernel, the unknown boundary functions in the functional equation are also expressed in terms of this parameter, referred to as the “uniformization variable”, and equations are derived and subsequently solved for these boundary functions. In our view, the concept of analytic (or meromorphic) continuation plays a more important role in these analyses than the “uniformization” itself, which does not really reflect the essence of the technique, but the terminology seems, by now, widely accepted. Often, analytic continuation can also be applied directly to the functional equation, without the need of parametrization (or “uniformization”); see, e.g., Cohen [10, 11] for the analysis of the so-called clocked buffered switch, and Devos et al. [13] in the study of a two-class randomly alternating service model.

We also mention the so-called “power-series technique”, mainly devised by Hooghiemstra, Keane and Van de Ree [20] and Blanc (see, e.g., [5]), and further developed by, among others, Hooghiemstra and Koole [21], as a useful method to approximately analyze the steady-state joint distribution of some two-queue systems. This technique consists of expanding the desired distribution (or the associated pgf) as a power series in terms of some system parameter (usually, the load in some queue), and then finding the coefficients of the consecutive powers in that power series as the solutions of “easier” equations than the original functional equation. An adapted version of the power-series technique was successfully applied by Walraevens et al. [30] for the approximate analysis of generalized processor sharing (GPS) queues.

Of course, there are other (ad-hoc) methods as well. An excellent overview of methods that have been used to find the joint distribution of the system contents in two-queue systems can be found in the paper by Adan et al. [1].

In the current paper, we look at the problem of simultaneously analyzing two coupled queues from yet another perspective. Instead of trying to solve the associated balance equations or functional equation, we focus on the asymptotic conditional behavior of the two-queue system when one queue is (temporarily) overloaded, i.e., when the system content of one queue is (temporarily) very high (goes to infinity). We do this for a very simple example system of two coupled parallel queues, where the coupling is caused solely by the fact that the two queues receive external arrival streams that are possibly mutually interdependent. In order to keep the discussion as “pure” as possible, we intentionally allow no other sources of coupling between the two queues; in particular, we assume that arrivals in either queue are not dependent on the states of the queues (as could be the case, for instance, when customers, upon arrival, always join the shortest queue, or when arrivals in one queue are departures from the other queue) and that both queues have their own dedicated server which is permanently available for the service of customers of that queue only. Systems of two parallel queues have been investigated frequently in the past, as illustrated by the numerous references mentioned earlier. We emphasize in particular the early (seminal) works by Kingman [24] and Flatto and McKean [19] who consider continuous-time models for the join-the-shorter-line scheduling scheme, and Konheim et al. [25] who consider one shared server for both queues, also through a continuous-time model. But the specific system considered in the current paper, i.e., two parallel queues with interdependent arrivals (and no other sources of coupling) has been dealt with in just a few papers, mainly in a discrete-time setting, especially in the context of the analysis of a clocked buffered switch, in papers by Jaffe [22, 23], Cohen [10, 11], Boxma and van Houtum [6] and Adan et al. [1], as mentioned earlier. The paper Bruneel [7] also falls within this category, albeit that the joint arrival distribution can be more general than “binomial of order two” (as is the case in the clocked buffered switch) there. In the current paper, we essentially investigate the same general model as Bruneel [7], but from the perspective of analyzing it under the specific condition that one of both queues contains a large number of customers. The approach taken in this paper does not require any specific assumptions with respect to the joint arrival distribution, and, to the best of our knowledge, is new.

The rest of the paper is organized as follows. Section 2 describes the full details of the mathematical model we consider. In Sect. 3, we establish the basic functional equation for the steady-state joint pgf of the two system contents, and derive explicit expressions for the two marginal pgfs (and mean values) of the system contents in the individual queues. In Sect. 4, we define the “asymptotic system” as a convenient short terminology for the original two-queue system, considered under the explicit condition that the system content in queue 1 is (temporarily) very large (goes to infinity). We then formally prove that the asymptotic system is nearly identical to the original (unconditional) system, i.e., it has two parallel discrete-time single-server queues, deterministic 1-slot service times, independent arrivals from slot to slot, but a modified joint arrival distribution, that can be computed explicitly from the original joint arrival distribution, regardless of its nature. We then apply this fundamental result to examine the stability condition and the steady-state queueing performance of queue 2 in the asymptotic system; we also derive accurate approximative closed-form expressions for the joint tail distribution of the two system contents in the original (unconditional) system. Section 5 illustrates our methodology extensively by considering a number of (well-known) example arrival distributions in great detail. Here, we easily retrieve previously known results, when these are available, but also various new results for systems that have not been solved so far. In Sect. 6, we compare the performance of queue 2 in the asymptotic system with its performance in the original system, in terms of the arrival rate, the mean system content and the (approximate) tail distribution of the system content, and try to explain the observed differences in terms of the nature of the intra-slot correlation in the arrival process. Some conclusions are stated in Sect. 7. The paper also has two appendices; “Appendix A” simply proves a mathematical lemma, required in Sect. 4, but “Appendix B” is important in its own right and shows how to solve the functional equation explicitly for a very specific joint arrival distribution that was also considered in one of the examples of Sect. 5; we had this interesting (non-trivial) result for a number of years but it was never published before.

2 Mathematical model

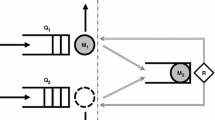
In this paper, we investigate a discrete-time queueing system, consisting of two parallel queues, named queue 1 and queue 2, with infinite waiting room and one server each. A graphical representation of the system is shown in Fig. 1.

Fig. 1

System of two parallel single-server queues with joint arrival pgf A(x, y). $A_1(x)$ and $A_2(y)$ denote the marginal arrival pgfs in queue 1 and queue 2, respectively

As in all discrete-time models, the time axis is divided into fixed-length intervals referred to as (time) slots. New customers may enter the system at any given (continuous) point on the time axis, but services are synchronized to (i.e., can only start and end at) slot boundaries. Customers arriving to queue 1 and to queue 2 are referred to as type-1 customers and type-2 customers, respectively. We assume that the service of each customer requires exactly one time slot, regardless of whether the customer is of type 1 or type 2.

The arrival process of new customers in the system is characterized by means of a sequence of i.i.d. nonnegative discrete random vectors $(a_{1,k},a_{2,k})$ with common joint probability mass function (pmf) a(i, j) and common joint probability generating function (pgf) A(x, y), respectively. Here $a_{1,k}$ and $a_{2,k}$ indicate the numbers of type-1 and type-2 arrivals, respectively, during slot k, and, hence, a(i, j) and A(x, y) are defined as

$$\begin{aligned} a(i,j) \triangleq \textrm{Prob}\!\left[ a_{1,k} = i \text { and }a_{2,k} = j \right] , \quad i,j \ge 0 \hspace{5.0pt},\\ \end{aligned}$$

$$\begin{aligned} A(x,y) \triangleq E\!\left[ x^{a_{1,k}}y^{a_{2,k}}\right] \triangleq \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty a(i,j) \, x^i y^j, \end{aligned}$$

(1)

which are independent of k. The (marginal) pgfs of $a_{1,k}$ and $a_{2,k}$ are given by

$$\begin{aligned} A_1(x) \triangleq E\!\left[ x^{a_{1,k}}\right] = A(x,1), \quad A_2(y) \triangleq E\!\left[ y^{a_{2,k}}\right] = A(1,y) , \end{aligned}$$

(2)

respectively. The mean number of arrivals of type i per slot is denoted as

$$\begin{aligned} \lambda _i \triangleq A_i'(1) . \end{aligned}$$

(3)

Note that, just as the joint pgf A(x, y), the marginal pgfs $A_1(x)$ and $A_2(y)$ and the mean arrival rates $\lambda _i$ do not depend on the slot index k.

3 Steady-state queueing analysis

3.1 Stability conditions of the system

The main purpose of our paper is to analyze some aspects of the steady-state behavior of the queueing system under study. It is not difficult to see that the system is stable, i.e., a steady state exists, if and only if both queue 1 and queue 2 are stable. As both queues are simple single-server queues with deterministic 1-slot service times, the stability conditions thus read

$$\begin{aligned} \lambda _1< 1 , \lambda _2 < 1 . \end{aligned}$$

(4)

3.2 System evolution as a function of time

Let $u_{1,k}$ and $u_{2,k}$ indicate the system contents, i.e., the numbers of customers present in queue 1 and queue 2, respectively, at the beginning of slot k. We indicate their joint pgf as

$$\begin{aligned} U_k(z_1,z_2) \triangleq E\!\left[ z_1^{u_{1,k}}z_2^{u_{2,k}}\right] . \end{aligned}$$

(5)

We note that, in this paper, the term system content always refers to the total number of customers in the queue, including the customer in service, if any. As each queue of the system has exactly one server that can serve exactly one customer per time slot, the following system equations are valid between the random variables $u_{1,k}$ and $u_{2,k}$ on the one hand, and the random variables $u_{1,k+1}$ and $u_{2,k+1}$, one slot later, on the other hand:

$$\begin{aligned} u_{1,k+1} = a_{1,k} + (u_{1,k}-1)^+, \quad u_{2,k+1} = a_{2,k} + (u_{2,k}-1)^+ . \end{aligned}$$

(6)

Here we have introduced the notation $(x)^+$ to indicate the quantity $\max (0,x)$. Equations (6) can be translated into one corresponding equation between the joint pgfs $U_{k}(z_1,z_2)$ and $U_{k+1}(z_1,z_2)$, by using definition (5), which results in

$$\begin{aligned} U_{k+1}(z_1,z_2){} & {} \triangleq E\!\left[ z_1^{u_{1,k+1}}z_2^{u_{2,k+1}}\right] = A(z_1,z_2) E\!\left[ z_1^{(u_{1,k}-1)^+}z_2^{(u_{2,k}-1)^+}\right] \nonumber \\{} & {} = \frac{A(z_1,z_2)}{z_1z_2} \left[ U_k(z_1,z_2) + (z_2-1)U_k(z_1,0) + (z_1-1)U_k(0,z_2)\right. \nonumber \\{} & {} \quad \left. + (z_1-1)(z_2-1)U_k(0,0) \right] . \end{aligned}$$

(7)

3.3 Steady state

We now let the time parameter k go to infinity. Assuming the system reaches a steady state, i.e., assuming the stability conditions (4) are met, then both functions $U_k(\cdot )$ and $U_{k+1}(\cdot )$ converge to a common limit function $U(\cdot )$, which denotes the joint pgf of the two system contents at the beginning of an arbitrary slot in the steady state. As a result, Eq. (7) translates into a linear equation for $U(z_1,z_2)$, which can be written as

$$\begin{aligned} K(z_1,z_2) U(z_1,z_2) = A(z_1,z_2) L(z_1,z_2), \end{aligned}$$

(8)

where the unknown function $L(z_1,z_2)$ is defined as

$$\begin{aligned} L(z_1,z_2) \triangleq (z_2-1)U(z_1,0) + (z_1-1)U(0,z_2) + (z_1-1)(z_2-1)U(0,0) \end{aligned}$$

and the “kernel” $K(z_1,z_2)$ is given by $K(z_1,z_2) \triangleq z_1z_2-A(z_1,z_2)$.

As has been discussed in e.g. Bruneel [7], the functional equation (8) is very hard to solve analytically, for general arrival pgfs $A(z_1,z_2)$. Only for specific classes of arrival pgfs, the explicit determination of the boundary functions $U(z_1,0)$ and $U(0,z_2)$, and, from this, the unknown function $L(z_1,z_2)$, and the whole pgf $U(z_1,z_2)$, in closed analytic form, seems feasible. We will discuss some rare examples in Sect. 5 (notably in Sects. 5.1 and 5.2.2). The marginal pgf $U_i(z)$ of the system content in queue i, however, can be easily deducted from (8) by choosing either {$z_1=z,z_2=1$} or {$z_1=1,z_2=z$}, which results in

$$\begin{aligned} U_i(z) = (1-\lambda _i)\frac{(z-1)A_i(z)}{z-A_i(z)} , \end{aligned}$$

(9)

where the marginal pgf $A_i(z)$ and mean value $\lambda _i$ of the number of type-i arrivals per slot were defined in Eqs. (2) and (3). The mean system content in queue i is given by

$$\begin{aligned} E\!\left[ u_i\right] = U_i'(1) = \lambda _i + \frac{A_i''(1)}{2(1-\lambda _i)} . \end{aligned}$$

(10)

These simple formulas for the individual queues are not surprising, as queue i is a single-server queue with 1-slot service times and arrival pgf $A_i(z)$. These formulas can be found in many papers and books on discrete-time queueing theory; see, e.g., chapter 4 of Bruneel and Kim [8].

4 Asymptotic behavior

From now on, let us assume that the system has reached a steady state. We then define the random variables $u_1$ and $u_2$ as the system contents in queues 1 and 2, respectively, at the beginning of an arbitrary slot in the steady state.

We now shift our focus from the analysis of the full joint distribution (or pgf) of the two system contents to the study of the conditional asymptotic behavior of one queue, say queue 2, given that the system content in the other queue, i.e., in queue 1, is very high. Specifically, we are interested in determining such quantities as the conditional pgf, mean value, approximate tail distribution,... of $u_2$, given that $u_1=n$, for large values of n. In order to do so, we first make some very mild assumptions on the marginal arrival pgfs $A_1(z)$ and $A_2(z)$, as stated in the “arrival assumption” below.

Arrival assumption

The pgf $A_i(z)$ has a radius of convergence $\Omega _i>1$ and $\lim _{z\rightarrow \Omega _i} A_i(z) = +\infty$.

Pgfs that satisfy the above condition are sometimes called “well-behaved”. The arrival assumption implies, among other things, that $A_1(z)$ and $A_2(z)$ do not have singularities on the unit circle in the complex z-plane, because their radius of convergence is strictly larger than 1. Note that most commonly used discrete arrival distributions have pgfs that satisfy these conditions.

4.1 Tail distribution of the system content in one queue

It is well known (see, e.g., Flajolet and Odlyzko [18], Bruneel and Kim [8], Bruneel et al. [9], Van Mieghem [29]) that the tail distribution of a discrete random variable can be very well approximated based on the so-called “dominant singularity” of the pgf of that random variable. Specifically, if the pgf X(z) of a discrete random variable X has a radius of convergence $\tau >1$, then $\tau$ (a positive real number) is a singularity of X(z) and X(z) cannot possess singularities with a smaller absolute value than $\tau$, i.e., $\tau$ is a “dominant” singularity of X(z). Moreover, in the very common case where X(z) has no other (complex) singularities with the same modulus as $\tau$ (i.e., $\tau$ is the only dominant singularity of X(z)), and $\tau$ is a pole of multiplicity 1, the tail distribution of X can be very well approximated by a geometric form with decay rate $\tau ^{-1}$:

$$\begin{aligned} \textrm{Prob}\!\left[ X=n\right] \approx c\tau ^{-n-1} , \end{aligned}$$

(11)

for large values of n. The constant c is the negative residue of the pgf X(z) at $z=\tau$, i.e.,

$$\begin{aligned} c = -\lim _{z\rightarrow \tau } (z-\tau )X(z) . \end{aligned}$$

(12)

This approximation is usually referred to as the “dominant-pole approximation” of the tail distribution of X. The terminology “dominant” stems from the fact that the exact value of the inverse z-transform of X(z), i.e., the pmf $\textrm{Prob}\!\left[ X=n\right]$, can be expressed as a sum of (geometric or similar) contributions of all the singularities of X(z), each with a decay rate inversely proportional to the singularity at hand; for large n, the contribution of the singularity with smallest modulus therefore “dominates” all the others, and the sum can be well approximated by the contribution of the dominant singularity alone.

We now apply the above approximation technique to the marginal pgf $U_i(z)$ of the queue-i system content. In order to do so, we first notice that the singularities of $U_i(z)$, as given by Eq. (9), are the zeroes of the expression $z-A_i(z)$. We show in “Appendix A” that, if $A_i(z)$ is “well-behaved” with radius of convergence $\Omega _i>1$, as defined above in the “arrival assumption”, then $z-A_i(z)$ has exactly one real positive zero, say $\tau _i$, with $1<\tau _i<\Omega _i$, which has multiplicity 1; obviously $\tau _i$ satisfies the equation

$$\begin{aligned} \tau _i = A_i(\tau _i) , \quad 1<\tau _i<\Omega _i ; \end{aligned}$$

(13)

furthermore, in “Appendix A”, we also show that

$$\begin{aligned} A_i'(\tau _i) > 1 \end{aligned}$$

(14)

and that $z-A_i(z)$ has no other zeroes outside the unit disk in the complex z-plane with modulus smaller than $\tau _i$. This means that $\tau _i$ is the dominant pole of the pgf $U_i(z)$ and an approximation such as (11) can be used. As a result, we obtain

$$\begin{aligned} \textrm{Prob}\!\left[ u_i=n\right] \approx c_i\tau _i^{-n-1} , \end{aligned}$$

(15)

where, according to (9) and (12),

$$\begin{aligned} c_i = -\lim _{z\rightarrow \tau _i} (z-\tau _i)U_i(z) = -\lim _{z\rightarrow \tau _i} (1-\lambda _i)\frac{(z-1)(z-\tau _i)A_i(z)}{z-A_i(z)} , \end{aligned}$$

or, upon use of de l’Hospital’s rule and Eq. (13),

$$\begin{aligned} c_i = \frac{(1-\lambda _i)(\tau _i-1)A_i(\tau _i)}{A'_i(\tau _i)-1} = \frac{(1-\lambda _i)(\tau _i-1) \tau _i}{A'_i(\tau _i)-1} . \end{aligned}$$

(16)

In Fig. 2, we compare the dominant-pole tail approximation (15), (16) for $\textrm{Prob}\!\left[ u_1=n\right]$ with simulation results for three different well-known arrival distributions with mean arrival rate $\lambda _1$:

• $A_1(z)=e^{\lambda _1(z-1)}$ (Poisson arrivals), with $\lambda _1=0.7$

• $A_1(z)=\frac{1}{1+\lambda _1-\lambda _1 z}$ (geometric arrivals), with $\lambda _1=0.8$

• $A_1(z) = \big (1-\frac{\lambda _1}{2} + \frac{\lambda _1}{2} z \big )^2$ (binomial arrivals of order two), with $\lambda _1=0.9$.

Fig. 2

Dominant-pole approximation for $\textrm{Prob}\!\left[ u_1=n\right]$ versus simulation results

The graphs show that the approximation is extremely accurate, even for small values of n. In Sect. 5.2.1, we shall see that, for geometric arrivals, $u_1$ happens to be geometrically distributed and the “tail approximation” is even exact for all values of n; see Eq. (60).

4.2 Conditional arrival process

Our main goal being the study of the conditional behavior of the system content in queue 2, given that the system content in queue 1 is (temporarily) very large, it would seem natural to focus immediately on the (existence and—if so—the computation of the) conditional pgf of the queue-2 system content $u_2$ given the (high) value (n) of $u_1$ at the beginning of the same (arbitrary) slot in the steady state, i.e., the conditional pgf

$$\begin{aligned} U^*_2(z|n) \triangleq E\!\left[ z^{u_2}|u_1=n\right] \end{aligned}$$

and its limit as $n\rightarrow \infty$, which we denote as

$$\begin{aligned} U^*_2(z) \triangleq \lim _{n\rightarrow \infty } U^*_2(z|n) . \end{aligned}$$

(17)

Here, however, we take a different approach. As the system content in queue 2 at the beginning of any slot in the steady state, say slot S, is merely the result of the arrivals and the services in queue 2 before slot S, and the services are, in fact, very deterministic, we first concentrate on the conditional arrival process in queue 2 before slot S, given that the system content in queue 1 at the start of slot S is equal to n, for large values of n. It turns out that it is not more difficult to analyze the conditional joint arrival process in both queues 1 and 2 than in just queue 2. Moreover, we shall see that this yields some interesting additional information. Our approach is based on this observation.

Formally, we proceed as follows. Let S be an arbitrary slot in the steady state. Let $u_{1,S}$ denote the system content at the beginning of slot S in queue 1. As S is an arbitrary slot, $u_{1,S}$ is distributed according to the known pgf $U_1(z)$ defined in (9). Let $a_{1,S-\ell }$ and $a_{2,S-\ell }$ ($\ell \ge 1$) denote the numbers of arriving customers of type 1 and 2, respectively, $\ell$ slots earlier than slot S, i.e., during slot $S-\ell$. For any integer $m \ge 1$, the (unconditional) joint distribution of the random variables $\{a_{1,S-\ell },a_{2,S-\ell }, 1 \le \ell \le m\}$ is well-known; as the arrivals in our system are independent from slot to slot, the associated joint pgf is given by a simple product form, i.e.,

$$\begin{aligned} B_m(x_1,y_1, \ldots , x_m,y_m) \triangleq E\!\left[ \prod _{\ell =1}^m (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }})\right] = \prod _{\ell =1}^m A(x_{\ell },y_{\ell }) . \end{aligned}$$

(18)

Note that this result is valid for any choice of the slot S, and therefore the notation ($B_m$) has no dependence on S.

Next, assume that, for the chosen slot S, $u_{1,S}$ is equal to a given value n; if desired, the probability that this is the case, i.e.,

$$\begin{aligned} u_1(n)\triangleq \textrm{Prob}\!\left[ u_{1,S}=n\right] , \end{aligned}$$

(19)

can be computed from the known pgf $U_1(z)$ (see Eq. (9)) by inverse z-transformation. Of course, if it is known that $u_{1,S}=n$, this has an impact on the possible values of the numbers of arrivals in the slots before S (and their probabilities). In general, it is to be expected that, under this condition, the random variables $\{a_{1,S-\ell },a_{2,S-\ell }, 1 \le \ell \le m\}$ have a different joint pgf than the above defined $B_m$, and are even not necessarily mutually independent anymore from slot to slot. We are therefore interested in the computation of the conditional joint pgf of the random variables $\{a_{1,S-\ell },a_{2,S-\ell }, 1 \le \ell \le m\}$ given that $u_{1,S}=n$. Formally, we define this conditional joint pgf as

$$\begin{aligned} F_{m|n}(x_1,y_1, \ldots , x_m,y_m) \triangleq E\!\left[ \prod _{\ell =1}^m (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}) | u_{1,S}=n\right] , \end{aligned}$$

(20)

where we may again suppress the dependence on S in the notation. We now go through a series of consecutive steps to derive an explicit expression for the function $F_{m|n}$, for large values of n.

4.2.1 Step 1: the joint pgf $V_m$

We start by defining the joint pgf of $\{a_{1,S-\ell },a_{2,S-\ell }, 1 \le \ell \le m\}$ and $u_{1,S}$ as

$$\begin{aligned} V_m(x_1,y_1, \ldots , x_m,y_m;z) \triangleq E\!\left[ \bigg (\prod _{\ell =1}^m (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}\bigg ) z^{u_{1,S}}\right] . \end{aligned}$$

(21)

This definition can be easily extended to include the boundary case $m=0$, by agreeing that an empty product is equal to 1, i.e.,

$$\begin{aligned} V_0(z) \triangleq E\!\left[ z^{u_{1,S}}\right] = U_1(z) = (1-\lambda _1)\frac{(z-1)A_1(z)}{z-A_1(z)} , \end{aligned}$$

(22)

where we have used (9). Note that, although the function $V_m$, as defined in (21), does not explicitly depend on the choice of the slot S, we will (temporarily) add a subscript S in our notation (i.e., $V_{m,S}=V_m$), in order to improve the clarity of the derivations that follow.

4.2.2 Step 2: a recurrence relation for $V_m$

Using system Eq. (6) for $k=S-1$ in (21), we can express $V_{m+1,S}$ in terms of $V_{m,S-1}$:

$$\begin{aligned} \begin{aligned} V_{m+1,S}&(x_1,y_1, \ldots , x_{m+1},y_{m+1};z) = E\!\left[ \bigg (\prod _{\ell =1}^{m+1} (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}\bigg ) z^{u_{1,S}}\right] \\&= E\!\left[ \bigg (\prod _{\ell =1}^{m+1} (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}\bigg )z^{a_{1,S-1} + (u_{1,S-1}-1)^+}\right] \\&= E\!\left[ \bigg ((x_1 z)^{a_{1,S-1}} y_1^{a_{2,S-1}}\bigg )\bigg (\prod _{\ell =2}^{m+1} (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}\bigg )z^{(u_{1,S-1}-1)^+}\right] . \end{aligned} \end{aligned}$$

Since the arrivals during slot $S-1$ are independent of all the earlier arrivals (and, hence, also of $u_{1,S-1}$), the above expected value can be expressed as a product of two expected values, i.e.,

$$\begin{aligned} V_{m+1,S}(x_1,y_1, \ldots , x_{m+1},y_{m+1};z) = A(x_1z,y_1)E\!\left[ \bigg (\prod _{\ell =2}^{m+1} (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}\bigg )z^{(u_{1,S-1}-1)^+}\right] . \end{aligned}$$

Here the second factor can be expressed in terms of the function $V_{m,S-1}$, and so

$$\begin{aligned} \begin{aligned} V&_{m+1,S}(x_1,y_1, \ldots , x_{m+1},y_{m+1};z) = A(x_1z,y_1)E\!\left[ \bigg (\prod _{\ell '=1}^m (x_{\ell '+1}^{a_{1,(S-1)-\ell '}} y_{\ell '^+1}^{a_{2,(S-1)-\ell '}}\bigg )z^{(u_{1,S-1}-1)^+}\right] \\&= A(x_1z,y_1) \frac{V_{m,S-1}(x_2,y_2, \ldots , x_{m+1},y_{m+1};z) + (z-1) V_{m,S-1}(x_2,y_2, \ldots , x_{m+1},y_{m+1};0)}{z} . \end{aligned} \end{aligned}$$

Suppressing the dependence on S (or $S-1$) again, we obtain the following (recurrence) relation between $V_{m+1}$ and $V_m$:

$$\begin{aligned} \begin{aligned} V&_{m+1}(x_1,y_1, \ldots , x_{m+1},y_{m+1};z) \\ {}&= \frac{A(x_1z,y_1)}{z} \big [V_m(x_2,y_2, \ldots , x_{m+1},y_{m+1};z) + (z-1) V_m(x_2,y_2, \ldots , x_{m+1},y_{m+1};0)\big ] . \end{aligned}\nonumber \\ \end{aligned}$$

(23)

4.2.3 Step 3: $z=\tau _1$ is the dominant pole of $V_m$

For $m=0$, (23) leads to

$$\begin{aligned} V_1(x_1,y_1;z) = \frac{A(x_1z,y_1)}{z} [V_0(z) + (z-1) V_0(0)] , \end{aligned}$$

(24)

or in view of (22),

$$\begin{aligned} V_1(x_1,y_1;z) = \frac{A(x_1z,y_1)}{z} [U_1(z) + (z-1) U_1(0)] = \frac{(1-\lambda _1)(z-1)A(x_1z,y_1)}{z-A_1(z)} .\nonumber \\ \end{aligned}$$

(25)

Similarly, for $m=1$, we get from (23) and (25)

$$\begin{aligned} \begin{aligned} V_2(x_1,y_1,&x_2,y_2;z) = \frac{A(x_1z,y_1)}{z} [V_1(x_2,y_2;z) + (z-1) V_1(x_2,y_2;0)] \\&= \frac{(1-\lambda _1)(z-1)A(x_1z,y_1)}{z} \bigg [\frac{A(x_2z,y_2)}{z-A_1(z)} + \frac{A(0,y_2)}{A_1(0)} \bigg ] . \end{aligned} \end{aligned}$$

(26)

Analogously, we could derive an explicit expression for the function $V_m$, for any finite value of m, from the recurrence relation (23). However, such an expression would be complicated (for general m), and, more importantly, is not really needed for the purpose of computing the function $F_{m|n}$, defined in (20), which is our true goal. The expressions (22), (25) and (26) for the functions $V_0$, $V_1$, $V_2$ do make clear that these functions, considered as functions of the variable z, all have a single pole at $z=\tau _1$, which is a zero of their common denominator $(z-A_1(z))$. It is readily seen that this statement holds true for all the functions $V_m, m \ge 0$. Moreover, the pole at $z=\tau _1$ is the dominant pole of the functions $V_m$ if – as usual – we restrict the values of the other variables ($x_\ell$ and $y_\ell$) to the closed unit disks in their respective complex planes, i.e., $|x_\ell | \le 1,|y_\ell | \le 1$. One easy intuitive way to see this is by observing that factors such as $A(x_\ell z,y_\ell )$, appearing in the numerators of the formulas for $V_m$ remain finite when $|z|<\tau _1$:

$$\begin{aligned} |A(x_\ell z,y_\ell )| = \bigg |\sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty a(i,j) \, (x_\ell z)^i y_\ell ^j \bigg | \le \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty a(i,j) \, |x_\ell z|^i |y_\ell |^j \end{aligned}$$

(27)

and, thus, if $|x_\ell | \le 1,|y_\ell | \le 1$,

$$\begin{aligned} |A(x_\ell z,y_\ell )| \le \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty a(i,j) \, |z|^i = A(|z|,1) = A_1(|z|) , \end{aligned}$$

(28)

which is certainly finite for $|z|<\tau _1$, since the radius of convergence $\Omega _1$ of the marginal arrival pgf $A_1(z)$ is larger than $\tau _1$, as discussed in Sect. 4.1 and “Appendix A”.

4.2.4 Step 4: deriving $F_{m|n}$ from $V_m$

From the definitions (20) and (21), it easily follows (by an application of the law of total expectation) that

$$\begin{aligned} \begin{aligned} V_m(x_1,y_1, \ldots , x_m,y_m;z)&\triangleq E\!\left[ \bigg (\prod _{\ell =1}^m (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}\bigg ) z^{u_{1,S}}\right] \\&= \sum _{n=0}^\infty u_1(n) z^n E\!\left[ \prod _{\ell =1}^m (x_\ell ^{a_{1,S-\ell }} y_\ell ^{a_{2,S-\ell }}) | u_{1,S}=n\right] \\&= \sum _{n=0}^\infty z^n u_1(n) F_{m|n}(x_1,y_1, \ldots , x_m,y_m) . \end{aligned}\qquad \end{aligned}$$

(29)

Hence, the product $u_1(n) F_{m|n}$ is nothing but the coefficient of the power $z^n$ in the power series expansion of the function $V_m$, considered as a function of the variable z, i.e., for given values of the variables $\{(x_\ell ,y_\ell ), 1 \le \ell \le m\}$. In principle, this product can thus be retrieved from $V_m$ through inverse z-transformation. Here, we are interested in large values of n, and, therefore, the inverse z-transform of $V_m$ is dominated by the term associated to its dominant pole, which is $z=\tau _1$. For large n, we can therefore use the following accurate dominant-pole approximation:

$$\begin{aligned} u_1(n) F_{m|n}(x_1,y_1, \ldots , x_m,y_m) \approx W_m(x_1,y_1, \ldots , x_m,y_m) \tau _1^{-n-1} , \end{aligned}$$

(30)

and, hence,

$$\begin{aligned} F_{m|n}(x_1,y_1, \ldots , x_m,y_m) \approx \frac{W_m(x_1,y_1, \ldots , x_m,y_m) \tau _1^{-n-1}}{u_1(n)} , \end{aligned}$$

(31)

where $W_m$ denotes the negative residue of $V_m$ at $z=\tau _1$, i.e.,

$$\begin{aligned} W_m(x_1,y_1, \ldots , x_m,y_m) \triangleq -\lim _{z\rightarrow \tau _1} (z-\tau _1) V_m(x_1,y_1, \ldots , x_m,y_m;z) . \end{aligned}$$

(32)

4.2.5 Step 5: determining $W_m$

Multiplying both sides of the recurrence relation (23) by a factor $-(z-\tau _1)$ and then taking the limit for $z\rightarrow \tau _1$, we easily get

$$\begin{aligned} W_{m+1}(x_1,y_1, \ldots , x_{m+1},y_{m+1})= & {} -\lim _{z\rightarrow \tau _1} (z-\tau _1) \frac{A(x_1z,y_1)}{z}\nonumber \\ {}{} & {} \times [V_m(x_2,y_2, \ldots , x_{m+1},y_{m+1};z)] \nonumber \\= & {} \frac{A(\tau _1 x_1,y_1)}{\tau _1} W_m(x_2,y_2, \ldots , x_{m+1},y_{m+1}) .\qquad \quad \end{aligned}$$

(33)

Equation (33) is a (very simple) recursive equation for the functions $W_m$; applying (33) repeatedly for consecutive values of m, we can express $W_m$ as

$$\begin{aligned} W_m(x_1,y_1, \ldots , x_m,y_m) = \bigg [ \prod _{\ell =1}^{m-1} \frac{A(\tau _1 x_\ell ,y_\ell )}{\tau _1} \bigg ] W_1(x_m,y_m) . \end{aligned}$$

(34)

The function $W_1$ can be easily derived from (25) as

$$\begin{aligned} W_1(x,y)= & {} -\lim _{z\rightarrow \tau _1} (z-\tau _1) V_1(x,y;z) = -\lim _{z\rightarrow \tau _1} (z-\tau _1) \frac{(1-\lambda _1)(z-1)A(xz,y)}{z-A_1(z)}\nonumber \\= & {} \frac{(1-\lambda _1)(\tau _1-1)A(\tau _1 x,y)}{A_1'(\tau _1)-1} , \end{aligned}$$

(35)

which, eventually, leads to

$$\begin{aligned} W_m(x_1,y_1, \ldots , x_m,y_m) = \frac{(1-\lambda _1)\tau _1(\tau _1-1)}{A_1'(\tau _1)-1} \bigg [ \prod _{\ell =1}^m \frac{A(\tau _1 x_\ell ,y_\ell )}{\tau _1} \bigg ] . \end{aligned}$$

(36)

4.2.6 Step 6: approximate expression for $F_{m|n}$

We have shown in Sect. 4.1 (Eqs. (15) and (16)) that, for large n, the probability $u_1(n)$ can be well approximated as

$$\begin{aligned} u_1(n) \approx \frac{(1-\lambda _1)\tau _1(\tau _1-1)}{A'_1(\tau _1)-1} \tau _1^{-n-1} . \end{aligned}$$

(37)

Using (36) and (37) in (31), we find that, for large values of n, the function $F_{m|n}$ can be accurately approximated as

$$\begin{aligned} F_{m|n}(x_1,y_1, \ldots , x_m,y_m) \approx \prod _{\ell =1}^m \frac{A(\tau _1 x_\ell ,y_\ell )}{\tau _1} , \end{aligned}$$

(38)

which turns out to be independent of n. Introducing the notation

$$\begin{aligned} A^*(x,y) \triangleq \frac{A(\tau _1 x,y)}{\tau _1} , \end{aligned}$$

(39)

we can thus conclude that, for large values of n,

$$\begin{aligned} F_{m|n}(x_1,y_1, \ldots , x_m,y_m) \approx \prod _{\ell =1}^m A^*( x_\ell ,y_\ell ) . \end{aligned}$$

(40)

As a consequence of the properties of dominant-pole approximations, as used in the above derivation (in both the numerator and the denominator of (31)), the above approximative equality becomes a true equality when $n\rightarrow \infty$. An easy way to see that this statement is true, without complicating the notations too much, is as follows. First, replace the approximative equality (30) by an exact equality by introducing a correction term $o_1(\tau _1^{-n-1})$ that summarizes the contributions of all the non-dominant singularities in the inverse z-transform of the function $V_m$:

$$\begin{aligned} u_1(n) F_{m|n} = W_m \tau _1^{-n-1} + o_1(\tau _1^{-n-1}) , \end{aligned}$$

(41)

where, for notational convenience we have (temporarily) omitted the arguments of the functions $F_{m|n}$ and $W_m$, and $o_1(\tau _1^{-n-1})$ is a function of n that goes to zero more rapidly than $\tau _1^{-n-1}$ as $n\rightarrow \infty$. Next, take a similar action on Eq. (37), introducing a similar function $o_2(\tau _1^{-n-1})$:

$$\begin{aligned} u_1(n) = \frac{(1-\lambda _1)\tau _1(\tau _1-1)}{A'_1(\tau _1)-1} \tau _1^{-n-1} + o_2(\tau _1^{-n-1}) . \end{aligned}$$

(42)

From (41) and (42), we then get the following exact expression for $F_{m|n}$:

$$\begin{aligned} F_{m|n} = \frac{W_m \tau _1^{-n-1} + o_1(\tau _1^{-n-1})}{\frac{(1-\lambda _1)\tau _1(\tau _1-1)}{A'_1(\tau _1)-1} \tau _1^{-n-1} + o_2(\tau _1^{-n-1})} = \frac{W_m + \frac{o_1(\tau _1^{-n-1})}{\tau _1^{-n-1}}}{\frac{(1-\lambda _1)\tau _1(\tau _1-1)}{A'_1(\tau _1)-1} + \frac{o_2(\tau _1^{-n-1})}{\tau _1^{-n-1}}} . \end{aligned}$$

(43)

Taking the limit for $n\rightarrow \infty$ in (43), and in view of the properties of the auxiliary functions $o_1$ and $o_2$, we then easily get

$$\begin{aligned} \lim _{n\rightarrow \infty }F_{m|n} = \frac{W_m}{\frac{(1-\lambda _1)\tau _1(\tau _1-1)}{A'_1(\tau _1)-1}} . \end{aligned}$$

(44)

Finally, restoring the full notations again, and using (36), we obtain the following exact result:

$$\begin{aligned} F_m(x_1,y_1, \ldots , x_m,y_m) \triangleq \lim _{n\rightarrow \infty } F_{m|n}(x_1,y_1, \ldots , x_m,y_m) = \prod _{\ell =1}^m A^*( x_\ell ,y_\ell ) . \end{aligned}$$

(45)

We note that the “asymptotic” conditional joint pgf $F_m$ has a similar product form as the unconditional joint pgf $B_m$, defined in (18), the only difference being that the unconditional joint pgf A(x, y) of the numbers of type-1 and type-2 arrivals in one slot has been replaced by the “asymptotic” conditional joint pgf $A^*(x,y)$, defined in (39).

4.3 The “asymptotic” system

In this paper, we basically study a system of two parallel single-server queues with 1-slot service times and independent arrivals from slot to slot, characterized by the joint pgf A(x, y), as defined in (1). Intuitively speaking, we have shown in the previous section that, conditional on the fact that the system content $u_1=n$ and n is large at the beginning of an arbitrary slot in the steady state, the arrivals into the two-queue system during the preceding slots are (approximately) independent from slot to slot, and distributed according to the joint pgf $A^*(x,y)$, as defined in (39); the approximation becomes exact when $n\rightarrow \infty$. Let us define the “asymptotic system” as the (conditional) “limit version” of the (original) system where the condition “$u_1 \rightarrow \infty$” is imposed. We have shown in the previous section that the asymptotic system is almost identical to the original system, the only difference being that the arrivals are characterized by the joint pgf $A^*(x,y)$ instead of A(x, y). We emphasize that the asymptotic system is not a new, different system than the original system; it is just a convenient short terminology to refer to the original system, whenever the latter is observed under the condition of $u_1$ approaching infinity.

In the asymptotic system, according to Eq. (39), the marginal pgfs of the numbers of arrivals (per slot) of type 1 and type 2 are given by

$$\begin{aligned} A_1^*(x) \triangleq A^*(x,1) = \frac{A(\tau _1 x,1)}{\tau _1} = \frac{A_1(\tau _1 x)}{\tau _1} \quad , \quad A_2^*(y) \triangleq A^*(1,y) = \frac{A(\tau _1,y)}{\tau _1}. \nonumber \\ \end{aligned}$$

(46)

The mean arrival rates (per slot) in queues 1 and 2 are

$$\begin{aligned} \lambda _1^* \triangleq A_1^{*'}(1) = A_1'(\tau _1) \quad , \quad \lambda _2^* \triangleq A_2^{*'}(1) = \frac{1}{\tau _1} \frac{\partial {A}}{\partial {y}}(\tau _1,1) . \end{aligned}$$

(47)

According to (14), $A_1'(\tau _1) > 1$, and we can thus conclude that

$$\begin{aligned} \lambda _1^* > 1 , \end{aligned}$$

(48)

i.e., in the asymptotic system, the arrival rate in queue 1 is strictly greater than 1. This matches perfectly with the defining condition of the asymptotic system: $u_1 \rightarrow \infty$, i.e., queue 1 builds up continuously in the asymptotic system. On the other hand, the stability of queue 2 in the asymptotic system depends on the value of $\lambda _2^*$. Specifically, in the asymptotic system, the second queue is stable if and only if

$$\begin{aligned} \lambda _2^* = \frac{1}{\tau _1} \frac{\partial {A}}{\partial {y}}(\tau _1,1)< 1 \,\Leftrightarrow \,\frac{\partial {A}}{\partial {y}}(\tau _1,1) < \tau _1 . \end{aligned}$$

The correct interpretation of these results deserves some discussion. Recall that we are studying the original two-queue system under the assumption that it has reached a steady state, globally speaking. To that end, we have assumed that both $\lambda _1$ and $\lambda _2$ are strictly smaller than 1, i.e., on average both queue 1 and queue 2 receive less than 1 customer per slot. However, this does not imply that the (conditional) mean arrival rate in either queue cannot be temporarily greater than 1. As far as queue 1 is concerned, according to (48), this is exactly what happens in the asymptotic system. We assume there that, at some moment in time, the system content $u_1$ is very large (theoretically: goes to infinity). Of course, this can only happen if the arrivals during (infinitely) many preceding slots have (on average) exceeded the service capacity of the queue. We emphasize that the probability of $u_1$ being very large may not be very high in a system that is globally stable, but yet the event is possible (as illustrated in equation (15)) and—in the asymptotic system—we study exactly this case. Our results reveal that, in the asymptotic system, i.e., the original system conditioned on the event that, at some time instant in the steady state, $u_1\rightarrow \infty$, the (conditional) mean arrival rate $\lambda _1^*$ in queue 1 (in the preceding slots) is indeed larger than 1, as could be expected. More interestingly, they also show that, if $u_1$ takes very large values, then queue 2 may be either stable or instable, depending on $\lambda _2^*$ being smaller or greater than 1.

The essential reason why the system content in queue 1 has an impact on the arrivals in queue 2 is, of course, that the arrival streams in both queues are possibly nonindependent (within a slot). It is therefore to be expected that, in the special case where the arrivals in queues 1 and 2 are strictly mutually independent, this phenomenon disappears. Indeed, assume that

$$\begin{aligned} A(x,y) = A_1(x) A_2(y) , \end{aligned}$$

then, according to (46) and (13),

$$\begin{aligned} A_2^*(y) = \frac{A(\tau _1,y)}{\tau _1} = \frac{A_1(\tau _1)A_2(y)}{\tau _1} = A_2(y) , \end{aligned}$$

i.e., the arrivals in queue 2 in the asymptotic system are identical to their counterparts in the original, unconditioned system.

4.4 Conditional system content in queue 2

We now take a closer look at the behavior of queue 2 in the asymptotic system. From our study of the conditional arrival process in Sect. 4.2, it follows that queue 2 behaves as a regular discrete-time single-server system with 1-slot service times, independent arrivals from slot to slot, and arrival pgf $A_2^*(y)$, as defined in Eq. (46). Queue 2 is stable if and only if $\lambda _2^*$, as defined in (48), is smaller than 1. If this is the case, then the steady-state pgf of the system content in queue 2, i.e., the pgf $U^*_2(z)$, defined in (17), exists and is given by a formula similar to the ones in Eq. (9), but with a modified arrival process:

$$\begin{aligned} U_2^*(z) = (1-\lambda _2^*)\frac{(z-1)A_2^*(z)}{z-A_2^*(z)} . \end{aligned}$$

(49)

Various (conditional) moments of $u_2$, given that $u_1 \rightarrow \infty$, can be easily computed from (49), in the usual way. For instance, the mean value can be obtained from

$$\begin{aligned} E\!\left[ u_2 | u_1 \rightarrow \infty \right] = U_2^{*'}(1) = \lambda _2^* + \frac{A_2^{*''}(1)}{2(1-\lambda _2^*)} . \end{aligned}$$

(50)

It is also possible to derive an accurate approximation for the (conditional) tail distribution of $u_2$, given that $u_1 \rightarrow \infty$, by using a dominant-pole approximation as summarized in the Eqs. (11) and (12), with X(z) replaced by $U_2^*(z)$, i.e., for large values of $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx \textrm{d}\sigma ^{-\ell -1} , \end{aligned}$$

(51)

where

$$\begin{aligned} d \triangleq -\lim _{z\rightarrow \sigma } (z-\sigma )U_2^*(z) , \end{aligned}$$

(52)

and where $\sigma$ denotes the dominant pole of $U_2^*(z)$, i.e., $\sigma$ is the smallest real positive solution, larger than 1, of the equation

$$\begin{aligned} \sigma = A_2^*(\sigma ) . \end{aligned}$$

(53)

The existence of a dominant pole $\sigma$ for the pgf $U_2^*(z)$ basically follows from the same kind of argument as the existence of the dominant pole $\tau _i$ of the pgf $U_i(z)$, as discussed in “Appendix A”, and the observation (in all the examples that we considered) that $A_2^*(z)$ is a well-behaved pgf if $A_2(z)$ is well-behaved.

5 Some specific examples

In this section, we explore some specific instances of the general two-queue model discussed in the previous sections. This amounts to considering specific choices for A(x, y).

5.1 Identical arrivals in both queues

Assume that the two queues receive exactly the same number of arrivals in each slot, i.e., for all values of the slot index k, $a_{1,k} = a_{2,k}$. In this case, A(x, y) can be expressed as a function of the product of its arguments x and y, i.e., $A(x,y) = B(xy)$, where B(z) is a well-behaved pgf with radius of convergence $\Omega >1$. The marginal arrival pgfs and mean values are

$$\begin{aligned} A_1(z) = A_2(z) = B(z) \quad , \quad \lambda _1 = \lambda _2 = B'(1) \triangleq \lambda <1 . \end{aligned}$$

It is very clear that, in the steady state (possibly after some finite transient period), the two queues contain exactly the same number of customers (at the beginning of each slot), and, consequently, the joint pgf $U(z_1,z_2)$ of the two system contents can also be expressed as a function of the product of its two arguments. Specifically,

$$\begin{aligned} U(z_1,z_2) = U_1(z_1 z_2) =U_2(z_1 z_2) = (1-\lambda )\frac{(z_1 z_2-1)B(z_1 z_2)}{z_1 z_2-B(z_1 z_2)} , \end{aligned}$$

where $U_1(\cdot )$ and $U_2(\cdot )$ are the known functions defined in (9). We note that, according to Bruneel [7], this is one of the few known cases in which a fully explicit analytic expression for the joint pgf $U(z_1,z_2)$ can be derived, which is, of course, due to the very specific and simple nature of the system.

From our formulas derived in Sect. 4, we easily find that the dominant poles $\tau _i$ (as defined in (13)) of the marginal system-content pgfs are $\tau _1=\tau _2 \triangleq \tau$, where $\tau$ is the only (real positive) solution of the equation $\tau = B(\tau ), 1< \tau < \Omega$, and from (14), we also know that $B'(\tau ) > 1$. According to (39), in the asymptotic system, the joint arrival pgf is given by

$$\begin{aligned} A^*(x,y) = \frac{A(\tau x,y)}{\tau } = \frac{B(\tau xy)}{\tau } , \end{aligned}$$

which is also a function of the product $x\cdot y$. It then easily follows that the marginal arrival pgfs and mean values in the asymptotic system are

$$\begin{aligned} A_1^*(z) = A^*(z,1) = A_2^*(z) = A^*(1,z) = \frac{B(\tau z)}{\tau } \quad , \quad \lambda _1^* = \lambda _2^* = B'(\tau ) . \end{aligned}$$

(54)

As expected, we find that $\lambda _1^* > 1$, signifying that, in the (conditional) asymptotic system, queue 1 is unstable, in accordance with its defining condition $u_1 \rightarrow \infty$. However, since in this particular case, $\lambda _1^* = \lambda _2^*$, we find that queue 2 is unstable too, i.e., if $u_1 \rightarrow \infty$ then also $u_2 \rightarrow \infty$, which is in complete agreement with the fact that the system contents in both queues, at the beginning of any slot in the steady state, are identical. In conclusion, our methodology clearly reveals that, in the case of identical arrivals in both queues, a steady-state pgf $U_2^*(z)$, as defined in (49), does not exist.

5.2 One global arrival stream probabilistically routed to both queues

In our model, the total number of arrivals into the system (i.e., both queues together) during slot k is given by $c_k = a_{1,k} + a_{2,k}$. It is easily seen that the $c_k$s also form a sequence of i.i.d. nonnegative discrete random variables with common pgf $C(z) \triangleq A(z,z)$. We call C(z) the “pgf of the global arrival stream”. In this subsection, we assume that a global arrival stream of customers with corresponding pgf C(z) presents itself at the entrance of our two-queue system. Consecutive customers are then routed probabilistically, i.e., independently from customer to customer, and with fixed probabilities, to queue 1 or queue 2, respectively. Let $\alpha$ and $1-\alpha$ denote the probabilities that an arriving customer is routed to queue 1 or queue 2, respectively. Figure 3 represents this setting graphically.

Fig. 3

A global arrival stream with pgf C(z) is split probabilistically into two substreams with pgfs $A_1(x)$ and $A_2(y)$, where $\alpha$ and $1-\alpha$ indicate the fractions of customers routed to queues 1 and 2, respectively

It is readily seen that, in this situation, the joint arrival pgf A(x, y) and the marginal arrival pgfs $A_1(x)$ and $A_2(y)$ are given by

$$\begin{aligned}{} & {} A(x,y) = C(\alpha x + (1-\alpha ) y), \quad A_1(x) = C(1-\alpha + \alpha x), \nonumber \\{} & {} A_2(y) = C(\alpha + (1-\alpha ) y) . \end{aligned}$$

(55)

Let $\mu$ indicate the total mean arrival rate, i.e., $\mu \triangleq C'(1)$. Then, the mean arrival rates in the individual queues (see (3)) are

$$\begin{aligned} \lambda _1 = \mu \alpha \quad , \quad \lambda _2 = \mu (1-\alpha ) , \end{aligned}$$

(56)

and, of course, $\lambda _1 + \lambda _2 = \mu$. The two-queue system is stable if and only if $\lambda _1<1$ and $\lambda _2<1$ (see (4)), or, in this setting, if and only if

$$\begin{aligned} \mu< \min \bigg (\frac{1}{\alpha }, \frac{1}{1-\alpha }\bigg ) \quad \text { or } \quad \max \bigg (0,\frac{\mu -1}{\mu }\bigg )< \alpha < \min \bigg (1,\frac{1}{\mu }\bigg ) . \end{aligned}$$

(57)

Note that this implies $\mu < 2$.

It is not possible to obtain more detailed results on the behavior of the asymptotic system for general C(z). In the following subsections, we therefore consider some specific choices for C(z).

5.2.1 Global geometric arrivals

Assume a geometric distribution with mean $\mu$ for the global arrival stream, i.e.,

$$\begin{aligned} C(z) = \frac{1}{1+\mu - \mu z} \quad , \quad C'(1) = \mu \ge 0 . \end{aligned}$$

The joint and marginal arrival pgfs A(x, y), $A_1(x)$ and $A_2(y)$ can be obtained from (55) as

$$\begin{aligned}{} & {} A(x,y) = \frac{1}{1+\lambda _1+\lambda _2 - \lambda _1 x - \lambda _2 y} , A_1(x) = \frac{1}{1+\lambda _1 - \lambda _1 x} , \nonumber \\{} & {} A_2(y) = \frac{1}{1+\lambda _2 - \lambda _2 y} . \end{aligned}$$

(58)

Note the remarkable property that the marginal arrival distributions in queues 1 and 2 are also geometric, with means $\lambda _1=\mu \alpha$ and $\lambda _2=\mu (1-\alpha )$, respectively. The marginal pgf and mean value of the system content in queue i can be found from (9) and (10) as

$$\begin{aligned} U_i(z) = \frac{1-\lambda _i}{1-\lambda _iz} , \quad E\!\left[ u_i\right] = \frac{\lambda _i}{1-\lambda _i} . \end{aligned}$$

(59)

We thus observe that the system content in queue i is also geometrically distributed, notably with parameter $\lambda _i$. The corresponding pmf is well-known:

$$\begin{aligned} \textrm{Prob}\!\left[ u_i=n\right] = (1-\lambda _i)\lambda _i^n , \quad n \ge 0 \hspace{5.0pt}. \end{aligned}$$

(60)

The dominant pole $\tau _i$ is the (only) zero of the denominator of $U_i(z)$, as given in (59):

$$\begin{aligned} \tau _1 = \frac{1}{\lambda _1} = \frac{1}{\mu \alpha }> 1, \quad \tau _2 = \frac{1}{\lambda _2} = \frac{1}{\mu (1-\alpha )} > 1 . \end{aligned}$$

(61)

According to (46), (58), the marginal arrival pgfs and mean values in the asymptotic system are

$$\begin{aligned} A_1^*(x) = \frac{\lambda _1}{1+\lambda _1 - x} = \frac{1}{1+\lambda _1^* - \lambda _1^* x}, \quad \lambda _1^* = \frac{1}{\lambda _1} \end{aligned}$$

(62)

and

$$\begin{aligned} A_2^*(y) = \frac{\lambda _1}{\lambda _1 + \lambda _2 - \lambda _2 y} = \frac{1}{1+\lambda _2^* - \lambda _2^* y} , \quad \lambda _2^* = \frac{\lambda _2}{\lambda _1} = \frac{1-\alpha }{\alpha } . \end{aligned}$$

(63)

Some first conclusions can be drawn from these results. In the asymptotic system, the marginal arrival distributions are geometric, just as in the original system, but the mean arrival rates are $\lambda _1^*$ and $\lambda _2^*$ instead of $\lambda _1$ and $\lambda _2$. From (62), we learn that $\lambda _1^*$ is strictly greater than one, because it is the inverse of $\lambda _1 <1$, which again illustrates the instability of queue 1 in the asymptotic system. On the other hand, (63) shows that the stability of queue 2 in the asymptotic system is determined solely by the value of the routing probability $\alpha$, or, equivalently, the ratio of $\lambda _1$ and $\lambda _2$. Queue 2 is stable if and only if

$$\begin{aligned} \lambda _2^*< 1 \,\Leftrightarrow \,\lambda _2 < \lambda _1 \,\Leftrightarrow \,\alpha > \frac{1}{2} . \end{aligned}$$

(64)

This result is intuitively appealing: in order for queue 2 to be stable when queue 1 goes into saturation (i.e., $u_1\rightarrow \infty$), it should receive less customers per slot than queue 1. Moreover, the (conditional) arrival process in queue 2 does not depend on the total arrival rate $\mu$ of the original system, but is fully determined by the value of $\alpha$, a most intriguing result.

Now let us assume that $\lambda _2 < \lambda _1$. Then, in the asymptotic system, queue 2 behaves as a stable single-server queue with 1-slot service times and geometric arrivals with mean $\lambda _2^*$, implying that the pgf and the mean value of the queue-2 system content exist and are given by

$$\begin{aligned}{} & {} U_2^*(z) = \frac{1-\lambda _2^*}{1-\lambda _2^* z} = \frac{\lambda _1-\lambda _2}{\lambda _1 - \lambda _2 z} = \frac{2\alpha -1}{\alpha - (1-\alpha ) z}, \nonumber \\{} & {} E\!\left[ u_2|u_1\rightarrow \infty \right] = \frac{\lambda _2^*}{1-\lambda _2^*} = \frac{1-\alpha }{2\alpha -1} . \end{aligned}$$

(65)

The dominant pole $\sigma$ of $U_2^*(z)$, as defined in (53), is the (only) zero of its denominator, i.e.,

$$\begin{aligned} \sigma = \frac{1}{\lambda _2^*} = \frac{\lambda _1}{\lambda _2} = \frac{\alpha }{1-\alpha } > 1 . \end{aligned}$$

(66)

As discussed in Sect. 4.4, the (conditional) tail distribution of $u_2$, given that $u_1 \rightarrow \infty$, can be well approximated by using the dominant-pole technique, i.e., for large $\ell$,

$$\begin{aligned}&\textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx d\sigma ^{-\ell -1} , \text { where } d \triangleq -\lim _{z\rightarrow \sigma } (z-\sigma )\nonumber \\&U_2^*(z) = \frac{1-\lambda _2^*}{\lambda _2^*} = \frac{2\alpha - 1}{1-\alpha } . \end{aligned}$$

(67)

Hence, combining (66) and (67), we get, for large $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx (1- \lambda _2^*)(\lambda _2^*)^\ell = \frac{2\alpha - 1}{\alpha } \bigg ( \frac{1-\alpha }{\alpha } \bigg )^{\ell } \hspace{5.0pt}. \end{aligned}$$

(68)

The joint pmf of $(u_1,u_2)$ can be expressed, in general, as

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] = \textrm{Prob}\!\left[ u_1=n\right] \textrm{Prob}\!\left[ u_2=\ell | u_1=n\right] . \end{aligned}$$

(69)

Here the first factor is given by the exact formula (60), valid for any n, and the second factor can be well approximated by the dominant-pole form (68), valid for large n and $\ell$. As a result, we obtain a closed-form approximation for the joint tail distribution of $(u_1,u_2)$, i.e., for large values of both n and $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] \approx \frac{(2\alpha - 1)(1-\mu \alpha )}{\alpha } (\mu \alpha )^n \bigg ( \frac{1-\alpha }{\alpha } \bigg )^{\ell } , \text { if } \quad \alpha >\frac{1}{2} . \end{aligned}$$

(70)

The high accuracy of formula (70) for large n (say $n \ge 10$), is illustrated by one specific example, in Fig. 4, where a comparison is made with simulation results. Note that we did not even select high values of $\ell$ here. We obtained a similar accuracy when keeping n fixed and varying $\ell$. Producing simulation results for high n and $\ell$ at the same time, is extremely time-consuming, since it concerns very rare events; evaluating the closed formula (70), on the contrary, requires virtually no time at all.

Fig. 4

Dominant-pole approximation (70) for $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$ versus simulation results, for fixed $\ell =1,2,3,4$ and $\alpha =0.7$ and $\mu =1$

An additional result can be obtained by exploiting the symmetry of our model. Indeed, we can interchange the roles of queue 1 and queue 2, in the sense that we define the asymptotic system by the condition “$u_2 \rightarrow \infty$” instead of “$u_1 \rightarrow \infty$”, and then study the behavior of queue 1 under this condition. This implies that the roles of the routing probabilities $\alpha$ and $1-\alpha$ must also be interchanged. As a result, we find,

$$\begin{aligned}{} & {} \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] \approx \frac{(1-2\alpha )[1-\mu (1-\alpha )]}{1-\alpha } \bigg ( \frac{\alpha }{1-\alpha } \bigg )^n [\mu (1-\alpha )]^\ell ,\nonumber \\{} & {} \qquad \text { if } \quad \alpha <\frac{1}{2} . \end{aligned}$$

(71)

We note that, to the best of our knowledge, a fully explicit analytic expression for the whole joint pgf $U(z_1,z_2)$ has never been derived for the specific joint arrival distribution considered here, i.e., for the joint arrival pgf A(x, y) defined in Eq. (58). We strongly suspect that the fact that the approximative expressions (70) and (71) for the joint tail distribution of $(u_1,u_2)$ are profoundly different depending on the routing probability $\alpha$ being greater or smaller than $\frac{1}{2}$ implies that such an analytic expression of $U(z_1,z_2)$, valid for all possible values of $\alpha$, may not exist. We also note that, if $\alpha$ is exactly equal to $\frac{1}{2}$, then queue 2 is unstable when $u_1\rightarrow \infty$ and queue 1 is unstable when $u_2\rightarrow \infty$, and we cannot find a joint tail approximation at all.

5.2.2 Global shifted geometric arrivals

Assume a shifted geometric distribution with mean $\mu \ge 1$ for the global arrival stream, i.e.,

$$\begin{aligned} C(z) = \frac{z}{\mu - (\mu -1)z} , \quad C'(1) = \mu \ge 1 . \end{aligned}$$

The joint and marginal arrival pgfs A(x, y), $A_1(x)$ and $A_2(y)$ can be obtained from (55) as

$$\begin{aligned} A(x,y) = \frac{\alpha x + (1-\alpha ) y}{\mu -(\mu -1)\alpha x -(\mu -1)(1-\alpha ) y} , \end{aligned}$$

(72)

$$\begin{aligned} A_1(x) = \frac{1-\alpha + \alpha x}{1+(\mu -1)\alpha (1-x)} , \quad A_2(y) = \frac{\alpha +(1-\alpha )y}{1+(\mu -1)(1-\alpha )(1-y)} \hspace{5.0pt}. \end{aligned}$$

The marginal pgfs of the system contents in queues 1 and 2 can be found from (9) as

$$\begin{aligned} U_1(z) = \frac{(1-\mu \alpha )(1-\alpha + \alpha z)}{1-\alpha -(\mu -1)\alpha z} , \quad U_2(z) = \frac{[1-\mu (1-\alpha )][\alpha + (1-\alpha )z]}{\alpha -(\mu -1)(1-\alpha )z} .\qquad \end{aligned}$$

(73)

The mean system content $E\!\left[ u_2\right] = U_2'(1)$ follows from (73) as

$$\begin{aligned} E\!\left[ u_2\right] = \frac{\mu \alpha (1-\alpha )}{1-\mu (1-\alpha )} = \frac{\lambda _1\lambda _2}{\mu (1-\lambda _2)} . \end{aligned}$$

(74)

The dominant pole $\tau _i$ is the (only) zero of the denominator of $U_i(z)$; from (73) we get

$$\begin{aligned} \tau _1 = \frac{1-\alpha }{(\mu -1)\alpha }> 1 , \quad \tau _2 = \frac{\alpha }{(\mu -1)(1-\alpha )} > 1 . \end{aligned}$$

(75)

According to (46), the marginal arrival pgfs in the asymptotic system are

$$\begin{aligned} A_1^*(x) = \frac{\mu \alpha + \alpha (x-1)}{\mu \alpha - (1-\alpha )(x-1)} , \quad A_2^*(y) = \frac{\alpha [1+(\mu - 1)y]}{\mu - (1-\alpha )[1+(\mu - 1)y]} . \end{aligned}$$

(76)

The corresponding mean arrival rates (per slot) in queues 1 and 2 are

$$\begin{aligned} \lambda _1^* \triangleq A_1^{*'}(1) = \frac{1}{\mu \alpha } = \frac{1}{\lambda _1} , \quad \lambda _2^* \triangleq A_2^{*'}(1) = \frac{\mu - 1}{\mu \alpha } = \frac{\mu -1}{\lambda _1} . \end{aligned}$$

(77)

Again, just as in the case of (unshifted) geometric arrivals, it is clear that $\lambda _1^*$ is strictly greater than one, because it is the inverse of $\lambda _1 <1$, reflecting the instability of queue 1 in the asymptotic system. On the other hand, in this case, $\lambda _2^*$ turns out to be always strictly smaller than one, regardless of the value of the routing probability $\alpha$. This follows easily from the stability condition (57). This means that queue 2 is always stable when $u_1\rightarrow \infty$, in this case. Hence, the asymptotic pgf and mean value of the system content in queue 2 always exist and can be found from (49), (76), (77) and (50):

$$\begin{aligned} U_2^*(z)= & {} \frac{[1-\mu (1-\alpha )][1+(\mu -1)z]}{\mu [\alpha - (\mu -1)(1-\alpha )z]} , \quad \nonumber \\ E\!\left[ u_2|u_1\rightarrow \infty \right]= & {} \frac{\mu -1}{\mu [1-\mu (1-\alpha )]} = \frac{\mu -1}{\mu (1-\lambda _2)} . \end{aligned}$$

(78)

It is remarkable that $U_2(z)$ and $U_2^*(z)$ have the same denominator (upon a multiplicative constant). The dominant pole $\sigma$ of $U_2^*(z)$ is therefore equal to $\tau _2$, i.e.,

$$\begin{aligned} \sigma = \frac{\alpha }{(\mu -1)(1-\alpha )} = \tau _2 . \end{aligned}$$

(79)

As discussed in Sect. 4.4, the (conditional) tail distribution of $u_2$, given that $u_1 \rightarrow \infty$, can be well approximated, for large values of $\ell$, as

$$\begin{aligned}&\textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx d\sigma ^{-\ell -1} , \text { where } d \triangleq -\lim _{z\rightarrow \sigma } (z-\sigma )\nonumber \\&\quad U_2^*(z) = \frac{1-\mu (1-\alpha )}{\mu (\mu -1)(1-\alpha )^2} . \end{aligned}$$

(80)

Hence, combining (79) and (80), we get

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx \frac{1-\mu (1-\alpha )}{\mu \alpha (1-\alpha )} \bigg ( \frac{(\mu -1)(1-\alpha )}{\alpha } \bigg )^{\ell } . \end{aligned}$$

(81)

Again, this can be combined with a tail approximation for the system-content distribution in queue 1, as per Eqs. (15) and (16), i.e., for large values of n,

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n\right] \approx c_1\tau _1^{-n-1} = c_1 \bigg (\frac{(\mu -1)\alpha }{1-\alpha }\bigg )^{n+1} \hspace{5.0pt}, \end{aligned}$$

(82)

where

$$\begin{aligned} c_1= \frac{(1-\lambda _1)(\tau _1-1)\tau _1}{A'_1(\tau _1)-1} = \lambda _1\tau _1(\tau _1-1) = \frac{\mu (1-\alpha )(1-\mu \alpha )}{(\mu -1)^2 \alpha } . \end{aligned}$$

(83)

Hence

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n\right] \approx \frac{\mu (1-\mu \alpha )}{\mu -1} \bigg (\frac{(\mu -1)\alpha }{1-\alpha }\bigg )^n . \end{aligned}$$

(84)

Combining (81) and (84), we find that, for large values of both n and $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] \approx \frac{(1-\mu \alpha )[1-\mu (1-\alpha )]}{(\mu -1)\alpha (1-\alpha )} \bigg (\frac{(\mu -1)\alpha }{1-\alpha }\bigg )^n \bigg ( \frac{(\mu -1)(1-\alpha )}{\alpha } \bigg )^{\ell } \hspace{5.0pt}. \nonumber \\ \end{aligned}$$

(85)

We note that, in this case, we have found an approximation which is valid for all values of the parameter $\alpha$. Moreover, formula (85) is invariant to the substitutions $\alpha \leftrightarrow 1-\alpha , n \leftrightarrow \ell$. In part, this is due to the remarkable property that the dominant poles $\sigma$ and $\tau _2$ are identical here, i.e., the decay rate of the tail distribution of $u_2$ is not influenced by $u_1$, and vice versa. The case of global shifted geometric arrivals is also one of the very few instances of our model where an explicit analytic expression for the whole joint pgf $U(z_1,z_2)$ of the two system contents can be found, as opposed, for instance, to the seemingly very similar case of (unshifted) geometric arrivals, where no solution has been reported so far. Indeed, using an adapted version of a technique briefly discussed in Bruneel [7], we have been able to derive such an expression. The details of this derivation—which is interesting in its own right—are discussed in “Appendix B”; here we merely state the final result:

$$\begin{aligned} U(z_1,z_2) = \frac{(\tau _1 -1)(\tau _2 -1)[\alpha z_1 + (1-\alpha )z_2]}{(\tau _1 -z_1)(\tau _2 -z_2)} , \end{aligned}$$

(86)

where $\tau _1$ and $\tau _2$ are the dominant poles of $U_1(z)$ and $U_2(z)$, respectively, given in (75). Note that, apparently, $\tau _1$ and $\tau _2$ are also the only singularities of the joint pgf $U(z_1,z_2)$.

Having an explicit expression for $U(z_1,z_2)$ at our disposal, gives a unique opportunity to check the correctness of the asymptotic results obtained through the methodology developed in this paper. First, consider the series expansion of $U(z_1,z_2)$ in powers of $z_1$, for given $z_2$:

$$\begin{aligned} U(z_1,z_2) = \sum _{n=0}^\infty z_1^n S_n(z_2) , \quad \text {where} \quad S_n(z_2) \triangleq \sum _{\ell =0}^\infty z_2^\ell \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] . \end{aligned}$$

If we consider $U(z_1,z_2)$ as a function of the variable $z_1$, then (86) shows that $U(z_1,z_2)$ has a single dominant pole at $z_1=\tau _1$, and hence, for large n, $S_n(z_2)$ can be well approximated as

$$\begin{aligned} S_n(z_2) \approx c_S(z_2) \tau _1^{-n-1} , \end{aligned}$$

(87)

where $c_S(z_2)$ is given by

$$\begin{aligned} c_S(z_2) \triangleq -\lim _{z_1\rightarrow \tau _1} (z_1-\tau _1)U(z_1,z_2) = \frac{(\tau _1-1)(\tau _2-1)[\alpha \tau _1+(1-\alpha )z_2]}{\tau _2-z_2} \hspace{5.0pt}.\qquad \end{aligned}$$

(88)

The conditional marginal pgf of the system content in queue 2, given that $u_1=n$, can be derived from this through

$$\begin{aligned} U_2^*(z|n){} & {} = \sum _{\ell =0}^\infty z^\ell \textrm{Prob}\!\left[ u_2=\ell |u_1=n\right] = \sum _{\ell =0}^\infty z^\ell \frac{\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] }{\textrm{Prob}\!\left[ u_1=n\right] } \\{} & {} = \frac{S_n(z)}{\textrm{Prob}\!\left[ u_1=n\right] } . \end{aligned}$$

For large n, according to (87), (83), (82) and (88), this can be well approximated by

$$\begin{aligned} U_2^*(z) = \frac{c_S(z)}{c_1} = \frac{(\tau _2-1)[\alpha \tau _1+(1-\alpha )z_2]}{\lambda _1\tau _1(\tau _2-z)}= \frac{[1-\mu (1-\alpha )][1+(\mu -1)z]}{\mu [\alpha - (\mu -1)(1-\alpha )z]} . \end{aligned}$$

This is exactly the same expression as we obtained earlier in Eq. (78).

Next, we can also invert the known pgf $U(z_1,z_2)$ completely, i.e., compute the joint probabilities $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$ such that

$$\begin{aligned} U(z_1,z_2) = \sum _{n=0}^\infty \sum _{\ell =0}^\infty z_1^n z_2^\ell \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] . \end{aligned}$$

(89)

Departing from expression (86), we easily get

$$\begin{aligned} \begin{aligned} U(z_1,z_2)&= [\alpha z_1 + (1-\alpha )z_2] \frac{1-\frac{1}{\tau _1}}{1-\frac{z_1}{\tau _1}} \frac{1-\frac{1}{\tau _2}}{1-\frac{z_2}{\tau _2}} \\&= [\alpha z_1 + (1-\alpha )z_2] (1-\frac{1}{\tau _1}) (1-\frac{1}{\tau _2}) \sum _{i=0}^\infty \sum _{j=0}^\infty \tau _1^{-i} \tau _2^{-j} z_1^i z_2^j \\&= \frac{(\tau _1-1)(\tau _2-1)}{\tau _1\tau _2} \bigg ( \sum _{i=0}^\infty \sum _{j=0}^\infty \alpha \tau _1^{-i} \tau _2^{-j} z_1^{i+1} z_2^j + \sum _{i=0}^\infty \sum _{j=0}^\infty (1-\alpha )\tau _1^{-i} \tau _2^{-j} z_1^i z_2^{j+1} \bigg ) \hspace{5.0pt}. \end{aligned} \end{aligned}$$

(90)

Identifying equal powers of $z_1$ and $z_2$ in (89) and (90), we can compute $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$ explicitly, for any $n,\ell \ge 0$. It is not difficult to see that this leads precisely to expression (85), as soon as $n \ge 1, \ell \ge 1$, which illustrates, once again, the accuracy, and, in this case even the exact nature of the asymptotic dominant-pole results derived via the methodology developed in this paper.

5.2.3 Global binomial arrivals of order two

Assume a binomial distribution of order two with mean $\mu$ for the global arrival stream, i.e.,

$$\begin{aligned} C(z) = \bigg (1-\frac{\mu }{2}+\frac{\mu }{2}z\bigg )^2 , \quad C'(1) = \mu . \end{aligned}$$

The mean arrival rates are $\lambda _1=\mu \alpha$ and $\lambda _2=\mu (1-\alpha )$ (see (56)) and the joint and marginal arrival pgfs can be expressed in terms of these as (see (55))

$$\begin{aligned} A(x,y)= & {} \bigg (1-\frac{\lambda _1}{2}-\frac{\lambda _2}{2}+\frac{\lambda _1}{2} x + \frac{\lambda _2}{2}y\bigg )^2 , A_1(x) = \bigg (1-\frac{\lambda _1}{2} + \frac{\lambda _1}{2} x \bigg )^2 , \nonumber \\ A_2(y)= & {} \bigg (1-\frac{\lambda _2}{2} + \frac{\lambda _2}{2} y \bigg )^2 . \end{aligned}$$

(91)

Here, again, we observe the remarkable property that the marginal arrival processes in queues 1 and 2 are also binomial of order two, with means $\lambda _1$ and $\lambda _2$, respectively. The marginal pgf and mean value of the system content in queue i are (see(9))

$$\begin{aligned} U_i(z) = \frac{4(1-\lambda _i)A_i(z)}{(2-\lambda _i)^2 - (\lambda _i)^2 z} , E\!\left[ u_i\right] = U_i'(1) = \frac{\lambda _i(4- 3\lambda _i)}{4(1-\lambda _i)} . \end{aligned}$$

(92)

The dominant pole $\tau _i$ is the (only) zero of the denominator of $U_i(z)$; from (92), we get

$$\begin{aligned} \tau _i = \bigg ( \frac{2-\lambda _i}{\lambda _i} \bigg )^2 \end{aligned}$$

(93)

According to (46), the marginal arrival pgfs and mean arrival rates in the asymptotic system are

$$\begin{aligned} A_1^*(x) = \frac{\big (1-\frac{\lambda _1}{2}+ \frac{\lambda _1}{2}\tau _1 x\big )^2}{\tau _1} = \bigg (1-\frac{\lambda _1^*}{2} + \frac{\lambda _1^*}{2} x \bigg )^2 , \quad \lambda _1^* = 2 - \lambda _1 > 1 , \\ \end{aligned}$$

$$\begin{aligned} \begin{aligned} A_2^*(y) = \frac{\big (1-\frac{\lambda _1}{2}-\frac{\lambda _2}{2}+\frac{\lambda _1\tau _1}{2} + \frac{\lambda _2}{2}y\big )^2}{\tau _1} = \bigg ( 1-\frac{\lambda _2^*}{2} + \frac{\lambda _2^*}{2} y \bigg )^2 , \quad \lambda _2^* = \frac{\lambda _1\lambda _2}{2-\lambda _1} < 1 . \end{aligned} \end{aligned}$$

(94)

Some conclusions can be drawn from these expressions. First, we observe that the two marginal arrival streams in the asymptotic system are also of type “binomial of order two”, but with different mean arrival rates, i.e., $\lambda _i^*$ instead of $\lambda _i$. Again, as expected, it is clear that $\lambda _1^*$ is strictly greater than one, because $\lambda _1 <1$. And, just as in the case of global shifted geometric arrivals, $\lambda _2^*$ turns out to be always strictly smaller than one, regardless of the value of the routing probability $\alpha$, because $\lambda _1 <1$ and $\lambda _2 <1$. So, queue 2 is always stable when $u_1\rightarrow \infty$. Hence, the asymptotic marginal pgf and mean value of the system content in queue 2 always exist. Exploiting the formal resemblance between $A_2^*(y)$ and $A_2(y)$, we easily find similar expressions as in the unconditional case (see (92)):

$$\begin{aligned} U_2^*(z) = \frac{4(1-\lambda _2^*)A_2^*(z)}{(2-\lambda _2^*)^2 - (\lambda _2^*)^2 z} , \quad E\!\left[ u_2|u_1\rightarrow \infty \right] = \frac{\lambda _2^*(4-3\lambda _2^*)}{4(1-\lambda _2^*)} . \end{aligned}$$

(95)

The dominant pole $\sigma$ of $U_2^*(z)$ is the (only) zero of its denominator, i.e.,

$$\begin{aligned} \sigma = \bigg ( \frac{2-\lambda _2^*}{\lambda _2^*} \bigg )^2 > 1 , \end{aligned}$$

(96)

i.e., a similar formula as for $\tau _i$ in (93). As before, the (conditional) tail distribution of $u_2$, given that $u_1 \rightarrow \infty$, can be well approximated by using the dominant-pole technique, i.e., for large $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx d\sigma ^{-\ell -1} , \end{aligned}$$

(97)

where

$$\begin{aligned} d \triangleq -\lim _{z\rightarrow \sigma } (z-\sigma )U_2^*(z) = \frac{4(1-\lambda _2^*)A_2^*(\sigma )}{(\lambda _2^*)^2} = \frac{4(1-\lambda _2^*)\sigma }{(\lambda _2^*)^2} . \end{aligned}$$

(98)

Hence, combining (96), (97) and (98), we get, for large $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx \frac{4(1-\lambda _2^*)}{(\lambda _2^*)^2} \bigg ( \frac{1}{\sigma } \bigg )^\ell = \frac{4(1-\lambda _2^*)}{(\lambda _2^*)^2} \bigg ( \frac{\lambda _2^*}{2-\lambda _2^*} \bigg )^{2\ell } . \end{aligned}$$

(99)

Again, this can be combined with a tail approximation for the system-content distribution in queue 1, as per Eqs. (15) and (16), i.e., for large values of n,

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n\right] \approx c_1\tau _1^{-n-1} , \text { where } c_1 \triangleq -\lim _{z\rightarrow \tau _1} (z-\tau _1)U_1(z) = \frac{4(1-\lambda _1)\tau _1}{(\lambda _1)^2} , \end{aligned}$$

so that

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n\right] \approx \frac{4(1-\lambda _1)}{(\lambda _1)^2} \bigg ( \frac{1}{\tau _1} \bigg )^n = \frac{4(1-\lambda _1)}{(\lambda _1)^2} \bigg ( \frac{\lambda _1}{2-\lambda _1} \bigg )^{2n} . \end{aligned}$$

(100)

Combining (99) and (100), we find that, for large values of both n and $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_1=n,u_2=\ell \right] \approx u_1(n,\ell ) \triangleq \frac{16(1-\lambda _1)(1-\lambda _2^*)}{(\lambda _1)^2(\lambda _2^*)^2} \bigg ( \frac{\lambda _1}{2-\lambda _1} \bigg )^{2n} \bigg ( \frac{\lambda _2^*}{2-\lambda _2^*} \bigg )^{2\ell } . \end{aligned}$$

(101)

In terms of the original parameters $\mu$ and $\alpha$ of our model, $u_1(n,\ell )$ can be expressed as

$$\begin{aligned} u_1(n,\ell )= & {} \frac{16(2-\mu \alpha )(1-\mu \alpha )[2-\mu \alpha -\mu ^2\alpha (1-\alpha )]}{\mu ^6\alpha ^4(1-\alpha )^2} \cdot \bigg ( \frac{\mu \alpha }{2-\mu \alpha } \bigg )^{2n} \nonumber \\{} & {} \quad \bigg ( \frac{\mu ^2\alpha (1-\alpha )}{4-2\mu \alpha -\mu ^2 \alpha (1-\alpha )} \bigg )^{2\ell } . \end{aligned}$$

(102)

Interchanging the roles of queues 1 and 2, we can similarly obtain a dual approximation:

$$\begin{aligned} u_2(n,\ell )\triangleq & {} \frac{16[2-\mu (1-\alpha )][1-\mu (1-\alpha )][2-\mu (1-\alpha )-\mu ^2\alpha (1-\alpha )]}{\mu ^6(1-\alpha )^4 \alpha ^2}\nonumber \\{} & {} \cdot \bigg ( \frac{\mu ^2\alpha (1-\alpha )}{4-2\mu (1-\alpha )-\mu ^2 \alpha (1-\alpha )} \bigg )^{2n} \bigg ( \frac{\mu (1-\alpha )}{2-\mu (1-\alpha )} \bigg )^{2\ell } . \end{aligned}$$

(103)

It may seem surprising that expressions (102) and (103) are not identical, i.e., are not invariant to the substitutions $\alpha \leftrightarrow 1-\alpha , n \leftrightarrow \ell$. In order to clarify this observation, let us consider the special case $\alpha =\frac{1}{2}$. Our model then reduces to the well-known model of the “(symmetric) clocked buffered switch”, that has been analyzed by various authors in the past (Jaffe [22, 23], Boxma and van Houtum [6], Cohen [10], Adan et al. [1]), by using various kinds of techniques. For $\alpha =\frac{1}{2}$, we get the following results for the dominant poles $\tau _1$, $\tau _2$ and $\sigma$:

$$\begin{aligned} \tau _1 = \tau _2 = \bigg ( \frac{4-\mu }{\mu } \bigg )^2 , \quad \sigma = \bigg ( \frac{16-4\mu -\mu ^2}{\mu ^2} \bigg )^2 . \end{aligned}$$

The joint tail approximations $u_1(n,\ell )$ and $u_2(n,\ell )$, given in (102) and (103), reduce to

$$\begin{aligned} u_1(n,\ell )= & {} \frac{64(2-\mu )^2(16-\mu ^2)}{\mu ^6} \tau _1^{-n} \sigma ^{-\ell } \\= & {} \frac{64(2-\mu )^2(16-\mu ^2)}{\mu ^6} \bigg ( \frac{\mu }{4-\mu } \bigg )^{2n} \bigg ( \frac{\mu ^2}{16-4\mu -\mu ^2} \bigg )^{2\ell } , \\ u_2(n,\ell )= & {} \frac{64(2-\mu )^2(16-\mu ^2)}{\mu ^6} \sigma ^{-n} \tau _2^{-\ell } \\= & {} \frac{64(2-\mu )^2(16-\mu ^2)}{\mu ^6} \bigg ( \frac{\mu ^2}{16-4\mu -\mu ^2} \bigg )^{2n} \bigg ( \frac{\mu }{4-\mu } \bigg )^{2\ell } . \end{aligned}$$

Jaffe [22, 23] also provides an approximative expression for the joint tail distribution of the two “queue contents” $(q_1,q_2)$, where the queue content $q_i$ in queue i is defined as the number of customers in queue i, excluding the customer in service, if any. It is clear that the “queue content” $q_i$ is related to the “system content” $u_i$ in queue i (as we use in this paper) by the simple equation $q_i=(u_i-1)^+$, and, therefore, for large values of n and $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ q_1=n,q_2=\ell \right] = \textrm{Prob}\!\left[ u_1=n+1,u_2=\ell +1\right] . \end{aligned}$$

Our two tail approximations $u_1(n,\ell )$ and $u_2(n,\ell )$ for $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$ can thus be translated to two corresponding tail approximations $q_1(n,\ell )$ and $q_2(n,\ell )$ for $\textrm{Prob}\!\left[ q_1=n,q_2=\ell \right]$ as follows:

$$\begin{aligned} q_1(n,\ell ) \triangleq u_1(n+1,\ell +1) = \frac{64(2-\mu )^2(16-\mu ^2)}{(4-\mu )^2(16-4\mu -\mu ^2)^2} \bigg ( \frac{\mu }{4-\mu } \bigg )^{2n} \bigg ( \frac{\mu ^2}{16-4\mu -\mu ^2} \bigg )^{2\ell } ,\nonumber \\ \end{aligned}$$

(104)

$$\begin{aligned} q_2(n,\ell ) \triangleq u_2(n+1,\ell +1) = \frac{64(2-\mu )^2(16-\mu ^2)}{(4-\mu )^2(16-4\mu -\mu ^2)^2} \bigg ( \frac{\mu ^2}{16-4\mu -\mu ^2} \bigg )^{2n} \bigg ( \frac{\mu }{4-\mu } \bigg )^{2\ell } . \end{aligned}$$

We illustrate the accuracy of formula (104) for large n (say $n \ge 10$) by one specific example, in Fig. 5, where a comparison is made with simulation results. Producing simulation results for high n and $\ell$ at the same time, is extremely time-consuming, since it concerns very rare events; evaluating the closed formula (104), on the contrary, requires virtually no time at all.

Fig. 5

Joint tail approximation $q_1(n,\ell )$ versus simulation results, for fixed $\ell =1,2,3,4$ and $\mu =1.8$

The corresponding result obtained by Jaffe [22, 23], in his original notations, is

$$\begin{aligned} \textrm{Prob}\!\left[ q_1=n,q_2=\ell \right] \approx q_3(n,\ell ) \triangleq \frac{M}{b_1 b_2} \left( \frac{1}{b_1 b_2} \right) ^{(n+\ell )/2} \left( \left( \frac{b_2}{b_1 } \right) ^{(n-\ell )/2} + \left( \frac{b_1}{ b_2} \right) ^{(n-\ell )/2}\right) , \end{aligned}$$

where

$$\begin{aligned} p \triangleq \frac{\mu }{2} , \quad M \triangleq \frac{16}{p^6} (1-p)^2(4-p^2) , \quad b_1 \triangleq \left( \frac{2}{p} -1 \right) ^2 , \quad b_2 \triangleq \left( 1 + \frac{2}{p} - \frac{4}{p^2} \right) ^2 . \end{aligned}$$

Translating this to our notations, we thus find that $b_1=\tau _1$, $b_2=\sigma$ and

$$\begin{aligned} q_3(n,\ell ) = q_1(n,\ell ) + q_2(n,\ell ) . \end{aligned}$$

Hence, we see that Jaffe’s approximation is symmetric in the parameters n and $\ell$, and corresponds to the sum of our two approximations; $q_3(n,\ell )$ is compared to simulation results in Fig. 6 and is clearly more accurate than $q_1(n,\ell )$ for lower values of n.

Fig. 6

Joint tail approximation $q_3(n,\ell )$ versus simulation results, for fixed $\ell =1,2,3,4$ and $\mu =1.8$

In order to better understand why this is the case, we need some context. First, it is important to know that both Cohen [10] and Jaffe [22, 23] prove that $U(z_1,z_2)$ has an infinite number of poles, and that the locations of the poles of $U(z_1,z_2)$, considered as a function of $z_1$, are independent of $z_2$, and vice versa. Thus, the joint pgf $U(z_1,z_2)$ has two countably infinite sets of poles, one set with respect to the variable $z_1$ and another set with respect to the variable $z_2$. Since $\alpha =\frac{1}{2}$, these two sets are identical. Using our notations, it turns out that, in both sets of poles, the dominant pole is $\tau _1=\tau _2$ and the second most dominant pole is $\sigma$. The reason why Jaffe obtains a more accurate result is that he – explicitly, from the very beginning – not only uses the most dominant poles, but also the second most dominant poles of $U(z_1,z_2)$ with respect to the dimensions $z_1$ and $z_2$, in his joint tail approximation, whereas we basically only use the most dominant pole in one direction, and then look for the most dominant pole in the other direction, given this earlier choice, which turns out to be the second most dominant pole in that direction. Apparently, as also explicitly noticed by Jaffe, there is no contribution to the joint tail from the two most dominant poles in both directions (i.e., $\tau _1=\tau _2$) together. We further note that, if n is much larger than $\ell$, then, since $b_1=\tau _1=\tau _2<b_2=\sigma$, $q_2(n,\ell )$ becomes negligible with respect to $q_1(n,\ell )$; the opposite is true if $\ell$ is much larger than n; in both cases, Jaffe’s approximation basically reduces to one of our two approximations.

Finally, we emphasize that our approach does lead to the same, more accurate, approximation as Jaffe’s analysis, if we simply add up our two approximations. This adding up is not just a heuristic trick: it corresponds to taking into account the contributions of more singularities (with respect to both $z_1$ and $z_2$) when inverting the pgf $U(z_1,z_2)$ to find the pmf $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$. This approach could be taken for other arrival processes A(x, y) too, if multiple expressions for $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$ are obtained. The reason we did not need it in Sect. 5.2.1 (global geometric arrivals) is that there, for a given routing probability $\alpha$, we only got one expression for $\textrm{Prob}\!\left[ u_1=n,u_2=\ell \right]$; in Sect. 5.2.2 (global shifted geometric arrivals), the two approximate expressions were identical.

6 Discussion of results

In the previous section, we have observed that, depending on the precise nature of the arrival pgf A(x, y), different scenarios may occur with respect to the behavior of queue 2 when the number of customers in queue 1 is large (i.e., in the asymptotic system). In case of identical arrivals, queue 2 is always unstable; for global geometric arrivals, queue 2 may be either stable or unstable, depending on the relative values of $\lambda _1$ and $\lambda _2$, whereas in case of global shifted geometric or binomial arrivals, queue 2 is always stable. Intuitively, one might expect that the amount and the nature of the intra-slot correlation between the arrivals of type 1 and type 2, should play an important role in the type of behavior that is observed. If this correlation is positive, we expect both queues to exhibit similar behavior, i.e., the system content in queue 2 is large (small) when the system content in queue 1 is large (small); if the correlation is positive and large, we even expect that $u_2\rightarrow \infty$ when $u_1\rightarrow \infty$, and this is what we observe in case of identical arrivals, indeed. On the other hand, if the arrival correlation is negative, queues 1 and 2 are expected to behave differently, in the sense that $u_2$ typically takes small values when $u_1$ takes high values, and vice versa, and therefore, queue 2 should remain stable when $u_1\rightarrow \infty$, i.e., in the asymptotic system. This looks like what we observe in case of global shifted geometric or binomial arrivals. But it is not a priori clear what should happen if the arrival correlation is moderately positive; this seems to be what happens in case of global geometric arrivals.

Let us corroborate these intuitive expectations by means of formulas. We start by computing the arrival correlation. Let $a_1$ and $a_2$ denote the numbers of type-1 arrivals and type-2 arrivals in one slot, respectively. Then, the correlation coefficient $\rho _a$ between $a_1$ and $a_2$ is defined as

$$\begin{aligned} \rho _a \triangleq \frac{E\!\left[ a_1a_2\right] -\lambda _1\lambda _2}{\sqrt{E\!\left[ a_1^2\right] -\lambda _1^2}\sqrt{E\!\left[ a_2^2\right] -\lambda _2^2}} = \frac{\textrm{cov}\!\left[ a_1,a_2\right] }{\sqrt{E\!\left[ a_1^2\right] -\lambda _1^2}\sqrt{E\!\left[ a_2^2\right] -\lambda _2^2}} , \end{aligned}$$

where $\lambda _1=E\!\left[ a_1\right]$ and $\lambda _2=E\!\left[ a_2\right]$ are the quantities defined earlier in Eq. (3), and

$$\begin{aligned} E\!\left[ a_1a_2\right] = \frac{\partial ^{2}{A}}{\partial {x}\partial {y}}(1,1) , \quad E\!\left[ a_1^2\right] = \frac{\partial ^{2}{A}}{\partial {x}^{2}}(1,1) + \lambda _1 , \quad E\!\left[ a_2^2\right] = \frac{\partial ^{2}{A}}{\partial {y}^{2}}(1,1) + \lambda _2 . \end{aligned}$$

The quantity $\textrm{cov}\!\left[ a_1,a_2\right] \triangleq E\!\left[ a_1a_2\right] -\lambda _1\lambda _2$ is the covariance of $a_1$ and $a_2$, and has the same sign as the correlation coefficient $\rho _a$, but is easier to compute.

6.1 Global geometric arrivals

For the case of global geometric arrivals, where A(x, y) is given in Eq. (58), the arrival correlation turns out to be positive, between 0 and $+1$, i.e.,

$$\begin{aligned} \rho _a(\text {geom}) = \frac{\mu \sqrt{\alpha (1-\alpha )}}{\sqrt{(1+\mu \alpha )[1+\mu (1-\alpha )]}} = \frac{\sqrt{\lambda _1\lambda _2}}{\sqrt{(1+\lambda _1)(1+\lambda _2)}} > 0 . \end{aligned}$$

We thus expect queue 2 in the asymptotic system (where $u_1\rightarrow \infty$) to be more heavily loaded than in the unconditional system. This expectation is confirmed by Eq. (63), i.e.,

$$\begin{aligned} \lambda _2^* = \frac{\lambda _2}{\lambda _1} > \lambda _2 . \end{aligned}$$

Moreover, $\lambda _2^*$ only remains smaller than one, i.e., the stability of queue 2 is only guaranteed, if $\lambda _2<\lambda _1<1$. Apparently, the correlation coefficient $\rho _a(\text {geom})$, which is an increasing function of $\lambda _2$, for given $\lambda _1$, gets too big to ensure stability of queue 2 beyond this point. But, if $\lambda _2 < \lambda _1$, then $E\!\left[ u_2|u_1\rightarrow \infty \right]$ exists and, according to (59) and (65), is greater than $E\!\left[ u_2\right]$:

$$\begin{aligned} E\!\left[ u_2|u_1\rightarrow \infty \right] = \frac{\lambda _2^*}{1-\lambda _2^*} > \frac{\lambda _2}{1-\lambda _2} = E\!\left[ u_2\right] . \end{aligned}$$

Comparing the tail distributions of $u_2$ in the asymptotic system and the original system, we also see a heavier tail in the asymptotic system, as, according to (60) and (68), for large $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx (1- \lambda _2^*)(\lambda _2^*)^\ell > (1-\lambda _2)\lambda _2^\ell \approx \textrm{Prob}\!\left[ u_2=\ell \right] . \end{aligned}$$

6.2 Global shifted geometric arrivals

The situation is different for global shifted geometric arrivals, where A(x, y) is given by expression (72) and we find

$$\begin{aligned} \rho _a(\text {shift}) = \frac{(\mu -2)\sqrt{\alpha (1-\alpha )}}{\sqrt{\mu -1+(2-\mu )^2\alpha (1-\alpha )}} = - \frac{\sqrt{(2-\mu )^2 \lambda _1\lambda _2}}{\sqrt{(2-\mu )^2 \lambda _1\lambda _2 + \mu ^2(\mu -1)}} , \end{aligned}$$

which is clearly negative, between 0 and $-1$, because $1\le \mu <2$. The mean asymptotic arrival rate in queue 2 is given by formula (77):

$$\begin{aligned} \lambda _2^* = \frac{\mu -1}{\lambda _1}< \frac{\lambda _1\lambda _2}{\lambda _1} = \lambda _2 < 1 , \end{aligned}$$

(105)

where we have used the inequality

$$\begin{aligned} \mu -1 < \lambda _1\lambda _2 \,\Leftrightarrow \,\lambda _1\lambda _2 -(\mu -1) = \lambda _1\lambda _2 -(\lambda _1 + \lambda _2) +1 =(1-\lambda _1)(1-\lambda _2) > 0 .\nonumber \\ \end{aligned}$$

(106)

Equation (105) not only implies that queue 2 is always stable in the asymptotic system, but also that it is less heavily loaded than in the original system. This observation is confirmed by a comparison of the expressions (74) and (78) for the mean system content in queue 2:

$$\begin{aligned} E\!\left[ u_2|u_1\rightarrow \infty \right] = \frac{\mu -1}{\mu (1-\lambda _2)} < \frac{\lambda _1\lambda _2}{\mu (1-\lambda _2)} = E\!\left[ u_2\right] , \end{aligned}$$

where we have, again, used the inequality (106). A comparison of the tail distributions of $u_2$ in the asymptotic system and the original system now reveals that both have the same decay rate, because, according to (79), in this case, the dominant poles $\tau _2$ (of $U_2(z)$) and $\sigma$ (of $U_2^*(z)$) coincide:

$$\begin{aligned} \sigma = \tau _2 = \frac{\alpha }{(\mu -1)(1-\alpha )} = \frac{\lambda _1}{(\mu -1)\lambda _2} . \end{aligned}$$

Nevertheless, we can derive from (81) and (84) that, for large $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right]\approx & {} \frac{\mu (1-\lambda _2)}{\lambda _1\lambda _2} \bigg ( \frac{(\mu -1)\lambda _2}{\lambda _1} \bigg )^{\ell } \\< & {} \frac{\mu (1-\lambda _2)}{\mu -1}\bigg ( \frac{(\mu -1)\lambda _2}{\lambda _1} \bigg )^{\ell } \approx \textrm{Prob}\!\left[ u_2=\ell \right] , \end{aligned}$$

using, once again, the inequality (106).

6.3 Global binomial arrivals

The case of global binomial arrivals of order two can be dealt with similarly. Here, A(x, y) is given by (91) and, again, we find a negative arrival correlation, between 0 and $-1$, i.e.,

$$\begin{aligned} \rho _a(\text {binom}) = - \frac{\sqrt{\lambda _1\lambda _2}}{\sqrt{(2-\lambda _1)(2-\lambda _2)}} < 0 . \end{aligned}$$

According to (94), the mean arrival rate in queue 2 in the asymptotic system is given by

$$\begin{aligned} \lambda _2^* = \frac{\lambda _1\lambda _2}{2-\lambda _1}< \lambda _2 < 1 . \end{aligned}$$

Here again, queue 2 is always stable in the asymptotic system, but less loaded than in the original system. Expressions (92), (95) for the mean system content in queue 2 confirm this:

$$\begin{aligned} E\!\left[ u_2|u_1\rightarrow \infty \right] = \frac{\lambda _2^*(4-3\lambda _2^*)}{4(1-\lambda _2^*)} < \frac{\lambda _2(4-3\lambda _2)}{4(1-\lambda _2)} = E\!\left[ u_2\right] , \end{aligned}$$

because the function

$$\begin{aligned} g(x) \triangleq \frac{x(4-3x)}{4(1-x)} \end{aligned}$$

is a monotonically increasing function of its argument x (since $g'(x)>0$, for all real x). Comparing the tail distributions of $u_2$ in the asymptotic system and the original system, we also see a lighter tail in the asymptotic system, as, according to (99) and (100), for large $\ell$,

$$\begin{aligned} \textrm{Prob}\!\left[ u_2=\ell | u_1 \rightarrow \infty \right] \approx \frac{4(1-\lambda _2^*)}{(\lambda _2^*)^2} \bigg ( \frac{\lambda _2^*}{2-\lambda _2^*} \bigg )^{2\ell } < \frac{4(1-\lambda _2)}{(\lambda _2)^2} \bigg ( \frac{\lambda _2}{2-\lambda _2} \bigg )^{2\ell } \approx \textrm{Prob}\!\left[ u_2=\ell \right] . \end{aligned}$$

6.4 General global arrivals

The above results for global geometric, shifted geometric and binomial arrivals with probabilistic routing to both queues, suggest that the (sign of) the correlation coefficient (or, the covariance) between $a_1$ and $a_2$ gives a good indication of the type of behavior we may expect for queue 2 in the asymptotic system: if the arrival correlation is positive, then queue 2 receives more arrivals in the asymptotic system than in the original system, whereas the opposite implication seems to hold in case of negative arrival correlation. In an attempt to examine this more generally, we have found that the reality is somewhat more subtle, and, in particular, that a second-order characteristic of the joint arrival process such as the covariance or the correlation coefficient cannot completely predict the type of behavior of the asymptotic system. Let us reconsider – more generally – the case where a global arrival stream with pgf C(z) is split into two substreams with routing probabilities $\alpha$ and $1-\alpha$ for queues 1 and 2, respectively, as discussed in the introduction of Sect. 5.2. Let us denote the mean and the variance of the total number of arrivals per slot in the system as $E\!\left[ c\right]$ and $\textrm{var}\!\left[ c\right]$, respectively. Then

$$\begin{aligned} E\!\left[ c\right] = C'(1) , \quad \textrm{var}\!\left[ c\right] = C''(1) + C'(1) - [C'(1)]^2 . \end{aligned}$$

As the joint pgf A(x, y) is given by $A(x,y) = C(\alpha x + (1-\alpha )y)$ (see (55)), we easily get

$$\begin{aligned} \lambda _1 = \alpha C'(1) , \quad \lambda _2 = (1-\alpha ) C'(1) , \quad E\!\left[ a_1 a_2\right] = \alpha (1-\alpha )C''(1) , \end{aligned}$$

and, from this,

$$\begin{aligned} \textrm{cov}\!\left[ a_1,a_2\right] = \alpha (1-\alpha )\{C''(1)-[C'(1)]^2\} = \alpha (1-\alpha ) \{\textrm{var}\!\left[ c\right] - E\!\left[ c\right] \} . \end{aligned}$$

(107)

Among other things, this simple result reveals that the arrival correlation is positive or negative depending on $\textrm{var}\!\left[ c\right]$ being larger or smaller than $E\!\left[ c\right]$.

We have seen in the earlier examples that $\lambda _2^*$ was larger than $\lambda _2$ when the arrival correlation was positive, and vice versa when it was negative. Let us examine whether this also holds more generally. More specifically, we examine whether the quantities $\Delta _2 \triangleq \lambda _2^* - \lambda _2$ and $\textrm{cov}\!\left[ a_1,a_2\right]$ always have the same sign. In order to do so, we compute $\Delta _2$ as

$$\begin{aligned} \Delta _2 \triangleq \lambda _2^* - \lambda _2 = \frac{1}{\tau _1} \frac{\partial {A}}{\partial {y}}(\tau _1,1) - (1-\alpha )C'(1) = \frac{1-\alpha }{\tau _1} [C'(1-\alpha + \alpha \tau _1) - \tau _1 C'(1)] , \end{aligned}$$

where we have used (47) and (55). From its definition, it follows that $\tau _1$ satisfies the equation $\tau _1=C(1-\alpha +\alpha \tau _1)$, and, therefore

$$\begin{aligned} \Delta _2 = \frac{1-\alpha }{\tau _1} [C'(1-\alpha + \alpha \tau _1) - C(1-\alpha +\alpha \tau _1) C'(1)] = \frac{1-\alpha }{\tau _1} D(1-\alpha +\alpha \tau _1) ,\qquad \end{aligned}$$

(108)

where $D(z) \triangleq C'(z)-C'(1)C(z)$. We now introduce the power series expansions of the functions C(z) and $C'(z)$ about $z=1$:

$$\begin{aligned} C(z) = 1 + \sum _{n=1}^\infty C^{(n)}(1) \frac{(z-1)^n}{n!} , \quad C'(z) = C'(1) + \sum _{n=1}^\infty C^{(n+1)}(1) \frac{(z-1)^n}{n!} , \end{aligned}$$

(109)

where $C^{(n)}(z)$ denotes the nth derivative of the function C(z). Using (109), we get D(z) as

$$\begin{aligned} D(z) = \sum _{n=1}^\infty [C^{(n+1)}(1) - C'(1)C^{(n)}(1)] \frac{(z-1)^n}{n!} . \end{aligned}$$

Inserting this result in (108), we obtain a useful expression for $\Delta _2$:

$$\begin{aligned} \Delta _2 = \frac{1}{\tau _1} \sum _{n=1}^\infty \omega _n[a_1,a_2] \frac{(\tau _1-1)^n}{n!} = \frac{\tau _1-1}{\tau _1}\textrm{cov}\!\left[ a_1,a_2\right] + \frac{1}{\tau _1} \sum _{n=2}^\infty \omega _n[a_1,a_2] \frac{(\tau _1-1)^n}{n!} ,\nonumber \\ \end{aligned}$$

(110)

where the quantities $\omega _n[a_1,a_2]$ are, in fact, higher-order covariances of the arrival process, i.e.,

$$\begin{aligned} \omega _n[a_1,a_2] \triangleq \alpha ^n(1-\alpha )[C^{(n+1)}(1) - C'(1)C^{(n)}(1)] = \textrm{cov}\!\left[ \prod _{j=0}^{n-1}(a_1-j),a_2\right] . \end{aligned}$$

Expression (110) reveals that, indeed, there is a relationship between the quantities $\Delta _2$ and $\textrm{cov}\!\left[ a_1,a_2\right]$, but $\textrm{cov}\!\left[ a_1,a_2\right]$ does not completely determine $\Delta _2$. It turns out that the higher-order covariances $\omega _n[a_1,a_2], n\ge 2,$ of the arrival process are also important. This implies that arrival distributions may exist for which $\Delta _2$ and $\textrm{cov}\!\left[ a_1,a_2\right]$ do not have the same sign. We have searched for an example, and, indeed, found one. Specifically, consider the case where the total number of arrivals per slot is either zero or two, i.e., the global arrival pgf C(z) takes the form

$$\begin{aligned} C(z) = 1-\frac{\mu }{2} + \frac{\mu }{2} z^2 , \quad C'(1) = \mu < 2 . \end{aligned}$$

In this case, the dominant pole $\tau _1$, solution of the equation $\tau _1=C(1-\alpha +\alpha \tau _1)$, is given by

$$\begin{aligned} \tau _1 = 1 + \frac{2(1-\mu \alpha )}{\mu \alpha ^2} , \end{aligned}$$

and the $\omega _n$s are

$$\begin{aligned} \omega _1[a_1,a_2] = \alpha (1-\alpha )\mu (1-\mu ) , \quad \omega _2[a_1,a_2] = -\mu ^2 , \quad \omega _n[a_1,a_2] = 0 , n>2 . \end{aligned}$$

According to (110), $\Delta _2$ is equal to

$$\begin{aligned} \Delta _2 = \frac{\tau _1-1}{\tau _1}\textrm{cov}\!\left[ a_1,a_2\right] + \frac{1}{\tau _1} \omega _2[a_1,a_2] \frac{(\tau _1-1)^2}{2!} = \mu (1-\alpha )^2\frac{1-\tau _1}{\tau _1} < 0 . \end{aligned}$$

We thus have the situation that $\Delta _2$ is clearly negative for all possible values of the system parameters, whereas the arrival covariance

$$\begin{aligned} \textrm{cov}\!\left[ a_1,a_2\right] = \omega _1[a_1,a_2] = \alpha (1-\alpha )\mu (1-\mu ) , \end{aligned}$$

can be either positive or negative, depending on $\mu$ being smaller or larger than one. So, in this particular example, the arrival covariance only predicts the behavior of the asymptotic system well in case the overall mean arrival rate $\mu$ is big enough. Whether this conclusion can be generalized to other global arrival distributions is not clear.

The main conclusion from Sect. 6 seems to be that the arrival covariance $\textrm{cov}\!\left[ a_1,a_2\right]$ is indeed related to the performance difference of queue 2 in a comparison between the original system and the asymptotic system, but does not simply predict it. The intuition that it should do so is thus not always correct.

7 Conclusions and further research

In this paper, we have considered a system of two parallel (coupled) discrete-time single-server queues with general independent arrivals per slot, but with possible intra-slot dependence between the arrival streams into both queues. To explicitly derive the joint steady-state pgf $U(z_1,z_2)$ of the system contents in queues 1 and 2 for a general joint arrival pgf A(x, y) is extremely hard for this system. Only for some classes of arrival pgfs, such explicit solutions are known (Bruneel [7]); we have provided two examples in Sect. 5, i.e., the cases of identical arrivals (Sect. 5.1) and global shifted-geometric arrivals (Sect. 5.2.2). We have therefore focused on the derivation of the performance of queue 2 under the condition that the system content $u_1$ in queue 1 is very large. We have shown that, under this condition, queue 2 behaves as a regular discrete-time single-server queue with independent arrivals from slot to slot, but with a modified pgf (i.e., $A_2^*(z)$ instead of $A_2(z)$) for the number of arrivals per slot. Moreover, this is true for any choice of the joint pgf A(x, y), i.e., even in cases where an explicit solution for $U(z_1,z_2)$ is not known, and we have derived a simple formula to deduct $A_2^*(z)$ from the original A(x, y). Using this fundamental result, we were able not only to determine the stability condition but also to derive all the usual performance characteristics of queue 2, such as the pgf $U_2^*(z)$, the mean value $E\!\left[ u_2|u_1\rightarrow \infty \right]$ (or any higher-order moment), and a very accurate approximation for the tail distribution of the system content of queue 2, in the so-called “asymptotic system”. Moreover, we could also derive closed-form approximative expressions for the joint tail distribution of the system contents $(u_1,u_2)$ in the two queues in the original system. These approximations, too, are very accurate, especially when we combine the two dual formulas (one for the condition $u_1\rightarrow \infty$ and one for the condition $u_2\rightarrow \infty$) that are obtained with our approach in some cases. Whether this concept can be further generalized could be subject of further research.

We have then applied our theoretical results to a number of specific choices of the arrival pgf A(x, y), especially for the setting where one global arrival stream into the two-queue system is split probabilistically into two substreams, each entering one of the two individual queues. This application gave rise to a large number of explicit closed-form formulas for the main performance metrics of queue 2 in the asymptotic system, which could then be compared with their counterparts in the original unconditioned system. A serious attempt was made to intuitively explain the observed differences, based on the intra-slot correlation (or covariance) in the arrival streams, but it turned out that this was not always possible.

For some choices of A(x, y), where the explicit solution for $U(z_1,z_2)$ or approximative closed-form expressions for the joint tail distribution of $(u_1,u_2)$ have been reported earlier in the literature, we have verified that our solution technique gives rise to the same results. However, our technique is applicable for any A(x, y) and can thus generate new - partial - results for arrival processes that were, until now, not amenable to exact solution. In particular, we hope that the dominant-pole approximation formulas that can be derived with our technique for the joint tail distribution of $(u_1,u_2)$ may, in some cases, be helpful in determining more (or even all) singularities of the joint pgf $U(z_1,z_2)$, both with respect to the variable $z_1$ and the variable $z_2$. The results in Sect. 5.2.3 with respect to global binomial arrivals point in that direction. This too could be a topic of future work.

Appendices

Appendix A: Dominant pole of $U_i(z)$

If $A_i(z)$ is “well-behaved” with radius of convergence $\Omega _i>1$, such that $\lim _{z\rightarrow \Omega _i} A_i(z) = +\infty$, then $z-A_i(z)$ has exactly one real positive zero, say $\tau _i$, with $1<\tau _i<\Omega _i$, which has multiplicity 1; $z-A_i(z)$ has no other zeroes outside the unit disk in the complex z-plane with modulus smaller than $\tau _i$, and $A_i'(\tau _i) > 1$.

Proof

Note that we may exclude the case where $A_i(z)$ is a linear function of z, because in such a case there is at most one arrival in each slot and no queue builds up, i.e., this case is not of interest in the current context where very large values of the system content are considered. So, either $A_i(z)$ is a nonlinear entire function, analytic in the whole complex plane, i.e., the radius of convergence $\Omega _i = +\infty$, and then $A_i(z)$ grows faster than linearly as $|z|\rightarrow \infty$, or $A_i(z)$ has a finite radius of convergence $\Omega _i>1$.

Let us consider the function $h(z) \triangleq z-A_i(z)$ for real values of its argument z, as graphically illustrated in Fig. 7. Because $h(1)=0$ and $h'(1) = 1 - \lambda _i>0$ (in view of the stability condition (4)), h(z) is positive in some real interval to the right of the value $z=1$. Taking into account that $\lim _{z\rightarrow \Omega _i}A_i(z)= + \infty$, it then follows that $\lim _{z\rightarrow \Omega _i}h(z)= -\infty$, both when $\Omega _i$ is finite or infinite. Since h(z) is a continuous function of z, there exist a $\tau _i\in ]1,\Omega _i[$ such that $h(\tau _i)=0$. Obviously, the slope of the curve h(z) is negative at $z=\tau _i$, where h(z) goes from positive to negative values, i.e.,

$$\begin{aligned} h'(\tau _i) < 0 \Leftrightarrow A_i'(\tau _i) > 1 . \end{aligned}$$

Recall that $A_i(z)$ is a pgf and hence a power series with non-negative coefficients. In particular, $A_i''(z)>0$ for positive real $z\in ]\tau _i,\Omega _i[$. It follows that $h''(z)<0$, i.e., $h'(z)$ decreases, for positive real $z\in ]\tau _i,\Omega _i[$, and, thus, since $h'(\tau _i)<0$, the slope $h'(z)$ remains negative for $z\in ]\tau _i,\Omega _i[$ and, since $h(\tau _i)=0$, the function h(z) does the same. We can thus conclude that $\tau _i$ is the only zero of h(z) in the real interval $]1,\Omega _i[$, i.e., h(z) has no real zeroes in $]1,\tau _i[$. By an application of Rouché’s theorem (see, e.g., [8]) on the circle $\{|z|=\tau _i\}$ in the complex z-plane, it can be shown that h(z) only has one single zero in the open complex disk $\{|z| < \tau _i\}$, i.e., the real zero $z=1$; hence, h(z) has no complex zeroes outside the unit disk either with a modulus smaller than $\tau _i$. This concludes the proof. $\square$

Fig. 7

The function $h(z) \triangleq z-A_i(z)$ versus z, for real values of z

Appendix B: Explicit computation of $U(z_1,z_2)$ in case of global shifted geometric arrivals

In this case, the joint arrival pgf $A(z_1,z_2)$ is given by Eq. (72), i.e.,

$$\begin{aligned} \begin{aligned} A(z_1,z_2)&= \frac{\alpha z_1 + (1-\alpha ) z_2}{\mu -(\mu -1)\alpha z_1 -(\mu -1)(1-\alpha ) z_2} \\&= \frac{\tau _1\tau _2[\alpha z_1 + (1-\alpha ) z_2]}{\tau _1 \tau _2 - \alpha \tau _1(z_2-1) - (1-\alpha )\tau _2(z_1-1)} , \end{aligned} \end{aligned}$$

(111)

where we have introduced the dominant poles $\tau _1$ and $\tau _2$, given in Eq. (75), in the expression. The unknown joint pgf $U(z_1,z_2)$ is the “solution” of the functional Eq. (8), i.e.,

$$\begin{aligned} K(z_1,z_2) U(z_1,z_2) = A(z_1,z_2) L(z_1,z_2), \end{aligned}$$

(112)

where the kernel $K(z_1,z_2)$ is defined as

$$\begin{aligned} K(z_1,z_2) \triangleq z_1z_2-A(z_1,z_2) = \frac{\alpha \tau _1 z_1(z_2-1)(\tau _2-z_2) + (1-\alpha )\tau _2 z_2(z_1-1)(\tau _1-z_1)}{\tau _1 \tau _2 - \alpha \tau _1(z_2-1) - (1-\alpha )\tau _2(z_1-1)} ,\nonumber \\ \end{aligned}$$

(113)

and $L(z_1,z_2)$ is an unknown function, defined as

$$\begin{aligned} L(z_1,z_2) \triangleq (z_2-1)U(z_1,0) + (z_1-1)U(0,z_2) + (z_1-1)(z_2-1)U(0,0) . \end{aligned}$$

(114)

As discussed in Sect. 4.1, the radius of convergence of the marginal pgf $U_i(z)$ is given by $\tau _i$, defined in (13). This means that

$$\begin{aligned} |U_i(z)| = \big |\sum _{n=0}^\infty \textrm{Prob}\!\left[ u_i=n\right] \, z^n \big |< \infty \,\Leftrightarrow \,|z|<\tau _i . \end{aligned}$$

Now, the joint pgf $U(z_1,z_2)$ can be expressed as

$$\begin{aligned} U(z_1,z_2) = \sum _{i=0}^\infty \sum _{j=0}^\infty \textrm{Prob}\!\left[ u_1=i,u_2=j\right] \, z_1^i z_2^j . \end{aligned}$$

Hence, if $|z_2| \le 1$, we have

$$\begin{aligned} |U(z_1,z_2)|\le & {} \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty \textrm{Prob}\!\left[ u_1=i,u_2=j\right] \, |z_1^i| |z_2^j| \le \sum \limits _{i=0}^\infty \sum \limits _{j=0}^\infty \textrm{Prob}\!\left[ u_1=i,u_2=j\right] \, |z_1|^i \nonumber \\= & {} \sum \limits _{i=0}^\infty \textrm{Prob}\!\left[ u_1=i\right] |z_1|^i = U_1(|z_1|)< \infty , \quad \text {if } |z_1|<\tau _1 . \end{aligned}$$

(115)

For reasons of symmetry, we can similarly prove that

$$\begin{aligned} |U(z_1,z_2)|< \infty , \quad \text {if } |z_1|\le 1,|z_2|<\tau _2 . \end{aligned}$$

(116)

From (115) and (116), we conclude that the area of convergence of the joint pgf $U(z_1,z_2)$ contains at least the region

$$\begin{aligned} \Phi \triangleq \{(z_1,z_2):|z_1|<\tau _1,|z_2|\le 1 \} \cup \{(z_1,z_2):|z_1|\le 1,|z_2|<\tau _2 \} . \end{aligned}$$

(117)

Now suppose that $(z_1,z_2)\in \Phi$ is a zero-tuple of the kernel $K(z_1,z_2)$, i.e., $K(z_1,z_2)=0$, then, since $|U(z_1,z_2)| < \infty$, Eq. (112) implies that $L(z_1,z_2)=0$, or, equivalently,

$$\begin{aligned} \frac{U(z_1,0)}{z_1-1} + \frac{U(0,z_2)}{z_2-1} + U(0,0) = 0 . \end{aligned}$$

(118)

Further, assume that, for some value of $z_2$, both $(\hat{z_1},z_2)\in \Phi$ and $(\tilde{z_1},z_2)\in \Phi$ are zero-tuples of $K(z_1,z_2)$. We then refer to $\hat{z_1}$ and $\tilde{z_1}$ as “connected” $z_1$-values. It then follows from (118) that, at the same time,

$$\begin{aligned} \frac{U(\hat{z_1},0)}{\hat{z_1}-1} + \frac{U(0,z_2)}{z_2-1} + U(0,0) = 0 \quad \text {and} \quad \frac{U(\tilde{z_1},0)}{\tilde{z_1}-1} + \frac{U(0,z_2)}{z_2-1} + U(0,0) = 0 , \end{aligned}$$

so that

$$\begin{aligned} \frac{U(\hat{z_1},0)}{\hat{z_1}-1} = \frac{U(\tilde{z_1},0)}{\tilde{z_1}-1} . \end{aligned}$$

(119)

We now show that, in this particular case, such connected $z_1$-values can indeed be found. Specifically, we choose two $z_1$-values on a circle with center in the origin and radius $\sqrt{\tau _1}$ in the complex $z_1$-plane as follows:

$$\begin{aligned} \hat{z_1} = \sqrt{\tau _1} e^{\imath \theta } \quad \text {and} \quad \tilde{z_1} = \sqrt{\tau _1} e^{-\imath \theta } . \end{aligned}$$

Here $\imath$ denotes the imaginary unit, i.e., $\imath ^2=-1$. From (113), it is clear that the equation $K(z_1,z_2)=0$ is equivalent to

$$\begin{aligned} \alpha \tau _1(z_2-1)(\tau _2-z_2) + (1-\alpha )\tau _2 z_2(z_1-1)(\frac{\tau _1}{z_1}-1) = 0 . \end{aligned}$$

If we substitute $z_1$ in the above equation for either $\hat{z_1}$ or $\tilde{z_1}$, we obtain the same equation in both cases:

$$\begin{aligned} f(z_2) \triangleq \alpha \tau _1(z_2-1)(\tau _2-z_2) + (1-\alpha )\tau _2 z_2(\sqrt{\tau _1} e^{\imath \theta }-1)(\sqrt{\tau _1} e^{-\imath \theta }-1) = 0 . \end{aligned}$$

The above equation is a quadratic equation in the variable $z_2$. It thus has two solutions for $z_2$. We now show that one of these solutions, say $z_2(\theta )$, is real and lies in the interval [0, 1]. Indeed, for $z_2=0$, we have

$$\begin{aligned} f(0) = -\alpha \tau _1\tau _2 < 0 , \end{aligned}$$

whereas for $z_2=1$, we get

$$\begin{aligned} f(1)= & {} (1-\alpha )\tau _2(\tau _1-2\sqrt{\tau _1}\cos {\theta } + 1) \ge (1-\alpha )\tau _2(\tau _1-2\sqrt{\tau _1} + 1) \\= & {} (1-\alpha )\tau _2(\sqrt{\tau _1} - 1)^2 > 0 . \end{aligned}$$

Hence, the polynomial f(z) (a continuous function) goes from negative to positive between $z_2=0$ and $z_2=1$. Therefore, it has a zero, $z_2(\theta ) \in [0,1]$. As $|\hat{z_1}| = |\tilde{z_1}| = \sqrt{\tau _1} < \tau _1$ and $|z_2(\theta )| \le 1$, we have thus shown that $\hat{z_1}$ and $\tilde{z_1}$ are connected $z_1$-values and, hence, (119) is valid. As $|e^{\imath \theta }|=1$ and $e^{-\imath \theta } = \frac{1}{e^{\imath \theta }}$, this can be written as

$$\begin{aligned} (\sqrt{\tau _1}z^{-1}-1)U(\sqrt{\tau _1}z,0) = (\sqrt{\tau _1}z-1)U(\sqrt{\tau _1}z^{-1},0) , \text { for } |z|=1 . \end{aligned}$$

(120)

Introducing the series expansion

$$\begin{aligned} U(z,0) = \sum _{n=0}^\infty u(n,0) z^n , \text { where } u(n,0) \triangleq \textrm{Prob}\!\left[ u_1=n,u_2=0\right] , \end{aligned}$$

we can express Eq. (120) as

$$\begin{aligned} (\sqrt{\tau _1}z^{-1}-1)\sum _{n=0}^\infty u(n,0) (\sqrt{\tau _1})^n z^n = (\sqrt{\tau _1}z-1)\sum _{n=0}^\infty u(n,0) (\sqrt{\tau _1})^n z^{-n} , \text { for } |z|=1 . \end{aligned}$$

Identifying equal (positive or negative) powers of z on both sides of the above equation leads to

$$\begin{aligned} \tau _1 u(2,0) - u(1,0) = u(0,0) , \quad \tau _1 u(n+1,0) - u(n,0) = 0 , n \ge 2 . \end{aligned}$$

We note that $u(0,0)=U(0,0)=0$ in this particular model, because the total number of arrivals during a slot into the system is always at least equal to 1 and, hence, the two-queue system can never be completely empty at the beginning of a slot. It thus follows that

$$\begin{aligned} \tau _1 u(n+1,0) - u(n,0) = 0 , \quad n \ge 1 , \end{aligned}$$

and, from this,

$$\begin{aligned} u(n,0) = (\tau _1)^{-(n-1)}u(1,0) , \end{aligned}$$

and, hence,

$$\begin{aligned} U(z,0) = \sum _{n=1}^\infty (\tau _1)^{-(n-1)}u(1,0) z^n = u(1,0)z \sum _{n=1}^\infty \bigg (\frac{z}{\tau _1}\bigg )^{n-1} = \frac{u(1,0)\tau _1 z}{\tau _1-z} . \end{aligned}$$

(121)

The remaining unknown u(1, 0) can be computed from the known equality

$$\begin{aligned} U(1,0) \triangleq U_2(0) = 1-\lambda _2 = 1-\mu (1-\alpha ) , \end{aligned}$$

where $U_2(z)$ and $\lambda _2$ were derived from (73) and (56). Choosing $z=1$ in (121), we easily get

$$\begin{aligned} u(1,0) = \frac{\tau _1 - 1}{\tau _1} U(1,0) , \end{aligned}$$

so that

$$\begin{aligned} U(z,0) = [1-\mu (1-\alpha )]\frac{(\tau _1 - 1)z}{\tau _1 - z} . \end{aligned}$$

(122)

Using a completely symmetric approach, we can also prove that

$$\begin{aligned} U(0,z) = [1-\mu \alpha ]\frac{(\tau _2 - 1)z}{\tau _2 - z} . \end{aligned}$$

(123)

This concludes the hardest part of our analysis, i.e., the explicit computation of the boundary functions U(z, 0) and U(0, z). Using (122) and (123) in (114) and keeping in mind that $U(0,0)=0$, we then get

$$\begin{aligned} \begin{aligned} L(z_1,&z_2) \triangleq (z_2-1)U(z_1,0) + (z_1-1)U(0,z_2) \\&= \frac{(\tau _1-1)(\tau _2-1)}{\tau _1\tau _2(\tau _1-z_1)(\tau _2-z_2)}[\alpha \tau _1 z_1(z_2-1)(\tau _2-z_2) + (1-\alpha )\tau _2 z_2(z_1-1)(\tau _1-z_1)] . \end{aligned}\nonumber \\ \end{aligned}$$

(124)

The resemblance between the numerators of $K(z_1,z_2)$ (Eq. (113)) and $L(z_1,z_2)$ (Eq. (124)) is striking. Combining these formulas and the known expression (111) for $A(z_1,z_2)$, we can now derive an explicit expression for the joint pgf $U(z_1,z_2)$ of the two system contents from the functional Eq. (112):

$$\begin{aligned} U(z_1,z_2) = \frac{A(z_1,z_2)L(z_1,z_2)}{K(z_1,z_2)} = \frac{(\tau _1 -1)(\tau _2 -1)[\alpha z_1 + (1-\alpha )z_2]}{(\tau _1 -z_1)(\tau _2 -z_2))} . \end{aligned}$$