Reward maximization in general dynamic matching systems

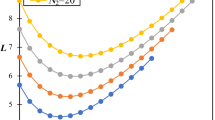
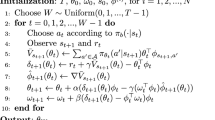Abstract

We consider a matching system with random arrivals of items of different types. The items wait in queues—one per item type—until they are “matched.” Each matching requires certain quantities of items of different types; after a matching is activated, the associated items leave the system. There exists a finite set of possible matchings, each producing a certain amount of “reward.” This model has a broad range of important applications, including assemble-to-order systems, Internet advertising, and matching web portals. We propose an optimal matching scheme in the sense that it asymptotically maximizes the long-term average matching reward, while keeping the queues stable. The scheme makes matching decisions in a specially constructed virtual system, which in turn controls decisions in the physical system. The key feature of the virtual system is that, unlike the physical one, it allows the queues to become negative. The matchings in the virtual system are controlled by an extended version of the greedy primal–dual (GPD) algorithm, which we prove to be asymptotically optimal—this in turn implies the asymptotic optimality of the entire scheme. The scheme is real time; at any time, it uses simple rules based on the current state of the virtual and physical queues. It is very robust in that it does not require any knowledge of the item arrival rates and automatically adapts to changing rates. The extended GPD algorithm and its asymptotic optimality apply to a quite general queueing network framework, not limited to matching problems, and therefore are of independent interest.