Improved semi-quantum key distribution with two almost-classical users

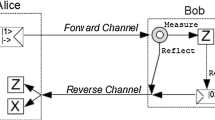
Abstract

Semi-quantum key distribution (SQKD) protocols attempt to establish a shared secret key between users, secure against computationally unbounded adversaries. Unlike standard quantum key distribution protocols, SQKD protocols contain at least one user who is limited in their quantum abilities and is almost “classical” in nature. In this paper, we revisit a mediated semi-quantum key distribution protocol, introduced by Massa et al. (Experimental quantum cryptography with classical users, 2019. arXiv preprint arXiv:1908.01780), where users need only the ability to detect a qubit, or reflect a qubit; they do not need to perform any other basis measurement; nor do they need to prepare quantum signals. Users require the services of a quantum server which may be controlled by the adversary. In this paper, we show how this protocol may be extended to improve its efficiency and also its noise tolerance. We discuss an extension which allows more communication rounds to be directly usable; we analyze the key-rate of this extension in the asymptotic scenario for a particular class of attacks and compare with prior work. Finally, we evaluate the protocol’s performance in a variety of lossy and noisy channels.

Appendices

Appendix

A.1 Parameter estimation

In this appendix, we determine bounds on the needed inner products (required to evaluate Eq. 14) by considering various, observable, events such as the probability of the server sending the message “1” given that both parties choose $\texttt {Reflect}$ (this should be small for instance). This can be done for arbitrary channels; however as discussed in the text, we derive expressions for a symmetric depolarization attack, a common approach in QKD security proofs. Note that our security proof does not require this as an assumption—it is only done in order to evaluate the performance on a standard channel scenario. Our steps below, however, may be followed for any observed channel. Under these evaluation conditions, we may parameterize the channel statistics as follows: $\phi$ will be the phase error of the channel; $p_l$ is the probability of loss in one direction (the server to users and the users to the server); and $p_d$ is the dark count rate of the server’s detectors.

Recall the density operator describing one round of the protocol (Eq. 9) which we copy here:

$$\begin{aligned} \rho _{ABE} =\,&\frac{1}{N}[{\mathbf {00}}]_{AB}\otimes ( [{\mathbf {1, t_1,}} {\varvec{\nu }}_{{\mathbf {0}}}] + [{\mathbf {0, t_0, 0, s_0}}] + [{\mathbf {0,t_0,1,s_1}}])\nonumber \\&+\frac{1}{N}[{\mathbf {11}}]_{AB}\otimes ( [{\mathbf {1, s_1,}} {\varvec{\nu }}_{{\mathbf {0}}}] + [{\mathbf {0, s_0, 0, t_0}}] + [{\mathbf {0,s_0,1,t_1}}])\nonumber \\&+\frac{1}{N}[{\mathbf {01}}]_{AB}\otimes ( [{\mathbf {1,r_1,}}{\varvec{\nu }}_{{\mathbf {0}}}] + [{\mathbf {0,r_0,0,g_0}}] + [{\mathbf {0,r_0,1,g_1}}])\nonumber \\&+\frac{1}{N}[{\mathbf {10}}]_{AB}\otimes ( [{\mathbf {1,g_1,}}{\varvec{\nu }}_{{\mathbf {0}}}] + [{\mathbf {0,g_0,0,r_0}}] + [{\mathbf {0,g_0,1,r_1}}]) \end{aligned}$$

(15)

We begin by considering ${\mathrm{Pr}}(C = 1 \text { }|\text { }A=B=\texttt {Reflect}) = P_{1|RR}$ which is the probability that conditioning on both Alice and Bob choosing $\texttt {Reflect}$, the server sends the message 1. It is clear, from the analysis in Sect. 4 and the state $\rho _{ABE}$, that this is $P_{1|RR} = {\langle r_1|r_1\rangle }$. Under our symmetric attack scenario, we set this to $P_{1|RR} = \frac{p_lp_d}{2} + (1-p_l)\left( \frac{p_lp_d}{2} + (1-p_l)\phi \right)$. Similarly, we find the following:

$$\begin{aligned} P_{1|RR}&= {\langle r_1|r_1\rangle } = \frac{p_lp_d}{2} + (1-p_l)\left( \frac{p_lp_d}{2} + (1-p_l)\phi \right) \\ P_{0|RR}&= {\langle r_0|r_0\rangle } = \frac{p_lp_d}{2} + (1-p_l)\left( \frac{p_lp_d}{2} + (1-p_l)(1-\phi )\right) \\\\ P_{1|MR}&= {\langle s_1|s_1\rangle } = \frac{p_lp_d}{2} + \frac{1-p_l}{2}\left( \frac{p_lp_d}{2} + \frac{1-p_l}{2}\right) \\ P_{0|MR}&= {\langle s_0|s_0\rangle } = \frac{p_lp_d}{2} + \frac{1-p_l}{2}\left( \frac{p_lp_d}{2} + \frac{1-p_l}{2}\right) \\\\ P_{1|RM}&= {\langle t_1|t_1\rangle } = \frac{p_lp_d}{2} + \frac{1-p_l}{2}\left( \frac{p_lp_d}{2} + \frac{1-p_l}{2}\right) \\ P_{0|RM}&= {\langle t_0|t_0\rangle } = \frac{p_lp_d}{2} + \frac{1-p_l}{2}\left( \frac{p_lp_d}{2} + \frac{1-p_l}{2}\right) \\\\ P_{1|MM}&= {\langle g_1|g_1\rangle } = \frac{p_lp_d}{2}\\ P_{0|MM}&= {\langle g_0|g_0\rangle } = \frac{p_lp_d}{2} \end{aligned}$$

Note that, in the above, we are defining $P_{i|RM}=P_{i|MR}$ to be the probability of the server sending message i and the measuring party not detecting the photon. These let us easily compute N using Eq. 10 and the above.

It is also clear that the values of $\alpha$, $\beta$, and $\gamma$ may be observed based on Alice and Bob’s measurements. Namely, $|\alpha |^2$ is the probability that conditioning on both parties choosing $\texttt {Measure}$ that Alice detects the photon. Similar observations may be made for $|\beta |^2$, while $|\gamma |^2$ is the probability that neither party detects a photon. Thus, these are:

$$\begin{aligned} |\alpha |^2 = |\beta |^2 = \frac{1-p_l}{2}; |\gamma |^2 = p_l, \end{aligned}$$

Next, we bound $|{\langle s_1|t_1\rangle }|$ and $|{\langle s_0|t_0\rangle }|$. From Eq. 8, we have:

$$\begin{aligned} {\langle r_1|r_1\rangle }&=\alpha ^2{\langle e_1|e_1\rangle }+\beta ^2 {\langle f_1|f_1\rangle }+\gamma ^2 {\langle g_1|g_1\rangle }\\&\quad +2\alpha \beta {\mathrm{Re}}{\langle e_1|f_1\rangle }+ 2\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }+2\gamma \alpha {\mathrm{Re}}{\langle g_1|e_1\rangle } \end{aligned}$$

Thus,

$$\begin{aligned} \alpha \beta {\mathrm{Re}}{\langle e_1|f_1\rangle }&=\frac{1}{2}({\langle r_1|r_1\rangle }-\alpha ^2{\langle e_1|e_1\rangle }-\beta ^2 {\langle f_1|f_1\rangle }-\gamma ^2{\langle g_1|g_1\rangle }\nonumber \\&\quad -2\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }-2\gamma \alpha {\mathrm{Re}}{\langle g_1|e_1\rangle })\nonumber \\&=\frac{1}{2}({\langle r_1|r_1\rangle }-\alpha ^2{\langle e_1|e_1\rangle }-\beta ^2 {\langle f_1|f_1\rangle }-\gamma ^2{\langle g_1|g_1\rangle })\nonumber \\&\quad -\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }-\gamma \alpha {\mathrm{Re}}{\langle g_1|e_1\rangle } \end{aligned}$$

(16)

Now, we can write ${\mathrm{Re}}{\langle s_1|t_1\rangle }$ as:

$$\begin{aligned} {\mathrm{Re}}{\langle s_1|t_1\rangle }= \alpha \beta {\mathrm{Re}}{\langle f_1|e_1\rangle }+\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }+\alpha \gamma {\mathrm{Re}}{\langle g_1|e_1\rangle }+\gamma ^2 {\langle g_1|g_1\rangle } \end{aligned}$$

By substituting in Eq. 16 and noting that ${\mathrm{Re}}{\langle e_1|f_1\rangle } = {\mathrm{Re}}{\langle f_1|e_1\rangle }$, we have:

$$\begin{aligned} {\mathrm{Re}}{\langle s_1|t_1\rangle }&=\frac{1}{2}({\langle r_1|r_1\rangle }-\alpha ^2{\langle e_1|e_1\rangle }-\beta ^2 {\langle f_1|f_1\rangle }-\gamma ^2{\langle g_1|g_1\rangle })\nonumber \\&\quad -\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }-\gamma \alpha {\mathrm{Re}}{\langle g_1|e_1\rangle }+\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }+\alpha \gamma {\mathrm{Re}}{\langle g_1|e_1\rangle }+\gamma ^2 {\langle g_1|g_1\rangle }\nonumber \\&=\frac{1}{2} {\langle r_1|r_1\rangle }-\frac{1}{2}\alpha ^2{\langle e_1|e_1\rangle }-\frac{1}{2}\beta ^2 {\langle f_1|f_1\rangle }+\frac{1}{2}\gamma ^2{\langle g_1|g_1\rangle } \end{aligned}$$

(17)

Next we may find an expression for $\alpha ^2{\langle e_1|e_1\rangle }$ by looking at ${\langle t_1|t_1\rangle }$ (which is an observable quantity as discussed above, namely $P_{1|RM}$):

$$\begin{aligned}&{\langle t_1| t_1\rangle }= \alpha ^2 {\langle e_1 |e_1\rangle } + \gamma ^2 {\langle g_1 |g_1\rangle } + 2 \alpha \gamma {\mathrm{Re}}{\langle e_1 |g_1\rangle } \\&\Longrightarrow \alpha ^2 {\langle e_1 |e_1\rangle }= {\langle t_1| t_1\rangle }- \gamma ^2 {\langle g_1| g_1\rangle } - 2 \alpha \gamma {\mathrm{Re}} {\langle e_1| g_1\rangle } \end{aligned}$$

Of course ${\langle t_1 |t_1\rangle }$ is an observable probability for Alice and Bob and, later, we may use Cauchy–Schwarz to bound $|{\langle e_1|g_1\rangle }|$ thus allowing them to bound $\alpha ^2{\langle e_1|e_1\rangle }$ used in the expansion of ${\langle s_1|t_1\rangle }$. Similarly, we find:

$$\begin{aligned}&{\langle s_1| s_1\rangle }= \beta ^2 {\langle f_1| f_1\rangle } + \gamma ^2 {\langle g_1|g_1\rangle } + 2 \beta \gamma {\mathrm{Re}} {\langle f_1|g_1\rangle } \\&\Longrightarrow \beta ^2 {\langle f_1|f_1\rangle }= {\langle s_1|s_1\rangle }- \gamma ^2 {\langle g_1|g_1\rangle } - 2 \beta \gamma {\mathrm{Re}} {\langle f_1|g_1\rangle } \end{aligned}$$

Combining this into Eq. 17 and using the (reverse) triangle inequality yields:

$$\begin{aligned} |{\langle s_1|t_1\rangle }|&\ge |{\mathrm{Re}}{\langle s_1|t_1\rangle }|= \frac{1}{2}\left| {\langle t_1|t_1\rangle } + {\langle s_1|s_1\rangle } - {\langle r_1|r_1\rangle } - 3{\langle g_1|g_1\rangle }- 2\alpha \gamma {\mathrm{Re}}{\langle e_1|g_1\rangle }\right. \nonumber \\&\quad \left. - 2\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }\right| \nonumber \\&\ge \frac{{\langle t_1|t_1\rangle } + {\langle s_1|s_1\rangle } - {\langle r_1|r_1\rangle }}{2} \nonumber \\&\quad - \frac{3}{2}{\langle g_1|g_1\rangle } - (\alpha \gamma + \beta \gamma )\sqrt{{\langle g_1|g_1\rangle }}, \end{aligned}$$

(18)

where, for the last inequality, we used the fact that $|{\langle e_1|g_1\rangle }| \le \sqrt{{\langle e_1|e_1\rangle }{\langle g_1|g_1\rangle }} \le \sqrt{{\langle g_1|g_1\rangle }}$. (Similarly for ${\langle f_1|g_1\rangle }$.) Similarly we may bound:

$$\begin{aligned} |{\langle s_0|t_0\rangle }|&\ge \frac{1}{2}\left| {\langle t_1|t_1\rangle } + {\langle s_1|s_1\rangle } - {\langle r_1|r_1\rangle } - 3{\langle g_1|g_1\rangle } - 2\alpha \gamma {\mathrm{Re}}{\langle e_1|g_1\rangle } - 2\beta \gamma {\mathrm{Re}}{\langle f_1|g_1\rangle }\right| \end{aligned}$$

(19)

$$\begin{aligned}&\ge \frac{{\langle t_0|t_0\rangle } + {\langle s_0|s_0\rangle } - {\langle r_1|r_1\rangle }}{2} - \frac{3}{2}{\langle g_1|g_1\rangle } - (\alpha \gamma + \beta \gamma )\sqrt{{\langle g_1|g_1\rangle }}. \end{aligned}$$

(20)