1 Introduction

Reconstruction of the quantum state of a system is of vital importance not only in fundamental studies of quantum mechanics but also in many practical applications of quantum information technology. The standard way to do it, the so-called quantum state tomography, requires an indirect computational reconstruction based on the measurement outcomes of a complete set of non-commuting observables on identically prepared systems [1]. Recently, an alternative method has been put forward and demonstrated experimentally [2, 3]. It has attracted much interest because it enables the complex-valued wave functions to be extracted directly and, from many points of view, in an experimentally less challenging manner. We call this method the direct tomography of wave functions. The direct tomography was originally proposed as a special case of weak measurement [2, 3]. Later it was extended to arbitrary measurement setup working regardless of the system-pointer coupling strength [4, 5]. More recently, the direct tomography has been reinterpreted in the so-called probe-controlled system framework. The latter allows experimenters for even wider variations of setup such as scan-free method of direct tomography [6], and in many cases leads to a higher efficiency. However, the metrological aspects of direct tomography have not been examined at all.

The statistical nature sets the standard quantum limit on the precision of standard measurement techniques [7, 8]. To reduce the statistical error, one needs to perform a large number N of repeated measurements. When it comes to direct tomography, it seems even worse as the post-selection procedure demands even more repetitions. Recent efforts in quantum metrology have shown new insights to overcome the standard quantum limit and achieve a higher precision by exploiting quantum resources, especially, quantum entanglement [7,8,9,10]. A great number of measurement strategies along the line have been proposed and demonstrated experimentally so far [11]. It is known that a genuine multi-particle entanglement is necessary to achieve the maximum precision, the so-called Heisenberg limit [10, 12].

In this paper, we investigate the ultimate precision of the direct tomography of wave functions. For the purpose, we generalize the idea of quantum metrology to the estimation of complex-valued phase. We show that the reformulation enables to identify the optimal measurements for efficient estimation and investigate the fundamental precision limit of direct tomography. We further propose two different measurement schemes that eventually approach the Heisenberg limit. In the first method, the pointers are prepared in special entangled states, either GHZ-like maximally entangled state or the symmetric Dicke state. In the other scheme, the ensemble of the measured systems is duplicated and the replica ensemble is time-reversal transformed before the start of the measurement.

Note that here we are concerned with the precision of statistical origin concerning measurement on an ensemble of systems. A notable exception is the so-called protected measurement [13, 14], where the expectation value of an observable is obtained from measurement on a single system as demonstrated in a recent experiment [15]. In this case, a higher precision may be achieved by preparing the pointer in a special state of minimum uncertainty such as a squeezed state [16].

2 Direct tomography as a phase estimation

In order to investigate the precision limit of the direct tomography of wave functions, it is convenient to reformulate it as a phase estimation. It allows a clearer picture of the optimal initial states and measurements and hence more convenient investigation of the precision limit.

Before the reformulation, we briefly summarize the procedure of direct tomography [2,3,4]. Here we follow Ref. [4] and examine the direct tomography beyond weak-coupling approximation. Consider an unknown pure state \(\mathinner {|{\textstyle \psi _\text {S}}\rangle }\) in a d dimensional Hilbert space and expand it in a given basis \(\{\mathinner {|{\textstyle x}\rangle }|x=1,\cdots ,d\}\) as

$$\begin{aligned} \mathinner {|{\textstyle \psi _\mathrm {S}}\rangle }=\sum _{x=1}^d\psi _x\mathinner {|{\textstyle x}\rangle }. \end{aligned}$$
(1)

A qubit is taken as the pointer and prepared in the state \(\mathinner {|{\textstyle \phi _\mathrm {in}}\rangle }\). The total wave function of the system plus the pointer is thus \(\mathinner {|{\textstyle \varPsi _\mathrm {in}}\rangle }=\mathinner {|{\textstyle \psi _S}\rangle }\otimes \mathinner {|{\textstyle \phi _\mathrm {in}}\rangle }\). The direct measurement of wave function \(\psi _x\) starts by coupling the system with the pointer. The system-pointer interaction can be described by a unitary operator of the form

$$\begin{aligned} {\hat{U}}_x =\mathrm {e}^{-\mathrm {i}\theta \mathinner {|{\textstyle x}\rangle }\mathinner {\langle {\textstyle x}|}\otimes \hat{K}/2} =(\hat{I}_\text {S}-\mathinner {|{\textstyle x}\rangle }\mathinner {\langle {\textstyle x}|})\otimes \hat{I}_\text {P}+\mathinner {|{\textstyle x}\rangle }\mathinner {\langle {\textstyle x}|}\otimes \mathrm {e}^{-\mathrm {i}\theta \hat{K}/2}, \end{aligned}$$
(2)

where \(\theta \) is the system-pointer coupling constant, \(\hat{K}/2\) is a traceless “angular momentum” operator (i.e., \(e^{-i\theta \hat{K}/2}\) is a “rotation” operator) on the pointer, and \(\hat{I}_\text {S}\) (\(\hat{I}_\text {P}\)) is the identity operator on the system (pointer). The initial state \(\mathinner {|{\textstyle \phi _\mathrm {in}}\rangle }\) and the coupling operator \(\hat{K}\) of the pointer are chosen such that \(\mathinner {\langle {\textstyle \phi _\mathrm {in}}|}\hat{K}\mathinner {|{\textstyle \phi _\mathrm {in}}\rangle }=0\). Metrologically, it corresponds to the requirement that the pointer rotates as much as possible in response to the system-pointer coupling and enables a higher precision [20]. After the interaction, the system is post-selected on to the state

$$\begin{aligned} |p_0\rangle =\frac{1}{\sqrt{d}}\sum _{x=1}^d\mathinner {|{\textstyle x}\rangle } , \end{aligned}$$
(3)

which leaves the pointer in the state

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle } = \frac{1}{\sqrt{|\alpha |^2+|\beta |^2}} \left( \alpha \hat{I}_P - \mathrm {i}\beta \hat{K}\right) \mathinner {|{\textstyle \phi _\mathrm {in}}\rangle } \,, \end{aligned}$$
(4)

where

$$\begin{aligned} \alpha = {\tilde{\psi }}-\psi _x+\psi _x\cos (\theta /2) \,,\quad \beta = \psi _x\sin (\theta /2) \,,\quad {\tilde{\psi }}=\sum _x\psi _x. \end{aligned}$$
(5)

Without loss of generality, \({\tilde{\psi }}\) is assumed to be real and positive as a global phase factor is physically irrelevant (if \({\tilde{\psi }}= 0\), then one can choose a post-selection to a different state). Now, extracting \(\psi _x\) is essentially equivalent to the single-qubit quantum state tomography. Accordingly, we choose three observables to measure, \(\hat{K}/2\) in the system-pointer coupling and two other angular momentum operators, \(\hat{K}_1/2\) and \(\hat{K}_2/2\), perpendicular to \(\hat{K}/2\). Through a number of independent measurements, the probabilities \(P_M\) for the measurements \(M=K,K_1,K_2\) to yield the outcome 1 (contrary to \(-1\)) are inferred, and then the wave function is extracted from the relation

$$\begin{aligned} \psi _x \propto (1-P_{K_1})\tan \frac{\theta }{4} + \left( P_{K_2}-\frac{1}{2}\right) + \mathrm {i}\left( P_K-\frac{1}{2}\right) . \end{aligned}$$
(6)

Therefore, in principle, the wave function \(\psi _x\) is estimated exactly as long as the probabilities \(P_M\) are inferred out of an infinite number of repeated measurements. In practice, however, the number of repetitions is finite and the accuracy is subject to the standard quantum limit.

Now let us reformulate the direct tomography outlined above as a phase estimation problem. To this end, we rewrite the normalized pointer state after post-selection into the form

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle } = \sqrt{\frac{\alpha ^2+\beta ^2}{|\alpha ^2+\beta ^2|}} \frac{\mathrm {e}^{-\mathrm {i}\varphi \hat{K}/2}|\phi _\mathrm {in}\rangle }{\sqrt{\langle \phi _\mathrm {in}|\mathrm {e}^{\mathrm {i}(\varphi ^*-\varphi )\hat{K}/2}|\phi _\mathrm {in}\rangle }} , \end{aligned}$$
(7)

where we have introduced a complex-valued phase \(\varphi \) by the relations

$$\begin{aligned} \cos \frac{\varphi }{2}=\frac{\alpha }{\sqrt{\alpha ^2+\beta ^2}} \,,\quad \sin \frac{\varphi }{2}=\frac{\beta }{\sqrt{\alpha ^2+\beta ^2}} \,. \end{aligned}$$
(8)

Once the complex parameter \(\varphi \) is estimated through experiments, one can extract the wave function \(\psi _x\) by

$$\begin{aligned} \psi _x=\frac{{\tilde{\psi }} \tan (\varphi /2)}{\sin (\theta /2)[1+\tan (\theta /4)\tan (\varphi /2)]}. \end{aligned}$$
(9)

Whereas the relation (7) between the final and initial state is formally the same as the standard phase estimation in quantum metrology [10], it involves two real parameters, \(\varphi _1:={\text {Re}}\varphi \) and \(\varphi _2:={\text {Im}}\varphi \), and corresponds to multi-parameter quantum metrology [17]. Naturally, it requires measurements of more than one observables. Throughout this work, the estimation of complex parameter \(\varphi =\varphi _1+\mathrm {i}\varphi _2\) will be used interchangeably with the multi-parameter estimation of real parameters \(\varphi _1\) and \(\varphi _2\).

To see how to estimate the complex phase \(\varphi \) in Eq. (7), we note that

$$\begin{aligned} \begin{bmatrix} \langle \hat{K}_1\rangle _\mathrm {f}\\ \langle \hat{K}_2\rangle _\mathrm {f} \end{bmatrix} = \frac{1}{\cosh (\varphi _2)+\sinh (\varphi _2)\mathinner {\langle {\textstyle \hat{K}}\rangle }_\mathrm {in}} \begin{bmatrix} \cos (\varphi _1) &{} -\sin (\varphi _1)\\ \sin (\varphi _1) &{} \cos (\varphi _1) \end{bmatrix} \begin{bmatrix} \langle \hat{K}_1\rangle _\mathrm {in}\\ \langle \hat{K}_2\rangle _\mathrm {in} \end{bmatrix} \end{aligned}$$
(10)

and

$$\begin{aligned} \mathinner {\langle {\textstyle \hat{K}}\rangle }_\mathrm {f} =\frac{ \sinh (\varphi _2) + \cosh (\varphi _2)\mathinner {\langle {\textstyle \hat{K}}\rangle }_\mathrm {in} }{ \cosh (\varphi _2)+\sinh (\varphi _2)\mathinner {\langle {\textstyle \hat{K}}\rangle }_\mathrm {in}}, \end{aligned}$$
(11)

where \(\langle ...\rangle _\mathrm {f}\) denotes the statistical average \(\langle \phi _\mathrm {f}|...\mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }\) and analogously \(\langle ...\rangle _\mathrm {in}\). It is observed from Eqs. (10) and (11) that \(\varphi _1\) rotates the classical vector \((\langle \hat{K}_1\rangle ,\langle \hat{K}_2\rangle )\) around the axis along \(\hat{K}\) whereas \(\varphi _2\) shifts \(\mathinner {\langle {\textstyle \hat{K}}\rangle }\). Such a rotation angle \(\varphi _1\) can be estimated by Ramsey-type interferometry whereas the estimation of \(\varphi _2\) requires an amplitude measurement scheme. In particular, for a choice of \(\mathinner {|{\textstyle \phi _\mathrm {in}}\rangle }\) consistent with the optimal sensitivity such that \(\mathinner {\langle {\textstyle \hat{K}_2}\rangle }_\mathrm {in}=\mathinner {\langle {\textstyle \hat{K}}\rangle }_\mathrm {in}=0\), one has

$$\begin{aligned} \mathinner {\langle {\textstyle \hat{K}_1}\rangle }_\mathrm {f} = \frac{\cos (\varphi _1)}{\cosh (\varphi _2)} \mathinner {\langle {\textstyle \hat{K}_1}\rangle }_\mathrm {in} \,,\quad \mathinner {\langle {\textstyle \hat{K}}\rangle }_\mathrm {f} = \tanh (\varphi _2). \end{aligned}$$
(12)

In short, the optimal estimation of the complex phase \(\varphi \), one needs first to (i) prepare the pointer in the initial state such that \(\mathinner {\langle {\textstyle \hat{K}_2}\rangle }=\mathinner {\langle {\textstyle \hat{K}}\rangle }=0\), and then (ii) perform measurements of two [rather than three as in Eq. (6)] observables \(\hat{K}_1\) and \(\hat{K}\). Therefore, the reformulation of direct tomography in the form of complex phase estimation is intuitively appealing and helps us find the optimal measurements for efficient estimation.

In passing, we remark that any measurement scheme involving post-selection can essentially be formulated as a complex phase estimation although the estimated phase carries different information depending on the specific measurements. An interesting example is sequential weak measurement [18], which has recently been realized experimentally for two non-commuting observables [19]. In this case, the estimated phase gives the sequential weak values.

3 Precision limits of the direct tomography

The estimation of a real-valued phase can reach the Heisenberg limit by exploiting quantum entanglements in the pointers [10]. The question is whether the same limit can be achieved for the estimation of a complex phase involved in the direct tomography. Here we demonstrate that it is indeed possible.

Using N00N state Consider an ensemble of N systems all in the same state \(\mathinner {|{\textstyle \psi _S}\rangle }\). We take a set of N qubits as the pointers and prepare them in the so-called NOON state (or the N-qubit GHZ state),

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {in}}\rangle } = \frac{|0\rangle ^{\otimes N}+|1\rangle ^{\otimes N}}{\sqrt{2}} , \end{aligned}$$
(13)

which has proved particularly interesting in high-precision quantum metrology [11]. We couple each system in the ensemble to each corresponding pointer qubit so that the overall unitary operator of the interaction is given by

$$\begin{aligned} \hat{U}_x^{\otimes N}=\left[ \exp \left( -\mathrm {i}\theta \mathinner {|{\textstyle x}\rangle }\mathinner {\langle {\textstyle x}|}\otimes \frac{{\hat{\sigma }}_z}{2}\right) \right] ^{\otimes N}. \end{aligned}$$
(14)

Here we have chosen \(\hat{K}={\hat{\sigma }}_z\) to be concrete. After post-selecting every system on to the state \(\mathinner {|{\textstyle p_0}\rangle }\) in Eq. (3), the (normalized) final state of the pointers is given by

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }_\text {N00N}=\frac{(\alpha -\mathrm {i}\beta )^N|0\rangle ^{\otimes N}+(\alpha +\mathrm {i}\beta )^N|1\rangle ^{\otimes N}}{\sqrt{|\alpha -\mathrm {i}\beta |^{2N}+|\alpha +\mathrm {i}\beta |^{2N}}} \end{aligned}$$
(15)

with \(\alpha \) and \(\beta \) defined in Eq. (5). Equivalently, in accordance with the phase-estimation formulation in Eq. (7), it can be rewritten as \(\mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }_\text {N00N}\) as follows (up to a global phase):

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }_\text {N00N} =\frac{\mathrm {e}^{-\mathrm {i}N\varphi /2}|0\rangle ^{\otimes N} +\mathrm {e}^{\mathrm {i}N\varphi /2}|1\rangle ^{\otimes N}}{\sqrt{2 \cosh (N\varphi _2)}}. \end{aligned}$$
(16)

Now consider two measurements \(\hat{M}_1:=\hat{\sigma }_x^{\otimes N}\) and \(\hat{M}_2:=\hat{\sigma }_z^{\otimes N}\). We note that

$$\begin{aligned} \langle \hat{M}_1\rangle :=\langle \hat{\sigma }_x^{\otimes N}\rangle&= \frac{\cos (N\varphi _1)}{\cosh (N\varphi _2)}, \end{aligned}$$
(17)
$$\begin{aligned} \langle \hat{M}_2\rangle :=\langle \hat{\sigma }_z^{\otimes N}\rangle&= \tanh (N\varphi _2) \quad (\text {for odd } N). \end{aligned}$$
(18)

Assuming small variations of the measurements with the parameter \(\varphi =\varphi _1+\mathrm {i}\varphi _2\), the covariance matrix \(C_{ij}(\varphi ):=\varDelta \varphi _i\varDelta \varphi _j\) (\(i,j=1,2\)) of the estimators \(\varphi _1\) and \(\varphi _2\) is related to the covariance of the measurement \(\mathinner {\langle {\textstyle \varDelta \hat{M}_\mu \varDelta \hat{M}_\nu }\rangle }\) (\(\mu ,\nu =1,2\)) by the error-propagation formula

$$\begin{aligned} \mathinner {\langle {\textstyle \varDelta \hat{M}_\mu \varDelta \hat{M}_\nu }\rangle } = \sum _{ij} \frac{\partial \langle \hat{M}_\mu \rangle }{\partial \varphi _i} C_{ij}(\varphi ) \frac{\partial \langle \hat{M}_\nu \rangle }{\partial \varphi _j}. \end{aligned}$$
(19)

Inverting the error propagation formula, we find that the precision is given by

$$\begin{aligned} (\varDelta \varphi _1)^2=(\varDelta \varphi _2)^2=\frac{\cosh ^2(N\varphi _2)}{N^2}. \end{aligned}$$
(20)

It is concluded that \(\hat{M}_1\) and \(\hat{M}_2\) are indeed optimal measurements under the optimal condition \(N\varphi _2\rightarrow 0\) for the Heisenberg limit. Here we have chosen specific measurements \(\hat{M}_1\) and \(\hat{M}_2\), but more general argument in terms of the Fisher information and the Cramer-Rao bound; see “Appendix A”.

Using Dicke state Thanks to their experimental relevance, the symmetric Dicke states have also been widely used for quantum entanglement [11]. In particular, it was illustrated that the entanglement in a Dicke state enables one to achieve the Heisenberg-limited interferometry for the single-parameter quantum metrology [20]. Given N qubits, the symmetric Dicke state \(\mathinner {|{\textstyle j\equiv N/2,m}\rangle }\) with \(m=j,j-1,\cdots ,-j\) is defined by

$$\begin{aligned} \mathinner {|{\textstyle j,m}\rangle } :=\sqrt{\frac{(j-m)!(j+m)!}{(2j)!}}\sum _P \hat{P}|\underbrace{11...}_{j-m}\underbrace{00...}_{j+m}\rangle , \end{aligned}$$
(21)

where the sum is over all possible permutations P and \(\hat{P}\) is the corresponding permutation operator.

We proceed in a similar manner as with the initial NOON state of pointers. The pointers of N qubits are initially prepared in the particular Dicke state \(\mathinner {|{\textstyle \phi _\mathrm {in}}\rangle }=\mathinner {|{\textstyle j\equiv N/2,0}\rangle }\). Each pointer is coupled with a system in the ensemble so that the unitary interaction is given by

$$\begin{aligned} \hat{U}_x^{\otimes N} =\left[ \exp (-\mathrm {i}\theta \mathinner {|{\textstyle x}\rangle }\mathinner {\langle {\textstyle x}|}\otimes {\hat{\sigma }}_y/2)\right] ^{\otimes N}. \end{aligned}$$
(22)

Here we have chosen \(\hat{K}={\hat{\sigma }}_y\) to make the best use of the characteristic of the Dicke state; namely, the sharp distribution along the equator of the generalized Bloch sphere [11]. After post-selection, the final state (7) of the pointers becomes

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }_\text {Dicke} =\frac{\mathrm {e}^{-\mathrm {i}\varphi \hat{J}_y}|j,0\rangle }{\sqrt{\langle j,0|\mathrm {e}^{\mathrm {i}(\varphi ^*-\varphi )\hat{J}_y}|j,0\rangle }}, \end{aligned}$$
(23)

where

$$\begin{aligned} {\hat{J}}_\mu =\frac{1}{2}\sum ^N_{k=1}\hat{\sigma }^{(k)}_\mu \quad (\mu =x,y,z) . \end{aligned}$$
(24)

For later use, we define the Wigner matrix element

$$\begin{aligned} W_{mm'}^{(j)} := \mathinner {\langle {\textstyle j,m}|}e^{-i\varphi \hat{J}_y}\mathinner {|{\textstyle j,m'}\rangle } . \end{aligned}$$
(25)

Here note that the phase \(\varphi \) is complex in general. For integer j, the expression for the matrix element \(W_{m0}^{(j)}\) is especially simple as

$$\begin{aligned} W^{(j)}_{m0}(\varphi ) = P^m_j(\cos \varphi )\sqrt{\frac{(j-m)!}{(j+m)!}} \quad (\varphi _1>0) \,, \end{aligned}$$
(26)

where \(P^m_j(z)\) denotes the associated Legendre polynomial of argument z.

Unlike the NOON state, the Dicke state does not allow for simple expressions for the Fisher information and the corresponding Cramer-Rao bound. Instead, we choose the optimal measurements based on the characteristics of the Dicke state and its behavior under the collective rotation \(e^{-i\varphi \hat{J}_y}\) by a complex angle \(\varphi \). As mentioned above, the Dicke state has a sharp distribution along the equator of the Bloch sphere. Then \(e^{-i\varphi _1\hat{J}_y}\) rotates this distribution off the equator. The resulting sharp contrast with the initial state can be detected most efficiently by measuring \(\hat{J}_z^2\). On the other hand, \(e^{\varphi _2\hat{J}_y}\) tends to pull the distribution along the positive y-axis. This deviation can be efficiently detected by measuring \(\hat{J}_y\). Below we demonstrate that \(\hat{J}_y\) and \(\hat{J}_z^2\) are indeed optimal measurements to achieve the Heisenberg limit.

We start with the analysis of the measurement of \(\hat{J}_y\): By virtue of the theory of angular momentum, we acquire

$$\begin{aligned} \langle \hat{J}_y\rangle&= \frac{\mathrm {i}W^{(j)}_{10}(2\mathrm {i}\varphi _2)}{W^{(j)}_{00}(2\mathrm {i}\varphi _2)}\sqrt{j(j+1)}, \end{aligned}$$
(27)
$$\begin{aligned} \langle \hat{J}^2_y\rangle&= j(j+1) - \frac{\mathrm {i}W^{(j)}_{10}(2\mathrm {i}\varphi _2)}{W^{(j)}_{00}(2\mathrm {i}\varphi _2)} \coth (2\varphi _2)\sqrt{j(j+1)}. \end{aligned}$$
(28)

It then follows from the error-propagation formula that

$$\begin{aligned} \frac{1}{(\varDelta \varphi _2)^2}&= \frac{1}{(\varDelta \hat{J}_y)^2} \left( \frac{\partial \mathinner {\langle {\textstyle \hat{J}_y}\rangle }}{\partial \varphi _2}\right) ^2 =4(\varDelta \hat{J}_y)^2\nonumber \\&= 4j(j+1)\left[ 1 - \frac{\mathrm {i}W^{(j)}_{10}(2\mathrm {i}\varphi _2)}{W^{(j)}_{00}(2\mathrm {i}\varphi _2)} \frac{\coth (2\varphi _2)}{\sqrt{j(j+1)}} - \left( \frac{\mathrm {i}W^{(j)}_{10}(2\mathrm {i}\varphi _2)}{W^{(j)}_{00}(2\mathrm {i}\varphi _2)}\right) ^2\right] . \end{aligned}$$
(29)

Equation (29) implies that the larger \((\varDelta \hat{J}_y)^2\) is the more precise the estimation of \(\varphi _2\) gets, which leads to the optimal condition \(\varphi _2=0\). Putting the optimal condition into Eq. (29) gives the Heisenberg limit

$$\begin{aligned} (\varDelta \varphi _2)^2_{\mathrm {opt}}=\frac{2}{N(N+2)} \end{aligned}$$
(30)

for the estimation of \(\varphi _2\). It is interesting to note that the variance \((\varDelta \varphi _2)^2\) in Eq. (29) depends only on \(\varphi _2\) but not on \(\varphi _1\). This is another important feature that allows \(\varphi _2\) to be estimated independently of \(\varphi _1\) through the measurement \(\hat{J}_y\).

To analyze the measurement \(\hat{J}_z^2\) as an estimator of \(\varphi _1\), we evaluate

$$\begin{aligned} \mathinner {\langle {\textstyle \hat{J}^2_z}\rangle }&= \frac{\mathrm {i}W^{(j)}_{10}(2\mathrm {i}\varphi _2)}{W^{(j)}_{00}(2\mathrm {i}\varphi _2)} \sqrt{j(j+1)}\sin (\varphi ) \left[ \coth (2\varphi _2)\sin (\varphi )-\mathrm {i}\cos (\varphi )\right] , \end{aligned}$$
(31)
$$\begin{aligned} \langle \hat{J}^4_z\rangle&= \frac{1}{W^{(j)}_{00}(2\mathrm {i}\varphi _2)} \sum _{m=-j}^j m^4| W^{(j)}_{m0}(\varphi )|^2 . \end{aligned}$$
(32)

Unlike the case with the measurement \(\hat{J}_y\), the moments \(\mathinner {\langle {\textstyle \hat{J}_z^2}\rangle }\) and \(\mathinner {\langle {\textstyle \hat{J}_z^4}\rangle }\) depend on both \(\varphi _1\) and \(\varphi _2\). Therefore one has to use the multi-parameter error-propagation formula (19) with \(\hat{M}_1=\hat{J}_z^2\) and \(\hat{M}_2=\hat{J}_y\), which leads to

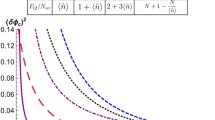
$$\begin{aligned} (\varDelta \varphi _1)^2 =\frac{\mathinner {\langle {\textstyle (\varDelta \hat{J}_z^2)^2}\rangle }+\left( \frac{\partial \langle \hat{J}^2_z\rangle }{\partial \varphi _2}\right) ^2(\varDelta \varphi _2)^2 -\frac{\partial \langle \hat{J}^2_z\rangle }{\partial \varphi _2} \left( \frac{\partial \langle \hat{J}_y\rangle }{\partial \varphi _2}\right) ^{-1} \mathinner {\langle {\textstyle \{\varDelta \hat{J}^2_z,\varDelta \hat{J}_y\}}\rangle }}{ \left( \frac{\partial \langle \hat{J}^2_z\rangle }{\partial \varphi _1}\right) ^2}, \end{aligned}$$
(33)

where we have defined \(\varDelta \hat{A}=\hat{A}-\mathinner {\langle {\textstyle \hat{A}}\rangle }\) for operator \(\hat{A}\) and noted that \(\partial \langle \hat{J}_y\rangle /\partial \varphi _1=0\). We refer the technical details of its calculations to “Appendix B”, and instead summarize its behavior in Fig. 1 as a function of \(\varphi _1\) and \(\varphi _2\) for the pointers of \(N=50\) qubits. It is clear from Fig. 1 that the optimal condition is given by \(\varphi _1=\varphi _2=0\). At this optimal condition, the precision of \(\varphi _1\) is given by the Heisenberg limit

$$\begin{aligned} (\varDelta \varphi _1)^2_\mathrm {opt} = \frac{2}{N(N+2)}. \end{aligned}$$
(34)

Incidentally, by putting the optimal condition \(\varphi _2=0\) obtained independently through the measurement \(\hat{J}_y\) above, we get

$$\begin{aligned} \left. (\varDelta \varphi _1)^{-2}\right| _{\varphi _2=0} = \frac{8j(j+1)}{(j^2+j-2)\tan ^2(\varphi _1)+4}, \end{aligned}$$
(35)

which coincides with the single-parameter estimation in Ref. [20] as it should.

Fig. 1
figure 1

The precision, \((\varDelta \varphi _1)^{-2}\), as a function \(\varphi _1\) for different values of \(\varphi _2\) and \(N=50\) qubits in the Dicke state

Full size image

Using time-reversal ensemble The reformulation of the direct tomography as a complex phase estimation in Eq. (7) inspires another interesting strategy based on time-reversal (TR) transformation. Given an ensemble of systems in the state in Eq. (1), we prepare another ensemble in the TR state

$$\begin{aligned} |\bar{\psi }_\text {S}\rangle := \hat{T}\mathinner {|{\textstyle \psi _\mathrm {S}}\rangle } = \sum _{x=1}^d\psi ^*_x\mathinner {|{\textstyle x}\rangle }, \end{aligned}$$
(36)

where \(\hat{T}\) is the (anti-unitary) TR operator (here we assume for simplicity that the basis state \(\mathinner {|{\textstyle x}\rangle }\) is invariant under the TR transformation). The pointers of 2N qubits are prepared, say, in the NOON state. The first N qubits interact with the systems in the original ensemble whereas the other N qubits are coupled with ones in the time-reversal ensemble. After post-selection, the pointers get in the final state of the form

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }_\text {TRS} =\frac{[(\alpha -\mathrm {i}\beta )(\alpha ^*-\mathrm {i}\beta ^*)]^N|0\rangle ^{\otimes 2N}+[(\alpha ^*+\mathrm {i}\beta ^*)(\alpha +\mathrm {i}\beta )]^N|1\rangle ^{\otimes 2N}}{\sqrt{|(\alpha -\mathrm {i}\beta )(\alpha ^*-\mathrm {i}\beta ^*)|^{2N}+|(\alpha ^*+\mathrm {i}\beta ^*)(\alpha +\mathrm {i}\beta )|^{2N}}} . \end{aligned}$$
(37)

Now recall that for any complex variables \(\alpha \) and \(\beta \),

$$\begin{aligned} |(\alpha -\mathrm {i}\beta )(\alpha ^*-\mathrm {i}\beta ^*)| = |(\alpha ^*+\mathrm {i}\beta ^*)(\alpha +\mathrm {i}\beta )|. \end{aligned}$$
(38)

It recasts Eq. (37) to the quantum metrologically appealing form

$$\begin{aligned} \mathinner {|{\textstyle \phi _\mathrm {f}}\rangle }_\text {TRS} =\frac{|0\rangle ^{\otimes 2N} + \mathrm {e}^{\mathrm {i}2N\varphi _1}|1\rangle ^{\otimes 2N}}{\sqrt{2}}. \end{aligned}$$
(39)

Namely, the above state is identical to the state with the amplified phase shift in interferometries with the NOON state, one of the earliest experimental demonstrations of the Heisenberg limit [21]. It is also worth noting that unlike the above two schemes, in which the estimation of \(\varphi _1\) strictly depends on that of \(\varphi _2\), the scheme using the TR ensemble enables the real part \(\varphi _1\) to be estimated independently. To estimate the imaginary part \(\varphi _2\), we can apply the measurement strategy proposed in Sect. 3.

As the TR transformation is anti-unitary, it cannot be implemented physically in isolated systems. However, it is achievable by embedding the system in a larger system. Therefore, as long as the setup permits additional capability of controlling the system, the TR ensemble provides an efficient strategy for direct precision measurement of wave functions.

4 Conclusion

Generalizing the idea of quantum metrology of phase estimation, we have reformulated the direct tomography of wave functions as the estimation of complex phase. It has turned out that the new formulation is intuitively appealing and inspires the proper choices of optimal measurements. We have further proposed two different measurement schemes that eventually approach the Heisenberg limit. In the first method, the pointers are prepared in special entangled states, either GHZ-like maximally entangled state or the symmetric Dicke state. In the other scheme, the ensemble of the measured systems is duplicated and the replica ensemble is time-reversal transformed before the start of the measurement. In both methods, the real part of the phase is estimated with Ramsey-type interferometry while the imaginary part is estimated by amplitude measurements. The optimal condition for the ultimate precision is achieved at small values of the complex phases, which provides possible explanations why the previous weak-measurement scheme was successful. The direct tomography relies inevitably on post-selection, and the proposed schemes offer asymptotic gains as the number of pointers in entanglement increases.