Skip to main content
SpringerLink
Log in

The Witten index for 1D supersymmetric quantum walks with anisotropic coins

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

Chiral symmetric discrete-time quantum walks possess supersymmetry, and their associated Witten indices can be naturally defined. The Witten index is known to give a lower bound for the number of topologically protected bound states. The purpose of this paper is to give a complete classification of the Witten index for a one-dimensional split-step quantum walk. It turns out that the Witten index of this model exhibits a striking similarity to that of a Dirac particle model in supersymmetric quantum mechanics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

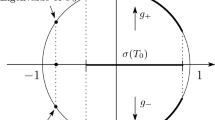
  1. That is to say, \(\pm 1\) are not accumulation points of the spectrum of U.

References

  1. Ambainis, A., Bach, E., Nayak, A., Vishwanath, A., Watrous, J.: One-dimensional quantum walks. In: Proceedings of 33th ACM Symposium of the Theory of Computing, pp. 37–49 (2001)

  2. Arai, A.: Analysis on Fock Spaces and Mathematical Theory of Quantum Fields: An Introduction to Mathematical Analysis of Quantum Fields. World Scientific Publishing Company, Singapore (2017)

    MATH  Google Scholar 

  3. Asbóth, J.K., Obuse, H.: Bulk-boundary correspondence for chiral symmetric quantum walks. Phys. Rev. B 88, 121406 (2013)

    Article  ADS  Google Scholar 

  4. Barkhofen, S., Lorz, L., Nitsche, T., Silberhorn, C., Schomerus, H.: Supersymmetric polarization anomaly in photonic discrete-time quantum walks. Phys. Rev. Lett. 121, 260501 (2018)

    Article  ADS  Google Scholar 

  5. Bolle, D., Gesztesy, F., Grosse, H., Schweiger, W., Simon, B.: Witten index, axial anomaly, and Krein’s spectral shift function in supersymmetric quantum mechanics. J. Math. Phys. 28, 1512–1525 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  6. Bracken, A.J., Ellinas, D., Smyrnakis, I.: Free-dirac-particle evolution as a quantum random walk. Phys. Rev. A 75, 022322 (2007)

    Article  ADS  Google Scholar 

  7. Cedzich, C., Geib, T., Stahl, C., VelÃązquez, L., Werner, A.H., Werner, R.F.: Complete homotopy invariants for translation invariant symmetric quantum walks on a chain. arXiv:1804.04520

  8. Cedzich, C., Geib, T., Grünbaum, F.A., Stahl, C., Velázquez, L., Werner, A.H., Werner, R.F.: The topological classification of one-dimensional symmetric quantum walks. Ann. Henri Poincaré 19, 325–383 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  9. Elaydi, S.: An Introduction to Difference Equations. Undergraduate Texts in Mathematics, 3rd edn. Springer, New York (2005)

    Google Scholar 

  10. Endo, S., Endo, T., Konno, N., Segawa, E., Takei, M.: Limit theorems of a two-phase quantum walk with one defect. Quantum Inf. Comput. 15, 1373–1396 (2015)

    MathSciNet  Google Scholar 

  11. Fuda, T., Funakawa, D., Suzuki, A.: Weak limit theorem for a one-dimensional split-step quantum walk. Rev. Math. Pures Appl. 64(2–3), 157–165 (2019)

    MathSciNet  MATH  Google Scholar 

  12. Fuda, T., Funakawa, D., Suzuki, A.: Localization of a multi-dimensional quantum walk with one defect. Quantum Inf. Process. 16, 203 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  13. Fuda, T., Funakawa, D., Suzuki, A.: Localization for a one-dimensional split-step quantum walk with bound states robust against perturbations. J. Math. Phys. 59, 082201 (2018). https://doi.org/10.1063/1.5035300

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Gesztesy, F., Simon, B.: Topological invariance of the witten index. J. Funct. Anal. 79, 91–102 (1988)

    Article  MathSciNet  Google Scholar 

  15. Grimmett, G., Janson, S., Scudo, P.: Weak limits for quantum random walks. Phys. Rev. E 69, 026119 (2004)

    Article  ADS  Google Scholar 

  16. Gross, D., Nesme, V., Vogts, H., Werner, R.F.: Index theory of one dimensional quantum walks and cellular automata. Commun. Math. Phys. 310, 419–454 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  17. Grover, L.: A fast quantum mechanical algorithm for database search. In: Proceeding of the 28th ACM Symposium on Theory of Computing, pp. 212–219 (1996)

  18. Higuchi, Yu., Segawa, E.: The spreading behavior of quantum walks induced by drifted random walks on some magnifier graph. Quantum Inf. Comput. 17, 0399–0414 (2017)

    MathSciNet  Google Scholar 

  19. Higuchi, Yu., Segawa, E.: Quantum walks induced by Dirichlet random walks on infinite trees. J. Phys. A Math. Theor. 51, 075303 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  20. Higuchi, Yu., Konno, N., Sato, I., Segawa, E.: Spectral and asymptotic properties of Grover walks on crystal lattices. J. Funct. Anal. 267, 4197–4235 (2014)

    Article  MathSciNet  Google Scholar 

  21. Kitagawa, T.: Topological phenomena in quantum walks: elementary introduction to the physics of topological phases. Quantum Inf. Process. 11, 1107–1148 (2012)

    Article  MathSciNet  Google Scholar 

  22. Kitagawa, T., Rudner, M.S., Berg, E., Demler, E.: Exploring topological phases with quantum walks. Phys. Rev. A 82, 033429 (2010)

    Article  ADS  Google Scholar 

  23. Kitagawa, T., Broome, M.A., Fedrizzi, A., Rudner, M.S., Berg, E., Kassal, I., Aspuru-Guzik, A., Demler, E., White, A.G.: Observation of topologically protected bound states in photonic quantum walks. Nat. Commun. 3, 882 (2012)

    Article  ADS  Google Scholar 

  24. Konno, N.: Quantum random walks in one dimension. Quantum Inf. Process. 1, 345–354 (2002)

    Article  MathSciNet  Google Scholar 

  25. Konno, N.: One-dimensional discrete-time quantum walks on random environment. Quantum Inf. Process. 8, 387–399 (2009)

    Article  MathSciNet  Google Scholar 

  26. Konno, N.: Localization of an inhomogeneous discrete-time quantum walk on the line. Quantum Inf. Process. 9, 405–418 (2010)

    Article  MathSciNet  Google Scholar 

  27. Konno, N., Łuczak, T., Segawa, E.: Limit measures of inhomogeneous discrete-time quantum walks in one dimensional. Quantum Inf. Process. 12, 33–53 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  28. Konno, K., Portugal, R., Sato, I., Segawa, E.: Partition-based discrete-time quantum walks. Qunatum Inf. Process. 17, 100 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  29. Kurzyński, P.: Relativistic effects in quantum walks: Klein’s paradox and zitterbewegung. Phys. Lett. A 372, 6125–6129 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  30. Maeda, M., Suzuki, A.: Continuous limits of linear and nonlinear quantum walks. Rev. Math. Phys. https://doi.org/10.1142/S0129055X20500087

  31. Magniez, F., Nayak, A., Roland, J., Santha, M.: Search via quantum walk. In: ACM Symposium on Theory of Computing, pp. 575–584 (2007)

  32. Magniez, F., Nayak, A., Richter, P., Santha, M.: On the hitting times of quantum versus random walks. Algorithmica 63, 91–116 (2012)

    Article  MathSciNet  Google Scholar 

  33. Meyer, D.A.: Quantum lattice gases and their invariants. Int. J. Mod. Phys. C 8, 717–735 (1997)

    Article  ADS  Google Scholar 

  34. Mochizuki, K., Kim, D., Obuse, H.: Explicit definition of PT symmetry for nonunitary quantum walks with gain and loss. Phys. Rev. A 93, 062116 (2016)

    Article  ADS  Google Scholar 

  35. Obuse, H., Kawakami, N.: Topological phases and delocalization of quantum walks in random environments. Phys. Rev. B 84, 195139 (2011)

    Article  ADS  Google Scholar 

  36. Obuse, H., Asbóth, J.K., Nishimura, Y., Kawakami, N.: Unveiling hidden topological phases of a one-dimensional Hadamard quantum walk. Phys. Rev. B 92, 045424 (2015)

    Article  ADS  Google Scholar 

  37. Ohno, H.: Unitary equivalent classes of one-dimensional quantum walks. Quantum Inf. Process. 15, 3599–3617 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  38. Portugal, R., Santos, R.A.M., Fernandes, T.D., GonÃğalves, D.N.: The staggered quantum walk model. Quantum Inf. Process. 15, 85 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  39. Richard, S., Suzuki, A., Tiedra de Aldecoa, R.: Quantum walks with an anisotropic coin I: spectral theory. Lett. Math. Phys. 108, 331–357 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  40. Richard, S., Suzuki, A., Tiedra de Aldecoa, R.: Quantum walks with an anisotropic coin II: scattering theory. Lett. Math. Phys. 109, 61–88 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  41. Segawa, E., Suzuki, A.: Spectral mapping theorem of an abstract quantum walk. Quantum Inf. Process. https://doi.org/10.1007/s11128-019-2448-6

  42. Segawa, E.: Localization of quantum walks induced by recurrence properties of random walks. J. Comput. Theor. Nanosci. 10, 1583–1590 (2013)

    Article  Google Scholar 

  43. Shikano, Y., Katsura, H.: Localization and fractality in inhomogeneous quantum walks with self-duality. Phys. Rev. E 82, 031122 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  44. Strauch, F.W.: Relativistic quantum walks. Phys. Rev. A 73, 054302 (2006). Erratum Phys. Rev. A 73, 069908, 2006

    Article  ADS  MathSciNet  Google Scholar 

  45. Strauch, F.W.: Relativistic effects and rigorous limits for discrete- and continuous-time quantum walks. J. Math. Phys. 48, 082102 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  46. Suzuki, A.: Supersymmetry for chiral symmetric quantum walks. Quantum Inf. Process. 18, 363 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  47. Suzuki, A.: Asymptotic velocity of a position-dependent quantum walk. Quantum Inf. Process. 15, 103–119 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  48. Szegedy, M.: Quantum speed-up of Markov chain based algorithms. In: Proceedings of 45th IEEE Symposium on Foundations of Computer Science, pp. 32–41 (2004)

  49. Thaller, B.: The Dirac equation. Texts and Monographs in Physics. Springer, Berlin (1992)

    Google Scholar 

  50. Xiao, L., Zhan, X., Bian, Z.H., Wang, K.K., Zhang, X., Wang, X.P., Li, J., Mochizuki, K., Kim, D., Kawakami, N., Yi, W., Obuse, H., Sanders, B.C., Xue, P.: Observation of topological edge states in parity-time-symmetric quantum walks. Nat. Phys. 13, 1117–1123 (2017)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are deeply indebted to the members of the Shinshu Mathematical Physics Group for extremely valuable discussions and comments. A. S. was supported by JSPS KAKENHI Grant Number JP18K03327. This work was also supported by the Research Institute for Mathematical Sciences, a Joint Usage/Research Center located in Kyoto University.

Author information

Authors and Affiliations

  1. Division of Mathematics and Physics, Faculty of Engineering, Shinshu University, Wakasato, Nagano, 380-8553, Japan

    Akito Suzuki

  2. School of Computer Science, Engineering and Mathematics, Flinders University, 1284 South Road, Clovelly Park, SA, 5042, Australia

    Yohei Tanaka

Authors
  1. Akito Suzuki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yohei Tanaka
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Akito Suzuki.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Suzuki, A., Tanaka, Y. The Witten index for 1D supersymmetric quantum walks with anisotropic coins. Quantum Inf Process 18, 377 (2019). https://doi.org/10.1007/s11128-019-2485-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-019-2485-1

Keywords

Search

Navigation