Skip to main content
SpringerLink
Log in

Approximating ground and excited state energies on a quantum computer

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

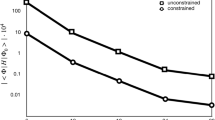
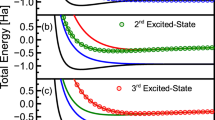
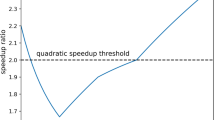
Abstract

Approximating ground and a fixed number of excited state energies, or equivalently low-order Hamiltonian eigenvalues, is an important but computationally hard problem. Typically, the cost of classical deterministic algorithms grows exponentially with the number of degrees of freedom. Under general conditions, and using a perturbation approach, we provide a quantum algorithm that produces estimates of a constant number \(j\) of different low-order eigenvalues. The algorithm relies on a set of trial eigenvectors, whose construction depends on the particular Hamiltonian properties. We illustrate our results by considering a special case of the time-independent Schrödinger equation with \(d\) degrees of freedom. Our algorithm computes estimates of a constant number \(j\) of different low-order eigenvalues with error \(O(\varepsilon )\) and success probability at least \(\frac{3}{4}\), with cost polynomial in \(\frac{1}{\varepsilon }\) and \(d\). This extends our earlier results on algorithms for estimating the ground state energy. The technique we present is sufficiently general to apply to problems beyond the application studied in this paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. For functions \(f,g\ge 0\) defined on \({\mathbb R}_+\), the notation \(f(\varepsilon )=\omega (g(\varepsilon ))\) means that for any \(M>0\), arbitrarily large, we have \(f(\varepsilon )\ge M g(\varepsilon )\) for sufficiently small \(\varepsilon \).

  2. We give an explicit construction for \(B\) in Eq. (17).

  3. Here and elsewhere, by reasonable overlap we mean that the magnitude of the projection is not exponentially small in \(d\).

  4. This follows immediately for \(m=O(1)\) from the bound \(\left( {\begin{array}{c}d\\ m\end{array}}\right) \le \frac{d^m}{m!} = poly(d)\).

References

  1. Abrams, D.S., Lloyd, S.: Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys. Rev. Lett. 83, 5162–5165 (1999)

    Article  ADS  Google Scholar 

  2. Aharonov, D., Ta-Shma, A.: Adiabatic quantum state generation and statistical zero knowledge. In: Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, pp. 20–29. ACM (2003)

  3. Andrews, B., Clutterbuck, J.: Proof of the fundamental gap conjecture. J. Am. Math. Soc. 24(3), 899–916 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  4. Aspuru-Guzik, A., Dutoi, A.D., Love, P.J., Head-Gordon, M.: Simulated quantum computation of molecular energies. Science 309(5741), 1704–1707 (2005)

    Article  ADS  Google Scholar 

  5. Babuska, I., Osborn, J.: Eigenvalue problems. Handb. Numer. Anal. 2, 641 (1991)

    MathSciNet  Google Scholar 

  6. Berry, D.W., Ahokas, G., Cleve, R., Sanders, B.C.: Efficient quantum algorithms for simulating sparse hamiltonians. Commun. Math. Phys. 270(2), 359–371 (2007)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  7. Bravyi, S., Divincenzo, D.P., Oliveira, R.I., Terhal, B.M.: The complexity of stoquastic local Hamiltonian problems. Quantum Inf. Comput. 8(5), 361–385 (2008)

    MathSciNet  Google Scholar 

  8. Cao, Y., Papageorgiou, A., Petras, I., Traub, J.F., Kais, S.: Quantum algorithm and circuit design solving the Poisson equation. New J. Phys. 15, 013021 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  9. Childs, A.M., Gosset, D., Webb, Z.: The Bose–Hubbard model is qma-complete. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) Automata, Languages, and Programming. Volume 8572 of Lecture Notes in Computer Science, pp. 308–319. Springer, Berlin (2014)

  10. Cullum, J.K., Willoughby, R.A.: Lanczos algorithms for large symmetric eigenvalue computations: vol. 1: theory, vol. 41. SIAM (2002)

  11. Demmel, J.W.: Applied Numerical Linear Algebra. SIAM, Philadelphia, PA (1997)

    Book  MATH  Google Scholar 

  12. Feynman, R.: Simulating physics with computers. SIAM J. Comput. 26, 1484–1509 (1982)

    Google Scholar 

  13. Forsythe, G.E., Wasow, W.R.: Finite-Difference Methods for Partial Differential Equations. Dover, New York (2004)

    MATH  Google Scholar 

  14. Furche, F., Rappoport, D.: Density functional methods for excited states: equilibrium structure and electronic spectra. In: Olivucci, M. (ed.) Computational Photochemistry. Theoretical and Computational Chemistry, vol. 16, pp. 93–128. Elsevier, Amsterdam (2005)

    Chapter  Google Scholar 

  15. Golub, G.H., Van Loan, C.F.: Matrix Computations. JHU Press, Baltimore (2012)

    Google Scholar 

  16. Gustafson, S.J., Sigal, I.M.: Mathematical Concepts of Quantum Mechanics. Springer, Berlin (2011)

    MATH  Google Scholar 

  17. Hislop, P.D., Sigal, I.M.: Introduction to Spectral Theory: With Applications to Schrödinger Operators. Number v. 113 in Applied Mathematical Sciences Series. Springer, New York (1996)

    MATH  Google Scholar 

  18. Hohenberg, P., Kohn, W.: Inhomogeneous electron gas. Phys. Rev. 136(3B), B864 (1964)

    Article  ADS  MathSciNet  Google Scholar 

  19. Kassal, I., Whitfield, J.D., Perdomo-Ortiz, A., Yung, M.-H., Aspuru-Guzik, A.: Simulating chemistry using quantum computers. Ann. Rev. Phys. Chem. 62, 185–207 (2011)

    Article  ADS  Google Scholar 

  20. Kempe, J., Kitaev, A., Regev, O.: The complexity of the local Hamiltonian problem. SIAM J. Comput. 35(5), 1070–1097 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  21. Klappenecker, A., Rötteler, M.: Discrete cosine transforms on quantum computers. In: Proceedings of the 2nd International Symposium on Image and Signal Processing and Analysis, pp. 464–468 (2001)

  22. Lanyon, B.P., Whitfield, J.D., Gillett, G.G., Goggin, M.E., Almeida, M.P., Kassal, I., Biamonte, J.D., Mohseni, M., Powell, B.J., Barbieri, M., Aspuru-Guzik, A., White, A.G.: Towards quantum chemistry on a quantum computer. Nat. Chem. 2, 106–111 (2010)

    Article  Google Scholar 

  23. Leveque, R.J.: Finite Difference Methods for Ordinary and Partial Differential Equations. SIAM, Philadelphia, PA (2007)

    Book  MATH  Google Scholar 

  24. Lloyd, S.: Universal quantum simulators. Science 273(5278), 1073–1078 (1996)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  25. Love, P.J.: Back to the future: a roadmap for quantum simulation from vintage quantum chemistry. In: Kais, S. (ed.) Quantum Information and Computation for Chemistry. Advances in Chemical Physics, vol. 154, pp. 39–66. Wiley, Hoboken, NJ (2014)

    Chapter  Google Scholar 

  26. Nielsen, M., Chuang, I.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  27. Papageorgiou, A.: On the complexity of the multivariate Sturm–Liouville eigenvalue problem. J. Complex. 23(4–6), 802–827 (2007)

    Article  MATH  Google Scholar 

  28. Papageorgiou, A., Petras, I.: Estimating the ground state energy of the Schrödinger equation for convex potentials. J. Complex. 30, 469–494 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  29. Papageorgiou, A., Petras, I., Traub, J.F., Zhang, C.: A fast algorithm for approximating the ground state energy on a quantum computer. Math. Comput. 82(284), 2293–2304 (2014)

    Article  MathSciNet  Google Scholar 

  30. Papageorgiou, A., Traub, J.F.: Measures of quantum computing speedup. Phys. Rev. A 88(2), 022316 (2013)

    Article  ADS  Google Scholar 

  31. Papageorgiou, A., Zhang, C.: On the efficiency of quantum algorithms for Hamiltonian simulation. Quantum Inf. Process. 11, 541–561 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  32. Parlett, B.N.: The Symmetric Eigenvalue Problem, vol. 7. SIAM, Philadelphia (1980)

    MATH  Google Scholar 

  33. Schuch, N., Verstraete, F.: Computational complexity of interacting electrons and fundamental limitations of density functional theory. Nat. Phys. 5(10), 732–735 (2009)

    Article  Google Scholar 

  34. Strang, G., Fix, G.J.: An Analysis of the Finite Element Method, 2nd edn. Wellesley-Cambridge Press, Wellesley (2008)

    Google Scholar 

  35. Suzuki, M.: Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations. Phys. Lett. A 146(6), 319–323 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  36. Suzuki, M.: General theory of fractal path integrals with application to many-body theories and statistical physics. J. Math. Phys. 32, 400–407 (1991)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  37. Titchmarsh, E.C.: Eigenfunction Expansions: Associated with Second-Order Differential Equations. Oxford University Press, Oxford (1962)

    MATH  Google Scholar 

  38. Wei, T.-C., Mosca, M., Nayak, A.: Interacting boson problems can be QMA hard. Phys. Rev. Lett. 104(4), 040501 (2010)

    Article  ADS  Google Scholar 

  39. Weinberger, H.F.: Upper and lower bounds for eigenvalues by finite difference methods. Commun. Pure Appl. Math. 9(3), 613–623 (1956)

    Article  MATH  MathSciNet  Google Scholar 

  40. Weinberger, H.F.: Lower bounds for higher eigenvalues by finite difference methods. Pac. J. Math. 8(2), 339–368 (1958)

    Article  MATH  MathSciNet  Google Scholar 

  41. Wickerhauser, M.V.: Adapted Wavelet Analysis from Theory to Software. A.K. Peters, Wellesley, MA (1994)

    MATH  Google Scholar 

  42. Zalka, C.: Efficient simulation of quantum systems by quantum computers. Fortschr. Phys. 46(6–8), 877–879 (1998)

    Article  MathSciNet  Google Scholar 

  43. Zalka, C.: Simulating quantum systems on a quantum computer. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 454(1969), 313–322 (1998)

    Article  ADS  MATH  Google Scholar 

Download references

Acknowledgments

The authors would like to thank Joseph F. Traub for useful comments and suggestions. This research has been supported in part by NSF/DMS.

Author information

Authors and Affiliations

  1. Department of Computer Science, Columbia University, New York, NY, 10027, USA

    Stuart Hadfield & Anargyros Papageorgiou

Authors
  1. Stuart Hadfield
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anargyros Papageorgiou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stuart Hadfield.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hadfield, S., Papageorgiou, A. Approximating ground and excited state energies on a quantum computer. Quantum Inf Process 14, 1151–1178 (2015). https://doi.org/10.1007/s11128-015-0927-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-015-0927-y

Keywords

Search

Navigation