Efficient estimation of true fixed-effects stochastic frontier models

Abstract

Fixed-effects modeling has become the method of choice in several panel data settings, including models for stochastic frontier analysis. A notable instance of stochastic frontier panel data models is the true fixed-effects model, which allows disentangling unit heterogeneity from efficiency evaluations. While such a model is theoretically appealing, its estimation is hampered by incidental parameters. This note proposes a simple and rather general estimation approach where the unit-specific intercepts are integrated out of the likelihood function. We apply the theory of composite group families to the model of interest and demonstrate that the resulting integrated likelihood is a marginal likelihood with desirable inferential properties. The derivation of the result is provided in full, along with some connections with the existing literature and computational details. The method is illustrated for three notable models, given by the normal-half normal model, the heteroscedastic exponential model, and the normal-gamma model. The results of simulation experiments highlight the properties of the methodology.

1 Introduction

Fixed-effects models are prominent in modern panel data econometrics since they adjust for unit heterogeneity, potentially correlated with the covariates. The robustness of fixed-effects models is rather important in stochastic frontier analysis, which explains the popularity of the true fixed-effects stochastic frontier model (Greene 2005a, b). For a production frontier model, the specification of the true fixed-effects model is given by

$${y}_{it}={\alpha }_{i}+{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}}-{u}_{it}+{v}_{it},$$

(1)

where i is the index for the unit of the panel (i = 1, …, n) and t is the index for time (t = 1, …, T), with T assumed to be the same across units without loss of generality. Here y_it is the output and x_it is a vector of exogenous inputs, both possibly in log form, β is a vector of coefficients and α_i the unit fixed effect. In the following, we will also employ y_i and X_i to denote the vector of outputs and the matrix of inputs for the i-th panel member, respectively. Furthermore, u_it is the one-sided inefficiency term, and v_it is the symmetric idiosyncratic error, independent of u_it. A simple change in the sign of u_it is required for a cost frontier model specification. We assume conditional independence (given α_i and x_i1, …, x_iT) of observations within the same panel member and independence across units. Finally, we denote by θ the set of structural model parameters, given by β plus all the parameters entering the distribution of the error term ε_it = v_it − u_it.

The introduction of the unit-specific intercepts α_i is the key to disentangle heterogeneity from efficiency, but at the same time, when the intercepts are estimated jointly with the other model parameters, the incidental parameters issue arises; see, for example, Bartolucci et al. (2016). In short, α_i is consistently estimated only for T → ∞. For finite T, the resulting bias accumulates across panel members, and it propagates to θ, thus affecting the efficiency evaluation for settings with short panels. Therefore, some caution is required when estimating the structural parameters.

There are some proposals in the econometric literature that overcome the incidental parameters problem for some notable true fixed-effects model specifications, but they all rely on specific distributional properties. This note aims to present a simple and $\sqrt{n}$-consistent estimation method that could be effectively applied to a broad array of distributions for ε_it. Moreover, it provides an efficient estimator which is at least as efficient as existing consistent estimators.

The outline of this note is as follows. Section 2 reviews the econometric literature on consistent estimation of true fixed-effects models. The proposal is presented in Section 3, where mathematical support is provided. Some numerical studies are reported in Section 4, including an application to the challenging normal-gamma model. Section 5 provides a brief discussion.

2 Background

A marginal maximum likelihood estimation for model (1) is developed in Chen et al. (2014) paralleling the usual derivation of the within estimator for linear models. In particular, the authors consider the deviation of each term of the model from the unit mean and then maximize the within likelihood defined on the (T − 1) deviations of the error term for the i-th unit. The method is specific to the normal-half normal model where the components of ε_it are half normally distributed ${u}_{it} \sim {N}^{+}(0,{\sigma }_{u}^{2})$, and normally distributed ${v}_{it} \sim N(0,{\sigma }_{v}^{2})$, respectively. Using the results from the multivariate closed skew normal distribution (see González-Farías et al. 2004, and the references therein), they show that neglecting a constant additive term, the within log-likelihood function is

$$\begin{array}{lll}{\ell }_{{{{\rm{W}}}}}({{{\boldsymbol{\theta }}}})&=&\mathop{\sum }\limits_{i\,=\,1}^{n}\log {\phi }_{T-1}\left({\tilde{{{{\boldsymbol{y}}}}}}_{i}^{* }-{\tilde{{{{\boldsymbol{X}}}}}}_{i}^{* }{{{\boldsymbol{\beta }}}};{{{{\bf{0}}}}}_{T-1},{\sigma }^{2}\,\left({{{{\boldsymbol{I}}}}}_{T-1}-\frac{{{{\boldsymbol{{E}}}_{T-1}}}}{T}\right)\right)\\ &&+\, \mathop{\sum }\limits_{i=1}^{n}\log {\Phi }_{T}\left(-\displaystyle\frac{\lambda }{\sigma }\,\left({\tilde{{{{\boldsymbol{y}}}}}}_{i}-{\tilde{{{{\boldsymbol{X}}}}}}_{i}{{{\boldsymbol{\beta }}}}\right);{{{{\bf{0}}}}}_{T},{{{{\boldsymbol{I}}}}}_{T}+\frac{{\lambda }^{2}}{T}\,{{{{\boldsymbol{E}}}}}_{T}\right),\end{array}$$

(2)

where ϕ_m(⋅) and Φ_m(⋅) denote the density function and the CDF of the m-dimensional normal distribution, ${\sigma }^{2}={\sigma }_{u}^{2}+{\sigma }_{v}^{2}$, and λ = σ_u/σ_v. Further, the notation $\tilde{{{{\boldsymbol{X}}}}}$ denotes the within transformation of the m-dimensional vector x, namely the deviation of the m values of x from its the sample mean, whereas the notation ${\tilde{{{{\boldsymbol{X}}}}}}^{* }$ denotes that only the first m − 1 such values are retained. Finally, 0_m is a vector of m zeros, I_m is the identity matrix of size m, and E_m is a m × m matrix of ones. The expression (2) is free of α_i, and its maximizer defines the maximum marginal likelihood estimator (MMLE), which is consistent for increasing n regardless of the value of the panel length T. Wang and Ho (2010) define a similar estimator, but for a different model where u_it = u_i h_it, with h_it being a non-random function of some covariates, and assuming u_i half normally distributed. See also Kutlu et al. (2020).

Another contribution is Wikström (2015), who defines a method-of-moments estimator and provides a simulation study for the same model considered by Chen et al. (2014). The proposal has some interesting properties, such as its logical simplicity. On the other hand, it is likely to be less efficient than the MMLE since the latter is based on a marginal likelihood (see Pace and Salvan 1997, Chap. 4), and the method of moments is at times prone to numerical instabilities, as testified by the “problematic replications” reported in Wikström (2015).

Belotti and Ilardi (2018) provide some notable estimation strategies. Among other things, they note that the proposal in Chen et al. (2014), exploiting the closure property of the skew normal distribution, could be applied to some extensions of the normal-half normal model, including the truncated normal distribution for the inefficiency term, heteroscedasticity, and autocorrelation between different inefficiencies. They also note that while the T-dimensional normal CDF involved in the log-likelihood (2) can be reduced to a one-dimensional integral, the within log-likelihood for such extensions would involve an irreducible T-dimensional normal CDF, whose computation for large panel lengths may become cumbersome. Hence, they propose another estimator, the pairwise difference estimator (PDE).

The PDE is the maximizer of an objective function involving the distribution of all the differences between pairs of observations belonging to the same panel member, much in the spirit of composite likelihood estimation (Varin et al. 2011). The results reported by Belotti and Ilardi (2018) illustrate the $\sqrt{n}$-consistency of the proposal, which is, however, feasible only for truncated normal or exponential inefficiency terms.

Finally, we note that Belotti and Ilardi (2018) propose another estimator, the marginal maximum simulated likelihood estimator (MMSLE), which approximates the MMLE by simulation, also covering some heteroscedastic extensions not considered by Chen et al. (2014). The simulations in Belotti and Ilardi (2018) show that the MMSLE is a good approximation to the MMLE for the normal-half normal model. At any rate, while theoretically interesting, its Monte Carlo nature makes it less appealing than the original MMLE.

3 Estimation via marginal likelihood

A general solution for consistent estimation of the structural parameters θ proceeds by noting that given the sample for the i-th unit, α_i acts as a location parameter.

We start by considering the order statistics for the i-th panel member $({y}_{i(1)},\ldots ,{y}_{i(T)})$, from which we define the following data vector

$${{{{\boldsymbol{s}}}}}_{i}={{{{\boldsymbol{s}}}}}_{i}({y}_{i1},\ldots ,{y}_{iT})=({y}_{i(2)}-{y}_{i(1)},\ldots ,{y}_{i(T)}-{y}_{i(1)}).$$

(3)

It is straightforward to verify that the distribution of s_i is free of the unit-specific intercept α_i, which is eliminated by pivoting on the smallest observation. This suggests the following marginal likelihood for θ

$${L}_{{{{\rm{M}}}}}({{{\boldsymbol{\theta }}}})=\mathop{\prod }\limits_{i=1}^{n}{f}_{S}({{{{\boldsymbol{s}}}}}_{i};{{{\boldsymbol{\theta }}}}),$$

where f_S(s_i; θ) is the density of s_i. The remaining task is to obtain an analytic expression for f_S(s_i; θ). To this end, we rely on the theory of composite group families. In particular, we follow the same steps as Pace and Salvan (1997, Theorem 7.5)¹ to express the marginal likelihood (aside from a constant factor) as

$${L}_{{{{\rm{M}}}}}({{{\boldsymbol{\theta }}}})=\mathop{\prod }\limits_{i=1}^{n}{f}_{S}({{{{\boldsymbol{s}}}}}_{i};{{{\boldsymbol{\theta }}}})=\mathop{\prod }\limits_{i=1}^{n}\int\nolimits_{-\infty }^{\infty }\mathop{\prod }\limits_{t=1}^{T}{f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})\,{{{{d}}}}{\alpha }_{i},$$

(4)

where f_Y(y_it; α_i, θ) is the density function of y_it, from which we readily define the marginal log-likelihood ${\ell }_{{{{\rm{M}}}}}({{{\boldsymbol{\theta }}}})=\log {L}_{{{{\rm{M}}}}}({{{\boldsymbol{\theta }}}})$. The expression (4) greatly facilitates the task of obtaining the marginal likelihood based on (3), which would be otherwise rather involved to obtain directly. The only issue is the approximation of the one-dimensional integrals in (4), for which we provide some guidelines in what follows. Moreover, note that the expression (4) requires the density f_Y(y_it; α_i, θ) of the response variable y_it, that in most cases is not difficult to obtain; at any rate, the example in section 4.3 illustrates how to proceed when this is not the case.

Since ℓ_M(θ) is a marginal log-likelihood based on n independent data vectors, it can be treated as a bona fide log-likelihood function for θ. Hence its maximizer is $\sqrt{n}$-consistent and the inverse of its negative Hessian evaluated at the maximizer is a valid estimate of the sampling variance. Note that for an incidental parameter of a different nature than a location parameter, the elimination through integration as in (4) may not provide any improvement on the incidental parameter bias; see Schumann et al. (2021) and the references therein. We note in passing that the marginal likelihood (4) is an instance of a class of integrated likelihood functions studied in Arellano and Bonhomme (2009). A connection between the results presented here and the theory of the latter paper is illustrated in Appendix B.

The marginal likelihood in (4) provides a rather general and relatively simple estimation approach without needing specific distributional properties. As a general fact in the frontier specification, the integrals in (4) do not have a closed-form solution, and they must be approximated by numerical methods. For panel data settings, however, the n integrals must be approximated with high accuracy; otherwise, the error in the approximation accumulates across panel groups. For this reason, we endorse the use of adaptive Gaussian quadrature (Liu and Pierce 1994) with Q quadrature points, which gives the following approximation to ℓ_M(θ) (neglecting a constant additive term)

$${\widehat{\ell }}_{{{{\rm{M}}}}}({{{\boldsymbol{\theta }}}})=\mathop{\sum }\limits_{i=1}^{n}\log \left[{{{{\rm{se}}}}}_{i}({{{\boldsymbol{\theta }}}})+\mathop{\sum }\limits_{q=1}^{Q}{w}_{q}\,\exp \left\{{z}_{q}^{2}+\mathop{\sum }\limits_{t=1}^{T}\log {f}_{Y}({y}_{it};{z}_{q}^{* },{{{\boldsymbol{\theta }}}})\right\}\right],$$

(5)

where z_q and w_q are the Gauss-Hermite quadrature nodes and weights. Furthermore, ${z}_{q}^{* }$ are the adjusted nodes ${z}_{q}^{* }=\sqrt{2}\,{{{{\rm{se}}}}}_{i}({{{\boldsymbol{\theta }}}})\,{z}_{q}+{\widehat{\alpha }}_{i}({{{\boldsymbol{\theta }}}})$, where ${\widehat{\alpha }}_{i}({{{\boldsymbol{\theta }}}})$ is the mode of $\sum_{t = 1}^{T}\log {f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})$ in α_i, and se_i(θ) is the reciprocal of the squared root of the second derivative of $-\sum_{t = 1}^{T}\log {f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})$ with respect to α_i, evaluated at ${\widehat{\alpha }}_{i}({{{\boldsymbol{\theta }}}})$.

The important advantage of the approximation (5) is that, by tuning Q, we can keep the approximation error under strict control. Indeed, having a $\sqrt{n}$-consistent estimator as a target, it seems reasonable to aim for an approximation error smaller than the inferential error n^−1/2. Following Stringer and Bilodeau (2022), we should choose Q at least equal to $\lceil (3/2){\log }_{T}(n)-2\rceil$, where ⌈⋅⌉ is the ceiling function. For instance, for T = 5, which is the smallest panel length considered in the aforementioned stochastic frontier literature, the latter formula implies that around 10 quadrature points are sufficient for n as large as 100,000. All the results of the next section were obtained with Q = 25, well above the required number, and indeed, we cross-checked the high accuracy of the approximation by comparison with the more computationally expensive Gauss-Kronrod quadrature.

4 Some notable models

In this section, we apply the Integrated Likelihood Estimator (ILE) defined by the maximizer of (4) to some models of interest.

4.1 The normal-half normal model

A fundamental model is the normal-half normal model, studied by both Chen et al. (2014) and Belotti and Ilardi (2018). For the case where ${u}_{it} \sim {{{{{N}}}}}^{+}(0,{\sigma }_{u}^{2})$ and ${v}_{it} \sim N(0,{\sigma }_{v}^{2})$, we followed these authors and considered the same single-input simulation scenario. Since we found that the ILE matches the MMLE for all the model parameters with high numerical accuracy, we do not report any results here. The equivalence between ILE and MMLE is encouraging since the latter is a benchmark estimator for the normal-half normal TFE model. Notice that the same equivalence occurs in the case of panel data models with fixed effects and normal errors (Schumann et al. 2021).

We end this example by noting that for the extension to truncated normal inefficiency coupled with heteroscedasticity, the computation of MMLE would require the evaluation of the T-dimensional normal CDF, with a computational burden increasing with the group size. On the contrary, the marginal likelihood (4) would retain the same order of complexity.

4.2 The heteroscedastic exponential model

This is another example considered in Belotti and Ilardi (2018), for which the PDE provides good estimation performance. Here we assume ${u}_{it} \sim {{{\mathcal{E}}}}({\sigma }_{iu})$ and ${v}_{it} \sim {{{{N}}}}(0,{\sigma }_{v}^{2})$, where ${\sigma }_{iu}=\exp ({\gamma }_{0}+{z}_{i}\,{\gamma }_{1})$. With such a specification, and after setting ${r}_{it}={y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}}$, the density of each observation of the i-th panel member becomes

$${f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})=\frac{1}{{\sigma }_{iu}}\,\exp \left\{\frac{{r}_{it}}{{\sigma }_{iu}}+\log \Phi \left(-\frac{{r}_{it}}{{\sigma }_{v}}-\frac{{\sigma }_{v}}{{\sigma }_{iu}}\right)+\frac{{\sigma }_{v}^{2}}{2\,{\sigma }_{iu}^{2}}\right\}.$$

We focus here on some of the simulation experiments reported in Belotti and Ilardi (2018) and compared our implementation of the ILE with the PDE; the latter was computed using the Stata code made available by Belotti et al. (2013).

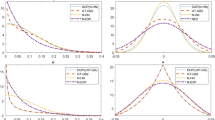
Plots in Fig. 1 display the results based on 1000 simulated datasets for the same simulation scenario of section 6.1 in Belotti and Ilardi (2018), with the setting corresponding to their Table 1, namely n = 100, T = 5, and “signal to noise ratio” set to 1; this setting was chosen since it is the most challenging, but the results for the other settings are rather similar and are reported in the Supplementary Material. The two estimators may differ on a sample-by-sample basis, yet they exhibit very little bias (if any). The ILE slightly outperforms the PDE in terms of MSE since it is based on a marginal likelihood rather than a pairwise likelihood, yet the difference in efficiency is small.

Fig. 1

Heteroscedastic exponential model. Scatterplots of PDE vs ILE results and boxplots of the two sets of estimates for the setting reported in Table 1 in Belotti and Ilardi (2018), with bisector line added (scatterplots) and horizontal line corresponding to the true parameter value (boxplots)

Table 1 Estimated power of the test of exponentiality

4.3 The normal-gamma model

As mentioned at the outset, the important property of the proposal (4) is its broad generality, and to illustrate this point, we consider here the normal-gamma model. First introduced by Greene (1990), this model has been somewhat underused in applications since it involves computations that are notoriously challenging; see Ritter and Simar (1997), Tsionas (2000), Greene (2003) and the references therein. To the best of our knowledge, the normal-gamma model has never been adopted for the true fixed-effects stochastic frontier model. While the results of Ritter and Simar (1997) illustrate the difficulties that may arise in estimating the efficiency parameters, they also suggest that estimation issues are much less severe with large sample sizes. Since, in the setting of interest, we can glean information about the efficiency parameter from n panel units, the total number of observations may be large enough for meaningful estimation. A similar positive note comes from the Bayesian inferential approach in Tsionas (2000), where it is reported that for a normal-gamma model with a total sample size of 1000, “results are satisfactory”.

The model assumes ${u}_{it} \sim {{{\mathcal{G}}}}(\gamma ,\lambda )$ and ${v}_{it} \sim N(0,{\sigma }_{v}^{2})$. The model density requires the numerical approximation of an integral; letting again ${r}_{it}={y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}}$, the density of each observation of the i-th panel member is

$${f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})=\int\nolimits_{0}^{\infty }\frac{1}{\sqrt{2\pi {\sigma }_{v}^{2}}}\exp \left\{-\frac{({r}_{it}+z)}{2\,{\sigma }_{v}^{2}}-\frac{z}{\lambda }\right\}\,\frac{{z}^{\gamma -1}}{{\lambda }^{\gamma }\,\Gamma (\gamma )}{{{{d}}}}z.$$

(6)

For the ILE, this implies that a double integral is required, and a meticulous numerical implementation is called for. Our strategy entails coding the normal-gamma convolution integral (6) in C++ using adaptive Gauss-Kronrod quadrature with a large number of nodes, plus other steps required for successful implementation of the approximation (5); further details are provided in the Supplementary Material. A fact worth mentioning is that the numerical optimization of the log-likelihood (5) is best achieved with the re-parameterization in which γ and σ_v are replaced by the mean and the standard deviation of the gamma term, namely

$${\mu }_{G}=\gamma \,\lambda , \quad {\sigma }_{G}=\sqrt{{\sigma }_{v}^{2}+\gamma \,{\lambda }^{2}}.$$

The fact that very high accuracy is required for both the inner and outer integrals involved in the log-likelihood function makes its optimization rather expensive; while other models are estimated in a matter of seconds, the estimation of the normal-gamma model may take several minutes.

Figure 2 summarizes the estimation results for 1000 data sets at each of four different settings, with the true efficiency parameter values set at γ = 2, λ = 1 and σ_v = 0.25. This choice of parameters avoids the “relatively difficult” case where γ < 1 (Tsionas 2000), for which, in our settings, the optimization becomes far too slow for a Monte Carlo study. Note that the minimum total sample size considered is 1250: compared to the previous example, the results for the setting n = 100 and T = 5 are not reported, since the estimation turned out to be unreliable.

Fig. 2

Normal-gamma model. Boxplots of ILE results in four different settings, with horizontal lines corresponding to the true parameter value

Despite the challenging estimation, the results are reasonably satisfactory since the distribution of each of the estimators has a median matching the true parameter value in all cases, and it becomes more concentrated around it when the total sample size increases. Though the two settings n = 500, T = 5 and n = 250, T = 10 have the same total sample size, the latter shows slightly better results.

Another useful point concerns the possibility of distinguishing the gamma model from simpler ones. A natural competitor is the normal-exponential, which is obtained as a special case of the model of section 4.2. Table 1 reports the estimated power for a fixed level α = 0.05 of the log-likelihood ratio test for the hypothesis γ = 1, i.e., the test of exponentiality

$$W=2\,\left\{{\widehat{\ell }}_{{{{\rm{M}}}}}(\widehat{{{{\boldsymbol{\theta }}}}})-{\widehat{\ell }}_{{{{\rm{M}}}}}({\widehat{{{{\boldsymbol{\theta }}}}}}_{0})\right\},$$

where $\widehat{{{{\boldsymbol{\theta }}}}}$ is the estimator from the normal-gamma model and ${\widehat{{{{\boldsymbol{\theta }}}}}}_{0}$ the estimator from the normal-exponential model. This is a power computation since the data were generated under the normal-gamma model with γ = 2.

The results suggest that while the setting n = 100 and T = 5 is very far from being suitable to distinguish the gamma model from the exponential one, things get progressively better for the four settings reported in Fig. 2.

5 Discussion

The estimator based on the marginal likelihood obtained by integrating out the panel-specific intercepts in the true fixed-effects stochastic frontier model represents a simple and efficient methodology. The proposal recovers the existing consistent estimators whenever available and can provide a useful solution in other cases. It seems worth noting that the same strategy where group-specific intercepts are integrated out may be relevant to other fixed-effects panel data models with continuous response as an alternative to differencing, providing a $\sqrt{n}$-consistent estimator and avoiding any issue related to the size of T.

The ILE may also be useful in connection with four-component panel stochastic frontier models; see Kumbhakar and Lai (2022) for a recent review. Such models include two random group-specific effects in place of α_i in (1), namely α_i = τ_i − η_i, where τ_i is a group effect and η_i is the persistent inefficiency components. Such an approach allows for more informative efficiency evaluations than the true fixed-effects setting, at the expense of stronger distributional specifications. For those researchers willing to adopt the four-component specification, a recommended approach may be to supplement the analysis with the estimates of several alternative models along the lines of what was done by Kumbhakar et al. (2014). We endorse the inclusion of the true fixed-effects model among the array of considered specifications since its robust nature will provide some coverage against input endogeneity issues. A simple comparison of the estimates of structural parameters and estimated inefficiencies across several models could then provide some valuable information. To this end, the availability of resources for true-fixed effects analysis, including software, may represent a useful addition.

In closing, among possible directions for extension of the current paper, we mention the adoption of other distributions for the inefficiency term or the inclusion of semiparametric effects for the production or cost function, along the lines of the proposal in Bellio and Grassetti (2011). The implementation of the latter, however, would require special care.

6 Software

A public repository with R code for fitting the models presented in this note is available at github.com/lucagrassetti/ilsfa.

Appendices

Appendix A: Inference based on the integrated likelihood

We need to show that marginal likelihood based on s_i in expression (3) of the main paper equals the integrated likelihood

$${f}_{S}({{{{\boldsymbol{s}}}}}_{i};{{{\boldsymbol{\theta }}}})=\int\nolimits_{-\infty }^{\infty }\mathop{\prod }_{t=1}^{T}{f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})\,{{{{d}}}}{\alpha }_{i},$$

(A.1)

To this end, we follow the same steps of the proof of Theorem 7.5 of Pace and Salvan (1997), which covers an even more complex setting for location and scale transformations.

Before proceeding, note that since α_i is a location parameter and ${{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}}$ acts on the location as well, we can define f₀(⋅) such that

$${f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})={f}_{0}({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}),$$

(A.2)

where ψ denotes the set of structural parameters without β, i.e., θ = (β, ψ).

First, we perform a sufficiency reduction to the order statistic for the i-th unit in the panel $\left({y}_{i(1)},\ldots ,{y}_{i(T)}\right)$, having density

$${f}_{{Y}_{{{{\rm{ord}}}}}}({y}_{i(1)},\ldots ,{y}_{i(T)};{\alpha }_{i},{{{\boldsymbol{\theta }}}})=T!\mathop{\prod }\limits_{t=1}^{T}{f}_{0}({y}_{i(t)}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{i(t)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}).$$

(A.3)

Since the distribution of s_i does not depend on α_i, without losing generality we may assume α_i = 0, and the distribution (A.3) becomes

$${f}_{{Y}_{{{{\rm{ord}}}}}}({y}_{i(1)},\ldots ,{y}_{i(T)};0,{{{\boldsymbol{\theta }}}})=T!{\prod }_{t=1}^{T}{f}_{0}({y}_{i(t)}-{{{{\boldsymbol{x}}}}}_{i(t)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}).$$

The next step is to consider the one-to-one transformation

$$\left\{\begin{array}{l}{z}_{i}={y}_{i(1)}\quad \\ {s}_{i2}={y}_{i(2)}-{y}_{i(1)}\quad \\ \vdots \quad \\ {s}_{iT}={y}_{i(T)}-{y}_{i(1)}\quad \end{array}\right.$$

having inverse

$$\left\{\begin{array}{l}{y}_{i(1)}={z}_{i}\quad \\ {y}_{i(2)}={s}_{i2}+{z}_{i}\quad \\ \vdots \quad \\ {y}_{i(T)}={s}_{iT}+{z}_{i}\quad \end{array}\right.,$$

and unitary Jacobian. It follows that

$${f}_{Z,S}({z}_{i},{s}_{i1},\ldots ,{s}_{iT};{{{\boldsymbol{\theta }}}})=T!{f}_{0}({z}_{i}-{{{{\boldsymbol{x}}}}}_{i(1)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,\mathop{\prod }\limits_{t=2}^{T}{f}_{0}({s}_{it}+{z}_{i}-{{{{\boldsymbol{x}}}}}_{i(t)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}),$$

from which we can integrate out z_i to obtain the marginal distribution of s_i

$${f}_{S}({{{{\boldsymbol{s}}}}}_{i};{{{\boldsymbol{\theta }}}})=T!\int\nolimits_{-\infty }^{\infty }{f}_{0}({z}_{i}-{{{{\boldsymbol{x}}}}}_{i(1)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,\mathop{\prod }\limits_{t=2}^{T}{f}_{0}({s}_{it}+{z}_{i}-{{{{\boldsymbol{x}}}}}_{i(t)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,{{{{d}}}}{z}_{i}.$$

Furthermore, note that the constant T! can be omitted in the likelihood definition, and then we proceed with another change of variable u_i = z_i − y_i(1), for i = 1, …, n, having again unitary Jacobian. With some simple algebra, we obtain

$${f}_{S}({{{{\boldsymbol{s}}}}}_{i};{{{\boldsymbol{\theta }}}})=\int\nolimits_{-\infty }^{\infty }\mathop{\prod }\limits_{t=1}^{T}{f}_{0}({y}_{i(t)}+{u}_{i}-{{{{\boldsymbol{x}}}}}_{i(t)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,{{{{d}}}}{u}_{i}.$$

A further change of variable α_i = − u_i finally gives the result (A.1), using again the identity (A.2), so that

$${f}_{S}({{{{\boldsymbol{s}}}}}_{i};{{{\boldsymbol{\theta }}}})=\int\nolimits_{-\infty }^{\infty }\mathop{\prod }\limits_{t=1}^{T}{f}_{0}({y}_{i(t)}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{i(t)}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,{{{{d}}}}{\alpha }_{i}=\int\nolimits_{-\infty }^{\infty }\mathop{\prod }\limits_{t=1}^{T}{f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})\,{{{{d}}}}{\alpha }_{i}.$$

Appendix B: Relation to the results in Arellano and Bonhomme (2009)

The integrated likelihood (4) corresponds to the choice of the uniform prior according to Arellano and Bonhomme (2009). The fact that it corresponds to the marginal likelihood obtained from the distribution of (3) implies that the uniform prior resolves the incidental parameter issue, and this, in turn, must imply that condition (11) in the cited article holds. In what follows, we illustrate that this is the case.

As reminded by the authors, to prove this fact, it suffices that ρ_i(θ, α_i) does not depend on α_i, where ρ_i(θ, α_i) is the following vector

$${\rho }_{i}({{{\boldsymbol{\theta }}}},{\alpha }_{i})=-\frac{{i}_{{{{\boldsymbol{\theta }}}}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})}{{i}_{{\alpha }_{i}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})},$$

with ${i}_{{{{\boldsymbol{\theta }}}}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})$ and ${i}_{{\alpha }_{i}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})$ denoting the θα_i-block and the α_iα_i-block of the expected Fisher information matrix, respectively.

The fact that the expected Fisher information does not depend on α_i is straightforward to verify. To this aim, let us consider the log-likelihood function for the i-th unit corresponding to the TFE model (1), using again the identity (A.2)

$${\ell }_{i}({\alpha }_{i},{{{\boldsymbol{\theta }}}})=\mathop{\sum }_{t=1}^{T}\log {f}_{Y}({y}_{it};{\alpha }_{i},{{{\boldsymbol{\theta }}}})=\mathop{\sum }_{t=1}^{T}\log {f}_{0}({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}).$$

From this, we obtain the score function for α_i

$$\frac{\partial {\ell }_{i}({\alpha }_{i},{{{\boldsymbol{\theta }}}})}{\partial {\alpha }_{i}}=\mathop{\sum }\limits_{t=1}^{T}-\frac{{f}_{0}^{{\prime} }({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})}{{f}_{0}({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})},$$

where ${f}_{0}^{{\prime} }(z;{{{\boldsymbol{\psi }}}})=\partial {f}_{0}(z;{{{\boldsymbol{\psi }}}})/\partial z$, and then the α_iα_i-block of the observed information matrix

$$-\frac{{\partial }^{2}{\ell }_{i}({\alpha }_{i},{{{\boldsymbol{\theta }}}})}{\partial {\alpha }_{i}^{2}}=\mathop{\sum }\limits_{t=1}^{T}-\frac{{f}_{0}^{{\prime\prime} }({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,{f}_{0}({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})-{({f}_{0}^{{\prime} }({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}))}^{2}}{{f}_{0}^{2}({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})},$$

where again ${f}_{0}^{{''} }(z;{{{\boldsymbol{\psi }}}})={\partial }^{2}{f}_{0}(z;{{{\boldsymbol{\psi }}}})/\partial {z}^{2}$. Note that we can write

$$-\frac{{\partial }^{2}{\ell }_{i}({\alpha }_{i},{{{\boldsymbol{\theta }}}})}{\partial {\alpha }_{i}^{2}}=\mathop{\sum }\limits_{t=1}^{T}q({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}}),$$

for a suitable q(⋅; ψ) function. Then

$${i}_{{\alpha }_{i}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})=\mathop{\sum }\limits_{t=1}^{T}\int\nolimits_{-\infty }^{\infty }q({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,{f}_{0}({y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}};{{{\boldsymbol{\psi }}}})\,{{{{d}}}}{y}_{it},$$

from which we make a change of variable ${r}_{it}={y}_{it}-{\alpha }_{i}-{{{{\boldsymbol{x}}}}}_{it}^{\top }{{{\boldsymbol{\beta }}}}$, obtaining

$${i}_{{\alpha }_{i}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})=\mathop{\sum }\limits_{t=1}^{T}\int\nolimits_{-\infty }^{\infty }q({r}_{it};{{{\boldsymbol{\psi }}}})\,{f}_{0}({r}_{it};{{{\boldsymbol{\psi }}}})\,{{{{d}}}}{r}_{it},$$

which shows that ${i}_{{\alpha }_{i}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})$ is a function of ψ only. Similarly, we obtain that the ${i}_{{{{\boldsymbol{\theta }}}}{\alpha }_{i}}({{{\boldsymbol{\theta }}}},{\alpha }_{i})$ depends on ψ only, and so does ρ_i(θ, α_i).