Regularized conditional estimators of unit inefficiency in stochastic frontier analysis, with application to electricity distribution market

Abstract

In stochastic frontier analysis, the conventional estimation of unit inefficiency is based on the mean/mode of the inefficiency, conditioned on the composite error. It is known that the conditional mean of inefficiency shrinks towards the mean rather than towards the unit inefficiency. In this paper, we analytically prove that the conditional mode cannot accurately estimate unit inefficiency, either. We propose regularized estimators of unit inefficiency that restrict the unit inefficiency estimators to satisfy some a priori assumptions, and derive the closed form regularized conditional mode estimators for the three most commonly used inefficiency densities. Extensive simulations show that, under common empirical situations, e.g., regarding sample size and signal-to-noise ratio, the regularized estimators outperform the conventional (unregularized) estimators when the inefficiency is greater than its mean/mode. Based on real data from the electricity distribution sector in Sweden, we demonstrate that the conventional conditional estimators and our regularized conditional estimators provide substantially different results for highly inefficient companies.

1 Introduction

Since the publication of the papers by Aigner et al. (1977) and Meeusen and van den Broeck (1977), stochastic frontier analysis (SFA) has been a common approach to gain deeper insights into the potential for productivity improvement (Kumbhakar et al. 2020) and cost reduction in monopolized markets (Bogetoft and Otto 2011). For unit inefficiency, the standard estimation approach was developed by Jondrow et al. (1982), acronymed “JLMS” in the SFA literature. The JLMS estimator is based on the mean (and the mode) of the inefficiency conditioned on the composite error (for later studies of JLMS estimators, see Kumbhakar and Lovell 2000, and Battese and Coelli 1988).

Despite its widespread use, the JLMS estimator has been criticized. Wang and Schmidt (2009) show that it shrinks the inefficiency towards its mean, leading to a distribution that is different from the distribution of the inefficiency. The mean and mode are not fully representative characteristics of the conditional distribution of the inefficiency, especially if each unit is observed once. Thus, in cross-sectional context, conditional estimator produces an inconsistent estimator of the inefficiency. Moreover, a conditional estimator is conditioned on an estimated composite error rather than on the composite error itself (Horrace 2005 and Kumbhakar et al. 2015). Therefore, the sampling distribution of the conditional estimator is different from the theoretically assumed conditional distribution of the inefficiency. Consequently, the inefficiencies are inaccurately estimated, something regulatory agencies have stated as an impediment for the practical use of SFA (Badunenko et al. 2012; Stone 2002 and Tsionas 2017). This is also illustrated in a simulation study by Andor et al. (2019), where they show that both the SFA and Data envelopment analysis (DEA) methods used by regulators underestimate the true efficiency values. One way to reduce this problem is to combine the SFA and the DEA (Andor et al. 2019 and Tsionas 2021), but such combinatory approaches are not able to eliminate the underestimation problem.

Our approach is similar to the combinatory approach in that it can be viewed as a weighted average of unit inefficiency estimators, but in contrast, it is a weighted average of the sample (industry), solely based on the SFA approach. The proposed regularized estimators can be used as stand-alone estimators along with any other estimators in a combinatory approach. In addition, the regularized estimators described here can be used in a variety of situations but in this paper, we limit ourselves to studying unit inefficiency estimation in a cross-sectional context, using the classical stochastic frontier model suggested by Aigner et al. (1977).

We propose a regularized (constrained) estimator based on Bayesian risk (expected loss) that restricts the inefficiencies to satisfy some underlying theoretical (and/or intuitive) conditions. Restrictions on the moments are common options for the imposed constraints upon the likelihood functions (e.g., Hall and Presnell 1999). Our regularized estimators are easily calculated, e.g., they can be the JLMS (unregularized) estimators, with imposed constraints on the first and the second moments of the conditional distribution of the inefficiency.

The proposed methodology is different from other recent contributions in the field. For example, Kumbhakar et al. (1991) suggest a single step procedure for the estimation of unit inefficiency when they deploy firm-specific determinants of the inefficiency in the maximum likelihood estimation of the SFA model. They show that ignoring the determinants would lead to biased and inconsistent estimators. However, firm-specific determinants are often unobserved, and even unknown. Another recent contribution is the use of non-parametric and semi-parametric estimation methods, in which the JLMS estimator is used for estimating unit inefficiency (Kumbhakar et al. 2007). Another avenue of research is the use of quantile regression into the estimation of the production function (Bernini et al. 2004; Wang et al. 2014 and Behr 2010). However, this approach introduces a new challenge, specifically that one needs to pay more attention to the selection of appropriate quantiles which can be different for distinct densities of the composite error (Jradi et al. 2019). In addition, no sound and clear post-estimation method for estimating unit inefficiency exists when using quantile regression (Kumbhakar et al. 2020).

Under mild assumptions, e.g., log-concavity of the distribution, which covers many of the distributions used in the SFA literature, we analytically investigate some properties of the conditional mode (maximum a posteriori probability estimator) and give a general formula for the conditional mode (and its functions) that can be used with any inefficiency density. Next, we derive a regularized conditional mode estimator with the three most commonly used inefficiency densities, i.e., the half-normal, truncated normal and exponential distributions. The proposed unit inefficiency estimation is considered a restricted or penalized estimation method that improves the estimation of unit inefficiency based on the conditional mean/mode. Therefore, the regularized estimators can be easily derived wherever the JLMS (unregularized) estimators are used. Therefore, the idea of our manuscript can be easily used in any context where the unit inefficiency estimation is calculated based on the optimization of an objective function, by imposing some restrictions to improve the accuracy of the unit inefficiency estimator.

An extensive simulation study is conducted, with varying factors, such as the sample size, inefficiency density and signal-to-noise ratio (relative variation of the inefficiency to the variation of random shocks). The simulation results show that the regularized estimators outperform the conventional (unregularized) estimators when the inefficiencies are greater than their mean/mode, especially with a larger signal-to-noise ratio. As the unregularized conditional mean/mode shrinks towards the mean/mode, the regularized conditional mean/mode shrinks less towards the mean/mode, especially for larger inefficiencies.

We apply both unregularized and regularized estimators to data from the Swedish electricity distribution sector. The results show that the estimated inefficiencies from the two regularized and unregularized estimators are substantially different, particularly for firms that are in the right tail of the inefficiency distribution. Considering the results from the simulations which are supported analytically (Theorem 3), we recommend that regulators use the results from the regularized estimators for the firms that are ranked highly inefficient, based on their estimated inefficiency scores using the conditional mean/mode.

The remainder of this paper is structured as follows. In Section 2, we derive a general formula for the conditional mode of the inefficiency and analytically investigate some of its properties under mild distributional assumptions of unconditional inefficiency. Next, the regularized estimator is discussed and formally derived for both production and cost functions. It is analytically shown that the regularized conditional mode estimators serve to reduce the shrinkage towards the mode. Regularized conditional mode estimators are presented under three different distributional assumptions. In Section 4, both regularized and unregularized estimators are evaluated using extensive Monte Carlo simulations. In Section 5, we present an application based on real data. The data represent electricity distribution firms in Sweden, and we estimate the cost inefficiency, which is used by the Energy Markets Inspectorate as an input in their revenue cap regulation. Section 6 concludes the paper and discusses avenues for future research.

2 Theory

A stochastic frontier, cross-sectional, production model can be formulated as

$$y_i = {{{\boldsymbol{x}}}}_i^\prime \beta + v_i - u_i$$

(1)

where i indicates the unit, y_i is the observed output, x_i is the given k × 1 vector of inputs, u_i is the unobserved inefficiency, v_i is the unobserved noise and β is an unknown k × 1 vector of functional parameters.

The conventions of a simple parametric cross-section SFA assume i.i.d. random noise terms with a density function g_v(v) that is symmetric around zero and i.i.d. nonnegative inefficiencies with a density function f_u(u). For example, the most common (semistandard) g_v(v) is assumed to be the density of a zero-mean normal distribution $N\left( {0,\,\sigma _v^2} \right)$¹, and the equivalent candidates for f_u(u) are assumed to be the densities of a half-normal distribution $N^ + \left( {0,\,\sigma _u^2} \right)$, an exponential distribution Exp(σ_u) with scale parameter σ_u, and a truncated normal distribution $N^ + \left( {\mu ,\,\sigma _u^2} \right)$ with a general μ that can take any real number.

The maximum likelihood estimation of an SFA model is based on maximizing the likelihood of the i.i.d. composite errors ε_i = v_i − u_i with the density function

$$h_\varepsilon \left( \varepsilon \right) = {\int}_0^{ + \infty } {f_u\left( u \right)\,g_v\left( {u + \varepsilon } \right)\,du}$$

where the composite error ε_i is ε_i = y_i−${{{\boldsymbol{x}}}}_i^\prime \beta$.

It has been argued (e.g., Greene 1990 and Ruggiero 1999), that the selection of different inefficiency density functions should not result in noticeable differences between the fit of the SFA models, or the ranks of the estimated conditional unit inefficiencies. However, they may differ in the magnitude of the estimated inefficiencies, especially for highly inefficient units.

As mentioned in the Introduction, the most common way of scoring the unit inefficiency is through the JLMS estimators. For the i^th unit, the inefficiency is estimated as $\widehat u_i = E\left( {u\left| {\varepsilon _i} \right.} \right)$ or $\widehat u_i = Mode\left( {u\left| {\varepsilon _i} \right.} \right)$ using the following conditional density function of inefficiency u given a composite error ε.

$$f_{u\left| \varepsilon \right.}\left( u \right) = \frac{{f_u\left( u \right)\,g_v\left( {u + \varepsilon } \right)}}{{h_\varepsilon \left( \varepsilon \right)}}$$

However, as stated by Kumbhakar et al. (2020), the conditional estimator of the inefficiency is an estimator of a characteristic (mean or mode) of the conditional inefficiency rather than of the inefficiency itself. Such a distinction between the two remains unchanged regardless of the sample size. In fact, it depends on the size of the noise variance rather than on the sample size. This fact is proven by Wang and Schmidt (2009) for the conditional mean when the inefficiency follows a half-normal distribution, and they argue that it also holds when the inefficiencies are drawn from exponential and general truncated normal distributions. However, such argument has not been proven for the conditional mode, although there is a general belief in the SFA literature that the JLMS estimators, whether mean or mode, are shrinkage estimators.

In Theorem 3, we provide a proof that, under mild distributional assumptions, the conditional mode of the inefficiency analogously shrinks towards the mode of the inefficiency. This means that the conditional mode estimator underestimates large inefficiencies. It also overestimates the inefficiencies of almost fully efficient firms when the inefficiency mode is a positive number (as it is the case for a truncated normal distribution with location parameter μ > 0).

The conditional mode estimator is the maximum a posteriori probability estimator, which is the mode of the a posteriori distribution, i.e., $Mode\left( {u\left| {\varepsilon _i} \right.} \right) = \mathop {{{{{\mathrm{Argmax}}}}}}\nolimits_{u \in {\Bbb R}^ + } \,f_{u\left| \varepsilon \right.}\left( u \right) = \mathop {{{{{\mathrm{Argmax}}}}}}\nolimits_{u \in {\Bbb R}^ + } \,\left( {f_u\left( u \right)g_v\left( {u + \varepsilon } \right)} \right)$. In Theorem 1, we give a general formula to calculate the conditional mode of the inefficiency for any inefficiency density function that fulfills the mild assumptions stated below. We take smooth density functions f_u(u) whose supports are the real numbers in the range $u\, \in \,\left[ {0,\,\infty } \right)$. For such densities, we define the “form” (kernel) of the density, denoted as K(w), for w ∈ ℝ, as follows,

$$f\left( u \right) = \left\{ {\begin{array}{*{20}{l}} {cK\left( u \right),\,if\,u\, \ge \,0} \\ {0,\,if\,u\, < \,0} \end{array}} \right.$$

where, c is a constant and possibly an expression containing the parameters of the density function, but not a function of the variable u itself. Note that the form of the density is in fact the kernel of the density defined for both the support of the density and its complement in the set of the real numbers. First, we present the following corollary.

Corollary: Suppose the function K(w) > 0 is defined for all w ∈ ℝ, with the following properties:

• 1. K(w) is continuously differentiable for all w ∈ ℝ, and log-concave.

• 2. $\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}$ is bounded above, such that $\mathop {{\lim }}\limits_{w\, \to \, + \,\infty } \,\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}\, < \,\left| M \right|\, < \, +\infty$.

• 3. $\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}$ is bounded below, such that $\mathop {{\lim }}\limits_{w\, \to \, - \,\infty } \,\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}\, > \, - \,\left| m \right|\, > \, - \infty$.

For the convergence of the integral ${\int}_{ - \infty }^{ + \infty } {e^{ - s\left[ {w - \frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}} \right]}dw}$, with l < s < r, we must have $\mathop {{\lim }}\limits_{w\, \to \, \pm \,\infty } \,\left| {\frac{{\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}}}{w}} \right|\, < \,1$.

We give the detailed proof in the Appendix. The results of the following theory are based on the results of the Corollary.

Theorem 1: Suppose the noise of the production function in (1) is $v\sim N\left( {0,\sigma _v^2} \right)$, and the inefficiency has the density f_u(u), for u ≥ 0. If f_u(u) has the form K(w) which is continuously differentiable, with its first derivative K′(w), such that $\mathop {{\lim }}\nolimits_{w\, \to \, \pm \,\infty } \,\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}$ is bounded, then the inefficiency mode conditioned on the composite error ε, denoted as $\widehat u = Mode\left( {u\left| \varepsilon \right.} \right)$, is unique. In addition, if

$$\mathop {{\lim }}\limits_{\tilde u\, \to \, \pm \,\infty } \,\left| {\frac{{\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}}}{{\tilde u}}} \right|\, < \,\frac{1}{{\sigma _v^2}}$$

then the conditional mode is $\widehat u = Mode\left( {u\left| \varepsilon \right.} \right) = {{{\mathrm{max}}}}\left\{ {0,\,\tilde u} \right\}$, where

$$\tilde u = - \varepsilon - \mathop {\sum}\limits_{k = 1}^{ + \infty } {\frac{{\left( {\sigma _v^2} \right)^k}}{{k!}}\left[ {\frac{\partial }{{\partial \varepsilon }}} \right]^{k - 1}\left\{ { - \frac{{K^\prime \left( { - \varepsilon } \right)}}{{K\left( { - \varepsilon } \right)}}} \right\}^k}$$

Proof:

Obviously, $\widehat u = Mode\left( {u\left| \varepsilon \right.} \right) = \mathop {{{{{\mathrm{Argmax}}}}}}\nolimits_{u \in {\Bbb R}^ + } \left( {f_u\left( u \right)g_v\left( {u + \varepsilon } \right)} \right) = {{{\mathrm{max}}}}\left\{ {0,\,\tilde u} \right\}$, where $\tilde u$ is defined as

$$\tilde u = \mathop {{{{{\mathrm{Argmax}}}}}}\limits_{u \in {\Bbb R}} \left( {K\left( u \right)g_v\left( {u + \varepsilon } \right)} \right)$$

By solving the above maximization problem, we have

$$\begin{array}{l}K^\prime \left( {\widetilde u} \right)\,g_v\left( {\tilde u + \varepsilon } \right) + g_v^\prime \left( {\tilde u + \varepsilon } \right)\,K\left( {\tilde u} \right)\, = \,K^\prime \left( {\tilde u} \right)\,g_v\left( {\tilde u + \varepsilon } \right)\\\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\;\;\; - \frac{{\left( {\tilde u + \varepsilon } \right)}}{{\sigma _v^2}}g_v\left( {\tilde u + \varepsilon } \right)\,K\left( {\tilde u} \right) = 0\end{array}$$

$$\tilde u\, = \, - \varepsilon + \sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}$$

(2)

With f_u(u) a log-concave density, $\frac{{d\,{{{\mathrm{ln}}}}\left[ {f_u\left( {\tilde u} \right)} \right]}}{{du}} = \frac{{f_u^\prime \left( {\tilde u} \right)}}{{f_u\left( {\tilde u} \right)}} = \frac{{K^\prime \left( u \right)}}{{K\left( u \right)}}$ is a decreasing function of u ≥ 0. Thus, there is a unique solution of $\tilde u$ in terms of bounded ε in (2), since $\sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}} - \widetilde u = \varepsilon$ also becomes a monotonically decreasing function of $\tilde u \ge 0$.

For the Lagrange reversion theorem (see Whittaker and Watson (1927), pp. 132–133, and Grossman (2005)²) of Eq. (2), we start with the bilateral Laplace transform of the function $\tilde u^\prime \left( { - \varepsilon } \right) = \frac{{d\tilde u}}{{d\left( { - \varepsilon } \right)}} = - \frac{{d\tilde u}}{{d\varepsilon }}$. Suppose for a complex number s whose real part is in the interval k < Re(s) < r, the bilateral Laplace transform exists, as follows.

$$\begin{array}{l}{{{\mathcal{L}}}}\left\{ {\frac{{d\tilde u}}{{d\left( { - \varepsilon } \right)}}} \right\}\left( s \right) = \mathop {\int}\limits_{ - \infty }^{ + \infty } {e^{ - s\left( { - \varepsilon } \right)}\frac{{d\tilde u}}{{d\left( { - \varepsilon } \right)}}d\left( { - \varepsilon } \right)}\\\qquad\qquad\qquad = \mathop {\int}\limits_{ - \infty }^{ + \infty } {e^{ - s\left[ {\tilde u - \sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}} \right]}d\tilde u} = \mathop {\int}\limits_{ - \infty }^{ + \infty } {e^{ - s\tilde u}\,e^{s\sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}}d\tilde u} \end{array}$$

For the convergence of the above integral, we must have the following condition (see Corollary above):

$$\mathop {{\lim }}\limits_{\tilde u \to \pm \infty } \left| {\frac{{\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}}}{{\tilde u}}} \right|\, < \,\frac{1}{{\sigma _v^2}}$$

Returning to the above integral, and using Taylor expansion of $s\sigma _v^2\frac{{K^\prime ( {\tilde u})}}{{K( {\tilde u})}}$, we have

$$\begin{array}{l}{{{\mathcal{L}}}}\left\{ {\frac{{d\tilde u}}{{d\left( { - \varepsilon } \right)}}} \right\}\left( s \right) = \mathop {\int}\limits_{ - \infty }^{ + \infty } {e^{ - s\tilde u}\left[ {\mathop {\sum}\limits_{k = 0}^{ + \infty } {\frac{{s^k}}{{k!}}\left( {\sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}} \right)^k} } \right]} d\tilde u \\\qquad\qquad\qquad = \mathop {\sum}\limits_{k = 0}^{ + \infty } {\left[ {{\int}_{ - \infty }^{ + \infty } {e^{ - s\tilde u}\,\frac{{s^k}}{{k!}}\left( {\sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}} \right)^kd\tilde u} } \right]} \end{array}$$

Applying the properties of bilateral Laplace transform $\left( {{{{\mathcal{L}}}}\left\{ {f^{\left( n \right)}} \right\}\left( s \right) = s^n{{{\mathcal{L}}}}\left\{ f \right\}\left( s \right)} \right)$ to the integral inside the summation, the summation is equal to

$$\begin{array}{l} = \mathop {\sum}\limits_{k = 0}^{ + \infty } {\left[ {\mathop {\int}\limits_{ - \infty }^{ + \infty } {\frac{1}{{k!}}e^{ - s\tilde u}\,\frac{{d^k}}{{du^k}}\left( {\sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}} \right)^kd\tilde u} } \right]}\\ = \mathop {\int}\limits_{ - \infty }^{ + \infty } {e^{ - s\tilde u}\left[ {\mathop {\sum}\limits_{k = 0}^{ + \infty } {\frac{1}{{k!}}.\frac{{d^k}}{{du^k}}\left( {\sigma _v^2\frac{{K^\prime \left( {\tilde u} \right)}}{{K\left( {\tilde u} \right)}}} \right)^k} } \right]} d\tilde u\end{array}$$

By changing the notation of the last integral and due to the uniqueness of bilateral Laplace transform,

$$\frac{{d\tilde u}}{{d\left( { - \varepsilon } \right)}} = \mathop {\sum}\limits_{k = 0}^{ + \infty } {\frac{{\left( {\sigma _v^2} \right)^k}}{{k!}}\frac{{d^k}}{{d\left( { - \varepsilon } \right)^k}}\left( {\frac{{K^\prime \left( { - \varepsilon } \right)}}{{K\left( { - \varepsilon } \right)}}} \right)^k}$$

$$\frac{{d\tilde u}}{{d\left( { - \varepsilon } \right)}} = 1 + \mathop {\sum}\limits_{k = 1}^{ + \infty } {\frac{{\left( {\sigma _v^2} \right)^k}}{{k!}}\frac{{d^k}}{{d\varepsilon ^k}}\left( { - \frac{{K^\prime \left( { - \varepsilon } \right)}}{{K\left( { - \varepsilon } \right)}}} \right)^k}$$

$$\frac{{d\tilde u}}{{d\varepsilon }} = - 1 - \mathop {\sum}\limits_{k = 1}^{ + \infty } {\frac{{\left( {\sigma _v^2} \right)^k}}{{k!}}\frac{{d^k}}{{d\varepsilon ^k}}\left( { - \frac{{K^\prime \left( { - \varepsilon } \right)}}{{K\left( { - \varepsilon } \right)}}} \right)^k}$$

Solving the above differential equation gives us the solution

$$\tilde u = - \varepsilon - \mathop {\sum}\limits_{k = 1}^{ + \infty } {\frac{{\left( {\sigma _v^2} \right)^k}}{{k!}}\frac{{d^{k - 1}}}{{d\varepsilon ^{k - 1}}}\left( { - \frac{{K^\prime \left( { - \varepsilon } \right)}}{{K\left( { - \varepsilon } \right)}}} \right)^k}$$

This completes the proof. ■

Note that the commonly used inefficiency densities of half normal, exponential, general truncated normal and gamma (with shape parameter ≥1) are log-concave distributions. When the noise v and the inefficiency u are distributed as assumed in Theorem 1, for each of the density and distribution functions $q \in \left\{ {\tilde f_{\widehat u\left| u \right.},\,\tilde F_{\widehat u\left| u \right.},\,\tilde f_{\widehat u\left| \varepsilon \right.},\,\tilde F_{\widehat u\left| \varepsilon \right.},\,\tilde f_{u|\widehat u},\,\tilde F_{u\left| {\widehat u} \right.},\,f_u,\,F_u,\,\tilde f_{\widehat u},\,\tilde F_{\widehat u}} \right\}$, and any other differentiable function of $\widehat u \ge 0$, we have,

$$q\left( {\widehat u} \right) = q\left( { - \varepsilon } \right) - \mathop {\sum}\limits_{k = 1}^{ + \infty } {\frac{{\left( {\sigma _v^2} \right)^k}}{{k!}}\left[ {\frac{\partial }{{\partial \varepsilon }}} \right]^{k - 1}\left\{ {\left( { - \frac{{f_u^\prime \left( { - \varepsilon } \right)}}{{f_u\left( { - \varepsilon } \right)}}} \right)^kq^\prime \left( { - \varepsilon } \right)} \right\}}$$

When the $\left[ {\ln \left( {f_u\left( u \right)} \right)} \right]^\prime = \frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( u \right)} \right]}}{{{{{\mathrm{d}}}}u}}$ is linear, as it is the case for the half-normal, exponential and general truncated normal densities, the conditional mode, in terms of the mode of inefficiency m, is simplified as

$$\widehat u = Mode\left( {u{{{\mathrm{|}}}}\varepsilon } \right) = \frac{{ - \varepsilon + \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime - \sigma _v^2m\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]{^{\prime\prime}} }}{{1 - \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]{^{\prime\prime}} }}$$

where, [ln(f_u(m))]′ and [ln(f_u(m))]^′′ are the first and second derivatives evaluated at the mode of the inefficiency (m). In general, the conditional mode, theoretically and empirically, is less covered in the SFA literature when JLMS estimators are used, in favor of the conditional mean. To the best of authors’ knowledge, the article by Papadopoulos (2021) is an exception, in that the author elaborates on the conditional model and proves its monotonicity in terms of the composite error when the inefficiency follows a generalized exponential distribution. Monotonicity of the conditional mode in terms of the composite error is important in that both (mean/mode) JLMS estimators must rank the unit inefficiencies identically. If so, using the conditional mode, the inefficiencies can be ranked based on their corresponding composite errors, i.e., the coefficient of ranked correlation between the conditional mode scores and the composite errors becomes almost negative one. A similar argument holds for conditional mean scores, as shown by Bera and Sharma (1999) and Ondrich and Ruggiero (2001). In Theorem 2, we show that under mild distributional assumptions, the monotonicity of the conditional mode in terms of the composite error is generalizable to any other inefficiency distribution.

Theorem 2: Suppose $v\sim N\left( {0,\,\sigma _v^2} \right)$. The inefficiency density f_u(u) is nonzero, twice differentiable and log-concave at u ≥ 0. The conditional mode estimator of the inefficiency conditioned on the composite error ε is a monotonically decreasing function of the composite error.

Proof:

Since f_u(u) is log-concave, we have $\frac{{{{{\mathrm{d}}}}^2\ln \left[ {f_u\left( u \right)} \right]}}{{\left( {{{{\mathrm{d}}}}u} \right)^2}} \le 0$ for all u ≥ 0. As shown in Theorem 1, we can write Eq. (2) as $\tilde u = - \varepsilon + \sigma _v^2\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{{{{\mathrm{d}}}}\widetilde u}}$. Then, by the chain rule of derivatives, we have

$$\frac{{\partial \tilde u}}{{\partial \varepsilon }} = - 1 + \sigma _v^2\frac{{{{{\mathrm{d}}}}^2\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{\left( {{{{\mathrm{d}}}}\tilde u} \right)^2}}\frac{{\partial \tilde u}}{{\partial \varepsilon }} = \frac{{ - 1}}{{1 - \sigma _v^2\frac{{{{{\mathrm{d}}}}^2\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{\left( {{{{\mathrm{d}}}}\tilde u} \right)^2}}}}\, < \,0$$

The above negative derivative would imply strict monotonicity if negative scores ($\tilde u$) were acceptable. Since they are restricted to $\widehat u = {{{\mathrm{max}}}}\left\{ {0,\,\tilde u} \right\}$, monotonicity is not strict, in general. Thus, the proof is complete. ■

Wang and Schmidt (2009) show that the conditional mean shrinks towards the mean of inefficiency rather than towards inefficiency itself. This property is disadvantageous to the unit inefficiencies that depart from the mean since it underestimates highly inefficient firms and overestimates the inefficiencies lower than the mean. It is also a disadvantage of the conditional mean for regulators to accurately estimate the inefficiency in the lower and, especially, in the upper tail of the inefficiency distribution. Although being able to rank the units based on their inefficiencies is of regulators’ interest, in some cases the magnitude of the inefficiency is of crucial importance, for instance, EU countries’ (in)efficiencies in their climate plans to cut emissions of greenhouse gases.

In Theorem 3, we prove that the conditional mode has a similar property, in that it is a shrinkage estimator towards the mode of inefficiency rather than towards inefficiency itself. With such property, although the conditional mode would outperform the conditional mean in estimating the lower tail of an inefficiency distribution with its mode in a narrow positive neighborhood of zero, it is still a poor estimator for highly inefficient firms, i.e., the right tail of the distribution.

Theorem 3: Suppose $v\sim N\left( {0,\sigma _v^2} \right)$ and, the inefficiency density f_u(u) is nonzero, twice differentiable, log-concave for u > 0 and with $m = Mode\left( u \right) = \mathop {{{{{\mathrm{Argmax}}}}}}\nolimits_{u \in {\Bbb R}^ + } \,f_u\left( u \right)$. Let the conditional mode estimator of the inefficiency be $\widehat u = Mode\left( {u\left| \varepsilon \right.} \right)$. Then,

a) as $\sigma _v^2 \to 0$, $\widehat u \to _pu$,

b) as $\sigma _v^2 \to 0$, $\widehat u \to _du$,

c) as $\sigma _v^2 \to 0$, $\frac{{\widehat{u} - u}}{{\sigma _v}} \to _dN\left( {0,1} \right)$,

d) as $\sigma _v^2 \to \infty$, $\widehat u \to _pm = Mode\left( u \right)$.

e) as $\sigma _v^2 \to \infty$, $\sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime + \left( {\sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} - 1} \right)\left( {\widehat u - m} \right) \to _d\left( {\varepsilon + m} \right)$.

Proof:

By assumption, f_u(u) is differentiable and nonzero, for u > 0. Then, $\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( u \right)} \right]}}{{{{{\mathrm{d}}}}u}}$ is bounded (differentiable functions have their derivatives bounded). Then, we can write $\tilde u = \mathop {{{{{\mathrm{Argmax}}}}}}\limits_{u \in {\Bbb R}^ + } \left( {f_u\left( u \right) \cdot g_v\left( {u + \varepsilon } \right)} \right)$,

$$f_u^\prime \left( {\tilde u} \right)\,g_v\left( {\tilde u + \varepsilon } \right) + f_u\left( {\tilde u} \right)\,g_v^\prime \left( {\tilde u + \varepsilon } \right) = 0$$

$$\frac{1}{{\sigma _v^2}} = \frac{1}{{\tilde u + \varepsilon }}\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{{{{\mathrm{d}}}}\widetilde u}}$$

In addition, as $\sigma _v^2 \to 0$, the normal density tends to Dirac’s delta function,³ with its mass concentrated around the mean, i.e., $g_v\left( v \right) \to _d\,\delta \left( {E\left( v \right)} \right)$. Then, $v \to _pE\left( v \right) = 0$. (Note that it might be that $\tilde u\, < \,0$, then the conditional mode is $\widehat u = {{{\mathrm{max}}}}\left\{ {0,\,\tilde u} \right\}$).

a) As $\sigma _v^2 \to 0$, $v \to _pE\left( v \right) = 0$ (Dirac’s delta function). Then $\varepsilon \to _p - u$ (since ε = v − u), or equivalently $- \varepsilon \to _pu$. Additionally, as $\sigma _v^2 \to 0$, $\frac{1}{{\widetilde u + \varepsilon }}\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{{{{\mathrm{d}}}}\widetilde u}} \to \infty$ (due to the fact that $\frac{1}{{\sigma _v^2}} = \frac{1}{{\widetilde u + \varepsilon }}\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{{{{\mathrm{d}}}}\widetilde u}}$). Since $\frac{{{{{\mathrm{d}}}}ln\left[ {f_u\left( u \right)} \right]}}{{{{{\mathrm{d}}}}u}}$ is bounded, then, for a bounded composite error, it must be that $\tilde u \to - \varepsilon$. It means $\tilde u \to _pu$. Then, $\widehat u = \max \left\{ {0,\,\tilde u} \right\} \to _p\max \left\{ {0,u} \right\} = u$.

b) Although the convergence in probability, as shown in point (a), automatically implies the convergence in distribution, another direct proof, independent from the result of point (a) above, can be as follows.

$$\varepsilon = \sigma _v^2\frac{{f_u^\prime \left( {\tilde u} \right)}}{{f_u\left( {\tilde u} \right)}} - \tilde u$$

Then,

$$\left| {\frac{{{{{\mathrm{d}}}}\varepsilon }}{{{{{\mathrm{d}}}}\tilde u}}} \right| = \left| {\sigma _v^2\frac{{{{{\mathrm{d}}}}^2\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{\left( {{{{\mathrm{d}}}}\tilde u} \right)^2}} - 1} \right|$$

$$\begin{array}{l}\tilde f_{\tilde u}\left( {\tilde u} \right) = h_\varepsilon \left( {\sigma _v^2\frac{{f_u^\prime \left( {\tilde u} \right)}}{{f_u\left( {\tilde u} \right)}} - \tilde u} \right)\left| {\frac{{{{{\mathrm{d}}}}\varepsilon }}{{{{{\mathrm{d}}}}\tilde u}}} \right| = \left| {\sigma _v^2\frac{{{{{\mathrm{d}}}}^2\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{\left( {{{{\mathrm{d}}}}\tilde u} \right)^2}} - 1} \right|\\ \times\mathop {\int}\limits_0^{ + \infty } {f_u\left( u \right)\,g_v\left( {u + \sigma _v^2\frac{{f_u^\prime \left( {\tilde u} \right)}}{{f_u\left( {\tilde u} \right)}} - \tilde u} \right)du} \end{array}$$

As $\sigma _v^2 \to 0$,

$$\begin{array}{l}\tilde f_{\tilde u}\left( {\tilde u} \right) \to _d\mathop {{\lim }}\limits_{\sigma _v^2} h_\varepsilon \left( {\sigma _v^2\frac{{f_u^\prime ( {\tilde u})}}{{f_u\left( {\tilde u} \right)}} - \tilde u} \right)\left| {\frac{{{{{\mathrm{d}}}}\varepsilon }}{{{{{\mathrm{d}}}}\tilde u}}} \right|\\\qquad\quad = \mathop {{\lim }}\limits_{\sigma _v^2} \left| {\sigma _v^2\frac{{{{{\mathrm{d}}}}^2\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{\left( {{{{\mathrm{d}}}}\tilde u} \right)^2}} - 1} \right|\mathop {\int}\limits_0^{ + \infty } {f_u\left( u \right)\,g_v\left( {u + \sigma _v^2\frac{{f_u^\prime ( {\tilde u})}}{{f_u\left( {\tilde u} \right)}} - \tilde u} \right)du} \end{array}$$

$$= {\int}_0^{ + \infty } {f_u\left( u \right)\,\delta \left( {u - \tilde u} \right)du = f_u\left( {\tilde u} \right)}$$

As $\sigma _v^2 \to 0$, $\Pr \left( {\tilde u\, < \,0} \right) \to 0$, and $\tilde f_{\widehat u}\left( u \right) = \frac{{\tilde f_{\tilde u}\left( u \right)}}{{1 - \Pr \left( {\tilde u < 0} \right)}} \to \tilde f_{\tilde u}\left( u \right)$, meaning that $\tilde f_{\widehat u}\left( u \right) \to f_u\left( u \right)$, for $u \ge 0$.

c) Since $v\sim N\left( {0,\sigma _v^2} \right)$, then $- \frac{v}{{\sigma _v}}\sim N\left( {0,1} \right)$. It means

$$- \frac{v}{{\sigma _v}} = - \frac{{u + \varepsilon }}{{\sigma _v}} = \frac{{\tilde u - u - \sigma _v^2\frac{{f_u^\prime \left( {\tilde u} \right)}}{{f_u\left( {\tilde u} \right)}}}}{{\sigma _v}}\sim N\left( {0,1} \right)$$

As $\sigma _v^2 \to 0$, $\frac{{\tilde u - u - \sigma _v^2\frac{{f_u^\prime ( {\tilde u})}}{{f_u( {\tilde u})}}}}{{\sigma _v}} \to _p\frac{{\tilde u - u}}{{\sigma _v}}$, then $\frac{{\tilde u - u}}{{\sigma _v}} \to _dN\left( {0,1} \right)$. From point b, as $\sigma _v^2 \to 0$, $\Pr \left( {\tilde u\, < \,0} \right) \to 0$, and we have $\widehat u = {{{\mathrm{max}}}}\left\{ {0,\,\tilde u} \right\}$, i.e., as $\sigma _v^2 \to 0$, $\widehat u \to _p\tilde u$. Then, $\frac{{\widehat u - u}}{{\sigma _v}} \to _p\frac{{\tilde u - u}}{{\sigma _v}}$, meaning that $\frac{{\widehat u - u}}{{\sigma _v}} \to _dN\left( {0,1} \right)$.

d) Since we have $\frac{1}{{\sigma _v^2}} = \frac{1}{{\tilde u + \varepsilon }}\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{{{{\mathrm{d}}}}\tilde u}}$, for a bounded value of ε, as $\sigma _v^2 \to \infty$, it implies two possibilities. First, if $\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u( {\tilde u})} \right]}}{{{{{\mathrm{d}}}}\tilde u}} \to 0$, then $\tilde u \to Mode\left( u \right)$ since f_u(u) is unimodal (log-concave). Whether the Mode(u) is zero or a positive number, we have $\widehat u = max\left\{ {0,\tilde u} \right\} \to Mode\left( u \right)$. Second, if $\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u( {\tilde u})} \right]}}{{{{{\mathrm{d}}}}\widetilde u}} /\!\!\!\!\!\to 0$, then we must have $\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( {\tilde u} \right)} \right]}}{{{{{\mathrm{d}}}}\widetilde u}}\, < \,0$ and the density must be a monotonically decreasing function of u ≥ 0, since for $\tilde u \to + \infty$, $\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u( {\tilde u})} \right]}}{{{{{\mathrm{d}}}}\tilde u}} \not > 0$. Thus, it must be that $\tilde u \to - \infty$ (with a bounded ε), which is restricted to $\widehat u = \max \left\{ {0,\tilde u} \right\} = 0$. In such case, $\widehat u = \max \left\{ {0,\,\tilde u} \right\} = 0$ is again the mode of u since f_u(u) (that cannot have $\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u\left( u \right)} \right]}}{{{{{\mathrm{d}}}}u}} = 0$, for any u > 0, according to the second possibility) must be strictly monotonically decreasing with its Mode(u) = 0.

e) As $\sigma _v^2 \to \infty$, we can use the fact in point d and the mean value theorem around the mode m to write $\mathop {{\lim }}\limits_{\sigma _v^2 \to \infty } \frac{{\left[ {\ln ( {f_u( {\tilde u} )} )} \right]^\prime - \left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime }}{{\widetilde u - m}} = \left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime}$, since $\mathop {{\lim }}\limits_{\sigma _v^2 \to \infty } \left( {\tilde u - m} \right) = 0$. Therefore, using this fact and the Eq. (2), $\tilde u = - \varepsilon \, + \,\sigma _v^2\frac{{{{{\mathrm{d}}}}\ln \left[ {f_u( {\tilde u})} \right]}}{{{{{\mathrm{d}}}}\tilde u}}$, we have $\mathop {{\lim }}\limits_{\sigma _v^2 \to \infty } \tilde u = \mathop {{{{{\mathrm{lim}}}}}}\limits_{\sigma _v^2 \to \infty } \frac{{ - \varepsilon + \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime - \sigma _v^2\,m\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime }}}{{1 - \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime }}}$. This means, as $\sigma _v^2 \to \infty$, $\sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime + \left( {\sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} - 1} \right)\left( {\widehat u - m} \right) \to _d\left( {\varepsilon + m} \right)$. ■

Note that in point e of Theorem 3, for half normal and general truncated normal densities, the first derivate of the log density evaluated at the mode is $\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime = 0$, while for the exponential density, only the second derivate at the mode is $\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} = 0$.

A question that might arise is, does a larger sample prevent the shrinkage of the JLMS estimators? In cross-sectional context, the simple answer to this question is ‘no’ in the literature, for several reasons. First, since the inefficiencies are unobservable, the conditional estimators cannot be improved by learning from more data (in contrast to regression models). Second, the productivity of each unit is observed only once, therefore, due to the assumption of independence between the units, conditional estimator of each unit inefficiency is conditioned on a single composite error which corresponds to the unit itself. Third, due to lack of replication, the JLMS estimator is based on a guess (a typical value, like the mean or the mode) from the conditional distribution of the inefficiency, conditioned on a single composite error. Therefore, inconsistency and high uncertainty of the JLMS estimators are expected in the cross-sectional context. In econometrics literature, it is known that regularization increases the accuracy of an estimator by reducing its variance. The accuracy of a regularized estimator is due to a trade-off between decreased variance and increased bias.

3 Regularization

It has been shown in the literature that a maximum likelihood estimator is improved by maximizing an a posteriori or regularized (penalized) likelihood function; see for example, Cox and O’Sullivan (1990) and Flynn et al. (2013). One can consider the conditional mode and the conditional mean from Bayes expected loss and the Bayes risk minimization perspective. For example, for the conditional mean, the loss function is $\left( {u - \widehat u} \right)^2$, whose risk minimization yields $\mathop {{{{{\mathrm{Argmin}}}}}}\nolimits_{\widehat u \in {\Bbb R}^ + } \,E\{ { {( {u - \widehat u} )^2} |\varepsilon } \} = E\left( {u\left| \varepsilon \right.} \right)$. For the conditional mode, the loss function is a zero-one indicator function $\left( {I\left( {u\, \ne \,\widehat u} \right)\, - \,1} \right)$, whose risk minimization yields $\mathop {{{{{\mathrm{Argmin}}}}}}\nolimits_{\hat u \in {\Bbb R}^ + } \,E\left\{ {\left. {I\left( {u \,\ne \,\widehat u} \right) - 1} \right|\varepsilon } \right\} = \mathop {{{{{\mathrm{Argmin}}}}}}\nolimits_{\widehat u \in {\Bbb R}^ + } \,\left[ { - f_{u|\varepsilon }\left( {\widehat u} \right)} \right] = \mathop {{{{{\mathrm{Argmax}}}}}}\nolimits_{\widehat u \in {\Bbb R}^ + } \,f_{u\left| \varepsilon \right.}\left( {\widehat u} \right) = Mode\left( {u\left| \varepsilon \right.} \right)$.

A regularization of the risk minimization is achieved by adding extra information to, or imposing more constraints on, the risk function (expected loss). Suppose the constraints are a set of m zero-equality equations of twice differentiable functions R(u), i.e., R(u) = 0_m×1. The regularized conditional mean of the inefficiency is the solution to the following constrained objective function.

$$\mathop {{\min }}\limits_{\widehat u \in {\Bbb R}^ + } E\{ { {( {u - \widehat u} )^2} |\varepsilon } \}$$

$${{{\mathrm{Subject}}}}\,{{{\mathrm{to}}}}:{{{\boldsymbol{R}}}}\left( {\widehat u} \right) = 0$$

The solution is $\mathop {{{{{\mathrm{Argmin}}}}}}\nolimits_{\widehat u \in {\Bbb R}^ + } \,E\,\{ { {( {u - \widehat u} )^2} |\varepsilon } \}\, + \,\lambda ^\prime {{{\boldsymbol{R}}}}\left( {\widehat u} \right)$, where λ is the vector of Lagrange multipliers. The regularized conditional mean is the solution to the following system of equations.

$$\left\{ {\begin{array}{*{20}{l}} {\hat u - E\left( {u{{{\mathrm{|}}}}\varepsilon } \right) + 0.5\lambda ^\prime \,\nabla R\left( {\hat u} \right) = 0} \\ {R\left( {\hat u} \right) = 0} \end{array}} \right.$$

For the conditional mode of the inefficiency, the objective function and the constraints are as follows.

$$\mathop {{\max }}\limits_{\widehat u \in {\Bbb R}^ + } f_{u\left| \varepsilon \right.}\left( {\widehat u} \right)$$

${{{\mathrm{Subject}}}}\,{{{\mathrm{to}}}}:{{{\boldsymbol{R}}}}\left( {\hat u} \right) = 0$

The regularized conditional mode is the solution to the following system of equations.

$$\left\{ {\begin{array}{*{20}{l}} {f_{u\left| \varepsilon \right.}^\prime \left( {\widehat u} \right) + \lambda ^\prime \nabla R\left( {\widehat u} \right) = 0} \\ {R\left( {\widehat u} \right) = 0} \end{array}} \right.$$

The regularized JLMS estimators can be developed for both the mean and the mode. However, in the next section, we develop only the regularized conditional mode estimators for the three most commonly used inefficiency densities, which are the half normal, exponential and general truncated normal. In fact, the idea of a restricted estimator of the unit inefficiency can be easily generalized to any method that estimates the unit inefficiency based on the optimization of an objective functions (e.g., methods based on the determinants of inefficiency, such as Wang and Schmidt; 2002, Tran and Tsionas; 2009, Simar et al. 2017, and Parmeter et al. 2017). This can be done by imposing proper restrictions on the optimization of the objective function that is used for estimating the unit inefficiency.

Restricted moments are common imposed constraints on the likelihood functions (e.g., Hall and Presnell 1999). The constraints can, for instance, be on the sum of the inefficiencies or the sum of squared inefficiencies. These are constraints on the first and second moments of the inefficiencies, respectively. Based on the result of point e from Theorem 3, we can write

$$\mathop {{\lim }}\limits_{\sigma _v^2 \to \infty } \left( {\tilde u - m} \right) = \mathop {{{{{\mathrm{lim}}}}}}\limits_{\sigma _v^2 \to \infty } \frac{{ - \left( {\varepsilon + m} \right) + \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime }}{{1 - \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} }} = - \frac{{\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime }}{{\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} }}$$

which shows the shrinkage of the conditional mode towards the mode in response to the noise variance inflation. For half normal and general truncated normal densities, the limit is zero. With an exponential density, the $\tilde u$ is restricted to be non-negative, i.e., $\hat u = {{{\mathrm{max}}}}\{ 0,\tilde u\}$ and m = 0. Then, $\mathop {{\lim }}\nolimits_{\sigma _v^2 \to \infty } (\hat u - m) = 0$. With a vector of constraints ${{{\boldsymbol{R}}}}\left( {\hat u} \right) = 0$, the mode-difference limit becomes

$$\mathop {{\lim }}\limits_{\sigma _v^2 \to \infty } \left( {\tilde u - m} \right) = \mathop {{{{{\mathrm{lim}}}}}}\limits_{\sigma _v^2 \to \infty } \frac{{ - \left( {\varepsilon + m} \right)\, +\, \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime \,+\, \sigma _v^2\,\lambda ^\prime \nabla {{{\boldsymbol{R}}}}\left( {\widehat u} \right)}}{{1 \,-\, \sigma _v^2\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} }}$$

$$= - \frac{{\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^\prime + \lambda ^\prime \nabla {{{\boldsymbol{R}}}}\left( {\hat u} \right)}}{{\left[ {\ln \left( {f_u\left( m \right)} \right)} \right]^{\prime\prime} }}$$

Therefore, the above limit can be different from zero with properly selected constraints. This means that regularization can serve to reduce the shrinkage of the conditional mode estimator towards the mode. For the developed regularized conditional modes in Table 1, this fact is obvious. For example, for the general truncated normal, the conditional mode is $\frac{{ - \sigma _u^2\varepsilon + \mu \sigma _v^2}}{{\sigma _v^2 + \sigma _u^2}}$, which shrinks toward the mode μ with noise variance inflation, i.e., $\mathop {{\lim }}\nolimits_{\sigma _v^2 \to \infty } \,\frac{{ - \sigma _u^2\varepsilon \, + \,\mu \sigma _v^2}}{{\sigma _v^2\, + \,\sigma _u^2}}\, = \,\mu$. But, its regularized version based on the first moment restriction is $- \frac{{\sigma _u^2\varepsilon + \sigma _v^2\bar \varepsilon }}{{\sigma _v^2 + \sigma _u^2}}$, and its limit when $\sigma _v^2 \to \infty$ is $\mathop {{\lim }}\nolimits_{\sigma _v^2 \to \infty } \, - \,\frac{{\sigma _u^2\varepsilon + \sigma _v^2\bar \varepsilon }}{{\sigma _v^2 + \sigma _u^2}} = - \bar \varepsilon \, \ne \,\mu$. The same argument holds for the other two cases (half normal and exponential densities and their conditional modes and regularized conditional modes). Therefore, a weaker shrinkage property of the regularized estimators, especially for highly inefficient units, is expected. This fact is also supported by the simulation results in Section 4, as expected.

Table 1 The unit inefficiency estimator $\widehat u = {{{\mathrm{max}}}}\left\{ {0,\, - \tilde u} \right\}$, with $\tilde u$ given in the cells of the following table

4 First- and second-moment constraints

Inconsistency and high uncertainty of the JLMS estimators are expected in the cross-sectional context since any JLMS estimator of a unit inefficiency is conditioned on a single composite error corresponding to the unit itself. For each unit inefficiency estimation, we can also exploit extra information from other composite errors. For example, one can impose a restriction on all estimated inefficiencies such that their sample mean equals the sample mean of the composite errors. Such a restriction is equivalent to a sample zero-mean constraint on the estimated random shocks.

In terms of economic theory, the zero-mean random shock constraint is interpreted as a condition where the unit’s productivity is invariant to the random shocks in the market. Let us take a production frontier model such as the Cobb-Douglas or a translog model with the inefficiency as the single source of shortfall.

$$y_i = f\left( {{{{\boldsymbol{x}}}}_i;\beta } \right)\,e^{ - u_i}$$

If firm i experiences a random shock (v_i), its production can expand or shrink, depending on the sign of v_i.

$$y_i = f\left( {{{{\boldsymbol{x}}}}_i;\beta } \right)\,e^{ - u_i}\,e^{v_i}$$

Random shocks for some units can cover part of their inefficiencies, while for others, they might worsen their productivities, depending on whether the random shocks and the firm specific inefficiencies are in the same or opposite directions. An assumption of the SFA model in (1) is the zero-mean random shocks with a normal distribution. A similar restriction can also be imposed on the estimated random shocks, such that their sample mean is equal to zero. This is equivalent to the counterfactual assumption that if a firm were consecutively exposed to the shocks from the whole market, its productivity would eventually return to the same level, since it is assumed that the sum of the random socks in the market is equal to zero.

$$\begin{array}{l}y_i\,\,\, = \,f\left( {{{{\boldsymbol{x}}}}_i;\beta } \right) \cdot e^{ - u_i} = f\left( {{{{\boldsymbol{x}}}}_i;\beta } \right) \cdot e^{ - u_i} \cdot e^{v_1} \ldots e^{v_i} \ldots e^{v_n}\, \\\qquad= \,f\left( {{{{\boldsymbol{x}}}}_i;\beta } \right) \cdot e^{ - u_i}e^{\mathop {\sum}\nolimits_{i = 1}^n {v_i} } = f\left( {{{{\boldsymbol{x}}}}_i;\beta } \right) \cdot e^{ - u_i}\end{array}$$

Imposing the above-mentioned market (industry) shock-invariance assumption on the conditional mode of the inefficiency and the constraint that $\varepsilon _i = v_i - u_i$, for i = 1, … , n, with a sample of n units, is translated into the inefficiency sum (mean) restriction. The regularized conditional mode is the solution of the following constrained objective function.

$$\mathop {{\max }}\limits_{u_1, \ldots ,u_n} \left\{ {\mathop {\sum}\limits_{i = 1}^n {\ln \left[ {g_v\left( {u_i + \varepsilon _i} \right)} \right] + \ln \left[ {f_u\left( {u_i} \right)} \right]} } \right\}$$

subject to:

$$\mathop {\sum}\limits_{i = 1}^n {\left( {u_i + \varepsilon _i} \right) = 0}$$

Using the Lagrange multiplier method, the above constrained objective function is written as

$$\begin{array}{l}m_0\left( {u_1, \ldots ,u_n|\varepsilon _1, \ldots ,\varepsilon _n} \right)\\ \,\,\, \quad = \mathop {{{{{\mathrm{Argmax}}}}}}\limits_{u_1, \ldots ,u_n} \left\{ {\mathop {\sum }\limits_{i = 1}^n \ln \left[ {g_v\left( {u_i + \varepsilon _i} \right)} \right] + \ln \left[ {f_u(u_i)} \right] + \lambda \mathop {\sum }\limits_{i = 1}^n (u_i + \varepsilon _i)} \right\}\end{array}$$

Then, the estimated inefficiencies are forced to fulfill the constraint $\mathop {\sum}\nolimits_{i = 1}^n {v_i = 0}$. We can extend the number of restrictions, for example, by adding a restriction on the variance or the sum of squares of the estimated conditional modes, as follows.

$$\mathop {{\max }}\limits_{u_1, \ldots ,u_n} \left\{ {\mathop {\sum}\limits_{i = 1}^n {\ln \left[ {g_v\left( {u_i + \varepsilon _i} \right)} \right] + \ln \left[ {f_u\left( {u_i} \right)} \right]} } \right\}$$

Subject to:

$$\mathop {\sum}\limits_{i = 1}^n {\left( {u_i + \varepsilon _i} \right) = 0}$$

$$\mathop {\sum}\limits_{i = 1}^n {u_i^2 = c}$$

The c on the right side of the second constraint can be, for example, c = nE(u²). With the Lagrange multiplier method, the above constrained objective function is written as

$$\begin{array}{l}m_0\left( {u_1, \ldots ,u_n\left| {\varepsilon _1, \ldots ,\varepsilon _n} \right.} \right) = \mathop {{{{{\mathrm{Argmax}}}}}}\limits_{u_1, \ldots ,u_n} \\ \left\{ {\mathop {\sum}\limits_{i = 1}^n {\ln \left[ {g_v\left( {u_i + \varepsilon _i} \right)} \right] + \ln \left[ {f_u(u_i)} \right] + } \lambda \mathop {\sum}\limits_{i = 1}^n {\left( {u_i + \varepsilon _i} \right) + \theta } \,\left[ {\mathop {\sum}\limits_{i = 1}^n {u_i^2 - c} } \right]} \right\}\end{array}$$

Table 1 shows the regularized conditional mode estimators for a production model. Note that; $\bar \varepsilon = \frac{{\mathop {\sum }\nolimits_{i = 1}^n \varepsilon _i}}{n}$ and $\hat \sigma _\varepsilon ^2 = \frac{{\mathop {\sum }\nolimits_{i = 0}^n \left( {\varepsilon _i - \bar \varepsilon } \right)^2}}{n}$, and for $u_i\sim N^ + (\mu ,\sigma _u^2)$,

$$E\left( {u^2} \right) = \sigma _u^2\left( {1 + \frac{\mu }{{\sigma _u}}\frac{{\phi \left( {\mu /\sigma _u} \right)}}{{{{\Phi }}\left( {\mu /\sigma _u} \right)}} + \frac{{\mu ^2}}{{\sigma _u^2}}} \right)$$

For half-normal and exponential distributions, E(u²) is $\sigma _u^2$ and $2\sigma _u^2$, respectively. Thus, with the first- and second-moment constraints, $\widetilde u$ has the same closed-form solution in terms of E(u²). The conditional mean E(u|ε_i) with each of the densities shown in Table 1, has the following general form:

$$E\left( {u\left| {\varepsilon _i} \right.} \right) = \tilde \sigma \frac{{\phi \left( {\tilde \mu /\tilde \sigma } \right)}}{{{{\Phi }}\left( {\tilde \mu /\tilde \sigma } \right)}} - \tilde \mu$$

where $\tilde \mu$ is the negative of the cells of the 1^st row in Table 1 (corresponding to $- \tilde u$ in Theorem 1), and $\tilde \sigma = \sigma _v$ for the exponential density and $\tilde \sigma = \frac{{\sigma _v\sigma _u}}{\sigma }$ for each of the half-normal and truncated normal densities, where $\sigma ^2 = \sigma _v^2 + \sigma _u^2$.

As stated in Theorem 3, the conditional mode of inefficiency shrinks towards the mode of inefficiency in response to any noise variance inflation. From Table 1, we realize that the regularized estimators (explicitly with the first-moment restriction) serve to hold the unit inefficiency estimators away from the inefficiency mode by adding fractions of the noise variance to the conditional mode estimators, i.e., they serve to reduce the shrinkage of the conditional mode estimator towards the mode of inefficiency (0 or μ > 0).

For each of the above inefficiency densities and the set of the constraints, the same estimators are developed for a cost function. To save space, they are not presented here, but they are obtained straightforwardly by altering the signs of ε and $\overline \varepsilon$ inside the above closed-form formulae in Table 1. The purpose of presenting regularized conditional mode estimators is to introduce the methodology with closed-form mathematical expressions. Analogous to the conditional mode, the methodology can also be applied to regularized conditional mean estimators, with properly selected constraints⁴.

5 Simulations

An extensive simulation study is conducted to assess the performance of the proposed methodology relative to the JLMS estimators. The varying factors of the simulation study are (i) the sample size, (ii) the inefficiency distribution, (iii) the noise variance, (iv) the inefficiency variance and (iv) the location parameter when the inefficiency follows a truncated normal distribution.

In addition, the performance of the regularized estimators is assessed when the distribution is incorrectly specified. For this purpose, we see Gompertz distribution a suitable option, due to its desirable characteristics for being a probability distribution of inefficiency. More precisely, Gompertz distribution is a non-negative and log-concave distribution with non-zero density and with flexibility to be skewed to the left and to the right, and to have its mode equal to zero or to a positive number. For more on Gompertz distribution, see e.g., Lenart 2012.

Samples of size 20, 30, 50, 100 and 250 were simulated. A Cobb-Douglas production model was assumed, and each sample consisted of three simulated variables: production output and labor and capital inputs. The values for the intercept, elasticities, and means and variances of labor and capital were selected to imitate a production model originally used in Cobb-Douglas (1928). Specifically, the regression coefficients were selected as $\beta = \left\{ { - 0.25,\,0.25,\,075} \right\}$ and labor and capital were drawn from the bivariate normal distribution ${{{\boldsymbol{x}}}}\sim N_2\left( {\left[ {5.5,\,5} \right],\,\left[ {\begin{array}{*{20}{c}} {0.25} & 0 \\ 0 & {0.04} \end{array}} \right]} \right)$.

The noise from $N\left( {0,\sigma _v^2} \right)$ and inefficiencies from $N^ + (0,\sigma _u^2)$, $N^ + (\mu ,\sigma _u^2)$, $Exp(\sigma _u)$, and $Gompertz\left( {\eta ,b} \right)$ are drawn and used to simulate the production model. The noise variance was given the values of $\sigma _v^2 = \left\{ {0.1,\,0.5,\,0.9} \right\}$ and the inefficiency variance Var(u) was selected such that $Var\left( u \right) = 1 - \sigma _v^2$, i.e., the variance of the composite error was kept at unity with each simulated sample ($\sigma _\varepsilon ^2 = 1$). For the truncated normal inefficiency, the variance is also affected by μ. In the simulations, μ = 0 (for half normal) and μ = 0.1, and (for truncated normal). We select the basic Gompertz distributions with their scale parameters equal to one (b = 1). Then, their shape parameters η are selected such that $Var\left( u \right) = 1 - \sigma _v^2$.

We randomly draw inefficiencies from basic Gompertz(η, b) distributions. However, to assess the performance of the regularized estimators of unit inefficiency with an incorrectly specified distribution, we use $N^ + (0,\sigma _u^2)$, $N^ + (\mu ,\sigma _u^2)$ and Exp(σ_u) when estimating the SFA model and the unit inefficiency scores. The results are shown in Fig. 4 for samples of size 100. The results are consistent with other sample sizes, too.

Distributional parameters must be properly selected for having $Var(u) = 1 - \sigma _v^2$. For Exp(σ_u), we select $\sigma _u = \sqrt {1 - \sigma _v^2}$, and for $N^ + (0,\sigma _u^2)$, we select $\sigma _u^2 = (1 - \sigma _v^2)/(1 - \frac{2}{\pi })$. However, for each of $N^ + (\mu ,\sigma _u^2)$ and Gompertz(η,b), there is no closed form solution to select the proper distributional parameters. We found the parameters numerically, as shown in Table 2.

Table 2 Distributional Parameters for $Var(u) = 1 - \sigma _v^2$

The simulations were implemented as follows. For each sample size, the simulated design matrix was fixed across all simulations. To assess the performance of each estimator across different ranks of inefficiency, we considered two different scenarios. The first scenario is to rank the firms constantly based on their inefficiencies such that the first simulated firm always receives the lowest simulated inefficiency, and the last simulated firm always receives the largest inefficiency. The second scenario is to randomly rank the firms based on their inefficiencies. The results of the two scenarios were consistent; hence, the second scenario was followed to avoid any potential effect due to differences in production input across the firms. This process was repeated 100 times, i.e., 100 samples of ranked inefficiencies were simulated from the above-mentioned inefficiency probability distributions. For each of the 100 samples of inefficiencies, 100 samples of noise terms were randomly generated from the normal distributions. This resulted in 10,000 replications for each of the 60 combinations of the above factors (sample size, probability distribution, $\sigma _v^2$, $\sigma _u^2$ and μ).

With each replication of the simulation process, the four measures of unit-level inefficiencies were calculated, which were the conditional mean, conditional mode, conditional mode with first-moment constraint and conditional mode with first- and second-moment constraint. The Mean Squared Error (MSE) for the i^th firm’s inefficiency was calculated as follows.

$$MSE\left( {\widehat u_i} \right) = \frac{{\mathop {\sum }\nolimits_{k = 1}^{100} \mathop {\sum }\nolimits_{j = 1}^{100} \left( {\widehat u_{ji} - u_{ki}} \right)^2}}{{10000}}$$

The squared bias for the i^th firm’s inefficiency measure was calculated as follows.

$$Bias^2\left( {\widehat u_i} \right) = \frac{{\mathop {\sum}\nolimits_{k = 1}^{100} {\left( {\frac{{\mathop {\sum }\nolimits_{j = 1}^{100} \widehat u_{ji}}}{{100}} - u_{ki}} \right)^2} }}{{100}}$$

Each measure’s relative efficiency to the conditional mean efficiency was calculated as

$$Relative\,MSE\left( {\widehat u_i} \right) = \frac{{MSE\left( {E\left( {u\left| {\varepsilon _i} \right.} \right)} \right)}}{{MSE\left( {\widehat u_i} \right)}}$$

In the above formulae, i represents the unit, j is the noise replication and k represents inefficiency replications. The results of the relative MSE are shown in Fig. 1, Fig. 2, Fig. 3 and Fig. 4. In the graphs, the x-axis represents the rank of the inefficiency⁵ and the y-axis represents the relative MSE. All the simulations and calculations were run in STATA/SE 16 for Windows 64 bit using the sfcross command by Belotti et al. (2013).

Fig. 1

Normal—Half-Normal Model: Relative Inefficiency (MSE Ratio) compared to E(u|ε). Note: The larger the noise variance, the choppier the curves of the regularized conditional mode estimators are

Fig. 2

Normal—Exponential Model: Relative Inefficiency (MSE Ratio) compared to E(u|ε). Note: The larger the noise variance, the choppier the curve of the unregularized conditional mode is

Fig. 3

Normal—Truncated Normal Model (with μ = 0.1): Relative Inefficiency (MSE Ratio) compared to E(u|ε). Note: The larger the noise variance, the choppier the curves of the regularized conditional mode estimators are

Fig. 4

Inefficiencies are drawn from basic Gompertz distributions (scale parameter b = 1), but the inefficiency distributions are incorrectly specified, using each of exponential, half normal and general truncated normal distributions. Relative Inefficiency (MSE Ratio) compared to E(u|ε), with sample size n = 100. Note: The larger the noise variance, the choppier the curves of the regularized conditional mode estimators are

The results of the simulations in Figs. 1–4 show that when estimating large inefficiencies, the regularized conditional mode estimator, especially with the first-moment constraint, outperforms the JLMS estimators as the signal-to-noise ratio (σ_u/σ_v) increases. While the signal-to-noise ratio seems to be more decisive for the relative performance of the regularized estimator than the sample size and distributional assumption, its performance improves further when inefficiencies are exponentially distributed and when the sample size is not very large. Also, the larger the signal-to-noise ratio, the more robust the regularized estimators are, if the distribution is incorrectly specified, especially for larger inefficiencies. Some points are listed as follows:

• The unregularized conditional mode is almost always the most accurate estimator for units with no or small inefficiency— a result that is expected due to its shrinkage-towards-mode property. ⁶

• The unregularized conditional mean is the most accurate estimator of the unit inefficiency for middle ranks since it is a shrinkage estimator towards the mean.

• Regularized conditional mode estimators, especially the one with the first-moment constraint, are the most accurate estimators of unit inefficiencies that are more to the right tail of the distribution (highly ranked), unless it is a case with low signal-to-noise ratio, in which the unconditional mode (for lower ranks) and unconditional mean (for higher ranks) outperform the regularized estimators. The same argument holds if the inefficiency distribution is incorrectly specified, especially when an exponential distribution is incorrectly chosen as the inefficiency distribution.

• A summary of the above 3 points is that the analysts should make an effort to learn the characterizing conditions of the application at hand since the preferred estimation approach is determined by the signal-to-noise ratio and the location of the inefficiencies (see Badunenko et al. 2012). The averaging of different estimators has been proposed by Sickles (2005) with simple (naïve) averaging, Huang and Lai (2012), with different functional models, Parmeter et al. (2019), Andor et al. (2019) and Tsionas (2021). A different weighted average estimator can be developed using the regularized estimators, depending on the signal-to-noise ratio and the rank of the inefficiency. The preferred estimator can be a mixture (or weighted sum) of the conditional mode (for lower inefficiency ranks), conditional mean (for middle inefficiency ranks) and regularized conditional mode, especially the one subject to the first-moment constraint (for high inefficiency ranks). Also, a smoother estimator rather than the averaging can be an interpolated one that passes through some points (nodes and their values), like the unconditional mode, the unconditional mean and the most extreme conditional inefficiencies from both tails (skipping the lowest inefficiency if the mode inefficiency is zero).

6 Application

We consider the Swedish electricity distribution market that consisted of 154 local monopolies with complete data in 2013. The regulator wants to know the extent to which each firm can improve relative to the efficient frontier. For that purpose, we specify and estimate a variable cost (c) function where the number of customers/connection points (s) is the relevant output variable and the price of labor (l) and electricity (e) are the corresponding input prices. This production process is similar to what has been used in the past in this field; see e.g., Söderberg (2008), p. 65-66, for an extensive literature review. The price of electricity is included because firms purchase electricity to cover network losses and pay for transit on the high voltage network. The electricity price is calculated as the total costs of transit and the losses divided by the sum of the losses and high voltage deliveries.

Since the estimation of the unit inefficiency is a post-estimation procedure in SFA, entering the discussion of the selection between different productivity models, for instance between Cobb-Douglas and translog, might divert our attention away from the purpose of our proposed regularized estimators. Therefore, to save space, we only assume a Cobb-Douglas production model, and specify the variable cost function as $c_i = \alpha s_i^\beta e_i^\gamma l_i^\delta$, where i denotes the firm. The homogeneity restriction can be imposed by normalizing c_i and l_i by e_i, which after natural logarithm transform allows us to write the model as:

$$ln\left( {\frac{{c_i}}{{e_i}}} \right) = \beta _0 + \beta _1\,{{{\mathrm{ln}}}}\left( {s_i} \right) + \beta _2\,ln\left( {\frac{{l_i}}{{e_i}}} \right)$$

This expression has normal Cobb-Douglas properties, e.g., β₁ reveals the nature of the scale of production. Specifically, if β₁ < 1, then there are economies of scale; if β₁ = 1, then there is constant returns to scale; and if β₁ > 1, there are diseconomies of scale. It is straightforward to extend this Cobb-Douglas model to a stochastic frontier setting with inefficiency (u) and idiosyncratic error (v) terms (Coelli et al. 2005):

$$ln\left( {\frac{{c_i}}{{e_i}}} \right) = \beta _0 + \beta _1\,{{{\mathrm{ln}}}}\left( {s_i} \right) + \beta _2\,ln\left( {\frac{{l_i}}{{e_i}}} \right) + \nu _i + u_i$$

Data on variable costs (Opex), the number of customers, and the price of electricity are collected from the Swedish energy regulator (the Energy Markets Inspectorate). The price of labor, which measures the average regional salary for employees in the public sector, is collected from Statistics Sweden. Data are cross-sectional from the year 2013. Because the objective function, or type of customers, can be different for different ownership forms, as shown by Meade and Söderberg (2020), we argue that the regulator has to restrict the benchmark to the firms that have the same type of owners. For Swedish electricity distribution, therefore, we need three different benchmark samples: (i) municipality owned firms (n = 99), (ii) cooperatively owned firms (n = 32), and (iii) firms owned by private investors (n = 23). Some descriptive statistics of the data are presented in Table 4 in the Appendix.

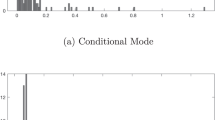
In Fig. 5, we see that the regularized estimators suggest that the highly inefficient firms have less technical efficiency (or equivalently larger inefficiency scores) compared to what the unregularized estimators estimate. Any inference regarding unit inefficiency can be poor when only a single sample is available, as it is in a cross-sectional context. However, we know that the conditional mean and the conditional mode (Theorem 3) are shrinkage estimators, i.e., they underestimate larger inefficiencies.

Fig. 5

Relative technical efficiency based on restricted and unrestricted conditional mode estimates, compared to technical efficiency based on unrestricted E(u|ε) estimtes

Therefore, our regularized estimators behave better in that sense, i.e., they estimated larger inefficiencies further from the mean/mode compared to the unregularized estimators. In addition, they have desired properties in the sense that they follow the theoretical first and second moments of inefficiency, i.e., their sample mean and variance are close to the estimated industry mean and variance.

The inference with a single sample is challenging. We checked the relative performance of each estimator by running a simulation with the same sampled data (number of customers and prices) but with the costs generated from the estimated parameters ($\widehat \sigma _v^2$, $\widehat \sigma _u^2$, $\widehat \mu$ and $\widehat \beta$) in Table 3. The simulation procedure was the same as that explained in the simulation section (Fig. 6 in the Appendix).

Table 3 Model estimates

7 Conclusions

The conditional mean/mode estimator of unit inefficiency is a shrinkage estimator towards the inefficiency mean/mode, depending on the noise variance (or signal-to-noise ratio). It is mostly different from the firm’s inefficiency itself unless there is no noise in the productivity model. The proposed regularized conditional mode estimators outperform the classical conditional mode/mean estimators, especially for highly inefficient units, and when the inefficiency distribution is incorrectly specified.

The constraints used in this paper were imposed on the first and the second moments of the inefficiencies when estimating the conditional mode of inefficiency. The idea can be further generalized to other types of constraints, distributions, or constraints on the conditional mean. In this article, the methodology is discussed in a cross-sectional context. However, it can be directly applied to a panel data context wherever the conditional mode/mean of the unit inefficiency is estimated. According to Tsionas (2017), one issue that continues to plague SFA is the endogeneity of the inputs. Our methodology is also directly applicable to SFA methods dealing with endogeneity. And most importantly, the proposed regularized estimators are beneficial to regulators for accurately estimating high unit inefficiencies since the benchmark methods systematically underestimate the inefficiency of less efficient units.

Appendix

Theorem: Suppose the function K(w) > 0 is defined for all $w \in {\Bbb R}$, with the properties:

• 1. K(w) is continuously differentiable for all $w \in {\Bbb R}$, and log-concave, with its first derivative K′(W).

• 2. $\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}$ is bounded above, such that $\mathop {{\lim }}\limits_{w \to + \infty } \frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}\, < \,\left| M \right|\, < \, +\infty.$

• 3. $\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}$ is bounded below, such that $\mathop {{\lim }}\limits_{w \to - \infty } \frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}\, > \, - \left| m \right|\, > \, -\! \infty.$

For the convergence of the integral ${\int}_{ - \infty }^{ + \infty } {e^{ - s\left[ {w - \frac{{K^\prime \left( w \right)}}{{K\left( w \right)}}} \right]}dw}$, with l < s < r, we must have $\mathop {{\lim }}\nolimits_{w\, \to \, \pm \,\infty } \left| {\frac{{\frac{{K^\prime (w)}}{{K(w)}}}}{w}} \right|\, < \,1$.

Proof:

We simplify the notation and use $\frac{{K^\prime \left( w \right)}}{{K\left( w \right)}} = H\left( w \right)$. Then, the integral can be written as follows.

$$\mathop {\int }\limits_{ - \infty }^{ + \infty } e^{ - s[w - H\left( w \right)]}dw = \mathop {\int }\limits_0^{ + \infty } e^{ - s[w - H\left( w \right)]}dw + \mathop {\int }\limits_0^{ + \infty } e^{s[w + H\left( { - w} \right)]}dw$$

Taking the first integral on the right side of the equation, [w − H(w)] is always increasing. Then, $\mathop {{\lim }}\nolimits_{w\, \to \, + \,\infty } \left[ {w\, - \,H\left( w \right)} \right]\, = \, +\infty$. In its functional form, it is similar to Laplace transform of $e^{sH\left( w \right)}$. Then, it must be the case that (see Widder 1946, Theorem 2.4a)

$$\mathop {{\lim }}\limits_{w\, \to \, + \,\infty } \,\frac{{sH\left( w \right)}}{w}\, = \,l\, \Rightarrow \,sl\, = \,\mathop {{\lim }}\limits_{w\, \to \, + \,\infty } \frac{{H\left( w \right)}}{w}\, < \,\mathop {{\lim }}\limits_{w\, \to \, + \,\infty } \frac{M}{w}\, = \,0$$

which implies that l < 0. For all s such that l < s, the integral converges if the rate of change is H(w) is slower than the rate of change in w, i.e., $\mathop {{\lim }}\limits_{w\, \to \, + \,\infty } \,\frac{{H\left( w \right)}}{w}\, < \,1$.

Taking the second integral on the right side of the equation, $\mathop {{\lim }}\nolimits_{w\, \to \, + \,\infty } \,\left[ {w + H\left( { - w} \right)} \right]\, = \, + \,\infty$. In its functional form, it is similar to Laplace transform of $e^{sH\left( w \right)}$ (with −s from s-domain). Then, it must be the case that

$$\mathop {{\lim }}\limits_{w \to + \infty } \frac{{sH\left( { - w} \right)}}{w} = r \Rightarrow sr = \mathop {{\lim }}\limits_{w \to + \infty } \frac{{H\left( { - w} \right)}}{w} > \mathop {{\lim }}\limits_{w \to + \infty } \frac{{ - \left| m \right|}}{w} = 0$$

which implies that r > 0. For all s such that s < r, the integral converges if the rate of change in H(−w) is faster than the rate of change in w, i.e.,

$1\, < \,\mathop {{\lim }}\nolimits_{w\, \to \, + \,\infty } \,\frac{{H\left( { - w} \right)}}{w}\, = \,\mathop {{\lim }}\nolimits_{w\, \to \, - \,\infty } \,\frac{{H\left( w \right)}}{{ - w}}$, which means $\mathop {{\lim }}\nolimits_{w\, \to \, - \,\infty } \,\frac{{H\left( w \right)}}{w}\, > \, - 1$.

Taking the conditions of both integrals together for the convergence, it means $\mathop {{\lim }}\limits_{w \to \pm \infty } \left| {\frac{{H\left( w \right)}}{{ - w}}} \right|\, <\, 1$. This completes the proof.

Figure 6 and Table 4

Fig. 6

The MSE ratio of unrestricted and restricted conditional mode estimators, compared to the unrestricted E(u|ε) with the simulations based on the data in the Application section

Table 4 Descriptive statistics of the data used in the application section