Abstract
Drawing on the puzzling behavior of ordinary knowledge ascriptions that embed an epistemic (im)possibility claim, we tentatively conclude that it is untenable to jointly endorse (i) an unfettered classical logic for epistemic language, (ii) the general veridicality of knowledge ascription, and (iii) an intuitive ‘negative transparency’ thesis that reduces knowledge of a simple negated ‘might’ claim to an epistemic claim without modal content. We motivate a strategic trade-off: preserve veridicality and (generalized) negative transparency, while abandoning the general validity of contraposition. We criticize various approaches to incorporating veridicality into domain semantics, a paradigmatic ‘information-sensitive’ framework for capturing negative transparency and, more generally, the non-classical behavior of sentences with epistemic modals. We then present a novel information-sensitive semantics that successfully executes our favored strategy: stable acceptance semantics, extending a vanilla bilateral state-based semantics for epistemic modals with a knowledge operator loosely inspired by the defeasibility theory of knowledge.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Despite sustained attention, epistemic modals remain a locus of controversy.Footnote 1 In this paper, we concern ourselves with the semantics and logic of ordinary knowledge ascriptions that embed an epistemic (im)possibility claim.
-
(1)
Ann knows that it might be raining.
-
(2)
Ann knows that it can’t be raining.
It is natural to interpret the modals in (1) and (2) as having an epistemic flavor. In particular, their meaning typically seems sensitive to Ann’s knowledge: intuitively, (1) communicates (perhaps inter alia) that Ann’s knowledge leaves it open that it is raining; (2) communicates (perhaps inter alia) that Ann’s knowledge rules out that it is raining. Notice how jarring the following sound:
-
(3)
# Ann knows that it might be raining and that it isn’t raining.
-
(4)
# Ann knows it can’t be raining, but for all she knows, it’s raining.
The first goal of this paper is to highlight (Sect. 2) some puzzling and subtle logical features of attitude ascriptions like (1) and (2). Here is a summary. On the face of it, each of the following represents valid reasoning:
-
(5)
Ann knows that it isn’t raining. So, Ann knows that it isn’t the case that it might be raining.
-
(6)
Ann knows that it isn’t the case that it might be raining. So, Ann knows that it can’t be raining.
-
(7)
Ann knows that it can’t be raining. So, it can’t be raining.
(5) showcases (what we call) the negative transparency of epistemic modal claims embedded in a knowledge ascription; (6) showcases the orthodox duality of epistemic possibility and necessity modals; (7) showcases the robust veridicality of knowledge ascription. But combining these properties with classical logic has a counter-intuitive consequence: a speaker rightly uses might claims to express her ignorance about p only if she accepts that everyone (in context) is ignorant about p. Notice that applying the transitivity of entailment to (5)–(7) yields:
-
(8)
Ann knows that it isn’t raining. So, it can’t be raining.
But then contraposition yields:
-
(9)
It might be raining. So, for all Ann knows, it is raining.
But (9) does not seem like valid reasoning. Suppose that I am playing poker with Ann. I mutter to myself ‘She might be holding an ace’. Surely I am not entitled to conclude from this that for all Ann knows, she is holding an ace (as far as I know, she can see that she isn’t holding an ace).
This isn’t a worry just for theorists that posit that natural language uniformly obeys classical logic: if classical logic governs discourse contexts where the semantic presuppositions of all relevant sentences are met, the puzzle applies to this constrained setting.
Section 3 proposes our strategy for answering the problem: accept veridicality and negative transparency, taking the data as evidence that contraposing an argument doesn’t always preserve validity. We thus extend a prominent strand in the literature that takes epistemic vocabulary to induce striking non-classical logical behavior.Footnote 2 Section 4 bolsters our choice by raising some problems for the alternative strategy of accepting only a restricted form of negative transparency, preserving classical logic. In particular, we observe how this plays out for a contextualist-descriptivist about epistemic modals.
Our second goal is to propose a formal semantics (with a natural intuitive interpretation) that successfully executes our strategy, in contrast to two extant rivals: first, domain semantics (per Yalcin (2007)) extended with a ‘classical’ account of knowledge operators (Sect. 5.1); second, domain semantics extended with a composite ‘safety’ account of knowledge operators (Sect. 5.2), per (Beddor & Goldstein, 2021). The novel theory we defend in Sect. 6—stable acceptance semantics—is of linguistic, technical, and philosophical interest.Footnote 3 On the linguistic side, we combine novel and known linguistic data to motivate a new entry in the tradition of ‘information-sensitive’ semantics for ordinary epistemic modals,Footnote 4 extending a standard ‘state-based’ account with a novel semantics for knowledge ascriptions. On the technical side, our system displays intriguing non-classical logical behavior, motivating, for future work, a fuller technical study of the underlying epistemic logic and its interactions with modals.Footnote 5 On the philosophical side, our semantics may be viewed as a new development in the expressivist tradition for epistemic vocabulary (cf. Yalcin (2011)), contributing to a line that treats assertibility and deniability conditions as primary.Footnote 6 What’s more, our account of knowledge operators is loosely inspired by the defeasibility theory of knowledge (Lehrer & Paxson, 1969), highlighting unexpected advantages of combining this perspective on knowledge ascription with our brand of expressivism.Footnote 7
Section 7 concludes with two outstanding issues for stable acceptance semantics, pointing to possible refinements for future work.
2 Negative Transparency and Veridicality
We now flesh out the puzzle outlined in Sect. 1: we note logical principles that, if true, neatly explain a variety of prima facie linguistic data, but have counter-intuitive effects when combined with classical logic.
To capture our candidate principles, we work with formal language \(\mathcal {L}\), intended to formalize a relevant fragment of declarative English. We use \(\varphi \) and \(\psi \) for arbitrary formulas in \(\mathcal {L}\). Intuitively, read \(K \varphi \) as ‘Ann knows that \(\varphi \)’. Ann is thus the name of the generic agent to whom we can ascribe knowledge; note that we do not in general assume, in our coming sentence examples, that the speaker is identical to Ann. Read \(\diamond \varphi \) as ‘It might be that \(\varphi \)’ or ‘it is possible that \(\varphi \)’, with the possibility modal stipulated to have an epistemic flavor. We assume that \(\lnot \diamond \varphi \) is read interchangeably as ‘it isn’t the case that it might be that \(\varphi \)’, ‘it can’t be that \(\varphi \)’, and ‘it must be that \(\lnot \varphi \)’ (assuming the orthodox duality of ‘might’ and ‘must’). We take atoms p and q to be declaratives without logical vocabulary (with \(\diamond \) included in the logical vocabulary). For simplicity, we assume that any semantic presuppositions for atoms are met, i.e., every atom is either true or false. We use \(\vdash \) to denote entailment and \(\equiv \) to denote logical equivalence, relative to our intended reading of \(\mathcal {L}\). We assume little at the outset about how entailment (i.e., logical consequence) is analyzed: for now, we leave it open whether it is best understood in terms of necessary truth-preservation, preservation of acceptability relative to information, or something else.Footnote 8
Now, there is prima facie reason to the think that the following logical principles are valid, and should be recovered by a formal semantics that aims to honor our intended reading of \(\mathcal {L}\):

For evidence, note that the following bare assertions, easily multiplied, have (to my ears at least) a distinct air of incoherence.
-
(10)
# Ann knows that it can’t be raining but, for all she knows, it is.
-
(11)
# Ann knows that it isn’t raining but, for all she knows, it might be.
-
(12)
# It might be raining, but Ann knows that it can’t be.
Compare (12) to the benign ‘It might be raining, but Ann (mistakenly) believes that it can’t be’. On the assumption that (10)–(12) are formalized as (13)–(15), NTrans explains this by predicting that (10) and (11) are contradictions; NeVer predicts that (12) is contradictory.
-
(13)
\(K \lnot \diamond p \wedge \lnot K \lnot p\)
-
(14)
\(K \lnot p \wedge \lnot K \lnot \diamond p\)
-
(15)
\(\diamond p \wedge K \lnot \diamond p\)
As further evidence for NTrans, note the difficulty in distinguishing what is communicated by the following:
-
(16)
For all Ann knows, Bob is here.
-
(17)
For all Ann knows, Bob might be here.
Conversationally, (16) and (17) come to the same thing: nothing that Ann knows rules out that Bob is here. Assuming that ‘for all Ann knows, \(\varphi \)’ is formalizable as ‘\(\lnot K \lnot \varphi \)’, NTrans predicts the equivalence of (16) and (17), as it entails (with minimal further assumptions) that \(\lnot K \lnot p\) is equivalent to \(\lnot K \lnot \diamond p\).
These observations have precedent. Though rarely considered in interaction with modal claims, the general veridicality of knowledge ascription is an orthodox assumption.Footnote 9NTrans recalls Łukasiewicz’ principle (i.e., \(\lnot p \vdash \lnot \diamond p\)), which is in turn related to the much-discussed incoherence of ‘epistemic contradictions’, i.e, claims of the form \(\lnot p \wedge \diamond p\) or \(p \wedge \diamond \lnot p\) (Bledin & Lando, 2018; Yalcin, 2007). Note, however, that accepting NTrans does not oblige one to accept Łukasiewicz’ principle.Footnote 10
But combining NTrans and NeVer with classical logic has untoward effects. To see this, first note a seemingly benign consequence of NTrans and NeVer.
Fact 1
NTrans+NeVer entails Epistemic Łukasiewicz (ELuk): \(K \lnot p \vdash \lnot \diamond p\)
Proof
\( K \lnot p \; \underset{\texttt{NTrans}}{\vdash } \; K \lnot \diamond p \; \underset{\texttt{NeVer}}{\vdash } \; \lnot \diamond p\) \(\square \)
There is again prima facie evidence that ELuk is an apt principle on our intended reading of \(\mathcal {L}\). Consider:
-
(18)
Ann knows that it isn’t raining. So, it can’t be raining.
-
(19)
Ann has conclusively established that it isn’t raining. So, it must not be.
-
(20)
# Ann knows that it isn’t snowing, but it might be.
-
(21)
# Ann has conclusively established that it isn’t snowing, but it might be.
(18) seems like unobjectionable ordinary reasoning (as does the closely related (19)). (20) has an air of incoherence (as does the closely related (21)). Assuming that (18) and (20) are respectively formalized as \(K \lnot p \vdash \lnot \diamond p\) and \(K \lnot q \wedge \diamond q\), ELuk explains both.
However, combining ELuk with unfettered classical logic yields a puzzling result.

Fact 2
ELuk+Con+DN entails Uniformity: \(\diamond p \vdash \lnot K \lnot p\)
Proof
\(\diamond p \; \underset{\texttt{DN}}{\vdash } \; \lnot \lnot \diamond p \; \underset{\mathtt {ELuk+Con}}{\vdash } \; \lnot K \lnot p \) \(\square \)
Uniformity says: ‘it might be that p’ entails ‘for all Ann knows, p’. This seems false, egregiously implying that if a speaker is aware of but rightly uncertain about p, then every agent is uncertain about p (remember, Ann is a generic agent). To see this, note that Uniformity (with minimal assumptions) entails:
But while ‘it might be raining and might not be raining’ predominantly serves to express the speaker’s ignorance about the rain, ‘Ann doesn’t know that it is raining and doesn’t know that it isn’t raining’ predominantly serves to express that Ann is ignorant.Footnote 11 As evidence, note the incoherence of the following:
-
(22)
# It might be raining and it might not be raining. Also, I know that it is raining.
-
(23)
# Ann knows that it might be raining and that it might not be raining. Also, she knows that it is raining.
To bolster our assessment that Uniformity is invalid, consider a banal context. Suppose that your dinner partner has a severe shellfish allergy. You ask Smith, your waiter: ‘Does the daily soup contain shellfish?’. Smith replies:
-
(24)
It might. The kitchen usually puts shellfish in the soup, but not always. I’ll check with Chef Jones. She always knows exactly what’s in the soup.
Upon hearing the banal (24), and waiting for Smith to return, one would normally happily accept (and say to your dinner partner) all of:
-
(25)
The soup might have shellfish (that’s why you shouldn’t eat it but should wait for Smith to return, as she is checking with the kitchen).
-
(26)
Unlike Smith, Jones knows whether the soup has shellfish (that’s why Smith is consulting Jones).
It would be odd to conclude from (25), per Uniformity, that it isn’t the case that Chef Jones knows that the soup doesn’t have shellfish. For (26) implies that either Jones knows that the soup has shellfish or she knows that it doesn’t have shellfish. An uncontentious application of disjunctive syllogism would thus yield (even before Smith returns): Chef Jones knows that the soup has shellfish. But surely one isn’t right to conclude this given only (24).
The general pattern here is emulated by other epistemic vocabulary. Let’s use \(\triangledown \varphi \) for ‘it is likely that \(\varphi \)’. Then \(K \lnot p \vdash \lnot \triangledown p\) and \(K \lnot p \vdash K \lnot \triangledown p\) are similarly well-supported by prima facie linguistic evidence, while \(\triangledown p\vdash \lnot K \lnot p\) does not seem true. Compare:
-
(27)
Ann knows that it isn’t raining. So, it isn’t likely to be raining.
-
(28)
# Ann knows it isn’t raining. But for all she knows, it’s likely to be raining.
-
(29)
It is likely that Ann will resign tomorrow. But only Ann knows for sure whether she will.
(27) strikes one as good, if unnecessarily cautious, reasoning. (28) seems incoherent. Contra \(\triangledown p\vdash \lnot K \lnot p\), (29) does not imply, via disjunctive syllogism, that Ann knows she will resign tomorrow (we formalize ‘Ann knows whether p’ as \(Kp \vee K\lnot p\)).
We add a last important wrinkle to our preliminary observations: both NeVer and NTrans have natural generalizations that, on the face of it, are as well supported by the evidence as the narrower principles. Consider:

For further evidence for Ver in the presence of epistemic modals, observe that the following has again an air of incoherence:
-
(30)
# It can’t be raining, though Ann knows it might be raining.
Compare the benign ‘it can’t be raining, though Ann mistakenly believes it might be’. If (30) is correctly formalized as \(\lnot \diamond p \wedge K \diamond p\), then Ver predicts that it is contradictory. More generally, Ver neatly explains the oddity (‘incoherence’ is sometimes too strong here) of speaker X saying that person Y knows that it might be that p when it is highly likely that X knows that p is false (even when Y clearly does not know that p is false):
-
(31)
?? Obviously, the earth isn’t flat. But the ancient Egyptians knew that it might be. (cf. Moss (2018), pg.122)
-
(32)
?? Lottie, my four-year-old, knows that frogs might be reptiles.
The explanation from Ver is that (31) entails ‘the earth might be flat’, shouldering a typical speaker that states (31) with a commitment which sits uneasily with their presumed knowledge that the earth isn’t flat; (32) entails ‘frogs might be reptiles’, sitting uneasily with the speaker’s presumed knowledge that frogs aren’t reptiles. Compare the banal ‘the ancient Egyptians thought that the earth might be flat’ and ‘Lottie thinks that frogs might be reptiles’. As thought ascriptions lack veridicality, analogous commitments are not imposed on the speaker.
It seems that NTrans can too be generalized. Consider:

For each formulation, NTrans is a special case (where \(p = \top \)). For convenience, I assume the above claims are equivalent. (Each formulation could be exclusively relied on in our coming argumentation, however.) The linguistic evidence in support of GeNT seems no worse than that for NTrans though, unsurprisingly, parsing the relevant sentences requires slightly more effort. Consider:
-
(33)
# Ann knows that it isn’t both raining and a nice day for a picnic, but for all she knows it’s both raining and might be a nice day for a picnic.
-
(34)
Ann knows that it isn’t both raining and a nice day for a picnic. So, Ann knows that either it isn’t raining or it must not be a nice day for a picnic.
-
(35)
# Ann knows that either it isn’t raining or must not be a nice day for a picnic, but for all she knows it’s both raining and a nice day for a picnic.
(33) and (35) sound incoherent; (34) sounds like good reasoning. GeNT neatly explains this, assuming that (33)–(35) are respectively formalized as follows:
-
(36)
\(K \lnot (r \wedge n) \wedge \lnot K \lnot (r \wedge \diamond n)\)
-
(37)
\(K \lnot (r \wedge n) \vdash K (\lnot r \vee \lnot \diamond n)\)
-
(38)
\(K (\lnot r \vee \lnot \diamond n) \wedge \lnot K \lnot (r \wedge n)\)
3 Strategies for response
We have a phenomenon that requires explanation: a pattern of presumed linguistic data that finds a simple explanation in logical principles that clash with classical logic. There are three broad strategies for accounting for this.
-
Strategy 1: predict the data by predicting the principles. Provide an independently motivated formal semantics that validates Ver and GeNT, and invalidates Uniformity (and thus Con).
-
Strategy 2: question the data. Explain away the alleged pattern of ordinary linguistic judgment (chiefly concerning coherence) exhibited in Sect. 2, perhaps using evidence that the alleged judgments aren’t sufficiently robust.
-
Strategy 3: predict the data without the principles. Provide an independently motivated formal semantics that preserves classical logic (in particular, Con) and argue, perhaps by appeal to pragmatics, that the validity of Ver and/or GeNT, and/or the falsity of Uniformity, is at best an illusion.
The present paper follows Strategy 1, taking the observations in Sect. 2 at face value, i.e., as prima facie evidence that embedded ‘might’ claims display an unusual logic. Note that independent motivation for rejecting Con has been tabled. For example, a proposed counterexample to modus tollens from Yalcin (2012), utilizing ‘likely’, is easily modified to bear against Con.
Marbles. Suppose an urn contains 100 marbles, big and small. Of the big, 10 are blue and 30 are red. Of the small, 50 are blue and 10 are red. A marble, m, is randomly selected and placed under a cup. Given only this information, (39) sounds like good reasoning, but (40) does not:
- (39)
Suppose that m is big. It follows that m is likely to be red.
- (40)
m isn’t likely to be red. # Thus, m isn’t big.
To see why the second inference in (40) seems incorrect, note that we already know that the marble isn’t likely to be red, yet accepting that it isn’t big is rash.
Let us immediately rule out a version of Strategy 1 according to which the invalidity of Uniformity and Con is explained using presupposition failure. It is commonly agreed that ‘knows’ is factive, as linguists use ‘factive’: ‘Ann knows that \(\varphi \)’ and ‘Ann doesn’t know that \(\varphi \)’ both typically imply that the speaker accepts \(\varphi \).Footnote 12 For example, a speaker that says ‘Ann doesn’t know that Raf is in Mexico’ is (typically) committed to ‘Raf is in Mexico’. Now, suppose that the presupposition is semantic in nature and that one’s favorite account of ‘knows’ and ‘might’ yields GeNT and Ver. Then ELuk holds, but failures of Con will be routine: \(K\varphi \) entails \(\varphi \), but \(\lnot \varphi \) will not entail \(\lnot K \varphi \), as the former marks the failure of the latter to have a truth value. Similarly, one expects Uniformity to fail: if both \(\diamond p\) and p hold, then \(\lnot K \lnot p\) does not have a truth value.
But the problem with this explanation is that it is unlikely that the factivity of ‘knows’ involves semantic presupposition (as Stalnaker (1974) influentially observes). Rather, it seems a matter of pragmatic presupposition: a speaker that states ‘Ann doesn’t know that \(\varphi \)’ can usually be assumed, on broadly Gricean grounds, to accept \(\varphi \). For the presupposition \(\varphi \) can be canceled: if Ann bets on black at the roulette table, there is nothing untoward about saying ‘Ann is taking a big risk—she doesn’t know that it won’t land on red’ or ‘for all Ann knows, it will land on red’. Obviously, this speaker is not committed to the truth of ‘it won’t land on red’.
4 Strategy 3 via flexible contextualism
We have motivated our chosen strategy on abductive grounds. Can alternative strategies provide an equally good, or better, explanation of the phenomenon? We put aside Strategy 2 but briefly explore Strategy 3 via a prominent descriptivist strand in the literature: we assess the proposal that the apparent validity of GeNT and/or Ver is an illusion created by the flexible context-sensitivity of epistemic modals (cf. Kratzer (1981), Dowell (2011)), in concert with systematic mechanisms governing discourse prominence (cf. Stojnić (2017)).
A common view is that ‘might’ is to some degree context-sensitive: exactly which body of knowledge/information such vocabulary is tuned to can vary by context (see, e.g., von Fintel and Gillies (2011)). To express this with perspicuity (more than natural language), we can enrich the syntax for \(\mathcal {L}\) to record the agent x (or, anyway, the information in their possession) that an instance of \(\diamond \) or K is ‘indexed’ to: we write \(\diamond _x\) and \(K_x\). We understand ‘agent’ loosely here, as including groups, or even mere sources of information. Then, with a nod to Dowell (2011), call the following view flexible contexualism: \(\diamond _x p\) has descriptive content, expressing the proposition that p is compatible with x’s knowledge, where x is fixed, in context, by the intentions of the speaker; \(\lnot \diamond _x p\) expresses that p is ruled out by x’s knowledge.
Given flexible contextualism, NTrans and ELuk are naturally explicated as follows (note that this explication is not mandatory in general):

But Unrestricted NTrans, on a flexible contextualist reading, is obviously false: \(K_a \lnot p\) does not imply \(K_a \lnot \diamond _b p\) when a and b aren’t identical (Ann knowing that p is false does not imply that Ann knows that p is ruled out by Bob’s knowledge). Unrestricted ELuk is also obviously false (Ann knowing that p is false does not imply that Bob’s knowledge rules out p). In contrast, qualified versions of NTrans and ELuk have significant appeal on the flexible contextualist picture:

Restricted NTrans says: Ann knows that her knowledge rules out p exactly when she knows that p is false (cf. the KK principle). Restricted ELuk says: from Ann knowing that p is false it follows that Ann’s knowledge rules out p.
Ver plus Restricted NTrans yields only Restricted ELuk. Unlike ELuk, there is nothing obviously problematic about contraposing instances of Restricted ELuk: \(\diamond _a p \vdash \lnot K_a \lnot p\) merely says that p being compatible with a’s knowledge entails that for all a knows, p is true. In short, the threat to Con is removed.
However, this story does not yet explain the data in Sect. 2. Consider again:
-
(39)
# Ann knows that it isn’t raining but, for all she knows, it might be.
-
(40)
# It can’t be raining, but Ann knows it might be.
To rehearse, these have a persistent air of incoherence: one struggles to imagine a context where they receive a smooth interpretation. Yet the flexible contextualist predicts that readily intelligible readings are available:
-
(41)
Ann knows that it isn’t raining but, for all she knows, nothing I know rules out rain.
-
(42)
My knowledge rules out rain but Ann knows that nothing she knows rules out rain.
However, the flexible contextualist can appeal to the pragmatic effects of discourse prominence to explain why hearers eschew benign interpretations of (39) and (40) in ordinary discourse.Footnote 13 The leading idea here is that the interpretation of a modal (in particular, the possibilities that it quantifies over) is typically (intended by the speaker to be) constrained by prior locutions that make relevant possibilities prominent. For epistemic modals, relevant possibilities are naturally raised to prominence by, at least, (i) prior (mention of) knowledge or belief ascriptions and (ii) prior bare epistemic modal claims (themselves presumably sensitive to the speaker’s knowledge as a default). Given this, the flexible contextualist can predict that hearers default to (something like) the following jarring interpretations when a speaker says (39) or (40):
-
(43)
# Ann knows that it isn’t raining but, for all she knows, her knowledge doesn’t rule out rain.
-
(44)
# My knowledge rules out rain but Ann knows that combining her knowledge with mine doesn’t rule out rain.
Flexible contextualism plus discourse prominence can also explain away (as an illusion) the apparent counter-examples to Con generated from contraposing instances of ELuk. For it can predict that the default interpretation of (45)is (47), and that of (46) is (48). But while (48) is indeed invalid, it is not the result of contraposing (47).
-
(45)
Chef Jones knows that there isn’t shellfish in the soup. So, there can’t be shellfish in the soup.
-
(46)
# There might be shellfish in the soup. So, for all Chef Jones knows, there is shellfish in the soup.
-
(47)
Chef Jones knows that there isn’t shellfish in the soup. So, the combination of my knowledge and Chef Jones’s knowledge rules out that there is shellfish in the soup.
-
(48)
# My own knowledge doesn’t rule out that there is shellfish in the soup. So, for all Chef Jones knows, there is shellfish in the soup.
So far so good. Still, it is far from clear that the resources we have given the flexible contextualist can account for all of our data. First, for all we’ve said, the view seems to erroneously predict that the default interpretation of (49) is (50).
-
(49)
The earth can’t be flat. Even the ancient Greeks knew that it can’t be flat.
-
(50)
My knowledge rules out that the earth is flat. Even the ancient Greeks knew that the combination of my knowledge and theirs rules out that the earth is flat.
But (49) and (50) are markedly different statements: in the mouth of a modern speaker, (49) is true and (50) is false (the ancient Greeks didn’t hold any views about this speaker’s knowledge).
Second, the order dependence of the mechanisms of discourse prominence (that we cited above to useful effect) seem to erroneously predict that the default interpretation of (51) is (53), and of (52) is (54):
-
(51)
# It can’t be raining. Jane knows it might be raining.
-
(52)
# Jane knows it might be raining. It can’t be raining.
-
(53)
# My knowledge rules out rain. Jane knows that rain is compatible with the combination of my knowledge and hers.
-
(54)
Jane knows that rain is compatible with what she knows. My knowledge rules out rain.
However, to my ears there is no discernible difference in meaning between (51) and (52) (for example, they both sound jarring), while there is a clear difference in meaning between (53) and (54) (for example, the former sounds jarring; the latter is readily intelligible).
Third, I see no reason why the mechanisms of discourse prominence would, given flexible contextualism, eliminate (56) as the default interpretation of (55)
-
(55)
?? The ancient Egyptians didn’t know much about the earth’s structure, but certainly knew that the earth might be flat.
-
(56)
The ancient Egyptians didn’t know much about earth’s structure, but certainly knew that a flat earth wasn’t ruled out by the knowledge that they had available at the time.
This seems the wrong prediction: (55) is markedly odd and plausibly false; (56) is readily intelligible and plausibly true.
Might it help to assume that the speaker’s knowledge is invariably prominent in discourse, even when prior modal locutions aren’t in play? No, for though this assumption helpfully predicts that (55) is typically interpreted as the odd and obviously false (57), it also predicts, egregiously, that (58) is typically interpreted as (59), and that (60) is typically interpreted as (61).
-
(57)
?? The ancient Egyptians didn’t know much about the earth’s structure, but certainly knew that a flat earth wasn’t ruled out by the combination of my knowledge and their knowledge.
-
(58)
The ancient Egyptians wrongly believed that the earth might be flat.
-
(59)
The ancient Egyptians wrongly believed that a flat earth wasn’t ruled out by the combination of my knowledge and their beliefs.
-
(60)
Ann knows that it might be raining.
-
(61)
Ann knows that it is compatible with the combination of my knowledge and her knowledge that it is raining.
Unlike (58), (59) is obviously false in the mouth of a modern speaker (the ancient Egyptians did not hold any beliefs about any modern speaker’s knowledge), and (60) and (61) clearly differ in content when the speaker is not Ann (consider a context where Ann has never heard of the speaker).
This is hardly the end of the road for (views like) flexible contextualism. Perhaps proponents can draw on further resources to challenge, ignore, or explain (away) our observations. Nevertheless, it is clear that executing Strategy 3 will not be plain sailing. We leave it to proponents to finesse the view.Footnote 14
5 Strategy 1 via domain semantics
We pursue the strategy of giving an independently motivated formal semantics that delivers Ver and GeNT, while invalidating Uniformity and Con. Before developing our positive view, we examine two extant competitors.
5.1 Classical domain semantics
Domain semantics invites a natural account of knowledge ascription that exhibits NTrans. This contrasts with the descriptivist school, according to which ‘it might be that p’ is taken as synonymous with, roughly, ‘p is not ruled out by what is mutually known, or easily known, by a relevant group of agents’. Negative transparency seems untenable on the descriptivist account: that Ann knows that the train isn’t late does not entail that Ann knows anything about what the mutual knowledge of a certain group rules out (even if the group includes only Ann: she might well be uncertain what she knows).
An information model \(\mathcal {I} = \langle W, \texttt{I} \rangle \) is a pair, with W the set of all possible worlds and \(\texttt{I}\) an assignment of an information state \(\texttt{I}(p)\) to each atomic sentence of \(\mathcal {L}\). We take an information state—generically denoted \({\textbf {i}}\)—to just be an intension, i.e., a subset of W. State \({\textbf {i}}\) is veridical at w when \(w \in {\textbf {i}}\). We evaluate sentences in \(\mathcal {L}\) as true in context (1) or false in context (0) relative to a possible world w and an information state \({\textbf {i}}\): the valuation function \(\llbracket \cdot \rrbracket ^{w, {\textbf {i}}}\) (mapping a sentence to a truth value, relative to an index of two shiftable parameters) is defined as follows.
Definition 1
(Domain Semantics) Given an information model \(\mathcal {I}\):

The following notion (following (Yalcin, 2007)) will be important for our account of attitude ascriptions:
Definition 2
(Acceptance)  : \(\llbracket \varphi \rrbracket ^{w, {\textbf {i}}} = 1\)
: \(\llbracket \varphi \rrbracket ^{w, {\textbf {i}}} = 1\)
If  , we say information \({\textbf {i}}\) accepts or supports sentence \(\varphi \), modeling the idea that having exactly the information \({\textbf {i}}\) is sufficient for conclusively establishing \(\varphi \), rendering \(\varphi \) correctly assertable (putting aside Gricean considerations). To get a feel for
, we say information \({\textbf {i}}\) accepts or supports sentence \(\varphi \), modeling the idea that having exactly the information \({\textbf {i}}\) is sufficient for conclusively establishing \(\varphi \), rendering \(\varphi \) correctly assertable (putting aside Gricean considerations). To get a feel for  , note that the following sensible properties are readily verified:
, note that the following sensible properties are readily verified:

Two notions of entailment are prominent in this framework. First, a truth-preservation relation \(\vDash \) is straightforwardly defined: \(\varphi \vDash \psi \) holds exactly when \(\llbracket \varphi \rrbracket ^{w, {\textbf {i}}} = 1\) implies \(\llbracket \psi \rrbracket ^{w, {\textbf {i}}} = 1\) for every w and \({\textbf {i}}\) in every model \(\mathcal {I}\). Second, an acceptance-preservation relation  is straightforwardly defined:
is straightforwardly defined:  holds exactly when
holds exactly when  implies
implies  for every \({\textbf {i}}\) in every model \(\mathcal {I}\). Both consequence relations serve as useful tools for explaining ordinary intuitions about entailment and contradiction. For example, the domain semanticist utilizes
for every \({\textbf {i}}\) in every model \(\mathcal {I}\). Both consequence relations serve as useful tools for explaining ordinary intuitions about entailment and contradiction. For example, the domain semanticist utilizes  , not \(\vDash \), to explain the incoherence of epistemic contradictions of the form \(p \wedge \diamond \lnot p\): while \(p \wedge \diamond \lnot p\) is consistent with respect to \(\vDash \), there is no \({\textbf {i}}\) such that
, not \(\vDash \), to explain the incoherence of epistemic contradictions of the form \(p \wedge \diamond \lnot p\): while \(p \wedge \diamond \lnot p\) is consistent with respect to \(\vDash \), there is no \({\textbf {i}}\) such that  .
.
To introduce attitude ascriptions, we transfer an account of belief ascription from Yalcin (2011) to knowledge ascription. Call this the classical approach. A classical model \(\mathcal {C}\) supplements an information model with function \({\textbf {k}}\), mapping a world to a non-empty intension \({\textbf {k}}^w\). The idea is that \({\textbf {k}}^w\) models Ann’s epistemic state at w as a set of epistemic alternatives (the total informational content of Ann’s knowledge). As an agent’s knowledge can never rule out the actual world, we stipulate: \(w \in {\textbf {k}}^w\) for all \(w \in W\).
Definition 3
(Classicism) Given classical \(\mathcal {C}\), we extend domain semantics with:

However, relative to Strategy 1 of Sect. 3, classicism is only a partial success.
Fact 3
For classicists, NTrans holds.
Proof
\(\llbracket K\lnot \diamond p \rrbracket ^{w, {\textbf {i}}} = 1\) iff  iff \(\forall u \in {\textbf {k}}^w\):
iff \(\forall u \in {\textbf {k}}^w\):  iff \(\forall u \in {\textbf {k}}^w\): \(u \notin \texttt{I}(p)\) iff
iff \(\forall u \in {\textbf {k}}^w\): \(u \notin \texttt{I}(p)\) iff  iff \(\llbracket K \lnot p \rrbracket ^{w, {\textbf {i}}} = 1\) \(\square \)
iff \(\llbracket K \lnot p \rrbracket ^{w, {\textbf {i}}} = 1\) \(\square \)
Fact 4
For classicists, Ver fails with respect to \(\vDash \).
Proof
Counter-model: consider \(\mathcal {C}\) where (i) \(W = \{w_1, w_2\}\), (ii) \(\texttt{I}(p) = \{w_2\}\), (iii) \({\textbf {k}}^{w_1} = W\). Let \({\textbf {i}} = \{w_1\}\). So, by (ii) and (iii), \(\llbracket K\diamond p \rrbracket ^{w_1, {\textbf {i}}} = 1\), as there is a p-world in \({\textbf {k}}^{w_1}\). But \(\llbracket \diamond p \rrbracket ^{w_1, {\textbf {i}}}=0\), as there is no p-world in \({\textbf {i}}\). \(\square \)
Of course, a small modification to the semantics secures Ver:

But the modified proposal abandons NTrans at the level of truth-preservation. For a counter-model, take \(\mathcal {C}\) where, for some \(@ \in W\), every world in \({\textbf {k}}^@\) (including @ itself) is a \(\lnot p\)-world (assuring  and \(\llbracket \lnot p \rrbracket ^{@, {\textbf {i}}} = 1\)), but there is a p-world in \({\textbf {i}}\) (so \(\llbracket \lnot \diamond p \rrbracket ^{@, {\textbf {i}}} = 0\)). So, given \(\mathcal {C}\), \(\llbracket K\lnot p \rrbracket ^{@, {\textbf {i}}} = 1\) and \(\llbracket K\lnot \diamond p \rrbracket ^{@, {\textbf {i}}} = 0\).
and \(\llbracket \lnot p \rrbracket ^{@, {\textbf {i}}} = 1\)), but there is a p-world in \({\textbf {i}}\) (so \(\llbracket \lnot \diamond p \rrbracket ^{@, {\textbf {i}}} = 0\)). So, given \(\mathcal {C}\), \(\llbracket K\lnot p \rrbracket ^{@, {\textbf {i}}} = 1\) and \(\llbracket K\lnot \diamond p \rrbracket ^{@, {\textbf {i}}} = 0\).
However, it is readily checked that the modified proposal yields:  iff
iff  . So, NTrans emerges at the level of acceptance, in tandem with Ver. This assuages its failure at the level of truth-preservation. Nevertheless, two worries remain. First, the modified proposal is, as it stands, markedly ad hoc: adding the clause \(\llbracket \varphi \rrbracket ^{w, {\textbf {i}}} = 1\) to the truth condition for \(K\varphi \) raises interpretive questions about the nature of \({\textbf {k}}^w\) (if \({\textbf {k}}^w\) simply represents Ann’s knowledge state, wouldn’t \({\textbf {k}}^w\) establishing \(\varphi \) invariably be sufficient for Ann to be positioned to know \(\varphi \)?) and serves purely to assure veridicality for modalized formulas (it is readily checked that Ver holds for \(\diamond \)-free formulas in the original account of \(K\varphi \)). Second, even more pointedly, the modified proposal does not yield GeNT: in particular, there exists \(\mathcal {C}\) and \({\textbf {i}}\) where
. So, NTrans emerges at the level of acceptance, in tandem with Ver. This assuages its failure at the level of truth-preservation. Nevertheless, two worries remain. First, the modified proposal is, as it stands, markedly ad hoc: adding the clause \(\llbracket \varphi \rrbracket ^{w, {\textbf {i}}} = 1\) to the truth condition for \(K\varphi \) raises interpretive questions about the nature of \({\textbf {k}}^w\) (if \({\textbf {k}}^w\) simply represents Ann’s knowledge state, wouldn’t \({\textbf {k}}^w\) establishing \(\varphi \) invariably be sufficient for Ann to be positioned to know \(\varphi \)?) and serves purely to assure veridicality for modalized formulas (it is readily checked that Ver holds for \(\diamond \)-free formulas in the original account of \(K\varphi \)). Second, even more pointedly, the modified proposal does not yield GeNT: in particular, there exists \(\mathcal {C}\) and \({\textbf {i}}\) where  but \({\textbf {i}} \nVdash K\lnot (p \wedge \diamond q)\).
but \({\textbf {i}} \nVdash K\lnot (p \wedge \diamond q)\).
Fact 5
For classicists, GeNT fails with respect to  .
.
Proof
Let \({\textbf {i}}\) contain only worlds \(w_1\) and \(w_2\), with p only true at \(w_1\), and q only true at \(w_2\). Thus,  but \({\textbf {i}} \nVdash \lnot (p \wedge \diamond q)\) (as \(\llbracket p \wedge \diamond q\rrbracket ^{w_1, {\textbf {i}}} = 1\)). If we further set \({\textbf {k}}^w\) to be \({\textbf {i}}\) for every \(w \in {\textbf {i}}\), we get:
but \({\textbf {i}} \nVdash \lnot (p \wedge \diamond q)\) (as \(\llbracket p \wedge \diamond q\rrbracket ^{w_1, {\textbf {i}}} = 1\)). If we further set \({\textbf {k}}^w\) to be \({\textbf {i}}\) for every \(w \in {\textbf {i}}\), we get:  but \({\textbf {i}} \nVdash K \lnot (p \wedge \diamond q)\). \(\square \)
but \({\textbf {i}} \nVdash K \lnot (p \wedge \diamond q)\). \(\square \)
5.2 Safety semantics
Inspired by Moss (2013, 2018), Beddor and Goldstein (2021) assure Ver by exploiting the traditional idea that knowledge is analyzed as a composite: on their view, knowledge is belief plus truth plus a condition that renders the belief ‘safe enough’ to yield knowledge. The safety requirement follows a tradition commenced by Sosa (1999) and Williamson (2000).
A safety model \(\mathcal {S}\) supplements an information model with functions \({\textbf {b}}\) and \(\mathfrak {i}\), each mapping a possible world to a non-empty intension: \({\textbf {b}}^w\) is the agent’s doxastic state at w (understood as a set of doxastic alternatives), while \(\mathfrak {i}(w)\) (we write \({\textbf {i}}^w\)) is the worldly information at w: a set of worlds that count intuitively as sufficiently ‘nearby’ w. We stipulate that \({\textbf {i}}^w\) is veridical at w, i.e., \(w \in {\textbf {i}}^w\).
How to think about ‘worldly information’? Beddor and Goldstein (2021) note various contenders (with respective complications) for cashing out this notion. Our formal preoccupations let us delay this critical issue for elsewhere. We assume that worldly information provides an inter-subjective limit on the veridical information that can be accrued by agents. Formally, we define: veridical \({\textbf {i}}\) is available at w when \({\textbf {i}}^w \subseteq {\textbf {i}}\).
We work temporarily with language  , replacing knowledge operator K with an objective possibility operator
, replacing knowledge operator K with an objective possibility operator  and belief operator B. Read
and belief operator B. Read  as ‘it is objectively possible that \(\varphi \)’ or, more colloquially, ‘it could easily have been that \(\varphi \)’. Read \(B\varphi \) as ‘Ann believes that \(\varphi \)’.
as ‘it is objectively possible that \(\varphi \)’ or, more colloquially, ‘it could easily have been that \(\varphi \)’. Read \(B\varphi \) as ‘Ann believes that \(\varphi \)’.
Definition 4
(Safety Semantics) Given safety model \(\mathcal {S}\), we extend domain semantics to  :
:

So  is true at \(\langle w,{\textbf {i}} \rangle \) when there is a world v compatible with the worldly information at w (intuitively, v is ‘nearby’ w) such that \(\varphi \) is true at \(\langle v,{\textbf {i}}^v \rangle \).
is true at \(\langle w,{\textbf {i}} \rangle \) when there is a world v compatible with the worldly information at w (intuitively, v is ‘nearby’ w) such that \(\varphi \) is true at \(\langle v,{\textbf {i}}^v \rangle \).
Then, \(K\varphi \) is defined as:

The intention is that  expresses that Ann’s belief that \(\varphi \) could not easily have been false. Define \(\blacksquare \varphi \) to mean
expresses that Ann’s belief that \(\varphi \) could not easily have been false. Define \(\blacksquare \varphi \) to mean  . Then the safety condition
. Then the safety condition  may be written as \(\blacksquare (B\varphi \supset \varphi )\).
may be written as \(\blacksquare (B\varphi \supset \varphi )\).
Fact 6
For safety semantics:
-
(1)
If \(\varphi \) is a boolean combination of atoms then: \(\llbracket \blacksquare (B \varphi \supset \varphi )\rrbracket ^{w,{\textbf {i}}} = 1\) iff, \(\forall v \in {\textbf {i}}^w\), if
 then v is a \(\varphi \)-world
then v is a \(\varphi \)-world -
(2)
\(\llbracket \blacksquare (B\diamond p\supset \diamond p)\rrbracket ^{w,{\textbf {i}}} = 1\) iff, \(\forall v \in {\textbf {i}}^w\), if a p-world is in \({\textbf {b}}^v\), a p-world is in \({\textbf {i}}^v\)
-
(3)
\(\llbracket \blacksquare (B\lnot \diamond p\supset \lnot \diamond p)\rrbracket ^{w,{\textbf {i}}} = 1\) iff, \(\forall v \in {\textbf {i}}^w\), if
 then
then 
Proof
A straightforward application of the relevant definitions. \(\square \)
It follows immediately from \(K\varphi \)’s definition that safety semantics yields Ver. Nevertheless, safety semantics fails to execute Strategy 1 of Sect. 3. (As proofs for safety semantics quickly become intricate, we now relegate them to “Appendix A.1”.)
Fact 7
According to safety semantics, NTrans fails: \(K\lnot p \nvDash K \lnot \diamond p\).
Safety semantics faces further fundamental difficulties in accounting for the logic of attitude ascriptions.
Fact 8
For any extension of domain semantics, \(p \wedge q \vDash p\) and \(\diamond (p \wedge q) \vDash \diamond p\).
Fact 9
According to safety semantics, \(K (p \wedge q) \nvDash K p \)
Fact 10
According to safety semantics, \(K\diamond (p \wedge q) \nvDash K\diamond p \)
One quickly confirms that safety semantics closes belief under logical consequence. So, it can hardly be replied that it is best conceived as modeling imperfect reasoners that may not execute every instance of conjunction elimination. Rather, safety semantics predicts, counter-intuitively, that ideal knowledge isn’t closed under logical consequence. Though the problem goes deeper: arguably, knowledge of a conjunction implies knowledge of its conjuncts even in the case of ordinary agents (it is odd to claim that ordinary Ed knows that it is stormy and windy but deny that he knows that it is stormy).
It is well known that austere implementations of the safety conception of knowledge issue problematic closure properties (Murphy, 2005; Alspector-Kelly, 2011). More sophisticated implementations mitigate this, though a completely satisfactory theory remains elusive (Williamson, 2009a, b; Goldstein and Hawthorne, 2024). Can a sophisticated variant of safety semantics avoid the problematic results detailed above? We leave investigation to proponents of the view.Footnote 15
6 Strategy 1 via stable acceptance semantics
We now present a novel information-sensitive semantic theory that does successfully execute Strategy 1 from Sect. 3. A leading idea behind this theory is that knowledge is stable under the refinement of one’s information: roughly, one knows \(\varphi \) only if one would still be positioned to know \(\varphi \) were one to possess the total available evidence. We start by drawing connections between influential examples in the literature on epistemic modals and knowledge ascriptions.
6.1 Objective constraints on (mighty) knowledge claims
Consider the well-known (alleged) insight that the truth/aptness of an epistemic possibility claim is sensitive to objective factors that go beyond the actual knowledge of the speaker or other relevant agents: in particular, it is sensitive to information/evidence that is not possessed but is in some sense available. Hacking (1967) provides two classic motivating examples.
Salvaging Operation. “Imagine a salvage crew searching for a ship that sank a long time ago. The mate of the salvage ship works from an old log, makes a mistake in his calculations, and concludes that the wreck may be in a certain bay. It is possible, he says, that the hulk is in these waters. No one knows anything to the contrary. But in fact, as it turns out later, it simply was not possible for the vessel to be in that bay; more careful examination of the log shows that the boat must have gone down at least thirty miles further south. The mate said something false when he said, “It is possible that we shall find the treasure here”, but the falsehood did not arise from what anyone actually knew at the time.” [Hacking 1967,pg. 148]
Lottery. “Consider a person who buys a lottery ticket. At the time he buys his ticket we shall say it is possible he will win, though probably he will not. As expected, he loses. But retrospectively it would be absurd to report that it only seemed possible that the man would win. It was perfectly possible that he would win.” [Hacking, 1967, pg. 148]
These suggest that whether an epistemic possibility claim is aptly assertible can depend on information that is available via “practicable investigation” (as Hacking puts it), or via “relevant way[s] by which members of the relevant community can come to know” (DeRose, 1991), or that the speaker or other relevant agents “easily might know” [Moore, 1962, pg. 402].
For our purposes, two observations suffice. First, one hesitates to say that the mate knew that we might find the treasure in the bay: as his claim could not be maintained were readily accessible and clearly relevant further evidence collected, it does not rise to knowledge. This by itself explains the temptation to judge it as (at least somewhat) inappropriate when the mate says ‘the treasure might be here’: one should, ideally, assert only what one knows. Second, it seems reasonable to say that we knew that the person with the fair lottery ticket might win, but probably would not. Our beliefs were sufficiently sensitive to the available information: given presumably intrinsic limits on predicting a lottery, no amount of available evidence could rule out his winning.
A theorist can incorporate these observations in two ways. First, one could incorporate objective factors as a constraint on apt epistemic possibility claims. As [MacFarlane, 2014, Sect.10.2.2] notes, this has the cost that it becomes hard to see how the casual ‘might’ claims we make in ordinary life are ever warranted. Alternatively, one could incorporate objective factors as a constraint on apt knowledge ascriptions (with an indirect effect upon epistemic possibility claims). As the conditions for asserting a knowledge claim are plausibly relatively demanding, the analogue of the previous objection has less force here. Our own theory exploits this second approach.
Precedent and independent motivation is provided by the tradition of defeasibility theories of knowledge (Lehrer & Paxson, 1969). The defeasibility approach we are chiefly interested says: knowledge is indefeasibly justified true belief, where indefeasible justification is justification that would not be defeated were the agent in possession of the total available evidence.Footnote 16 For our purposes, the core position boils down to this:
Indefeasibility. In any context c, a knows that \(\varphi \) in c only if \({\textbf {e}}^c\) supports \(\varphi \), where \({\textbf {e}}^c\) is a body of evidence called the total available evidence (in c).
Not only does Indefeasibility gel with our intuitive assessment of Salvaging Operation and Lottery, it neatly explains influential examples that don’t involve mighty knowledge (due to Lehrer and Paxson (1969); we quote Harman (1973)).
Book Thief. “While I am watching him, Tom takes a library book from the shelf and conceals it beneath his coat...I am sure that it was Tom, for I know him well. I saw Tom steal a book and that is the testimony that I give before the University Judicial Council...Later that day, Tom’s mother testifies that Tom has an identical twin, Buck. Tom, she says, was thousands of miles away at the time of the theft....It was Tom that took the book. His mother was lying when she said that he was thousands of miles away. I do not know that she was lying, of course, since I do not know anything about her, even that she exists. Nor does anyone at the hearing know that she is lying, although some suspect that she is. In these circumstances I do not know that Tom stole the book. My knowledge is undermined by evidence I do not possess.” [Harman,1973, pp.142-143]
Notorious Mother. “Suppose that Tom’s mother was known to the Judicial Council as a pathological liar. Everyone at the hearing realizes that Buck, Tom’s supposed twin, is a figment of her imagination....In such a case, my knowledge would not be undermined by her testimony; but if I were told only that she had just testified that Tom has a twin brother and was himself thousands of miles away from the scene of the crime at the time that book was stolen, I would no longer be justified in believing as I do now that Tom stole the book. Here I know even though there is evidence which, if I knew about it, would cause me not to be justified in believing my conclusion.” [Harman, 1973, pg.146]
Indefeasibility accounts for the contrast. In Book Thief, the library detective fails to know because the total available evidence does not indicate that Tom is the thief: coming to know this evidence would undermine the detective’s justified belief. But in Notorious Mother, the total available evidence does indicate that Tom is the thief: coming to know it (including that Tom’s mother is a pathological liar) would not undermine the detective’s justified belief that Tom stole the book.
How to characterize ‘availability’? We put aside this subtle and vexed issue.Footnote 17 We shall show that an Indefeasibility-respecting formal semantics delivers our target logical properties, whatever substantive account of availability is best.
A satisfactory account of ‘availability’ will be subtle. Consider:
Picnic. You and Ann are deciding whether to picnic in Monterey. She is risk-averse: she won’t drive out if she knows it might be raining there. As neither of you has checked the weather report, neither of you knows whether or not it might be raining in Monterey. So, Ann checks the report: it predicts that rain is 70% likely. Since Ann now knows that it might be raining in Monterey, she rightly states ‘It might be raining in Monterey’. She decides not to drive out.
‘Ann knows that it might be raining’ seems unobjectionably deployed in Picnic, despite there plausibly being further relevant evidence that Ann could feasibly collect (she could drive to Monterey; she could phone her friend Bob, who lives in Monterey). Suppose that this additional evidence would establish that it isn’t raining in Monterey. It doesn’t seem that Ann’s mighty knowledge is blocked by these particular possible defeaters. Why not? A satisfactory account of ‘availability’ will tell us, drawing a distinction between the (context-sensitive?) notion of ‘availability’ that informs knowledge ascription, and ‘availability’ in a looser sense: evidence that can in principle be collected.
6.2 Stable acceptance semantics
In contrast to domain semantics, we offer a bilateral acceptance semantics: instead of evaluating sentences at world-information pairs and deriving acceptance conditions, sentences are evaluated at just an information state. That is, acceptance (and rejection) conditions are directly provided.Footnote 18 (Sect. 6.4 will consider whether we would fare just as well by incorporating some of our key proposals into domain semantics, then generating acceptance conditions.) Relatedly, our account of logical consequence is based on acceptance preservation rather than truth preservation.
A bounded model \(\mathcal {M}\) supplements an information model with functions \({\textbf {k}}\) and \({\textbf {e}}\), each mapping a world to an information state (i.e., an intension), respectively denoted \({\textbf {k}}^w\) and \({\textbf {e}}^w\). We call \({\textbf {e}}^w\) the total available evidence at w, while \({\textbf {k}}^w\) is, again, Ann’s epistemic alternatives: the possible worlds compatible with what she knows. We stipulate that \({\textbf {k}}^w\) and \({\textbf {e}}^w\) are always veridical at w, i.e., \(w \in {\textbf {k}}^w\) and \(w \in {\textbf {e}}^w\) for all w. We say that intension \({\textbf {j}}\) refines intension \({\textbf {i}}\) when \({\textbf {j}} \subseteq {\textbf {i}}\). We say that \({\textbf {i}}\) is internally coherent when \({\textbf {e}}^w\) refines \({\textbf {i}}\) for every \(w \in {\textbf {i}}\). Intuitively, to be internally coherent is to be coherent in the following sense: if \({\textbf {i}}\) leaves it open that the total available evidence (i.e., the best available information) cannot rule out a certain possibility, then \({\textbf {i}}\) does not itself rule out that possibility.
Lemma 1
If \({\textbf {i}}\) is internally coherent then \({\textbf {i}} = \bigcup _{w \in {\textbf {i}}} {\textbf {e}}^w\).
Proof
As \({\textbf {e}}^w\) refines \({\textbf {i}}\) for all \(w \in {\textbf {i}}\), we have \(\bigcup _{w \in {\textbf {i}}} {\textbf {e}}^w \subseteq {\textbf {i}}\). Suppose that \(w \in {\textbf {i}}\). As \({\textbf {e}}^w\) is veridical at w, \(w \in {\textbf {e}}^w\). So, \({\textbf {i}} \subseteq \bigcup _{w \in {\textbf {i}}} {\textbf {e}}^w \). \(\square \)
We stipulate, for all \(w \in W\), that \({\textbf {k}}^w\) and \({\textbf {e}}^w\) are internally coherent. This yields a formal version of Indefeasibility: \({\textbf {e}}^w \subseteq {\textbf {k}}^w\) for all w, i.e., any proposition entailed by Ann’s total knowledge state is entailed by the total available evidence.
Definition 5
(Stable Acceptance Semantics) Given bounded \(\mathcal {M}\), intension \({\textbf {i}}\):

Read  as ‘\({\textbf {i}}\) accepts \(\varphi \)’ or ‘\({\textbf {i}}\) supports \(\varphi \)’, and
as ‘\({\textbf {i}}\) accepts \(\varphi \)’ or ‘\({\textbf {i}}\) supports \(\varphi \)’, and  as ‘\({\textbf {i}}\) rejects \(\varphi \)’ or ‘\({\textbf {i}}\) refutes \(\varphi \)’. Intuitively, a speaker is positioned (pragmatic considerations aside) to assert \(\varphi \) when the information that she robustly possesses (presumably corresponding to what she knows, or at least believes) accepts \(\varphi \); she is positioned to deny \(\varphi \) when the information in her possession rejects \(\varphi \).
as ‘\({\textbf {i}}\) rejects \(\varphi \)’ or ‘\({\textbf {i}}\) refutes \(\varphi \)’. Intuitively, a speaker is positioned (pragmatic considerations aside) to assert \(\varphi \) when the information that she robustly possesses (presumably corresponding to what she knows, or at least believes) accepts \(\varphi \); she is positioned to deny \(\varphi \) when the information in her possession rejects \(\varphi \).
The most unusual entry is that for \(K\varphi \): ‘Ann knows that \(\varphi \)’ is accepted by \({\textbf {i}}\) exactly when \({\textbf {i}}\) guarantees that Ann’s knowledge guarantees that the total available evidence supports \(\varphi \); ‘Ann knows that \(\varphi \)’ is rejected by \({\textbf {i}}\) exactly when \({\textbf {i}}\) establishes that Ann’s knowledge is consistent with the total available evidence not supporting \(\varphi \). An ‘assertoric’ version of Indefeasibility follows: if a speaker can assert that the total available evidence doesn’t support \(\varphi \), they should deny that Ann knows that \(\varphi \).
The following gives a natural account of logical consequence for stable acceptance semantics:
Definition 6
(Coherent Consequence)  iff, for every bounded model \(\mathcal {M}\), if \({\textbf {i}}\) is internally coherent and
iff, for every bounded model \(\mathcal {M}\), if \({\textbf {i}}\) is internally coherent and  , then
, then  .
.
6.3 Key results
We now show that stable acceptance semantics, equipped with coherent consequence, successfully executes Strategy 1. We start with preliminary results that render our main proofs direct enough to be philosophically instructive.
Definition 7
A sentence \(\varphi \) is \(\diamond \)-restricted if the only occurrences of \(\diamond \) are in the scope of a K operator.
For example, \(\lnot (p \wedge q)\) and \(K\diamond p\) are \(\diamond \)-restricted; \(\diamond p\) and \(\lnot \diamond (p \vee q)\) aren’t.
Lemma 2
If \(\varphi \) is \(\diamond \)-restricted then:
-
(1)
 iff \(\forall w \in {\textbf {i}}\):
iff \(\forall w \in {\textbf {i}}\): 
-
(2)
 iff \(\forall w \in {\textbf {i}}\):
iff \(\forall w \in {\textbf {i}}\): 
Proof
A routine induction. \(\square \)
Lemma 3
If \(\varphi \) is \(\diamond \)-restricted then: 
Proof
Suppose that  . Thus, \(\forall w \in {\textbf {i}}\):
. Thus, \(\forall w \in {\textbf {i}}\):  . Thus, by Lemma 2,
. Thus, by Lemma 2,  . The reasoning can be reversed. \(\square \)
. The reasoning can be reversed. \(\square \)
Theorem 1
(Normal Form) For every sentence \(\varphi \), there exists \(n \ge 0\) and \(\diamond \)-restricted sentences \(\alpha _0, \alpha _1, \ldots , \alpha _n\) such that for any \({\textbf {i}}\):

Proof
See the “Appendix”. \(\square \)
Fact 11
Generalized Negative Transparency holds:  .
.
Proof
Suppose that  . So, \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\): there exists \({\textbf {1}}^u\) and \({\textbf {2}}^u\) such that \({\textbf {1}}^u \cup {\textbf {2}}^u = {\textbf {e}}^u\), and
. So, \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\): there exists \({\textbf {1}}^u\) and \({\textbf {2}}^u\) such that \({\textbf {1}}^u \cup {\textbf {2}}^u = {\textbf {e}}^u\), and  and
and  . By Lemma 3: \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\):
. By Lemma 3: \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\):  . So,
. So,  . The reasoning can be reversed. \(\square \)
. The reasoning can be reversed. \(\square \)
Fact 12
K-Veridicality holds:  .
.
Proof
Assume that \({\textbf {i}}\) is internally coherent and  . So, \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\):
. So, \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\):  . By Theorem 1, there exists \(n \ge 0\) and \(\diamond \)-restricted sentences \(\alpha _0, \alpha _1, \ldots , \alpha _n\) such that, \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\):
. By Theorem 1, there exists \(n \ge 0\) and \(\diamond \)-restricted sentences \(\alpha _0, \alpha _1, \ldots , \alpha _n\) such that, \(\forall w \in {\textbf {i}}\), \(\forall u \in {\textbf {k}}^w\):  .
.
We show that  . Let \(w \in {\textbf {i}}\). Now, as \(w \in {\textbf {k}}^w\) and
. Let \(w \in {\textbf {i}}\). Now, as \(w \in {\textbf {k}}^w\) and  for any \(u \in {\textbf {k}}^w\), we have
for any \(u \in {\textbf {k}}^w\), we have  . So, by Lemma 2, we have \(\forall u \in {\textbf {e}}^w\):
. So, by Lemma 2, we have \(\forall u \in {\textbf {e}}^w\):  . Thus, as \(w \in {\textbf {e}}^w\), we have
. Thus, as \(w \in {\textbf {e}}^w\), we have  . Generalizing: \(\forall w \in {\textbf {i}}\):
. Generalizing: \(\forall w \in {\textbf {i}}\):  . So, by Lemma 2,
. So, by Lemma 2,  .
.
We show that  for \(1 \le k \le n\). Let \(w \in {\textbf {i}}\). Now, for any \(u \in {\textbf {k}}^w\), there exists \(v \in {\textbf {e}}^u\) such that
for \(1 \le k \le n\). Let \(w \in {\textbf {i}}\). Now, for any \(u \in {\textbf {k}}^w\), there exists \(v \in {\textbf {e}}^u\) such that  , as
, as  . As \(w \in {\textbf {k}}^w\), it follows that there exists \(v \in {\textbf {e}}^w\) such that
. As \(w \in {\textbf {k}}^w\), it follows that there exists \(v \in {\textbf {e}}^w\) such that  . Thus, as \({\textbf {i}}\) is internally coherent, \(\exists v \in {\textbf {i}}\) such that
. Thus, as \({\textbf {i}}\) is internally coherent, \(\exists v \in {\textbf {i}}\) such that  . So,
. So,  .
.
Altogether:  . So, by Theorem 1,
. So, by Theorem 1,  . \(\square \)
. \(\square \)
Less formally, suppose that \({\textbf {i}}\) is internally coherent and supports \(K \diamond p\). Thus, \({\textbf {i}}\) guarantees that Ann’s knowledge state guarantees that the total available evidence establishes \(\diamond p\). Thus, the candidates for the total available evidence—those \({\textbf {i}}\) cannot rule out—all contain a p-world. As \({\textbf {i}}\) is internally coherent, \({\textbf {i}}\) cannot itself rule out these worlds. So, \({\textbf {i}}\) accepts \(\diamond p\).
Fact 13
Uniformity fails: \(\diamond p \nVDash \lnot K \lnot p\).
Proof
Consider any bounded model \(\mathcal {M}\) where: (i) \(w_1 \in \texttt{I}(p)\) and \(w_2 \notin \texttt{I}(p)\); (ii) \({\textbf {e}}^{w_1} = {\textbf {k}}^{w_1} = \{w_1\}\) and \({\textbf {e}}^{w_2} = {\textbf {k}}^{w_2} = \{w_2\}\). Set \({\textbf {i}} = \{w_1, w_2\}\). Note that \({\textbf {i}}\) is internally coherent.
By (i),  . So, \(\exists w \in {\textbf {i}}\):
. So, \(\exists w \in {\textbf {i}}\):  . So,
. So,  .
.
By (i),  . Thus, by Lemma 2 and (ii),
. Thus, by Lemma 2 and (ii),  . Thus, by (ii), \(\forall u \in {\textbf {k}}^{w_2}\):
. Thus, by (ii), \(\forall u \in {\textbf {k}}^{w_2}\):  . Thus, \(\exists w \in {\textbf {i}}\) such that \(\forall u \in {\textbf {k}}^w\):
. Thus, \(\exists w \in {\textbf {i}}\) such that \(\forall u \in {\textbf {k}}^w\):  . Thus,
. Thus,  . Thus, \({\textbf {i}} \nVdash \lnot K \lnot p\). \(\square \)
. Thus, \({\textbf {i}} \nVdash \lnot K \lnot p\). \(\square \)
Less formally, Uniformity fails because it is possible for information \({\textbf {i}}\) to have the following properties simultaneously: (i) it is consistent with \({\textbf {i}}\) that p holds; (ii) it is consistent with \({\textbf {i}}\) that Ann’s knowledge rules out that the total available evidence is compatible with p.
6.4 Domain semantics with stable knowledge
We have been working directly with acceptance and rejection conditions. Would we fare just as well if we enhanced domain semantics with our ‘stability’ account of knowledge ascription, and generate acceptance conditions therefrom? The answer is ‘no’. Consider:
Definition 8
(Domain Semantics + Stable Knowledge) Given bounded \(\mathcal {M}\):

We can then define a version of coherent consequence:  means that if \({\textbf {i}}\) is internally coherent and
means that if \({\textbf {i}}\) is internally coherent and  then
then  , for every \({\textbf {i}}\) in every bounded \(\mathcal {M}\).
, for every \({\textbf {i}}\) in every bounded \(\mathcal {M}\).
Fact 14
According to domain semantics with stable knowledge:
-
a.
Ver fails: in particular, \(K \lnot (\diamond p \wedge \diamond q) \nVDash \lnot (\diamond p \wedge \diamond q)\)
-
b.
GeNT fails.
Proof
See “Appendix A.3”. \(\square \)
7 Outstanding issues
Our stable acceptance semantics is somewhat preliminary. I conclude by noting two outstanding issues that, I believe, motivate refinements. However, the exact choice of refinement is an important decision point, best left to future work.
7.1 First issue
How best to extend stable acceptance semantics to the multi-agent setting? Consider another mundane scenario:
Cards. For a card game, three cards (Ace of Spades, Ace of Diamonds, Ace of Hearts) are to be distributed (face down). The Ace of Spades is given to Ann, the Ace of Diamonds is given to Bob, and the Ace of Hearts is placed face down on the table. Ann and Bob know the set-up, except for the exact card distribution. After examining their cards, Ann knows the card on the table might be the Ace of Diamonds and might be the Ace of Hearts (as she is holding the Ace of Spades). Meanwhile, Bob knows the card on the table cannot be the Ace of Diamonds (as this, he observes, is the card he is holding).
At first glance, there is something puzzling here: given Ver, ‘Ann knows the card on the table might be the Ace of Diamonds’ entails ‘the card on the table might be the Ace of Diamonds’, and ‘Bob knows the card on the table cannot be the Ace of Diamonds’ entails ‘the card on the table cannot be the Ace of Diamonds’. Together, this seems a contradiction.
The flexible contextualist has a ready reply: the appearance of contradiction is an illusion generated by a shift in the knowledge that the modals are indexed to (the ‘might’ is indexed to Ann’s knowledge; the ‘cannot’ to Bob’s knowledge).
What should a proponent of stable acceptance semantics say? Given Indefeasibility, a promising thought is that there is plausibly a shift in what counts as the total available evidence when ascribing knowledge to Ann as opposed to Bob. The truth of ‘Ann knows the card on the table might be the Ace of Diamonds’ depends on the evidence available to Ann not including the (defeating) fact that Bob holds the Ace of Diamonds; the truth of ‘Bob knows the card on the table cannot be the Ace of Diamonds’ depends on the evidence available to Bob including the fact that Bob holds the Ace of Diamonds. This explains why ‘the card on the table might be the Ace of Diamonds’ and ‘the card on the table cannot be the Ace of Diamonds’ aren’t simultaneously assertable relative to a fixed body of available evidence.
But does this rough assessment withstand scrutiny? How best to incorporate it into stable acceptance semantics? Should the shiftiness of ‘availability’ be given a contextualist treatment or an invariantist but subject-sensitive treatment? This is for future work.
7.2 Second issue
According to our stable acceptance semantics, sentences with the appearance of a contradiction are satisfiable. It is readily checked that bounded models exist that satisfy \(\diamond p \wedge \diamond \lnot p \wedge \lnot (\diamond p \wedge \diamond \lnot p)\). Take any information state \({\textbf {i}}\) that includes both a p-world and a \(\lnot p\)-world. Note that Lemma 3, together with De Morgan’s Laws, implies that \(\lnot (\diamond p \wedge \diamond \lnot p)\) is accepted by \({\textbf {i}}\) exactly when \(\lnot p \vee p\) is accepted, rendering it a logical truth.
It follows quickly that our stable acceptance semantics does not respect the principle of explosion (nor reductio ad absurdum) in full generality. This prevents the collapse of its logic into triviality. Still, it is odd to predict that sentences with the form of a contradiction are satisfiable: it hardly sounds kosher to first assert that it might be raining and it might not be raining, and then assert that it isn’t the case that it might be raining and might not be raining.
However, all this points to a deeper (and independently interesting) problem: any theory that conservatively executes Strategy 1 of Sect. 3 must yield such ‘contradictions’. Consider this chain of reasoning:
-
\(\diamond p \wedge \diamond \lnot p \wedge (K\lnot p \vee K p)\)
-
\(\therefore \) \(\diamond p \wedge \diamond \lnot p \wedge (K\lnot \diamond p \vee K\lnot \diamond \lnot p)\)
-
\(\therefore \) \(\diamond p \wedge \diamond \lnot p \wedge (\lnot \diamond p \vee \lnot \diamond \lnot p)\)
-
\(\therefore \) \(\diamond p \wedge \diamond \lnot p \wedge \lnot (\diamond p \wedge \diamond \lnot p)\)
The first line is consistent, presumably, on any sensible theory that rejects Uniformity. The second line follows by NTrans, double negation equivalence, and constructive dilemma. The third follows by Ver and constructive dilemma. The fourth deploys De Morgan. We have a worry here for Strategy 1, but not one with an easy moral: anyone (proponent of Strategy 1 or not) that wishes to extricate themselves from the above reasoning must abandon at least one intuitively attractive logical principle.
One style of response continues the theme of rejecting classical logic when epistemic modals are in play. Theorists have motivated and explored the option of abandoning constructive dilemma in full generality: see [Bledin, 2014, Sect.7], [Aloni et al. 2022, Sect.3]. Theorists have motivated and explored the option of abandoning De Morgan’s laws in full generality: see [Hawke and Steinert-Threlkeld, 2021, Sect.7.3]. I am inclined to think the latter is the better option for explaining away the above paradox and, anyway, is more easily incorporated into a refined stable acceptance semantics. This is for future work: it points to a subtle treatment of \(\wedge \) and \(\vee \) that distracts from the present paper’s main concerns.
Notes
See the papers in Egan and Weatherson (2011) for a sense of the debate. See Bledin (2014), Stojnić (2017), Moss (2018), Bledin and Lando (2018), Incurvati and Schlöder (2019), Hawke and Steinert-Threlkeld (2021), Beddor and Goldstein (2021), Aloni (2022), and Aloni et al. (2022) for some recent developments.
The present paper fleshes out a preliminary version of our theory defended in Hawke (2023).
See Smets et al. (2022) for another formal theory of knowledge ascription inspired by the defeasibility tradition. This theory has little in common with our own proposal: for example, it does not incorporate epistemic modals and is not state-based.
See Bledin (2014) for a comparison of some relevant accounts of logical consequence.
Orthodoxy has been challenged: see Hazlett (2012) for a summary. The debate centers on whether \(\varphi \) is a genuine entailment of ‘Ann knows that \(\varphi \)’, or simply a pragmatic presupposition. A key issue is the status of ordinary claims like ‘everything that the Ancients knew about cosmology turned out to be wrong’. Is this a literal or non-literal (e.g., sarcastic, or projective) use of ‘knows’? As we embrace orthodoxy in this paper, we assume the latter without argument.
A skeptic about Łukasiewicz’ principle can use NTrans to explain why the former seems valid in conversation. Suppose that Ann rightly asserts \(\lnot p\). Thus, given a knowledge norm of assertion, Ann represents herself as knowing \(\lnot p\), i.e., she pragmatically communicates that \(K \lnot p\) is true. Using NTrans, a listener rightly concludes that Ann knows that it can’t be that p, i.e., \(K \lnot \diamond p\). Thus, Ann has also represented herself as committed to \(\lnot \diamond p\). Hence, ‘it can’t be that p’ must be assertible for her.
It is commonly agreed that a bare \(\diamond p\) has a solipsistic reading as a default, or something close (e.g., expression of the information state of a select group of agents that includes the speaker). For discussion, see MacFarlane (2011), especially Sect.1, and von Fintel and Gillies (2011), especially Sect. 2.
See Hazlett (2012) for an overview.
See (Stojnić 2017) for a detailed attempt to use discourse prominence to explain away the threat posed to non-classical logic by examples like Marbles.
As a reviewer points out, our observations likely transfer to other broadly descriptivist theories that are suitably ‘flexible’ in the interpretation of epistemic modals. For example, consider the flexible relativism of Beddor and Egan (2018). Details/nuances aside, this view agrees with flexible contextualism that \(\diamond p\) canonically expresses that p is compatible with agent x’s knowledge; unlike flexible contextualism, it posits that x is fixed by the intentions/context of a relevant assessor of an utterance of \(\diamond p\), who may well differ from the speaker. This again allows sensible interpretations of (39) and (40); so again pragmatics must be deployed to explain their infelicity. But if principles of order-sensitive discourse prominence are posited (as might again seem natural), the flexible relativist presumably confronts analogous recalcitrant data.
I am skeptical that safety theorists can avoid Fact 9 without resorting to an overly baroque theory. To illustrate, consider the popular strategy of incorporating methods of belief into one’s safety conception of knowledge: S knows p if and only if S could not easily have falsely believed p using their actual method of belief formation. Now suppose we supplement this with a thesis we call Extended Methods (framed by Goldstein and Hawthorne (2024), drawing on Williamson (2009b), p.326 and Williamson (2009a)): if S competently deduces a conclusion from some premises, then S’s method for believing the conclusion includes as an essential part S’s method for believing each premise. This view closes knowledge under competent deduction: competent conclusions drawn from safe premises will themselves be safe. But it does not assure that knowing a conjunction implies knowing the conjuncts. Suppose S believes p via an act of perception \(M_1\) and believes q via a separate act of perception \(M_2\), and goes on to believe \(p \wedge q\) via complex method \(M_3\) that essentially includes \(M_1\), \(M_2\), and a competent act of deduction. We stipulate that there are no nearby worlds where S deploys \(M_3\) yet \(p \wedge q\) is false. Thus, on our current safety account, S knows \(p \wedge q\). However, we add that there is a nearby world \(w_1\) where S believes p via \(M_1\), yet p is false: we need simply stipulate that S does not use method \(M_2\) to come to believe q at \(w_1\) (indeed, q is false at \(w_1\), so cannot be perceived at \(w_1\)). On our current safety account, S therefore fails to know p.
See Swain (1998) for an overview of the debate.
For independent advantages of working with an acceptance semantics, see Veltman (1985), Schroeder (2008), Hawke and Steinert-Threlkeld (2018), Hawke and Steinert-Threlkeld (2021), Ciardelli (2021) and Aloni (2022); for independent drawbacks to domain semantics, see Hawke and Steinert-Threlkeld (2021).
References
Aloni, M. (2022). Logic and conversation: The case of free choice. Semantics and Pragmatics, 15(5), 565–589.
Aloni, M., Incurvati, L., & Schlöder, J. (2022). Epistemic modals in hypothetical reasoning. Erkenntnis, 88(8), 3551–3581. https://doi.org/10.1007/s10670-022-00517-x
Alspector-Kelly, M. (2011). Why safety doesn’t save closure. Synthese, 183(2), 127–142. https://doi.org/10.1007/s11229-010-9755-x
Barker, J. (1976). What you don’t know won’t hurt you. American Philosophical Quarterly, 13, 303–308.
Beddor, B., & Egan, A. (2018). Might do better: Flexible relativism and the QUD. Semantics and Pragmatics, 11
Beddor, B., & Goldstein, S. (2021). Mighty knowledge. The Journal of Philosophy, 118(5), 229–269.
Bledin, J. (2014). Logic informed. Mind, 123(490), 277–316. https://doi.org/10.1093/mind/fzu073
Bledin, J., & Lando, T. (2018). Closure and epistemic modals. Philosophy and Phenomenological Research, 97(1), 3–22.
Ciardelli, I. (2021). Restriction without quantification: Embedding and probability for indicative conditionals. Ergo, 8
Dabrowski, A., Moss, L. S., & Parikh, R. (1996). Topological reasoning and the logic of knowledge. Annals of Pure and Applied Logic, 78, 73–110. https://doi.org/10.1016/0168-0072(95)00016-X
DeRose, K. (1991). Epistemic possibilities. Philosophical Review, 100(4), 581–605. https://doi.org/10.2307/2185175
Dowell, J. L. (2011). A flexible contextualist account of epistemic modals. Philosophers, 11(14), 1–25.
Egan, A., & Weatherson, B. (eds.) (2011). Epistemic modality. Oxford University Press.
Goldstein, S., & Hawthorne, J. (2024). Safety, closure, and extended methods. Journal of Philosophy, 121(1), 26–54.
Hacking, I. (1967). Possibility. Philosophical Review, 76, 143–168.
Harman, G. (1973). Thought. Princeton University Press.
Hawke, P. (2023). An acceptance semantics for stable modal knowledge. Electronic Proceedings in Theoretical Computer Science, 379, 331–343. https://doi.org/10.4204/eptcs.379.27
Hawke, P., & Steinert-Threlkeld, S. (2018). Informational dynamics of epistemic possibility modals. Synthese, 195(10), 4309–4302. https://doi.org/10.1007/s11229-016-1216-8
Hawke, P., & Steinert-Threlkeld, S. (2021). Semantic expressivism for epistemic modals. Linguistics and Philosophy, 44(2), 475–511.
Hazlett, A. (2012). Factive presupposition and the truth condition on knowledge. Acta Analytica, 27, 461–478.
Incurvati, L., & Schlöder, J. (2019). Weak assertion. The Philosophical Quarterly, 69(277), 741–770.
Klinedinst, N., & Rothschild, D. (2012). Connectives without truth tables. Natural Language Semantics, 20(2), 137–175. https://doi.org/10.1007/s11050-011-9079-5
Kratzer, A. (1981). The notional category of modality. In H.-J. Eikmeyer & H. Rieser (Eds.), Words, worlds, and context (pp. 38–74). Walter de Gruyter.
Lehrer, K., & Paxson, T. (1969). Knowledge: Undefeated justified true belief. Journal of Philosophy, 66, 225–37.
MacFarlane, J. (2011). Epistemic modals are assessment-sensitive. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 144–179). Oxford University Press.
MacFarlane, J. (2014). Assessment sensitivity. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199682751.001.0001
Moore, G. E. (1962). Commonplace Book, 1919-53. Allen and Unwin.
Moss, S. (2013). Epistemology formalized. The Philosophical Review, 122(1), 1–43.
Moss, S. (2018). Probabilistic knowledge. Oxford University Press.
Murphy, P. (2005). Closure failures for safety. Philosophia, 33(1–4), 331–334. https://doi.org/10.1007/bf02652659
Pollock, J. (1986). Contemporary theories of knowledge. Rowman and Littlefield.
Punčochář, V. (2015). Weak negation in inquisitive semantics. Journal of Logic, Language and Information, 24(3), 323–355. https://doi.org/10.1007/s10849-015-9219-2
Schroeder, M. (2008). Expression for expressivists. Philosophy and Phenomenological Research, 76(1), 86–116.
Smets, S., Özgün, A., Bezhanishvili, N., & Baltag, A. (2022). Justified belief, knowledge, and the topology of evidence. Synthese, 200(6), 1–51. https://doi.org/10.1007/s11229-022-03967-6
Sosa, E. (1999). How to defeat opposition to moore. Philosophical Perspectives, 13, 141–154.
Stalnaker, R. (1974). Pragmatic presuppositions. In M. Munitz & P. Unger (Eds.), Semantics and philosophy (pp. 197–214). New York University Press.
Stojnić, U. (2017). One’s modus ponens: Modality, coherence, and logic. Philosophy and Phenomenological Research, 95, 167–214.
Swain, M. (1974). Epistemic defeasibility. The. American Philosophical Quarterly, 11, 15–25.
Swain, M. (1998). Knowledge, defeasibility theory of. https://doi.org/10.4324/9780415249126-P012-1. https://www.rep.routledge.com/articles/thematic/knowledge-defeasibility-theory-of/v-1.
Veltman, F. (1985). Logics for conditionals. PhD thesis, Universiteit van Amsterdam.
Veltman, F. (1996). Defaults in update semantics. Journal of Philosophical Logic, 25(3), 221–261. https://doi.org/10.1007/BF00248150
von Fintel, K., & Gillies, A. S. (2011). ‘Might’ made right. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 108–130). Oxford: Oxford University Press.
Williamson, T. (2000). Knowledge and its limits. Oxford: Oxford University Press.
Williamson, T. (2009). Replies to critics. In D. Pritchard & P. Greenough (Eds.), Williamson on knowledge (pp. 279–384). Oxford: Oxford University Press.
Williamson, T. (2009b). Probability and danger. In Amherst lecture in philosophy, pp. 1–35.
Yalcin, S. (2007). Epistemic modals. Mind, 116(464), 983–1026.
Yalcin, S. (2011). Nonfactualism about epistemic modality. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 295–332). Oxford: Oxford University Press.
Yalcin, S. (2012). A counterexample to modus tollens. Journal of Philosophical Logic, 6(41), 1001–1024.
Yang, F., & Väänänen, J. (2017). Propositional team logics. Annals of Pure and Applied Logic, 168(7), 1406–1441. https://doi.org/10.1016/j.apal.2017.01.007
Acknowledgements
Thanks to my reviewers for suggestions that improved the paper. Variants of (parts of) this paper were presented at the 2023 Pacific Division APA Meeting at the Westin St. Francis in San Francisco, CA (April 5–8, 2023) and at the 19th conference on Theoretical Aspects of Rationality & Knowledge conference (TARK XIX) at Worcester College, University of Oxford, UK (June 28–30, 2023). Thanks to members of these audiences for helpful comments, especially David Boylan, Simon Goldstein, Jeremy Goodman, Harvey Lederman, Bernhard Salow, Lesley Walker, and Francesca Zaffora Blando. This publication is part of the project ‘The Semantics of Knowledge and Ignorance’ (ECS Project Number 23603221), funded by the Early Career Scheme of the University Grants Committee (UGC) of Hong Kong.
Funding
Open Access Publishing Support Fund provided by Lingnan University. This work was supported by the University Grants Committee of Hong Kong via Early Career Scheme (ECS) Grant No. 23603221.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author certifies that they have no affiliation with or involvement in any organization or entity with any financial interest or non-financial interest inthe subject matter or materials discussed in this manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Proofs
Appendix A: Proofs
1.1 Safety theory
Fact 7. \(K\lnot p \nvDash K \lnot \diamond p\)
Proof
For a counter-model, take any \(\mathcal {S}\) where (i) \(\texttt{I}(p) = \{w_2\}\) and (ii) \({\textbf {b}}^{w_1} ={\textbf {i}}^{w_1}=\{w_1\}\). Set \({\textbf {i}}=\{w_1, w_2\}\). By (i), \(\llbracket \lnot p \rrbracket ^{w_1, {\textbf {i}}} = 1 \). As \({\textbf {b}}^{w_1}\) contains only \(\lnot p\)-worlds, we have \(\llbracket B\lnot p \rrbracket ^{w_1, {\textbf {i}}} = 1 \). Thus, for all \(v \in {\textbf {i}}^{w_1}\), if \(\llbracket B\lnot p \rrbracket ^{v, {\textbf {i}}} = 1 \) then \(\llbracket \lnot p \rrbracket ^{v, {\textbf {i}}} = 1 \). By Fact 6 part (1), \(\llbracket \blacksquare ( B\lnot p \supset \lnot p) \rrbracket ^{w_1, {\textbf {i}}} = 1 \). However, \(\llbracket \lnot \diamond p \rrbracket ^{w_1, {\textbf {i}}} = 0 \), as \(w_2 \in {\textbf {i}}\) and \(\llbracket \lnot p \rrbracket ^{w_2, {\textbf {i}}} = 0 \). So, \(\llbracket K \lnot p \rrbracket ^{w_1, {\textbf {i}}} = 1 \) but \(\llbracket K \lnot \diamond p \rrbracket ^{w_1, {\textbf {i}}} = 0 \). \(\square \)
Fact 9. \(K (p \wedge q) \nvDash K p \)
Proof
Let \(\mathcal {S}\) be a model where (i) \(W = \{w_1, w_2, w_3\}\), (ii) \(\texttt{I}(p)=\{w_1, w_3\}\), (iii) \(\texttt{I}(q)= \{w_1, w_2\}\), (iv) \({\textbf {b}}^{w_1}= \{ w_1\}\), (v) \({\textbf {b}}^{w_2}= {\textbf {b}}^{w_3}= \{ w_3\}\), (vi) \({\textbf {i}}^{w_1} = \{w_1, w_2\}\), and (vii) \({\textbf {i}}^{w_2} = \{w_2\}\). Let \({\textbf {i}} = \{ w_1, w_2\}\).
By (ii) and (iii), \(w_1\) is a \(p\wedge q\)-world; \(w_2\) is a \(\lnot p\wedge q\)-world; \(w_3\) is a \(p\wedge \lnot q\)-world.
So, \(\llbracket p \wedge q \rrbracket ^{w_1, {\textbf {i}}} = 1\). Further, by (iv),  . So, \(\llbracket B(p \wedge q) \rrbracket ^{w_1, {\textbf {i}}} = 1\). Further, by (vi), \(\forall v \in {\textbf {i}}^{w_1}\): if
. So, \(\llbracket B(p \wedge q) \rrbracket ^{w_1, {\textbf {i}}} = 1\). Further, by (vi), \(\forall v \in {\textbf {i}}^{w_1}\): if  then v is a \(p\wedge q\)-world. So, \(\llbracket \blacksquare (B(p \wedge q) \supset (p \wedge q))\rrbracket ^{w_1, {\textbf {i}}} = 1\). Altogether: \(\llbracket K(p \wedge q) \rrbracket ^{w_1, {\textbf {i}}} = 1\).
then v is a \(p\wedge q\)-world. So, \(\llbracket \blacksquare (B(p \wedge q) \supset (p \wedge q))\rrbracket ^{w_1, {\textbf {i}}} = 1\). Altogether: \(\llbracket K(p \wedge q) \rrbracket ^{w_1, {\textbf {i}}} = 1\).
However, by (v),  . So, \(\exists w \in {\textbf {i}}^{w_1}\):
. So, \(\exists w \in {\textbf {i}}^{w_1}\):  but w is \(\lnot p\)-world. So, \(\llbracket \blacksquare (Bp \supset p) \rrbracket ^{w_1, {\textbf {i}}} = 0\). So, \(\llbracket Kp \rrbracket ^{w_1, {\textbf {i}}} = 0 \).\(\square \)
but w is \(\lnot p\)-world. So, \(\llbracket \blacksquare (Bp \supset p) \rrbracket ^{w_1, {\textbf {i}}} = 0\). So, \(\llbracket Kp \rrbracket ^{w_1, {\textbf {i}}} = 0 \).\(\square \)
Fact 10. \(K\diamond (p \wedge q) \nvDash K\diamond p \)
Proof
The model \(\mathcal {S}\) in the previous proof works as a counter-example here too. There is a \(p \wedge q\)-world in \({\textbf {i}}\) (so, \(\llbracket \diamond (p \wedge q) \rrbracket ^{w_1, {\textbf {i}}}=1\)) and in \({\textbf {b}}^{w_1}\) (so, \(\llbracket B\diamond (p \wedge q) \rrbracket ^{w_1, {\textbf {i}}}=1\)). Further, \(\forall w \in {\textbf {i}}^{w_1}\): if there is a \(p\wedge q\)-world in \({\textbf {b}}^w\) then there’s one in \({\textbf {i}}^w\) (so, \(\llbracket \blacksquare (B\diamond (p \wedge q) \supset \diamond (p \wedge q))\rrbracket ^{w_1, {\textbf {i}}}=1\)). Thus, \(\llbracket K\diamond (p \wedge q) \rrbracket ^{w_1, {\textbf {i}}}=1\). However, by (v) and (vii), there is a p-world in \({\textbf {b}}^{w_2}\) but not in \({\textbf {i}}^{w_2}\). So, \(\exists w \in {\textbf {i}}^{w_1}\): there’s a p-world in \({\textbf {b}}^w\) but not in \({\textbf {i}}^w\). So, \(\llbracket \blacksquare (B\diamond p \supset \diamond p)\rrbracket ^{w_1, {\textbf {i}}}=0\). So, \(\llbracket K\diamond p \rrbracket ^{w_1, {\textbf {i}}}=0\). \(\square \)
1.2 Normal Form for Stable Acceptance Semantics
Theorem 1. For every sentence \(\varphi \), there exists \(n \ge 0\) and \(\diamond \)-restricted sentences \(\alpha _0, \alpha _1, \ldots , \alpha _n\) such that for any \({\textbf {i}}\):

Proof
We proceed by induction on sentence structure, with respect to the following stronger property: there exists \(m, n \ge 0\) and \(\diamond \)-restricted sentences \(\alpha _0, \alpha _1, \ldots , \alpha _m\) and \(\beta _0, \beta _1, \ldots , \beta _n\) such that, for any \({\textbf {i}}\):
-
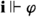 iff
iff 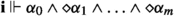
-
 iff
iff 
The case for atom p is trivial, as this sentence is itself \(\diamond \)-restricted: set \(m=n=0\), \(\alpha _0 = p\) and \(\beta _0 = \lnot p\).
The case for knowledge ascription \(K\varphi \) is trivial, as this sentence is itself \(\diamond \)-restricted: set \(m=n=0\), \(\alpha _0 = K\varphi \) and \(\beta _0 = \lnot K \varphi \).
For the induction hypothesis IH, assume, for arbitrary \(\varphi \) and \(\psi \), that there exists \(m, n, x, y \ge 0\) and \(\diamond \)-restricted sentences
such that, for any \({\textbf {i}}\):
-
 iff
iff 
-
 iff
iff 
-
 iff
iff 
-
 iff
iff 
Using the IH, we can prove the following.






\(\square \)
1.3 Domain Semantics with Stable Knowledge
Fact 14. According to domain semantics with stable knowledge:
-
a.
Ver fails.
-
b.
GeNT fails.
Proof
-
a.
Counter-model: \(W = \{w_1, w_2\}\); \(\texttt{I}(p)=\{w_1\}\) and \(\texttt{I}(q)=\{w_2\}\); \({\textbf {k}}^{w_1}={\textbf {k}}^{w_2} = W\); \({\textbf {e}}^{w_1}=\{w_1\}\) and \({\textbf {e}}^{w_2}=\{w_2\}\). Let \({\textbf {i}} = W = \{w_1, w_2\}\). One readily confirms: \(\llbracket \lnot (\diamond p \wedge \diamond q) \rrbracket ^{w_1, {\textbf {e}}^{w_1}} = 1\) and \(\llbracket \lnot (\diamond p \wedge \diamond q) \rrbracket ^{w_2, {\textbf {e}}^{w_2}} = 1\). Thus,
 and
and  . Thus, \(\forall w \in {\textbf {i}}\): \(\forall u \in {\textbf {k}}^w\):
. Thus, \(\forall w \in {\textbf {i}}\): \(\forall u \in {\textbf {k}}^w\):  . Thus,
. Thus, 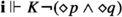 . It is also readily confirmed that \(\llbracket \diamond p \wedge \diamond q \rrbracket ^{w_1, {\textbf {i}}} = 1\). Hence, \(\exists w \in {\textbf {i}}\): \(\llbracket \lnot (\diamond p \wedge \diamond q) \rrbracket ^{w, {\textbf {i}}} = 0\). Hence, \({\textbf {i}} \nVdash \lnot (\diamond p \wedge \diamond q)\).
. It is also readily confirmed that \(\llbracket \diamond p \wedge \diamond q \rrbracket ^{w_1, {\textbf {i}}} = 1\). Hence, \(\exists w \in {\textbf {i}}\): \(\llbracket \lnot (\diamond p \wedge \diamond q) \rrbracket ^{w, {\textbf {i}}} = 0\). Hence, \({\textbf {i}} \nVdash \lnot (\diamond p \wedge \diamond q)\). -
b.
Counter-model: \(W = \{w_1, w_2\}\); \(\texttt{I}(p)=\{w_1\}\) and \(\texttt{I}(q)=\{w_2\}\); \({\textbf {k}}^{w_1}={\textbf {e}}^{w_1}={\textbf {k}}^{w_2} = {\textbf {e}}^{w_2} = W\). Let \({\textbf {i}} = W = \{w_1, w_2\}\). We then proceed as in Fact 5.
\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hawke, P. Stable acceptance for mighty knowledge. Philos Stud 181, 1627–1653 (2024). https://doi.org/10.1007/s11098-024-02103-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-024-02103-z





 then v is a
then v is a  then
then 
 iff
iff 
 iff
iff 
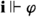 iff
iff 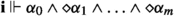
 iff
iff 
 iff
iff 
 iff
iff 
 iff
iff 
 iff
iff 
 and
and  . Thus,
. Thus,  . Thus,
. Thus, 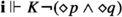 . It is also readily confirmed that
. It is also readily confirmed that