Mind the gap: noncausal explanations of dual properties

Abstract

I identify and characterize a type of noncausal explanation in physics. I first introduce a distinction, between the physical properties of a system, and the representational properties of the mathematical expressions of the system’s physical properties. Then I introduce a novel kind of property, which I shall call a dual property. This is a special kind of representational property, one for which there is an interpretation as a physical property. It is these dual properties that, I claim, are amenable to noncausal (mathematical, in fact) explanations. I discuss a typical example of such a dual property, and an example of an explanation as to why that dual property holds (the explanation of the quantization of the linear momentum).

1 Introduction

Not all explanatory requests in science are the same. Some can be met by indicating the cause of the phenomenon of interest; others cannot. This paper identifies and examines certain why-questions in physics that belong, I shall argue, to this second category. Their answers are given by appealing to what I shall call here representational features of the mathematical formalism which expresses the physical properties of the system of interest.

These answers are philosophically relevant for two reasons. First, since they answer why-questions, they can be considered ‘explanations’; second, in virtue of their mathematical character, these answers-explanations are arguably ‘noncausal’. Hence—my thesis here—such answers should count as noncausal scientific explanations. In holding this, I aim to provide support for a much-debated more general thesis, that there are noncausal scientific explanations of physical phenomena.¹ This is a claim which, it seems, is still far from been definitively established—Michael Strevens, for one, has recently maintained that, in essence, none of the currently discussed examples of noncausal explanations passes the bar²—hence any additional examples will help supporting it.

I begin in Sect. 2 by engaging the view (causal ‘exclusivism’) which contests the existence of noncausal explanations; then, I sketch what I take to be a novel path around exclusivism. In Sects. 3 and 4, I examine closely a (new) example of mathematical noncausal explanation: the quantization of linear momentum. While discussing this example, which is in fact representative for a whole family of examples, I also gesture at some other illustrations and suggest that our notion here, of a formal-mathematical explanation, may have a distinguished predecessor in relativistic quantum mechanics: the idea of formal- mathematical prediction, illustrated by Paul Dirac’s postulation of the positron in the early 1930s. In Sect. 5 I propose a general account of this kind of explanation. In Sect. 6, I highlight the virtues of my account by comparing it, and my examples, with other accounts (and other examples) offered in the literature.

2 Dual properties: a strategy to identify noncausal explanation in physics

So, let causal ‘exclusivism’ be the view that scientific explanations can only be causal. The view has been influential in the past, and it is popular among recent authors. Angela Potochnik, for instance, maintains that “to explain something is to show what is responsible for that thing—and whatever is responsible for something is its cause.” (Potochnik, 2020: 22–23). In the same vein, Brad Skow writes that “maybe causal explanation is not just one kind of explanation. Maybe, instead what it is to be an explanation is to be a causal explanation. Whatever set of features constitutes the nature of causal explanation also constitutes the nature of explanation” (Skow, 2014: 445).

The opponents of exclusivism, the (explanatory) ‘pluralists’, do not foreclose the possibility that, in addition to causal explanations, there could also be noncausal ones.³ Pluralists typically question the two commitments taken on by the exclusivists: to a theory of causal explanation, and to this theory’s relevance for science. The latter commitment is important since the exclusivists maintain that such a theory of explanation is not merely a philosophical fantasy, but is able to accommodate examples of explanations one finds in scientific practice. Unsurprisingly then, one of the pluralist strategies against exclusivism has been to scrutinize this commitment; more concretely, two kinds of problems with it have been flagged up.

First, the pluralists noted that the causal exclusivist theories of explanation have difficulties to capture some central explanatory practices in science. Wesley Salmon’s theory, for instance, faces such a difficulty when it comes to quantum mechanics, as he honestly acknowledged himself:

In answer to the question of this section, ‘Can quantum mechanics explain?’ the answer must be, for the time being at least, ‘In a sense ‘yes,’ but in another sense ‘no.’’ In Salmon, (1984, 242–59) I had admitted only the negative answer to this question. (Salmon, 1998, 76)

Second, the pluralists have remarked that the exclusivists theories are not able to do justice to a number of examples of scientific explanations of a seemingly noncausal type. Marc Lange (2017) has most recently adopted this strategy, by presenting a variety of cases of what he calls ‘distinctively mathematical explanations’. Among the examples he has discussed, we can find earlier examples by Lipton (2004), Baker (2005), and Pincock (2007, 2012), as well as several of his own. Batterman’s (2001) asymptotic explanations are also often cited as examples of noncausal explanations.

Yet, in fairness to the causal exclusivists, I should also note that all these contributions have come under heavy criticism. Actually, Lange (2015, 2017) rejects Lipton’s, Baker’s and Batterman and Rice’s (2014) claims that they have offered examples of noncausal explanations. Moreover, Lange’s own position has been contested (see Craver and Povich (2017), Skow (2017), Andersen (2018)). As it will become clear later, the kind of strategy and the examples I articulate here are of a very different nature from Lange’s and others’ proposals—hence, I shall argue, they are not exposed to these objections.

The pluralist approach advanced here is a variant of the abovementioned strategy of arguing by (counter-)example; the gist of my argument is an extended exposition and analysis of such a putative counterexample (from quantum mechanics). I chose this example because, I believe, it is possible to classify it as an explanation without an appeal to our intuitions about, or theories of, explanation.⁴ Thus, our main object of investigation here is a special case of a true and relevant answer to a why-question, answer that should count as a genuine explanation. Yet, I stress, this is so not because this answer fits our intuitions regarding what is explanatory, and also not because it is deemed so by a certain theory of explanation. Rather, this answer has this status in virtue of adopting ‘minimalism’ about scientific explanation: namely, that to explain is, first and foremost (i.e., minimally), to provide a true and informative answer to a why-question.⁵

Another worry to address at the outset is the characterization of this answer-explanation as ‘noncausal’. To a first approximation, I claim that it deserves this label in so far as it is given by appealing to a representational property—of a mathematical formula. Since, as we’ll see, this answer exploits only features of the mathematical description of the physical systems of interest, this answer will a fortiori bypass any considerations regarding the stuff described. We shall return to this crucial point later.

Now, I would like to introduce a key distinction, between two kinds of properties: physical properties, on one hand, and representational properties, on the other. Physical properties are the usual properties of physical systems, e.g., mass, velocity, momentum, energy, etc. By contrast, what I call here a ‘representational’ property is not a property of the physical system per se; it is a property of a canonical mathematical expression of one of the system’s physical properties. Based on this distinction, I next introduce what I shall call here dual properties. These are properties that have a special dual nature, in that they are representational properties and also have an interpretation as physical properties.

To be sure, more needs to be said about the very notion of a dual property. We will encounter one below (actually, a whole class), but let me first try to clarify the concept of a representational property. An example will help, so consider the standard mathematical expression of the potential energy stored in a simple harmonic oscillator, i.e., the formula $k{x}^{2}/2$, standardly abbreviated as ‘U’ (as usual, k is the force constant and x the coordinate of the position of the oscillating mass). That the oscillator stores energy is (obviously) a physical property of this physical system. A representational property, on the other hand, is a certain kind of property of this very formula, property that it has in virtue of its specific symbolic constitution—here, ‘is quadratic’ would be such a property of formula U. Representational properties like these⁶ will be central in what follows, since some of them will turn out to also be dual properties. But note the emphasis: not all representational properties are dual properties; for instance, the one we just encountered—call it ‘quadradicity’—is not.

So, dual properties will be those representational properties which are also properties of the system itself (i.e., physical properties); or, put as above, they are representational properties with a (natural) interpretation as physical properties. And, as already noted, the answers to the why-questions of interest here will consist in essence in accounts as to why such dual properties hold. Therefore, I shall argue, these answers/explanations, in virtue of being entirely formal, will fall outside the domain of causality, no matter how large and inclusive one takes this domain to be.

To dispel some possible confusion regarding dual properties, let me also note that many mathematical formulae admit physical interpretations. (To take a most crude illustration, consider formula ‘x + y’. A natural interpretation of it is to assign the variables x and y values of the masses of a two-component physical system, and to take this expression as giving the total mass of such a system.) However, it is crucial to understand that here we shall focus on certain properties of such formulae, not on the formulae themselves. To stress: it is these properties that have to admit physical interpretations, not the formulae per se. So, when we consider a representational property of a given formula (e.g., that it is invariant under certain substitutions), the question to ask is whether this property corresponds, or not, to a physical property (physical fact).

Returning to the example above of the potential energy stored in a simple harmonic oscillator, we saw that the formula U = kx²/2 has the property 'is quadratic'. I also said that this was only a representational property of U, and not a dual property. But we now note that in addition to its quadradicity, formula U has another representational property, namely invariance under the x→–x substitution. (Trivially, we have U(x) = U(–x), since kx²/2 = k(–x)²/2.)⁷ Importantly, this symmetry is a representational property of the formula U which does have a physical interpretation—namely, that the amount of energy stored in the oscillator when it is located at the left of the equilibrium point is the same as the amount of energy it stores when it finds itself at the same distance to the right side of that point. Hence, this symmetry counts as a dual property, too.

To consider another example, which provides us with a template more relevant for the discussion in the later sections, it may be that a formula φ (expressing a physical quantity Q) lacks a term for a certain quantity W. This—‘lacks a term for W’—qualifies as a representational property of φ, and moreover it is a property that has a (trivial) physical interpretation; namely, that the Q of the system does not depend on the W of the system,⁸ hence it is a dual property. In more concrete terms, one can take the formula φ to be giving the period T of a simple pendulum (of length L, in a gravitational field g), and as quantity Q its period T. That is, φ = 2π $\sqrt{L/g}$, a formula which does not contain the term for the mass of the pendulum’s bob (here, mass is the generic quantity W above). The physical interpretation of this representational property of φ (namely, that it does not feature a mass term) is clear and admittedly surprising: the period of a simple pendulum does not depend on the mass of the bob.

Below I shall discuss a certain dual property in detail; however, before I do this, let me say more about what I mean by a ‘representational property’ of a mathematical expression. As intimated above, this is a property of the structured symbolic constitution of an expression. We call two expressions representationally equivalent when, despite some superficial differences, they can be (mathematically) transformed into each other; e.g., φ = (x + y)² and θ = x² + 2xy + y² are representationally equivalent. On the other hand, other expressions, e.g., $\sqrt{2xy}$ and (x²–y²)/3, or sin(x) and cos(x), can’t be so transformed, so we will say that they are not representationally equivalent. Thus, to identify the representational properties of an expression is to describe how it is constructed (from what mathematical operations, or functions) and, most importantly, to indicate how it behaves under mathematical transformations.⁹ Moreover, we can think of representational equivalence as identity of the range of values. This is relevant because although two expressions look markedly different, they may yield the same numerical value for certain substitutions of the variables in them. For instance, if we substitute x = 4 and y = 2 in the formulae $\sqrt{2xy}$ and (x²–y²)/3, they both yield the same numerical value, namely 4. But this does not always hold, as there are values of the variables (e.g., x = 2 and y = 1) for which the output of the two formulae is different (2 and 1, respectively). On the other hand, substitutions of numerical values for variable(s) in formulae that are representationally equivalent always produce the same numerical output.

Thus understood, the representational properties of a mathematical expression of a physical quantity (or process) are quite important in physics. It is well-known that sometimes it makes a significant difference whether a formula contains only linear terms, whether it is continuous or discrete, whether it is an ordinary differential equation or a partial one, whether it is a vectorial or a scalar quantity, whether it is factorizable or not, and so on. One well-known episode in the history of physics when the representational properties of an expression were regarded as essential involves Paul Dirac’s search for the relativistic equation for the electron (we will encounter it in Sect. 4). His dissatisfaction with the earlier Klein–Gordon equation (also meant to describe the relativistic electron) stemmed from the fact that that equation was not linear. Pais (1986, 289) quotes Dirac as saying that “The linearity in $\partial /\partial t$ was absolutely essential for me”. Indeed, the equation he eventually found ((5) below) was linear.

Returning to the general strategy that I intend to implement here, the leading idea is to identify a special class of cases in physics having the following remarkable feature: the explanation as to why a certain physical property (of the system) holds amounts to an explanation as to why a certain representational property (of a mathematical expression of a physical property of the system) holds. These are cases where such physical and representational properties appear ‘fused’ as dual properties—metaphorically, they are like the two sides of the same coin. Thus, a dual property will have a representational facet and a physical one, and hence—in virtue of having a representational facet—it lends itself to a formal-mathematical noncausal explanation. The example(s) below will hopefully make this somewhat abstract characterization clearer.

Finally, another distinguishing feature of the why-questions discussed here is that the formal-mathematical answers-explanations they receive are the only ones available. They are not replaceable—that is, by other, more ‘substantial’, presumably causal, answers. Since there is consensus in physics that such replacements are missing, the causal exclusivists (who would reject these formal-mathematical explanations) are pressed hard to accept that physics simply has no explanations to offer in these cases.

Now, this position is admittedly available in the logical space; after all, physics is not omniscient. Yet raising the white flag for the kind of examples discussed here is, I urge, unwarranted, if not ill-advised. This is so since my case studies, and especially the main one below, the quantization of linear momentum, belong to mainstream physics, and have extensively been treated in research papers and textbooks; they are well-understood, and far from the cutting edge of knowledge. Therefore, such a defeatist stance is prima facie less plausible than the one I endorse—to wit, that the physicists are not helpless when it comes to these why-questions, since they can formulate some answers-explanations. It is just that these explanations have to be recognized for what they are: a special kind, i.e., formal-mathematical.

3 A formal-mathematical explanation of a dual property

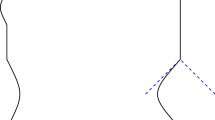
As announced above, the main case study I discuss here is the quantization of linear momentum for a particle in circular motion on a ring. See Fig. 1.

Fig. 1

A particle, described by its wave-function $\psi$, moving on a circumference of length $2\pi r$

We consider a free particle of energy E and mass m moving in one dimension on a circle of circumference $2\pi r$. It is well known that the linear momentum p of the particle has a surprising property: the spectrum of values for this quantity is not continuous, but discrete. In striking contrast with the classical situation (where the momentum of such a particle is allowed to take any values), only a discrete array of values exists. Thus, the request for an explanation suggests itself: why is the motion of the particle constrained like this? Why is its momentum ‘quantized’?

More specifically, the textbook expression for the values of the momentum is the following¹⁰:

$${p}_{n}=(\hslash /r)n$$

(1)

where n takes values $\pm 1, \pm 2,\dots$

This expression shows, as expected, that the momentum is quantized; however, one would like to know why this is so. So, naturally, the causal exclusivist would recommend here to look for some physical-causal factor which somehow cancels, and thus eliminates, the other possible values of the momentum. But, as the physicists assure us, such factor(s) are not to be found.

Note, moreover, that this is not merely an epistemic limitation. This is not due to our ignorance—as if this physical system were new and insufficiently studied, and surprises are still possible. After almost a century of working with quantum mechanics, physicists are pretty confident that there are no such (yet undetected) physical-causal ‘blocking’ processes whose effect is that certain types of motions do not happen (e.g., those motions in which p = 1.5 $(\hslash /r))$

Thus, from the exclusivist perspective, this is the end of the story: absent such ‘cancelling’ factors, the puzzling phenomenon has no explanation. However, as I noted, this is too early a capitulation. There is another way to address the why-question, and the proposal is to explore the possibility of an explanation by focusing on the representational properties of expression (1) above. The property of interest here is the fact that (1) consists in a discrete array of values.

Next, I claim that this discreteness is an example of what I have called above a dual property. On the one hand, it is a representational property; namely, a property of the very expression (1) above. There, momentum p appears as an array of discrete values, and not as a continuous function. On the other hand, it is obvious that discreteness can also be seen as a physical property of the system: it indicates that certain motions of the particle (or, more generally, certain physical states) are physically prohibited.

Yet, this duality is not an accident, but has a deeper root. It exists in virtue of a general interpretive principle, which can be formulated roughly in the following conditional form: if the spectrum of values for a physical quantity Q is not continuous, but discrete, then certain physical states, corresponding to the values missing from the spectrum, do not exist. Let me abbreviate this principle as P_D.

Principle P_D is, I submit, fairly uncontroversial, perhaps even trivial; it is widely used in scientific practice, and not only in physics. It is a connective principle, in that it links the discreteness of the spectrum of a physical quantity Q—discreteness which, again, is a representational property (of the formula expressing Q)—with the physical fact that certain states do not exist, which is a bona fide physical property of the system of interest. Given this connection, it is natural to think that one may try to explain the latter by accounting for the former, i.e., for the representational property. Then, the next question to consider is, why does the expression for the momentum p take discrete form (1) above?

The answer is, as we shall now see, of a mathematical nature. It does not rely on identifying a physical-causal factor responsible for eliminating the other possible motions of the particle (and implicitly for the elimination of other values of its linear momentum). The argument consists in a mathematical derivation, embedded in the formalism, as follows.

We know that states of definite momentum p = ℏk are given by the wave-function

$$\psi (x)=(1/\sqrt{2\pi r}){e}^{ipx/\hslash }$$

(2)

Since the particle moves on a closed trajectory, the state (2) has to be periodic of period $2\pi r$. Hence, we must have that $\psi (x) = \psi (x+2\pi r)$. By imposing this condition, we obtain

$${e}^{2\pi ipr/\hslash } = 1$$

(3)

Note that we have reached this point by codifying all the physics available; and yet we still do not have an answer as to why p takes a discrete form. But now we can account for this form in exclusively mathematical terms: as a matter of pure mathematics, Eq. (3) is satisfied only for a discrete set of values for p. Thus, we have an answer to the question as to why the representational property holds, i.e., why the momentum p has the discrete form given by (1). And, given our assumptions above, I contend that such an answer should count as an explanation.

Before we move on, let me parse the example more carefully.¹¹ The explanation was formulated in two stages. The first, preliminary step identified a representational property—discreteness; again, this is the property that the values of the momentum of the particle ‘jump’ from one integer multiple of $(\hslash /r)$ to another, without taking the intermediary values. This property is representational, since it is a property of the mathematical expression of the momentum given by (1). Yet discreteness is also a physical property of the system (of its momentum) and, as such, it is a dual property. As a dual property, it features two facets, or aspects: a representational one, and a physical-causal one.

The next step in explaining why this dual property holds consisted in offering a purely mathematical argument as to why it holds: more precisely, as to why its representational facet holds, i.e., as to why expression (1) has a discrete form. Thus, what we wanted was an explanation as to why the dual property qua representational property held. This explanation was formulated as a mathematical derivation. Crucially, note that this derivation was performed after we used all the physical-causal information available.

In essence, what we did can be characterized as follows. We managed to turn the initial why-question about a physical property of the system into a why-question about the representational property of a mathematical expression (namely, that (1) is an array of discrete values.) And, once this representational property was accounted for, we found ourselves in the position to claim that a complete and correct explanation of a dual property was provided. Then, given the nature of dual properties, this also functioned as an explanation of a physical property as well.¹² Finally, note that a large burden of the explanatory work has been carried by the interpretation of the formalism. The underlying general interpretive principle instrumental here (P_D above) is what connects the representational property with the physical property, and thus generates the dual property of interest here.

4 Further clarifications

To return to our main why-question (why is the momentum quantized?), one may wonder whether the two-step argument above really explains this quantization of the linear momentum—for one may feel that it does not. Thus, one may face an uncomfortable sentiment already experienced in other situations involving quantum mechanics, that something is missing. And this is, unsurprisingly, a physical-causal factor that removes (eliminates, cancels, blocks, stops, etc.), in a causal-mechanical fashion, the other ways the particle might move on the ring. A candid confession that Salmon made a long time ago in a different context¹³ is relevant here: “I do have a profound sense that something that has not been explained needs to be explained.” (1989, 186).

Salmon’s sense of dissatisfaction is shared by many, among them the prominent philosopher-physicist James Cushing. He made a somewhat similar complaint: “I do not see how an understanding of physical processes is possible if the move to a causal story is blocked.” (Cushing, 1991, 350) He says this while also aware of that this reaction may be subjective; he realizes that “of course, this may be a difficulty peculiar to me” (1991, 350). As is clear from the quotation, Cushing’s focus is on how understanding is a product of explanation (actually, the main topic of his insightful paper), issue which, for reasons of space, is unfortunately not possible to discuss here. He embraces the pessimistic hypothesis that the explanations offered within quantum mechanics may not yield understanding—but, importantly, we should not forget that he construes understanding in a causal-mechanical, even pictural-visual way. On the other hand, the more recent accounts of the notion of understanding “find this [construal] implausible”—as Khalifa (2017, 116) put it in direct reference to his views. However, the Cushing-type of discontent is not to be quickly dismissed. This is so especially since, as we will see below, there are situations when such canceling causal factors can be found.

Before we investigate these situations, let me note that this kind of dissatisfaction stems, on reflection, from two sources. The first is some kind of (classically-induced?) causal exclusivist nostalgia. To confront it, one just has to be reminded that there is no requirement in physics or philosophy that all explanations must be of one kind, i.e., causal. The second source is not epistemological, but metaphysical. What is felt to be missing is, in fact, not so much a specific (causal) factor responsible for the gaps, but an answer to a much deeper concern, about the very nature of reality. It can be expressed as another why-question: ‘but, why is Nature quantized?’.

When facing such a profound query, one has to consider the possibility that maybe an issue of this magnitude is just not physics’ business to address. Thus, by separating the grand metaphysical (why-)question from the initial specific (why-)question, we are led to making a constructive suggestion about the latter: admit that at least in a sense (precisely the formal-mathematical sense of explanation isolated here) the answer above does explain why the momentum is quantized. Thus, what one could (and should) do—in order to alleviate the tension between physics’ (limited) resources and one’s (legitimate) metaphysical anxieties—is to simply recognize this formal-mathematical sense of explanation as epistemically valid.

A general account of this kind of explanation will be sketched in the next section. Now, we shall take a brief detour and look at a (famous) example from classical mechanics, the double-slit experiment. This is one of those cases where the why-question of interest regards the existence of some ‘gaps’ as well, but in which a physical-causal cancelling factor responsible for their existence can be found. Thus, despite the similarity of the explananda in the two examples (the discreteness of the spectrum), in this new case we will not deal with an instance of a noncausal explanation (although we will make use of mathematics).

The well-known (idealized) physical setup is presented in Fig. 2. A water wave comes from the left, hits a dam, and passes through two openings in it (O₁ and O₂), drilled at distance d of each other. The baffling phenomenon to explain is the existence of certain points (in fact, narrow regions) on the shore (‘screen’) where no wave arrives.

Fig. 2

A water wave coming from the left passes through two openings O₁ and O₂

The explanation of the existence of these ‘gaps’ is as follows. Once the wave reaches the dam’s openings, two new waves are created at each opening, of equal wavelength λ. (One is depicted in the diagram). They travel together toward the shore. Now consider an arbitrary point P on the shore. It will be located at distances O₁P and O₂P, respectively, from the two openings. Let us assume that O₂P > O₁P.

Different numbers of wavelengths λ fit into each of the paths O₁P and O₂P. The key observation is that if P is located on the shore such that the two paths differ in length by half a wavelength (e.g., O₂P–O₁P = $\frac{1}{2}$ λ, or $\frac{3}{2}$ λ, etc.), then the waves that leave the openings in phase (crest to crest) arrive at P out of phase (crest to trough). Thus, no wave hits the shore at P because of destructive interference. On the other hand, for those points on the shore where the two paths differ by a whole wavelength, the waves arrive in phase (crest to crest). In this case, there is a maximum positive value for the intensity of the wave, because of constructive interference. Most points on the screen are of course somewhere in between these minima (zeros) and maxima.

However, what interests us here is (the property of the system) that these minima do occur. We have established that there are points on the shore where destructive interference takes place, and thus no waves arrive. They correspond to ‘gaps’. The question then is why do these gaps arise?¹⁴

These gaps can be easily characterized mathematically, as follows. Assuming that the distance between the dam and the shore is much larger than d, the angle θ between path O₁P and a perpendicular to the dam is approximately equal to the angle between O₂P and that perpendicular. Then, simple trigonometry shows that the path difference can be calculated to be O₂P–O₁P = $dsin\theta$. As argued above, the points of destructive interference are located where this difference is a half-integral multiple of the wavelength, so they can be identified from the following discrete set:

$$dsin\theta = \left( {n + \frac{1}{2}} \right)\;\lambda ,$$

(4)

where n = 0,$\pm$ 1, $\pm$ 2…¹⁵

To conclude, the point of this example is to show that there are cases when the explanation of the existence of some gaps (a physical property) is given by indicating a physical-causal mechanism responsible for the appearance of these gaps; here, the mechanism is destructive interference. Thus, although this is an explanation making use of mathematics, it is not a mathematical-noncausal explanation, but a causal one.

Back to the main argument, we are now in the position to see the general structure of the kind of formal-mathematical noncausal explanation I aim to articulate in this paper. I will do this in the next section. Meanwhile, however, let us note that the central idea here—that in order to gain physical insight physicists sometimes exploit the representational features of the mathematical descriptions of the physical systems—is actually known, and has been studied in the literature on the history and philosophy of physics. I shall now briefly present what seems to be a ‘cousin’ of the central notion here, namely a case of formal-mathematical prediction. The case study that illustrates it is well-known, and hence in no need of extensive elaboration: Dirac’s prediction of the positron in 1931.

What is now called the ‘positron’, Dirac named initially the ‘anti-electron’.¹⁶ The beginning of the story is the equation for the (free) electron he found in 1928, equation whose remarkable property was that it accommodated Special Relativity:

$$\left({i\gamma }^{\mu }{\partial }_{\mu }-m\right)\psi =0$$

(5)

where ${\gamma }^{\mu }$ are the 4 × 4 Dirac matrices (and we put $\hslash =c=1)$. From (5), it is clear that two of its four solutions, wave-functions ψ₁ and ψ₂, describe the states they were meant to describe, the spin-up and spin-down electron.¹⁷ But in 1928 no physical sense could be made of the other two solutions, ψ₃ and ψ₄ (the so-called ‘negative-energy’ states). As a testament to his genius, Dirac did not dispose of these two other solutions. Instead, fully aware that the new quantum theory he was elaborating may allow them, he went on and took these two pieces of mathematical formalism to be as descriptive as the other two solutions. He conjectured that they, too, correspond to a yet-undetected particle: the spin-up and spin-down positron. Essentially, his argument was that both spinors ψ₁ and ψ₂, and the ‘surplus’ ones ψ₃ and ψ₄, are solutions to the same equation, and this makes them formally similar. Thus, since the former have a physical correspondent, so could/should the latter. This reasoning puts his prediction in the same category as the kind of formal reasoning investigated here.

However, note an important dissimilarity between the Dirac case and the cases discussed above. In making his prediction, Dirac did not rely on an entirely unproblematic interpretive principle such as P_D. So, although one can say that he, too, interpreted the formalism (in a referential way), his interpretation was quite different from the interpretation we have encountered above. As we recall, that was an interpretation supported by a widely accepted understanding of the connection between the representational and physical properties; so, the dual property that resulted was not arrived at in a controversial way at all. By comparison, Dirac’s interpretation¹⁸ was of a different type: a much bolder move, not often used in scientific practice, a genuine step in the dark. It can be called a ‘Pythagorean’ interpretation, an apt name since it licensed reading the existence of a physical entity directly off the mathematical formalism.¹⁹

5 How formal-mathematical noncausal explanations work

I have maintained that the quantization of momentum case study presented above exemplifies a specific kind of scientific explanation. It is an instance of a formal-mathematical/noncausal explanation insofar as we

• (i) Identify a dual property,

  and

• (ii) Account for its representational facet (a representational property) in mathematical/noncausal terms.

As indicated, such an explanation proceeds in two steps. First, we find a very special kind of property: a dual property, whose two facets (the representational and the physical) are ‘fused’ together, as it were, by the interpretive principle P_D. Second, we formulate a mathematical derivation, hence (I submit) a noncausal explanation, of the representational facet of the dual property (i.e., of the representational property). Then, given the interpretation linking the representational and the physical property, I maintain that we are entitled to say that we have accounted for the physical property as well. To insist, although the mathematical expression in question is a piece of formalism, it is linked to physical reality through a natural interpretation ensured by the principle P_D. I stress this link in order to forestall a serious objection: the explanatory exercise described here does not take place in a void, and it is not a manipulation of empty mathematical symbols; on the contrary, it has immediate physical significance.²⁰ Finally, note that this exercise is generalizable. The example presented here illustrates one (type of) interpretation, i.e., via principle P_D above, but I conjecture that others can be envisaged.

A diagram summarizing the dialectic we have followed here may help; see below. Overall, we offer a formal-mathematical explanation as to why a ‘composite’ dual property holds. The essential fact that the physical property (understood as one facet of the dual property) receives a formal-mathematical explanation is indicated by the dotted diagonal arrow:

The way to read this diagram is as follows: “a formal-mathematical explanation of a dual property is an explanation of a representational property (i.e., of the representational facet of the dual property), and thus, since the representational property is interpreted as a physical property (vertical arrow down), it is an explanation of a physical property (dotted diagonal arrow).”

This diagram has been extracted from the example analyzed above, and it reflects its structure. As we recall, the example involved a situation in which what required explanation was the existence of some puzzling physical ‘gaps’. Moreover, it should be stressed that such type of phenomenon is by no means singular in physics. In addition to the quantization of momentum, one could also mention the quantization of the energy for the particle on a ring, or the same kind of quantization results for a particle in an infinite square well, or for the simple harmonic oscillator, or the quantization of intrinsic angular momentum/spin, and so on. Indeed, the example we have been dealing with here is not isolated, but a member of a whole family of examples. For instance, the energy of the particle of mass m moving on the ring is also quantized, and the values are given by the following array of values:

$${E}_{n}=({n}^{2}{\hslash }^{2})/2m{r}^{2}$$

(6)

where n = 0,$\pm$ 1, $\pm$ 2, $\pm$ 3…

The explanation in this situation is entirely analogous to the one formulated for the quantization of the momentum: we identify the same kind of dual property, consisting of a representational property (the discreteness expressed by the mathematical representation (6)) which receives a natural physical interpretation (via principle P_D)—namely, that certain physical configurations do not exist, i.e., those states in which the energy of the particle has certain ‘intermediary’ values. In the absence of a physical-causal element responsible for these gaps—showing, for instance, that such states are annihilated, in the same manner in which a particle interacts with its antiparticle—the second step in the formal-mathematical explanation has to be formulated, and it consists in an analogous mathematical argument which elucidates why the representational property of (6) holds.

The important idea is that a representational property (of a mathematical expression) takes center stage in the explanatory endeavor; then, our main concern becomes how to account for it.²¹ But something else is also remarkable here: both elements of this kind of explanation (the merely representational and the physical) are directly connected, and in an unproblematic fashion. This is noteworthy, and we shall focus on this aspect in the next section. The way we establish the link between the abstract formalism and the actual physics is precisely what marks the significant difference between the kind of formal-mathematical noncausal explanation identified here, and other cases of mathematical-noncausal explanations currently discussed in the literature.

6 A comparison

As noted above, the recent analyses of noncausal mathematical explanations appeal to a variety of examples—e.g., Lipton’s flying sticks (Lipton, 2004), Baker’s cicadas (Baker, 2005), Lyon and Colyvan’s honeycombs (Lyon & Colyvan, 2008), Pincock’s Koenigsberg bridges (Pincock, 2007, 2012), Baron’s Levy walks (Baron, 2014), Lange’s strawberries (Lange, 2017), and so on.²² I do not deny that in these explanations mathematics plays an essential role—although I do concur with some of Lange’s (and others’) objections that some of these may fail to qualify as noncausal. So, while the latter label (‘noncausal’) may not always be warranted, I agree that in all these cases of explanations mathematics carries the explanatory burden indeed.

Now, I would like to close this paper by pointing out an important comparative aspect; namely, that the examples above (those which do qualify as noncausal explanations) rely on mathematics in a different way than do the examples I introduced here. The main difference consists in how one deals with the connection between the mathematical formalism and the physical reality. While for my explanations this connection is natural and vindicated by scientific practice (principle P_D is, as we recall, uncontroversial), such connection is not presented explicitly in these other explanations; more importantly, when probed, it turns out to be deeply problematic. The way in which the formal-abstract part of these explanations (the mathematical results they employ) is related to the concrete-physical part is left unelucidated.

All these other examples face this problem, and showing this would require analyzing all of them in detail. Since this is not possible here, I will only consider the most recent, and also the simplest, example from the list above: Lange’s much-discussed explanation as to why Mother cannot distribute 23 uncut strawberries evenly to her three children. Crucial to our comparison is that in the explanation of this impossibility what bears the explanatory burden is the pure mathematical fact that 23 is not divisible by 3. A more precise way to formulate this distinctly mathematical explanation [DME] is as follows:

[DME]

Given two constitutive assumptions, that (A) Mother has 23 strawberries and three children, and (S), that the strawberries (and the children) are not modified during the distribution process,

Mother’s attempt (D) to distribute evenly 23 uncut strawberries to her 3 children,

must fail because

(M) 23 does not divide evenly by 3.

This, Lange notes, is a ‘because without cause’, and thus the DME above is a typical instance of a class of noncausal explanations. For them,

the explanatory power arises in some other way. Even if they happen to appeal to causes [(A) above; my note²³], they do not appeal to them as causes— they do not exploit their causal powers. [Lange 2013: 496] (see also [Lange, 2017: 20])

More generally, the notion of a ‘distinctively mathematical explanation’, can be spelled out in the following terms:

• (a) The explanans (M above) is a mathematical truth, and thus it is noncausal

• (b) The explanation may mention causal facts (e.g. (A)), yet it is noncausal in so far as it does not exploit them,

• (c) The explanans constrains the physical setup

• (d) The explanandum (D) is a special kind of necessary fact (about the natural world)

The issue I signaled above can be re-expressed as follows: it is unclear what is the nature of the connection between (M) and (D), i.e., point (c) above. As noted, this problem is in fact more general and affects, as far as I can tell, all examples mentioned above.²⁴ More specifically, there is no indication in Lange’s theory of DMEs as to how the ‘constraint’ that mathematics is supposed to impose, actually operates. This notion is, I insist, unaccounted for, despite the numerous appearances of the word (‘constraint’) in Lange’s works.²⁵ We are told that these mathematical constraints “apply to causal processes” (Lange, 2017: xvi, among other places), but virtually nothing specific about how they do the constraining (so to speak).

Now, in fairness to Lange, he does mention that the constraints have a “modal” and “counterfactual” nature (see e.g., Lange (2017: 10) and other places). Yet in making such observations, he only mentions the issue without really addressing it: the appeal to such notoriously murky notions (modality and counter-factuality) does not actually help here, but makes the clarification a case of obscurum per obscurius. He describes what the constraints are meant to be doing, while remaining silent, once again, on any details about how they (might possibly) do it. To repeat, the key-question, left unanswered, is precisely how the explanandum “arises” (Lange 2013, 496)—or, to be even more precise, how properties of numbers (can) constrain properties of strawberries and people.

Note, finally, that this objection may not constitute a decisive refutation of Lange’s account. Several ways out are still open to him, but the lingering worry is that all of them seem to require taking onboard metaphysical commitments which, all things considered, should be avoided (and which, as far as I can tell, I do avoid). This is so since, in the end, such metaphysical ‘baggage’ can only weaken the credibility of a theory. For instance, one such commitment may be to a (rather hard to defend) empiricist philosophy of mathematics, according to which numbers, and facts about them, are not abstract, but concrete, and thus are able to operate constraints, by interacting, in the usual sense of the word, with the world. Another metaphysics to appeal to, and equally unpalatable to many, may be some form of interactionist dualism, in which mathematical entities, while remaining abstract, do affect (somehow!) objects and events in the physical world.²⁶

To close, let me address one more way out available to Lange²⁷ which, once articulated, may also pose a problem for my strategy. Suppose we ask: don't (virtually) all representational properties of mathematical expressions have interpretations as physical properties, in some context or other? Hence, isn’t there an abundance of dual properties out there? I claimed that dual properties exist, and suggested that they are sparse. But if there are many of them around, then one may wonder whether Lange's strawberry explanation can also be approached in these terms as well—and then it, too, can be classified as a noncausal explanation, through my own lenses. More precisely, the idea is to propose that ‘indivisibility’ is such a dual property; thus, the indivisibility (of 23 by 3) would be a representational property, while the indivisibility of the given collection of strawberries into smaller collections is a physical property.

This is a thoughtful suggestion, but I believe it should be resisted. The key point against it is that indivisibility (by 3) is a property of the number 23; as such, it is not a representational property as understood here, since representational properties are properties of mathematical expressions, i.e., of the formulae themselves, and not of what they stand for (here, a mathematical object, viz. a number). Of course, a mathematical formula can be identified here, and this is ‘23’, which is how we express number twenty-three in base 10. As such, the expression/formula ‘23’ does have representational properties, e.g., that it consists of two digits. This is a representational property indeed, but not a dual property, insofar as it seems to lack a physical interpretation in the sense discussed here. Moreover, if we consider a different expression of the number twenty-three, e.g., in base 2, we find this to be ‘10111’. This new formula has several representational properties too, e.g., it contains five digits, its last three digits are identical, and so on. And yet, once again, none of these is a dual property in the sense relevant here.

7 Conclusion

The idea that there can be noncausal/mathematical explanations of physical phenomena is admittedly intriguing; it has many and influential opponents (the ‘exclusivists’), and a few supporters (the ‘pluralists’). The latter have proposed a series of examples of such putative explanations, but most of them, if not all, have been met with disbelief. It was rightly (I believe) pointed out that, upon closer inspection, such explanations turned out to draw on what intuitively seemed like causal factors, or (as I objected here) neglected to account satisfactorily for the nature of the connection between the mathematical and the physical. Thus, to bolster pluralism, new strategies and examples are welcome. Moreover, the strategy and the example(s) pursued here, built around the notion of a dual property, have been especially chosen to bypass these objections. If what I have argued so far is anywhere close to the mark, then this type of explanation, of dual properties, is most securely located outside the domain of causality indeed.