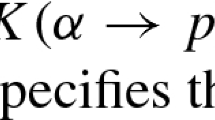Abstract
Famously, the Church–Fitch paradox of knowability is a deductive argument from the thesis that all truths are knowable to the conclusion that all truths are known. In this argument, knowability is analyzed in terms of having the possibility to know. Several philosophers have objected to this analysis, because it turns knowability into a nonfactive notion. In addition, they claim that, if the knowability thesis is reformulated with the help of factive concepts of knowability, then omniscience can be avoided. In this article we will look closer at two proposals along these lines (Edgington in Mind 94(376):557–568, 1985; Fuhrmann in Synthese 191(7):1627–1648, 2014a), because there are formal models available for each. It will be argued that, even though the problem of omniscience can be averted, the problem of possible or potential omniscience cannot: there is an accessible state at which all (actual) truths are known. Furthermore, it will be argued that possible or potential omniscience is a price that is too high to pay. Others who have proposed to solve the paradox with the help of a factive concept of knowability should take note (Fara in Synthese 173(1):53–73, 2010; Spencer in Mind 126(502):466–497, 2017).
Similar content being viewed by others
Notes
Maffezioli et al. (1963) show the inadmissibility of omniscience in an intuitionistic knowability logic.
If we had analytic proof systems for factive notions of knowability, then we could also use those. Maffezioli et al. (1963) do this for intuitionistic knowability logic.
See (Hughes and Cresswell 1996, pp. 217–220) for more information on ‘multi-modal’ (incl. ‘bi-modal’) logics.
These definitions are epistemic variations on the definitions for belief and actuality models in (Heylen 2016, pp. 1654–1655), which are essentially the models in (Rabinowicz and Segerberg 1994) with one exception. In (Rabinowicz and Segerberg 1994, Sect. 3) each model contains a set \(\varPi\) of propositions (i.e. subsets of \(W \times W\)), which (i) contains the truth sets that correspond to atomic formulas and (ii) is closed under complement, finite intersection and operations that correspond to the knowledge operator, the necessity operator and the actuality operator. Each formula corresponds in their models to a proposition, but in principle there can be propositions that do not correspond to a formula. Adding a set of propositions is for the purposes of this article a needless complication, since we will be using schemes in the object language and quantify over formulas in the meta-language rather than quantify over propositions in the object language.
See (Heylen 2016, p. 1655, Theorem 3.7).
In (Rabinowicz and Segerberg 1994, Sect. 3) the following condition for the weak validity of \(\phi \rightarrow \Diamond K A \phi\) is put forward: for every \(w \in W\) and every proposition \(\pi \in \varPi\) (see 4), if \(\langle w, w \rangle \in \pi\), then there exists some \(v \in W\), such that \(wR_{M}v\) and, for every \(w', v' \in W\), if \(\langle v, w \rangle E \langle v', w' \rangle\), then \(\langle w', w' \rangle \in \pi\). This condition is more general than is needed for the (weak) validity of the scheme\(\phi \rightarrow \Diamond K A \phi\), since there can be propositions that are not expressed by formulas, although every formula expresses a proposition (see footnote 4). It is easy to transform the model used in the left-to-right direction of the proof of Lemma 2.1 into a full-fledged (Rabinowicz and Segerberg 1994)-model. The proposition \(\pi\) is the singleton \(\{ \langle w', w' \rangle \}\) and it has to be included in the set of propositions \(\varPi\), because the latter by stipulation includes the truth set of atomic formula p.
It might be objected that in these models one has logical omniscience and, since there are infinitely many logical truths, an infinite numbers of truths is known. In response one could, for instance, change Definition 2.1 by adding a set \(W^{*}\) of sets of formulas of the language (‘impossible worlds’), with \(R_{M}\) a two-place relation on W and with \(R_{E}\) a two-place reflexive relation on \(W \cup W^{*} \times W \cup W^{*}\) such that, if \(\langle w, w' \rangle R_{E} \langle v, v' \rangle\) and \(w= w'\), then \(v = v'\). The relation of truth relative to a model and a state with an evaluation world belonging to W remains the same. The relation of truth relative to a model and a state with an evaluation world belonging to \(W^{*}\) is determined by membership of the elements of \(W^{*}\). Logical truth is defined relative to states where both the evaluation and the reference world are from W. It is easy to check that logical omniscience no longer holds. Moreover, Lemma 2.1 still holds, although at one point in the proof of the left-to-right direction a slight generalisation, viz. \(V\left( p, u' \right) = 0\) or \(p \not \in u'\), is needed. I leave it to the reader to check this.
One the one hand, for the purpose of checking that the validity of the knowability thesis does not entail omniscience, it is actually an advantage that the models have logical omniscience built into them, for it makes the inadmissibility claim stronger. On the other hand, the admissibility of possible omniscience is stronger, if one does not assume logical omniscience. See footnote 7 for more on this.
In (Fuhrmann 2014a, p. 1644) the w-index is missing, but X is supposed to be a subset of W, whereas \(S'\) is a subset in \(W \times W\).
Here both accessibility relations are interpreted as epistemic accessibility relations, whereas in Sect. 2.1 one of the accessibility relations is glossed as a modal one and the other accessibility relation is glossed as an epistemic one.
References
Boolos, G. S., Burgess, J. P., & Jeffrey, R. C. (2003). Computability and logic (4th ed.). New York: Cambridge University Press.
Carnap, R. (1931). Die Physikalische Sprache als Universalsprache der Wissenschaft. Erkenntnis, 2(1), 432–465.
De Clercq, R., & Horsten, L. (2004). Perceptual indiscriminability: In defence of Wright’s proof. Philosophical Quarterly, 54(216), 439–444.
Dummett, M. (1977). Elements of intuitionism. Oxford: Oxford University Press.
Edgington, D. (1985). The paradox of knowability. Mind, 94(376), 557–568.
Edgington, D. (2010). Possible knowledge of unknown truth. Synthese, 173(1), 41–52.
Fara, M. (2010). Knowability and the capacity to know. Synthese, 173(1), 53–73.
Fischer, M. (2013). Some remarks on restricting the knowability principle. Synthese, 190(1), 63–88.
Fitch, F. B. (1963). A logical analysis of some value concepts. Journal of Symbolic Logic, 28(2), 135–142.
Fuhrmann, A. (2014a). Knowability as potential knowledge. Synthese, 191(7), 1627–1648.
Fuhrmann, A. (2014b). Erratum to: Knowability as potential knowledge. Synthese, 191(7), 1649.
Hart, W. D. (1979). The epistemology of abstract objects: Access and inference. Aristotelian Society Supplementary, 53(1), 153–166.
Hart, W. D., & McGinn, C. (1976). Knowledge and necessity. Journal of Philosophical Logic, 5(2), 205–208.
Heylen, J. (2016). Counterfactual theories of knowledge and the notion of actuality. Philosophical Studies, 173(6), 1647–1673.
Hughes, G. E., & Cresswell, M. J. (1996). A new introduction to modal logic. London: Routledge.
Kaplan, D. (1977). Demonstratives. In J. Almog, J. Perry, & H. Wettstein (Eds.), Themes from Kaplan (pp. 481–563). Oxford: Oxford University Press.
Kripke, S. A. (1963). Semantical analysis of modal logic I. Normal propositional calculi. Zeitschrift fur mathematische Logik und Grundlagen der Mathematik, 9(56), 67–96.
Maffezioli, P., Naibo, A., & Negri, S. (2013). The Church–Fitch knowability paradox in the light of structural proof theory. Synthese, 190(14), 2677–2716.
Moore, G. E. (1942). A reply to my critics. In P. A. Schilpp (Ed.), The philosophy of G. E. Moore. Chicago, IL: Open Court.
Percival, P. (1990). Fitch and intuitionistic knowability. Analysis, 50(3), 182–187.
Rabinowicz, W., & Segerberg, K. (1994). Actual truth, possible knowledge. Topoi, 13(2), 101–115.
Spencer, J. (2017). Able to do the impossible. Mind, 126(502), 466–497.
Williamson, T. (1982). Intuitionism disproved? Analysis, 42(4), 203–207.
Williamson, T. (1987). On the paradox of knowability. Mind, 96(382), 256–261.
Williamson, T. (1988). Knowability and constructivism. Philosophical Quarterly, 38(153), 422–432.
Williamson, T. (1992). On intuitionistic modal epistemic logic. Journal of Philosophical Logic, 21(1), 63–89.
Williamson, T. (1994). Never say never. Topoi, 13(2), 135–145.
Williamson, T. (2000). Knowledge and its limits. New York: Oxford University Press.
Williamson, T. (2016). Absolute provability and safe knowledge of axioms. In L. Horsten & P. Welch (Eds.), Gödel’s Disjunction: The scope and limits of mathematical knowledge (pp. 243–252). Oxford: Oxford University Press.
Yap, A. (2014). Idealization, epistemic logic, and epistemology. Synthese, 191(14), 3351–3366.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Heylen, J. Factive knowability and the problem of possible omniscience. Philos Stud 177, 65–87 (2020). https://doi.org/10.1007/s11098-018-1180-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-018-1180-x