Introduction

Arc interruption is a critical process in circuit breakers (CBs) as arcs impose thermal and electromagnetic stress on CB components [1, 2]. In order to expedite arc interruption, a solid insulation material is strategically positioned around a movable contact and a fixed contact. When the arc interacts with the insulation material, it undergoes ablation, wherein the material decomposes, generating a gas. This gas, in turn, cools the arc and extends its length by blowing it away. Commonly used material for the arc interruption include PA6, POM and PTFE [3, 4]. Currently, polymer ablation assisted CBs have been developed [5,6,7,8], which represents a significant advancement in this field. These CBs leverage the ablation phenomenon to enhance arc interruption capabilities, ensuring more efficient and reliable operation. Furthermore, controlling the ablation has been attracting attention to develop the CBs using SF6 gas alternatives, since SF6 gas has much higher global warming potential (GWP) of 25,200 of CO2 [9,10,11]. A comprehensive understanding of polymer ablated arc holds significant importance for various technical equpiment such as circuit breakers, arcing horns and electrical fuses. Additionally, predicting polymer wall wear caused by ablation and its effect on the mass flux within the polymer are critical issues in configuration design, selection of materials and device operation. So far, polymer and electrode vapors contaminated arc plasmas and their characteristics and influence on plasmas have been investigated [12,13,14]. Especially, for large current more than kA in high voltage CBs, photodegradation mechanism would be dominant for polymer ablation [15,16,17,18]. In such the nozzle ablation in the high-voltage CB, the arc plasma was not directly in contact with the polymer wall, resulting in radiation becoming the dominant factor. On the other hand, for low-voltage/ low-current switches, like moldeled case circuit breaker (MCCB), ablation is more likely to occur due to contact with high-temperature plasma. This difference in ablation mechanisms emphasizes the need for tailored approaches when addressing the challenges posed by polymer ablation in different types of CBs. Understanding the underlying processes, characteristics and factors influencing polymer ablation enables researchers and engineers to optimize design configurations, select appropriate materials, and ensure and reliable operation of these devices in various voltage and current ranges.

The purpose of the present research is to gain a better understanding of the thermal interaction between polymers and arc plasma. To achieve this, a simplified model was devised, incorporating both experimental and numerical simulation approaches. The model consisted of an electrode pair and a cylindrical polymer, allowing for an examination of the effect of polymer ablation and electrode evaporatoin on arc interruption characteristics. In this configuration, one electrode was embedded in the cylindrical polymer, forming a one-side flow outlet model. This configuration aims to enhance arc interruption performance by facilitating the pressure rise and gas blowing by polymer ablation. In this model, the polymer ablation can mainly be caused by pyrolysis rather than photodegradation because the arc plasma definitely contacts the polymer. This is also based on the observation results of the polymer surface after the experiment. The polymer ablation caused by radiation causes deterioration to even the inside of the polymer, but no such deterioration was observed under low current conditions. The constructed simulation model considered the ablation flux resulting from the heat flux by the arc plasma. In the numerical simulation, no unknown coefficients and parameters depending on the configuration were used. By comparing the results of arc voltage and mass of ablation per unit arc energy obtained from both experiment and simulation, the simulation results were found to agree fairly with the experimental results. This outcome suggests that the polymer-plasma interaction can be well simulated by the constructed simulation model with pyrolitic ablation. The validity of the model demonstrated in the present paper can contribute to make the results of the previous paper [19] more reliable.

The findings of this study contribute to advancing our understanding of the thermal dynamics involved in polymer ablation and the influence of electrode evaporation on arc interruption. The validated simulation model provides a valuable tool for further investigations and the design of optimization of low voltage CBs.

Experimental Details

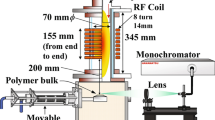
Figure 1 shows the experimental setup used for the polymer ablated arc. The electrode configuration consists of a pair of metal electrode of iron (Fe) of 6 mm diameter and a polymer cylinder of inner diameter of 6 mm. The polymer material was made of PA6 (Polyamide6, [-C6H11ON-]n) POM (Polyoxy-methlene, [-CH2O-]n) and PTFE (Polytetrafluoroethylene, [-C2F4-]n), which were generally used for the nozzle and the arc interruption chamber in circuit breakers. The gap distance between electrodes was set at 50 mm. A part of one electrode was covered with the cylindrical polymer with a depth of 30 mm. A steady DC current of 20 A was generated by a current source for DC (Komatsu Industries Corp., G9150II). Light emission images of polymer ablated arc were observed through the high-speed video camera (Keyence Corporation, VW-6000), whose frame rate and exposure time were set at 1000 fps and 12.5 μs. Current and voltage across electrodes were measured by using current transformer (CT) (Yokogawa Electric Corporation, CT701931) and CR voltage divider, respectively. The DC arc was ignited using a thin copper wire of ϕ0.1 mm located between the electrodes. Before and after the experiment, the weight difference of polymer materials was measured for their mass loss by polymer ablation.

Fig. 1
figure 1

Experimental setup for polymer ablated arc

Full size image

Experimental Results

High Speed Images of Polymer Ablated Arc for Each Polymer Material

Figure 2 shows the light emission images of polymer ablated arc for different polymer materials of PA6, POM and PTFE. In all cases, a strong gas flow was blown from the gas flow outlet of cylindrical polymer to the anode. The strong luminescence near the anode originates from the evaporation of the electrode metal. Among three kinds of polymers, the arc was contracted the most in the case with POM, followed by PA6 and PTFE. The spread of the arc on the anode side would also be due to the difference in gas flow velocity.

Fig. 2
figure 2

Observed images of polymer ablation arc (1 frame selected from images captured by high-speed video camera)

Full size image

Current and Voltage Waveform

Figure 3 shows the current and voltage waveforms measured for different polymer materials of PA6, POM and PTFE. Due to the specification of the current source, a current of 3 A initially flowed. Then, a constant current of 20 A was applied. First, at t = 0.3 s, the arc ignited through the thin copper wire between the electrodes with the increase in voltage. After that, the arc would become stable because the voltage and current became almost constant. The average arc voltage of this period was 220.0 V, 229.4 V and 99.6 V in PA6, POM and PTFE, respectively, as summarized in Fig. 4. Finally, at t = 0.88 s, the arc was interrupted by stopping the current supply from the DC current source.

Fig. 3
figure 3

Current and voltage waveforms of polymer ablated arc for different polymer materials

Full size image
Fig. 4
figure 4

Averaged arc voltage for different polymer materials during steady state under current of 20 A

Full size image

Mass Loss by Polymer Ablation

Figure 5 shows the mass difference measured before and after the single arc experiment. The mass loss of POM was almost twice as much as that of PTFE. The order of mass loss of polymer corresponds to the arc diameter and the arc voltage. PA6 would be more effective than POM for improving the arc voltage with smaller mass loss of the material. Therefore, the higher arc voltage was obtained by a larger amount of polymer ablation. This can also be explained by the arc contraction, decreasing in arc cross-section.

Fig. 5
figure 5

Mass difference in polymer due to ablation

Full size image

From results of the waveform measured, the arc image observed and the mass loss by polymer ablation measured above, the polymer ablation can make the arc diameter decreased, leading to the increase in arc voltage.

Numerical Simulations for Polymer Ablated Arc

To explain the experimental results, from the standpoint of theoretical physics, the calculation of atomic and molecular transport coefficients of ablated polymer vapor and electromagnetic thermofluid simulation of the polymer ablated arc without using any experimental values were performed.

As the calculation procedure, first, the particle composition of air and polymer vapors in the thermal equilibrium state was calculated by minimizing the Gibbs free energy [20]. Then, their thermodynamic and transport properties were calculated by using the equilibrium particle composition calculated in the previous chapter and collision integrals with first-order approximation of Chapman-Enskog method [21]. The polymer ablation in the present model would dominantly occur due to the pyrolysis rather than photodegradation the arc plasma was reliably in contact with the polymer inner wall. However, the influence of radiation should be considered. Therefore, the radiation coefficient of the thermal plasma was obtained by calculating the line spectrum and continuous spectrum, quoting correponding variables from NIST Standard Reference Database 78 [22]. Using the calculated thermodynamic and transport properties and radiation power, the electromagnetic thermofluid simulation for polymer ablated arc under steady state was carried out.

Calculation Domains

From the specification of polymer ablated arc using the present electrode configuration with cylindrical polymer, a two-dimensional axisymmetric model, as presented in Fig. 6, was constructed. For the calculation domain, two models were prepared; one is only for the left electrode and cylindrical polymer part (Model A), the other is the whole electrode configuration including an opposite electrode (Model B). Based on the finite volume method, in model A, the calculation domain was divided into 100 parts in the axial direction and 40 parts in the radial direction, including electrode and polymer, while 180 parts in the axial direction and 100 parts in radial direction in model B, respectively. A cell with a length of 100 mm was set at the left side of the same calculation space. This is hypothetically provided to prevent excessive cooling of the arc plasma by the electrodes. Comparing the simulation results from both models, the interference from outside the cylinder could be taken into consideration.

Fig. 6
figure 6

2D-axisymmetric calculation domain for polymer ablated arc. (Model A for inner region of cylindrical polymer only, model B for whole region of electrode configuration with opposite electrode)

Full size image

Assumptions in Calculations

In the electromagnetic thermofluid simulation for polymer-ablated arc, the followings were assumed.

  1. (1)

    The calculation space is axisymmetric. This is applicable due to the experimental observation of polymer-ablated arc model used.

  2. (2)

    In the calculation space, local thermal equilibrium (LTE) holds, where the electron temperature, gas temperature, and excitation temperature can be described as one temperature. Chemical reactions are in an equilibrium state.

  3. (3)

    The flow in arc plasma is laminar.

  4. (4)

    The arc plasma is optically thin for light with 200 nm or greater wavelength; re-absorption of emitted light is not examined. However, for light with less than 200 nm wavelength, the radiation loss is set to 20% of the calculated total radiation coefficient considering re-absorption.

  5. (5)

    The electric field exists only in axial direction.

  6. (6)

    Pressure propagation with sound velocity is considered as a compressible flow.

The heat transfer between thermal plasma, electrode, and polymer materials and the thermal conduction in electrode and polymer were also considered.

Boundary Conditions

As the boundary condition, the cylindrical symmetry condition was applied at the axis center at r = 0. The free flow at the end face of the polymer material with z = 50 mm in model A, and boundaries of top, bottom and right in air space in model B. The heat transfer from the fluid to the solid considers the energy transfer to the polymer material as described later, and the energy loss due to the temperature rise, melting and vaporization of the polymer material and the electrode material. The values of source terms accounting for ablation and evaporation, given from boundary surface, were given to control volume.

Governing Equations for Arc Plasmas and Polymer Ablation

The present model assumed that behaviors of polymer-ablated arc such as temperature, gas flow velocity, etc. was governed by the conservation equations for mass, momentum, energy and mass of polymer vapor [23]. These equations were described with time-dependent terms so that the transient simulation can also be conducted in the same model.

Polymer ablation can occur by heat flux and radiation flux from the arc plasma. In the present paper, the contribution from radiation flux was neglected because the arc plasmas was definitely in contact with the polymer wall and also the current treated here was low less than 50 A.

The numerical calculation model has taken into account the electron emission phenomena at electrode surface, as well as the above electrode evaporation.

All the equations used for calculation were shown in reference [23].

Numerical Simulation Results of Polymer Ablated Arc

Distributions of Temperature, Gas Flow Velocity and Mass Fraction of Polymer Vapor in Arcs in Cylindrical Polymer

Figure 7a shows the temperature distribution in PA6, POM and PTFE ablated arc in model A under the current of 20 A. Figure 8 shows the radial distribution in temperature at 10 mm away from the cathode (z = 30 mm) and gas flow outlet (z = 50 mm), respectively. The temperature distribution was almost uniform along the axial direction. For the radial distribution, the temperature at the arc core increased in the order of POM, PA6 and PTFE, reaching approximately 10,000 K. On the other hand, the temperature near the polymer wall decreased to about the thermal decomposition temperature less than 1000 K for all three polymers. Thus, the temperature would radially distribute as the arc plasma contraction due to the polymer ablation. This can indicate that the higher temperature gas contact dominantly induces the polymer ablation, which is different from the polymer ablation due to photodegradation in the puffer type circuit breakers, where the cold gas is injected around the arc core.

Fig. 7
figure 7

Temperature, gas flow velocity and mass fraction of ablated polymer vapor distributions in different polymer materials of PA6, POM and PTFE under DC20 A steady state

Full size image
Fig. 8
figure 8

Radial distributions of temperature and gas flow velocity at positions of 10 mm away from cathode tip and outlet of cylindrical polymer

Full size image

Figure 7b shows the distribution of axial gas flow velocity in PA6, POM and PTFE ablated arc. The gas flow velocity increased toward the outlet because the ablated polymer vapor. At the outlet, the gas flow velocity reached 141.9 m/s, 178.8 m/s and 36.6 m/s in cases with PA6, POM and PTFE, respectively, which were accelerated by the increase in mass internal cylindrical polymer due to the polymer ablation. The calculation results of gas flow velocity would correspond to the experimental observation images of polymer ablated arc. From results of mass fraction of ablated polymer vapor in Fig. 7c, it filled the entire cylinder and then exhausted. Therefore, the arc characteristics are completely dominated by the properties of polymer vapor. On the other hand, almost no evaporation of the electrode metal occurred.

Distributions of Temperature, Gas Flow Velocity and Mass Fraction of Polymer Vapor in Outside of Cylinder

Figure 9 shows the calculation results of distributions of temperature, axial gas flow velocity and mass fraction of polymer vapor in PA6, POM and PTFE ablated arc using model B. The color scale is the same shown in Fig. 7. From the figure, the hot gas composed of polymer vapor emitted from the cylindrical polymer was blown onto the opposite electrode, where the temperature gradient became higher. Then, the high temperature gas was diffused toward the radial direction and partly transported to electrode rear. This difference from the experimental observation would be influenced of the calculation boundary and the edge shape in opposite electrode. The radial temperature distribution at z = 60 mm in outside of the cylinder, the arc diameter was smaller in the order of POM, PA6 and PTFE. In the cylindrical polymer region, the temperature and mass fraction of polymer vapor were almost the same with model A, which indicates the interaction between arc plasma and polymer wall including the ablation phenomenon could be well simulated even by considering only the inside of the polymer cylinder. The difference between models A and B was seen in gas flow velocity at the outlet. This is because of the boundary at the outlet of cylinder in model A, and thus its influence was clarified.

Fig. 9
figure 9

Temperature, gas flow velocity and mass fraction of ablated polymer vapor distributions in different polymer materials of PA6, POM and PTFE (model B)

Full size image

Mass Loss Rate by Pyrolytic Ablation

Figure 10 shows the mass loss rate by ablation for different polymer materials compared in two models. The numerical simulation modelled the polymer ablation with the heat flux into solid polymer. The total mass production rate due to polymer ablation at each position was calculated by integrating it along inner wall of the cylindrical polymer with following equation.

$$ M_{{{\text{abl}}}} = 2\pi R\smallint S_{{\text{p}}}^{C} dz $$
(1)

where R [m] is inner diameter of the cylindrical polymer and \({S}_{{\text{p}}}^{C}\) [kg/(m3∙s)] is rate of mass production by polymer ablation.

Fig. 10
figure 10

Calculated mass loss rate by ablation for different polymer materials under DC20 A in two calculation models

Full size image

From the calculation result in both models, the magnitude relationship of the ablation rates was almost the same. POM and PA6 showed high ablation rate. This is because the heat of the high-temperature arc was conducted more than the PTFE due to the high thermal conductivity of the ablated polymer vapor based on the presence of H atom. POM has the highest mass loss rate among polymer materials compared. This high ablation rate caused the contraction of the arc and resulting the high flow velocity at the outlet. Since the arc duration is the same for all polymer conditions, the trends in the amount of polymer loss agree with those in the experimental results of mass difference in polymer, in Fig. 5.

Arc Column Voltage and Mass Loss Rate by Polymer Ablation

Figure 11 shows the arc column voltage of polymer ablated arc with different polymer materials. The arc column voltage for model A represents the voltage in axial position from 20 mm (electrode) to 50 mm (outlet), as well as the voltage between electrodes for model B, which were calculated by integrating the electrical conductivity inner region of cylindrical polymer with following equation.

$$ v_{{{\text{arc}}}} = I \cdot r_{{{\text{arc}}}} = I\mathop \sum \limits_{i} \frac{1}{{g_{i} }} = \mathop \sum \limits_{i} \frac{1}{{\mathop \sum \nolimits_{j} \frac{{\sigma_{ij} S_{ij} }}{{l_{ij} }}}} $$
(2)

where\(i\), index in axial direction;\(j\), index in radial direction; \({g}_{ij}\) [S], arc conductance; \({\sigma }_{ij}\) [S/m], unit electrical conductivity; \({S}_{ij} \left[{{\text{m}}}^{2}\right]\), cross sectional area; and\({l}_{ij} \left[{\text{m}}\right]\), unit length.

Fig. 11
figure 11

Calculated arc column voltage of polymer ablated arc with different polymer materials under DC20 A. (Gap distances of 30 mm from electrode to outlet for Model A and 50 mm between electrodes for model B)

Full size image

The figure shows that PA6 and POM have the higher arc voltage than PTFE in both models. In relation to the temperature distribution and gas flow velocity distribution in the previous section, the increase in arc voltage would be due to contraction of the arc due to polymer ablation. The arc contraction reduced the conductive diameter, that is, the cross-sectional area, and contributed to the increase in arc resistance \({r}_{{\text{arc}}}\). In case with PTFE, the same holds for the decrease in conductive area due to polymer ablation. However, since the electrical conductivity of mixed PTFE vapor is higher than that of air, PA6, and POM [23], the arc resistance did not increase rather decreased. To compare the arc voltages obtained in experiment and calcualted in numerical simulation, it is necessary to add a cathode fall voltage to arc column voltage calculated above.

Figure 12 shows the comparison of arc voltage per unit length in experiment and numerical simulation. The additional electrode fall voltage was estimated approximately 10 V in model A and 16 V in model B, respectively [24]. Since both arc voltages matched well, it was indicated that the constructed arc simulation model was appropriate. The arc voltage in model A was higher than that in model B. This would be explained by the radial expansion of conductive cross-section in outer space.

Fig. 12
figure 12

Arc voltage per unit length of polymer ablated arc with different polymer materials under DC20 A considering electrode fall voltage 10 V and 16 V for models A and B, respectively

Full size image

Figure 13 shows the mass loss per unit arc energy between experiment and numerical simulation. The arc energy was calculated with following equations.

$$ W_{{{\text{exp}}}} = \frac{{M_{{{\text{exp}}}} }}{{\smallint I_{{{\text{arc}}}} \cdot v_{{{\text{arc}}}} dt}} $$
(3)
$$ W_{{{\text{cal}}}} = \frac{{M_{{{\text{abl}}}} }}{{I_{{{\text{cal}}}} \cdot v_{{{\text{arc}}}} }} $$
(4)

where \({W}_{{\text{exp}}}\) and \({W}_{{\text{cal}}}\) represent the mass loss per unit arc energy in experiment and numerical simulation. \({M}_{{\text{exp}}}\) is the mass difference by ablation shown in Fig. 4. The total energy during arcing in experiment was calculated from the waveforms measured. \({M}_{{\text{abl}}}\) represents the mass loss rate by polymer ablation, calculated by Eq. (1), shown in Fig. 9. \({I}_{{\text{cal}}}\) was fixed at 20 A and \({v}_{{\text{arc}}}\) was calculated by Eq. (2).

Fig. 13
figure 13

Comparison of mass loss per unit arc energy with different polymer materials under DC20 A

Full size image

Using these values, the mass of ablation per unit arc energy can be derived. From the results, higher energy is necessary for PTFE to be ablated, while PA6 can effectively be ablated and act on the arc plasma. These values were relatively higher than other previous researches [25, 26]. This would be due to differences in geometry and current value. These papers discussed under higher current condition above 1 kA. In such cases, most of the arc energy becomes radiation loss and would account for a small proportion of the ablation. In our study, the energy contributing to polymer ablation increased because the arc plasma was definitely in contact with the polymer. On the other hand, the difference between experimental and calculated values in POM can be affected by radiation because the temperature of the arc core was higher than other two polymers. These differences can also be improved by considering the transient state of arc ignition, where the ablation rate changes significantly [23].

Conclusion

The purpose of research is to gain a better understanding of the thermal interaction between polymers and arc plasma. The experiment and numerical simulation for polymer-ablated arc were performed with one-side flow outlet model. In the model used, the pyrolysis rather the photodegradation would be dominant for ablation because the arc plasma was definitely in contact with the polymer. The simulation results are in good agreement with the experimental results, indicating that the simulation modeling without using experimental values and unknown coefficients is valid. This outcome suggests that the polymer-plasma interaction can be well simulated by the constructed simulation model with pyrolitic ablation. Both results also indicate that POM can improve the arc voltage due to the high ablation rate, and PA6 can effectively be ablated and act on the arc plasma.