1 Introduction

It is apparent that information technologies and cryptography are the most demanding industries for random numbers, and therefore random number generation devices. There are however many other uses that heavily depend on random number generation, like the gambling industry or fundamental investigation.

Random number generators can be classified into three categories (Mannalath et al. 2022):

  1. (1)

    Pseudorandom number generators (PRNG): seemingly random numbers are generated by means of an algorithm. The output sequence is hard to distinguish from a truly random one, but its order is totally predefined.

  2. (2)

    True random number generators (TRNG):

    1. a.

      Physical random number generators: random numbers are generated upon measurements of classic systems parameters with chaotic behaviors; in special, chaos in lasers has been successfully used as a source of random bits at high frequencies (Kanter et al. 2010; Li et al. 2010; Li et al. 2018; Uchida et al. 2008). Output sequences are usually considered random, but at a fundamental level they are deterministic.

    2. b.

      Quantum random number generators (QRNG): random numbers are generated based on the uncertainty inherent to quantum physics (Gabriel et al. 2010).

In the last years, many experiments have been conducted relying on the quantum nature of light. In particular several authors have shown the operation of homodyne detectors in laboratory setups (Collett et al. 1987; Herrero-Collantes and Garcia-Escartin 2017) that can be extended to commercial use (Huang and Zhou 2019; Qi 2017; Raffaelli et al. 2018). There have also been shown major improvements obtained with the introduction of an Erbium-Doped Fiber Amplifier EDFA (Qi 2017). Those experiments used, nonetheless, different components, circuits and measurement equipment. In this paper we will present a thorough comparison of these methods, using a homogeneous setup for all of them. On top of that, we will conduct new experiments destined to analyze the influence of parameters such as laser power, EDFA pumping power or laser wavelength on a QRNG based on a homodyne receptor.

Classical monochromatic light waves have a quantum mechanical equivalence known as coherent states, which can be represented as a superposition of the photon number states. Unlike classical electromagnetic waves, phase and photon number of a coherent state have uncertainty in them and are always fluctuating around their average values.

The zero photon number state, more commonly known as the vacuum state, possesses a non-zero energy originated from a randomly fluctuating electromagnetic field (Glauber 1963) present even in the absence of photons. Measuring these random fluctuations will be one source of randomness in our experiments. The second source of randomness will rely on the phenomenon of amplified spontaneous emission (ASE) present in an EDFA, in which random noise from the spontaneous emission in the medium with population inversion is in turn amplified by stimulated emission in the medium. Lastly, we used as a source of randomness the phase noise resulting from spontaneous emission on two independent lasers operating at the same frequency.

2 Experimental setup

Table 1 Measured parameters in each experiment
Full size table

We present eight experiments based on the same laboratory setup, under the same conditions and with the same pieces of equipment (see Table 1), so the influence of laser wavelength or EDFA pumping power on QRNGs based on vacuum fluctuations or ASE as a randomness source can be compared and studied.

The general homodyne detector setup consists of a 50:50 beam splitter, in which a laser is connected with a source of randomness (vacuum fluctuations/ASE). The outputs of the beam splitter are sent to two photoreceptors by optical fiber cables of the same length to avoid phase delays between the branches.

Both photodiodes must have similar characteristics so that the classical noise and oscillations from the laser get canceled out by taking the photocurrent difference which is proportional to the shot noise of the laser (Schumaker 1984; Yuen and Chan 1983).

The digitized difference of the photocurrents is recorded with an oscilloscope at a sampling frequency of 250 MS/s and 8 bits of resolution.

Fig. 1
figure 1

Diagrams of laboratory setups for experiments 1–3 (top), 4–7 (middle) and 8 (bottom)

Full size image

2.1 Vacuum fluctuations measurement

In experiments 1, 2, and 3 (Fig. 1a) the quantum noise was obtained by measuring the vacuum fluctuations in the electromagnetic field.

Experiments 1 and 3 used a laser source of 1549.32 and 1308.8 nm respectively.

Experiment 2 was designed to measure the effect of an unbalanced setup: one 1-meter fiber was used to connect the splitter to the first photodiode, while two 1-meter fibers were used in the connecting between the splitter and the second photodiode, thus changing the length of the path that each light beam has to go through. The optical source was the same 1549.32 nm laser from experiment 1.

Laser sources, photodiodes, and beam splitter in the setup were the ones contained in the OptoSci ED-WDM kit.

2.2 ASE measurement

In experiments 4, 5, 6, and 7 (Fig. 1b) the setup is modified so ASE becomes the source of the quantum noise to be measured. That was accomplished by connecting an EDFA to the beam splitter input that was left open in experiments 1, 2, and 3. The used EDFA (from OptoSci ED-AMP kit) reaches saturation with a pumping power of 20 mW, so powers of 10 mW and 13 mW were selected in order to stay away from the upper limit.

Once again, two different laser wavelengths (1549.32 and 1308.8 nm) were alternatively connected to the first input of the beam splitter.

2.3 Vacuum fluctuations with channel multiplexing

In experiment 8 (Fig. 1c), two independent 1550 nm lasers were connected to the inputs of the beam splitter, thus producing a beat between the phase noise of both signals.

2.4 Electronic (non-quantum) noise measurement

Electronic noise measurements were performed by sampling the input signal in the oscilloscope while keeping the laser sources off. Four types can be distinguished:

  1. (1)

    Electronic noise #1: tests without EDFA. Noise sources are photodiodes and the oscilloscope.

  2. (2)

    Electronic noise #2: tests with EDFA at 10 mW pumping power. Noise sources are ASE, photodiodes, and the oscilloscope.

  3. (3)

    Electronic noise #3: tests with EDFA at 13 mW pumping power. Noise sources are ASE, photodiodes, and the oscilloscope.

  4. (4)

    Electronic noise #4: tests with a single laser to avoid noise beat. Noise sources are the photodiode, the oscilloscope, and the laser.

3 Measured data and postprocessing

3.1 Noise types and entropy

For each experiment, \(5\times {10}^{5}\) samples of data have been recorded. The same number of samples have been taken for each of the four electronic noise types.

These sequences have been then undergone a normality test battery (Chi-square goodness of fit test, Lilliefors test, Kolmogorov-Smirnov test, and Jarque-Bera test) thus ensuring they fit a Gaussian distribution as predicted by theory (Glauber 1963) (except for experiment number 8).

The means and variances of the 11 Gaussian distributions are shown in Table 2:

Table 2 Means and variances of measured Gaussian distributions
Full size table

The signals recorded in each test are the combination of noises from quantum and non-quantum sources, being the latter unwanted because of not being purely non-deterministic.

Taking into account that both noises have different nature and origin, we can consider the quantum and the electronic noise to be independent (Sanguinetti et al. 2014; Ma et al. 2013), so the variance of the quantum noise can be calculated by subtracting the variance due to the electronic noise from the variance of the signal measured in the experiment (Table 3, second column).

For measuring and comparing the uncertainty of the sequences obtained in the different experiments, we calculated the min-entropy of experiments 1–7 as

$${H}_{min}=\underset{1\le i\le k}{\text{min}}\left({-\text{log}}_{2}{p}_{i}\right)={-\text{log}}_{2}\left(\underset{1\le i\le k}{\text{max}}{p}_{i}\right)$$
(1)

where N = {x1, x2,...,xk} is the set of measurements with probabilities \({p}_{i}\) for i = 1,...,k [12].

As the noise distribution in experiment 8 is not gaussian, an special analysis was required. The min-entropy was estimated by calculating the amount of bits that can be influenced by three standard deviations of the non-quantum noise associated to the experiment.

With an 8-bit digitalization of the raw data, the min-entropy calculation is shown in Table 3, third column:

Table 3 Variance due to quantum noise and associated entropy
Full size table

It can be observed that entropy obtained in tests 4 and 6 is significantly higher than the others, thus demonstrating that min-entropy, and therefore, the random bits generation rate, increases with EDFA’s pumping power.

Tests 5 and 7 yielded the lowest values for the min-entropy, thus showing that EDFA’s improvement can only be leveraged by a laser with a wavelength within the amplification range.

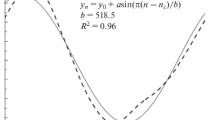
Entropy values from tests 1, 2 and 3 are very similar, which can lead us to think that neither wavelength nor fiber-optic links length make a difference. However, when comparing autocorrelation values for tests 1 and 2 (Fig. 2), a clear advantage of the balanced fibers setup over the unbalanced one is appreciated.

Fig. 2
figure 2

autocorrelation coefficients from test 1 (left) and 2 (right). Positive values are in blue and negative values in red. (Color figure online)

Full size image

The two-laser setup from test 8 yields similar min-entropy values to those involving an EDFA.

3.2 Randomness extractors

The relatively low-entropy gaussian noise data obtained from the generator needs to be postprocessed with a randomness extractor, which will output a shorter, uniformly distributed sequence with higher entropy.

There are different techniques for this purpose, from which the Toeplitz matrix hashing has been chosen (Mansour et al. 1993; Krawczyk 1994) due to the high rate of generation it allows.

Let n be the length of the input sequence S, with min-entropy k. The length of the output sequence O can be calculated as \(m=k+{{log}}_{2}\epsilon\), where ε is the security parameter, representing how close the distribution is from an ideal homogeneous one.

With this formula we computed for each experiment the length of the output sequence required for obtaining a security parameter of \(\epsilon ={2}^{-50}\) when setting an input length \(n=5000\). These results are shown in Table 4.

Table 4 Length of the output sequence (\(\epsilon ={2}^{-50}\), \(n=5000\))
Full size table

The output random sequence is finally generated according to the following procedure:

  1. (1)

    We generated a sequence seed of \(d=n+m-1\) uniformly distributed pseudorandom numbers in the range {\(\text{0,1}\)}.

  2. (2)

    From the previous sequence {\({a}_{i}\)}, we built a Toeplitz matrix \(T \in {\mathcal{M}}\;_{{n \times m}} /a\;_{{ij}} = a_{{i + 1,j + 1}} \;\forall a\;_{{ij}} \in T\).

  3. (3)

    The output non-binary vector is calculated as \({O}^{{\prime }}=S\times T\).

  4. (4)

    Finally, a binarizing technique is applied so we get the final true random sequence \(O=\left\{{o}_{i}\right\}\) where \({o}_{i}={o}_{i}^{{\prime }}\text{m}\text{o}\text{d} 2\).

4 Randomness evaluation

Given a finite sequence of numbers, it is impossible to determine with absolute certainty whether they are random or not: a series of apparently random numbers may have a large repetition period so it is unnoticed and, conversely, a perfectly random sequence of numbers can show some repetitive patterns produced by chance.

Having that in mind, we decided to subject the outcome of our experiments to the NIST Statistical Test Suite (Bassham et al. 2010), consisting of a battery of 15 tests that compare different parameters of the sequence under study against the ones expected from a homogeneous random one. A test will be regarded as passed if the obtained p-value is over 0.01.

Our results (Fig. 3) show a high proportion of successful tests, with some values under 0.01 in experiments 1, 2, 3, 5 and 8. In spite of these under threshold values, since their proportion is very low, we can conclude with a high probability that the sequences are random and uniformly distributed.

5 Conclusion

It is possible to build a discrete quantum random number generator based on a homodyne detector.

The random number generation rate can be increased by using the ASE from and EDFA instead of solely the vacuum fluctuations.

Random bits generation rate increases with EDFA’s pumping power while an imbalance in the length of the optical paths in the setup increases the autocorrelation coefficients of the measurements.

Finally, it is demonstrated that the use of two lasers provides better entropy values and higher random generation rates than setups relying on a single laser and vacuum fluctuations.

Fig. 3
figure 3

: results of NIST Statistical Test Suite. Blue: values equal or over 0.01. Red: values under 0.01. a Test 1, sequence length \(1.70\times 1{0}^{6}\); b Test 2, sequence length \(1.74\times 1{0}^{6}\); c Test 3, sequence length \(1.69\times 1{0}^{6}\); d Test 4, sequence length \(2.54\times 1{0}^{6}\); e Test 5, sequence length \(1.65\times 1{0}^{6}\); f Test 6, sequence length \(2.85\times 1{0}^{6}\); g Test 7, sequence length \(1.63\times 1{0}^{6}\); h Test 8, sequence length\(5.18\times 1{0}^{6}\) (Color figure online)

Full size image