Analysis of material susceptibility in silicon on insulator waveguides with combined simulation of four-wave mixing and linear mode coupling

Abstract

We derive propagation equations modeling third-order susceptibility-induced nonlinear interaction and linear mode coupling in waveguides. We model material susceptibility with Raman and electronic response which include approximations suited for optical communications. We validate our model by comparing numerical integration of the propagation equations to continuous wave measurements of a silicon on insulator waveguide.

1 Introduction

All-optical signal processing is a promising technique for various applications. Two prominent examples are optical phase conjugation (OPC) for mitigating nonlinear impairments in optical fiber links (Vukovic et al. 2015) and wavelength conversion (WLC) which shows high potential for several scenarios. In a narrowband sense, WLC can enable all-optical routing in datacenters or metropolitan networks. In a broadband sense, WLC allows to jointly multiplex several fully-loaded C-bands into one fiber by shifting them to distinct bands. Different approaches based on highly non-linear fibers (Rademacher et al. 2020), LiNbO$^{3}$ waveguides (Minzioni et al. 2010), and silicon on insulator (SOI) waveguides (Gajda et al. 2018; Ronniger et al. 2020) have been investigated. We present a simulation for the latter, including nonlinear effects and linear mode coupling, with an accurate model of the susceptibility in silicon.

Third-order material nonlinearity—the origin of four-wave mixing (FWM)—is the basis for all-optical signal processing. Due to the high nonlinear potential of silicon, the application of an SOI waveguide demands a more detailed consideration of nonlinearity than it is provided by the optical nonlinear Schrödinger equation. Therefore, we derive a set of coupled differential equations that model linear and nonlinear interaction based on the third-order susceptibility (resembling pulse propagation in Agrawal (2013)). As a result of the high Raman gain coefficient in silicon—which is three to four orders of magnitude higher compared to silica (Jalali et al. 2006)—it is essential to include the effect of molecular vibrations (Raman response) besides the commonly considered electron vibrations (Kerr effect).

The input-output conversion efficiency (CE) defined as idler output power over signal input power is a critical measure of the nonlinear process’s performance. For achieving a strong idler build-up, phase matching (PM) has to be performed and multi-mode operation is usually preferred since an additional degree of freedom is obtained. We refer to Kernetzky et al. (2020) for a detailed analysis of geometry optimization for PM in SOI waveguides. In Höfler et al. (2021) we described a model for the susceptibility calculation in silicon. This is extended in this work by applying the susceptibility model to the propagation equations of an SOI waveguide, as well as by comparing the results to a continuous wave measurement of the waveguide.

2 Modeling light propagation

For investigating the spatial development of the amplitudes of the interacting frequencies along the waveguide, the corresponding differential equations will be stated, starting from the wave equation

(1)

The electric displacement field is defined as

$$\begin{aligned} \vec {D}= \epsilon _0\cdot \left( \varvec{\epsilon }_{{\textbf {r}}}\vec {E}+ \vec {P}^{\text {nl}}\right) , \end{aligned}$$

(2)

where the extended material permittivity matrix

$$\begin{aligned} \varvec{\epsilon }_{\mathrm {r}} = \epsilon _\mathrm {r}' \varvec{I} + \varvec{\delta \epsilon }_{{\textbf {r}}}- j \epsilon _\mathrm {r}'' \varvec{I} \end{aligned}$$

(3)

models material dispersion by $\epsilon _\mathrm {r}' (x,y)=n^2(x,y)$, linear perturbations by the matrix $\varvec{\delta \epsilon }_{{\textbf {r}}}(x,y,z)$, light attenuation by $\epsilon _\mathrm {r}'' (x,y)$, and where $\varvec{I}$ is the identity matrix. Rearranging all perturbations into one vector yields

$$\begin{aligned} \vec {D}= \epsilon _0\cdot \left( \epsilon _\mathrm {r}' \vec {E}+ \vec {{ P}}^{\prime }\right) \end{aligned}$$

(4)

with $\vec {{ P}}^{\prime }= \varvec{\delta \epsilon }_{{\textbf {r}}}\vec {E}-j \epsilon _\mathrm {r}'' \vec {E}+\vec {{ P}}^{\text {nl}}$. Inserting $\vec {D}$ in Eq. 1 gives

(5)

We model the nonlinear polarization vector as

(6)

which contains the susceptibility tensor ${\overset{\leftrightarrow }{\varvec{\chi }}}^{[3]}$ $\in \mathbb {C}^{3\times 3\times 3\times 3}$, and where represents the tensor product. Stating Eq. 6 in sum-notation gives

$$\begin{aligned} P_\text {i}^{\text {nl}}=\iiint \sum _{\text {j,k,l}}\chi ^{[3]}_{\mathrm{ijkl}}(\tau _{\zeta },\tau _{\eta },\tau _{\rho }) \cdot E_\text {j}(t-\tau _{\zeta })\cdot E_\text {k}(t-\tau _{\eta })\cdot E_\text {l}(t-\tau _{\rho })\,\mathrm {d}\tau _{\zeta }\,\mathrm {d}\tau _{\eta }\,\mathrm {d}\tau _{\rho } \end{aligned}$$

(7)

with i, j, k, l $\in \{x,y,z\}$.

The unmodulated total propagating electrical field can be written as a superposition of modes (m) at discrete positive frequencies $\mathrm {f}_i$

$$\begin{aligned} \begin{aligned} \vec {E}= \Re \left\{ \sum _{i,m}\vec {{ E}}_{\mathrm {f}_{i}}^{(m)}\right\} = \frac{1}{2} \sum _{i,m} \hat{E}_{\mathrm {f}_{i}}^{(m)} \, \vec {\Psi }_{\mathrm {f}_{i}}^{(m)} \text {e}^{j\left( 2\pi \mathrm {f}_i t-\beta _{{\mathrm{f}}_{i}}^{(m)} z\right) } +\ c.c. \,, \end{aligned} \end{aligned}$$

(8)

with real part $\Re \{\cdot \}$, amplitudes $\hat{E}_{\mathrm {f}_{i}}^{(m)}{(z)}\in \mathbb {C}$, transversal field distributions $\vec {\Psi }_{\mathrm {f}_{i}}^{(m)}(x,y)$, and propagation constants $\beta _{{\mathrm{f}}_{i}}^{(m)}$. In the following, we make the common assumption that $\vec {P}^{\prime }$ causes a z-dependence of $\hat{E}$, but does not have any effect on $\vec {\Psi }$. Since the outer gradient in term in Eq. 5 alters the transversal field profiles, $\nabla \cdot \vec {P}^{\prime } = 0, \, \forall \vec {P}^{\prime }$ has to hold to fulfill the assumption that $\vec {P}^{\prime }$ does not affect $\vec {\Psi }$. With that, evaluating Eq. 5 at the positive frequency $\mathrm {f}_0$ (analytic signal) leads to

(9)

with $\vec {\mathcal {P}}_{}':= \vec {P}'\big |_{+\mathrm {f}_0}$ and $\vec {\mathcal {E}}{:}{=}\vec {E}|_{+\mathrm {f}_0}$.

After quite some calculus, algebra and by assuming $\partial _{z}\epsilon _{\mathrm{r}}^{\prime } = 0$, the x component of Eq. 9 becomes

(10)

with $\beta _0 = 2\pi \mathrm {f}_0 / \mathrm {c}_0$. Since the field amplitude $\hat{E}_{\mathrm {f}_{0}}^{(m)}{(z)}$ only changes due to perturbations $\vec {P}'$, all addends with $\partial _{z}\hat{E}$ vanish in the homogeneous equation ($\vec {P}' = \vec {0}$). This indicates that due to mode orthogonality all m summands needs to be equal to zero, i.e., . Based on the assumption that $\vec {P}'$ does not alter $\vec {\Psi }$, this also has to hold for $\vec {P}'\ne \vec {0}$. Consequently, by extending Eq. 10 by the y and z component one gets

$$\begin{aligned} \sum _m -j \beta _{{\mathrm{f}}_{0}}^{(m)}\, \partial _{z} \left( \hat{E}_{\mathrm {f}_{0}}^{(m)} \right) \cdot \vec {\Psi }_{\mathrm {f}_{0}}^{(m)} {\text {e}}^{j\left( 2\pi \mathrm {f}_0 t-\beta _{{\mathrm{f}}_{0}}^{(m)}z\right) }= \mu _0\epsilon _0\, {\partial _{t}}^{2}{\vec {\mathcal {P}}_{}'}, \end{aligned}$$

(11)

which also makes use of the slowly varying wave approximation $\left| \partial _{z}^{2}\hat{E}_{\mathrm {f}_{0}}^{(m)} \right| \ll \left| 2\beta _{{\mathrm{f}}_{0}}^{(m)} \partial _{z}\hat{E}_{\mathrm {f}_{0}}^{(m)} \right|$, as well as $\left| \partial _{z}\hat{E}_{\mathrm {f}_{0}}^{(m)} \right| \ll \left| \beta _{{\mathrm{f}}_{0}}^{(m)}\, \hat{E}_{\mathrm {f}_{0}}^{(m)} \right|$ for the z component.

The nonlinear part of $\vec {\mathcal {P}}_{}'$ is governed by the third-order material susceptibility $\overset{\varvec{\leftrightarrow }}{\varvec{\chi }}^{\left[ 3\right] }$. This tensor generates a nonlinear perturbation at frequency $\mathrm {f}_0$ by combining three interacting light waves. Inserting Eq. 8 into Eq. 6 and only considering frequency combinations $(\mathrm {f}_{\zeta },\mathrm {f}_{\eta },\mathrm {f}_{\rho })$ with two positive and one negative contribution (thus, considering processes such as OPC and Bragg scattering (BS)) gives

(12)

where $\overset{\varvec{\leftrightarrow }}{\varvec{X}}^{\left[ 3\right] }$ is the Fourier transform of $\overset{\varvec{\leftrightarrow }}{\varvec{\chi }}^{\left[ 3\right] }$, i.e., $\mathcal {F}\Big \{\overset{\varvec{\leftrightarrow }}{\varvec{\chi }}^{\left[ 3\right] }\Big \} = \overset{\varvec{\leftrightarrow }}{\varvec{X}}^{\left[ 3\right] }$.

Inserting Eq. 12 in Eq. 11, multiplying with $\vec {\Psi }_{\mathrm {f}_{0}}^{{(a)}^{*}}$ from the left and integrating over the cross section (making use of mode orthogonality), we obtain the propagation equation for mode (a) at frequency $\mathrm {f}_0$

(13)

with

(14)

The mode coupling (MC) coefficient $\mathop {C_{(m)}^{(a)}}$ couples modes at the same frequency whereas the nonlinearity coefficient ${N_{(m_1,m_2,m_3)}^{(a)}}$ couples between modes at all possible frequency combinations. This leads to a set of coupled differential equations of the type of Eq. 13 which has to be solved numerically. While the source fields can propagate in different modes and at arbitrary frequencies, the efficiency of the linear and nonlinear processes is determined by energy conservation and by the phase mismatches $\Delta \beta _\text {lin}$ and $\Delta \beta$, respectively.

3 Susceptibility in silicon

In the following, the third-order susceptibility for silicon as origin of nonlinear effects is analyzed. In silicon, there are two main parts that account for nonlinear processes, namely the electronic contribution (e) due to bound electrons and the Raman contribution (R) stemming from atomic lattice vibrations. Hence, it is reasonable to split the third-order nonlinear susceptibility tensor into its main parts, i.e., $\overset{\varvec{\leftrightarrow }}{\varvec{X}}^{\left[ 3\right] }= \overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e} + \overset{\varvec{\leftrightarrow }}{\varvec{X}}_{R}$, and investigate each part separately (Lin et al. 2007). Throughout this section, we assume a waveguide fabricated on a (001) surface and parallel to the [110] direction.

3.1 Electronic susceptibility in frequency domain

Due to spatial symmetry, only 21 out of 81 entries of $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}$ are nonzero, of which four are independent of each other (Boyd 2003). If only wavelengths $\lambda > \lambda _{\text {min}} = 1.10\,\mu \text {m}$ are considered, the Kleinmann condition is satisfied and three of the four independent elements can be approximated to be equal (Lin et al. 2007; Bristow et al. 2007; Osgood et al. 2009). Usually the electronic susceptibility is considered as nearly constant, since variations of the interacting frequencies lead to only small fluctuations of $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}$. For a wavelength range including the commonly used optical bands from O to L, the spacing between interacting frequencies is small enough to treat nonlinearity caused by the electronic contribution as being independent of the interacting frequencies, i.e., $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}({\mathrm {f}_{0}};{\mathrm {f}_{\zeta }},{\mathrm {f}_{\eta }},{\mathrm {f}_{\rho }}) \approx \overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}(\mathrm {f}_{0})$. With this assumption and for $\lambda \in [1.2\,\mu \text {m},2.4\,\mu \text {m}]$ (also including bands O to L), the last two independent entries of $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}$ can be related to each other as well (Zhang et al. 2007). Furthermore, the real and imaginary part of the last independent entry is linked to the Kerr coefficient $n_2$ and the two-photon absorption coefficient $\beta _{\text {tpa}}$, respectively. Altogether, this leads to the 21 nonzero elements

$$\begin{aligned} \begin{aligned} X_e^{xxxx}&= \Re \{X_e^{xxxx}\} + j \Im \{X_e^{xxxx}\}\\&= X_e^{yyyy} = X_e^{zzzz},\\[1em] \frac{X_e^{xxxx}}{2.36}&= X_e^{xxyy} = X_e^{zzyy} = X_e^{yyzz} = X_e^{zzxx} = X_e^{xxzz} \\&= X_e^{yyxx} = X_e^{xyxy} = X_e^{zyzy} = X_e^{yzyz} = X_e^{zxzx} \\&= X_e^{xzxz} = X_e^{yxyx} = X_e^{xyyx} = X_e^{zyyz} = X_e^{yzzy}\\&= X_e^{zxxz} = X_e^{yxxy} = X_e^{xzzx}, \end{aligned} \end{aligned}$$

(15)

with $\Re \{X_e^{xxxx}\} = 2.3482 \cdot n_2(\mathrm {f}_{0}) \cdot \epsilon _0 \cdot c_0 \cdot n^2(\mathrm {f}_{0})$, $\Im \{X_e^{xxxx}\} = \frac{1.1741}{2 \pi \mathrm {f}_{0}}\cdot \beta _{\text {tpa}}(\mathrm {f}_{0}) \cdot \epsilon _0 \cdot c_0^2 \cdot n^2(\mathrm {f}_{0})$ (Osgood et al. 2009; Hon et al. 2011), where the characteristics of $n_2$ and $\beta _{\text {tpa}}$ can be found in Bristow et al. (2007).

3.2 Raman susceptibility in frequency domain

The Raman contribution $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{R}$ emerges from the interaction of light with lattice vibrations (phonons) of the material. If the difference of two incident light waves coincides with the frequency of the lattice vibration (resonance), the atom is excited to a higher vibrational eigenstate. The susceptibility elements induced by Raman scattering can be stated as Dimitropoulos et al. (2003); Jalali et al. (2006); Lin et al. (2007)

$$\begin{aligned} \begin{aligned} {X_{R}}^{\mathrm{ijkl}}({\mathrm {f}_{0}};{\mathrm {f}_{\zeta }},{\mathrm {f}_{\eta }},{\mathrm {f}_{\rho }})&= {X_{R}}^{\mathrm{ijkl}}({\mathrm {f}_{0}};{\mathrm {f}_{1}},{-\mathrm {f}_{2}},{\mathrm {f}_{3}})\\&= \dfrac{1}{\pi } \cdot \mathrm {f}_{v} \cdot \Gamma \cdot \dfrac{c_0}{Z_0}\cdot \\&\quad \left( {X_{1}}^{\mathrm{ijkl}}(\mathrm {f}_{2}-\mathrm {f}_{3})\cdot \sum _{n=1}^{3}(R_{ij})_n \cdot (R_{kl})_n + \right. \left. {X_{1}}^{\mathrm{ijkl}}(\mathrm {f}_{2}-\mathrm {f}_{1})\cdot \sum _{n=1}^{3}(R_{il})_n \cdot (R_{jk})_n\right) , \end{aligned} \end{aligned}$$

(16)

with $\{\mathrm {f}_{0},\mathrm {f}_{1},\mathrm {f}_{2},\mathrm {f}_{3}\}>0$, , $a \in \{1,3\}$, and $i,j,k,l \in \{x,y,z\}$, where $\Gamma = 105\,\mathrm{GHz}$ is the FWHM-bandwidth, $\mathrm {f}_{v} = 15.6\,\mathrm{THz}$ the vibrational eigenstate frequency, $Z_0 = \sqrt{\frac{\mu _0}{\epsilon _0}}$, $g_R$ the Raman gain coefficient, and $R_n$, $n \in \{1,2,3\}$ the three Raman matrices with

Each Raman matrix corresponds to the respective displacement of the phonons along the crystallographic directions of the medium and reflects its crystal symmetry. The terms $\sum _{n=1}^{3}(R_{ij})_n\cdot (R_{kl})_n$ and $\sum _{n=1}^{3}(R_{il})_n \cdot (R_{jk})_n$ determine the 18 nonzero elements of $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{R}$. All denoted frequency values apply only at room temperature, i.e., $T\approx 300\,\mathrm{K}$. The formula and the required parameters for the approximation of $g_R$ can be found in Jalali et al. (2006); Dimitropoulos et al. (2003); Ralston and Chang (1970); Renucci et al. (1975).

As indicated by Eq. (16), the entries of the Raman susceptibility consist of two contributions, ${X_{1}}^{\mathrm{ijkl}}(\mathrm {f}_{2}-\mathrm {f}_{1})$ and ${X_{1}}^{\mathrm{ijkl}}(\mathrm {f}_{2}-\mathrm {f}_{3})$. This can be derived from the fact that there exist two potential ways to promote atoms from the ground state to a higher vibrational eigenstate. Figure 1 illustrates the Raman process $\mathrm {f}_{0}=\mathrm {f}_{1}-\mathrm {f}_{2}+\mathrm {f}_{3}$ in the special case of resonance. A photon of energy $h\mathrm {f}_{1,3}$ excites the atom from the ground state to a virtual energy state $E_1'$. Then, stimulated by a photon of frequency $\mathrm {f}_{2}$, part of the energy is used to promote the atom to the vibrational eigenstate $E_v = h\mathrm {f}_{v}$, the other part is emitted as a photon with frequency $\mathrm {f}_{2}$. Thus, photons with energy $h\mathrm {f}_{1,3}$ can be understood as the driving force for providing atoms to the vibrational eigenstate $E_v$. If a photon of energy $h\mathrm {f}_{3,1}$ is absorbed by an atom located at the vibrational eigenstate $E_v$, the atom is excited to the virtual state $E_2'$ and falls back to the ground state immediately while emitting a photon of frequency $\mathrm {f}_{0}$. Considering $\mathrm {f}_{1}$ as the frequency that implicitly provides atoms to the vibrational eigenstate, $X_1^{ijkl}$ is differently pronounced depending on how precisely the resonance frequency $\mathrm {f}_{v}$ is hit by the frequency difference $\mathrm {f}_{1} - \mathrm {f}_{2}$. In the case of resonance, i.e., $\mathrm {f}_{1} - \mathrm {f}_{2} = \mathrm {f}_{v}$, the maximal value of $X_1^{ijkl}$ is obtained. Analogously, $X_2^{ijkl}$ considers the possibility of resonance between $\mathrm {f}_{2}$ and $\mathrm {f}_{3}$, by regarding $\mathrm {f}_{3}$ as the frequency that implicitly supplies atoms to the vibrational eigenstate.

Fig. 1

Energy-diagram of the possible Raman processes in resonance. Virtual states, represented by the dashed lines, can only be used as transitions and cannot be occupied in contrast to eigenstates

4 Numerical impelementation

In our simulation, we launch three waves (two pumps and one signal) with discrete frequencies into an SOI waveguide. By linear MC, waves at all frequencies couple into all available modes at the same frequencies. Due to the nonlinear interaction, waves at all possible frequency combinations are generated in all available modes. Both interactions occur differently pronounced depending on phase mismatches $\Delta \beta _\text {lin}$ and $\Delta \beta$ and coefficients C and N. Consequently, the number of possible combinations for interaction quickly rises. We limit the simulation by only considering light propagation in the guided modes of the waveguide ($\text {TE}_{0}$, $\text {TE}_{1}$, $\text {TE}_{2}$) and by only taking frequencies into account that will be generated with non-negligible efficiency. Thus, the frequencies of the three input waves, i.e., $\mathrm {f}_{\mathrm {P}_1},\mathrm {f}_{\mathrm {P}_2},\mathrm {f}_{\mathrm {S}}$, and the two generated frequencies $\mathrm {f}_{\mathrm {BS}} = - \mathrm {f}_{\mathrm {P}_1} + \mathrm {f}_{\mathrm {S}} + \mathrm {f}_{\mathrm {P}_2}$ and $\mathrm {f}_{\mathrm {OPC}} = + \mathrm {f}_{\mathrm {P}_1} - \mathrm {f}_{\mathrm {S}} + \mathrm {f}_{\mathrm {P}_2}$ (arising from the BS and OPC FWM processes) are considered. Although this limitation drastically reduces complexity, still 15 coupled differential equations have to be solved simultaneously as summarized in Table 1.

The transversal field distributions $\vec {\Psi }_{\mathrm {f}_{i}}^{(m)}$ and their corresponding propagation constants $\beta _{{\mathrm{f}}_{i}}^{(m)}$ for the considered waveguide were calculated with an own full-vectorial mode solver based on Fallahkhair et al. (2008). After determining the required $\overset{\varvec{\leftrightarrow }}{\varvec{X}}^{\left[ 3\right] }(\mathrm {f}_{\zeta },\mathrm {f}_{\eta },\mathrm {f}_{\rho })$ (for all possible frequency combinations accounting to $\mathrm {f}_{i}$), the nonlinear coupling coefficients $N_{(m_1,m_2,m_3)}^{(a)}$ can be calculated. The influence of linear coupling and thus the magnitude of the linear coupling coefficients $\mathop {C_{(m)}^{(a)}}$ is determined by the coupling matrix $\varvec{\delta \epsilon }_{{\textbf {r}}}$ which models deviations from the unperturbed refractive index profile, e.g., caused by waveguide roughness or mechanical stress. Since $\varvec{\delta \epsilon }_{{\textbf {r}}}$ depends on various factors it is difficult to find analytic expressions for its entries. Therefore, a heuristic approach is often preferred that uses $\varvec{\delta \epsilon }_{{\textbf {r}}}$ to match the simulation and measurement results of linear coupling.

We numerically integrate the system of coupled differential equations (Eq. (13)) based on the third-order susceptibility (Sect. 3) with a variable order, variable step-size Adams-Bashforth-Moulton solver (ode113).

Table 1 The considered set of coupled differential equations which has to be solved simultaneously

5 Idler evolution in an SOI waveguide

5.1 Simulation (I)

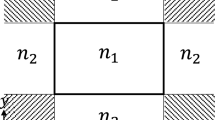
First, an SOI waveguide with rib width 1800 nm, slab height 100 nm, SOI height 220 nm, propagation length 2 cm and one dip of width 400 nm and depth 70 nm is considered. Figure 2 shows the waveguide’s geometry, which is the same as in Kernetzky et al. (2020).

Fig. 2

Refractive index geometry of the nano-rib waveguide with slab, SOI and dip heights, as well as rib and dip widths

Table 2 Simulation (I) parameters: wavelengths and modes of propagating waves with high conversion efficiency as well as input powers and mode-dependent attenuation coefficients. The asterisk at $\mathrm {I}_{\mathrm {OPC}^*}$ indicates that PM was optimized for the OPC process

Table 2 summarizes the input/output wavelengths and their corresponding modes, optimized for best efficiency of the OPC process. We select realistic values for input powers, and mode-dependent attenuation coefficients, which are also included in Table 2. The resulting power evolution along the waveguide—without linear MC ($C = 0$)—is shown in Fig. 3a. It can be seen, that the propagation of the input waves (marked as , and ) is dominated by the linear waveguide attenuation; the power decrease caused by the nonlinear power transfer to the OPC and BS idler is hardly visible in the log-domain. The OPC process () with best PM is created with highest efficiency, while the BS process () with slightly worse PM is created with less efficiency. The additional decrease in BS idler power compared to the OPC idler is caused by the larger phase mismatch $\Delta \beta$. All other potential FWM products at other modes and frequencies are not shown, since they are highly phase-mismatched, and thus have negligible power.

Fig. 3

a Simulated power evolution of pumps, signal and idlers along the waveguide without linear MC. The mode distribution is corresponding to Table 2. b Simulated power evolution of selected waves with linear and nonlinear coupling. c Vertical zoom on the OPC idler in $\text {TE}_{0}$ in (b)

For the analysis of MC, we heuristically set

$$\begin{aligned} \varvec{\delta \epsilon }_{{\textbf {r}}}= \begin{bmatrix}1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix} \end{aligned}$$

to introduce MC. This breaks the orthogonality of modes in the computation of C in Eq. 14, by not taking into account the small but non-negligible y and z components of the transversal field profiles. We emphasize again, that more meaningful entries in this matrix need to be found by matching simulation with experimental data.

Figure 3b shows the power evolution with additional linear MC. In principle, all waves couple into all considered modes. We exemplarily show one pump and one idler ( , ). The oscillation periods depend on the corresponding $\Delta \beta _\text {lin}$ values as $\mathrm {L}_\text {Oscillation} = \frac{2\pi }{\left| \Delta \beta _\text {lin} \right| }$ and the coupled powers on both, C and $\Delta \beta _\text {lin}$. For instance, the magnitude of the normalized coupling coefficient of the OPC idler from $\text {TE}_{1}$ to $\text {TE}_{0}$ ( ) is $\left| \mathop {C_{(\text {TE}_{1})}^{(\text {TE}_{0})}}\right| \bigg /\iint \left| \vec {\Psi }_{\mathrm {f}_{\mathrm {I}_{\mathrm {OPC}}}}^{(\text {TE}_{0})} \right| ^2 \mathrm {d}A= 1.3\times 10^{-4}$, whereas from $\text {TE}_{1}$ to $\text {TE}_{2}$ ( ) it is $\left| \mathop {C_{(\text {TE}_{1})}^{(\text {TE}_{2})}}\right| \bigg /\iint \left| \vec {\Psi }_{\mathrm {f}_{\mathrm {I}_{\mathrm {OPC}}}}^{(\text {TE}_{2})} \right| ^2 \mathrm {d}A=3.6\times 10^{-3}$. The corresponding phase mismatches $|\Delta \beta _\text {lin}|$ are $|\beta _{{f}_{\mathrm {I}_{\mathrm {OPC}}}}^{(\text {TE}_{1})} - \beta _{{f}_{\mathrm {I}_{\mathrm {OPC}}}}^{(\text {TE}_{0})}| = 9.1\times 10^{4}\,\mathrm{m}^{-1}$ ( ), and $|\beta _{{f}_{\mathrm {I}_{\mathrm {OPC}}}}^{(\text {TE}_{1})} - \beta _{{f}_{\mathrm {I}_{\mathrm {OPC}}}}^{(\text {TE}_{2})}| =9.2\times 10^{5}\,\mathrm{m}^{-1}$ ( ), respectively. While the coupling coefficient C from $\text {TE}_{1}$ to $\text {TE}_{2}$ is greater than from $\text {TE}_{1}$ to $\text {TE}_{0}$ (large values induce more coupled power), the phase mismatch $\Delta \beta _\text {lin}$ from $\text {TE}_{1}$ to $\text {TE}_{2}$ is also greater than from $\text {TE}_{1}$ to $\text {TE}_{0}$ (large values induce less coupled power). This leads to similar power levels of the OPC idler in $\text {TE}_{0}$ and $\text {TE}_{2}$ ( , ). Figure 3c shows a closeup of $\mathrm {I}_{\mathrm {OPC}}$ in mode $\text {TE}_{0}$ and reveals two oscillations. The slower one with period of roughly the plotted range is caused by direct coupling from $\text {TE}_{1}$. The fast oscillation arises from second-order linear coupling from $\text {TE}_{2}$ and is therefore only weakly pronounced.

5.2 Simulation (II) with experimental verification

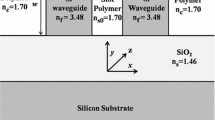
For verifying the simulation results we use measured data from an SOI waveguide with rib width 1672 nm, slab height 100 nm, SOI height 220 nm, and propagation length 11.3 mm (Ronniger et al. (2021); Kernetzky et al. (2021)). Table 3 summarizes the simulation parameters optimized for best efficiency of the BS process.

Table 3 Simulation (II) parameters: wavelengths and modes of propagating waves with high conversion efficiency as well as input powers and mode-dependent attenuation coefficients. The asterisk at $\mathrm {I}_{\mathrm {BS}^*}$ indicates that PM was optimized for the BS process

Since mode multiplexer and grating coupler at the input and output of the waveguide are lossy, the simulation parameters have to be adjusted accordingly which is reflected in a reduced input power, i.e., $\mathrm {P_{\mathrm {P}_1}} = 13.92 \ \mathrm{d Bm}$, $\mathrm {P_{\mathrm {P}_2}} = 18.75\ \mathrm{d Bm}$, and $\mathrm {P_{\mathrm {S}}} = 6.28\ \mathrm{d Bm}$. A suitable means to evaluate the generation process of the BS idler is the input-output conversion efficiency (CE): $\mathrm {CE} = \mathrm {P_{\mathrm {I}_\mathrm {BS}}} / \mathrm {P_S}$ (or $\mathrm {CE} = \mathrm {P_{\mathrm {I}_\mathrm {BS}}} - \mathrm {P_S}$ in log-domain), where the signal and idler power is defined at the input (before mode multiplexer and grating coupler) and at the output (after mode demultiplexer and grating coupler) of the chip, respectively. Figure 4a shows that the simulated idler power is $\mathrm {P_{\mathrm {I}_\mathrm {BS}}} = -22.5\ \mathrm{d Bm}$ at the end of the waveguide. This results in a CE of $\mathrm {CE}_{\mathrm {sim}}= -22.5\ \mathrm{d Bm} - 5\ \mathrm{d B} - 11.28\ \mathrm{d Bm} \approx -39\ \mathrm{d B}$, where -5 dB includes the losses caused by demultiplexer and grating coupler at the output. From Fig. 4b, the measured CE for $\lambda _{\mathrm {I}_{\mathrm {BS}}} = 1303.44\ \mathrm{n m}$ is $\mathrm {CE}_{\mathrm {meas}}\approx -42\ \mathrm{d B}$. This is a very good match between measurement and simulation, since the remaining CE difference of 3 dB is very small considering measurement imperfections, material parameter, temperature variations, etc.

Fig. 4

a Simulated BS idler and signal power evolution. The mode distribution is corresponding to Table 2. b Measured CE output of the SOI waveguide, fromRonniger et al. (2021)

6 Conclusions

We modeled electronic and molecular parts $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}$ and $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{R}$ of the silicon susceptibility $\overset{\varvec{\leftrightarrow }}{\varvec{X}}^{\left[ 3\right] }$. We linked the components of $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{e}$ to material parameters and presented a closed-form solution for $\overset{\varvec{\leftrightarrow }}{\varvec{X}}_{R}$. Although the approximations we applied limit the usable wavelength region, they are valid for commonly used optical transmission bands.

We derived and numerically integrated a set of coupled differential equations, which model linear and nonlinear light evolution along waveguides. Each frequency component in each mode is modeled by an equation that includes linear attenuation, linear MC, and FWM nonlinearity caused by the material susceptibility $\overset{\varvec{\leftrightarrow }}{\varvec{X}}^{\left[ 3\right] }$. We verified the validity of the proposed model by measured data of an SOI waveguide.