1 Introduction

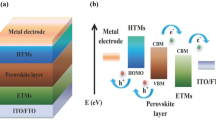
Perovskite solar cells (PSCs) have significant attention for academia and industry, Due to outstanding qualities such as efficiency, low cost, and simple assembly using roll-to-roll processing (Yang et al. 2017; Park et al. 2016; Han et al. 2018). In photovoltaics, perovskite materials are game-changers. The performance of perovskite solar cells has recently increased from 3.7 to 25.2% in a brief period, making it a formidable competitor to silicon solar cells (NREL 2019). A light-absorbing layer is commonly placed between the electron transport material (ETM) and PSCs' hole transport material (HTM). At the interface between the HTM and the perovskite layer, the HTM's role is to allow hole extraction while preventing charge recombination. To justify their use, suitable materials should have tremendous hole transport capacity and conductivity, high mobility (Kou et al. 2017). In addition, the HOMO orbital energy level should be well aligned with the valence band of the perovskite material (Sun et al. xxxx) and good solubility to aid processability, and low cost (Maciejczyk et al. 2016).

The efficiency of a solar device is determined mainly by charge generation and passage to the appropriate electrodes. After the electrons/holes are generated and transferred to their charge transport layers, they are collected at their corresponding electrodes, resulting in a photocurrent. Solar cells are also subject to undesired processes, such as recombining charged species, which reduces efficiency (Calió et al. 2016). The charge generation, separation, and extraction processes must occur faster than the recombination process to achieve high efficiency. Charges (holes/electrons) are better extracted and transported from the absorbing layer to the electrodes when interfacial layers are present; they also prevent the flow of oppositely charged ions.

HTMs are critical to device performance because they: i) change the energy barrier height between an electrode and the active layer; ii) form a specific contact for carriers; iii) protect a physical and chemical reaction between the electrode and the active layer; iv) aid in charge transport and collection; and v) improve the stability of the active layer/electrode and, ultimately, the device. Perovskite solar cells use a variety of HTMs, including inorganic, polymer, and small organic molecules. Inorganic HTMs need thermal deposition, whereas solution-processable deposition destroys perovskite film, leading to a degraded absorption layer (Park et al. 2016). On the other hand, polymers have been associated with poor reproducibility due to batch to batch variance in polymerization or polydispersity. Another drawback of polymer HTMs is their low hole mobility, which their weak stacking would cause compared to small molecules. Molecules, on either hand, can be used as HTM to tackle repeatability difficulties since structural changes can easily change the purity, mobility, and optical properties (Shahjad et al. 2017).

To create smaller molecules that make good HTMs for perovskite solar cells, researchers must first investigate the structure-properties relationship, including the electronic structure of molecules as their constituents. Useful data about any molecule can be gathered by conducting a comprehensive theoretical and experimental study to understand bandgap, highest occupied molecular orbital (HOMO) and lowest occupied molecular orbital (LUMO) energy levels. This knowledge is crucial for understanding and designing appropriate compounds for solar cells. It has previously been reported that using DFT theory to predict geometry, electronic structure, and properties of conjugated materials is a good and trustworthy method (Zade and Bendikov 2006; Zade et al. 2011).

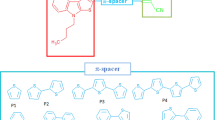
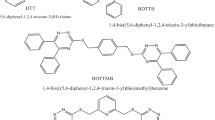
The present study focused on derivates of 1,3,5–tris (diphenylamino) benzene (TDAB) molecule. Scheme 1 depicts the design of novel 1,3,5–tris (diphenylamino) benzene (TDAB) derivatives. The computational investigation of various efficient small molecules-based HTMs in perovskite solar cells employing the DFT method at B3LYP/6-311G level of theory is presented here. The systematic theoretical study sought a comprehensive knowledge of structure–property co-relationships and explored numerous optimal geometry properties such as bandgap, HOMO, and LUMO.

Scheme 1
scheme 1

Chemical structures, abbreviations of 1,3,5–tris (diphenylamino) benzene (TDAB) unit and derivates

Full size image

2 Computational methodology

The structural, electronic, and optical properties of the studied hole transport materials HTM1-HTM9 have been explored using density functional theory (DFT) and time-dependent density functional theory (TD–DFT). S0 and S1 geometries of all HTMs were optimized using Beckethree–Lee–Yang–Parr (B3LYP) (Becke 1988; Lee et al. 1988). For forecasting such geometries and attributes, functional analysis is effective (Chi and Li 2015; Chen et al. 2014; Bagheri Novir and Hashemianzadeh 2015). The optimizations were carried out using using the standard 6-311G basis set (Tomasi et al. 2005; Cossi and Barone 2001; Adamo and Barone 2000). The polarizable continuum model (PCM) (Tomasi et al. 2005; Cossi and Barone 2001; Adamo and Barone 2000) has been used to study the influence of acetonitrile (with 35.09 measurement value of dielectric constant) solvation. Gaussian 09 W was used to calculate the geometries and electrical characteristics of neutral (ground and first excited states), cationic, and anionic forms, as well as reorganization energies (Frisch et al. 2016). Gauss View (version 5.0.8) (Roy Dennington and Millam 2009) was used to do visual checks as part of this process. As a result, none of the HTM1-HTM9 geometries has imaginary frequencies, ensuring energy minima.

3 Result and discussion

3.1 Geometry parameters- dihedral angles

Six dihedral angles of the three connecting units to the central benzene ring were selected for the TDAB and HTM1-HTM9 at the ground state for gas and solvent optimization and are presented in Table 1. The optimized structures (Fig. 1) in the gas and solvent phase show that all molecules are non-planar with selected dihedral angles between 20° and 50°, and the non-planarity is due to the presence of nitrogen atoms with sp3 hybridized (McKelvey xxxx). Removal or addition of an electron from a molecule causes a noticeable effect on the value of dihedral angle as observed in the gas phase in Fig. 2, where the larger dihedral angle of anion optimized molecules for the angle C1-C6-N7-C12was observed compared to the dihedral angle of the cation indicating that much higher reorganization energy is required for the formation of anion from neutral molecule compared to the formation of cation from the neutral molecule. The TDAB and HTM1-HTM9 quickly form cation than anion molecule, thus efficiently transporting holes than an electron.

Table 1 The dihedral angles for TDAB and HTM1-HTM9 in gas and acetonitrile solvent
Full size table
Fig. 1
figure 1

Optimized structures of the TDAB and HTM 1–9 in gas phase by using DFT/B3LYP method with 6-311G basis set

Full size image
Fig. 2
figure 2

Dihedral angles TDAB and HTM 1-9 in the gas phase by using DFT/B3LYP method with 6-311G basis set

Full size image

3.2 Ionization potential and electron affinity

The ionization potential (IP) and electron affinity (EA) have been determined by DFT approach using the following equations, respectively (Chitpakdee et al. 2014)

$${\text{IP }} = {\text{ E}}_{{{\text{cation}}}} - {\text{ E}}_{{{\text{neutral}}}}$$
(1)
$${\text{EA }} = {\text{ E}}_{{{\text{anion}}}} - {\text{ E}}_{{{\text{neutral}}}}$$
(2)

During the working of the perovskite solar cell, after an electron has been excited from the valence band of the perovskite active layer, an electron from the HOMO of the HTM has to drop and fill the hole left in the valence band of the perovskite; thus the ionization potential of the HTM has to be considerably lower to favour the process of electron transfer from the HTM to the perovskite active layer, hence hole transfer from perovskite material to the HTM (Naqvi 2021). The lower the IP value, the easy formation of holes in the molecules under study; It is seen from Fig. 3 that the lowest IP value in the examined molecules here was obtained from HTM 9 and thus, tri addition of -NH2 providing much more contribution to the HOMO energy level than the others has led to lower IP value (Wazzan et al. 2018).

Fig. 3
figure 3

Ionization potentials (IP) of TDAB and HTM 1–9 in gas phase by using DFT/B3LYP method with 6-311G basis set

Full size image

3.3 Frontier molecular orbitals (HOMO–LUMO)

The HOMO and LUMO distributions and the energy levels of the structures examined are presented in Fig. 4 to help comprehend the electronic structure. In general, a good HOMO delocalization and an appropriate HOMO energy level relative to the valence band of perovskite are advantageous for improving the hole transfer integral and hole transport. The HOMO of the structures is estimated to be distributed over the entire molecule, whereas the LUMO is concentrated on the substitution core. It turns out that the HOMO is more broadly dispersed than the LUMO in the two derivatives, indicating that the derivatives have a good chance of being used as hole transport materials. Thus, energy and distribution of frontier molecular orbitals (FMOs) could be used to explain carrier transport features.

Fig. 4
figure 4

HOMO and LUMO surface plots of the TDAB and HTM 1–9 in gas phase by using DFT/B3LYP method with 6-311G basis set

Full size image

HOMO originated mainly from the entire molecule, while LUMO was primarily given by substituted groups benzene rings side. Hole transport is aided by the strengthening of the delocalization effect. There was also an increase in HTM/valence band overlaps between the HOMO of the TDAB as the HTM and the perovskite material, leading to enhanced charge extraction (Naqvi 2021). HTM9, which is produced by adding –NH2 to TDAB in tri addition, has the greatest HOMO level, as seen in Fig. 4. Due to the existence of two lone pairs, HTM 2, HTM 5, and HTM 8 deviate from the increasing trend of HOMO energies due to increases and in the strength of the electron-donating group attached. HTM 8 has the lowest HOMO energy level of all the compounds under research and the spiro-OMeTAD, indicating a favorable overlap with the MAPbI3 perovskite active layer, according to the study.

3.4 Bandgap energy

The quantities of HOMO energy (EHOMO), LUMO energy (ELUMO), and their energy gap (H–L) were determined to understand the effect of the electrical characteristics better. Energy gaps represent the difference between HOMO and LUMO levels. The smaller the energy gap, the more likely the electronic transition (Sahli et al. 2018; Chiba et al. 2017; Frost et al. 2014), and the energy gap can be calculated using the following formula:

$$\Delta_{H - L} = \left| {HOMO - LUMO} \right|$$
(3)

The calculated HOMO, LUMO and ∆H–L values TDAB and HTM1-HTM9 are listed in Table 2. The FMOs of TDAB and the designed HTM1-HTM9 must be compared to the MAPbI3 perovskite molecule shown in Fig. 5, which has HOMO energy of − 5.44 eV and LUMO energy of − 4.0 eV, and the spiro-OMeTAD, which is currently in use and has HOMO energy of − 5.07 eV. The LUMO energy levels for the TDAB and HTM1-HTM9 were all above the LUMO energy level of the MAPbI3 perovskite active layer and hence prevention of an electron excited from the valence band (VB) of the perovskite to the conduction band (CB) of the perovskite to fall in LUMO energy level of the HTM instead of the CB of the electron transport material.

Table 2 HOMO, LUMO and bandgap energy in eV for TDAB and HTM1-HTM9
Full size table
Fig. 5
figure 5

HOMO and LUMO energy level diagram of TDAB and HTM 1–9 in the gas phase

Full size image

When the sun illuminates the PSC, electrons must be ejected from the perovskite active layer whose band energy gap is 2 eV or less (Naqvi and Patra 2021). For the HTM, the band energy gap has to be more than 2 eV to avoid the parasitic loss of energy from the sun. The TDAB and HTM 1–9 show a band energy gap of between 4.0 and 4.3 eV; thus, the low parasitic loss is expected to occur when used with the perovskite material. The solvent acetonitrile does not affect the band energy gap, as observed in Fig. 6. On the other hand, HTM3, HTM6and HTM9, which mono, di, and tri substitution of –NH2 respectively, were have lower values of band energy gaps. This has been due to the highest HOMO energy levels attained because the –NH2 is the most influential electron-donating group among the selected groups and with a smaller bandgap, a redshift is expected to occur (Qui and Pie et al. 2019).

Fig. 6
figure 6

Band energy gaps for TDAB and HTM 1–9 in gas and acetonitrile solvent by using DFT/B3LYP method with 6-311G basis set

Full size image

3.5 Charge transport properties

The reorganization energy (λh/e) refers to the energy change of the system, which is caused by the structural relaxation after the gain or loss of electrons. After a molecule has gained or lost an electron to form an anion or cation, the energy required for geometry modification is called reorganization energy. A change in dihedral angle gives a good prediction of a molecule's reorganization energy, but the reorganization energy of a molecule is inversely proportional to the charge mobility of the molecule. Thus lower reorganization energy of holes is a relevant factor for a hole transport material (Ashassi-Sorkhabi and Salehi-Abar 2018). The reorganization energy is of two types: reorganization energy for the hole (λh) and electronic reorganization energy (λe). To optimize the anions and cations of the TDAB molecule and its derivatives, it could be benefited from the reorganization energies.

The λh and λe energies were calculated using the following equations (Shi et al. 2019; Christians et al. 2014; Sha et al. 2018):

$$\lambda_{h} = (E_{0}^{ + } - E_{ + } ) + (E_{ + }^{0} - E_{0} )$$
(4)
$$\lambda_{e} = (E_{0}^{ - } - E_{ - } ) + (E_{ - }^{0} - E_{0} )$$
(5)

where \(E_{0}^{ + }\)(\(E_{0}^{ - }\)) denotes the energy of cations (anions) resultant by optimizing the structure of neutral molecules. \(E_{ + }\)(\(E_{ - }\)) is the cation (anion) energy calculated using the optimized cation (anion) structure. E0 denotes the energy of the neutral molecule in its ground state. The calculated reorganization energies of the hole for HTM1-HTM9 are present in Table 3 and show in Fig. 7. From the Table 3, the order of hole reorganization energies are as follows: HTM8 > HTM9 > HTM3 > HTM5 > HTM6 > HTM2 > HTM7 > TDAB ≈ HTM1 > HTM4.

Table 3 Charge transfer integral (V), Reorganization energies (λ), and charge transfer rate (K) for the TDAB and HTM1-HTM9
Full size table
Fig. 7
figure 7

Reorganization energy of holes and electrons for TDAB and HTM 1–9 in gas phase by using DFT/B3LYP method with 6-311G basis set

Full size image

From Table 3, we can find that λhole of HTM4, HTM1 and HTM7 (0.159,0.165 and 0.170 eV, respectively) are smaller than other respective HTMs. Furthermore, it was observed that HTM 1, HTM 4 and HTM 7 with mono, di and tri substitutions of the –CH3, respectively; this means that the hole transfer rates for HTM4, HTM1 and HTM7 might be higher than other HTMs. Comparing λhole and λelec values of the four HTM4, HTM1, HTM2 and HTM7 indicate that the λhole < λelec. This also implies that the hole carrier mobility of such HTMs is greater than the electron carrier mobility. This means that these chemicals have the most significant hole-transporting potential.

3.6 Charge transfer rate (K)

It is widely known that reorganization energy (λ) no single parameter can explain the nature of charge transfer; consequently, we estimated the hole and electron transfer integrals and the intrinsic mobilities. The hole mobility of nine molecules was investigated using the Marcus theory. Marcus theory has been frequently used to determine the hole hopping rate (kh) at room temperature, which may be stated as (Irfan et al. 2018; Zhang et al. 2017):

$$k_{h} = \frac{{V^{2} }}{\hbar }\left( {\frac{\pi }{{\lambda_{h} k_{B} T}}} \right)^{1/2} \exp \left( {\frac{{ - \lambda_{h} }}{{4k_{B} T}}} \right)$$
(6)

V is the charge transfer integral, h is the reorganization energy, kB is the Boltzmann constant, while T is the temperature (we usually use T = 300 K.) (Lan and Huang 2008; Marcus 1964). According to the preceding equation, the hole hopping rate Kh is influenced by two crucial parameters: V and λ are broken into two parts: the electron transfer integral Ve and the hole transfer integral Vh (Gapol et al. 2017). The specific structure of molecular stacking is difficult (Ashassi-Sorkhabi et al. 2019; Kirkpatrick and Nelson 2005), but the level-splitting approach gives good accessibility to face-to-face stacking (Kirkpatrick and Nelson 2005), and this configuration can improve − coupling (Valeev et al. 2006). Vh is the hole transfer integral, and it can be calculated as follows (Xu et al. 2018; Berlin et al. 2003; Brédas et al. 2002; Li et al. 2019; Zhang et al. 2018):

$$V_{h} = \frac{{E_{HOMO} - E_{HOMO - 1} }}{2}$$
(5)

Vh is hole transport integral, EHOMO and EHOMO−1 are the HOMO level and HOMO-1 level of face-to-face model HTMs dimer (Ashassi-Sorkhabi et al. 2019). For a good HTM, the hole transfer rate must be more than the electron transfer rate in magnitude to ensure effective charge extraction and transfer to prevent electron and hole recombination. From Table 3 and Fig. 8, HTM 9, having the highest hole transfer rate compared to other molecules, is not suitable as HTM because of its higher magnitude of the electron transfer rate. Thus, HTM6 showed the highest hole transfer rate of 1888.5 × 10–10 s−1 with a minimum magnitude of the electron transfer rate.

Fig. 8
figure 8

Charge transport rate diagram for holes and electrons of TDAB and HTM 1–9 in the gas by using TD-DFT/B3LYP method with 6-311G basis set

Full size image

3.7 Absorption spectra

The absorption properties were characterized using the TD-DFT method with a 6-311G basis set on the ground state optimized structures in both gas and solvent (acetonitrile) to obtain information about the involved in the electronic transitions. The calculated maximum absorption wavelength (λmax) of TDAB and HTM1-HMT9 in the gas and solvent state are listed in Table 4.

Table 4 The ground state maximum absorption (λ max) wavelength of TDAB and HTM1-HTM9 in gas and acetonitrile
Full size table

The absorption spectrum of each HTM is represented in Figs. 9 and 10, the absorption of TDAB and HTM1-HMT9 in the gas phase was observed to occur within the UV region; thus, no absorption occurred in the visible region that will cause a parasitic loss due to decreased amount of energy from the sun to cause the excitation in the perovskite active layer. Instead, all the energy from the sun in the visible region of the spectrum will cause electron transitions in the perovskite active layer. Thus the TDAB and HTM1-HMT9 are transparent in the visible region of the spectrum in gas-phase calculations, with HTM 7 having the lowest value of λ max. A redshift was also observed in solvent phase calculations, and this can be explained by the use of high dielectric constant solvent, acetonitrile, which contributes to the electron density, causing a decrease in the band gap.

Fig. 9
figure 9

The calculated UV absorption spectra for TDAB and HTM 1–9 in the gas using TD-DFT/B3LYP method with 6-311G basis set in the gas phase

Full size image
Fig. 10
figure 10

The calculated UV absorption spectra for TDAB and HTM 1–9 in the solvent using TD-DFT/B3LYP method with 6-311G basis set in solvent phase

Full size image

4 Conclusions

DFT and TD–DFT methods have been used to investigate the studied HTM molecules for structural, electronic and optical properties. Six dihedral angles of the three connecting units to the central benzene ring were selected for the TDAB and HTM 1–9 show that all molecules are non-planarity. The FMOs of TDAB and the designed HTM 1–9 must be compared to the MAPbI3 perovskite molecule and all of the compounds under investigation, and the spiro-OMeTAD, HTM 8 has the lowest HOMO energy level, indicating a favourable overlap with the MAPbI3 perovskite active layer. The TDAB and HTM 1–9 show a band energy gap of between 4.0 to 4.3 eV; thus, the low parasitic loss is expected to occur when used with the perovskite material. On the other hand, HTM 3, HTM 6and HTM 9, which mono, di, and tri substitution of –NH2 respectively, were honoured to have lower values of band energy gaps. From UV absorption calculations, the TDAB and HTM 1–9 are transparent in the visible spectrum region in gas-phase calculations, with HTM 7 having the lowest value of λmax. The reorganization energy of holes and electrons was calculated, and it was observed that HTM 1, HTM 4 and HTM 7 with mono, di and tri addition of the –CH3, respectively and HTM 9, having the highest hole transfer rate compared to other molecules.