Indirect Inference and Small Sample Bias — Some Recent Results

Abstract

Macroeconomic researchers use a variety of estimators to parameterise their models empirically. One such is FIML; another is indirect inference (II). One form of indirect inference is ‘informal’ whereby data features are ‘targeted’ by the model — i.e. parameters are chosen so that model-simulated features replicate the data features closely. Monte Carlo experiments show that in the small samples prevalent in macro data, both FIML informal II produce high bias, while formal II, in which the joint probability of the data- generated auxiliary model is maximised under the model simulated distribution, produces low bias. They also show that FII gets this low bias from its high power in rejecting misspecified models, which comes in turn from the fact that this distribution is restricted by the model-specified parameters, so sharply distinguishing it from rival misspecified models.

1 Introduction

Macroeconomists are naturally interested in estimating DSGE models on the available data without involving the use of Bayesian priors that are uncertain and so would possibly bias their results. Unbiased estimates of these models’ parameters is important both to guide our knowledge of macroeconomic channels of causation and for good policy analysis. In this paper we consider the ability of two widely used empirical estimators to generate estimates with low bias in the small samples usually available in macroeconomics: FIML and indirect inference. With indirect inference we distinguish two methods of proceeding: one we term Informal Indirect Inference (III) in which model parameters are chosen to ‘target’ (i.e. replicate in simulation) a set of data features, usually moments: the estimated parameters are those whose simulated moments get closest on average to the targeted data moments. The other we term Formal Indirect Inference (FII) in which an auxiliary model, such as moments or a VAR, is chosen to describe the data and the DSGE model is simulated to match this auxiliary model: the estimated parameters are those for which the simulated auxiliary model has the the highest probability of generating the auxiliary model found in the data. In what follows we consider the small sample bias in estimation of all these methods revealed by Monte Carlo experiment. To anticipate, we find that the III targeting procedure produces high bias, whereas FII has low bias and should therefore be used in preference. Also, building on earlier work that has shown by Monte Carlo experiment the high and well-known small sample bias coming from the FIML estimator, as against the low-bias FII estimator, we ask what it is about these two procedures that produces this relative bias outcome; we find that this is essentially derived from FII’s high power in rejecting misspecified models. The overall conclusion of this paper is that researchers should estimate their DSGE models by formal Indirect Inference (FII), eschewing both FIML and the III targeting method of indirect inference.

2 Should We Target Data Features in Estimating DSGE Model

A popular way to calibrate dynamic stochastic general equilibrium (DSGE) models is to calibrate them with parameter values chosen to ‘target’ (i.e. exactly replicate) a set of moments. The model is then asked how well it can match some other moments when simulated; this match is informally carried out, in the hope that the simulated and data moments are ‘similar’. An early example of this method is Chari et al. (2002); two recent examples are Baslandze (2022), and Khan and Thomas (2013).

Chari et al. (2002) choose a set of parameters for a sticky-price benchmark model that approximately fits about a dozen moments; they then test the model against a real exchange rate-cross-country-consumption correlation, showing that it badly fails to replicate the absence of this correlation in the data. They interpret this result as showing that a New Keynesian model of the US is unable to fit key open economy data.

Baslandze (2022) sets out a model of innovation by firms, both regular and spinouts. She derives the steady state growth equilibrium for the model outcomes. The moments of these when simulated with heterogeneous firm shocks are compared with the data moments; a subset of the model parameters is chosen to minimise the distance between a weighted average of several moments, mostly with unit weights but one with a double weight. Various relationships in the data are then compared with those implied by the model and found to be similar — e.g. the share of spinouts in states with different non-compete laws.

Khan and Thomas (2013) set out a DSGE model of an economy with credit constraints. They calibrate the parameters to match moments of aggregate and firm-level data. Later they compare its simulated aggregate business cycle moments with US data moments, suggesting it is broadly similar.

This methodology — which we call ‘informal indirect inference’, III — is presented as a way of finding a model version sufficiently ‘close to’ the data that it can be treated as the true model. We evaluate this methodology via Monte Carlo (MC) experiments. What we find is that it leads to highly biased ‘estimates’ of the model parameters in small samples. By contrast we know from previous MC experiments that formal indirect inference (FII) using moments as the auxiliary model produce estimates with very low bias.

Under FII a set of around 9 moments are chosen from among those available, this number being sufficient to generate high, but not excessively high, power against parameter inaccuracy. The joint distribution of the model-simulated moments is then calculated. Which particular moments are chosen makes little difference; the key to ‘goldilocks’ power lies in the number used. This is because all the moments are nonlinear functions of the structural parameters; hence any set of the data-based moments as a group will in all cases only have a high probability of occurring in the model-simulated joint distribution if the model is the true one. The estimated parameters are those that maximise this probability.

By contrast under III, the joint distribution of the model-simulated moments is not calculated, and so neither is the joint probability of the data-based moments. Hence in general the parameter set chosen does not maximise this probability. It might be thought that in practice it would come close; asymptotically, i.e. in large samples, it would be the same. However, in small samples there is no reason to believe that the set of parameters which generates mean simulated behaviour closest to the mean of the data moments will also have the highest joint probability of generating these data moments. The two matching criteria are entirely different. Nor does using the same number of moments make them the same. Only one of them, FII, chooses the most likely set of parameters, conditional on the data moments. We confirm this in our Monte Carlo experiments below.

2.1 Indirect Inference on a DSGE Model

DSGE models (possibly after linearization) have the general form:

$$\begin{aligned} \begin{aligned} A_{0}E_{t}y_{t+1}= & {} A_{1}y_{t}+Bz_{t} \\ z_{t}= & {} Rz_{t-1}+\varepsilon _{t} \end{aligned} \end{aligned}$$

(1)

where $y_{t}$ contains the endogenous variables and $z_{t}$ the exogenous variables. The exogenous variables may be observable or unobservable. For example, they may be structural disturbances. We assume that $z_{t}$ may be represented by an autoregressive process with disturbances $\varepsilon _{t}$ that are $NID(0,\Sigma )$. Assuming that the conditions of Fernandez-Villaverde et al. (2007) are satisfied, the solution to this model can be represented by a VAR of form

$$\begin{aligned} \left[ \begin{array}{c} y_{t} \\ z_{t} \end{array} \right] =F\left[ \begin{array}{c} y_{t-1} \\ z_{t-1} \end{array} \right] +G\left[ \begin{array}{c} \xi _{t} \\ \varepsilon _{t} \end{array} \right] . \end{aligned}$$

(2)

where $\xi _{t}$ are innovations.

A special case of the DSGE model is where all of the exogenous variables are unobservable and may be regarded as structural shocks. An example is the Smets and Wouters (2007) US model to be examined below. This case, and its solution, can be represented as above for the complete DSGE model.

2.1.1 FII Estimation

The FII criterion is based on the difference between features of the auxiliary model (such as coefficients estimates, impulse response functions, moments or scores) obtained using data simulated from an estimated (or calibrated) DSGE model and those obtained using actual data; these differences are then represented by a Wald statistic; we call it the IIW (Indirect Inference Wald) statistic. The specification of the auxiliary model reflects the choice of descriptor variables.

If the DSGE model is correct (the null hypothesis) then, whatever the descriptors chosen, the features of the auxiliary model on which the test is based will not be significantly different whether based on simulated or actual data. The simulated data from the DSGE model are obtained by bootstrapping the model using the structural shocks implied by the given (or previously estimated) model and computed from the historical data. We estimate the auxiliary model, using both the actual data and the N samples of bootstrapped data to obtain estimates $a_{T}$ and $a_{S}(\theta _{0})$ of the vector $\alpha$. We then use a Wald statistic (WS) based on the difference between $a_{T}$, the estimates of the data descriptors derived from actual data, and $\overline{a_{S}(\theta _{0})}$, the mean of their distribution based on the simulated data, which is given by:

$$\begin{aligned} WS=(a_{T}-\overline{a_{S}(\theta _{0})})^{\prime }W^{-1}(\theta _{0})(a_{T}- \overline{a_{S}(\theta _{0})}) \end{aligned}$$

where $\theta _{0}$ is the vector of parameters of the DSGE model on the null hypothesis that it is true and $W(\theta _{0})$ is the weighting matrix. Following Guerron-Quintana et al. (2017) and Le et al. (2011, 2016), $W(\theta _{0})$ can be obtained from the variance-covariance matrix of the distribution of simulated estimates $a_{S}$

$$\begin{aligned} W(\theta _{0})=\frac{1}{N}\Sigma _{s=1}^{N}(a_{s}-\overline{a_{s}})^{\prime }(a_{s}-\overline{a_{s}}) \end{aligned}$$

(3)

where $\overline{a_{s}}=\frac{1}{N}\Sigma _{s=1}^{N}a_{s}$. WS is asymptotically a $\chi ^{2}(r)$ distribution, with the number of restrictions, r, equal to the number of elements in $a_{T}.$ An account of the detailed steps of involved in finding the Wald statistic can be found in Le et al. (2016) and Minford et al. (2016).

Estimation based on indirect inference focuses on extracting estimates of the structural parameters from estimates of the coefficients of the auxiliary model by choosing parameter values that minimise the distance between estimates of the auxiliary model based on simulated and actual data. A scalar measure of the distance may be obtained using a Wald statistic. This can be minimised using any suitable algorithm. The FII estimation may be expressed as

$$\hat{\theta }=\mathrm{argmin}\;WS(\theta )$$

(4)

Under the null hypothesis of full encompassing and some regularity conditions, Dridi et al. (2007) show the asymptotic normality of II estimator $\widehat{\varvec{\theta }}$,

$$\begin{aligned} \sqrt{T}(\widehat{\varvec{\theta }}-\varvec{\theta }_{0})\backsim N( \textbf{0},\Xi (N,W) \end{aligned}$$

(5)

with

$$\begin{aligned} \Xi (N,W)=\left\{ \frac{\partial ^{\prime }(a)}{\partial (\theta _{0})} W(\theta _{0})^{-1}\frac{\partial ^{\prime }(a)}{\partial (\theta _{0})} \right\} ^{-1}. \end{aligned}$$

(6)

$W{({\theta _{0}})}$ is the weighting matrix, which can obtained from bootstrap samples as in Eq. (3).

2.1.2 The Auxiliary Models

Le et al. (2017) show that the particular DSGE models we are examining are over-identified, so that the addition of more VAR coefficients (e.g. by raising the order of the VAR) increases the power of the test, because more nonlinear combinations of the DSGE structural coefficients need to be matched. Le et al. (2016) note that increasing the power in this way also reduces the chances of finding a tractable model that would pass the test, so that there is a trade-off for users between power and tractability. Le et al. (2016) and others (for example Minford et al. 2018; Meenagh et al. 2019; Meenagh et al. 2022) suggest the use of a three variable VAR (1) as auxiliary model. In this case, there are 9 VAR coefficients to match in the Wald statistics. Minford et al. (2016) also consider the Impulse Response Functions and simulated moments, which all have 9 elements to match in the Wald statistics, as the auxiliary model, and show that the power of the II tests when using the different auxiliary models are similar. Considering the covariance matrix and using its lower triangular elements, there are 3(3+1)/2=6 elements to compare in a three variable case.

In the Monte Carlo experiments below, we consider estimation with three different auxiliary models: 1) II using 9 VAR coefficients from a VAR(1); 2) II using 9 moments, consisting of 6 covariance elements and 3 first order autocorrelation; 3) II using the average of 6 moments, only including 6 covariance elements as a single auxiliary model of ‘targeted moments’ — where the remaining moments are left for informal checking. 4) II using the average of 9 moments as a single auxiliary model of targeted moments, where all moments are thus used for estimation. The first two of these carry out formal II estimation, while the last two are considered as informal II estimation.

2.1.3 Monte Carlo Experiments

We now perform some experiments comparing the formal and informal II estimation in small samples. The sample size is chosen as 200, which is typical for macro data. We take the Smets-Wouters (2007) model, with their estimated parameters to be the true model and generate 1000 samples of data from it. These are treated as the observed data in the II estimation. We design Monte Carlo simulation following the same approach as Le et al. (2016), Meenagh et al. (2019, 2022).

The true parameter values are from Smets and Wouters (2007), Table 4. In estimation, we start the initial parameter values by falsifying them by $10\%$ in both directions ($+/-$ alternately). We then estimate each sample and report the absolute bias and standard deviation of the II estimators. The results are reported in the Table 1, where y: real GDP, pi : inflation rate, r : real interest rate.

Table 1 Bias of II estimates by using different data descriptors

We find that the FII estimator has a very small bias. The average absolute biases of the FII estimator based on using VAR coefficients and the 9 moments as auxiliary models are $2.26\%$ and $3.02\%$ respectively.

In carrying out the III estimator, we first target only 6 moments, leaving 3 to be checked informally after estimation. We then extend the number of targeted moments to the full 9. The average bias of the III estimator, based on 6 moments as the auxiliary model, is twice to three times as large at $6.75\%$; nor is it much reduced if more moments are used, as illustrated here with 9 moments, where the bias is $6.08\%$. The informal II estimator thus has a much higher bias than the two formal II estimators. The standard deviations of the four estimators are roughly the same.

The three variables we choose follow Le et al. (2016). To check if our results are stable across different variables, we redo the Monte Carlo experiment by using three principal components of the 7 endogenous variables in Smets and Wouters (2007)’s model. The results, available on request, are similar.

2.2 Summary of Finding

A common practice in estimating parameters in DSGE models is to find a set that, when simulated, gets close to an average of certain data moments; the model’s simulated performance for other moments is then compared to the data for these as an informal test of the model. We call this procedure informal Indirect Inference, III. By contrast what we call Formal Indirect Inference, FII, chooses a set of moments as the auxiliary model and computes the Wald statistic for the joint distribution of these moments according to the structural DSGE model; it tests the model according to the probability of obtaining the data moments. The FII estimator then chooses structural parameters that maximise this probability, hence are the most likely conditional on the data moments. We show via Monte Carlo experiments that the FII estimator has low bias in small samples, whereas the III estimator has much higher bias. It follows that models estimated by III will frequently be substantially different from the true model and hence rejected by formal indirect inference tests.

3 How Should We Account For the Low Bias of the Formal Indirect Inference Estimator

We have found so far that in carrying out indirect inference, the appropriate procedure is the one we have described above and termed Formal Indirect Inference. Previous work - Le et al. (2016) and Meenagh et al. (2022) -has shown also that FIML estimation (ML for short) produces high small sample bias compared with FII, which is, by contrast, as we have seen, almost unbiased- clearly a very useful property for those using DSGE models in practice. In this final section of our paper we investigate the reason for this difference in bias between FII and ML. We suggest that it comes from the high relative power of FII in rejecting misspecified models.

In two recent surveys of indirect inference estimation Le et al. (2016) and Meenagh et al. (2019) have found by Monte Carlo experiment that in small samples the formal indirect inference (FII) test has much greater power than direct inference in its most widely used form of maximum likelihood (ML). So much so that in practice the power of the FII procedure needs to be limited by reducing the size of the auxiliary model in order to ensure finding a tractable model that can pass the test threshold. These surveys also found that in small sample estimation FII produced much lower bias than ML. Meenagh et al. (2019) noted (p.606): ‘This property (of low small sample bias) comes from the high power of the test in rejecting false parameter values.’ In this section we attempt to quantify this small sample relationship between power and bias under ML and FII.

Let us first recap each procedure. In ML the structural model is taken to the data and the estimation searches over its parameters, including those of the ARMA error processes, to minimise the sum of squared reduced form residuals.The joint likelihood of the data, conditional on the model, is maximised when this sum is minimised.

The FII method is set out in the previous section. Suppose we examine the VAR parameters, we can think of the structural model we are estimating as implying a joint normal distribution of these reduced form parameters, which we illustrate for two parameters as follows:

Fig. 1

Bivariate normal distribution with correlation of 0 and 0.9. Two possible data points shown: x=0.1, 0.9 and y=0.0

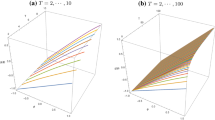
We can generate this Likelihood distribution of the two parameters, $\rho _{1}$.$\rho _{2}$, by bootstrapping the structural model with its shocks and estimating a VAR on each bootstrap. The cumulative probability of these two parameters’ squared deviation from the model’s mean prediction (the peak likelihood point) weighted by the inverse of their variance-covariance matrix, V, is represented by a chi-squared distribution where k, the degrees of freedom, is given by the number of VAR parameters. If the two parameters have a low correlation, then each is weighted by 1/its variance. The weight on $\rho _{1}$ falls relative to the other’s with a rising covariance/its variance.

On Fig. 1 above one can see the likelihood distribution of the different data-estimated reduced form coefficients, $\rho _{1}$.$\rho _{2}$, according to the model parameters — the top frame showing one with zero correlation between the two $\rho$s, the bottom frame one with a high positive correlation. In FII the parameters of the model are searched over to find those that have the highest likelihood, given the data-estimated coefficients shown by the red or blue dots; the parameters whose peak likelihood gets closest to the data dots will be the FII estimates. In ML the red or blue dots of the data are directly taken as the ML reduced form coefficients; and the model structural parameters are reverse-engineered to produce the ones closest to them.

Thus take a model $y=f(\theta ;\epsilon )$ which has a reduced form $y=v(\theta ;\epsilon )$. Assume it is identified so that there is a unique v corresponding to a particular f; thus given v we can discover f and vice versa. Suppose now on a sample $y_{0}$ we obtain an estimate $\widehat{v}(y_{0}).$ In FII we compute the likelihood of $\widehat{v}(y_{0})$ conditional on the model and the data, thus $L[\widehat{v}(y_{0})\mid y_{0},f(\theta ;\epsilon )]$; we then search over $\theta$ to find the maximum likelihood; this is the FII estimate. If unbiased, it will on average be the f corresponding to v. In general we find low bias in FII. In terms of our diagram $\widehat{v}$ is the blue or red dot and the joint distribution of the estimated model will be close to being centred around it. Now ML in principle does the same, choosing the ML values of $\theta$ that generate $\widehat{v}$ as their solution of $y_{0}=$ $f(\theta ;\epsilon ).$

It would seem therefore that the two estimates of the structural parameters should be the same. Indeed, it has been shown (e.g. by Gourieroux et al. 1993) that this is the case asymptotically, i.e. for very large samples. Both estimators are consistent in large samples, implying no bias.

However, in small samples — such as are typical in macroeconomics — they are not typically the same and we find bias in both according to our Monte Carlo experiments.

The question we wish to answer here is why the two estimates differ in small samples and the quantitative contribution of the causes.

Le et al. (2016) showed that the power of the FII and the ML-based LR tests of the model $f(\theta ;\epsilon )$ differed; specifically FII was substantially more powerful. This occurred when the FII test used as the distribution of v implied by $f(\theta ;\epsilon )$ the model-restricted distribution. If on the other hand it used the distribution of v from the reduced form data-implied distribution, then the power of FII was reduced to equality with that of LR. Thus the power of the FII test was considerably greater than that of the ML-based LR test — the reason being that the FII test used the distribution of v as restricted by the model under test, whereas the LR test used the reduced form v distribution from the data. In Fig. 2 we show a stylised illustration of this point: the figure shows the situation for the likelihood distribution of $\widehat{v}(\phi )$,the vector of auxiliary model features (ordered according to their Wald value under the model, with parameter vector $\phi$, indicated), under the restricted and unrestricted cases. To the left we see the distribution under the true model, with $\phi _{TRUE}$; to the right we see the distribution under the false model, $\phi _{FALSE}$. In the top panel this is given by the unrestricted distribution taken from the data, which is the same as the left hand distribution. In the bottom panel, it is given by the distribution generated by the false parameter model in conjunction with the errors implied by the model and the data. It can be seen that this latter distribution lies more narrowly around the central false average due to the inward pull of the false parameters on the simulations.

Fig. 2

Comparison of rejection rates of unrestricted and restricted distributions of $\widehat{v}(\phi _{FALSE})$

Table 2 shows the relative power of the FII and ML tests on a 3 variable VAR (1) and is replicated from Le et al. (2016) Table 1, where the Direct Inference column shows the results based on the LR test. What we see in this Table is that as the degree of mis-specification (the average Falsity of the model parameters) rises from 0 (True) through 1% to 20%, the rejection rate rises far more rapidly under Indirect Inference (FII) than under Direct Inference (ML). Thus once it reaches 7%, the rejection rate is already 99% under FII, but has only reached 21.6% under ML. Under ML to reject 99% requires mis-specification to be as high as 20%.

Table 2 Rejection Rates for Wald and Likelihood Ratio for 3 Variable VAR(1)

We can now turn to the implications of this greater power in FII testing for the bias that arises in estimation by FII and ML on small samples. The bias we estimate in our Monte Carlo (MC) experiments is defined as $B=E(\widehat{\theta })-\theta$, where the expectation is across all the MC pseudo-samples from the true model. We can express this definition in terms of all the possible sets of $\theta$ arranged in order of falsity, thus $B=\sum \limits _{i=\%F}(\theta _{i}-\theta )P_{i}$ where each $\theta _{i}$ is the set of parameters of $i\%$ falseness and $P_{i}$ is the frequency with which these are estimated in the MC samples. We can think of estimation by FII or ML as a process related to rejecting model parameters that fail each test respectively; if a false parameter set is rejected, it cannot become an estimate, and if not rejected for a sample, it can go on to become an estimate for that sample. We also need to know the probability for either FII or ML that, conditional on not being rejected, a parameter set $\theta$ will then be chosen as an estimate. Call these probabilities in turn $P_{1}$ for the probability of non-rejection, and $P_{2}$ for the probability of selection conditional on non-rejection. The MC experiments give us directly $P_{i1}$ as one minus the rejection rate for $\theta _{i}$, while we can obtain $P_{i}$ from our MC results directly as the proportion of estimates that are False to each extent. Then we derive $P_{i2}$ from $P_{i}=P_{i1}\times P_{i2}$. To gauge $P_{i2}$ we argue as follows: a $\theta$ parameter set that has not been rejected will still not be selected as an estimate if there is an unrejected $\theta$ of lesser falseness available instead that dominates it in the competition to become an estimate.

Table 3 shows the small sample bias of the two estimators in the Monte Carlo experiment, replicated from Table 3 from Le et al. (2016), clearly showing the big reduction in the bias under FII versus ML.

Table 3 Bias of Formal Indirect Inference and FIML

We show next the predicted two probabilities and biases for FII and ML in Table 4. For this table we have repeated the bias analysis with a fresh set of 1000 samples from the same model, yielding different absolute mean biases, as one would expect; in this set the ML bias is about the same, the FII bias rather smaller. What we see is that on average an unrejected $\theta$ is $60\%$ more likely to survive to being estimated under FII as under ML [0.42/0.26]. We suggest this is because FII has a generally higher rejection rate than ML, so that an unrejected $\theta$ faces less competition from other unrejected $\theta$, and so has a greater probability of surviving to estimation. Under ML the probability of survival is inversely correlated with the probability of non-rejection of the neighbouring $\theta$ closer to the truth: we suggest this is because the higher the chances of their non-rejection, the greater is the competition from them — see the right frame of Fig. 3. What we see under FII is different — the left frame of Fig. 3. Survival chances of false $\theta$, if unrejected, are low at the two extremes — both when close to true and when extremely false. Thus competition from better alternatives is greatest either close to the truth (when the truth is a serious rival), or very far from the truth (when the less absurdly false are serious rivals). This shift of survival probability to the extremes weakens the tendency for FII to reduce bias, by increasing the estimation chances of the middlingly false values which contribute most to the bias after taking account of rejection.

Table 4 Predicted probabilities and bias

Fig. 3

Predicted probabilities and biases for II and ML

Summarising our findings, our Monte Carlo experiments have shown that the lower bias of FII compared to ML comes primarily from a much higher rejection rate of false coefficients. This advantage is to a modest extent offset by the higher probability under FII that unrejected false coefficients will survive to become estimates. We interpret this in terms of the competition between unrejected coefficients: this is greater under ML than FII because there are more unrejected coefficients to choose from at all levels of falseness. This competition also behaves differently across the range of falseness, increasing with falseness under ML as nonrejection falls, but intensifying under FII at both extremes, either close to truth or highly false.

3.1 Summary of Findings

In this part we have reflected on the reasons that Maximum Likelihood (ML) shows both lower power and higher bias in small samples than formal Indirect Inference (FII ), drawing on the earlier work of Le et al. (2016) and Meenagh et al. (2019), based on extensive Monte Carlo experiments. It emerges from this work that when ML is being used, the likelihood distribution of $\widehat{v}$, the auxiliary parameter vector from the model under test, has a variance given by the unrestricted distribution of the errors whereas when FII is used it is given by the variance of their distribution as restricted by the $\theta$ of the model being tested, which is much smaller. This is the source of the higher power of FII, as explained by Le et al. (2016). This in turn implies that FII will have lower bias, because as sample data from the true model varies, false parameter values will be rejected much more frequently under FII ; this greater rejection frequency is partly offset by a lower tendency for ML to choose unrejected false parameters as estimates, due again to its lower power allowing greater competition from rival unrejected parameter sets.

4 Conclusions

In practice macroeconomic researchers use a variety of estimators to parameterise their models empirically and get as close as possible to what the data implies is the true model. One such is FIML; another is a form of indirect inference we term ‘informal’ under which data features are ‘targeted’ by the model — i.e. parameters are chosen so that model-simulated features replicate the data features closely. In this paper we show, based on Monte Carlo experiments, that in the small samples prevalent in macro data, both these methods produce high bias, while formal indirect inference, in which the joint probability of the data-generated auxiliary model is maximised under the model simulated distribution, produces low bias. We also show that FII gets this low bias from its high power in rejecting misspecified models, which comes in turn from the fact that this distribution is restricted by the model-specified parameters, so sharply distinguishing it from rival misspecified models.

We think our findings here have important practical implications for the estimation of structural macroeconomic models on the limited, small sample, macro data typically available. To obtain estimates with low bias Formal Indirect Inference should be used, with its considerable power in rejecting misspecified models¹.