Global Shocks in the US Economy: Effects on Output and the Real Exchange Rate

Abstract

This paper studies the effects of global shocks, relative to domestic shocks (productivity, mark-up, and demand shocks), in accounting for US business cycle fluctuations. We do this by developing and estimating a two-sector open economy dynamic stochastic general equilibrium model that features several real frictions and structural shocks. The central finding from the estimated model is that global shocks are the main driver of movements in many US macroeconomic aggregates. Particularly, we find that they explain around 40% of the variations in our main variables of interest—output and real exchange rate. This important quantitative contribution is achieved by using indirect inference estimation techniques to test the model. We identify exogenous world demand, oil price shocks, preference for exported energy-intensive goods, and the price of imported energy-intensive goods as the global shocks most prominent in causing the largest variations in economic outcomes. By contrast, foreign interest rates and preference for aggregate exported goods are found to be bystanders.

1 Introduction

How important are global shocks for economic fluctuations? Which kind of global shocks can most account for observed business cycles? How big are the impacts of domestic shocks, as captured by productivity, mark-up, and demand shocks, as sources of variation in real economic activities, once we allow for global shocks? For any country, obtaining answers to these questions is fundamental to designing and implementing relevant macroeconomic and regulatory policies. The focus of our analysis in this paper is the US. In particular, we examine to what extent US output and real exchange rate are driven by global shocks, and to what extent they are caused by domestic shocks. As the world’s largest economic power, most existing theoretical and empirical studies tend to treat the US as the source of external shocks for other countries (e.g., Belke et al. 2019; Canova 2005; Justiniano and Preston 2010; Kazi et al. 2013; Kim 2001; Schmitt-Grohé 1998). Yet, history shows us that the US itself is not immune to disturbances originating from abroad (e.g., the Arab-Israeli war of the early 1970s and the East Asian crisis of 1997-98). Our goal in this paper is to contribute to this line of discourse by using an estimated two-sector open economy dynamic stochastic general equilibrium (DSGE) model to structurally account for the size of the effects of global shocks on the US economy.

Our paper has two main contributions. First, our theoretical analysis builds on a two-sector open economy DSGE model first presented in Meenagh et al. (2015). In order to establish whether the US economy experiences energy business cycles, these authors advanced a novel two-sector model of the US with varying intensities of oil demand in production that also incorporates a high number of real frictions and shocks. Besides, the model allows for two types (energy-intensive and non-energy intensive) of final goods and a commodity (crude oil) to be traded on the world markets. From a modelling perspective, this was a notable contribution to the DSGE literature because previous work on this topic had generally been based on one-sector one-good autarky model except for oil imports (e.g., Dhawan and Jeske 2008; Kim and Loungani 1992).¹ Our paper extends their model in two distinct ways: (i) we let households have access to both home and foreign bonds, and (ii) we include ten more structural shocks in the version that we use in this paper.²

The paper’s second contribution is that the model is tested and estimated by the method of indirect inference on unfiltered data.³ In testing, we apply the indirect inference procedure to a set of initial parameters put forward as true for our model, and ask: could these coefficients, within this model framework, be the true model generating the data? Of course, only one true model with one set of coefficients is feasible. Nevertheless, we may have chosen coefficients that are not precisely right numerically so that the same model with other coefficient values could be correct. Only when we have evaluated the model with all coefficient values that are credible within the model theory will we have adequately tested it. Hence, in estimation, we further utilise our indirect inference procedure to seek alternative coefficient sets that could do better in duplicating US macroeconomy features. The primary reason why we favour the use of indirect inference is that it involves a powerful test of the model on the data. On this basis, we are able to say categorically that the model fits the data. As our empirical approach is less popular, we elaborate on it further in Sect 3. In addition, the use of unfiltered data allows us to add non-stationary shocks. So, beyond the theoretical refinements of Meenagh et al. (2015), we have also improved empirically on their work. As a result, our model can more appropriately mimic the dynamic properties of the US and the rest of the world data over the period under study.

To preview our results, employing a two-equation VARX(1) of output and real exchange rate, we find that the model is not rejected and is able to reproduce the features of the US data jointly, passing the Wald test with a p-value of 0.063. The central result that we document is the pivotal role of global shocks on US economic fluctuations. According to the estimated model, global shocks explain nearly 40% of the variances of US output and real exchange rate, as well as the variations in consumption, labour hours, and foreign bonds. Furthermore, global shocks account for well over 50% of the variabilities in the remaining macroeconomic aggregates: investment, imports, exports, wages, interest rate, and oil use. Unbundling global shocks, the results of the structural variance decomposition indicate that exogenous world demand and oil price shocks are the most important driving variables; these are followed by the preference for exported energy-intensive goods and the price of imported energy-intensive goods. Of the six global shocks modelled, the only two with negligible contributions to the US business cycle behaviour are the preference for aggregate exported goods and foreign interest rates. Using historical decomposition, we also show that global shocks were dominant in causing changes to US output and real exchange rate. Then, in an application motivated by the continuing debate in the existing literature about the importance of oil price shocks, we use the estimated model to predict the frequency of occurrence of output expansions and contractions in the presence (absence) of oil crisis for the US economy.

Our modelling strategy is derived broadly in the tradition of early international real business cycle (IRBC) literature (e.g., Ahmed et al. 1993; Backus et al. 1992, 1995; Baxter and Crucini 1995; Dellas 1986; Stockman and Tesar 1995). The main departures of our paper from that literature are two. First, we have adopted the assumption of incomplete asset markets to limit the degree of risk-sharing across countries implied by the structure of models in the early IRBC literature. In this regard, our model is in the fashion of the new open economy macroeconomics (NOEM) literature (e.g., Adolfson et al. 2007; Justiniano and Preston 2010). Second, the foundational element of the production structure in our model is in the spirit of Kim and Loungani (1992), who extended Kydland and Prescott’s (1982) model to allow a role for energy price shocks. Building on their approach, an added feature of our model is that we disaggregate the US economy into energy-intensive and non-energy intensive sectors, with both producing goods that are tradeable internationally. Consequently, we are able to study the business cycle implications of global and domestic shocks for US aggregate and disaggregate macroeconomic data.

The rest of the paper proceeds as follows. Section 2 describes our two-sector open economy DSGE model. Section 3 discusses the unfiltered data and the estimation methodology. Section 4 contains our findings. The final section concludes with a summary of the paper’s findings, policy implications, and suggestions for future research.

2 Model

In this section, we outline the model framework adopted in our analysis of the effects of global shocks on output and real exchange rate. The model structure (based on Meenagh et al. (2015)) combines several features of the models developed in Kim and Loungani (1992) and Backus et al. (1995). Similar to those papers, for example, we retain the intertemporal utility-maximizing behaviour of households and the perfectly competitive profit-maximizing nature of firms. Particularly, we allow production to involve energy demand, as in Kim and Loungani (1992). Additionally, we closely follow the model of Backus et al. (1995) and Bodenstein et al. (2011) along a two-country substructure to build a two-sector open economy DSGE model. Thus, there are two economic blocks in the model setup. We take the US to represent the home economy, and the rest of the world (ROW) to constitute the foreign economy. Our discussion focuses on key economic decisions of the US, which we assume to consist of four agents: firms, households, a government and traders. The foreign economy (taken to be exogenous) is assumed to have equal numbers of counterpart agents that are making equivalent choices. Following the now standard practice in the DSGE literature, we have also added an array of real rigidities, such as consumption habit formation, capital adjustment costs and variable capital utilisation rate, that are emphasised in many benchmark models (Christiano et al. 2005; Smets and Wouters 2007). For brevity, we present the specific functional forms on technologies and preferences, together with the decision problems faced by firms, households, and traders. We also show that the behaviour of the government is fully Ricardian. For full log-linearized model listing, the reader is referred to Sect. A of the Online Appendix. In what follows, $i\in \left\{H, F\right\}$ (H designates the home economy and F the foreign economy) and $j\in \left\{E, N\right\}$ (E signifies energy-intensive sector and N the non-energy intensive sector) will be utilised when we need to distinguish between economies and sectors, respectively.

2.1 Firms

The total output of the US economy in period t, ${Y}_{t}$, is given as the sum of the gross outputs of the energy-intensive, ${Y}_{E,t}$, and the non-energy intensive, ${Y}_{N,t}$, sectors:

$${Y}_{t}={Y}_{E,t}+{Y}_{N,t}$$

(1)

where, in each sector, there exists a continuum of identical, profit-maximising firms occupying the interval $\left[0, 1\right]$. The US sectoral outputs, ${Y}_{j,t}$, are produced using the constant elasticity of substitution (CES) technology that employs three factors:

$${Y}_{j,t}={A}_{j,t}{L}_{j,t}^{1-{\alpha }_{j}}{\left[{\theta }_{j}{\left({{U}_{j,t}K}_{j,t-1}\right)}^{-{\nu }_{j}}+\left(1-{\theta }_{j}\right){\left({{Q}_{j,t}O}_{j,t}\right)}^{-{\nu }_{j}}\right]}^{-\frac{{\alpha }_{j}}{{\nu }_{j}}}$$

(2)

where ${\alpha }_{j}, {\theta }_{j}\in \left(0, 1\right)$ and ${\nu }_{j}\in \left(0, \infty \right)$ are technology parameters that capture output elasticity of labour hours ($1-{\alpha }_{j}$), weight of capital services in production, and elasticity of substitution in production, respectively. ${L}_{j,t}$, ${U}_{j,t}{K}_{j,t-1}$, and ${O}_{j,t}$ represent labour hours, capital services (with ${U}_{j,t}$ denoting variable capital utilisation rate and ${K}_{j,t-1}$ the quantity of physical capital at the end of period $t-1$), and oil use, respectively; ${A}_{j,t}$ is sector-specific productivity shock and, motivated by Nordhaus et al. (1980), ${Q}_{j,t}$ is sector-specific oil efficiency shock—this type of shock captures the effect of exogenous stochastic factors that may additionally affect the intensity with which energy is used.

The period t profits of firms in each sector can be summarised by: ${\Pi }_{j,t}={P}_{j,t}{Y}_{j,t}-\left({W}_{t}+{\xi }_{j,t}\right){L}_{j,t}-\left({R}_{j,t}+{\vartheta }_{j,t}\right){{U}_{j,t}K}_{j,t-1}-{{P}_{O,t}O}_{j,t}$, where ${P}_{j,t}$, ${W}_{t}$, ${R}_{j,t}$, and ${P}_{O,t}$ are, respectively, the relative prices of sectoral goods, real wage rate, real rental rate of sectoral capital services, and the exogenous real world price of oil. ${\xi }_{j,t}$ is exogenous wage bill shifter and ${\vartheta }_{j,t}$ is exogenous capital cost shifter. Note that aggregate demand for oil in the economy is taken to be the sum of the sectoral oil demands: ${O}_{t}={O}_{E,t}+{O}_{N,t}$.

2.2 Households

The US is assumed to be populated by a continuum of identical, infinitely lived households occupying the interval $\left[0, 1\right]$. Their lifetime utility function is described by:

$${E}_{t}\sum_{t=0}^{\infty }{\beta }^{t}{\tau }_{t}\left[\frac{{\left({C}_{t}-{\iota C}_{t-1}\right)}^{1-\sigma }}{1-\sigma }-{\zeta }_{t}\frac{{\left({L}_{t}\right)}^{1+\omega }}{1+\omega }\right]$$

(3)

where $\beta , \iota \in \left(0, 1\right)$, and $\sigma , \omega \ge 0$ are preference parameters that denote the discount factor, consumption habit formation, the inverse of intertemporal elasticity of substitution, and the inverse of Frisch elasticity of labour supply, respectively. ${C}_{t}$ is consumption, ${L}_{t}={L}_{E,t}+{L}_{N,t}$ is total labour hours, ${\tau }_{t}$ is the intertemporal preference shock, and ${\zeta }_{t}$ is the labour supply shock.

Households add to their stocks of sectoral physical capital by investing in corresponding capital goods, ${I}_{j,t}$. The law of motion for physical capital stock in sector j can thus be written as:

$${K}_{j,t}=\left(1-\delta \left({U}_{j,t}\right)\right){K}_{j,t-1}+{{Z}_{j,t}I}_{j,t}-{AC}_{j,t}^{K}$$

(4)

with $\delta \left({U}_{j,t}\right)={\delta }_{j,0}+{\delta }_{j,1}{\left({U}_{j,t}\right)}^{{\delta }_{j,2}}/{\delta }_{j,2}$ and ${AC}_{j,t}^{K}={\psi }_{j}{\left({K}_{j,t}/{K}_{j,t-1}-1\right)}^{2}{K}_{j,t-1}/2$ denoting the time-varying depreciation rates and the capital adjustment costs, respectively (Basu and Kimball 1997; Dhawan and Jeske 2008), where ${\delta }_{j,0}, {\psi }_{j}\ge 0$, ${\delta }_{j,1}>0$, and ${\delta }_{j,2}>1$. ${Z}_{j,t}$ is sector-specific investment technology shock. From this, total investment is: ${I}_{t}={I}_{E,t}+{I}_{N,t}$. Households rent these capital stocks to firms in the two sectors. They also hold US (foreign) bonds denoted by ${B}_{t-1}$ (${B}_{F,t-1}$), earning gross returns ${R}_{t-1}$ (${R}_{F,t-1}$), and receive profits, ${\Pi }_{t}={\Pi }_{j,t}+{\Pi }_{T,t}$, from firms and traders.

On the assumption that the income of households covers their expenses, their flow budget constraint in real terms is:

$$\begin{aligned}{W}_{t}{L}_{t}&+{R}_{t-1}{B}_{t-1}+{R}_{F,t-1}{B}_{F,t-1}/{P}_{t}+{{R}_{E,t}{U}_{E,t}K}_{E,t-1}+{{R}_{N,t}{U}_{N,t}K}_{N,t-1}+{\Pi }_{t}\ge {C}_{t}\\&+{I}_{t}+{T}_{t}+{B}_{t}+{B}_{F,t}/{P}_{t}+{AC}_{F,t}^{B}/{P}_{t}\end{aligned}$$

(5)

where ${P}_{t}$ is the consumer price index (CPI) in the US (or the real exchange rate, with ${P}_{F,t}$, the consumer price index in the foreign economy, being the numeraire), ${T}_{t}$ is a lump-sum transfer, and following Schmitt-Grohé and Uribe (2003), we specify adjustment costs for procuring additional foreign bonds to be quadratic ${AC}_{F,t}^{B}={\psi }_{F}{\left({B}_{F,t}-{B}_{F}\right)}^{2}/2$ (with ${\psi }_{F}\ge 0$, the adjustment cost parameter, and ${B}_{F}$, the steady state level of foreign bonds).

2.3 US Government

The exogenous government spending takes up a fraction of domestic absorption; this is achieved by borrowing from the households and levying taxes on them. Thus, the government balances its budget in each period t:

$${G}_{t}={T}_{t}+{B}_{t}-{R}_{t-1}{B}_{t-1}$$

(6)

Implicit in the above budget constraint is that government debt does not change over time: ${B}_{t-1}={B}_{t}$.

2.4 Traders

Following the approach of Backus et al. (1995), we now assume that goods produced in the two sectors of the US economy are imperfect substitutes for similar goods originating from the counterpart sectors in the foreign economy. The innovation of our model is that we have two goods from each country rather than one. On this basis, consumption, investment, and government spending in both economies are assumed to be composites of four goods. For the US, the respective definitions are:

$${C}_{t}={\Phi }_{C}\left({C}_{i,t}^{j}\right)$$

(7)

$${I}_{t}={\Phi }_{I}\left({I}_{i,t}^{j}\right)$$

(8)

and

$${G}_{t}={\Phi }_{G}\left({G}_{i,t}^{j}\right)$$

(9)

where the aggregator functions ${\Phi }_{C}$, ${\Phi }_{I}$, and ${\Phi }_{G}$ (and all the ones defined hereafter) are assumed to be increasing and homogeneous-of-degree-one in their arguments. This aggregation approach is due to Armington (1969); see Feenstra et al. (2018) for a recent exposition.

Meanwhile, to retain our focus on the effects of global shocks on aggregate economic activities, we use total expenditures by US households and government. Formally, this is given as:

$${D}_{t}={C}_{t}+{I}_{t}+{G}_{t}$$

(10)

where ${D}_{t}$ is domestic absorption (and can now be interpreted as a composite of the four final goods in this world economy). Hence, we can write that:

$${D}_{t}={\Phi }_{D}\left({D}_{H,t}, {M}_{t}\right)$$

(11)

with ${\Phi }_{D}\left(.\right)={({\kappa }^{1/\phi }({{D}_{H,t})}^{\left(\phi -1\right)/\phi }+{(1-\kappa )}^{1/\phi }{\varpi }_{t}({{M}_{t})}^{\left(\phi -1\right)/\phi })}^{\phi /(\phi -1)}$. ${D}_{H,t}$ is domestic absorption of goods produced in the US, ${M}_{t}$ is total imports, and ${\varpi }_{t}$ is exogenous preference for aggregate imports; $\phi >0$ is the elasticity of substitution between home and foreign goods, and $\kappa \in (0, 1)$ is the home bias parameter.

As shown by Backus et al. (1995), the aggregator function (${\Phi }_{D}$) is sufficient for use if one is modelling two countries with two goods as they did. We, however, need further disaggregation since we have a model of two countries and four goods. We achieve this by defining US domestic absorption and aggregate imports of goods as functions of energy-intensive and non-energy intensive goods:

$${D}_{t}={\Gamma }_{D}\left({D}_{j,t}\right)$$

(12)

and

$${M}_{t}={\Gamma }_{M}\left({M}_{j,t}\right)$$

(13)

with ${\Gamma }_{D}\left(.\right)={({\lambda }^{1/\mu }{\gamma }_{t}({{D}_{E,t})}^{\left(\mu -1\right)/\mu }+{(1-\lambda )}^{1/\mu }({{D}_{N,t})}^{\left(\mu -1\right)/\mu })}^{\mu /(\mu -1)}$ and ${\Gamma }_{M}\left(.\right)={({\chi }^{1/\varrho }{\varphi }_{t}({{M}_{E,t})}^{\left(\varrho -1\right)/\varrho }+{(1-\chi )}^{1/\varrho }({{M}_{N,t})}^{\left(\varrho -1\right)/\varrho })}^{\varrho /(\varrho -1)}$. ${D}_{j,t}$ and ${M}_{j,t}$ are, respectively, the total demand of US households and government of sector j goods produced in home and foreign economies; $\mu , \varrho >0$ are the elasticity of substitution parameters across the sectoral goods, and $\lambda , \chi \in (0, 1)$ are the bias parameters for the energy-intensive goods. Lastly, ${\gamma }_{t}$ and ${\varphi }_{t}$ denote the respective exogenous preferences for energy-intensive goods produced in home and foreign economies.

The profits of traders are composed of three parts: ${\Pi }_{T,t}={\Pi }_{{\Phi }_{D},t}+{\Pi }_{{\Gamma }_{D},t}+{\Pi }_{{\Gamma }_{M},t}$, with ${\Pi }_{{\Phi }_{D},t}={P}_{t}{D}_{t}-{{P}_{H,t}D}_{H,t}-{M}_{t},$ ${\Pi }_{{\Gamma }_{D},t}={P}_{t}{D}_{t}-{{P}_{E,t}D}_{E,t}-{{P}_{N,t}D}_{N,t}$, and ${\Pi }_{{\Gamma }_{M},t}={M}_{t}-{P}_{E,t}^{F}{M}_{E,t}-{P}_{N,t}^{F}{M}_{N,t}$. We define US CPI (real exchange rate) as ${P}_{t}={(\lambda {\left({\gamma }_{t}\right)}^{\mu }({{P}_{E,t})}^{1-\mu }+(1-\lambda )({{P}_{N,t})}^{1-\mu })}^{1/(1-\mu )}$. The other price that showed up in the solved (log-linearized) model is the exogenous world price of imported energy-intensive goods, ${P}_{E,t}^{F}$. ${P}_{H,t}$ and ${P}_{N,t}^{F}$, which are, respectively, the price index of composite goods produced in the home economy and the exogenous world price of non-energy intensive goods, do not enter into the equations used for model simulation.⁴

While all the agents (firms, households, the government, and traders) in the foreign economy are making decisions symmetric to those presented above for the US economy, the two equilibrium conditions that will suffice to complete the characterisation of trade transactions concern aggregate imports and imports of energy-intensive goods by traders in the foreign economy. In what follows, all variables and parameters, though written for the foreign economy, have identical meanings to their home economy equivalents, such that we only elaborate on key ones. To begin with, we assume that the exogenous total foreign absorption, ${D}_{F,t}$, can analogously be written as: ${D}_{F,t}={C}_{F,t}+{I}_{F,t}+{G}_{F,t}$. Noting first that ${D}_{F,t}$ is a composite of foreign and US goods, we can write that: ${D}_{F,t}={\Phi }_{{D}_{F}}\left({D}_{W,t}, {M}_{F,t}\right)={\Phi }_{{D}_{F}}\left({D}_{W,t}, {X}_{t}\right)$, where ${D}_{W,t}$ is the foreign absorption of goods produced in the ROW, and ${M}_{F,t}={X}_{t}$ is either total imports (from the standpoint of foreign traders) or total exports (from the viewpoint of US traders). We can then write that: ${\Phi }_{{D}_{F}}\left(.\right)={({\left({\kappa }_{F}\right)}^{1/{\phi }_{F}}({{D}_{W,t})}^{\left({\phi }_{F}-1\right)/{\phi }_{F}}+{(1-{\kappa }_{F})}^{1/{\phi }_{F}}{\varpi }_{F,t}({{X}_{t})}^{\left({\phi }_{F}-1\right)/{\phi }_{F}})}^{{\phi }_{F}/({\phi }_{F}-1)}$, using the latter anatomization.

Moreover, our discussion so far dictates that ${D}_{F,t}$ is likewise a composite of four types of goods. Hence, we cast an expression for US exports as:

$${X}_{t}={\Gamma }_{X}\left({X}_{j,t}\right)$$

(14)

where ${\Gamma }_{X}\left(.\right)={({\left({\chi }_{F}\right)}^{1/{\varrho }_{F}}{\varphi }_{F,t}({{X}_{E,t})}^{\left({\varrho }_{F}-1\right)/{\varrho }_{F}}+{(1-{\chi }_{F})}^{1/{\varrho }_{F}}({{X}_{N,t})}^{\left({\varrho }_{F}-1\right)/{\varrho }_{F}})}^{{\varrho }_{F}/({\varrho }_{F}-1)}$.

2.5 Aggregation, Exogenous Processes, and Competitive Equilibrium

The market clears for energy-intensive goods:

$${Y}_{E,t}={D}_{E,t}+{X}_{E,t}-{M}_{E,t}$$

(15)

where, by Walras’ Law, the market also clears for non-energy intensive goods. The aggregate resource constraint in the home economy is satisfied by:

$${Y}_{t}={C}_{t}+{I}_{t}+{G}_{t}+{X}_{t}-{M}_{t}-{P}_{O,t}{O}_{t}$$

(16)

Furthermore, the dynamics of the current account implies that the market for foreign bonds is cleared by:

$${B}_{F,t}={R}_{F,t-1}{B}_{F,t-1}+{P}_{t}{X}_{t}-{M}_{t}-{P}_{O,t}{O}_{t}$$

(17)

Turning now to the exogenous shocks in our model, we note that there are twenty-two of them. A number of these shocks can be directly observed in the data (government spending, world demand, foreign interest rate, oil price, and the price of imported energy-intensive goods); see Sect. 3.2 below for further discussion. The remaining shocks are wedges in the model’s equilibrium equations (e.g., intertemporal preference, labour supply, and sectoral productivity shocks);⁵ these ones are derived as residuals (the difference between data and model).⁶ As our data are unfiltered, we carry out tests of stationarity for all shocks (see Sect. B of the Online Appendix). Based on the tests’ results, we treat one half of the shocks as stationary (or trend-stationary) and the remaining one half as non-stationary. We model the former group of shocks as AR(1) processes in levels:

$${\varepsilon }_{{s}_{1},t}={\rho }_{{s}_{1}}{\varepsilon }_{{s}_{1},t-1}+{\eta }_{{s}_{1},t}$$

(18)

for ${s}_{1}=\left\{{\tau }_{t}, {\zeta }_{t}, {R}_{F,t}, {Z}_{j,t}, {\vartheta }_{j,t}, {Q}_{j,t},{\varpi }_{t}, {\varpi }_{F,t}\right\}$. Whereas the non-stationary shocks are estimated using AR(1) processes in first differences:

$$\Delta {\varepsilon }_{{s}_{2},t}={\rho }_{{s}_{2}}\Delta {\varepsilon }_{{s}_{2},t-1}+{\eta }_{{s}_{2},t}$$

(19)

for ${s}_{2}=\left\{{\xi }_{j,t}, {P}_{O,t}, {A}_{j,t}, {G}_{t}, {\gamma }_{t}, {P}_{E,t}^{F}, {\varphi }_{t}, {\varphi }_{F,t}, {D}_{F,t}\right\}$. In equations (18) and (19), the innovations ${\eta }_{{s}_{1},t}$ and ${\eta }_{{s}_{2},t}$ are mutually independent, serially uncorrelated, and normally distributed with mean zero and variances ${\sigma }_{{s}_{1}}^{2}$ and ${\sigma }_{{s}_{2}}^{2}$, respectively.

Finally, an equilibrium is a set of endogenous stochastic processes for quantities and prices ${\left\{{C}_{t}, {L}_{t}, {L}_{j,t}, {B}_{F,t}, {I}_{t},{I}_{j,t}, {U}_{j,t}, {K}_{j,t}, {Y}_{t},{Y}_{j,t},{O}_{t},{O}_{j,t},{D}_{t},{D}_{E,t},{M}_{t},{M}_{E,t},{X}_{t},{X}_{E,t},{P}_{t},{P}_{j,t},{W}_{t},{R}_{t}, {R}_{j,t}\right\}}_{t=0}^{\infty }$, such that given the initial conditions for consumption (${C}_{t-1})$, bonds (${B}_{t-1}, {B}_{F,t-1}$), capital $({K}_{j,t-1}$), and the realisations of a set of exogenous stochastic processes driving the model ${\left\{{\tau }_{t}, {\zeta }_{t}, {R}_{F,t}, {Z}_{j,t}, {\vartheta }_{j,t}, {Q}_{j,t},{\varpi }_{t}, {\varpi }_{F,t}, {\xi }_{j,t}, {P}_{O,t}, {A}_{j,t}, {G}_{t}, {\gamma }_{t}, {P}_{E,t}^{F}, {\varphi }_{t}, {\varphi }_{F,t}, {D}_{F,t}\right\}}_{t=0}^{\infty }$, firms maximise their profits given the prices, households maximise their utility given the prices, traders maximise their profits given the prices, the government’s budget constraint is met, and all markets clear.

3 Estimation

3.1 Data

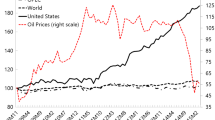
The model is estimated on US annual data over the 1949-2013 period. The constructed dataset includes 29 observations, falling within four categories: (i) the aggregate and sectoral measures on output, investment, labour hours, oil use, and prices of goods, (ii) the time series for consumption, wages, interest rate, and foreign bonds, (iii) the aggregate and energy-intensive sector measures of exports, imports, and domestic absorption, and (iv) the sectoral measures on capital stock and capital utilisation rate. Details on the data sources and construction of the variables are described in Sect. C of the Online Appendix. Fig. 1 depicts US unfiltered data.

Fig. 1

US unfiltered data used for estimation (1949-2013)

3.2 Indirect Inference

Indirect inference techniques from Le et al. (2011) are employed in estimating our model. Meenagh et al. (2012) extend this methodology to non-stationary data, which is more suited to our purpose. Furthermore, Le et al. (2016) provide a detailed account of their application to DSGE models. Adopting the canonical US model of Smets and Wouters (2007) as the ‘true’ one, these authors establish, via Monte Carlo experiments, that indirect inference methodology achieves low bias and larger power in small samples compared to the other main frequentist estimation technique, classical Maximum Likelihood. As a frequentist method, it also does not rely on priors, which in macroeconomics remain controversial, because for some coefficients we may not have a strong understanding of what the priors should be. To make progress in building up support for modelling approaches, we require a method that tests the model against the data, without appeal to priors. The advantage of using indirect inference is that it provides a highly powerful test of our model against the data. In the rest of this section, we give a brief description of the intuition behind the method of indirect inference and its estimation procedures.

The notion of indirect inference is built on choosing parameter sets ${\theta }_{0}$ to minimise the distance between coefficients generated from simulated data and those obtained from actual data. The simulated data are computed by bootstrap simulations of our DSGE model. The description of the data properties is done by means of an auxiliary model. In practice, our choice of the auxiliary model for testing by indirect inference draws on the fact that the solution to a log-linearised DSGE model can be represented as a restricted vector autoregressive moving average (VARMA) model either in levels, if the shocks are stationary, or in first differences, if the shocks are permanent, and that this can be approximated by a VAR. Moreover, rational expectations are generated as the solution to the model, based on the VAR (e.g., Del Negro and Schorfheide 2004, 2006; Canova 2007; Dave and DeJong 2007; Del Negro et al. 2007). With unfiltered data, the auxiliary model is taken to be a vector error correction model (VECM). For a structural model like ours, this can be written as a VARX(1) for the macroeconomic variables of interest:

$${\widetilde{w}}_{t}={[I-\mathcal{F}]\widetilde{w}}_{t-1}+{\Upsilon \overline{x} }_{t-1}+\pi t+{\upsilon }_{t}$$

(20)

where ${\overline{x} }_{t-1}$ are stochastic trends, $\pi t$ are deterministic trends, and ${\upsilon }_{t}$ are VECM innovations. The derivation of the above representation of the auxiliary model is contained in Sect. D of the Online Appendix.

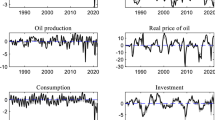
The implementation of indirect inference estimation involves three steps.⁷ First, the residuals and innovations of the structural DSGE model in Sect. 2 are computed based on actual data and model parameters ${\theta }_{0}$. As stated earlier in Sect. 2.5, five exogenous variables are observed in the actual data, while the remaining structural shocks are to be backed out directly as errors using the model equations and actual data. Fig. 2 shows the single equation residuals (based on estimated parameters; see Sect. 4 for details); Fig. 3 displays the accompanying estimated innovations that are employed to shock the model. Second, simulated data are generated from the DSGE model; this is done by bootstrapping its estimated innovations to obtain $S=1000$ independent samples. Third and finally, our auxiliary model is estimated for all data samples (actual and simulated). When applied to the simulated data, the variance-covariance matrix $\Omega$ of the distribution implied for the model’s coefficient vectors ${a}_{s} \left(s=1, \dots , S\right)$ is obtained. The resulting Wald statistic $WS$ is given by:

$$WS={\left({a}_{T}-\overline{{a }_{S}\left({\theta }_{0}\right)}\right)}^{^{\prime}}\Omega {\left({\theta }_{0}\right)}^{-1}\left({a}_{T}-\overline{{a }_{S}\left({\theta }_{0}\right)}\right)$$

(21)

where ${a}_{T}$ is the estimated vector of coefficients from actual US data, $\overline{{a }_{S}\left({\theta }_{0}\right)}$ is the mean of the estimated vector of coefficients from model-based data, and $\Omega {\left({\theta }_{0}\right)}^{-1}$ is the inverse of the estimated variance-covariance matrix. The task before us when using indirect inference techniques is that of judging the proximity of the restricted reduced-form VARX(1) approximation derived from the model to the unrestricted counterparts calculated from the data (i.e., $\left({a}_{T}-\overline{{a }_{S}\left({\theta }_{0}\right)}\right)$). The inference is based on the above Wald statistic, which tests the model in total against the data. Here, we have chosen a test threshold of 5% so that VARX(1) coefficients of actual data with a Wald percentile above 95% will mark rejection. We also present this information using transformed Mahalanobis distance and p-value ($=1- \mathrm{Wald percentile}/100$).

Fig. 2

Residuals

Fig. 3

Innovations

We note that the estimation by indirect inference is carried out by using a powerful search algorithm based on simulated annealing in which a search takes place over a wide range around the initial values, with an optimising search accompanied by random jumps around the suggested parameter space. We use calibrated values as the initial points for the search algorithm; the aim of the search is to find optimal coefficient sets that will make the model not to be rejected by the data. In the Online Appendix, Sect. E provides additional discussion on simulated annealing and Sect. F reports the initial values used to initiate the search procedure.

In our empirical analysis, meanwhile, we are concerned with whether the model can fit the main macroeconomic variables of interest. For our purpose, this is a combination of output and the real exchange rate; we select to estimate a VARX(1) on them with time trends and several shocks with unit roots. By doing this, we are utilising what Le et al. (2011) labelled a ‘directed’ Wald evaluation approach. Besides, we have chosen to cap the number of macroeconomic variables at 2 and the VAR order at 1 because of the power of indirect inference testing procedure, which needs to be high to achieve discrimination between models; but not so high that only almost exactly accurate models can pass. Indirect inference is a test of whether the parameters can be matched jointly, taking also into account the dynamics of all non-stationary shocks, rather than just those of output and the real exchange rate individually. As the number of variables and the VAR order are raised, so is the power of the test. Past work has found by Monte Carlo experiment that a VAR(1) with two variables typically gives the right level of power for testing macro models (Le et al. 2016; Meenagh et al. 2019).

4 Findings

4.1 Estimation Results

Indirect inference estimates of the structural parameters and the corresponding Wald test results are reported in Table 1. The inverse of Frisch elasticity of labour supply, $\upomega$, is 6.03, which indicates that labour hours react more to changes in the real wage. The inverse of intertemporal elasticity of substitution, $\sigma$, of 1.24 found here implies that households are more willing to spread consumption across time in response to a change in real interest rate. The estimated elasticity of substitution between capital services and oil use in both sectors (${\nu }_{E}$ and ${\nu }_{N}$) are similar: 0.29 in the energy-intensive sector and 0.27 in the non-energy intensive sector. These values mean that there are high elasticities of substitution between the two factors in both sectors. Output elasticities of labour hours are sizable in the two sectors, with $1-{\alpha }_{E}=0.75$ and $1-{\alpha }_{N}=0.63$. The estimated value of consumption habit formation parameter, $\iota$, is 0.3, which, although lower compared to estimates in existing literature employing closed-economy models (e.g., Merola 2015; Smets and Wouters 2007), is in accord with open-economy analyses (e.g., Justiniano and Preston 2010; Matheson 2010).

Table 1 Indirect inference estimates of structural parameters

Further, the estimates of the marginal costs of capital utilisation in the energy-intensive and non-energy intensive sectors, ${\delta }_{j,1}{u}_{j}^{{\delta }_{j,2}}$ (denoted by ${\delta }_{j}$), are 3% and 6%, respectively. These estimates indicate that return to investment in the non-energy intensive sector is higher than in the energy-intensive sector. The estimate of the elasticity of capital utilisation rate is lower in the energy-intensive sector (${\delta }_{E,2}=1.90$) than in the non-energy intensive sector (${\delta }_{N,2}=4.72$). Adjustment cost parameters for sectoral stocks of physical capital and foreign bonds are all estimated to be close to zero. We find that the elasticity of substitution between absorption of home-produced goods in the US and the imports of foreign goods is larger ($\phi =0.97$), being more than double that between foreign economy’s absorption of its own goods and US exports (${\phi }_{F}=0.43$). The elasticities of substitution between the components (energy-intensive and non-energy intensive goods) of each of total imports and total exports are, however, much smaller ($\varrho =0.07$ and ${\varrho }_{F}=0.04$). The model estimates of the elasticity of substitution between the absorption of energy-intensive and non-energy intensive goods in the US, $\mu$, is 0.44. The bias parameter for energy-intensive goods in the US is estimated to be low ($\lambda =0.26$).

Meanwhile, the weight of capital services in both sectors (${\theta }_{j}$) are not directly estimated, but are instead implicitly obtained by using the expression:

$${\theta }_{j}=\frac{1}{1+\frac{{\left({o}_{j}/{k}_{j}\right)}^{1+{\nu }_{j}}}{1/\beta -\left(1-{\delta u}_{j}\right)}}$$

(22)

where ${o}_{j}/{k}_{j}$ is the respective sector’s historical oil-capital ratio (${o}_{E}/{k}_{E}=0.011$ and ${o}_{N}/{k}_{N}=0.014$) obtained from US post-war data, $\beta$ is set equal to 0.96 to match the annual real interest rate of 4% over the sample period, and ${\delta u}_{j}$ is the steady state depreciation function of capital in the two sectors (${\delta u}_{E}=0.09$ and ${\delta u}_{N}=0.06$). We fix the values of the rest of the parameters in our model; see Sect. F of the Online Appendix.

Using these estimated values, the last three rows of Table 1 summarise the results which demonstrate whether or not the model is able to reproduce the features of the data jointly. We find that the model adequately fits the joint distribution of the data with a Wald statistic of 12.905. The transformed Mahalanobis distance of 1.444 provides support for this conclusion, because a value that is less than 1.645 is usually considered to confirm that the model is not rejected. Finally, the p-value of 0.063 confirms that the model passes the Wald test comfortably at the 95% confidence level. Table 2 reveals that many of the shocks are estimated to be mildly persistent, except for the autocorrelation coefficients of the first-differenced shocks that are treated as non-stationary. Besides, it is estimated that the sectoral oil use efficiency shocks are the most volatile, while intertemporal preference shock is the least volatile.

Table 2 Indirect inference estimates of shock processes

4.2 Variance Decomposition

The primary question that we ask of the estimated model is: how crucial are global shocks in accounting for the US business cycle fluctuations? To answer this question, we first cluster the shocks following Smets and Wouters (2007), except that we follow the NOEM literature in assigning foreign interest rate to the global shocks’ block (e.g., Kose 2002; Justiniano and Preston 2010; Matheson 2010). We categorise the shocks into four groups: (i) productivity shocks, (ii) mark-up shocks, (iii) demand shocks, and (iv) global shocks. Productivity shocks consist of the two sectoral productivity and the two sectoral oil use efficiency shocks. We include the exogenous wage bill and the exogenous capital cost shifters from both sectors in the mark-up shocks. The global shocks are represented by the exogenous world demand, exogenous foreign interest rate, exogenous world oil price, exogenous world price of imported energy-intensive goods, and preferences for aggregate exported goods and exported energy-intensive goods. All the remaining exogenous variables are combined into demand shocks.

Using these classifications, we report variance decomposition for aggregate macroeconomic variables in our model in Table 3. Clearly, global shocks have been the most influential determinants of movements in the US aggregate macroeconomic variables under study. For instance, we find that global shocks play a dominant role in the determination of six variables, accounting for well over 50% of their variances. More particularly, they explain 64% of the variance of investment, with productivity (10%), mark-up (10%) and demand (16%) shocks contributing the rest. In a similar vein, global shocks determine 65% of the variation in exports, 72% in imports, 58% in wages, 60% in interest rate, and 63% in oil use. As shown in the cases of these latter variables, productivity, mark-up, and demand shocks continue to play second fiddle to global shocks.

Table 3 Variance decomposition for the aggregate variables

We find that global shocks are the most important sources of changes in the remaining variables. They explain 38% of output variability, with productivity, mark-up, and demand shocks adding 18%, 18%, and 26%, respectively. Further, the variances of consumption (36%), labour hours (36%), the real exchange rate (42%), domestic absorption (39%), and foreign bonds (37%) are largely determined by global shocks, while the other groups of shocks supply the rest of the explanations. The findings here are consistent with McCarthy and Dhareshwar (1992) and Meenagh et al. (2010) on the importance of external shocks. Additionally, we confirm that global shocks are equally as important in explaining sectoral macroeconomic variables; see Sect. G of the Online Appendix.

4.3 Shock Decomposition

Next, we look at the historical contributions of the groups of shocks in our model to output and real exchange rate. This is done to further shed light on how our estimated model interprets business cycle fluctuations over the sample period. Figs. 4 and 5 show the shock decompositions for output and real exchange rate, respectively. In the diagrams, we illustrate the relative, per year, importance of each shock cluster in a stacked bar chart, and also include, as a line plot, the predicted actual (i.e., the model-based stochastic trends) of our variables of interest. According to our model, global shocks were the significant drivers of output in the US in the decades immediately following World War II until the close of the 20^th Century. Nevertheless, productivity shocks were also crucial in stimulating output over this period. After the year 2000, productivity shocks gain in importance in their role for explaining US output fluctuations, with the main additional contributions coming from global and demand shocks. This finding accords well with Le et al. (2019), who treated materials productivity shock as non-stationary, such that their effects are permanent. Moreover, the group of productivity shocks in our model includes oil use efficiency shocks in both sectors. We find that this empirical result, that productivity shocks remain relatively important post-1980, also derives from their additional impacts.⁸

Fig. 4

Shock decomposition (output)

Fig. 5

Shock decomposition (real exchange rate)

Generally, the cohorts of global and productivity shocks played more prominent roles in output changes than those of mark-up and demand shocks over the sample period. It is also of interest that productivity and global shocks tend to work contrary to mark-up and demand shocks over the majority of the period under study. The influence of global shocks may have been more extensive than the results indicate, had it not been for the offsetting effects that some of their components at times exerted on one another. For instance, in the periods marked by oil crises (e.g., 1973-1974 and 1978-1981), the adverse effects worked to depress the economy’s output, but these effects were soaked up by the positive shocks to world demand and preference for US products. As a result, the total impact on output was still positive in most instances. However, when the negative forces of rising oil/commodity prices outweigh the realised positive effects from the other global shocks, or when most of the shocks have reinforcing (whether positive or negative) contributions, we observe what the model predicts for 1952-1954 or 2007-2013, for example.

Turning to the shock decomposition for real exchange rate (Fig. 5), we see some similarities in the ability of global shocks to have meaningful impacts at the beginning of the sample, just as in the case of output. This is more apparent in the results of the 1950s, such that one can conjecture that the model's interpretation of the major influence of global shocks on the American economy is highly concentrated at the beginning of our sample. Their contributions, however, appear to peter out towards the end, especially in the case of the real exchange rate. Here, the predominant factors leading US competitiveness against ROW are productivity shocks, which appear to have had sole responsibility for most of the variations in real exchange rate since the early 1980s.

4.4 Additional Results and Robustness

So far, we have seen that global shocks are fundamental to explaining movements in key US macroeconomic variables. Now, we show the significance of its components by measuring their individual shares in the total variance contributed by the composite global shocks to the aggregate macroeconomic variables in our model. Fig. 6 shows the results. For example, it is demonstrated that exogenous world demand is responsible for over 30% of the effects of global shocks (38.19%; see Table 3) on output variance. The remaining 70% is largely contributed by oil price, preference for exported energy-intensive goods, and the price of imported energy-intensive goods. In all cases, exogenous world demand captures the lion share of the contributions by global shocks. Also, we find that oil price shocks are slightly more significant than the preference for exported energy-intensive goods and the price of imported energy-intensive goods. Meanwhile, in the variations of output and all the other macroeconomic variables (except exports), preference for aggregate exported goods plays a very subdued role. Lastly, the effect of foreign real interest rates on US macroeconomic variables are largely non-existent, which is consistent with strong domestic monetary policy (Iacoviello and Navarro 2019).

Fig. 6

Unbundling global shocks

Further, there remains a great debate in the literature about whether or not oil price shocks matter for business cycles in the US. While the focus of our paper has been broader than this aspect of global shocks, we find it useful to exploit the structure of our model to confront the issue. Thus, we consider the question: What does our model say about the role of oil price shocks in explaining US output fluctuations? Our approach here is to demonstrate the ability of the bootstrap simulated model samples to predict output expansions and contractions in the actual data, given oil price shocks.⁹ Our assessment of the simulated data focuses on two facts: (i) the frequency of occurrence (in 1000 years) of expansions and contractions in tandem with oil price changes, and (ii) the percentage of events (per 1000 years) involving movements in oil price. As shown in Table 4, oil price decreases (increases) account for around 17% (16%) of the occurrence of output expansions (contractions) in the full sample. Additionally, the experiment reveals that there will be no output contractions (expansions) and no oil price increases (decreases) every 2 years. Further, in approximately every 5 years, on average, there is an oil price rise (fall) that does not affect output fluctuation. We split the sample period into two periods (pre-1980 and post-1980) and find that the results remain consistent across time. A lesson to take from this is that, although oil prices sometimes matter for output changes, there are still many instances when the booms and busts are either merely systemic or due to other factors (see, e.g., Blanchard and Gali 2007; Davidson et al. 2010).

Table 4 An illustration of the model’s predictions of expansions and contractions

Moreover, the estimated structural parameter values reported in Table 1 imply that our model is not rejected at the 5% level of significance based on the Wald test. One may, however, want to test the sensitivity of the theoretical model to pass this empirical test given different parameter values, and the implication of such, for the baseline result. To do this, we focused on the parameter determining the Frisch elasticity of labour supply, $\omega$, which we held constant while we re-estimated the model. In particular, our aim was to see what lower value, if any, of $\omega$ compared to the estimated coefficient of 6.03 would yield a fit between our model and data. The results of fixing $\omega$ at 1, 2, …, 5 are shown in Table 5, which reveals that the model is not rejected only when the value of $\omega$ is as high as 5.¹⁰ On this basis, it appears that our empirical contribution is suggesting that previous lower estimates of this parameter ($\omega$) do not match the data behaviour, at least within our model framework.

Table 5 Indirect inference test results for lower values of the inverse of Frisch elasticity

In any case, we recalculated the variance decompositions of shocks for the aggregate macro-variables using the estimates from setting $\omega$ to 5, 4, and 3;¹¹ these are reported in Sect. H of the Online Appendix. As shown, our baseline finding that global shocks are important for driving US business cycles remains largely unaltered. However, the reported variance decompositions indicate that the estimated values of model parameters may also play a key role with regards to which groups of shocks are important. This is particularly obvious in the reported variance decompositions, when $\omega =5$, for which mark-up shocks played a dominant role. Although, the model did not fit the data when we set $\omega$ equal to 4 or 3, we observe that global shocks take a preeminent position, just as in our baseline finding.

Finally, the test’s robustness can be examined by Monte Carlo experiment, as in Le et al. (2016), where the model parameters are falsified by progressively larger amounts to check the power of the test. We find in this exercise for this model and the auxiliary model we have used, that the power of the test is fairly good and rises steadily as falsity increases. The Monte Carlo experiment is shown in Table 6 below. The experiment implies that once the estimated model parameters are 15% wide of the truth, there is a 20% chance of rejection. If 50% wide, there is close to certainty of rejection. Thus, the researcher knows that if the estimated model passes, it is likely to be reasonably close to the truth. We can think of this as showing that the model estimates are reasonably robust to errors of specification and estimation.

Table 6 Power of the indirect inference test

5 Conclusions

This paper has: (i) investigated the role of global shocks (relative to productivity, mark-up, and demand shocks) in the determination of US business cycle fluctuations, and (ii) identified which of the global shocks are most prominent in causing variations in US macroeconomic aggregates. For this purpose, we constructed a two-sector open economy DSGE model which features a large number of real frictions and several structural shocks. We estimated the model by the method of indirect inference on unfiltered data and were therefore able to admit non-stationary shocks. This empirical procedure showed that the model successfully matched the reality seen in US data. The central finding was that global shocks account for nearly 40% of the variances of output and the real exchange rate in the US economy between 1949 and 2013. Exogenous world demand, oil price shocks, preference for exported energy-intensive goods, and the price of imported energy-intensive goods were the global shocks responsible for causing these variations. In contrast, preference for aggregate exported goods was largely a bystander. Moreover, the estimated model appears to cast productivity shocks in a supporting role. Generally, the results underscored the supremacy of global and productivity shocks over mark-up and demand shocks in determining US business cycles.

We assert that these findings have salient policy implications both for the US and ROW, especially in this age of remarkable international economic integration. For the US, supposing that the policy makers have concerns about output fluctuations and the economy’s competitiveness vis-à-vis ROW, uncovering ways to raise exports, tighten domestic absorption, and increase productivity should be high on their agenda. Considering also the significant role played by the components of global shocks individually, it is crucial to design targeted government policy responses. Turning to exogenous world demand, the global shock identified by our model as having the most impact, the US policy makers would need to implement policies that can adjust the composition of imports and exports appropriately, without creating additional external debt burdens. Expanding world economic integration implies that synced cross-national macroeconomic events will increasingly become the norm. So, the question to be contemplated by ROW is: If global shocks can exert such significant quantitative effects on an economic superpower such as the US, which country is safe? It appears that greater trade liberalization and lower defensive postures (e.g., trade wars) must also be on the menu in this highly connected global village market.

To finish the paper, we note that our analysis has centred on comparing the model-data properties of output and real exchange rate for a developed country (US). One may therefore want to engage the proposed model as a possible data generating mechanism for similar (or different) macroeconomic variables in other types of economies (e.g., a developing country) in other regions of the world. (Of course, any such extensions could include financial and/or nominal frictions if the researcher so desires.) Such an endeavour could lead to purpose-built, country-specific policy statements. Finally, we have used a two-country model of the US and ROW for our study. Future work could extend this to a three-country world economy, including another major economic block (e.g., Euro Area). We would then be able to examine whether there are differences in the business cycle responses of the US and the Euro Area to various global shocks.