1 Introduction

The study of vibrational and stability analysis of the planar motion of pendulum dynamical systems near resonance has attracted considerable interest from several researchers [1,2,3,4,5,6,7,8,9]. The reason goes back to its wide-ranging applications across fields such as robotics, rotor dynamics, pump compressors, and transportation systems.

In [1], the author has shed light on the intricate dynamics of the DP under various conditions. He explored the nonlinear dynamics of a planar DP with a moving base near resonance using the MSM to provide valuable insights into its vibrational behavior. Stability analysis is conducted, employing the normal form theory, and BDs were generated to depict the shift from periodic to chaotic motion. Building upon this foundation, the author delved deeper into the vibrational behavior near second-order resonance in [2], further enriching our understanding of this complex system.

The transition from period-1 motion to chaos in a DP subjected to periodic forcing and damping was investigated in [3]. The authors analyzed the system's behavior using mathematical modeling and numerical simulations. A detailed understanding of how chaos emerges in such a system under specific conditions was provided.

Numerous investigations have been carried out to examine the motion of DPs through theoretical and experimental methods. In [4], a modified midpoint integrator is utilized to numerically examine the planar motion of a DP. Specifically, BDs and Poincaré sections were shown for particular energy values. The phenomenon of parametric excitation in an internally resonant DP is investigated in [5]. The bifurcation structure of a parametrically excited DP at low oscillation amplitudes is explored in [6]. The analysis for the situations of resonance is addressed in [7]. Furthermore, the rotational motions of a model comprising two pivotally connected pendulums about horizontal axes, are investigated in [8]. The dynamical behavior of a DP system under the influence of a vibrating suspension point is explored in [9].

The study of nonlinear dynamical systems is significant in various fields, such as industry, biology, and medicine, as demonstrated in [10,11,12,13]. Perturbation techniques, including [14], can be utilized to obtain approximate AS for the equations of motion (EOM) of these systems. The MSM, in particular, has garnered the attention of investigators due to its exceptional accuracy. Pendulum models, known for their relative simplicity, are commonly utilized to simulate the dynamics of diverse technical apparatuses and machine components. Various types of pendulums have been extensively explored in scientific literature, offering valuable insights for practical applications in the realm of nonlinear dynamics. In [15], a general solution procedure is developed for analyzing the vibrations (including primary resonance and nonlinear natural frequency) of systems with cubic nonlinearities, subjected to nonlinear and time-dependent internal boundary conditions. The nonlinear dynamic modeling, free vibration, and nonlinear analysis of a three-dimensional viscoelastic Euler–Bernoulli beam with a significant tip mass undergoing hub motion is accomplished in [16]. The dynamic EOM are discretized using the obtained mode shapes, and the system's response under rotary hub motion is analyzed. Steady-state solutions and frequency response curves, exhibiting bi-stable and tri-stable regions, are derived using the MSM. Additionally, BDs are studied for resonance conditions when the frequency of the rotary motion is equal to or nearly equal to the normalized beam frequencies. The mathematical modeling and nonlinear dynamics of the beam with three-dimensional tip mass undergoing large deformation in lateral and transverse directions is presented in [17]. The Galerkin’s method is exploited for discretization using the obtained modal parameters and MSM is used to obtain the steady state solutions under combined resonance conditions. In [18], a comprehensive AS algorithm for the nonlinear vibrations and stability of parametrically excited continuous systems with intermediate concentrated elements is developed. The method of multiple timescales is directly applied to the EOM, which consist of a set of nonlinear partial differential equations with nonlinear coupled terms.

Simple pendulum motion has been extensively investigated in [19, 20]. An exploration of their approximate periodic motion can be found in [21], employing the small parameter method [14] when the suspension point follows an elliptical trajectory, as in [22]. Furthermore, researchers in [23] delved into the motion of a weakly nonlinear 2DOF dynamical model, specifically focusing on its chaotic behavior during internal resonance. Additionally, the MSM is utilized in [14] to analyze the stationary behavior of a nonlinear spring pendulum (SP), with subsequent work in [24].

Various types of pendulums have undergone examination in different studies, such as those cited in [25,26,27,28]. In [25], a movable dynamic absorber was utilized along either the transverse or longitudinal direction of an excited pendulum, demonstrating high efficiency for minimally damped systems. The impact of fluid flow on the movement of both simple and SP is analyzed in [26] and [27], respectively. In [28], the dynamics of a vibrating absorber pendulum affixed to a rotating base is investigated. Chaos in the motion of an undamped SP is explored in [29] when its connection point moves along a circular route, with further investigation in [30]. The analysis of motion for a damped spring with linear stiffness, exhibiting behavior on a Lissajous curve, is elucidated in [31], considering the impact of harmonically forced moments and forces. Employing the MSM, the motion of a tuned absorber connected to a simple pendulum near resonance is investigated in [32].

Various pendulum systems have been investigated in related studies [33,34,35,36]. In [33], an exploration of the motion of a pendulum consisting of a triple-rigid body under the influence of some external moments is undertaken. Additionally, [34] examines an in-depth analysis of oscillating control applied to a pendulum with 3DOF mounted on a cart. This examination encompasses the scrutiny of stability criteria, bifurcations, and the stability of periodic frequency motions is characterized by constrained amplitudes. Furthermore, [35] investigates the stability analysis of subjected unscratched multiple pendulums to external harmonic forces. The study in [36] focuses on stability analysis under external harmonic moments. These studies also investigate the assessment of stability/instability zones across various frequency response characteristics.

The utilization of Lyapunov distribution patterns plays a pivotal role in probing the stability and chaos within dynamic systems, particularly those incorporating energy harvesting (EH) devices. EH systems face the challenge of optimizing device performance and efficiency amidst fluctuating and uncertain environmental conditions. Using the Lyapunov distribution pattern, one can delineate regions of stability, periodicity, and chaos within these systems [37]. In [38], the oscillations of a spherical pendulum subjected to horizontal Lissajous excitation are analyzed. The pendulum has 2DOF: a rotational angle in the horizontal plane and an inclination angle relative to the vertical z-axis. Numerical simulation results are presented using a mathematical model, depicted through multi-colored maps of the largest Lyapunov exponent (LE). Additionally, graphical representations of the attractors' geometric structures on Poincaré cross sections are shown, accompanied by maps illustrating the resolution density of trajectory points passing through a control plane.

This research delves into the movement of a 2DOF double pendulum, where the pivot point is constrained to trace a Lissajous curve. Employing the second type of Lagrange's equations, nonlinear differential EOM are derived. The MSM is applied to derive higher-order AS, which are then compared with the NS obtained through the fourth-order Runge–Kutta method. Criteria for solvability and modulation equations (ME) are derived to address various resonance scenarios. The stability of steady-state solutions is assessed through the RHC. The nonlinear stability analysis of the ME is performed to explore both the stability and instability ranges within the frequency responses. Resonance curves and time histories are plotted to analyze the influence of distinct physical parameters on system behavior. Additionally, BDs, LEs, and Poincaré maps are provided to elucidate various types of system dynamics.

2 Overview of the problem

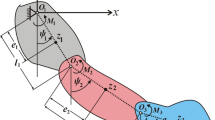
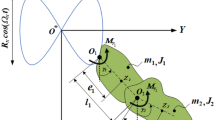
The dynamical system under investigation comprises DPs connected pivotally, with masses \(m_{k} \,(k = 1,2)\), viscous rotation \(b_{k}\), and attached at the points \(O_{k}\). The motion of the first pivot at \(O_{1}\) is constrained to follow a Lissajous curve in a counterclockwise direction. Meanwhile, the second pivot at \(O_{2} = (R_{x} \sin (\Omega_{x\,} t) + l_{1} \sin \theta ,R_{y} \cos (\Omega_{y} t) + l_{1} \cos \theta )\) serves as the connecting point between the two pendulums, as illustrated in Fig. 1. Hence, the location of \(O_{1}\) are given by

$$ \begin{gathered} x = R_{x} \sin (\Omega_{x\,} t), \hfill \\ y = R_{y} \cos (\Omega_{y} t)\,, \hfill \\ \end{gathered} $$
(1)

where \(R_{x} ,R_{y} ,\Omega_{x} ,\) and \(\Omega_{y}\) denote given parameters.

Fig. 1
figure 1

Dynamical motion of the system

Full size image

It's worth noting that the parameters \(l_{1}\) and \(l_{2}\) represent the lengths of the DPs. Toexamine the motion, let us consider the movement of the model in the plane \(xy\) with origin \(O^{*}\) in addition to the action of periodic force \(G(t)\) is applied to the second particle. It is appropriate to express both kinetic and potential energy as follows

$$ \begin{aligned} T & = \frac{1}{2}m_{1} [(l_{1} \dot{\theta }\cos \theta + R_{x} \Omega_{x} \cos \,\Omega_{y} t)^{2} \\ & \quad + (R_{y} \Omega_{y} \sin \,\Omega_{y} t - l_{1} \dot{\theta }\sin \theta )^{2} ] \\ & \quad + \frac{1}{2}m_{2} [(l_{1} \dot{\theta }\cos \,\theta + l_{2} \dot{\phi }\cos \phi + R_{x} \Omega_{x} \cos \,\Omega_{x} t)^{2} \\ & \quad + (l_{1} \dot{\theta }\sin \theta + l_{2} \dot{\phi } \times \sin \phi t + R_{y} \Omega_{y} \sin \,\Omega_{y} t)^{2} ], \\ V & = - m_{1} g(l_{1} \cos \theta + R_{y} \cos \,\Omega_{y} t) \\ & \quad - m_{2} g(l_{1} \cos \theta + l_{2} \cos \phi + R_{y} \cos \,\Omega_{y} t). \\ \end{aligned} $$
(2)

Here, is the gravitational acceleration and the over dots refer to the differentiation with respect to time \(t\). The EOM for the system described by the Lagrangian \(S = T - V\) can be derived using the below particular form of Lagrange's equations

$$ \,\frac{d}{dt}(\frac{\partial S}{{\partial \dot{\theta }}}) - \frac{\partial S}{{\partial \theta }} = Q_{1} ,\,\,\frac{d}{dt}(\frac{\partial S}{{\partial \dot{\phi }}}) - \frac{\partial S}{{\partial \phi }} = Q_{2} , $$
(3)

where the generalized velocities \(\dot{\theta }\) and \(\dot{\phi }\) are associated with specific generalized coordinates \(\theta\) and \(\phi\) of the system, while the generalized forces \(Q_{k} \,(k = 1,2)\) can be expressed in certain mathematical forms

$$ \begin{aligned} Q_{1} & = - l_{1} (b_{1} + b_{2} )[l_{1} \dot{\theta } + R_{x} \Omega_{x} \cos \,\theta \cos \,\Omega_{x} t \\ & \quad + R_{y} \Omega_{y} \sin \theta \sin \,\Omega_{y} t] \\ & \quad - l_{1} \,\cos (\theta - \phi )[b_{2} \,l_{2} \,\dot{\phi } + G(t)], \\ \end{aligned} $$
(4)
$$ \begin{aligned} Q_{2} & = - b_{2} \,l_{2} [l_{1} \,\dot{\theta }\cos (\theta - \phi ) + l_{2} \,\dot{\phi } \\ & \quad + R_{x} \Omega_{x} \cos \phi \cos \Omega_{x} t + \,R_{y} \Omega_{y} \sin \phi \sin \Omega_{y} t] \\ & \quad - l_{2} \,G(t);\,\,\,\,\,\,G(t) = Q\cos \,\Omega \,t, \\ \end{aligned} $$
(5)

where \(Q,\) and \(\Omega\) are the amplitude and frequency of \(G(t)\).

To simplify the analysis of the system, we introduce dimensionless versions of system parameters, frequencies, and time variables

$$ \begin{aligned} B_{1} & = \frac{{b_{1} + b_{2} }}{{(m_{1} + m_{2} )\omega_{1} }},B_{2} = \frac{{b_{2} \,l_{2} }}{{(m_{1} + m_{2} )\,l_{1} \,\omega_{1} }}, \\ M_{1} & = \frac{{m_{2} l_{2} }}{{(m_{1} + m_{2} )l_{1} }},M_{2} = \frac{{l_{1} }}{{l_{2} }}, \\ G_{1} & = \frac{Q}{{(m_{1} + m_{2} )\,l_{1} }},G_{2} = \frac{Q}{{m_{2} l_{2} }}, \\ C_{2} & = \frac{{b_{2} }}{{m_{2} \,\omega_{1} }},C_{1} = \frac{{l_{1} }}{{l_{2} }}C_{2} , \\ r_{x} & = \frac{{R_{x} }}{{l_{1} }},r_{y} = \frac{{R_{y} }}{{l_{1} }},r_{2x} = \frac{{R_{x} }}{{l_{2} }}, \\ r_{2y} & = \frac{{R_{y} }}{{l_{2} }},p = \frac{\Omega }{{\omega_{1} }},p_{x} = \frac{{\Omega_{x} }}{{\omega_{1} }}, \\ p_{y} & = \frac{{\Omega_{y} }}{{\omega_{1} }},\omega = \frac{{\omega_{2} }}{{\omega_{1} }},\omega_{1}^{2} = \frac{g}{{l_{1} }}, \\ \omega_{2}^{2} & = \frac{g}{{l_{2} }},\tau = \omega_{1} t. \\ \end{aligned} $$
(6)

Referring to the above equations, we can write the desired EOM in their dimensionless forms as follows

$$ \begin{aligned} & \theta^{\prime\prime} + \cos (\theta - \phi )(M_{1} \,\phi^{\prime\prime} + B_{2} \,\phi^{\prime}) + B_{1} \,\theta^{\prime} \\ & \quad + p_{x} \,r_{x} \cos \theta [B_{1} \cos (p_{x} \tau ) - p_{x} \sin (p_{x} \tau )] + \sin \theta \\ & \quad \times [B_{1} p_{y} r_{y} \sin (p_{y} \tau ) + p_{y}^{2} \,r_{y} \cos (p_{y} \tau ) + 1] \\ & \quad + M_{1} \phi^{{\prime}{2}} \sin (\theta - \phi ) = - G_{1} \cos (p\,\tau )\cos (\theta - \phi ), \\ \end{aligned} $$
(7)
$$ \begin{aligned} \phi^{\prime\prime} + \cos (\theta - \phi )(M_{2} \theta^{\prime\prime} + C_{1} \theta^{\prime}) + p_{x} \,\cos \phi [C_{2} r_{2x} \cos (p_{x} \tau ) \\ & \quad - p_{x} \sin (p_{x} \tau )] + p_{y} \,r_{2y} \sin \phi \\ & \quad \times [C_{2} \sin (p_{y} \tau ) + p_{y} \cos (p_{y} \tau )] + C_{2} \phi^{\prime} \\ & \quad - M_{2} \theta^{{\prime}{2}} \sin (\theta - \phi ) + \omega^{2} \sin \phi = - G_{2} \cos (p\,\tau ), \\ \end{aligned} $$
(8)

where primes here denote the differentiation regarding the dimensionless time \(\tau\).

3 The proposed perturbation approach

This section employs the MSM to categorize different resonance scenarios and ascertain the system's AS for Eqs. (7) and (8). This is accomplished according to the estimation of the trigonometric functions of \(\theta\) and \(\phi\) till the third-order around the static equilibrium's position. Consequently, Eqs. (7) and (8) can be expressed as follows

$$ \begin{aligned} & \theta^{\prime\prime} + \frac{1}{36}M_{1} [\theta \phi (\theta^{2} - 6)(\phi^{2} - 6) + \frac{1}{4}(\theta^{2} - 2)(\phi^{2} - 2)]\phi^{\prime\prime} \\ & \quad + \theta - \frac{{\theta^{3} }}{6} - \frac{{p_{y} \,r_{y} }}{6}[B_{1} \,p_{y} \,r_{y} \sin (p_{y} \tau ) + p_{y} r_{y} \cos (p_{y} \tau )]\theta (\theta^{2} - 6) \\ & \quad - \frac{1}{2}B_{1} (\theta^{2} - 2)p_{x} r_{x} \cos (p_{x} \tau ) + B_{1} \theta^{\prime} + \frac{1}{36}B_{2} [\theta \phi (\theta^{2} - 6)(\phi^{2} - 6) \\ & \quad + \frac{1}{4}(\theta^{2} - 2)(\phi^{2} - 2)]\phi^{\prime} + \frac{1}{36}G_{1} [\theta \phi (\theta^{2} - 6)(\phi^{2} - 6) \\ & \quad + \frac{1}{4}(\theta^{2} - 2)(\phi^{2} - 2)]\cos (p\,\tau ) + \frac{1}{12}M_{1} \\ & \quad \times \left[ {\frac{1}{36}\theta (\theta^{2} - 6)(\phi^{2} - 2) - \phi (\theta^{2} - 2)(\phi^{2} - 6)} \right]\phi^{2} \\ & \quad + \frac{1}{2}(\theta^{2} - 2)p_{x}^{2} r_{x} \sin (p_{x} \tau ) = 0, \\ \end{aligned} $$
(9)
$$ \begin{aligned} & \phi^{\prime\prime} + 9[(\phi^{2} - 2)G_{2} \cos (p\,\tau )]\theta^{\prime\prime} \\ & \quad - \frac{1}{2}C_{2} p_{x} r_{2x} (\phi^{2} - 2)\cos (p_{x} \tau ) + \frac{1}{2}p_{x}^{2} (\phi^{2} - 2)\sin (p_{x} \tau ) \\ & \quad + \left( {\phi - \frac{{\phi^{3} }}{6}} \right)\left[ {\omega^{2} + C_{2} \,p_{y} \,r_{2y} \sin (p_{y} \tau )} \right. \\ & \quad \left. { + p_{y}^{2} \,r_{2y} \cos (p_{y} \tau )} \right] + \frac{1}{36}C_{1} [\theta \phi (\theta^{2} - 6)(\phi^{2} - 6) \\ & \quad + 9(\theta^{2} - 2)(\phi^{2} - 2)]\theta^{\prime} - C_{2} \phi^{\prime} \\ & \quad + \frac{{M_{2} }}{12}\left\{ {\frac{\theta \phi }{3}(\theta^{2} - 6)(\phi^{2} - 6) + (\theta - \phi )[\theta^{2} (\phi^{2} - 2)} \right. \\ & \quad \left. { + 4\theta \phi - 2\phi^{2} + 12]\theta^{\prime 2} } \right\} = 0. \\ \end{aligned} $$
(10)

Understanding that the coordinates \(\theta\) and \(\phi\) need to be redefined with a small parameter \(0 < \,\varepsilon < < 1\) is essential. Subsequently, additional variables \(\psi\) and \(\gamma\) can be introduced as follows:

$$ \theta = \varepsilon \psi (\tau ;\varepsilon ),\,\,\,\,\,\,\,\,\phi = \varepsilon \gamma (\tau ;\varepsilon ). $$
(11)

Now, these variables can be considered as series expansions of this parameter [39].

$$ \Lambda (\tau ;\varepsilon ) = \sum\limits_{k = 1}^{3} {\varepsilon^{k - 1} \Lambda_{k} (\tau_{0} ,\tau_{1} ,\tau_{2} )} + O(\varepsilon^{3} );\,\,\,\,\,\Lambda = (\psi ,\gamma ), $$
(12)

where \(\tau_{n} = \varepsilon^{n} t\,\,\,(n = 0,\,1\,,\,2)\) represents different time scales. Thus, the subsequent operators may be utilized to convert both first and second derivatives concerning time \(t\) are computed to the new time scales [14]

$$ \begin{aligned} \frac{d}{dt} & = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial \tau_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial \tau_{2} }}, \\ \frac{{d^{2} }}{{dt^{2} }} & = \frac{{\partial^{2} }}{{\partial \tau_{0}^{2} }} + 2\varepsilon \frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad + \varepsilon^{2} \left( {\frac{{\partial^{2} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} }}{{\partial \tau_{0} \partial \tau_{2} }}} \right) + O(\varepsilon^{3} ). \\ \end{aligned} $$
(13)

Furthermore, we propose

$$ \begin{aligned} M_{1} & = \varepsilon \,\tilde{M}_{1} ,M_{2} = \varepsilon \,\tilde{M}_{2} ,B_{1} = \varepsilon \,\tilde{B}_{1} , \\ B_{2} & = \varepsilon \,\tilde{B}_{2} ,G_{1} = \varepsilon^{3} \,\tilde{G}_{1} ,G_{2} = \varepsilon^{3} \,\tilde{G}_{2} , \\ C_{1} & = \varepsilon \,\tilde{C}_{1} ,C_{2} = \varepsilon \,\tilde{C}_{2} ,r_{y} = \varepsilon \,\tilde{r}_{y} , \\ r_{x} & = \varepsilon \,\tilde{r}_{x} ,r_{2y} = \varepsilon \,\tilde{r}_{2y} ,r_{2x} = \varepsilon \,\tilde{r}_{2x} . \\ \end{aligned} $$
(14)

where \(\tilde{B}_{k} ,\tilde{M}_{k} \,,\tilde{G}_{k} \,,\tilde{C}_{k} ,\tilde{r}_{x} \,,\tilde{r}_{y} ,\tilde{r}_{2x} ,\,\,\,(k = 1,2)\) and \(\tilde{r}_{2y}\) are parameters of unity-order.

Inserting (11)–(14) in both (9) and (10), we can establish a relationship between the same power's coefficients of the variable \(\varepsilon\), which leads to the next sets of partial differential equations (PDEs) in accordance with the powers of \(\varepsilon.\)


Order of ε:

$$ \frac{{\partial^{2} \psi_{1} }}{{\partial^{2} \tau_{0} }} + \psi_{1} - p_{x}^{2} r_{x} \sin (p_{x} \,\tau ) = 0, $$
(15)
$$ \frac{{\partial^{2} \gamma_{1} }}{{\partial \tau_{0}^{2} }} + \,\omega^{2} \gamma_{1} = 0. $$
(16)

Order of ε2:

$$ \begin{aligned} & \frac{{\partial^{2} \psi_{2} }}{{\partial \tau_{0}^{2} }} + \psi_{2} + 2\frac{{\partial^{2} \psi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} + B_{2} \frac{{\partial \gamma_{1} }}{{\partial \tau_{0} }} + B_{1} \frac{{\partial \psi_{1} }}{{\partial \tau_{0} }} \\ & \quad + M_{1} \frac{{\partial^{2} \gamma_{1} }}{{\partial \tau_{0}^{2} }} + p_{y}^{2} \,r_{y} \,\psi_{1} \cos (p_{y} \,\tau ) \\ & \quad + B_{1} \,p_{x} \,r_{x} \cos (p_{x} \,\tau ) = 0, \\ \end{aligned} $$
(17)
$$ \begin{aligned} & \frac{{\partial^{2} \gamma_{2} }}{{\partial \tau_{0}^{2} }} + \omega^{2} \gamma_{2} + C_{2} \frac{{\partial \gamma_{1} }}{{\partial \tau_{0} }} + C_{1} \frac{{\partial \psi_{1} }}{{\partial \tau_{0} }} + M_{2} \frac{{\partial^{2} \psi_{1} }}{{\partial \tau_{0}^{2} }} \\ & \quad + p_{y}^{2} \,r_{2y} \,\gamma_{1} \cos (p_{y} \,\tau ) + 2\frac{{\partial^{2} \gamma_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad + C_{2} p_{x} \,r_{2x} \cos (p_{x} \,\tau ) + \frac{1}{2}p_{x}^{2} \,\gamma_{1}^{2} \sin (p_{x} \,\tau ) = 0. \\ \end{aligned} $$
(18)

Order of ε3:

$$ \begin{aligned} & \frac{{\partial^{2} \psi_{3} }}{{\partial \tau_{0}^{2} }} + \psi_{3} + \frac{{\partial^{2} \psi_{1} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} \psi_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} + 2\frac{{\partial^{2} \psi_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} \\ & \quad + B_{2} \left( {\frac{{\partial \gamma_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \gamma_{2} }}{{\partial \tau_{0} }}} \right) + B_{1} \left( {\frac{{\partial \psi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \psi_{2} }}{{\partial \tau_{0} }}} \right) \\ & \quad + M_{1} \left( {2\frac{{\partial^{2} \gamma_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{{\partial^{2} \gamma_{2} }}{{\partial \tau_{0}^{2} }}} \right) + G_{1} \cos (p\,\tau ) \\ & \quad + B_{1} p_{y} \,r_{y} \psi_{1} \sin (p_{y} \,\tau ) + \frac{1}{2}p_{x}^{2} \,r_{x} \,\psi_{1}^{2} \\ & \quad \times \sin (p_{x} \,\tau ) - \frac{1}{6}\psi_{1}^{3} + p_{y}^{2} \,r_{y} \,\psi_{2} \cos (p_{y} \,\tau ) = 0, \\ \end{aligned} $$
(19)
$$ \begin{aligned} & \frac{{\partial^{2} \gamma_{1} }}{{\partial \tau_{1}^{2} }} + 2\frac{{\partial^{2} \gamma_{1} }}{{\partial \tau_{0} \partial \tau_{2} }} + 2\frac{{\partial^{2} \gamma_{2} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{{\partial^{2} \gamma_{3} }}{{\partial \tau_{0}^{2} }} \\ & \quad + C_{2} \left( {\frac{{\partial \gamma_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \gamma_{2} }}{{\partial \tau_{0} }}} \right) + C_{1} \left( {\frac{{\partial \psi_{1} }}{{\partial \tau_{1} }} + \frac{{\partial \psi_{2} }}{{\partial \tau_{0} }}} \right) \\ & \quad + M_{2} \left( {2\frac{{\partial^{2} \psi_{1} }}{{\partial \tau_{0} \partial \tau_{1} }} + \frac{{\partial^{2} \psi_{2} }}{{\partial \tau_{0}^{2} }}} \right) + \omega^{2} \left( {\gamma_{3} - \frac{1}{6}\gamma_{1}^{3} } \right) \\ & \quad + \gamma_{1} C_{2} \,p_{y} \,r_{2y} \sin (p_{y} \,\tau ) \\ & \quad + G_{2} \cos (p\,\tau )\, + \gamma_{2} p_{y}^{2} \,r_{2y} \cos (p_{y} \,\tau ) \\ & \quad + \gamma_{2} \,\gamma_{1} p_{x}^{2} \sin (p_{x} \,\tau ) = 0. \\ \end{aligned} $$
(20)

Based on the PDEs (15)–(20), we can solve them subsequently. Therefore, the general solutions of equations (15)–(16) may be written as follows

$$ \psi_{1} = A_{1} e^{{i\tau_{0} }} + \overline{A}_{1} e^{{ - i\tau_{0} }} + \frac{{p_{x}^{2} \,\tilde{r}_{x} }}{{2(1 - p_{x}^{2} )}}(e^{{ip_{x} \tau_{0} }} + e^{{ - ip_{x} \tau_{0} }} ), $$
(21)
$$ \gamma_{1} = A_{2} e^{{i\omega \tau_{0} }} + \overline{A}_{2} e^{{ - i\omega \tau_{0} }} ;\,\,\,\,\,i = \sqrt { - 1} \,. $$
(22)

In this context, \(A_{k} \,\,(k = 1,2)\) represent complex functions related to the scales \(\tau_{n}\), and it may be determined at a later stage. On the other hand, \(\overline{A}_{k}\) signifies their complex conjugate.

Inserting the solutions (21) and (22) in both Eqs. (17) and (18), then eliminating the produced secular terms to obtain the subsequent conditions

$$ 2i\frac{{\partial A_{1} }}{{\partial \tau_{1} }} + (i\tilde{B}_{1} + \tilde{r}_{y} \,p_{y}^{2} )A_{1} = 0, $$
(23)
$$ 2i\omega \frac{{\partial A_{2} }}{{\partial \tau_{1} }} + (\tilde{r}_{2y} \,p_{y}^{2} + i\omega \,\tilde{C}_{2} )A_{2} = 0, $$
(24)

It states that the second-order system's solutions can be presented in a form

$$ \begin{aligned} \psi_{2} & = \frac{{(\tilde{M}_{1} \omega - i\tilde{B}_{2} )\omega A_{2} }}{{1 - \omega^{2} }}e^{{i\omega \tau_{0} }} \\ & \quad - \frac{{(p_{x} + p_{y}^{2} \,\tilde{r}_{y} )p_{x}^{2} \,\tilde{r}_{x} }}{{2(1 - p_{x}^{2} )^{2} }}e^{{ip_{x} \,\tau_{0} }} + cc, \\ \end{aligned} $$
(25)
$$ \begin{aligned} \gamma_{2} & = \frac{{A_{1} (\tilde{M}_{2} - i\tilde{C}_{1} )e^{{i\tau_{0} }} }}{{(\omega^{2} - 1)}} \\ & \quad - \left\{ {\frac{{(p_{x} \,A_{2} \overline{A}_{2} + 2\tilde{C}_{2} \,\tilde{r}_{2x} )}}{{4(\omega^{2} - p_{x}^{2} )}}} \right. \\ & \quad + \frac{{e^{{2i\,\omega \tau_{0} }} p_{x} \,A_{2}^{2} }}{{2(\omega^{2} - (p_{x} + 2\omega )^{2} )}} \\ & \quad + \frac{{e^{{ - 2i\,\omega \tau_{0} }} p_{x} \,\overline{A}_{2}^{2} }}{{2(\omega^{2} - (p_{x} - 2\omega )^{2} )}} \\ & \quad \left. { - \frac{{(\tilde{M}_{2} \,p_{x} - 1)p_{x}^{2} \,\tilde{r}_{x} }}{{2(1 - p_{x}^{2} )(\omega^{2} - p_{x}^{2} )}}} \right\}p_{x} e^{{ip_{x} \tau_{0} }} \\ & \quad + cc, \\ \end{aligned} $$
(26)

where cc represents the complex conjugates of the preceding terms.

It is possible to derive the subsequent criteria for eliminating secular terms from the third-order estimation considering the replacement of solutions (21)–(22) and (25)–(26) into equations (19)–(20).

$$ \begin{aligned} & \frac{{\partial^{2} A_{1} }}{{\partial \tau_{1}^{2} }} + 2i\frac{{\partial A_{1} }}{{\partial \tau_{2} }} + \tilde{B}_{1} \frac{{\partial A_{1} }}{{\partial \tau_{1} }} \\ & \quad + \left( {\frac{{(i\tilde{C}_{1} - \tilde{M}_{2} )\tilde{M}_{1} }}{{\omega^{2} - 1}}} \right)A_{1} = 0, \\ \end{aligned} $$
(27)
$$ \begin{aligned} & \frac{{\partial^{2} A_{2} }}{{\partial \tau_{1}^{2} }} + 2i\omega \frac{{\partial A_{2} }}{{\partial \tau_{2} }} + \tilde{C}_{2} \frac{{\partial A_{2} }}{{\partial \tau_{1} }} \\ & \quad + \frac{{\omega^{2} }}{{1 - \omega^{2} }}(\tilde{C}_{1} \,\tilde{B}_{2} + i\omega \tilde{M}_{1} \tilde{C}_{1} \\ & \quad + i\omega \tilde{B}_{2} \tilde{M}_{2} - \tilde{M}_{1} \tilde{M}_{2} )A_{2} \\ & \quad - \frac{1}{2}\omega^{2} A_{2}^{2} \overline{A}_{2} = 0. \\ \end{aligned} $$
(28)

As a result, the approximations \(\psi_{3}\), and \(\gamma_{3}\) of third-order have the forms

$$ \begin{aligned} \psi_{3} & = \tilde{B}_{2} \,s_{1} + \tilde{B}_{1} \,s_{3} + \frac{{\tilde{r}_{y} \,p_{y} }}{4}(p_{y} \,s_{4} + 2iB_{1} s_{2} ) \\ & \quad - \frac{1}{4}ip_{x}^{2} \,\tilde{r}_{x} \,s_{5} - \frac{{G_{1} e^{ip\tau } }}{{2(1 - p^{2} )}} + cc, \\ \end{aligned} $$
(29)
$$ \begin{aligned} \gamma_{3} & = \frac{{iB_{2} \,\tilde{r}_{x} \,p_{x} \,s_{6} }}{2} + \tilde{B}_{1} \,s_{7} + \frac{{p_{x}^{2} \,\tilde{r}_{x} \,s_{8} }}{2} \\ & \quad + s_{9} + s_{10} - \frac{{G_{2} e^{i\,p\tau } }}{{2(\omega^{2} - p^{2} )}} + cc. \\ \end{aligned} $$
(30)

where \(s_{1} ,\,s_{2} ,...,s_{10}\) are functions that can be seen in Appendix 1.

Upon analyzing conditions (23), (24), (27), and (28), the unknown functions \(A_{1} ,\,A_{2}\) may be determined. To efficiently get the desired AS, one can insert solutions (21), (22), (25), (26), (29), (30), and the series (12) in the assumption (11).

As mentioned earlier, the MS method involves utilizing an infinite array of distinct time scales rather than relying solely on a single time variable. This versatility is essential for meeting solvability criteria, which necessitate the elimination of secular components. The presence of fast time scales limits the structure of the calculated solutions. It's essential to ensure the consistency of solvability criteria across various orders. These criteria impose limitations on the amplitudes of "free" resonant terms that emerge in each expansion order. Failure to meet these constraints may result in inaccurate analysis outcomes or only permit basic solutions. It's worth noting that alternative free amplitude possibilities could lead to conflicting results [39].

4 Resonance classifications

It's important to emphasize that the categorization of resonance scenarios may occur in the final two orders of solution. Furthermore, the analysis of three of these identified scenarios constitutes a vital aspect of this section. Resonance occurrences are commonly understood to arise when the denominators of these components approach zero [40]. This can be described as:

  1. (i)

    Primary external resonance:

    This resonance occurs when an external force matches the natural frequency of a system, leading to significant oscillations. Therefore, it is presented at \(p \approx 1\) and \(p \approx \omega.\)

    Moreover, it's a fundamental aspect of vibrational dynamics and is crucial for understanding the response of structures to dynamic loads.

  2. (ii)

    Internal resonance:

    It occurs when different modes of a system's natural frequencies interact. Consequently, it takes place at \(1 \approx \omega ,p_{x} \approx \omega ,p_{x} \approx 1\,,\,p_{x} \approx 2\,,\) and \(p_{y} \approx 1 - \,\omega.\)

Investigating two of the above resonances simultaneously in a vibrating dynamical model entails analyzing the interplay between primary resonance and internal resonance. This comprehensive approach is essential for understanding the dynamic behavior of complex systems subjected to multifaceted loading conditions.

It is worth mentioning that as oscillations move away from resonance positions, the AS discussed in the earlier segment remain valid. Let's examine two significant external and internal resonances that occur simultaneously. Expressing the proximity of \(p,1\) by \(1,\omega\) can be achieved through the detuning parameters \(\sigma_{1}\) and \(\sigma_{2}\), which denote the deviation between vibrations and the precise resonance, as indicated:

$$ p = 1 + \sigma_{1} ,\,\,\,\,\,1 = \,\omega + \sigma_{2} . $$
(31)

We can represent these concepts using the variable \(\varepsilon\) by

$$ \sigma_{k} = \varepsilon \,\tilde{\sigma }_{k} \,\,\,(k = 1,2). $$
(32)

To fulfill the necessary solvability conditions, replace expressions (31) and (32) with Eqs. (17)–(20), and subsequently eliminate any component factors resulting in secular terms.

  • Requirements for the approximation of second-order

    $$ \frac{{\partial A_{1} }}{{\partial \tau_{1} }} = \frac{1}{2}(i\tilde{r}_{y} \,p_{y}^{2} - \tilde{B}_{1} )A_{1} , $$
    (33)
    $$ \frac{{\partial A_{2} }}{{\partial \tau_{1} }} = \frac{1}{2\omega }(i\tilde{r}_{2y} \,p_{y}^{2} - \omega \,\tilde{C}_{2} )A_{2} . $$
    (34)

  • Requirements for the estimation at the third-order

    $$ \begin{aligned} & 3i\frac{{\partial A_{1} }}{{\partial \tau_{2} }} + \left[ {\frac{{(i\tilde{C}_{1} - \tilde{M}_{2} )\tilde{M}_{1} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { - \frac{{(\tilde{r}_{y}^{2} \,p_{y}^{4} + 3\tilde{B}_{1}^{2} )}}{4}} \right]A_{1} \\ & \quad + \frac{{\tilde{G}_{1} }}{2}e^{{i\tilde{\sigma }_{1} \tau_{1} }} = 0, \\ \end{aligned} $$
    (35)
    $$ \begin{aligned} & 2i\omega \frac{{\partial A_{2} }}{{\partial \tau_{2} }} - \left\{ {\frac{{(\tilde{C}_{2} + \tilde{r}_{2y}^{2} \,p_{y}^{4} )}}{4}} \right. \\ & \quad + \frac{{\omega^{2} \,[\tilde{C}_{2} \,\tilde{B}_{2} + i\omega (\tilde{M}_{1} \,\tilde{C}_{1} + \tilde{B}_{2} \tilde{M}_{2} ) - \tilde{M}_{1} \tilde{M}_{2} ]}}{{1 - \omega^{2} }} \\ & \quad \left. { - \frac{1}{2}\omega^{2} A_{2} \overline{A}_{2} } \right\}\frac{{A_{2} }}{2} \\ & \quad + \frac{{(\tilde{M}_{2} - i\tilde{C}_{1} )(i\tilde{B}_{1} + \tilde{r}_{y} \,p_{y}^{2} - i\tilde{C}_{2} )}}{{\omega^{2} - 1}}A_{1} \,e^{{i\tilde{\sigma }_{2} \tau_{2} }} = 0. \\ \end{aligned} $$
    (36)

The mentioned criteria (33)–(36) possesses the ability to delineate the functions \(A_{1} ,\,A_{2}\) that can alternatively be represented in polar notation

$$ \begin{array}{*{20}l} {A_{k} (\tau_{1} ,\tau_{2} ) = \frac{1}{2}\tilde{a}_{j} (\tau_{1} ,\tau_{2} )e^{{i\psi_{k} (\tau_{1} ,\tau_{2} )}} ,} \hfill & {a_{k} = \varepsilon \tilde{a}_{k} ,} \hfill \\ {\theta_{1} (\tau_{1} ,\tau_{2} ) = \tilde{\sigma }_{1} \tau_{1} - \psi_{1} (\tau_{1} ,\tau_{2} ),} \hfill & {} \hfill \\ {\theta_{2} (\tau_{1} ,\tau_{2} ) = \tilde{\sigma }_{2} \tau_{1} - \psi_{1} (\tau_{1} ,\tau_{2} ) - \psi_{2} (\tau_{1} ,\tau_{2} ),} \hfill & {\sigma_{k} = \varepsilon \tilde{\sigma }_{k} \quad (k = 1,2),} \hfill \\ \end{array} $$
(37)

where \(\psi_{k}\) represent the phase angles, \(\theta_{k}\) denote the adjusted phases, and \(a_{k}\) stand for the amplitudes.

Replacing Eq. (37) into Eqs. (33)–(36) and subsequently separating the real and imaginary components of the resulting equations yields the modulation of ordinary differential equations (ODEs) as follows

$$ \begin{aligned} \frac{{d\theta_{1} }}{d\tau } & = \frac{1}{12}\left\{ {\left( {12\sigma_{1} + B_{1}^{2} + \frac{{4M_{1} \,M_{2} }}{{(\omega^{2} - 1)}}} \right.} \right. \\ & \quad \left. { + p_{y}^{2} \,r_{y} (p_{y}^{2} \,r_{y} - 6))a_{1} - 4G_{1} \cos \theta_{1} } \right\}, \\ \frac{{da_{1} }}{d\tau } & = - \frac{1}{6}\left( {a_{1} \left( {B_{1} + \frac{{C_{1} \,M_{1} }}{{\omega^{2} - 1}}} \right) + 2G_{1} \sin \theta_{1} } \right), \\ \frac{{d\theta_{2} }}{d\tau } & = \frac{1}{16}\left\{ {16\sigma_{2} + \frac{2}{{\omega^{3} }}\left( {\omega^{2} C_{2}^{2} - p_{y}^{2} (4\omega^{2} \,r_{y} - p_{y}^{2} \,r_{2y}^{2} )} \right)} \right. \\ & \quad - \frac{{8\omega (B_{2} \,C_{2} - M_{1} M_{2} )}}{{(1 - \omega^{2} )}} + \omega \,a_{2}^{2} \\ & \quad - \frac{{4\cos \theta_{2} }}{{\,\omega \,a_{2} }}\left( {\frac{{\,C_{1} (B_{1} - C_{2} ) + M_{2} \,p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad + B_{1} \,C_{1} + 2M_{2} \,p_{y}^{2} \,r_{y} )\} \\ & \quad + \frac{{\sin \theta_{2} }}{{2\omega a_{2} }}\left( {\frac{{B_{1} \,M_{2} - C_{1} \,p_{y}^{2} \,r_{y} - C_{2} M_{2} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { + \frac{{C_{1} \,p_{y}^{2} \,r_{y} - 2B_{1} \,M_{2} }}{2}} \right) + \sigma_{1} - \frac{{d\theta_{1} }}{d\tau }, \\ \frac{{da_{2} }}{d\tau } & = - \frac{{a_{2} }}{2}\left( {\frac{{\omega^{2} (B_{2} \,M_{2} + C_{1} M_{1} )}}{{1 - \omega^{2} }} + C_{2} } \right) \\ & \quad - \frac{1}{4\omega }\left\{ {\cos \theta_{2} \left( {\frac{{2(M_{2} (B_{1} - C_{2} \,) - C_{1} \,p_{y}^{2} \,r_{y} )}}{{\omega^{2} - 1}}} \right.} \right. \\ & \quad + C_{1} \,p_{y}^{2} \,r_{y} - 2B_{1} M_{2} ) \\ & \quad + \sin \theta_{2} \left( {\frac{{2(\,C_{1} (B_{1} - C_{2} ) + M_{2} \,p_{y}^{2} \,r_{y} )}}{{\omega^{2} - 1}}} \right. \\ & \quad + 2M_{2} \,p_{y}^{2} \,r_{y} - B_{1} \,C_{1} )\} . \\ \end{aligned} $$
(38)

It's important to emphasize that this system involves a set of four first-order ODEs, which are numerically solved using Mathematica software 12.0.0.0 to illustrate the time-dependent changes of the amplitudes \(a_{k} \,(k = 1,2)\) and modified phases \(\theta_{k}\). To achieve this, the supplied information has been utilized as shown in Table 1.

Table 1 The used data
Full size table

A close examination of Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 indicates that these figures are graphed when \(\omega ( = 1.41,1.58,\,1.64),\) \(G_{1} ( = 0.0001,0.0002,0.0003),\,\) and \(C_{1} ( = 0.00001,0.00003,0.00005)\). The analysis of the curves depicted in Figs. 2 and 3 reveals the temporal evolution of both amplitudes \(a_{k}\) and adjusted phases \(\theta_{k}\) across varying frequencies. A recurring pattern emerges, indicating that the generated waves exhibit periodic tendencies. Specifically, the amplitudes illustrated in Fig. 2 exhibit a diminishing trend as the values of the frequency \(\omega\) ascend. Conversely, the amplitudes of the drawn waves in Fig. 3 increase according to the increase in \(\omega\) values.

Fig. 2
figure 2

Impact of the various values of \(\omega \,( = 1.41,1.58,\,1.64)\) on the time history characteristics of the modified amplitudes: a a1, and b a2

Full size image
Fig. 3
figure 3

Beneficial effect of \(\omega \,( = 1.41,1.58,\,1.64)\) on time history behavior of the adjusted phases: a \(\theta_{1}\), and b \(\theta_{2}\)

Full size image
Fig. 4
figure 4

The nature of projections of \(a_{k} \,\,(k = 1,2)\) and \(\theta_{k}\) at \(\omega ( = 1.41,1.58,\,1.64)\) in the planes: a, b \(a_{1} \theta_{1}\), and c \(a_{2} \theta_{2}\)

Full size image
Fig. 5
figure 5

Demonstrates how changes in \(\omega \,( = 1.41,1.58,\,1.64)\) values effect on the solutions: a \(\theta\), and b \(\phi\)

Full size image
Fig. 6
figure 6

Phase plane diagrams according to \(\omega ( = 1.41,1.58,\,1.64)\) in the planes: a \(\theta \dot{\theta }\), and b \(\phi \dot{\phi }\)

Full size image
Fig. 7
figure 7

Compatibility between AS and NS for the waves describing: a \(\theta\), and b \(\phi\)

Full size image
Fig. 8
figure 8

Influence of various values of \(G_{1} ( = 0.0001,0.0002,0.0003)\) on the behavior of: a \(a_{1}\), and b \(a_{2}\)

Full size image
Fig. 9
figure 9

The positive impact of \(G_{1} ( = 0.0001,0.0002,0.0003)\) on the behavior of: a \(\theta_{1} ,\) and b \(\theta_{2}\)

Full size image
Fig. 10
figure 10

The projections of \(a_{k} \,\,(k = 1,2)\) and \(\theta_{k}\) at \(G_{1} ( = 0.0001,0.0002,0.0003)\) in the planes: a \(a_{1} \theta_{1}\), b \(a_{1} \theta_{1}\), and c \(a_{2} \theta_{2}\)

Full size image
Fig. 11
figure 11

The influence of \(G_{1} ( = 0.0001,0.0002,0.0003)\) on the time response solutions: a \(\theta\), and b \(\phi\)

Full size image
Fig. 12
figure 12

The phase plane diagrams when \(G_{1} ( = 0.0001,0.0002,0.0003)\) varies in the planes: a \(\theta \dot{\theta }\), and b \(\phi \dot{\phi }\)

Full size image
Fig. 13
figure 13

The effect of various values of \(C_{1} ( = 0.00001,0.00003,0.00005)\) on: a \(a_{1}\), and b \(a_{2}\)

Full size image
Fig. 14
figure 14

The positive effect of \(C_{1} ( = 0.00001,0.00003,0.00005)\) on: a \(\theta_{1}\), and b \(\theta_{2}\)

Full size image
Fig. 15
figure 15

The projections of \(a_{k} \,\,(k = 1,2)\) and \(\theta_{k}\) at \(C_{1} ( = 0.00001,0.00003,0.00005)\) in: a, b \(a_{1} \theta_{1}\), and c \(a_{2} \theta_{2}\)

Full size image
Fig. 16
figure 16

The influence of \(C_{1} ( = 0.00001,0.00003,0.00005)\) values on the waves describing the solutions: a \(\theta\), and b \(\phi\)

Full size image
Fig. 17
figure 17

The phase plane diagrams at \(C_{1} ( = 0.00001,0.00003,0.00005)\) in the planes: a \(\theta \dot{\theta }\), and b \(\phi \dot{\phi }\)

Full size image

Obtaining periodic behavior indicates that the vibrating dynamical system exhibits regular, repetitive behavior over time. Additionally, it indicates that the system operates within stable bounds, providing confidence in its mathematical procedures. This behavior provides insights into the stability of the dynamical system. By analyzing the behavior of the system over time, engineers and scientists can determine whether the system will settle into a predictable, repeating pattern, indicating stability. Once a periodic pattern is identified, it can be used to forecast the system's response to different inputs or perturbations, aiding in the design and optimization of control strategies. It serves as benchmarks for validating the design of vibrating dynamical systems [41, 42].

Closed curves in phase planes indicate stable behavior in the dynamical system, as in Fig. 4. This stability is crucial for ensuring predictable and controlled responses to external inputs or disturbances. Additionally, they provide insights into the long-term behavior of the system. Understanding closed curves helps in designing effective control strategies for vibrating dynamical systems. Engineers can use feedback control techniques to stabilize the system around these closed curves, ensuring robust performance under varying operating conditions. These curves can guide the optimization of system parameters to enhance performance. By adjusting parameters such as damping coefficients or excitation frequencies, engineers can maximize stability margins and minimize energy consumption while meeting performance requirements. Therefore, the phase plane curves depicted in Fig. 4 within the \(\theta_{1} a_{1}\) and \(\theta_{2} a_{2}\) planes are investigated. These curves emerge when the temporal variable t is eliminated from the mathematical expressions governing of \(\theta_{1} ,a_{1}\) and \(\theta_{2} ,a_{2}\). The resulting curves in this figure exhibit closed-loop formations, affirming the earlier prediction regarding the stability characteristics of the waves depicted in Figs. 2 and 3.

The evolution of the achieved solutions \(\theta \,\) and \(\phi\) over time has been graphed in Fig. 5a, b, respectively. In these figures, quasi-periodic wave packets have been observed evolving over time, confirming the quasi-periodicity nature of the approximate solutions obtained through the perturbation method referenced earlier. It is shown that the amplitudes of the depicted waves diminish with the increase of \(\omega\) values. When these solutions are visualized through their first derivatives, the phase plane diagrams are generated, see portions (a) and (b) of Fig. 6. The quasi-periodic nature introduces some disturbance in the plotted closed curves.

To validate the obtained AS, numerical solutions (NS) of Eqs. (7) and (8) are computed using the fourth-order Runge–Kutta algorithms. The comparison between the two is depicted in portions (a) and (b) of Fig. 7 for the solutions \(\theta \,\) and \(\phi\), respectively. Remarkably, a high degree of consistency is observed between them. Comparison between both solutions helps validate the accuracy and reliability of the analytical approximations. Discrepancies between them can highlight limitations or inaccuracies in the approximation methods, prompting refinements or adjustments to improve their predictive capabilities.

The beneficial effects of varying the force’s amplitude \(G_{1}\) on the adjusted amplitudes \(a_{k}\) and phases \(\theta_{k}\) are presented in Figs. 8 and 9, respectively. Notably, periodic behaviors are observed in the depicted waves over time, in which \(a_{1}\) being notably impacted by the change of \(G_{1}\) values, as indicated in Fig. 8a. Moreover, when the values of \(G_{1}\) increase, the waves’ amplitudes increase, while the wavelengths remain unaffected. Conversely, the temporal behavior of \(a_{2}\) has periodic manner over the investigated time interval, with no discernible impact from changes of \(G_{1}\), as demonstrated in Fig. 8b.

It's worth noting that the amplitudes of the periodic plotted time response describing the behavior of \(\theta_{1}\) over time decrease as the \(G_{1}\) values increase, while the number of waves remains unchanged, as depicted in Fig. 9a. On the other hand, the plotted time response for \(\theta_{2}\) exhibit a periodic pattern without any variation regarding the values of \(G_{1}\), as seen in Fig. 9b. The rationale behind this lies in the fourth mathematical formula within the system of equations (38), which remains independent of \(G_{1}\).

In the planes the \(\theta_{1} a_{1}\) and \(\theta_{2} a_{2}\), the projections of the plotted curves in Fig. 10a, b are plotted, each corresponding to various values of \(G_{1}\). As previously mentioned, the curves of \(a_{1}\) and \(\theta_{1}\) are impacted by the change in \(G_{1}\) values, and then curves in the respective planes change also, as illustrated in Fig. 10a. However, the plotted ones in the \(\theta_{2} a_{2}\) exhibit only one closed curve, confirming that \(a_{2}\) and \(\theta_{2}\) are independent on \(G_{1}\).

Based on the various values of \(G_{1}\), the AS of the gained results \(\theta\) and \(\phi\) are plotted in Fig. 11, where the wave packet amplitudes increase with the increase of \(G_{1}\) values. The relations between \(\theta ,\dot{\theta }\) and \(\phi ,\dot{\phi }\) has been illustrated graphically in Fig. 12 in accordance with the same values of \(G_{1}\). The disturbances observed are attributed to the quasi-periodicity inherent in the solutions.

The curves depicted in Figs. 13, 14, 15, 16, and 17 illustrate how the various values of the damping coefficient \(C_{1}\) variation influences on the behavior of the modified amplitudes, phases, their projections in the planes \(\theta_{1} a_{1} ,\)\(\theta_{2} a_{2} ,\) the obtained solutions \(\theta ,\phi ,\) and their phase planes. It is seen that the periodic waves in Fig. 13 are influenced with the change in \(C_{1}\) values, as seen from the system of equations (38) that \(a_{1}\) and \(a_{2}\) depend directly on \(C_{1}\) values. Moreover, the amplitudes of these waves decrease in accordance with the increase of \(C_{1}\) values. The drawn curves in Fig. 14 shows the time variations of the modified phases \(\theta_{1}\) and \(\theta_{2}\) as dictated by the values of \(C_{1}\). These curves have periodicity forms and vary in accordance with the values of \(C_{1}\). The projections of the graphed curves in Figs. 13 and 14 are depicted in the \(\theta_{1} a_{1}\) and \(\theta_{2} a_{2}\) planes, as seen in Fig. 15, to generate closed curves, affirming the stability of the waves describing \(\theta_{1} ,a_{1} ,\theta_{2} ,\) and \(a_{2}\). The impact of \(C_{1}\) values on the behavior of the AS for the time response representing \(\theta\) and \(\phi\) is illustrated in parts (a) and (b) of Fig. 16. As stated earlier, these solutions exhibit quasi-periodic wave packets throughout the entire duration, wherein their amplitudes decrease with the rise of \(C_{1}\) values. The corresponding phase plane diagrams of these solutions are drawn in portions (a) and (b) of Fig. 17, showing some distortions attributed to the quasi-periodic nature of the solutions.

It must be noted that the key advantage of using time histories in dynamic system analysis is the ability to understand the system's evolution and identify behavioral patterns and trends over time. These histories play a crucial role in providing insights into a system's behavior, indicating whether it remains stable or transitions to an unstable state over the examined time interval. They can help identify periodic or quasi-periodic intervals in a system's behavior, making them valuable for tracking changes over time. By allowing early detection of deviations from expected performance, time histories are crucial for maintenance and operational decisions. Moreover, they are useful for detecting chaotic behavior in a system.

5 Analysing the case of steady-state

This section’s title refers to the examination and investigation of a system or phenomenon when it has reached a state of equilibrium, where its properties or variables no longer change with time. This analysis typically involves studying the behavior, characteristics, and stability of the system under steady-state conditions. This indicates a deliberate action taken to achieve a specific objective within the context of a mathematical or scientific analysis. By setting the initial derivatives of variables \(\theta_{k} \,(k = 1,2)\) and \(a_{k}\) to zero [43]. Therefore, a subsequent set of algebraic equations involving the variables \(\theta_{k}\) and \(a_{k}\) may be written as follows

$$ \begin{aligned} & G_{1} \cos \theta_{1} = a_{1} \left[ {3\sigma_{1} + \frac{{B_{1}^{2} }}{4}} \right. \\ & \quad \left. { + \frac{{p_{y}^{2} \,r_{y} }}{6}(p_{y}^{2} \,r_{y} - 6) + \frac{{M_{1} M_{2} }}{{\omega^{2} - 1}}} \right], \\ & G_{1} \sin \theta_{1} = - a_{1} \left( {\frac{{3B_{1} }}{2} + \frac{{M_{1} C_{1} }}{{\omega^{2} - 1}}} \right), \\ & a_{1} \left[ {\frac{{C_{1} (B_{1} - C_{2} ) + M_{2} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { + \frac{{(B_{1} C_{1} + 2M_{2} p_{y}^{2} \,r_{y} )}}{2}} \right]\cos \theta_{2} \\ & \quad + a_{1} \left[ {\frac{{M_{2} (B_{1} - C_{2} ) + C_{1} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { - \frac{{(B_{1} \,M_{2} - C_{1} \,p_{y}^{2} \,r_{y} )}}{2}} \right]\,\sin \theta_{2} \\ & = a_{2} \left\{ {\omega (\sigma_{1} + \sigma_{2} ) - \frac{1}{{8\omega^{2} }}\left[ {a_{2}^{2} \omega^{4} } \right.} \right. \\ & \quad - 2C_{2}^{2} \omega^{2} + (1 - r_{2y} )p_{y}^{2} \,r_{2y} \\ & \quad \left. {\left. { + \frac{{\omega^{2} (B_{2} C_{2} - M_{1} M_{2} )}}{{1 - \omega^{2} }}} \right]} \right\}, \\ & a_{1} \left[ {\frac{{\,M_{2} (B_{1} - C_{2} ) + C_{1} \,p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { - \frac{1}{2}(B_{1} \,M_{2} - C_{1} \,p_{y}^{2} \,r_{y} )} \right]\cos \theta_{2} \\ & \quad + a_{1} \left[ {\frac{{\,C_{1} (B_{1} - C_{2} ) + M_{2} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { + \frac{1}{2}\left( {B_{1} C_{1} + 2M_{2} \,B_{1} \,M_{2} - C_{1} \,p_{y}^{2} \,r_{y} } \right)} \right]\sin \theta_{2} \\ & = a_{2} \left[ {C_{2} \omega + \frac{{\omega^{3} (B_{1} M_{2} + C_{1} M_{1} )}}{{1 - \omega^{2} }}} \right]. \\ \end{aligned} $$
(39)

The reduction processes of this system to another suitable one, demand the removal of certain components (the modified phases \(\theta_{k}\)). Therefore, the desired new system, which is characterized by two nonlinear algebraic equations involving amplitudes \(a_{k}\) and frequency response functions \(\sigma_{k}\), can be obtained as follows:

$$ \begin{aligned} G_{1}^{2} & = 9a_{1}^{2} \left( {\sigma_{1} + \frac{{B_{1} }}{12}(B_{1} - 6) + \frac{{p_{y}^{2} \,r_{y} }}{12}(p_{y}^{2} \,r_{y} - 6)} \right. \\ & \quad \left. { + \frac{{M_{1} (M_{2} - C_{1} )}}{{3(\omega^{2} - 1)}}} \right)^{2} ,a_{1}^{2} \left\{ {\left[ {\frac{{C_{1} (B_{1} - C_{2} ) + M_{2} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right.} \right. \\ & \quad \left. { + \frac{{(B_{1} C_{1} + 2M_{2} p_{y}^{2} \,r_{y} )}}{2}} \right]^{2} + \left[ {\frac{{M_{2} (B_{1} - C_{2} ) + C_{1} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. {\left. { - \frac{{(B_{1} M_{2} - C_{1} p_{y}^{2} \,r_{y} )}}{2}} \right]^{2} } \right\} = a_{2}^{2} \left\{ {\left[ {\frac{{C_{2}^{2} \omega^{2} - p_{y}^{2} \,r_{2y}^{2} }}{{4\omega^{2} }}} \right.} \right. \\ & \quad - \frac{{C_{2}^{2} }}{2} + p_{y}^{2} \,r_{2y} + 2(\sigma_{1} + \sigma_{2} )\omega - \frac{1}{8}a_{20}^{2} \omega^{2} \\ & \quad \left. {\left. { + \frac{{\omega^{2} }}{{1 - \omega^{2} }}(\omega (B_{1} M_{2} + C_{1} M_{1} ) + (B_{2} C_{2} - M_{1} M_{2} )) + C_{2} \omega } \right]^{2} } \right\}. \\ \end{aligned} $$
(40)

It's important to emphasize that an essential aspect of assessing stability involves examining the scenario of steady-state solutions. To explore the behavior around a neighborhood of fixed points, we'll substitute the following expressions into the aforementioned system (38) [44, 45]

$$ a_{j} = a_{k0} + a_{k1} ,\,\,\,\,\,\,\,\theta_{k} = \theta_{k0} + \theta_{k1} \,\,\,\,\,(k = 1,2), $$
(41)

where \(a_{k1}\) and \(\theta_{k1}\) represent respective small perturbations from the solutions \(a_{k0}\) and \(\theta_{k0}\) at the steady-state of the system (39). Consequently, we can express the linearized system of (38) as

$$ \begin{aligned} & a_{10} \frac{{d\theta_{11} }}{d\tau } = \frac{{a_{11} }}{12}\left\{ {\left( {12\sigma_{1} + B_{1}^{2} + \frac{{4M_{1} \,M_{2} }}{{(\omega^{2} - 1)}}} \right.} \right. \\ & \quad \left. {\left. { + p_{y}^{2} \,r_{y} (p_{y}^{2} \,r_{y} - 6)} \right)} \right\} + \frac{{G_{1} }}{3}\theta_{11} \sin \theta_{10} , \\ & \frac{{da_{11} }}{d\tau } = - \frac{{G_{1} \theta_{11} }}{3}\cos \theta_{10} - \frac{{a_{11} }}{6}\left[ {B_{1} + \frac{{M_{1} C_{1} }}{{(\omega^{2} - 1)}}} \right], \\ & a_{20} \omega \left( {\frac{{d\theta_{11} }}{d\tau } + \frac{{d\theta_{21} }}{d\tau }} \right) = (\sigma_{1} + \sigma_{2} )\omega a_{21} \\ & \quad - \frac{{a_{21} }}{2}\left[ {\frac{{C_{2}^{2} \omega^{2} - p_{y}^{4} \,r_{2y}^{2} }}{{4\omega^{2} }} - \frac{{C_{2}^{2} }}{2} + \frac{{\omega^{2} (B_{2} C_{2} - M_{1} M_{2} )}}{{1 - \omega^{2} }}} \right. \\ & \quad \left. { + p_{y}^{2} \,r_{2y} - \frac{1}{8}a_{20}^{2} \omega^{2} } \right] - \frac{{a_{10} }}{2}\theta_{21} \sin \theta_{20} \left[ {\frac{1}{{\omega^{2} - 1}}(B_{1} C_{1} } \right. \\ & \quad \left. {\left. { - C_{1} C_{2} + M_{2} p_{y}^{2} \,r_{y} } \right) + \frac{1}{2}(B_{1} C_{1} + 2M_{2} p_{y}^{2} \,r_{y} )} \right] \\ & \quad + \frac{{a_{10} }}{2}\theta_{21} \cos \theta_{20} \left[ {\frac{{M_{2} (B_{1} - C_{2} ) + C_{1} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}}} \right. \\ & \quad \left. { - \frac{{(B_{1} M_{2} - C_{1} p_{y}^{2} \,r_{y} )}}{2}} \right], \\ & \omega \frac{{da_{21} }}{d\tau } = - \frac{{a_{21} }}{2}\left[ {\frac{{\omega^{3} (B_{1} M_{2} + C_{1} M_{1} )}}{{1 - \omega^{2} }} + C_{2} \omega } \right] \\ & \quad - \frac{{a_{10} \theta_{21} }}{2}\cos \theta_{20} \left[ {\frac{1}{{\omega^{2} - 1}}(C_{1} (B_{1} - C_{2} ) + M_{2} p_{y}^{2} \,r_{y} )} \right. \\ & \quad \left. { + \frac{{(B_{1} C_{1} + 2M_{2} p_{y}^{2} \,r_{y} )}}{2}} \right] \\ & \quad - \frac{{a_{10} \theta_{21} }}{2}\sin \theta_{20} \left[ {\frac{1}{{\omega^{2} - 1}}(B_{1} M_{2} + C_{1} p_{y}^{2} \,r_{y} - C_{2} M_{2} )} \right. \\ & \quad \left. { - \frac{{(B_{1} M_{2} - C_{1} p_{y}^{2} r_{y} )}}{2}} \right]. \\ \end{aligned} $$
(42)

The solutions of the above system can be easily derived when \(a_{k1}\) and \(\theta_{k1}\) are represented exponentially as \(q_{d} \,e^{\lambda T}\). Here, \(q_{d} \,(d = 1,2,3,4)\) represent constants and \(\lambda\) describes unknown perturbations of the eigenvalues. For the steady-state solutions \(a_{k0}\) and \(\theta_{k0}\) to be asymptotically stable, the real parts of the roots of the characteristic equations below must be negative [46].

$$ \lambda^{4} + \Gamma_{1} \lambda^{3} + \Gamma_{2} \lambda^{2} + \Gamma_{3} \lambda + \Gamma_{4} = 0, $$
(43)

Thus, \(\Gamma_{d}\) denote functions of the unperturbed parameters \(a_{k0}\) and \(\theta_{k0}\) (see Appendix 1).

Since RHC [47] is a tool for determining the conditions under which steady-state solutions are viable, it implies that these criteria establish both the essential and complete conditions for such solutions to exist, as follows:

$$ \begin{aligned} & \Gamma_{1} > 0, \\ & \Gamma_{3} \left( {\Gamma_{1} \Gamma_{2} - \Gamma_{3} } \right) - \Gamma_{1}^{2} \Gamma_{4} > 0, \\ & \Gamma_{1} \Gamma_{2} - \Gamma_{3} > 0, \\ & \Gamma_{4} > 0. \\ \end{aligned} $$
(44)

To enhance accessibility, the preceding theoretical findings can be visually represented through computational means in the following section.

6 System stability examination

In this section, we delve into the dynamic behavior of the system through linear stability analysis. In addition to formulating the equations that describe the nonlinear aspects of the system, we also scrutinize the conditions necessary for stability. It has been observed that certain characteristics, such as the frequencies \(1,\omega ,\) and detuning parameters \(\sigma_{k} \,(k = 1,2)\), play a crucial role in meeting stability criteria.

The stability plots of the system are generated through a meticulously developed procedure, according to the parameters of equations (42) by using the parameters in Table 1. Mapping the amplitudes \(a_{k}\) of the oscillations against \(\sigma_{k}\) across multiple parametric domains illustrate the potential influence of these parameters on the existence of fixed points, as depicted in Figs. 18, 19, 20, 21, 22, 23. It should be mentioned that equations (42) are being used to yield Figs. 18, 19, 20, 21, 22, 23. These graphs depict the results obtained using selected values of the parameter \(\omega ,\,G_{1} ,\) and \(C_{1}\). Broadly speaking, the stable and unstable areas have been noted in the ranges \(\sigma_{j} \le - 0.06\) and \(- 0.06 < \sigma_{j}\) according to the prescribed parameters.

Fig. 18
figure 18

The FRC in the planes \(\sigma_{1} a_{k} \,\,(k = 1,2)\) at \(\omega \,( = 1.41,1.58,\,1.64)\), and \(\sigma_{2} = 0.2\)

Full size image
Fig. 19
figure 19

The FRC in the planes \(\sigma_{2} a_{k} \,\,(k = 1,2)\) at \(\omega \,( = 1.41,1.58,\,1.64)\), and \(\sigma_{1} = 0.1\)

Full size image
Fig. 20
figure 20

The resonance curves with the planes \(\sigma_{1} a_{k} \,\,(k = 1,2)\) at \(G_{1} ( = 0.0001,0.0002,0.0003)\), and \(\sigma_{2} = 0.2\)

Full size image
Fig. 21
figure 21

Resonance curves with the planes \(\sigma_{2} a_{k} \,\,(k = 1,2)\) at \(G_{1} ( = 0.0001,0.0002,0.0003)\), and \(\sigma_{1} = 0.1\)

Full size image
Fig. 22
figure 22

Resonance curves with the plane \(\sigma_{1} a_{k} \,\,(k = 1,2)\) at \(C_{1} ( = 0.00001,0.00003,0.00005)\), and \(\sigma_{2} = 0.2\)

Full size image
Fig. 23
figure 23

The FRC with the planes \(\sigma_{2} a_{k} \,\,(k = 1,2)\) at \(C_{1} ( = 0.00001,0.00003,0.00005)\), and \(\sigma_{1} = 0.1\)

Full size image

It's crucial to highlight that solid curves delineate the domain of stable fixed points, whereas dashed curves signify regions of instability. The frequency response curves (FRC) in Fig. 20 are drawn in the planes \(\sigma_{1} a_{k}\) when \(\omega\) has the aforementioned values of, \(\sigma_{2} = 0.2\), and \(C_{1} = 0.00001\) to generate the stability and instability areas. It is noted that the regions depicted in part (a) are affected by variations in \(\omega\) values, whereas no discernible alteration is observed in the represented FRC depicted in part (b). In Fig. 18a, b, three peaks fixed points are discerned. These points may be stable or not, where they are situated between the stable and unstable areas. However, within the plane \(\sigma_{1} a_{2}\), a solitary unstable peak fixed point is evident, while no peaks are observed in the plane \(\sigma_{1} a_{1}\).

On the other hand, the FRC in the planes \(\sigma_{2} a_{k}\) are drawn, to reveal the stability areas at \(\sigma_{1} = 0.1\), and \(C_{1} = 0.00001\) when \(\omega ( = 1.41,1.58,\,1.64)\). The information conveyed in Fig. 18a remains entirely consistent with the depicted curves in Fig. 19a concerning stability regions, critical points, and peak points. In Fig. 19b, the FRC exhibits one critical fixed point, which could be situated within either stable or unstable regions. Additionally, three peak fixed points are discerned within the unstable region of fixed points.

Examination of the plotted curves in Figs. 20 and 21 shows they are represented, respectively, in the \(\sigma_{1} a_{k}\) and \(\sigma_{2} a_{k}\) planes when the force’s amplitude \(G_{1}\) has the values \((0.0001,0.0002,0.0003)\). The FRC in Figs. 20b and 21b are not influenced with the change in \(G_{1}\) values, whereas those illustrated in Figs. 20a, and 21a exhibit sensitivity to such changes. The positive influence of the values of \(C_{1} ( = 0.00001,0.00003,0.00005)\) on the plotted FRC in the analyzed planes \(\sigma_{1} a_{k}\) and \(\sigma_{2} a_{k}\) is evident in Figs. 22 and 23, respectively. One can easily calculate the numbers of the fixed points whether critical or not in Figs. 20, 21, 22, 23.

Studying the characteristics of FRC for vibrating dynamical systems offers several benefits:

  • Insight into system’s behavior: FRC provide a comprehensive understanding of how a system responds to varying frequencies of excitation. By analysing these curves, engineers can gain insights into the system's natural frequencies, resonance behavior, damping characteristics, and overall dynamic response.

  • Design optimization: Understanding FRC helps engineers optimize the design of vibrating systems to meet specific performance criteria. By identifying resonance frequencies and critical points, designers can adjust parameters to enhance system stability, minimize vibrations, and improve efficiency.

  • Performance prediction: FRC analysis enables engineers to predict the performance of vibrating systems under different operating conditions. By studying the curves, they can anticipate how changes in input frequency, damping, or other parameters will affect system behavior, allowing for better performance prediction and control.

  • Fault diagnosis: Abnormalities in FRC can indicate potential faults or malfunctions within a vibrating system. By comparing measured FRC with expected or theoretical curves, specialists can diagnose issues such as structural damage, component wear, or improper tuning, facilitating timely maintenance or repairs.

  • Control system design: FRC serve as valuable tools in the design of control systems for vibrating systems. Engineers can use FRC information to develop control strategies that mitigate undesirable vibrations, regulate system responses, and improve overall performance.

Overall, studying the characteristics of frequency response curves enhances the understanding, design, prediction, diagnosis, and control of vibrating dynamical systems, leading to more efficient and reliable engineering solutions.

7 Nonlinear analysis

This section elucidates the characteristics of the nonlinear amplitude of the system (38) and their stabilities. To achieve this, let's delve into the following transformations [48, 49]

$$ \begin{gathered} A_{j} = \frac{1}{2}[\tilde{u}_{k} (\tau_{1} ,\tau_{2} ) + i\,\tilde{v}_{k} (\tau_{1} ,\tau_{2} )]e^{{ - i\tilde{\sigma }_{k} \tau_{1} }} \,\,\,(k = 1,2); \hfill \\ u_{k} = \varepsilon \tilde{u}_{k} ,\,\,\,\,\,\,\,\,\,\,\,v_{k} = \varepsilon \tilde{v}_{k} . \hfill \\ \end{gathered} $$
(45)

Here, the real and imaginary parts of the amplitudes are denoted by \(u_{k}\) and \(v_{k}\), respectively. Substituting these transformations into equations (23), (24), (27), and (28), and then segregating the real and imaginary components, we obtain

$$ \begin{aligned} & \frac{{dv_{1} }}{d\tau } - \frac{{u_{1} }}{12}\left[ {p_{y}^{2} \,r_{y} (6 - p_{y}^{2} \,r_{y} ) - B_{1}^{2} - \frac{{4M_{1} M_{2} }}{{(\omega^{2} - 1)}}} \right]v_{1} \\ & \quad + \left[ {\frac{{B_{1} }}{2} + \frac{{C_{1} M_{1} }}{{3(\omega^{2} - 1)}} + \sigma_{1} } \right] - \frac{{G_{1} }}{3} = 0, \\ & \frac{{du_{1} }}{d\tau } + \frac{{u_{1} }}{6}\left[ {3B_{1} + \frac{{2C_{1} M_{1} }}{{(\omega^{2} - 1)}} + 6\sigma_{1} } \right] \\ & \quad - \frac{{v_{1} }}{12}\left[ {B_{1}^{2} + \frac{{4M_{1} M_{2} }}{{(\omega^{2} - 1)}} - p_{y}^{2} \,r_{y} (6 - p_{y}^{2} \,r_{y} )} \right] = 0, \\ & \omega \frac{{du_{2} }}{d\tau } + \frac{{v_{2} }}{{8\omega^{2} }}\left[ {\frac{{4\omega^{4} (B_{2} C_{2} - M_{1} M_{2} )}}{{(\omega^{2} - 1)}}} \right. \\ & \quad \left. { - 2(C_{2}^{2} \omega^{2} + p_{y}^{4} \,r_{2y}^{2} ) + 8\omega^{2} p_{y}^{2} \,r_{y} - 4\omega^{4} (u_{2}^{2} + v_{2}^{2} )} \right] \\ & \quad - \frac{{u_{2} }}{2}\left[ {\frac{{\omega^{3} (B_{2} M_{2} + C_{1} M_{1} )}}{{2(1 - \omega^{2} )}} + C_{2} \omega + 2\sigma_{2} } \right] \\ & \quad + \frac{{B_{1} (C_{1} - C_{2} ) + M_{2} p_{y}^{2} \,r_{y} }}{{\omega^{2} - 1}} = 0, \\ & \omega \frac{{dv_{2} }}{d\tau } + \frac{{u_{2} }}{{8\omega^{2} }}\left[ {\frac{{4\omega^{4} (B_{2} C_{2} - M_{1} M_{2} )}}{{(1 - \omega^{2} )}}} \right. \\ & \quad \left. { - C_{2}^{2} \omega^{2} + (4\omega^{2} - p_{y}^{2} \,r_{2y} )p_{y}^{2} \,r_{2y} - 4\omega^{4} (u_{2}^{2} + v_{2}^{2} )} \right] \\ & \quad + \frac{{(B_{1} M_{2} - C_{1} p_{y}^{2} \,r_{y} - C_{2} M_{2} )}}{{\omega^{2} - 1}} \\ & \quad + \frac{{v_{2} }}{4}\left[ {\frac{{\omega^{3} (B_{2} M_{2} + C_{1} M_{1} )}}{{(1 - \omega^{2} )}} + 2(C_{2} \omega + 2\sigma_{2} )} \right] = 0. \\ \end{aligned} $$
(46)

The aforementioned system has been numerically solved and visually depicted in Figs. 24, 25, 26, 27, 28, 29, based on the provided parameters outlined below

$$ \begin{aligned} & \omega ( = 1.41,1.58,1.64),\quad G_{1} ( = 0.0001,0.0002,0.0003), \\ & C_{1} ( = 0.00001,0.00003,0.00005), \\ & \sigma_{1} = 0.1,\quad \sigma_{2} = 0.2,\quad u_{1} (0) = 0.1, \\ & v_{1} (0) = 0.8,\quad u_{2} (0) = 0.5,\quad v_{2} (0) = 0.4. \\ \end{aligned} $$
Fig. 24
figure 24

Positive impact of \(\omega ( = 1.41,1.58,1.64)\) values on: a the evolution of \(u_{1} (\tau )\), b the variation of \(v_{1} (\tau )\), and c the projections of the amplitudes’ trajectories within the plane \(u_{1} v_{1}\)

Full size image
Fig. 25
figure 25

The favorable influence of \(\omega ( = 1.41,1.58,1.64)\) values on: a the function \(u_{2} (\tau )\), b the function \(v_{2} (\tau )\), and c the curves in the plane \(u_{2} v_{2}\)

Full size image
Fig. 26
figure 26

Positive impact of \(\,G_{1}\) values on: a the evolution of \(u_{1} (\tau )\), b the variation of \(v_{1} (\tau )\), and c the projections of the amplitudes’ trajectories within the plane \(u_{1} v_{1}\)

Full size image
Fig. 27
figure 27

Influence of \(\,G_{1}\) values on: a \(u_{2} (\tau )\), b \(v_{2} (\tau )\), and c the curves in the plane \(u_{2} v_{2}\)

Full size image
Fig. 28
figure 28

The good impact of \(\,C_{1}\) values on: a \(u_{1} (\tau )\), b \(v_{1} (\tau )\), and c the curves within the plane \(u_{1} v_{1}\)

Full size image
Fig. 29
figure 29

Influence of \(\,C_{1}\) values on: a \(u_{2} (\tau )\), b \(v_{2} (\tau )\), and c the curves in the plane \(u_{2} v_{2}\)

Full size image

The adjusted amplitudes \(u_{k} \,\,(k = 1,2)\) and \(v_{k}\) versus \(\tau\) were meticulously examined across diverse parametric domains, and the projections of these amplitudes in phase-planes \(u_{k} v_{k}\) have been illustrated, delineated across segments (a), (b), and (c) within these figures. The depicted curves are calculated for distinct values of \(\omega ,\,G_{1} ,\) and \(C_{1}\).

The impact of the various values of \(\omega\) on the paths of \(u_{1} ,v_{1}\) and \(u_{2} ,v_{2}\) is depicted through the diagrams in Figs. 24 and 25, respectively. In these figures, periodic waves are depicted in sections (a) and (b), where the number of oscillations moderately rises with increasing values of the natural frequency \(\omega\), while the wavelengths decrease, as seen in Fig. 24. Conversely, the oscillation count of the illustrated waves diminishes as the values of \(\omega\) increase, consequently leading to an elongation of their wavelengths over time and then their wavelengths increase during over time, as displayed in Fig. 25. The related phase plane curves in \(u_{1} v_{1}\) and \(u_{2} v_{2}\) are depicted Figs. 24c and 25c, respectively.

Analyzing the temporal patterns of waves for both variables \(u_{k}\) and \(v_{k}\), alongside the associated phase plane trajectories in the \(u_{k} v_{k}\) planes, considering the influence of varying values of \(G_{1}\), is depicted in Fig. 26 and 27. The drawn waves in portions (a) and (b) of these figures have periodic forms. One can observe that the amplitudes of the waves decrease with the increase in \(G_{1}\) values, as explored in Fig. 26a, b. The curves with the plane \(u_{1} v_{1}\) have been impacted with \(G_{1}\) values, which correspond to the happened change in \(u_{1}\) and \(v_{1}\), see Fig. 26c. On the contrary, there is no alteration in the amplitudes of the waves describing \(u_{2}\) and \(v_{2}\), as illustrated in Fig. 27a, b. Hence, only a singular closed curve is depicted in Fig. 27c. This limitation stems from the non-explicit dependence of the system of equations (57) on \(G_{1}\).

The inspection of the presented curves in Figs. 28 and 29 shows that they are calculated when the values \(C_{1}\) vary. It is noted that the equations of system (57) depend on the parameter \(C_{1}\). Therefore, it can be anticipated that the diverse values of this parameter exert a beneficial influence on the depicted curves in these figures, whether in terms of time history or phase plane graphs. The amplitude of the waves diminishes along with their wavelengths, to some degree, with the increase in \(C_{1}\) values, as observed in parts of these figures. It's crucial to emphasize that the plotted closed symmetric trajectories provide insight into the stable behavior of the illustrated waves, and consequently, of the entire system.

8 Chaotic motion

Chaotic motion, a fascinating phenomenon within dynamic systems, defies traditional notions of predictability and stability. It's characterized by seemingly random, yet deterministic behavior, where tiny variations in initial conditions lead to drastically different outcomes over time. Chaotic systems often exhibit complex, irregular patterns that defy straightforward analysis, making them a subject of intense study across various scientific disciplines. Understanding chaotic motion provides valuable insights into the underlying dynamics of natural and engineered systems, shedding light on everything from turbulent fluid flow to the behavior of celestial bodies.

In the examined dynamical system, small adjustments to its parameters can significantly influence its behavior. Consequently, the system exhibits three distinct types of movement, as detailed in the following. We will specifically illustrate LE for \(\lambda_{s} \,\,(s = 1,2,3,4)\), BDs for variables \(\theta\) and \(\phi\), and the spectrum under the influence of \(C_{2}\) at step 0.00001.

In Fig. 30a, b, a stable limit cycle representing periodic behavior gives rise to a quasi-periodic orbit as a parameter changes, which can lead to the breakdown of quasi-periodicity and the onset of chaos, known as torus bifurcation. The Lyapunov spectrum exhibited various forms of movement, with two distinct ranges of \(C_{2}\), each corresponding to a different type of dynamics as seen in Fig. 30c. Within the first region of \(C_{2} \in [0,0.125]\), there are multiple Lyapunov spectrums divided into two groups with positive and negative values. Therefore, the system's behavior can be described as chaotic motion. we observed that the Lyapunov spectrum lines are grouped in a form close to a straight line whose coordinates start from a point close to zero. This indicates that the movement adheres to a quasi-periodic pattern, which is also apparent in the BDs for the corresponding range of \(\theta\) and \(\phi\). In the second range \(\left( {0.125,0.25} \right]\), we observed that the Lyapunov spectrum lines are grouped in a form close to a straight line whose coordinates start from a point close to zero. This indicates that the movement adheres to a quasi-periodic pattern, which is also apparent in the BDs for the corresponding range of \(\theta\) and \(\phi\).

Fig. 30
figure 30

(a, b) present BDs for \(\theta\) and \(\phi\), while c shows their spectrum of Lyapunov

Full size image

The Poincaré maps dots and phase portraits are depicted in Fig. 31, with blue curves representing the phase portraits and red dots symbolizing the Poincaré maps. In this figure, we choose two values of \(C_{2} ( = 0.17,\,0.2)\) within the second range. There are closed blue curves that eventually turn into one red point as seen in Fig. 31a, which means that the motion is periodic. In Fig. 31c, the pattern of red dots in the Poincaré map reveals nearly a closed trajectory for both variables \(\theta\) and \(\phi\) confirming the earlier conclusion regarding the quasi-periodic motion of the system. Conversely, due to the chaotic behavior, the red dots at \(C_{2} = 0.01\) in Fig. 31b starts to exhibit random divergence.

Fig. 31
figure 31

Poincaré maps and phase portraits for the variables \(\theta\) and \(\phi\) at a \(C_{2} = 0.17\), b \(C_{2} = 0.01\), c \(C_{2} = 0.2\)

Full size image

One can conclude from this section that Lyapunov spectra, BDs, phase portraits, and Poincaré maps provide valuable tools for characterizing the behavior of vibrating dynamical systems, enabling researchers to analyze stability, predict bifurcations, visualize trajectories, and understand the underlying dynamics.

9 Conclusion

The two-dimensional movement of a dynamical system with 2DOF has been investigated. Employing Lagrange’s equation, the equations that govern the system were deduced and solved asymptotically using the MS techniques, yielding results up to the approximation of third-order. All resonance scenarios have been categorized, with two examined concurrently to derive modulation formulations. Graphical illustrations of the frequency–response curves and frequency-amplitude curves have been utilized to underscore the favorable influence of parameters on movement. The NS for the original system are derived using the fourth-order Runge–Kutta numerical approach and emulated against perturbation approach results archived previously. The stability and lack of stability regions of fixed points in steady-state scenarios are assessed through the root-locus criterion. Additionally, nonlinear stability analysis has been conducted to verify the system's steady behavior. The system exhibits three distinct types of motion: periodic, quasi-periodic, and chaotic which are illustrated and analyzed via bifurcation plots, Poincaré graphs, and Lyapunov spectra.

Overall, these items are indispensable tools for researchers working with vibrating dynamical systems, enabling them to analyze system behavior, predict stability, design optimal systems, and validate mathematical models. Given the potential applicability of the achieved outcomes of this work in various engineering contexts involving vibrational control, this research carries substantial scientific significance and relevance.

10 Future work

Exploring other dynamical models with 3DOF or 4DOF could be a direction for future research. More importantly, different perturbation methods could be used to derive analytical solutions. Moreover, the rigid body problem could be modeled as a pendulum, with the support point moving along different paths. We will also investigate periodic and quasi-periodic solutions, along with the chaotic behavior of the parameters affecting the motion. Additionally, we will compare our results with previous studies to assess the novelty of our work.