Stochastic optimal control of a coupled tri-stable energy harvester under correlated colored noises

Abstract

In this paper, the stochastic optimal control of a tri-stable energy harvester (TEH) under a standard rectifier circuit driven by correlated colored noises is considered. From the view of physical intuition, the control force is directly separated into conservative component and dissipative one. Then, the stationary probability density function (SPDF) and the DC power of the controlled electromechanical coupled TEH can be derived by using the stochastic averaging based on energy-dependent frequency. The weighted combination of mean DC power and rectification efficiency is regarded as a performance index to transform the stochastic optimal control problem into an extremum problem of a multivariable function. The stochastic direct optimal control strategy developed in this paper avoids the trouble of dealing with complex differential equations. In contrast with the uncontrolled case, the TEH under direct optimal control achieves significant optimization of harvesting performance. The cross-correlation between the additive and multiplicative colored noises can break the symmetry of SPDF to induce random transition. The power conversion efficiency of the harvesting system can be optimized by choosing the appropriate noise intensities.

1 Introduction

With the rapid development of microelectronics and microfabrication technologies, the vibration energy harvesting that converts ambient vibration into electrical energy has been flourishing in recent years [1, 2]. Compared with the chemical battery, it is a potential way to provide a continuous scalable energy source. Many researches [3,4,5,6] have shown that the nonlinear vibration energy harvesters (VEHs) (such as mono-stable VEH [4], bi-stable VEH [7, 8], TEH [9, 10]) constructed by intentionally introducing nonlinear restoring force can effectively enhance power output with a higher harvesting potential. The TEH has received extensive attention because of its sustained high output level even under low frequency or ultra-low frequency vibration [10,11,12,13]. For instance, Kim et al. [10] established a mathematical model of the TEH to study its multi-stable state and nonlinear dynamic behavior. They pointed out that the harvester system can exhibit multi-stable behavior, which depended on the position and distance of the magnets. Zhang et al. [12] investigated the dynamics of mono-, bi- and tri-stable VEHs under colored noise and periodic excitation. They found that the mean harvested power of TEH was better than that of mono- and bi-stable VEHs. Unfortunately, the alternating current harvested by the harvester from ambient vibration cannot directly supply electronics. It must be converted into direct current through a nonlinear rectifier circuit to achieve the purpose of supplying power to the external electronics [14]. However, the nonlinear rectifier circuit will bring complex mutual coupling behavior to the harvesting system, which leads researchers to tend to simplify it as a load resistance [15,16,17]. Besides, the previous investigations on TEHs under nonlinear rectifier circuits rarely consider random excitation, especially in the case of correlated additive and multiplicative colored noises.

Most researches on TEHs are used to employ the deterministic harmonic excitation or Gaussian white noise to replace the actual environmental excitation [18,19,20,21]. In fact, engineering systems are usually related to random ambient vibrations [22,23,24]. In addition, Gaussian white noise is an ideal case of the stochastic fluctuations with zero correlation time [25]. Yet, the environmental vibration often deviates from the ideal case in actual applications. The colored noise with nonzero correlation time is necessary to be chosen to describe the random fluctuating vibration with large correlation time [26,27,28]. In energy harvesting applications, noise is usually assumed to be additive. In fact, multiplicative noise is ubiquitous in nature, such as the roll motion of a ship under random wave [29] and the energy harvesting through pendulum motion [30]. In fact, energy harvesting driven by correlated additive and multiplicative noises has gradually attracted the attention of researchers [31,32,33,34]. For example, Vocca et al. [32] compared the energy harvesting of nonlinear cantilever beams and buckled beams driven by correlated Gaussian white noise. Liu et al. [34] proposed a new quasi-conservative stochastic averaging to analyze the probabilistic response of nonlinear vibration energy harvesting system driven by exponentially correlated Gaussian colored noise. Thus, the correlated colored noises are considered in this paper to simulate the ambient vibration to drive the coupled TEH.

How to improve the efficiency of the harvesting device to efficiently supply electronic equipment has always been a crucial issue. The control method is considered to be a promising technology to improve energy harvesting, which can enhance the interaction between environmental excitation and cantilever vibration [35]. In fact, the control strategy has been successfully applied to the performance optimization of the harvester [36,37,38,39,40,41,42,43,44,45,46,47]. For example, Scruggs et al. [36] presented a technique to optimize the power generated from random vibration using a resonant energy harvester to enhance wave energy harvesting. Zhang et al. [37] proposed a sliding mode control algorithm to improve energy harvesting. They pointed out that for mono-stable VEH or bi-stable one in the multi-solution region, the rotatable magnet based on sliding mode control is beneficial to reach the high-energy orbit. Zhang et al. [42] constructed the time-delay feedback control as an electromechanical coupled VEH mounted on a rotational tire to improve the performance of a bi-stable VEH. Mohammadpour et al. [43] proposed the control of chaos based on a chaos detection algorithm and delayed feedback control to improve the efficiency of a bi-stable energy harvester. Telles Ribeiro et al. [45] realized the chaos control mechanism by combining a displacement actuator and a digital controller to stabilize the system dynamics. Kumar et al. [46] utilized Ott Grebogi Yorke [48] chaotic control method combined with Linear Quadratic Regulator to design the control force to maintain high-energy orbit, which improved the output power of the harvester. From the perspective of optimal energy harvesting, the stochastic optimal control can be employed to optimize the harvesting system [49]. However, traditional stochastic optimal control strategies usually involve complex differential equations [50]. Moreover, few researchers have carried out stochastic optimal control for the TEHs with strong nonlinear electromechanical coupled. Therefore, to achieve the performance optimization, this paper is devoted to using stochastic direct optimal control to realize the performance optimization of the TEH interfaced with a standard circuit driven by correlated colored noises. Where, the stochastic averaging based on energy-dependent frequency is utilized to solve the strongly nonlinear harvesting system. In addition, Table 1 gives the potential advantages and disadvantages of the stochastic optimal control strategy proposed in this paper by comparing with control of chaos.

Table 1 Potential advantages and disadvantages of the control strategy

The purpose of this work is to investigate the stochastic optimal control of a TEH interfaced with a standard rectifier circuit driven by correlated colored noises to improve the harvesting performance. The paper is organized as follows: Sect. 2 gives a detailed description of the stochastic-optimal-controlled TEH interfaced with a standard rectifier circuit driven by correlated colored noises. In Sect. 3, the stochastic optimal control problem is described in detail. Then, the SPDF of the controlled system is derived by the stochastic averaging based on energy-dependent frequency. The effects of correlated colored noises, control and system parameters on the steady-state dynamical behaviors of the harvester are further studied to enhance harvesting performance. Section 4 investigates the performance optimization of the harvester from the perspectives of stochastic response analysis and direct optimal control. In Sect. 5, some specific conclusions are discussed.

2 Stochastic-optimal-controlled electromechanical TEH

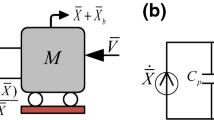
The structure diagram of the stochastic-optimal-controlled electromechanical TEH considered in this paper is shown in Fig. 1. The harvesting device consists of a TEH, a standard rectifier circuit and a stochastic optimal controller. The TEH is coupled with the rectifier circuit to realize the conversion from vibration to DC power. The correlated multiplicative and additive colored noises are employed to describe the actual road excitation. According to Fig. 1, the dimensionless electromechanical coupled system with the stochastic optimal control can be written as

$$ \begin{aligned} &\ddot{X} + \beta_{0} \dot{X} + \frac{{{\text{d}}U_{0} \left( X \right)}}{{{\text{d}}X}} + \kappa Y = - \ddot{X}_{b} + u\left( {X,\dot{X}} \right), \hfill \\ & \dot{Y} + I = \dot{X}, \hfill \\ \end{aligned} $$

(1)

where X represents the dimensionless displacement; $\beta_{0}$ is the dimensionless damping coefficient; $\kappa$ denotes the electromechanical coupled coefficient; $Y$ is the piezoelectric voltage; $u\left( {X,\dot{X}} \right)$ denotes the undetermined feedback control. The dimensionless current I flowing into the rectifier circuit can be described as [9]

$$ I = \left\{ \begin{array}{l} \lambda \dot{Y}_{R} + \alpha Y_{R} ,\quad Y = Y_{R} \hfill \\ - \lambda \dot{Y}_{R} - \alpha Y_{R} ,\quad Y = - Y_{R} \hfill \\ 0,\quad \left| Y \right| < Y_{R} \hfill \\ \end{array} \right., $$

(2)

where $\lambda = {{C_{R} } \mathord{\left/ {\vphantom {{C_{R} } {C_{P} }}} \right. \kern-0pt} {C_{P} }}$ is the ratio of the filter capacitance $C_{R}$ to the capacitance $C_{P}$ of the piezoelectric material. $\alpha$ is the time constant ratio. And $Y_{R}$ is the dimensionless rectified voltage.

Fig. 1

Schematic plot of the controlled TEH interfaced with a standard rectifier circuit

The symmetric potential function $U_{0} \left( X \right)$ in Eq. (1) is

$$ U_{0} \left( X \right) = \frac{1}{2}k_{1} X^{2} + \frac{1}{4}k_{3} X^{4} + \frac{1}{6}k_{5} X^{6} , $$

(3)

in which, $k_{i} \,\;(i = 1,3,5)$ define the dimensionless linear, cubic and quintic stiffness coefficients, respectively.

In Eq. (1), $- \ddot{X}_{b}$ represents the base acceleration, specifically $- \ddot{X}_{b} = \xi_{1} \left( t \right) + X\xi_{2} \left( t \right)$. The additive noise $\xi_{1} \left( t \right)$ and multiplicative noise $\xi_{2} \left( t \right)$ are correlated colored noises, which satisfy the following statistical properties

$$ \begin{gathered} \left\langle {\xi_{1} \left( t \right)} \right\rangle = 0,\left\langle {\xi_{1} \left( t \right)\xi_{1} \left( s \right)} \right\rangle = \frac{{D_{1} }}{{\tau_{1} }}\exp \left[ { - \frac{{\left| {t - s} \right|}}{{\tau_{1} }}} \right],S_{1} \left( \omega \right) = \frac{{D_{1} }}{{1 + \tau_{1}^{2} \omega^{2} }}, \hfill \\ \left\langle {\xi_{2} \left( t \right)} \right\rangle = 0,\left\langle {\xi_{2} \left( t \right)\xi_{2} \left( s \right)} \right\rangle = \frac{{D_{2} }}{{\tau_{2} }}\exp \left[ { - \frac{{\left| {t - s} \right|}}{{\tau_{2} }}} \right],S_{2} \left( \omega \right) = \frac{{D_{2} }}{{1 + \tau_{2}^{2} \omega^{2} }}, \hfill \\ \left\langle {\xi_{1} \left( t \right)\xi_{2} \left( s \right)} \right\rangle = \left\langle {\xi_{2} \left( t \right)\xi_{1} \left( s \right)} \right\rangle = \frac{{\gamma \sqrt {D_{1} D_{2} } }}{{\tau_{1} \tau_{2} }}\exp \left[ { - \frac{{\left| {t - s} \right|}}{{\tau_{1} \tau_{2} }}} \right], \hfill \\ \end{gathered} $$

(4)

where $S_{i} \left( \omega \right)$ (i = 1, 2) are the power spectral densities of the colored noises $\xi_{i} \left( t \right)$ (i = 1, 2). D₁ and D₂ are the intensity of colored noises $\xi_{1} \left( t \right)$ and $\xi_{2} \left( t \right)$, while $\tau_{1}$ and $\tau_{2}$ are the correlation time. $\gamma$ denotes the cross-correlation between the additive and the multiplicative colored noises.

3 Stochastic-optimal-controlled stationary response

3.1 Description of stochastic optimal control problem

Motivated by the performance optimization of the harvester, the stochastic optimal control is employed to design the feedback control rate $u\left( {X,\dot{X}} \right)$ in this paper. Undoubtedly, the output power is an important quantitative index of the harvesting performance. In fact, the rectification capacity of the nonlinear circuit is also crucial to the evaluation of harvesting performance. As shown in Fig. 2, the harvesting device typically requires two stages to convert the ambient vibration into direct current for supplying external electronics. That is, the transducer converts the mechanical energy in the environmental vibration into alternating current (AC), and then the harvested AC is converted into direct current (DC) through the rectifier circuit. Obviously, it is necessary to consider the rectification efficiency $\eta \%$ as an index to evaluate the harvesting capacity.

Fig. 2

Energy flowchart of an electromechanical coupled TEH device

Unfortunately, the trends of harvested DC power $E\left[ P \right]$ and $\eta$ are not always consistent. Therefore, in order to provide a compromise solution for nonlinear stochastic optimal control problems, the performance index is introduced as follows:

$$ J = w \cdot E\left[ P \right] + \left( {1 - w} \right) \cdot \eta , $$

(5)

where $E\left[ P \right]$ is the mean harvested DC power, while the $\eta$ represents the rectification efficiency of the nonlinear circuit. The constant $w \in \left[ {0,1} \right]$ is weighted factor, which balances the distance between output power and rectification efficiency. Particularly, when $w = 0$, $J = \eta$. In this case, $J$ characterizes the rectification efficiency. For $w = 1$, $J = E\left[ P \right]$, and $J$ measures the harvested DC power. For index (5), the order of magnitude of $E\left[ P \right]$ is different from that of $\eta$. For achieving multi-objective optimization, they are first transformed into objective functions $\overline{E}\left[ P \right]$ and $\overline{\eta }$ of the same order of magnitude, that is,

$$ \overline{E}\left[ P \right] = \frac{{E\left[ P \right] - m_{\rm{p}} }}{{n_{\rm{p}} - m_{\rm{p}} }}, $$

(6)

$$ \overline{\eta } = \frac{{\eta - m_{\eta } }}{{n_{\eta } - m_{\eta } }}, $$

(7)

where $\left[ {m_{P} ,n_{P} } \right]$ and $\left[ {m_{\eta } ,n_{\eta } } \right]$ represent the variation range of $E\left[ P \right]$ and $\eta$, respectively.

Thus, the performance index of the optimal control can be rewritten as

$$ J_{{{\text{opt}}}} = w \cdot \overline{E}\left[ P \right] + \left( {1 - w} \right) \cdot \overline{\eta }, $$

(8)

then, the system (1) and performance index (8) constitute the performance optimization problem of the controlled harvester. That is, the optimization problem is to search an optimal control force $u^{*} \left( {X,\dot{X}} \right)$ to maximize the index (8).

The feedback control directly depends on the generalized displacement and momentum. In other words, the control can change the restoring force (i.e., conservative component) and damping force (i.e., dissipation one). Therefore, inspired by physical intuition, the undetermined feedback control $u\left( {X,\dot{X}} \right)$ can be separated into two terms [51], that is

$$ u\left( {X,\dot{X}} \right) = - \frac{\partial G\left( X \right)}{{\partial X}} - f\left( {\tilde{H}\left( {X,\dot{X}} \right)} \right)\dot{X}, $$

(9)

where G(X) denotes the additional potential energy introduced by the stochastic direct optimal control method. And $f\left( {\tilde{H}\left( {X,\dot{X}} \right)} \right)$ represents the energy-dependent quasi-linear damping coefficient. The energy $\tilde{H}\left( {X,\dot{X}} \right)$ of the controlled system (1), disregarding the electromechanical coupling mechanism [i.e., $\kappa = 0$ in Eq. (1)], can be expressed as

$$ \tilde{H}\left( {X,\dot{X}} \right) = \frac{1}{2}\dot{X}^{2} + U_{0} \left( X \right) + G\left( X \right). $$

(10)

For convenience, $\tilde{H}\left( {X,\dot{X}} \right)$ is written as $\tilde{H}$ in the following analysis.

In addition, for the purpose of ensuring that the symmetrical tri-stable structure of the harvester is not destroyed, the G(X) and $f\left( {\tilde{H}} \right)$ in Eq. (9) can be further approximately expanded into the truncated Taylor series as follows.

$$ G\left( X \right) = b_{1} X^{2} + b_{2} X^{4} + b_{3} X^{6} , $$

(11)

$$ f\left( {\tilde{H}} \right) = a_{0} + a_{1} \tilde{H} + a_{2} \tilde{H}^{2} , $$

(12)

where $a_{i}$, $b_{j}$$\left( {i = 0,1,2,j = 1,2,3} \right)$ are the control parameters.

Then, substituting Eqs. (9), (11) and (12) into Eq. (1), the controlled system (1) can be transformed as follows

$$ \begin{aligned} & \ddot{X} + \tilde{\beta }\left( {\tilde{H}} \right)\dot{X} + \frac{{{\text{d}}\tilde{U}\left( X \right)}}{{{\text{d}}X}} + \kappa Y = \xi_{1} \left( t \right) + X\xi_{2} \left( t \right), \\ & \dot{Y} + I = \dot{X}, \\ \end{aligned} $$

(13)

where $\tilde{\beta }\left( {\tilde{H}} \right) = \beta_{0} + a_{0} + a_{1} \tilde{H} + a_{2} \tilde{H}^{2}$ represents the equivalent mechanical damping coefficient. The equivalent potential energy $\tilde{U}\left( X \right)$ of the controlled system (13) can be described as $\tilde{U}\left( X \right) = \frac{1}{2}\delta_{1} X^{2} + \frac{1}{4}\delta_{3} X^{4} + \frac{1}{6}\delta_{5} X^{6}$. And, $\delta_{1} = k_{1} + 2b_{1}$, $\delta_{3} = k_{3} + 4b_{2}$ and $\delta_{5} = k_{5} + 6b_{3}$ represent the equivalent linear, cubic and quintic stiffness coefficients, respectively. The $\tilde{U}\left( X \right)$ is a tri-stable potential with three stable equilibria ($X_{si}^{*} = \pm \sqrt {{{\left( { - \delta_{3} + \sqrt {\delta_{3}^{2} - 4\delta_{1} \delta_{5} } } \right)} \mathord{\left/ {\vphantom {{\left( { - \delta_{3} + \sqrt {\delta_{3}^{2} - 4\delta_{1} \delta_{5} } } \right)} {2\delta_{5} }}} \right. \kern-0pt} {2\delta_{5} }}}$, 0, i = 1, 2, 3) and two unstable saddle points ($X_{u}^{*} = \pm \sqrt {{{\left( { - \delta_{3} - \sqrt {\delta_{3}^{2} - 4\delta_{1} \delta_{5} } } \right)} \mathord{\left/ {\vphantom {{\left( { - \delta_{3} - \sqrt {\delta_{3}^{2} - 4\delta_{1} \delta_{5} } } \right)} {2\delta_{5} }}} \right. \kern-0pt} {2\delta_{5} }}}$). Then, the depths of the wells in the middle and on both sides can be expressed as

$$ \begin{aligned} \Delta V_{\rm{m}} & = \frac{1}{{24\delta_{5}^{2} }}\left[ { - 6\delta_{1} \delta_{3} \delta_{5} + \delta_{3}^{3} + \left( {\delta_{3}^{2} - 4\delta_{1} \delta_{5} } \right)^{3/2} } \right] \\ \Delta V_{l,r} & = \frac{1}{{12\delta_{5}^{2} }}\left( {\delta_{3}^{2} - 4\delta_{1} \delta_{5} } \right)^{3/2} . \\ \end{aligned} $$

(14)

Then, the well-depth ratio is defined as $R_{\Delta } {{ = \Delta V_{\rm{m}} } \mathord{\left/ {\vphantom {{ = \Delta V_{\rm{m}} } {\Delta V_{l,r} }}} \right. \kern-0pt} {\Delta V_{l,r} }}$. Figure 3a depicts the equivalent potential function $\tilde{U}\left( X \right)$ when the control parameters are set 0. It is observed that if the total energy is higher than the critical value $\tilde{U}_{1}$, the particle will jump among three potential wells with a higher output performance. Otherwise, it will be restricted in the well determined by the initial condition for intra-well vibration. From Fig. 3b, with the increase in control parameter b₂ or b₃, $\Delta V_{l,r}$ decreases while $\Delta V_{\rm{m}}$ remains almost unchanged. This means that the particle will be more likely to fall into the middle potential well with a mono-stable characteristic. Figure 3c–d investigates the influence of b₁ on the shape of the potential function. It is found that the well-depth ratio $R_{\Delta }$ increases with the increase in b₁, while $\Delta V_{\rm{m}}$ increases but $\Delta V_{l,r}$ decreases. Obviously, the control parameters $b_{j}$$\left( {j = 1,2,3} \right)$ have an important influence on the tri-stable potential, which means that they can affect the harvesting performance.

Fig. 3

a The equivalent potential $\tilde{U}\left( X \right)$ when the control parameters are 0, b the $\tilde{U}\left( X \right)$ under different control parameters b₂, b₃ with b₁ = 0, c the well-depth ratio $R_{\Delta }$ versus control parameter b₁ with b₂ = 0, b₃ = 0, d The variation of well-depth $\Delta V_{\rm{m}}$ or $\Delta V_{l}$ with $R_{\Delta }$. The stiffness coefficients are k₁ = 1, k₃ =  − 2.6, k₅ = 1

In short, the stochastic optimal control problem of the original system (1) is transformed into the parameter optimization problem of the controlled system (13), that is, the performance index (8) is minimized by searching the optimal $a_{i}^{*} ,\;b_{j}^{*} \left( {i = 0,1,2,j = 1,2,3} \right)$.

3.2 Stochastic stationary response of controlled system

From Eq. (8), to enhance the harvesting performance by using stochastic optimal control, it is necessary to obtain the stationary solution of the harvesting system. Therefore, the stochastic averaging based on energy-dependent frequency is employed in this paper to solve the stationary probability density function (SPDF) of the electromechanical coupled TEH.

According to the generalized harmonic transformation, the displacement and velocity of the controlled system (13) can be expressed as

$$ \begin{gathered} X\left( t \right) = A\left( H \right)\cos \left[ {\omega \left( H \right)t} \right] + X_{i}^{*} , \hfill \\ \dot{X}\left( t \right) = - A\left( H \right)\omega \left( H \right)\sin \left[ {\omega \left( H \right)t} \right], \hfill \\ \end{gathered} $$

(15)

where H(t) represents the total energy of the controlled system (13) when considering the rectifier circuit. $X_{i}^{*} \left( {i = 1, \ldots ,5} \right)$ define the equilibrium points. The $\omega \left( H \right)$ and $A\left( H \right)$ denote the energy-dependent frequency and amplitude, respectively. For convenience, $\omega \left( H \right)$ is recorded as $\omega$.

Combined with Eqs. (2), (13) and (15) , the piecewise piezoelectric voltage in Eq. (13) can be derived as [9]

$$ Y\left( t \right) = \left\{ \begin{array}{l} A\left( H \right)\left( {\cos \left( {\omega t} \right) - 1} \right) + Y_{R} ,\omega t \in \left[ {0,\theta \left( \omega \right)} \right) \hfill \\ - Y_{R} ,\omega t \in \left[ {\theta \left( \omega \right),\pi } \right) \hfill \\ A\left( H \right)\left( {\cos \left( {\omega t} \right) + 1} \right) - Y_{R} ,\omega t \in \left[ {\pi ,\theta \left( \omega \right) + \pi } \right) \hfill \\ Y_{R} ,\omega t \in \left[ {\theta \left( \omega \right) + \pi ,2\pi } \right] \hfill \\ \end{array} \right., $$

(16)

where $\theta \left( \omega \right) \in \left( {0,\pi } \right)$ is the blocked angle of the standard rectifier circuit in half one period. Y_R is the rectification voltage. The relationship between the two is as follows

$$ Y_{R} =\frac{{A\left( H \right)\left( {1 - \cos \theta \left( \omega \right)} \right)}}{2}. $$

(17)

According to Kirchhoff’s current law and Eqs. (2), (17), the Y_R and $\theta \left( \omega \right)$ can be derived as

$$ Y_{R} =\frac{2A\left( H \right)}{{2 + {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } \omega }} \right. \kern-0pt} \omega }}},\theta \left( \omega \right) = \arccos \left( {1 - \frac{4}{{2 + {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } \omega }} \right. \kern-0pt} \omega }}}} \right). $$

(18)

In general, the influence of the higher harmonic component generated by the rectifier circuit on the VEH can be ignored compared with that caused by the fundamental one. Thereby, the fundamental harmonic component $Y_{f} \left( t \right)$ can be utilized to approximate the piecewise voltage $Y\left( t \right)$ [9]. That is,

$$ Y\left( t \right) \approx Y_{f} \left( t \right) = \frac{1}{2\pi }\left( {X - X_{i}^{*} } \right)\left( {2\theta \left( \omega \right) - \sin \left[ {2\theta \left( \omega \right)} \right]} \right) + \frac{{\sin^{2} \left[ {\theta \left( \omega \right)} \right]}}{\pi \omega }\dot{X}. $$

(19)

Then, substituting Eq. (19) into System (13), the equivalent uncoupled equation of the controlled system can be approximately derived as

$$ \ddot{X} + \beta \left( {\tilde{H},\omega } \right)\dot{X} + \frac{{{\text{d}}U\left( X \right)}}{{{\text{d}}X}} = \xi_{1} \left( t \right) + X\xi_{2} \left( t \right), $$

(20)

where ${{{\text{d}}U\left( X \right)} \mathord{\left/ {\vphantom {{{\text{d}}U\left( X \right)} {{\text{d}}X}}} \right. \kern-0pt} {{\text{d}}X}} = {{{\text{d}}\tilde{U}\left( X \right)} \mathord{\left/ {\vphantom {{{\text{d}}\tilde{U}\left( X \right)} {{\text{d}}X}}} \right. \kern-0pt} {{\text{d}}X}} + {1 \mathord{\left/ {\vphantom {1 {2\pi }}} \right. \kern-0pt} {2\pi }} \cdot \kappa \left( {2\theta \left( \omega \right) - \sin \left[ {2\theta \left( \omega \right)} \right]} \right)\left( {X - X_{i}^{*} } \right)$. The $\beta \left( {\tilde{H},\omega } \right) = \tilde{\beta }\left( {\tilde{H}} \right) + {{\kappa \sin^{2} \left[ {\theta \left( \omega \right)} \right]} \mathord{\left/ {\vphantom {{\kappa \sin^{2} \left[ {\theta \left( \omega \right)} \right]} {\pi \omega }}} \right. \kern-0pt} {\pi \omega }}$ is the equivalent damping coefficient.

From Eq. (20), the equivalent potential energy $U\left( X \right)$ and the total energy $H\left( {X,\dot{X}} \right)$ of the uncoupled system can be written as [52]

$$ U\left( X \right) = \tilde{U}\left( X \right) + \frac{{\kappa \left( {2\theta \left( \omega \right) - \sin \left[ {2\theta \left( \omega \right)} \right]} \right)}}{4\pi }X^{2} , $$

(21)

$$ H\left( {X,\dot{X}} \right) = \frac{1}{2}\dot{X}^{2} + U\left( X \right). $$

(22)

The controlled equivalent uncoupled system (20) can be reconstructed by two first-order differential equations as follows:

$$ \dot{X} = \pm \sqrt {2H\left( {X,\dot{X}} \right) - 2U\left( X \right)} , $$

(23)

$$ \dot{H} = \dot{X}\xi_{1} \left( t \right) + \dot{X}X\xi_{2} \left( t \right) - \dot{X}g\left( {X,\dot{X}} \right), $$

(24)

where $g\left( {X,\dot{X}} \right) = \beta \left( {\tilde{H},\omega } \right)\dot{X} - \frac{{\kappa \left( {2\theta \left( \omega \right) - \sin \left[ {2\theta \left( \omega \right)} \right]} \right)}}{2\pi }X_{i}^{*}$.

Owing to the energy process in Eq. (24) being an approximate Markovian, the stochastic averaging based on energy-dependent frequency is utilized in this paper to obtain its averaged equation as follows:

$$ {\text{d}} H = m\left( H \right) + \sigma \left( H \right){\text{d}} B\left( t \right) $$

(25)

where the drift coefficient $m\left( H \right)$ and diffusion coefficient $\sigma^{2} \left( H \right)$ can be expressed as

$$ \begin{aligned} m\left( H \right) & = - \left\langle {\dot{X} \cdot g\left( {X,\dot{X}} \right)} \right\rangle_{t} + S_{1} \left( \omega \right) + S_{2} \left( \omega \right)\left\langle {X^{2} } \right\rangle_{t} + 2\gamma \cdot W\left( H \right)\left\langle X \right\rangle_{t} \\ \sigma^{2} \left( H \right) & = 2S_{1} \left( \omega \right)\left\langle {\dot{X}^{2} } \right\rangle_{t} + 2S_{2} \left( \omega \right)\left\langle {\dot{X}^{2} X^{2} } \right\rangle_{t} + 4\gamma \cdot W\left( H \right)\left\langle {\dot{X}^{2} X} \right\rangle_{t} , \\ \end{aligned} $$

(26)

in which, $S_{i} \left( \omega \right)$, $\left( {i = 1,2} \right)$ represent the power spectral density of additive colored noise $\xi_{1} \left( t \right)$ and multiplicative colored noise $\xi_{2} \left( t \right)$, which are defined in Eq. (4). And, $W\left( H \right) = {{\sqrt {D_{1} D_{2} } } \mathord{\left/ {\vphantom {{\sqrt {D_{1} D_{2} } } {\left[ {1 + \tau_{1}^{2} \tau_{2}^{2} \omega^{2} \left( H \right)} \right]}}} \right. \kern-0pt} {\left[ {1 + \tau_{1}^{2} \tau_{2}^{2} \omega^{2} \left( H \right)} \right]}}$. The $\left\langle \cdot \right\rangle_{t}$ denotes the time average, that is, $\left\langle \cdot \right\rangle_{t} = \frac{1}{T}\int_{0}^{T} {\left[ \cdot \right]} {\text{d}} t = \frac{1}{T}\oint {\frac{\left[ \cdot \right]}{{\dot{X}}}} {\text{d}} X$. By making H = U (A) in Eqs. (21) and (22), the closed-loop integral under different energy envelopes in the absence of stochastic optimal control is determined. Then, the motion period can be calculated as $T\left( H \right) = \oint {\frac{{{\text{d}} X}}{{\sqrt {2H\left( {X,\dot{X}} \right) - 2U\left( X \right)} }}}$. The energy-dependent frequency is $\omega \left( H \right) = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {T\left( H \right)}}} \right. \kern-0pt} {T\left( H \right)}}$. Obviously, $U\left( X \right)$ in Eq. (21) contains an unknown term $\omega$, which means that the iterative method is required to calculate the frequency $\omega$.

According to Eq. (25), the SPDF of total energy can be derived as

$$ P\left( H \right) = \frac{{C_{0} }}{{\sigma^{2} \left( H \right)}}\exp \left[ {\int {\frac{2m\left( H \right)}{{\sigma^{2} \left( H \right)}}{\text{d}} H} } \right]. $$

(27)

here, C₀ denotes a normalized constant.

Due to $P\left( {X_{1} ,X_{2} } \right) = {{P\left( H \right)} \mathord{\left/ {\vphantom {{P\left( H \right)} {T\left( H \right)}}} \right. \kern-0pt} {T\left( H \right)}}$, the joint SPDF of system (20) can be derived as

$$ P\left( {X,\dot{X}} \right) = \frac{{\left\langle {\dot{X}^{2} } \right\rangle_{t} C_{0} }}{{\sigma^{2} \left( H \right)}}\exp \left[ {\int_{0}^{H} {\left( {\frac{2m\left( \psi \right)}{{\sigma^{2} \left( \psi \right)}} - \frac{1}{{\left\langle {\dot{X}^{2} } \right\rangle_{t} }}} \right)} {\text{d}} \psi } \right]. $$

(28)

Then, the marginal SPDF can be described as

$$ \begin{gathered} P\left( X \right) = \int_{ - \infty }^{ + \infty } {p\left( {X,\dot{X}} \right)} {\text{d}} \dot{X}, \hfill \\ P\left( {\dot{X}} \right) = \int_{ - \infty }^{ + \infty } {p\left( {X,\dot{X}} \right)} {\text{d}} X. \hfill \\ \end{gathered} $$

(29)

3.3 Stochastic response analysis

Motivated to enhance harvesting performance, the effects of correlated colored noises, stochastic optimal control and system parameters on the steady-state dynamical behaviors of the TEH (1) are further studied.

The Monte Carlo simulation (MCS) based on Euler–Maruyama scheme [53, 54] for system (1) is used to validate the improved stochastic averaging based on energy-dependent frequency. Let $X_{1} = X$, $X_{2} = \dot{X}$, $X_{3} = Y$, $X_{4} = \xi_{1}$, $X_{5} = \xi_{2}$, the Itô stochastic differential equation of system (1) can be described as

$$ \begin{aligned} {\text{d}}X_{1} & = X_{2} {\text{d}}t \\ {\text{d}}X_{2} & = \left( {X_{4} + X_{1} X_{5} + u\left( {X_{1} ,X_{2} } \right) - \beta_{0} X_{2} - \frac{{{\text{d}} U_{0} \left( {X_{1} } \right)}}{{{\text{d}} X_{1} }} - \kappa X_{3} } \right){\text{d}}t \\ {\text{d}}X_{3} & = \left( {X_{2} - I} \right){\text{d}}t \\ {\text{d}}X_{4} & = - \frac{1}{{\tau_{1} }}X_{4} {\text{d}}t + \frac{1}{{\tau_{1} }}\sqrt {1 - \gamma^{2} } {\text{d}} B_{1} \left( t \right) + \frac{1}{{\tau_{1} }}\gamma {\text{d}} B_{2} \left( t \right) \\ {\text{d}}X_{5} & = - \frac{1}{{\tau_{2} }}X_{5} {\text{d}}t + \frac{1}{{\tau_{2} }}{\text{d}} B_{2} \left( t \right) \\ \end{aligned} $$

(30)

where B_i(t), (i = 1, 2) are the standard Brownian motion. For convenience, Eq. (30) can be rewritten as the following matrix form

$$ {\text{d}}{\mathbf{X}}\left( t \right) = {\mathbf{M}}\left( {{\mathbf{X}}\left( t \right),t} \right){\text{d}}t + {\mathbf{L}}\left( {{\mathbf{X}}\left( t \right),t} \right){\text{d}}{\mathbf{B}}\left( t \right) $$

(31)

where ${\mathbf{X}} = \left[ {X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} } \right]^{T}$, ${\mathbf{B}}\left( t \right) = \left[ {B_{1} \left( t \right),\,B_{2} \left( t \right)} \right]$. ${\mathbf{M}}\left( {{\mathbf{X}}\left( t \right),t} \right)$ is the drift term, and ${\mathbf{L}}\left( {{\mathbf{X}}\left( t \right),t} \right)$ is the diffusion term, that is,

${\mathbf{M}}\left( {{\mathbf{X}}\left( t \right),t} \right) = \left[ {\begin{array}{*{20}c} {X_{2} } \\ {X_{4} + X_{1} X_{5} + u\left( {X_{1} ,X_{2} } \right) - \beta_{0} X_{2} - \frac{{{\text{d}} U_{0} \left( {X_{1} } \right)}}{{{\text{d}} X_{1} }} - \kappa X_{3} } \\ {X_{2} - I} \\ { - \frac{1}{{\tau_{1} }}X_{4} } \\ { - \frac{1}{{\tau_{2} }}X_{5} } \\ \end{array} } \right],\;\;{\mathbf{L}}\left( {{\mathbf{X}}\left( t \right),t} \right) = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ {\frac{1}{{\tau_{1} }}\sqrt {1 - \gamma^{2} } } & {\frac{1}{{\tau_{1} }}\gamma } \\ 0 & {\frac{1}{{\tau_{2} }}} \\ \end{array} } \right].$

For Euler–Maruyama scheme, do the following at each step j,

• 1. Draw the random variable $\Delta {\mathbf{B}}_{j}$ from the distribution

  $$ \Delta {\mathbf{B}}_{j} \sim N\left( {{\mathbf{0}},{\mathbf{D}}\,\Delta t} \right) $$

  (32)

• 2. Compute

  $$ {\hat{\mathbf{X}}}\left( {t_{j + 1} } \right) = {\hat{\mathbf{X}}}\left( {t_{j} } \right) + {\mathbf{M}}\left( {{\hat{\mathbf{X}}}\left( {t_{j} } \right),t_{j} } \right)\Delta t + {\mathbf{L}}\left( {{\hat{\mathbf{X}}}\left( {t_{j} } \right),t_{j} } \right)\Delta {\mathbf{B}}_{j} $$

  (33)

  where ${\mathbf{D}} = \left[ {D_{1} ,\,D_{2} } \right]$, $\Delta t = t_{j + 1} - t_{j}$, $\Delta {\mathbf{B}}_{j} = {\mathbf{B}}\left( {t_{j + 1} } \right) - {\mathbf{B}}\left( {t_{j} } \right)$.

Then, the joint SPDF is plotted based on the numerical method and the analytical solution (28), respectively, as shown in Fig. 4. The two show good consistency, which verifies the effectiveness of the theoretical method. Motivated to further investigate the system response, the theoretical solutions (28) and (29) will be utilized to analyze the stochastic dynamics of controlled system (20).

Fig. 4

The joint SPDF. a Numerical result of system (1) under step size dt = 0.001, time span $\left[0, 8000\right]$ and b theoretical result based on Eq. (27) . The control parameters are set to 0. Other parameters are $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $D_{1} =0.003$, $D_{2} =0.003$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\beta =0.06$, $\lambda =100$, $\gamma = 0$

Then, the influence of correlated colored noises on the marginal SPDF based on Eq. (29) is analyzed. From Fig. 5, P(X) at the equilibrium points on both sides decreases with the increase in noises intensities. The P(X) at X = 0 increases with increasing the multiplicative noise intensity D₂, while it remains almost unchanged as the additive noise intensity D₁ increases. This indicates that the noise intensity of additive or multiplicative colored noise can strengthen the transition among the three potential wells, and the intensity D₂ plays a more significant role than that of D₁. However, the correlation times of correlated colored noises play the opposite role. In Fig. 6, the increase in correlation times increases the peak value on both sides of P(X) while the middle peak decreases, and the decrease caused by $\tau_{2}$ is more obvious. In this case, the particle becomes more likely to fall into one of the potential wells on both sides for intra-well vibration with a lower output level. As displayed in Fig. 7, the symmetry of P(X) is destroyed by the cross-correlation $\gamma$ between the additive and multiplicative colored noises. When $\gamma = 0$, the curve of P(X) is axisymmetric with respect to X = 0. Otherwise, the peaks on both sides of P(X) are no longer equal, that is, the curve is tilted. When $\gamma > 0$, the left peak of P(X) is higher than the right one (as $\gamma = 0.2$ in the figure), that is, the curve of P(X) tilts to the left, while for $\gamma < 0$, it tilts to the right. With the increase of $\left| \gamma \right|$, the tilt of the curve becomes worse. Yet, the tilted curve caused by the positive or negative value of $\gamma$ is antisymmetric with respect to X = 0. This implies that the correlation between additive and multiplicative colored noises can induce random transition.

Fig. 5

The marginal SPDF of system displacement under different noises intensities. a $D_{2} =0.003$, b $D_{1} =0.003$. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\beta =0.06$, $\lambda =100$, $\gamma = 0$

Fig. 6

The marginal SPDF of system displacement under different correlation times. a $\tau_{2} =0.2$, b $\tau_{1} =0.2$. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $D_{1} =0.003$, $D_{2} =0.003$, $\beta =0.06$, $\lambda =100$, $\gamma = 0$

Fig. 7

The marginal SPDF of system displacement under different noise cross-correlations. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $D_{1} =0.003$, $D_{2} =0.003$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\beta =0.06$, $\lambda =100$

4 Performance optimization of the controlled system

4.1 Energy harvesting performance

According to Eqs. (18) and (28), the mean harvested DC power $E\left[ P \right]$ can be expressed as

$$ E\left[ P \right] = \kappa \alpha \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\frac{{4A^{2} \left( H \right)}}{{\left( {2 + {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } \omega }} \right. \kern-0pt} \omega }} \right)^{2} }}P\left( {X,\dot{X}} \right){\text{d}} X} } {\text{d}} \dot{X}. $$

(34)

From Fig. 2, energy harvesting involves two conversion processes, namely, mechanical energy to AC and AC to DC. The conversion efficiency of the former is defined by the power conversion ratio $\rho \%$[31], while that of the latter is defined as the rectification efficiency $\eta \%$[52]. That is,

$$ \rho \% ={{P_{\rm{e}} } \mathord{\left/ {\vphantom {{P_{\rm{e}} } {P_{\rm{m}} }}} \right. \kern-0pt} {P_{\rm{m}} }}\left[ {100\% } \right], $$

(35)

$$ \eta \% = {{P_{\rm{d}} } \mathord{\left/ {\vphantom {{P_{\rm{d}} } {P_{\rm{e}} }}} \right. \kern-0pt} {P_{\rm{e}} }}\left[ {100\% } \right], $$

(36)

where $P_{\rm{m}} = \left\langle {\dot{X}\xi_{1} \left( t \right) + \dot{X}X\xi_{2} \left( t \right)} \right\rangle$ characterizes the effective mechanical energy in random environmental vibration. $P_{\rm{e}} = \kappa \left\langle {Y \cdot I} \right\rangle$ represents the average alternating current harvested by the TEH from random vibration. And $P_{\rm{d}} = \kappa \alpha \left\langle {Y_{R}^{2} } \right\rangle$ is the mean DC power of the nonlinear rectifier circuit. The $\left\langle \cdot \right\rangle = {{\left[ {\sum\limits_{i = 1}^{N} {\mathop {\lim }\limits_{{t_{n} \to \infty }} \frac{1}{{t_{n} }}\int_{0}^{{t_{n} }} {\left( \cdot \right){\text{d}} t} } } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum_{i = 1}^{N} {\mathop {\lim }\limits_{{t_{n} \to \infty }} \frac{1}{{t_{n} }}\int_{0}^{{t_{n} }} {\left( \cdot \right){\text{d}} t} } } \right]} N}} \right. \kern-0pt} N}$ is the time average and ensemble average.

Thereby, the expression of performance index $J_{\rm{opt}}$ in Eq. (8) can be further obtained as

$$ J_{\rm{opt}} = \frac{w}{{n_{\rm{p}} - m_{\rm{p}} }} \cdot \left\{ {\left[ {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\frac{{4\kappa \alpha A^{2} P\left( {X,\dot{X}} \right)}}{{\left( {2 + {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } \omega }} \right. \kern-0pt} \omega }} \right)^{2} }}{\text{d}} X} } {\text{d}} \dot{X}} \right] - m_{\rm{p}} } \right\} + \left( {1 - w} \right) \cdot \frac{{\eta - m_{\eta } }}{{n_{\eta } - m_{\eta } }}. $$

(37)

For convenience, make the function $J^{\prime} = - J_{\rm{opt}}$, that is,

$$ J^{\prime} = - \frac{w}{{n_{\rm{p}} - m_{\rm{p}} }} \cdot \left\{ {\left[ {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\frac{{4\kappa \alpha A^{2} P\left( {X,\dot{X}} \right)}}{{\left( {2 + {{\alpha \pi } \mathord{\left/ {\vphantom {{\alpha \pi } \omega }} \right. \kern-0pt} \omega }} \right)^{2} }}{\text{d}} X} } {\text{d}} \dot{X}} \right] - m_{\rm{p}} } \right\} - \left( {1 - w} \right) \cdot \frac{{\eta - m_{\eta } }}{{n_{\eta } - m_{\eta } }}. $$

(38)

Obviously, the stochastic optimal control problem of system (1) is transformed into searching the optimal parameters $a_{i}^{*} ,\;b_{j}^{*} \left( {i = 0,1,2,j = 1,2,3} \right)$ which minimizes the performance index (38). And, the direct control force can be written as

$$ u_{\rm{d}} \left( {X,\dot{X}} \right) \equiv u^{*} \left( {X,\dot{X}} \right) = - 2b_{1}^{*} X - 4b_{2}^{*} X^{3} - 6b_{3}^{*} X^{5} - \left[ {a_{0}^{*} + a_{1}^{*} \tilde{H} + a_{2}^{*} \tilde{H}^{2} } \right]\dot{X}. $$

(39)

4.2 Effects of noises and structure parameters on harvesting performance

Figure 8 displays the variation of power conversion efficiency $\rho \%$ in Eq. (35) and rectification efficiency $\eta \%$ in Eq. (36) with the additive colored noise intensity D₁ under different electromechanical coupled coefficient $\kappa$. It is found that with the increase of D₁, the $\rho \%$ shows a trend of increasing first and then decreasing, that is, there is an optimal D₁ to maximize the power conversion efficiency (e.g., $D_{1} = D_{{1_{{\kappa_{1} }} }}$ when $\kappa = 0.05$ in Fig. 8a). The increase in $\kappa$ promotes stronger additive colored noise to be required to maximize $\rho \%$ (as shown in Fig. 8a, $D_{{1_{{\kappa_{1} }} }} < D_{{1_{{\kappa_{2} }} }} < D_{{1_{{\kappa_{3} }} }}$). For smaller $\kappa$, there exists noise intensity to optimize $\eta \%$, e.g., $D_{1} = D_{{1_{\eta } }}$ for $\kappa = 0.05$ in Fig. 8b. Moreover, the increase in $\kappa$ can reduce the noise intensity required to achieve the optimal $\eta \%$. When $\kappa$ is large, the $\eta \%$ decreases monotonically with the increase of D₁. In general, the increase of $\kappa$ can improve the efficiency of the harvesting system, that is, $\kappa$ plays a positive role in energy harvesting.

Fig. 8

The power conversion efficiency $\rho \%$ and rectification efficiency $\eta \%$ vary with noise intensity D₁ under different $\kappa$. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $D_{1} =0.003$, $D_{2} =0.003$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\beta =0.06$, $\lambda =100$,$\gamma = 0$

In Fig. 9, the curves of $\rho \%$ and $\eta \%$ with multiplicative colored noise intensity D₂ under different time constant ratio $\alpha$ are plotted. With the increase in D₂, $\eta \%$ decreases monotonously. The decreasing trend tends to be fast and then slow. For example, for $\alpha = 0.05$ and $D_{2} > D_{{2_{\eta } }}$ in Fig. 9b, $\eta \%$ almost remains unchanged with D₂. However, $\rho \%$ increases first and then decreases as D₂ increases, and the optimal power conversion efficiency can be approximately obtained at $D_{{2_{\rho } }}$ in Fig. 9a. Moreover, $\alpha$ can significantly improve the harvesting efficiency $\rho \%$ or $\eta \%$. Figure 10 further explores the influence of noise cross-correlation $\gamma$ and correlation times of colored noises $\tau_{1} ,\;\tau_{2}$ on harvesting performance. It is observed that the curves of $E\left[ P \right]$ and $\eta \%$ are axisymmetric about $\gamma = 0$ with similar trends. Obviously, the optimal mean DC power and rectification efficiency are obtained at $\gamma = 0$. Furthermore, the correlation time of additive colored noise $\tau_{1}$ plays a negative role for $E\left[ P \right]$. The multiplicative or additive colored noise correlation time can improve the rectification efficiency $\eta \%$ of the circuit.

Fig. 9

The power conversion efficiency $\rho \%$ and rectification efficiency $\eta \%$ vary with noise intensity D₂ under different time constant ratio $\alpha$. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\kappa =0.1$, $D_{1} =0.003$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\beta =0.06$, $\lambda =100$,$\gamma = 0$

Fig. 10

The mean DC power $E\left[ P \right]$ and rectification efficiency $\eta \%$ vary with noise cross-correlation $\gamma$ under different correlation times $\tau_{1} ,\;\tau_{2}$. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $D_{1} =0.003$, $D_{2} =0.003$, $\beta =0.06$, $\lambda =100$

Figure 11 depicts the curves of $E\left[ P \right]$ or $\eta \%$ as a function of the noise intensity D₁. It is observed that $E\left[ P \right]$ increases approximately linearly with D₁, while the damping coefficient $\beta$ weakens the harvested DC power. For a smaller damping coefficient (i.e., $\beta = 0.06$ in Fig. 11b), $\eta \%$ increases first and then decreases with the increase in D₁, which indicates that there is an appropriate D₁ to maximize $\eta \%$. When $\beta$ is large (i.e., $\beta = 0.12$), $\eta \%$ decreases monotonically with D₁. Besides, $\beta$ plays a positive role for $\eta \%$. Therefore, in order to obtain a relatively ideal output level, balancing power output and rectification efficiency is crucial for the performance optimization of the harvester.

Fig. 11

The mean DC power $E\left[ P \right]$ and rectification efficiency $\eta \%$ vary with noise intensity D₁ under different damping coefficient $\beta$. The control parameters are set to 0. Other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $D_{2} =0.003$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\lambda =100$, $\gamma = 0$

4.3 Performance optimization under different weighted factors

The stochastic direct optimal control developed in this paper essentially modifies the system stiffness and damping term to optimize the performance index. As shown in Fig. 12, the stochastic optimal control of the strongly nonlinear coupled TEH driven by correlated colored noises is transformed into an optimization problem of multivariable function (38) including control parameters $b_{j} ,\;\left( {j = 1,2,3} \right)$ and $a_{i} ,\;\left( {i = 0,1,2} \right)$. From Fig. 3b, the control parameters $b_{j} ,\;\left( {j = 1,2,3} \right)$ have an important influence on the tri-stable potential structure. In order to simplify the calculation and improve the operation efficiency, the control parameters $a_{i} ,\;\left( {i = 0,1,2} \right)$ related to damping term are set to 0 in this paper. Then, the fminsearch function in MATLAB software is employed to search the optimal control parameters $b_{j}^{*} ,\;\left( {j = 1,2,3} \right)$ to minimize the performance index (38). The other parameters are chosen as $k_{1} =1$, $k_{3} = - 2.6$, $k_{5} =1$, $\alpha =0.05$, $\kappa =0.1$, $D_{1} =0.003$, $\tau_{1} =0.2$, $\tau_{2} =0.2$, $\beta =0.06$, $\lambda =100$, $\gamma = 0$, unless otherwise mentioned.

Fig. 12

The flowchart of stochastic optimal control based on equivalent uncoupled controlled Eq. (20)

The weighted factor in the index (38) is firstly set to w = 1. In this case, the performance index of the optimal control is to maximize the mean DC power without considering the magnitude conversion problem, i.e., $m_{\rm{p}} = 0,\;n_{\rm{p}} = 1$, $\overline{E}\left[ P \right] = E\left[ P \right]$. In Fig. 13a, with the increase in the number of iterations, the performance index $J^{\prime}$ first decreases rapidly and then tends to a fixed constant, which means the optimal control parameters $b_{i}^{*} ,\;(i = 1,2,3)$ that minimize the index $J^{\prime}$ have been searched. And the direct control force in Eq. (39) can be calculated as $u_{\rm{d}} \left( X \right) = {0}{\text{.0078}}X - {0}{\text{.042}}0X^{3} - {0}{\text{.1266}}X^{5}$ for fixed D₂ = 0.003 based on the stochastic optimal control developed in this paper. And, the optimal DC power is $E\left[ P \right]_{\rm{opt}} = 8.149 \times 10^{ - 3}$. In Fig. 13b, the curves of mean DC power $E\left[ P \right]$ with noise intensity D₂ under direct control force and uncontrolled case are plotted. Obviously, for D₂ = 0.003, the DC power under direct optimal control is higher than that under uncontrolled case. That is, the stochastic direct optimal control based on the improved stochastic averaging can effectively enhance the output power. Notably, although the optimal control force is calculated at a fixed D₂ = 0.003, it can obtain better output performance than the uncontrolled system in its neighborhood (e.g., in the interval $\left[ {0,D_{{2_{P} }} } \right]$).

Fig. 13

a Optimization process and b the dependence of $E\left[ P \right]$ of the controlled and uncontrolled cases on intensity D₂. The weighted factor is w = 1. The control parameters are b_i = 0, i = 1, 2, 3 in the uncontrolled case, while they are calculated as b₁ = − 0.0039, b₂ = 0.0105, b₃ = 0.0211 in the controlled case

Besides, Fig. 14 depicts the variation of power conversion efficiency $\rho \%$ with noise intensity D₂, where the efficiency of controlled case and uncontrolled one are compared. It is found that $\rho \%$ under optimal control is also superior to that under uncontrolled case. And the direct optimal control force reduces the noise intensity required to maximize $\rho \%$. Under the above weighted factor (i.e., w = 1), the $E\left[ P \right]$ and $\rho \%$ of controlled TEH are enhanced. However, $\eta \%$ obtained under direct optimal control is lower than that of the uncontrolled system, as shown in Fig. 15c when w = 1. This means that the performance index designed only with the maximum mean DC power is not sufficient. $\eta \%$ characterizes the ability of the rectifier circuit to convert the alternating current harvested from random vibration to direct current, which has an important impact on achieving efficient power supply.

Fig. 14

The dependence of power conversion efficiency $\rho \%$ of the controlled and uncontrolled cases on D₂. The weighted factor is w = 1. The control parameters are b_i = 0, i = 1, 2, 3 in the uncontrolled case, while they are calculated as b₁ = − 0.0039, b₂ = 0.0105, b₃ = 0.0211 in the controlled case

Fig. 15

The optimization process and the dependence of harvesting performance on D₂. The weighted factor is w = 0.8, and m_p = 0, $n_{\rm{p}} = 8 * 10^{ - 3}$, $m_{\eta } = 0$, $n_{\eta } = 0.4$. The control parameters are b_i = 0, i = 1, 2, 3 in the uncontrolled case, while they are b₁ = 0.0019, b₂ = 0.0016, b₃ = − 0.0351 in the controlled case

Thus, the weighted factor in index (38) is reset to w = 0.8. Figure 15a displays the variation of index (38) with the number of iterations during the optimization process. In this case, the direct optimal control force can be calculated as $u_{\rm{d}} \left( X \right) = - {0}{\text{.0038}}X - {0}{\text{.0064}}X^{3} + {0}{\text{.2106}}X^{5}$, while the optimal DC power and rectification ratio are $E\left[ P \right]_{\rm{opt}} = 7.885 \times 10^{ - 3}$, $\eta \%_{\rm{opt}} = 29.875\%$ as shown in Table 2. From Fig. 15b–d, for D₂ = 0.003, the $E\left[ P \right]$ and efficiencies ($\rho \%$ and $\eta \%$) of the controlled system are higher than those of the uncontrolled one. In particular, in the neighborhood of D₂ = 0.003 (e.g., interval $\left[ {0,D_{{2_{P} }} } \right]$), the harvesting performance under direct optimal control is also superior to that of uncontrolled case. It is found that the weighted factor of the performance index is of great significance to the optimization of the harvesting performance. By adjusting the weighted factor to balance the distance between the output power and the rectification efficiency, the harvester can obtain a higher output level.

Table 2 The performance comparison between the controlled and uncontrolled cases at different weighted factors

5 Conclusions

This paper aims to research the stochastic optimal control of a TEH under a standard rectifier circuit driven by correlated colored noises to enhance the performance of harvesting system. From the physical intuition, the direct control force is divided into conservative component and dissipative one. The additional potential gradient is utilized to characterize the conservative component, while the energy-dependent quasi-linear damping represents the dissipative one. Then, the analytical expressions of the SPDF and mean DC power are derived using the stochastic averaging based on energy-dependent frequency. In order to balance the distance between harvested power and harvesting efficiency, the weighted combination of mean DC power and rectification efficiency is employed as the performance index of the optimal control. The semi-analytical expression of the index is obtained to transform the stochastic optimal control problem into a multivariable function extremum problem. The influence of the index under different weighted factor on the harvesting performance of controlled TEH is further investigated.

It is found that the stochastic optimal control strategy based on the improved energy envelope stochastic averaging avoids solving complex differential equations. Compared with uncontrolled TEH, the harvesting performances including DC power, power conversion efficiency and rectification efficiency under direct optimal control are significantly improved. By adjusting the weighted factor of the performance index to balance the output power and the rectification efficiency, the harvesting system can achieve a relatively ideal output level. There are optimal correlated colored noises intensities D₁, D₂ to maximize the power conversion efficiency of the harvester. The cross-correlation of correlated colored noises can destroy the symmetry of SPDF, which is conducive to the occurrence of random transition.