Coupled nonlinear Schrödinger (CNLS) equations for two interacting electrostatic wavepackets in a non-Maxwellian fluid plasma model

Abstract

The nonlinear dynamics of two co-propagating electrostatic wavepackets in a one-dimensional non-magnetized plasma fluid model is considered, from first principles. The coupled waves are characterized by different (carrier) wavenumbers and amplitudes. A plasma consisting of non-thermalized ($\kappa$-distributed) electrons evolving against a cold (stationary) ion background is considered. The original model is reduced, by means of a multiple-scale perturbation method, to a pair of coupled nonlinear Schrödinger (CNLS) equations for the dynamics of the wavepacket envelopes. For arbitrary wavenumbers, the resulting CNLS equations exhibit no known symmetry and thus intrinsically differ from the Manakov system, in general. Exact analytical expressions have been derived for the dispersion, self-modulation (nonlinearity) and cross-modulation (coupling) coefficients involved in the CNLS equations, as functions of the wavenumbers ($k_1$, $k_2$) and of the spectral index $\kappa$ characterizing the electron profile. An analytical investigation has thus been carried out of the modulational instability (MI) properties of this pair of wavepackets, focusing on the role of the intrinsic (variable) parameters. Modulational instability is shown to occur in most parts of the parameter space. The instability window(s) and the corresponding growth rate are calculated numerically in a number of case studies. Two-wave interaction favors MI by extending its range of occurrence and by enhancing its growth rate. Growth rate patterns obtained for different $\kappa$ index (values) suggest that deviation from thermal (Maxwellian) equilibrium, for low $\kappa$ values, leads to enhance MI of the interacting wave pair. To the best of our knowledge, the dynamics of two co-propagating wavepackets in a plasma described by a fluid model with $\kappa$-distributed electrons is investigated thoroughly with respect to their MI properties as a function of $\kappa$ for the first time, in the framework of an asymmetric CNLS system whose coefficients present no obvious symmetries for arbitrary $k_1$ and $k_2$. Although we have focused on electrostatic wavepacket propagation in non-thermal (non-Maxwellian) plasma, the results of this study are generic and may be used as basis to model energy localization in nonlinear optics, in hydrodynamics or in dispersive media with Kerr-type nonlinearities where MI is relevant.

1 Introduction

Research on plasma dynamics has grown significantly during the last decades, because of the prospects for a wide range of applications related to space and fusion, among others. Plasmas in a state of collisional equilibrium exhibit a Maxwellian distribution. Space plasmas, however, are very often in stationary states out of equilibrium that can be described by kappa distributions, which are characterized by a Maxwellian-like “core” and a high-energy tail that follows a power law. Such distributions have been observed in the solar wind and planetary magnetospheres [1,2,3,4,5]. The intrinsic dispersion and nonlinearity in plasmas can be balanced to lead to collective dynamics and the emergence of localized excitation in the form of solitons, breathers, rogue waves, or shocks. Plasma fluid models mimicking Navier–Stokes equation in hydrodynamics (see e.g., in [6, 7]), can be reduced through standard perturbative methods to the celebrated nonlinear Schrödinger (NLS) equation known to govern the envelope dynamics of a modulated wavepacket in nonlinear and dispersive media. In the context of plasma fluids, the NLS equations have been derived for the first times in the early 1970 s [8, 9] and subsequently for a large variety of electrostatic plasma models. Recently, its localized solutions (envelope solitons, breathers) have in fact been associated with freak or rogue waves in plasmas [10,11,12,13]. Formally analogous NLS equations focusing on electromagnetic waves in plasmas modeled by fluid-Maxwell equations have been also derived [14,15,16]. In recent years, the kappa distribution of electrons has been used more and more in NLS-reduced plasma fluid models [17,18,19,20,21,22,23].

Different versions of NLS equations have been employed in other contexts, e.g., in the investigation of the dynamics of blow-up solutions in trapped quantum gases modeled by the Gross-Pitaevskii equation [24] which in a sense generalizes the three-dimensional NLS equation. Alternatively, plasma fluid model may be reduced to the Korteweg-de Vries (KdV) equation, which has been recently investigated in a generalized form (i.e., with high power nonlinearities) with respect to solitary, compacton, and periodic types of solutions [25]. Furthermore, the NLS equation with higher-order dispersion and parabolic nonlinearity has been found to admit dark, bright, kink, as well as triangular solitary wave solutions [26]. Also, several types of localized excitations have been constructed for extended Kadomtsev-Petviashvili equations of the B type, such as dromion- and lump-lattice structures as well as various folded solitary waves [27, 28].

The consideration of two co-propagating wavepackets in a particular plasma fluid and their mutual interaction, results in a pair of coupled NLS (CNLS) equations, whose coefficients generally depend on the carrier wavenumber(s) of the respective carrier waves. Electron plasma (Langmuir) waves and ion acoustic waves [29,30,31], amidst other studies, focused mostly on electromagnetic modes [32,33,34,35,36,37,38]. Beyond plasma science, general forms of CNLS equations have been investigated in recent years with respect to the existence of vector solitons, breathers, and rogue wave solutions, in contexts including higher-order coupled NLS systems [39, 40], coupled mixed-derivative NLS equations [41,42,43], variable coefficients CNLS equations [44], non-autonomous CNLS equations [45,46,47], systems involving four-wave mixing terms [48], coupled cubic-quintic NLS equations [49], space-shifted CNLS equations [50], and non-autonomous partially non-local CNLS equations [51], among others.

More specifically, pairs of CNLS equations have been employed as the workhorse model in diverse areas of science such in nonlinear optics, hydrodynamics, and dispersive media, for the investigation of their dynamics and their modulational instability properties. Below we refer to some of these work in which formally equivalent forms of CNLS equations to those presented in Sects. 2.3 or 2.5 were employed.

Systems of CNLS equations have been obtained in Ref. [52] for the description of interacting nonlinear wave envelopes and formation of rogue waves in deep water. A condition for rogue wave formation was introduced which relates the angle of interaction with the group velocities of these waves. The CNLS system exhibits modulational instability (MI), which develops much faster (i.e., it has higher growth rates) than in each of the corresponding (decoupled) NLS equations and constitutes an important aspect of rogue wave dynamics. Further, CNLS equations were employed as a model describing the formation of rogue waves of the Peregrine breather type in water, in interpretation of experimental observations. Indeed, in Ref. [53], it was demonstrated that nonlinear wave focusing resulting in strong localization on the water surface originates from MI evolving from two counter-propagating water waves. The observed experimental results are in excellent agreement with the corresponding results obtained from the hydrodynamic CNLS equation model. In another relevant work [54], a weakly nonlinear model consisting of a pair of CNLS equations was derived for two water wave systems known as crossing sea states in the context of ocean waves which propagate in two different directions. It was shown that when the first wave is modulationally unstable, then a second wave propagating in different direction results in an increase of the MI growth rates and enlargement of the instability region through their interaction.

Furthermore, a pair of CNLS equations which describe the interaction between the high-frequency Langmuir and low-frequency ion-acoustic waves in a plasma, and breather and rogue wave solutions have been investigated via the Darboux transformation [55]. The co-propagation of two circularly polarized strong laser pulses in a magnetized plasma in a weakly relativistic regime and their MI properties were investigated in Ref. [38] within the framework of two CNLS equations. Further works on dispersive media include the investigation of a CNLS equations model resulted from Maxwell’s equations with nonlinear permittivity and permeability in a left-handed metamaterial [56], for which several types of vector solitons were identified, the investigation of the MI profile of the coupled plane-wave solutions in left-handed metamaterials using CNLS equations in Ref. [57], and the investigation of the coupling between backward- and forward-propagating waves, with the same group velocity, in a composite right- and left-handed nonlinear transmission line [58].

Perhaps the largest amount of work on CNLS equations has been performed in optics, in which long ago those equations were shown to govern light propagation in isotropic Kerr materials [59]. In that work, the existence of a novel class of vector solitary waves was revealed, which bifurcate from circularly polarized solitons. Also, the generation of vector dark-soliton trains by induced MI in a highly birefringent fiber was experimentally observed in Ref. [60], in excellent agreement with theoretical predictions from numerical simulations of the CNLS equations. More recent works include the emergence of temporal patterns such as bright solitons and rogue waves in optical fibers investigated theoretically via a special version of CNLS equations, i.e., the Manakov system, which are initiated by the MI process [61]. The Manakov system has been also recently investigated with respect to the existence of novel, non-degenerate fundamental solitons corresponding to different wavenumbers [62]. More optical solitons have been obtained for the Manakov system of CNLS equations in Ref. [63], while analytical one- and two-soliton solutions in birefringent fibers have been obtained through the Hirota bilinear method in Ref. [64].

In the present work, a pair of CNLS equations is derived from a plasma model comprising of a cold inertial ion fluid evolving against a thermalized electron background that follows a kappa distribution, using a standard multiple scale approach (the Newell method). The coefficients of the CNLS equations have been calculated as functions of the wavenumbers of the two interacting waves and the coefficients of a Mc Laurin expansion of the kappa distribution (which depend on the spectral index $\kappa$). For arbitrary wavenumbers, the coefficients of the CNLS equations do not exhibit any known symmetry and hence the system is rendered non-integrable. A compatibility condition is derived for that system through a detailed modulational instability analysis that provides a polynomial relation (fourth order in the perturbation frequency) between the perturbation frequency and wavenumber [65]. The MI properties of the CNLS equations are then investigated with respect to the wavenumbers of the two carrier waves and the wavenumber of the perturbation for several values of the spectral index $\kappa$ of the electron distribution.

In comparison with earlier similar works, which in the context of plasma are rather scarce, we should stress that the obtained CNLS equations for the envelops of the two interacting wavepackets are the most general as far as the values of their coefficient are concerned; those coefficients are derived exactly in terms of $k_1$, $k_2$, and $\kappa$ without any other additional assumption (e.g., equal group velocities of the wavepackets). The choice of the fluid model was made on the basis on simplicity; it contains only one parameter, the spectral index $\kappa$ (besides the externally determined $k_1$ and $k_2$). This constitutes advantage to other models since it isolates the effect of $\kappa$ on the investigated MI properties. Moreover, a thorough MI analysis is performed as a function of $\kappa$ for the first time, which illuminates its role for values that are relevant to space plasmas and have been deduced from observational data. A comparison of the results for small values of $\kappa$ (in the interval [2,3]) with those using the common Maxwell–Boltzmann electron distribution reveals dramatic differences as far as the strength of the growth rate of MI and the MI window is concerned, which have not been shown before.

In following Sect. 2 the plasma fluid model equations are introduced, from which the CNLS equations are derived using the multiple-scale perturbation method. In Sect. 3, we undertake an analytical study of the modulational instability analysis of plane wave solutions of the CNLS equations. A detailed parametric analysis of MI occurrence is carried out, based on numerical calculation of the growth rate in Sect. 4. Our main results are briefly discussed and summarized in Sect. 5.

2 Derivation of a system of CNLS equations for two interacting wavepackets

2.1 Plasma fluid model equations and electron distribution

A one-dimensional (1D), non-magnetized plasma model is considered here for electrostatic excitations that consists of a cold inertial ion fluid of number density $n_i =n$ and velocity $u_i =u$, evolving against a thermalized, kappa-distributed electron background of number density $n_e$. The continuity, momentum, and Poisson partial differential equation(s) governing the dynamics of that model are given by [66]

$$\begin{aligned}{} & {} \frac{\partial n}{\partial t} +\frac{\partial (n u)}{\partial x} =0, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \frac{\partial u}{\partial t} +u \frac{\partial u}{\partial x} = -\frac{\partial \phi }{\partial x}, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \frac{\partial ^2 \phi }{\partial x^2} = n_e -n, \end{aligned}$$

(3)

respectively, with $\phi$ being the electrostatic potential. In Eqs. (1)–(3) above, the spatial and temporal variables x and t are normalized to the inverse ion plasma frequency $\omega _{pi}^{-1}$ and to the Debye screening length $\lambda _D$, respectively, where

$$\begin{aligned}{} & {} \lambda _D =\left( \frac{\varepsilon _0 k_B T_e}{z_i n_{i0} e^2}\right) ^{1/2}, \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \omega _{pi}=\left[ \frac{n_{0, i} (z_i e)^2}{\varepsilon _0 m_i}\right] ^{1/2} \,. \end{aligned}$$

(5)

The number density variable(s) of the ions n and the electrons $n_e$ are normalized to their respective equilibrium values $n_{i, 0}$ and $n_{e, 0} = z_i n_{i, 0}$; the ion velocity u is normalized to

$$\begin{aligned} c_s = \lambda _D \, \omega _{pi} =\left( \frac{z_i k_B T_e}{m_e}\right) ^{1/2}, \end{aligned}$$

(6)

i.e., essentially the (ion-acoustic) sound speed. Finally, the electrostatic potential $\phi$ is normalized to $k_B T_e/e$. Adopting a standard notation, the symbols $\varepsilon _0$, $k_B$, $T_e$, e, $m_i$, $z_i$ appearing in the latter expressions denote, respectively, the dielectric permittivity in vacuum, the Boltzmann’s constant, the (absolute) electron temperature, the electron charge, the ion mass, and the degree of ionization ($z_i = q_i/e$, where $q_i$ is the ion charge).

As announced above, we shall assume the electrons to follow a kappa distribution [1, 67, 68] that is given by [69, 70]

$$\begin{aligned} n_e =\left( 1 -\frac{\phi }{\kappa -\frac{3}{2}} \right) ^{-\kappa +\frac{1}{2} }. \end{aligned}$$

(7)

Note that this function is characterized by a real parameter $\kappa$ (known as the spectral index).

The kappa distribution adopted here for the non-thermal electrons is a straightforward replacement for the Maxwell–Boltzmann distribution when dealing with systems in stationary states out of equilibrium [71]. Such stationary states are commonly found in space and astrophysical plasmas [2, 3], whose nature allows for extracting the spectral index $\kappa$ in each particular case. Possible values of $\kappa$ in Eq. (7) lie in the interval $(3/2, \infty )$, while for $\kappa =+\infty$ the kappa distribution reverts to the Maxwell–Boltzmann one. Lower values of $\kappa$ are associated with a long tail in the particle (velocity) distribution, in account of a strong suprathermal component (i.e., for large velocity) [68]. This is a common occurrence e.g., in Space plasmas [1].

Space plasma observations have shown an empirical separation for the spectrum of the values of $\kappa$ into a near- ($3/2< \kappa < 2.5$) and a far- ($2.5< \kappa < \infty$) equilibrium region. In particular, kappa distributions with $2< \kappa < 6$ have been found to fit the observations and satellite data in the solar wind [67] (and references therein). In later sections, we are using values of $\kappa$ evenly distributed in the interval $2< \kappa < 6$ as well as a large value of $\kappa =100$ for which practically the electron component in the considered plasma model has reached equilibrium (Maxwell–Boltzmann).

Kappa distributions have by now become one of the most widely used tools for characterizing and describing space plasmas and are known to affect the fundamental properties of plasma waves and also of electrostatic solitary waves [72]. For low values of the electrostatic potential $\phi$, i.e., for $|\phi | \ll 1$ (in normalized units), kappa distribution Eq. (6) can be expanded in a Mc Laurin series in powers of $\phi$ as

$$\begin{aligned} n_e \approx 1 +c_1 \phi +c_2 \phi ^2 +c_3 \phi ^3 +\cdots \,, \end{aligned}$$

(8)

from which we shall keep terms up to order $\phi ^3$. In that case, the first three expansion coefficients are given by

$$\begin{aligned} c_1= & {} \frac{\kappa -\frac{1}{2}}{\kappa -\frac{3}{2}} \,, \end{aligned}$$

(9)

$$\begin{aligned} c_2= & {} \frac{\left( \kappa -\frac{1}{2}\right) \left( \kappa +\frac{1}{2}\right) }{2! \left( \kappa -\frac{3}{2} \right) ^2} \,, \end{aligned}$$

(10)

$$\begin{aligned} c_3= & {} \frac{\left( \kappa -\frac{1}{2}\right) \left( \kappa +\frac{1}{2}\right) \left( \kappa +\frac{3}{2}\right) }{3! \left( \kappa -\frac{3}{2}\right) ^3} \,. \end{aligned}$$

(11)

2.2 Application of the reductive perturbation method

We introduce fast and slow variables so that the derivatives are approximated as

$$\begin{aligned} \frac{\partial }{\partial t} \rightarrow \sum _{k=0}^\infty \varepsilon ^k \frac{\partial }{\partial t_k}, ~~~ \frac{\partial }{\partial x} \rightarrow \sum _{k=0}^\infty \varepsilon ^k \frac{\partial }{\partial x_k} \end{aligned}$$

(12)

where $\varepsilon$ is a small quantity, and $x_k=\varepsilon ^k x$, $t_k=\varepsilon ^k t$ (for $k = 0, 1, 2, 3,\ldots$). The dependent variables n, u, and $\phi$ can be expanded around their equilibrium value as

$$\begin{aligned} n= & {} 1 +\sum _{k=1}^\infty \varepsilon ^k n_k, \end{aligned}$$

(13)

$$\begin{aligned} u= & {} \sum _{k=1}^\infty \varepsilon ^k u_k, \end{aligned}$$

(14)

$$\begin{aligned} \phi= & {} \sum _{k=1}^\infty \varepsilon ^k \phi _k. \end{aligned}$$

(15)

The expansions of $\{n, u, \phi \}$ in Eqs. (13)–(15) along with those for the derivatives in Eq. (12) and the expansion of the electron distribution in Eq. (7) are substituted into model equations Eqs. (1)–(3), in order to obtain sets of perturbative equation of different orders in $\varepsilon$ up to order $\varepsilon ^3$.

The fluid equations obtained at first order ($\propto \varepsilon ^1$) read

$$\begin{aligned}{} & {} \frac{\partial n_1}{\partial t_0} +\frac{\partial (u_1)}{\partial x_0} =0, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \frac{\partial u_1}{\partial t_0} +\frac{\partial \phi _1}{\partial x_0} =0, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \frac{\partial ^2 \phi _1}{\partial x_0^2} +n_1 -c_1 \phi _1 =0, \end{aligned}$$

(18)

where $x_0 =x$ and $t_0 =t$. In these equations, the following Ansatz will be introduced

$$\begin{aligned} S_1 =S_{1,1}^{(1)} \, e^{+i \theta _1} +S_{1,2}^{(1)} \, e^{+i \theta _2} +c.c., \end{aligned}$$

(19)

where $S_1=\{n_1, u_1, \phi _1\}$ and the phases are $\theta _j =k_j x -\omega _j t$ with $k_j$ and $\omega _j$ being the wavevector and the corresponding (angular) frequency of the j-th wave (for $j=1, 2$). Note that the derivatives with respect to $t=t_0$ and $x=x_0$ that appear in Eqs. (16)–(18) do not act on the amplitude(s) $S_{1,j}^{(1)}$—(but only on the harmonic carrier functions, i.e., the exponentials, above), since the latter does not depend on these variables. After some straightforward calculations we get the equations ($j=1,2$)

$$\begin{aligned} -\omega _j n_{1,j}^{(1)} +k_j u_{1,j}^{(1)} =0, \nonumber \\ -\omega _j u_{1,j}^{(1)} +k_j \phi _{1,j}^{(1)} =0, \nonumber \\ +n_{1,j}^{(1)} -(k_j^2 +c_1) \phi _{1,j}^{(1)} =0. \end{aligned}$$

(20)

The equations for $j=1$ are not coupled to those with $j=2$, and thus, the two waves do not interact at this order of approximation. As a result, two uncoupled $3\times 3$ systems with unknowns $\{n_{1,j}^{(1)}, u_{1,j}^{(1)}, \phi _{1,j}^{(1)}\}$ for $j=1$ and $j=2$, respectively, are obtained as ($j=1,2$)

$$\begin{aligned} \begin{bmatrix} -i \omega _j &{} +i k_j &{} 0 \\ 0 &{} -i \omega _j &{} +i k_j \\ 1 &{} 0 &{} -(k_j^2 +c_1) \end{bmatrix} \begin{bmatrix} n_{1,j}^{(1)} \\ u_{1,j}^{(1)} \\ \phi _{1,j}^{(1)} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}, \end{aligned}$$

(21)

For these systems to have a non-trivial solution, it is required that their determinants should vanish, i.e.,

$$\begin{aligned} D_j = \begin{vmatrix} -\omega _j&+k_j&0 \\ 0&-\omega _1&+k_j \\ 1&0&-(k_j^2 +c_1) \end{vmatrix} =0, \end{aligned}$$

(22)

which provides the linear frequency dispersion relation ($\omega$) and the corresponding group ($v_g$) and phase ($v_{ph}$) velocity for the j-th wave ($j=1$ or 2) as

$$\begin{aligned} \omega _j= & {} \frac{k_j}{[k_j^2 +c_1(\kappa )]^{1/2}}, \end{aligned}$$

(23)

$$\begin{aligned} v_{g,j}= & {} \frac{c_1(\kappa )}{[k_j^2 +c_1(\kappa )]^{3/2}}, \end{aligned}$$

(24)

$$\begin{aligned} v_{ph,j}= & {} \frac{\omega _j}{k_j} =\frac{1}{[k_j^2 +c_1(\kappa )]^{1/2}}, \end{aligned}$$

(25)

where the dependence of the expansion coefficient $c_1$ on the spectral index $\kappa$ is explicitly indicated. The systems of Eqs. (21) can be solved in terms of the variables ($j=1,2$)

$$\begin{aligned} \phi _{1,j}^{(1)} =\Psi _j \end{aligned}$$

(26)

to give

$$\begin{aligned} n_{1,j}^{(1)} =\left( \frac{k_j}{\omega _j}\right) ^2 \Psi _j, ~~~~ u_{1,j}^{(1)} =\frac{k_j}{\omega _j} \Psi _j. \end{aligned}$$

(27)

Fig. 1

The frequency dispersion $\omega _1$ (a), the corresponding group velocity $v_{g,1}$ (b) as calculated from Eq. (24), and the phase velocity $v_{ph,1} =\omega _1/k_1$ (c) as calculated from Eq. (25), as a function of the wavenumber $k_1$ for the values (in ascending order, bottom to top curves): $\kappa =2$ (black), $\kappa =3$ (red), $\kappa =4$ (green), $\kappa =5$ (blue), $\kappa =6$ (orange), $\kappa =100$ (brown). (Color figure online)

The frequency dispersion $\omega _1$ and the group velocity $v_{g,1}$ which have been calculated from Eqs. (23) and (24) are shown in Fig. 1 as a function of the wavenumber $k_1$ for six values of the spectral index $\kappa$. The frequency dispersion curves seem to have the same qualitative features for any value of $\kappa$. However, the frequency (or fixed $k_1$) increases with increasing $\kappa$ for any $k_1$ in the (physically relevant) interval shown, while it saturates for large spectral index $\kappa$ to its Maxwell–Boltzmann value. Note that the curve obtained for $\kappa =100$, shown as brown curve in Fig. 1a, is practically identical to a curve that would have been obtained using the Maxwell–Boltzmann distribution for the electrons.

The corresponding group velocity curves in Fig. 1b, exhibit two distinct behaviors; for low $k_1$ (i.e., $k_1 \lesssim 0.9$) the group velocity $v_{g,1}$ increases with increasing $\kappa$ just as the frequency does in Fig. 1a. However, for high $k_1$ (i.e., $k_1 \gtrsim 0.9$) that tendency is reversed, and the group velocity $v_{g,1}$ decreases with increasing $\kappa$. Note that for very low $k_1$ (i.e., for $k_1 \rightarrow 0$), the group velocity increases from $v_{g,1} \simeq 0.59$ for $\kappa =2$ to $v_{g,1} =1$ for $\kappa =100$ (practically the same as in the case of Maxwell–Boltzmann distributed electrons, as expected for large values of $\kappa$). This constitutes a relative increase of up to $\simeq 70\%$ in group velocity (value) between the extreme values of $\kappa$ adopted here. We draw the conclusion that lower values of $\kappa$, i.e., a stronger deviation from the thermal (Maxwellian) picture, result in lower group velocity (i.e., slower wavepackets/envelopes) for electrostatic wavepackets of this kind, at least for long wavelengths (i.e., $\gtrsim$ the Debye length, more or less). The inverse trend is observed for short (sub-screening-radius) wavelengths (i.e., for wavenumber exceeding unity, roughly), since lower $\kappa$ values entail a slightly faster $v_g$ (value).

The phase velocity $v_{ph, 1}$, on the other hand, exhibits a simpler behavior, as illustrated in Fig. 1c. It turns out that $v_{ph, 1}$ increases with increasing $\kappa$ for all wavenumbers, while at the same time the phase speed decreases asymptotically toward zero for large $k_1$ (i.e., for vanishing wavelength), regardless of the value of $\kappa$, as expected from analytical expression (25). For negligible $k_1$ (i.e., in the infinite wavelength limit), the expressions for both group and phase speeds recover the sound speed $\lim _{k_1 \rightarrow 0} v_{g,1} =\lim _{k_1 \rightarrow 0} v_{ph,1} = 1/\sqrt{c_1(\kappa )}$, as can be inferred from Eqs. (24) and (25).

Obviously, all of the observations in the latter two paragraphs hold for the second wave also, upon a simple subscript permutation $1 \rightarrow 2$.

The equations obtained at the second order in $\varepsilon$ are

$$\begin{aligned} \frac{\partial n_2}{\partial t_0} +\frac{\partial (u_2)}{\partial x_0} =\mathcal{F}_1, \nonumber \\ \frac{\partial u_2}{\partial t_0} +\frac{\partial \phi _2}{\partial x_0} =\mathcal{F}_2, \nonumber \\ \frac{\partial ^2 \phi _2}{\partial x_0^2} -c_1 \phi _2 +n_2 =\mathcal{F}_3, \end{aligned}$$

(28)

where $\mathcal{F}_1$, $\mathcal{F}_2$, and $\mathcal{F}_3$ are known functions of $\Psi _j$ which are given in “Appendix B.” To solve Eqs. (28), we use the following ansatz

$$\begin{aligned} S_2 =S_{2}^{(0)} +\left[ S_{2,1}^{(1)} e^{i \theta _1} +S_{2,1}^{(2)} e^{2 i \theta _1} +S_{2,2}^{(1)} e^{i \theta _2} +S_{2,2}^{(2)} e^{2 i \theta _2} \right. \nonumber \\ \left. +S_{2,+}^{(1)} e^{i (\theta _1 +\theta _2)} +S_{2,-}^{(1)} e^{2 i (\theta _1 -\theta _2)} +c.c. \right] ,\nonumber \\ \end{aligned}$$

(29)

where $S =n, u$ or $\phi$; by “c.c” we have denoted the complex conjugate of the expression within the curly brackets. Upon substitution of Eqs. (29) into Eqs. (28), we obtain the systems of equations

$$\begin{aligned}{} & {} -\omega _j n_{2,j}^{(1)} +k_j u_{2,j}^{(1)} =\mu _{1,j}, \nonumber \\{} & {} -\omega _j u_{2,j}^{(1)} +k_j \phi _{2,j}^{(1)} =\mu _{2,j}, \nonumber \\{} & {} -(k_j^2 +c_1) \phi _{2,j}^{(1)} +n_{2,j}^{(1)} =\mu _{3,j}, \end{aligned}$$

(30)

resulting from all terms proportional to $e^{i \theta _1}$ and $e^{i \theta _2}$, respectively (to be discussed later; note that $\mu _{1,j}$, $\mu _{2,j}$, and $\mu _{3,j}$, involving temporal and spatial derivatives of $\Psi _j$, for $j=1,2$, are given in “Appendix B”),

$$\begin{aligned}{} & {} -2 \omega _j n_{2,j}^{(2)} +2 k_j u_{2,j}^{(2)} =-2 k_j n_{1,j}^{(1)} u_{1,j}^{(1)}, \nonumber \\{} & {} -2 \omega _j u_{2,j}^{(2)} +2 k_j \phi _{2,j}^{(2)} =-k_j u_{1,j}^{(1)}{^2}, \nonumber \\{} & {} -(4 k_j^2 +c_1) \phi _{2,j}^{(2)} +n_{2,j}^{(2)}=c_2 \Psi _j^2, \end{aligned}$$

(31)

for $j=1$ and 2, the latter resulting from the terms proportional to $e^{2 i \theta _1}$ and $e^{2 i \theta _2}$, respectively. The second harmonic amplitudes are given by solutions in the form

$$\begin{aligned} n_{2,j}^{(2)}= & {} C_{n,2,j}^{(2)} \Psi _j^2, \nonumber \\ u_{2,j}^{(2)}= & {} C_{u,2,j}^{(2)} \Psi _j^2, \nonumber \\ \phi _{2,j}^{(2)}= & {} C_{\phi ,2,j}^{(2)} \Psi _j^2, \end{aligned}$$

(32)

where the coefficients $C_{n,2,j}^{(2)}$, $C_{u,2,j}^{(2)}$, and $C_{\phi ,2,j}^{(2)}$ are given in “Appendix A,” and finally

$$\begin{aligned}{} & {} -(\omega _1 +\omega _2) n_{2,+}^{(1)} +(k_1 +k_2) u_{2,+}^{(1)} =f_1^{(+)} \Psi _1 \Psi _2, \end{aligned}$$

(33)

$$\begin{aligned}{} & {} -(\omega _1 +\omega _2) u_{2,+}^{(1)} +(k_1 +k_2) \phi _{2,+}^{(1)} =f_2^{(+)} \Psi _1 \Psi _2, \end{aligned}$$

(34)

$$\begin{aligned}{} & {} -\left[ (k_1+k_2)^2 +c_1 \right] \phi _{2,+}^{(2)} +n_{2,+}^{(1)} =f_3^{(+)} \Psi _1 \Psi _2, \end{aligned}$$

(35)

and

$$\begin{aligned}{} & {} -(\omega _1 -\omega _2) n_{2,-}^{(1)} +(k_1 -k_2) u_{2,-}^{(1)} =f_1^{(-)} \Psi _1 \Psi _2^\star , \end{aligned}$$

(36)

$$\begin{aligned}{} & {} -(\omega _1 -\omega _2) u_{2,-}^{(1)} +(k_1 -k_2) \phi _{2,-}^{(1)} =f_2^{(-)} \Psi _1 \Psi _2^\star , \end{aligned}$$

(37)

$$\begin{aligned}{} & {} -\left[ (k_1 -k_2)^2 +c_1 \right] \phi _{2,-}^{(2)} +n_{2,-}^{(1)}= =f_3^{(-)} \Psi _1 \Psi _2^\star , \end{aligned}$$

(38)

where $f_1^{(\pm )}$, $f_2^{(\pm )}$, and $f_3^{(\pm )}$ are functions of $k_1$ and $k_2$ and are given in “Appendix B.” The last two systems result from the terms proportional to $e^{i (\theta _1 +\theta _2)}$ and $e^{i (\theta _2 -\theta _2)}$, respectively. Their solution reads:

$$\begin{aligned}{} & {} n_{2,+}^{(1)} =C_{n,2,+}^{(1)} \Psi _1 \Psi _2, ~~~~ n_{2,-}^{(1)} =C_{n,2,-}^{(1)} \Psi _1 \Psi _2^\star , \end{aligned}$$

(39)

$$\begin{aligned}{} & {} u_{2,+}^{(1)} =C_{u,2,+}^{(1)} \Psi _1 \Psi _2, ~~~~ u_{2,-}^{(1)} =C_{u,2,-}^{(1)} \Psi _1 \Psi _2^\star , \end{aligned}$$

(40)

$$\begin{aligned}{} & {} \phi _{2,+}^{(1)} =C_{\phi ,2,+}^{(1)} \Psi _1 \Psi _2, ~~~~ \phi _{2,-}^{(1)} =C_{\phi ,2,-}^{(1)} \Psi _1 \Psi _2^\star , \end{aligned}$$

(41)

where again the coefficients $C_{n,2,\pm }^{(1)}$, $C_{u,2,\pm }^{(1)}$, and $C_{\phi ,2,\pm }^{(1)}$ are given in “Appendix A.”

In the same (second) order ($\sim \varepsilon ^2$), we also obtain an equation involving the “constant” terms (zeroth-order harmonics) in the form

$$\begin{aligned} -c_1 \phi _2^{(0)} +n_2^{(0)} =+2 c_2 \left( |\Psi _1|^2 +|\Psi _2|^2 \right) , \end{aligned}$$

(42)

which will be used in the next subsection.

Before moving on to the equations which are third order in $\varepsilon$, we return to the discussion of the solution of Eqs. (30). The latter, which actually consists of two $3\times 3$ uncoupled systems for the variables $\{ n_{2,1}^{(1)}, u_{2,1}^{(1)}, \phi _{2,1}^{(1)} \}$ and $\{ n_{2,2}^{(1)}, u_{2,2}^{(1)}, \phi _{2,2}^{(1)} \}$, can be written in matrix form as

$$\begin{aligned} \begin{bmatrix} -\omega _j &{} +k_j &{} 0 \\ 0 &{} -\omega _j &{} +k_j \\ 1 &{} 0 &{} -(k_j^2 +c_1) \end{bmatrix} \begin{bmatrix} n_{2,j}^{(1)} \\ u_{2,j}^{(1)} \\ \phi _{2,j}^{(1)} \end{bmatrix} = \begin{bmatrix} \mu _{1,j} \\ \mu _{2,j} \\ \mu _{3,j} \end{bmatrix}, \end{aligned}$$

(43)

where $\mu _{m,j}$ ($m=1,2,3$ and $j=1,2$) are provided in “Appendix B.” Note that the determinants of the two inhomogeneous systems of Eqs. (13) are zero, since this was the requirement for obtaining the frequency dispersion relations. Thus, in order to find non-trivial solutions for the two inhomogeneous systems of Eqs. (13), it is imposed that the following determinants should also vanish:

$$\begin{aligned} D_j' = \begin{vmatrix} \mu _{1,j}&+k_j&0 \\ \mu _{2,j}&-\omega _1&+k_j \\ \mu _{3,j}&0&-(k_j^2 +c_1) \end{vmatrix} =0. \end{aligned}$$

(44)

These determinants result from the replacement of the first column of the determinant $D_j$ with the vector $\mathbf{\mu }_j =[ \mu _{1,j} \, \mu _{2,j} \, \mu _{3,j} ]^T$. After calculations we obtain that in order for $D_j'$ to vanish, the following compatibility conditions

$$\begin{aligned} \frac{\partial \Psi _j}{\partial t_1} = -v_{g,j} \frac{\partial \Psi _j}{\partial x_1} \end{aligned}$$

(45)

(for both $j = 1$ and 2) should hold. The physical implication is that the (two) wavepacket envelopes travel at their respective group velocity. This was qualitatively expected from earlier works [10, 73].

2.3 Derivation of a system of coupled NLS equations

The equations in order $\varepsilon ^3$ are

$$\begin{aligned} \frac{\partial n_3}{\partial t_0} +\frac{\partial (u_3)}{\partial x_0} =\mathcal{G}_1, \nonumber \\ \frac{\partial u_3}{\partial t_0} +\frac{\partial \phi _3}{\partial x_0} =\mathcal{G}_2, \nonumber \\ \frac{\partial ^2 \phi _3}{\partial x_0^2} -c_1 \phi _3 +n_3 =\mathcal{G}_3, \end{aligned}$$

(46)

where $\mathcal{G}_1$, $\mathcal{G}_2$, and $\mathcal{G}_3$ are expressions involving lower ($\le 2$)-order harmonics of n, u, and $\phi$, which are given in “Appendix B.” We shall seek a multi-harmonic solution by substituting into the system of Eqs. (46) the following Ansatz

$$\begin{aligned} S_3= & {} S_{3}^{(0)} +\left[ ] S_{3,1}^{(1)} e^{i \theta _1} +S_{3,1}^{(2)} e^{2 i \theta _1} +S_{3,1}^{(3)} e^{3 i \theta _1} +S_{3,2}^{(1)} e^{i \theta _2} \right. \nonumber \\{} & {} \left. +S_{3,2}^{(2)} e^{2 i \theta _2} +S_{3,2}^{(3)} e^{3 i \theta _2} \right. \nonumber \\{} & {} \left. +S_{3,+}^{(1)} e^{i (\theta _1 +\theta _2)} +S_{3,-}^{(1)} e^{2 i (\theta _1 -\theta _2)} +S_{3,+12}^{(1)} e^{i (\theta _1 +2\theta _2)}\right. \nonumber \\{} & {} \left. +S_{3,-12}^{(1)} e^{i (\theta _1 -2\theta _2)} \right. \nonumber \\{} & {} \left. +S_{3,+21}^{(1)} e^{i (2\theta _1 +\theta _2)} +S_{3,-21}^{(1)} e^{i (2\theta _1 -\theta _2)} +c.c. \right] , \end{aligned}$$

(47)

where $S =n, u$, and $\phi$ and c.c. denotes the complex conjugate of the expression within the curly brackets.

Isolating the $\ell =0$ contributions, we obtain two equations for the zeroth harmonic amplitudes which can be combined with Eq. (42) to provide a $3\times 3$ system to be satisfied by the (3) unknowns $n_2^{(0)}$, $u_2^{(0)}$, and $\phi _2^{(0)}$, i.e.,

$$\begin{aligned} \frac{\partial n_2^{(0)}}{\partial t_1} +\frac{\partial u_2^{(0)}}{\partial x_1}= & {} -2 \frac{\partial }{\partial x_1} \left[ \left( \frac{k_1}{\omega _1} \right) ^3 |\Psi _1|^2 +\left( \frac{k_2}{\omega _2} \right) ^3 |\Psi _2|^2 \right] , \end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial u_2^{(0)} }{\partial t_1} +\frac{\partial \phi _2^{(0)}}{\partial x_1}= & {} -\frac{\partial }{\partial x_1} \left[ \left( \frac{k_1}{\omega _1} \right) ^2 |\Psi _1|^2 +\left( \frac{k_2}{\omega _2} \right) ^2 |\Psi _2|^2 \right] \end{aligned}$$

(49)

$$\begin{aligned} n_2^{(0)}= & {} c_1 \phi _2^{(0)} +2 c_2 \left( |\Psi _1|^2 +|\Psi _2|^2 \right) \,. \end{aligned}$$

(50)

relations (27). To solve the $3\times 3$ system thus obtained for the zeroth harmonics, we shall introduce the Ansatz

$$\begin{aligned} \phi _2^{(0)} =C_{\phi ,2,1}^{(0)} |\Psi _1|^2 +C_{\phi ,2,2}^{(0)} |\Psi _2|^2, \nonumber \\ u_2^{(0)} =C_{u,2,1}^{(0)} |\Psi _1|^2 +C_{u,2,2}^{(0)} |\Psi _2|^2, \nonumber \\ n_2^{(0)} =C_{n,2,1}^{(0)} |\Psi _1|^2 +C_{n,2,2}^{(0)} |\Psi _2|^2, \end{aligned}$$

(51)

into Eqs. (48)–(50) and use Eq. (15) to determine the coefficients $C_{\phi ,2,j}$, $C_{u,2,j}$, and $C_{n,2,j}$ whose expressions are given in “Appendix A.”

Finally, the equations obtained (in third order in $\varepsilon$) for the (3rd-order) first harmonic mode $\ell =1$ read

$$\begin{aligned} -i \omega _j n_{3,j}^{(1)} +i k_j u_{3,j}^{(1)} =\mathcal{R}_{1,j}, \nonumber \\ -i \omega _j u_{3,j}^{(1)} +i k_j \phi _{3,j}^{(1)} =\mathcal{R}_{2,j}, \nonumber \\ -\left( k_j^2 +c_1 \right) \phi _{3,j}^{(1)} +n_{3,j}^{(1)} =\mathcal{R}_{3,j}, \end{aligned}$$

(52)

where the functions $\mathcal{R}_{1,j}$, $\mathcal{R}_{2,j}$, and $\mathcal{R}_{3,j}$ are given in “Appendix B.”

A lengthy algebraic manipulation of Eqs. (52)—aimed at eliminating the variables $n_{3,j}^{(1)}$, $u_{3,j}^{(1)}$, and $\phi _{3,j}^{(1)}$—leads us to an equation in the form:

$$\begin{aligned} -i \omega _j \mathcal{R}_{1,j} -i k_j \mathcal{R}_{2,j} +\omega _j^2 \mathcal{R}_{2,j} =0, \end{aligned}$$

(53)

where the expressions for $\mathcal{R}_{m,j}$ ($m=1,2,3$ and $j=1,2$) are given by Eqs. (B20)–(B22) in “Appendix B.”

Finally, by substituting the expressions for $\mathcal{R}_{m,j}$ into Eq. (53) and using the obtained solutions for the harmonic amplitudes $n_{1,j}^{(1)}$, $u_{1,j}^{(1)}$, $\phi _{1,j}^{(1)} =\Psi _j$, $n_{2,j}^{(2)}$, $u_{2,j}^{(2)}$, $\phi _{2,j}^{(2)}$, $n_{2}^{(0)}$, $u_{2}^{(0)}$, and $\phi _{2}^{(0)}$, we obtain after a tedious and lengthy calculation with equations

$$\begin{aligned}{} & {} 4 \omega _1 k_1 \frac{\partial ^2 \Psi _1 }{\partial t_1 \partial x_1} -\frac{k_1^2}{\omega _1^2} \frac{\partial ^2 \Psi _1 }{\partial t_1^2} +(1-\omega _1^2) \frac{\partial ^2 \Psi _1 }{\partial x_1^2} \nonumber \\{} & {} \quad +2 i \frac{k_1^2}{\omega _1} \frac{\partial ^2 \Psi _1 }{\partial t_2^2} +2 i k_1 (1-\omega _1^2) \frac{\partial \Psi _1 }{\partial x_2} \nonumber \\{} & {} \quad +\left( \tilde{Q}_{11} |\Psi _1|^2 +\tilde{Q}_{12} |\Psi _2|^2 \right) \Psi _1 =0, \end{aligned}$$

(54)

$$\begin{aligned}{} & {} 4 \omega _2 k_2 \frac{\partial ^2 \Psi _2 }{\partial t_1 \partial x_1} -\frac{k_2^2}{\omega _2^2} \frac{\partial ^2 \Psi _2 }{\partial t_1^2} +(1-\omega _2^2) \frac{\partial ^2 \Psi _2 }{\partial x_1^2} \nonumber \\{} & {} \quad +2 i \frac{k_2^2}{\omega _2} \frac{\partial ^2 \Psi _2 }{\partial t_2^2} +2 i k_2 (1-\omega _2^2) \frac{\partial \Psi _2 }{\partial x_2} \nonumber \\{} & {} \quad +\left( \tilde{Q}_{21} |\Psi _1|^2 +\tilde{Q}_{22} |\Psi _2|^2 \right) \Psi _2 =0, \end{aligned}$$

(55)

where

$$\begin{aligned} \tilde{Q}_{jj}= & {} -2 \frac{k_j^3}{\omega _j} \left( C_{u,2,j}^{(2)} +C_{u,2,j}^{(0)} \right) -k_j^2 \left( C_{n,2,j}^{(2)} +C_{n,2,j}^{(0)} \right) \nonumber \\{} & {} +2 c_2 \omega _j^2 \left( C_{\phi ,2,j}^{(2)} +C_{\phi ,2,j}^{(0)} \right) +3 c_3 \omega _j^2, \end{aligned}$$

(56)

and

$$\begin{aligned} \tilde{Q}_{12}= & {} -2 \frac{k_1^3}{\omega _1} C_{u,2,2}^{(0)} -k_1 \frac{k_2}{\omega _2} \left( \omega _1 \frac{k_2}{\omega _2} +k_1 \right) \left( C_{u,2,+}^{(1)} +C_{u,2,-}^{(1)} \right) \nonumber \\{} & {} -k_1^2 C_{n,2,2}^{(0)} -\omega _1 k_1 \frac{k_2}{\omega _2} \left( C_{n,2,+}^{(1)} +C_{n,2,-}^{(1)} \right) \nonumber \\{} & {} +2 c_2 \omega _1^2 \left( C_{\phi ,2,2}^{(0)} +C_{\phi ,2,+}^{(1)} +C_{\phi ,2,-}^{(1)} \right) +6 c_3 \omega _1^2, \end{aligned}$$

(57)

$$\begin{aligned} \tilde{Q}_{21}= & {} -2 \frac{k_2^3}{\omega _2} C_{u,2,1}^{(0)} -k_2 \frac{k_1}{\omega _1} \left( \omega _2 \frac{k_1}{\omega _1} +k_2 \right) \nonumber \\{} & {} \left( C_{u,2,+}^{(1)} +C_{u,2,-}^{(1)} \right) -k_2^2 C_{n,2,1}^{(0)} \nonumber \\{} & {} -\omega _2 k_2 \frac{k_1}{\omega _1} \left( C_{n,2,+}^{(1)} +C_{n,2,-}^{(1)} \right) \nonumber \\{} & {} +2 c_2 \omega _2^2 \left( C_{\phi ,2,1}^{(0)} +C_{\phi ,2,+}^{(1)} +C_{\phi ,2,-}^{(1)} \right) +6 c_3 \omega _2^2. \end{aligned}$$

(58)

Note that the terms proportional to the variables $n_{2,j}^{(1)}$, $u_{2,j}^{(1)}$, and $\phi _{2,j}^{(1)}$ were eliminated with the help of Eqs. (30).

From Eqs. (54) and (55), it is straightforward to obtain a pair of coupled NLS equations in the familiar form

$$\begin{aligned}{} & {} i \left( \frac{\partial \Psi _1}{\partial t_2} +v_{g,1} \frac{\partial \Psi _1}{\partial x_2} \right) +P_1 \frac{\partial ^2 \Psi _1}{\partial x_1^2} \nonumber \\{} & {} \quad +\left( Q_{11} |\Psi _1|^2 +Q_{12} |\Psi _2|^2 \right) \Psi _1 =0, \end{aligned}$$

(59)

$$\begin{aligned}{} & {} i \left( \frac{\partial \Psi _2}{\partial t_2} +v_{g,2} \frac{\partial \Psi _2}{\partial x_2} \right) +P_2 \frac{\partial ^2 \Psi _2}{\partial x_1^2} \nonumber \\{} & {} \quad +\left( Q_{21} |\Psi _1|^2 +Q_{22} |\Psi _2|^2 \right) \Psi _2 =0 \,, \end{aligned}$$

(60)

where (for $j=1,2$)

$$\begin{aligned} P_j =-\frac{3}{2} c_1 \frac{k_j}{ (k_j^2 +c_1)^{5/2} }, \end{aligned}$$

(61)

are the (2) dispersion coefficients (analogous to the group-velocity-dispersion/GVD terms in nonlinear optics; note that $P_j = \frac{1}{2}\frac{\partial \omega _j}{\partial k_j}$, and

$$\begin{aligned} Q_{jj} = \frac{\omega _j}{2 k_j^2} \tilde{Q}_{jj}, ~~~~ Q_{12} = \frac{\omega _1}{2 k_1^2} \tilde{Q}_{12}, ~~~~ Q_{21} = \frac{\omega _2}{2 k_2^2} \tilde{Q}_{21}\nonumber \\ \end{aligned}$$

(62)

are the self-modulation (self-nonlinearity) coefficient and the (2) cross-modulation (coupling nonlinearity) coefficients, respectively. (The tilted quantities in the latter three expressions were defined above.)

Fig. 2

The frequency dispersion coefficient $P_1$, and the nonlinearity coefficient $Q_{11}$, calculated from Eqs. (61) and the first of Eqs. (62), as a function of the wavenumber $k_1$ for the values (in descending order, i.e. top to bottom top curves): $\kappa =2$ (black), $\kappa =3$ (red), $\kappa =4$ (green), $\kappa =5$ (blue), $\kappa =6$ (orange), $\kappa =100$ (brown). (Color figure online)

In Fig. 2, the dispersion coefficient $P_1$ and the nonlinearity coefficient $Q_{11}$ are shown as a function of the wavenumber of the first carrier wave $k_1$. Note that the corresponding quantities for the second carrier wave (i.e., $P_2$, $Q_{22}$, etc.) as a function of the wavenumber $k_2$ have exactly the same form. As evident in Fig. 2a, for the model considered here, the dispersion coefficients $P_j$ ($j=1,2$) are negative for any $k_j$, converging to zero for large values of $k_j$. Also, for the interval of $k_1$ values shown in the figure, the magnitude of $P_1$ increases with increasing spectral parameter $\kappa$. In the Maxwell–Boltzmann case (i.e., corresponding practically to the value of $\kappa =100$), the minimum value of $P_1$ is located at $k_1 \simeq 0.5$, while it shifts to high values of $k_1$ with increasing $\kappa$.

On the other hand, the nonlinearity coefficients $Q_{jj}$ can be either positive or negative, depending on the value of $k_j$, as can be seen in Fig. 2b. In the Maxwell–Boltzmann case that corresponds to very high values of the spectral index $\kappa$ of the kappa distribution of the electrons, the coefficients $Q_{jj}$ change sign at a particular value of the wavenumber of the carrier wave $k_j$, i.e., at $k_j \equiv k_r =1.47$, in agreement with earlier results [8, 9, 66].

2.4 Critical carrier wavenumbers for non-Maxwellian plasmas

Generally, for arbitrary $\kappa$, the symbol $k_r$ denotes the value of $k_1$ at which $Q_{jj}$ has a single root, i.e., $k_r$ is defined as that $k_1$ for which $Q_{jj} (k_j; \kappa ) =0$. As it can be implied from the definition of $Q_{jj}$ (for either $j=1$ or 2), $k_r$ is a(n undisclosed) function of $\kappa$.

Fig. 3

a The root $k_r$ of $Q_{11}$ as a function of the spectral index $\kappa$. For large values of $\kappa$ that root converges asymptotically to the value $k_1 =k_r =1.47$, i.e., its value in the Maxwell–Boltzmann case. The inset shows a magnified part of the main figure for physically relevant values of $\kappa$. The orange-dashed line is located at $k_r =1.47$. b The zeroes of the coupling coefficient $Q_{12}$ on the $k_1 - k_2$ plane are shown (in ascending order, bottom to top) for $\kappa =2$ (black), $\kappa =3$ (red), $\kappa =4$ (green), $\kappa =5$ (blue), $\kappa =6$ (orange), $\kappa =100$ (brown). The coupling coefficient $Q_{12}$ is negative in the area of the $k_1 - k_2$ plane above the corresponding curve (and positive underneath). Note that the coupling coefficient $Q_{21}$ can be obtained from $Q_{12}$ by interchanging $k_1$ and $k_2$ in the corresponding expressions. The corresponding curves for the zeros of $Q_{21}$ can be obtained by a reflection with respect to the diagonal $k_1 =k_2$ (and thus $Q_{21}$ would be positive in the area above the curves, and negative underneath). (Color figure online)

The dependence of the root $k_r$ on the spectral index $\kappa$ is shown in Fig. 3a for a large interval of $\kappa$ values. As it can be observed in Fig. 3a, the root $k_r$ diverges as $\kappa \rightarrow 3/2$. The value of the root $k_r$ decreases rapidly as $\kappa$ increases from the value 3/2, then reaches a minimum around $\kappa \simeq 2.5$ close to the border of far- to near-equilibrium, and then, with further increasing $\kappa$, it increases slowly to converge to $k_r =1.47$ from below for very large values of $\kappa$ (Maxwell–Boltzmann regime).

The coupling coefficients $Q_{12}$ and $Q_{21}$, on the other hand, depend on both $k_1$ and $k_2$ as can be observed from Eqs. (62). It turns out that, on the $k_1 -k_2$ plane, these coefficients may have either positive or negative values. The boundary between the regions corresponding to opposite signs for $Q_{12}$ is shown for several values of $\kappa$ in Fig. 3b, in which $Q_{12}$ is negative in the areas of the $k_1 -k_2$ plane above the boundary. It is obvious from the above figure that smaller values of the 2nd wavenumber ($k_2$) that might be associated with negative $Q_{12}$ for Maxwellian electrons (i.e. large $\kappa$) now switch to a positive $Q_{12}$ in the case of suprathermal electrons, i.e., for smaller $\kappa$. The analogous curves (boundaries) for $Q_{21}$ are obtained upon reflection with respect to the diagonal $k_1 - k_2$; hence, in the areas above the boundaries $Q_{21}$ are positive (and negative underneath).

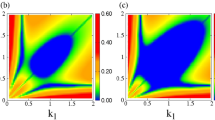
It is certainly useful to see not only these boundaries but all the values that $Q_{12}$ and $Q_{21}$ can take on the $k_1 -k_2$ plane. The first of them, i.e., the coefficient $Q_{12}$, is mapped on the $k_1 -k_2$ plane in Fig. 4 for several values of $\kappa$. (Note that $Q_{12}$ and $Q_{21}$ exhibit reflection symmetry around $k_1 =k_2$.) As it can be observed in Fig. 4, the coefficient $Q_{12}$ is mostly negative on the $k_1 -k_2$ plane for $\kappa =2$ (Fig. 4a), while the areas of negative and positive values are more or less of the same size for the other values of $\kappa$, i.e., for $\kappa =3,4,5,6,100$ (Fig. 4b–f). Also, it is clear that $Q_{12}$ takes very large positive or negative values in certain areas of the $k_1 -k_2$ plane. In particular, $Q_{12}$ is very large and positive for low $k_2$, while it has very large negative values in the upper left corner of the $k_1 -k_2$ plane. Actually, the plots of $Q_{12}$ are shown only for $k_2 > 0.1$ to avoid very large and divergent values. These large values of the coupling coefficients $Q_{12}$ and $Q_{21}$ are probably responsible for the wide occurrence of modulational instability in the CNLS system that will be discussed in the next section. Interestingly, only one (i.e., not both) of the $Q_{12}$ and $Q_{21}$ coefficients can become zero for a (any) particular pair of $k_1$ and $k_2$ values. In that case, for, say, $Q_{21} =0$, the second of CNLS equations Eq. (60) decouples from the first one, Eq. (59), although the latter is still affected by the former [66].

Fig. 4

The nonlinear coupling coefficient $Q_{12}$ mapped on the plane of the wavenumbers of the carrier waves $k_1$ and $k_2$, for a $\kappa =2$, b $\kappa =3$, c $\kappa =4$, d $\kappa =5$, e $\kappa =6$, f $\kappa =100$. In (f), the $\kappa$ distribution practically coincides with the Maxwell–Boltzmann distribution. The black contour indicates the boundary between positive and negative values of $Q_{12}$. Note that the plots above are shown from $k_2 =0.1$ to 2 when comparing the boundaries (the contours) with the curves in Fig. 3b. At low $k_2$ values, $Q_{12}$ becomes very large and has been omitted, for clarity. The corresponding coupling coefficients $Q_{21}$ are obtained upon a reflection around the line $k_1 =k_2$ (i.e., upon a permutation between $k_1$ and $k_2$.)

2.5 Reduced form of the CNLS system

Equations (49) and (50) can be transformed to a more common form of CNLS equations with a change of the independent variables, followed by a transformation of the wavefunctions $\Psi _1$ and $\Psi _2$. Let us introduce the new independent variables $\xi$ and $\tau$ through $\xi = x -v t$ and $\tau =t$, where the subscript in x and t has been dropped, and $v =( v_{g,1} +v_{g,2} )/2$ is the half-sum of the group velocities $v_{g,1}$ and $v_{g,2}$. By applying this change of variables to Eqs. (49) and (50) we get

$$\begin{aligned}{} & {} i \left( \frac{\partial \Psi _1}{\partial \tau } +\delta \frac{\partial \Psi _1}{\partial \xi } \right) +P_1 \frac{\partial ^2 \Psi _1}{\partial \xi ^2} \nonumber \\{} & {} \quad +\left\{ Q_{11} |\Psi _1|^2 +Q_{12} |\Psi _2|^2 \right\} \Psi _1 =0, \end{aligned}$$

(63)

$$\begin{aligned}{} & {} i \left( \frac{\partial \Psi _2}{\partial \tau } -\delta \frac{\partial \Psi _2}{\partial \xi } \right) +P_2 \frac{\partial ^2 \Psi _2}{\partial \xi ^2} \nonumber \\{} & {} \quad +\left\{ Q_{21} |\Psi _1|^2 +Q_{22} |\Psi _2|^2 \right\} \Psi _2 =0, \end{aligned}$$

(64)

where $\delta =( v_{g,1} -v_{g,2} )/2$ is the half-difference of the group velocities. In writing Eqs. (63) and (64), it is implicitly understood that the differentiations involved in the dispersive terms are with respect to the variable $\xi _1$, while the higher-order differentiation in the beginning of the left-hand side is with respect to $\xi _2$. The subscripts are nonetheless omitted, for simplicity, as they will not affect the final result. Then, by applying to transformation $\Psi _j =\bar{\Psi }_j\exp \left[ i\left( \frac{\delta ^2}{4 P_j} \tau -s_j\frac{\delta }{2P_j} \xi \right) \right]$ (with $s_1 = - s_2 =+1$), where $j=1,2$, we obtain

$$\begin{aligned}{} & {} i \frac{\partial \bar{\Psi }_1}{\partial \tau } \!+\!P_1 \frac{\partial ^2 \bar{\Psi }_1}{\partial \xi ^2} \!+\!\left\{ Q_{11} |\bar{\Psi }_1|^2 \!+\!Q_{12} |\bar{\Psi }_2|^2 \right\} \bar{\Psi }_1 \!=\!0,\nonumber \\ \end{aligned}$$

(65)

$$\begin{aligned}{} & {} i \frac{\partial \bar{\Psi }_2}{\partial \tau } \!+\!P_2 \frac{\partial ^2 \bar{\Psi }_2}{\partial \xi ^2} \!+\!\left\{ Q_{21} |\bar{\Psi }_1|^2 \!+Q_{22} |\bar{\Psi }_2|^2 \right\} \bar{\Psi }_2 =0,\nonumber \\ \end{aligned}$$

(66)

where $\bar{\Psi }_j$ are complex functions of the new variables $\xi$ and $\tau$.

It should be noted that CNLS equations analogous (and formally equivalent) to either Eqs. (59)–(60) or to Eqs. (65) and (66) above, have been obtained in various physical contexts earlier, describing nonlinear processes including pulse propagation in water waves [53], deep water wave propagation [52], soliton propagation in left-handed transmission lines [58], pulse propagation in optical nonlinear media [74], emergence of vector solitons in left-handed metamaterials [56], propagation of pulses with different polarization in anisotropic dispersive media [75]. Analogous systems of equations have been obtained from various plasma fluid models [29, 30, 32,33,34,35, 37, 38, 66], but never in the case of a (non-symmetric) pair of electrostatic wavepackets (i.e., with different wavenumbers and amplitude), which is the focus of this study.

3 Modulational instability analysis—analytical setting

Modulational instability (MI) analysis for two co-propagating pulses in the plasma fluid described by Eqs. (1) can be performed on CNLS equations (63) and (64) following the procedure in Refs. [38, 65]. We shall first seek a plane-wave solution for the system, which turns out to be of the form

$$\begin{aligned} \Psi _j =\Psi _{j,0} \, e^{i \tilde{\omega }_j \tau }, \end{aligned}$$

(67)

where $\Psi _{j,0}$ ($j=1,2$) is a constant amplitude (here assumed to be real) and $\tilde{\omega }_j$ is a frequency, to be determined. By inserting Eq. (67) into Eqs. (63) and (64), we obtain

$$\begin{aligned} \tilde{\omega }_1= & {} Q_{11} \Psi _{1,0}^2 +Q_{12} \Psi _{2,0}^2, \end{aligned}$$

(68)

$$\begin{aligned} \tilde{\omega }_2= & {} Q_{21} \Psi _{1,0}^2 +Q_{22} \Psi _{2,0}^2. \end{aligned}$$

(69)

Equations (67) with the amplitude-dependent frequencies given in Eqs. (68) and (69) provide a nonlinear mode of the CNLS system wherein the propagation of waves is governed by Eqs. (63) and (64). The stability behavior of these modes against a small perturbation can be addressed through standard MI analysis. Let us perturb the nonlinear modes by adding a small complex quantity $\varepsilon _j$ to their amplitudes ($|\varepsilon _j| \ll |\Psi _{j,0}|$), as

$$\begin{aligned} \Psi _j =( \Psi _{j,0} +\varepsilon _j ) \, e^{i \phi _j \tau }. \end{aligned}$$

(70)

By inserting the perturbed $\Psi _j$ into Eqs. (63) and (64) we obtain

$$\begin{aligned}{} & {} i \left( \frac{\partial \varepsilon _1}{\partial \tau } +\delta \frac{\partial \varepsilon _1}{\partial \xi } \right) +\Psi _{1,0} \phi _1 +P_1 \frac{\partial ^2 \varepsilon _1}{\partial \xi ^2} \nonumber \\{} & {} \quad +Q_{11} \Psi _{1,0}^2 (\varepsilon _1 +\varepsilon _1^\star ) +Q_{12} {\Psi }_{1,0} \Psi _{2,0} (\varepsilon _2 +\varepsilon _2^\star ) =0, \end{aligned}$$

(71)

$$\begin{aligned}{} & {} i \left( \frac{\partial \varepsilon _2}{\partial \tau } -\delta \frac{\partial \varepsilon _2}{\partial \xi } \right) +\Psi _{2,0} \phi _2 +P_2 \frac{\partial ^2 \varepsilon _2}{\partial \xi ^2} \nonumber \\{} & {} \quad +Q_{22} \Psi _{2,0}^2 (\varepsilon _2 +\varepsilon _2^\star ) +Q_{21} \Psi _{2,0} \Psi _{1,0} (\varepsilon _1 +\varepsilon _1^\star ) =0. \end{aligned}$$

(72)

Then, by setting $\varepsilon _j =g_j +i h_j$, where $g_j$ and $h_j$ are real functions, and subsequently substituting into Eqs. (71) and (72) and eliminating $h_j$ from the equations, we get

$$\begin{aligned}{} & {} \left\{ \left( \frac{\partial }{\partial \tau } +\delta \frac{\partial }{\partial \xi } \right) ^2 +P_1 \left( P_1 \frac{\partial ^2}{\partial \xi ^2} +2 Q_{11} \Psi _{1,0}^2 \right) \frac{\partial ^2}{\partial \xi ^2} \right\} g_1 \nonumber \\{} & {} \quad +2 P_1 Q_{12} \Psi _{2,0} \Psi _{1,0} \frac{\partial ^2}{\partial \xi ^2} g_2 =0 \,, \end{aligned}$$

(73)

$$\begin{aligned}{} & {} \left\{ \left( \frac{\partial }{\partial \tau } -\delta \frac{\partial }{\partial \xi } \right) ^2 +P_2 \left( P_2 \frac{\partial ^2}{\partial \xi ^2} +2 Q_{22} \Psi _{2,0}^2 \right) \frac{\partial ^2}{\partial \xi ^2} \right\} g_2 \nonumber \\{} & {} \quad +2 P_2 Q_{21} \Psi _{1,0} \Psi _{2,0} \frac{\partial ^2}{\partial \xi ^2} g_1 =0 \,. \end{aligned}$$

(74)

Eventually, by setting

$$\begin{aligned} g_j =g_{j,0} \, e^{i (K \xi -\Omega \tau )} \end{aligned}$$

(75)

and then substituting into the earlier equations, we obtain after some algebra the compatibility condition

$$\begin{aligned} \left[ (\Omega -\delta K)^2 -\Omega _1^2 \right] \left[ (\Omega +\delta K)^2 -\Omega _2^2 \right] =\Omega _c^4, \end{aligned}$$

(76)

where ($j=1,2$)

$$\begin{aligned} \Omega _j^2= & {} P_j K^2 \left( P_j K^2 -2 Q_{jj} \Psi _{j,0}^2 \right) , \end{aligned}$$

(77)

$$\begin{aligned} \Omega _c^4= & {} 4 P_1 P_2 Q_{12} Q_{21} \Psi _{1,0}^2 \Psi _{2,0}^2. \end{aligned}$$

(78)

Fig. 5

Maps of the growth rate $\Gamma$ on the plane of the wavenumber of the second carrier wave $k_2$ and the wavenumber of the perturbation K for $k_1 =0.4$, $\Psi _{1,0} =\Psi _{2,0} =0.15$, and a $\kappa =2$; b $\kappa =3$; c $\kappa =4$; d $\kappa =5$; e $\kappa =6$; f $\kappa =100$. For the selected value of $k_1$, the two single NLS equations resulting from decoupling the CNLS equations (e.g., by setting $Q_{12} =Q_{21} =0$ in Eqs. (63) and (64) are either both in the stable regime (for $k_2 < k_r$ where $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$), or the first is in the stable regime and the second in the unstable (for $k_2 > k_r$ where $P_1 Q_{11} < 0$ and $P_2 Q_{22} > 0$). Note that $k_r$ depends on the particular value of the spectral index $\kappa$ in accordance with the inset of Fig. 3a

For modulational instability to set in, Eq. (76) must have at least one pair of complex conjugate roots, so that the (positive) imaginary part of these roots can be identified as the growth rate of the modulationally unstable modes $\Gamma$. When Eq. (76) has two pairs of complex conjugate roots, then the largest of their imaginary parts is identified as the growth rate of the modulationally unstable modes, $\Gamma$, i.e.,

$$\begin{aligned} \Gamma =\max [Im(\Omega _r)], \end{aligned}$$

(79)

where $\Omega _r$ denotes one (each) of the four roots of the compatibility condition.

Fig. 6

Maps of the growth rate $\Gamma$ on the $k_2 - K$ plane for a $\kappa =1.75$; b $\kappa =2.00$; c $\kappa =2.25$; d $\kappa =2.50$. The other parameters as in Fig. 5. The vertical black-solid line indicates the boundary between two different regimes of the decoupled CNLS equations, i.e., the stable-stable regime for which $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$ ($k_2 < k_r$, left from the vertical line) and the stable–unstable regime for which $P_1 Q_{11} < 0$ and $P_2 Q_{22} > 0$ ($k_2 > k_r$, right from the vertical line). Note that $k_r$ depends weakly on the spectral index $\kappa$, but the differences cannot be observed in this scale

Note that a similar analysis may be applied to incoherent pairs of CNLS equations [64] as well as to higher-dimensional, non-autonomous CNLS equations [46].

3.1 Decoupled envelopes

In order to facilitate later discussion, we consider now the special case in which CNLS equations (73) and (74) are decoupled, i.e., the case in which either $Q_{12}$ or $Q_{21}$ (or even both) is equal to zero. In that case, compatibility conditions Eq. (76) simplifies significantly, and the perturbation frequencies $\Omega$ as a function of the perturbation wavenumber K are given by

$$\begin{aligned} \Omega =+\delta K \pm \Omega _1, ~~~~\Omega =-\delta K \pm \Omega _2, \end{aligned}$$

(80)

for the first and the second NLS equation that results from decoupling Eqs. (73) and (74), respectively. Correspondingly, the criterion for modulational instability in the first and second decoupled equation becomes, respectively, $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$. Note that these products depend on $k_1$ only and $k_2$ only, respectively. Since $P_j$ ($j=1,2$) in the considered model is always negative, the sign of the product $P_j Q_{jj}$ depends here on $Q_{jj}$. Now, if we recall that $Q_{jj} > 0$ for $k_j < k_r (\kappa )$ while $Q_{jj} < 0$ for $k_j > k_r (\kappa )$, we arrive at the following result: Within the considered model, the first NLS equation (for the 1st wavepacket) is modulationally stable for $k_1 < k_r (\kappa )$, while it is modulationally unstable otherwise. An identical conclusion is drawn and can be formulated for the second wavepacket (if decoupled from the first), upon formally shifting $1 \rightarrow 2$, i.e., it will be stable for $k_2 < k_r (\kappa )$ and unstable otherwise.

The conclusions in the latter paragraph recover what has long been known for the modulational stability profile of the NLS equation [76], summarized in that stability is prescribed for $P Q < 0$ and instability occurs otherwise.

4 Modulational instability: numerical parametric analysis

We have calculated the growth rate $\Gamma$ numerically for the CNLS equations by finding the roots of the polynomial in $\Omega$ function resulting from Eq. (76) and subsequently identifying the one with the highest imaginary part. That highest imaginary part is plotted as a function of the wavenumber of the perturbation K and the wavenumber of the second carrier wave $k_2$ for six values of the spectra index $\kappa$, i.e., for $\kappa =2,3,4,5,6,100$, and fixed value of $k_1$ and the amplitudes of the nonlinear wave modes $A_{1,0}$ and $A_{2,0}$ (the latter are fixed throughout the paper to $A_{1,0} =A_{2,0} =0.15$).

In Fig. 5, in particular, the growth rate $\Gamma$ is mapped on the $k_2 - K$ plane for $k_1 =0.4 < k_r (\kappa )$ and the six values of the spectral index $\kappa$ mentioned earlier. For that value of $k_1$, the first of the decoupled CNLS equations is modulationally stable ($P_1 Q_{11} < 0$), while the second one is also modulationally stable for $k_2 < k_r (\kappa )$ ($P_2 Q_{22} < 0$), while it is modulationally unstable for $k_2 > k_r (\kappa )$ ($P_2 Q_{22} > 0$). The instability boundary for the second decoupled CNLS equation is indicated in Fig. 5 (as well as in Figs. 7 and 9) by the black-solid vertical line. All the sub-figures Fig. 5 reveal complex instability patterns, in which modulational instability appears both in areas of the $k_2 - K$ plane where $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$ (stable-stable regime), as well as in areas where $P_1 Q_{11} < 0$ and $P_2 Q_{22} > 0$ (stable–unstable regime). The growth rate $\Gamma$ has not been mapped for $k_2 < 0.1$ on the $k_2 - K$ plane in all sub-figures for clarity, since it acquires very large and even divergent values in this areas.

Fig. 7

Maps of the growth rate $\Gamma$ on the plane of the wavenumber of the second carrier wave $k_2$ and the wavenumber of the perturbation K for $k_1 =0.7$, $\Psi _{1,0} =\Psi _{2,0} =0.15$, and a $\kappa =2$; b $\kappa =3$; c $\kappa =4$; d $\kappa =5$; e $\kappa =6$; f $\kappa =100$. For the selected value of $k_1$, the two single NLS equations resulting from decoupling the CNLS equations (e.g., by setting $Q_{12} =Q_{21} =0$ in Eqs. (63) and (64) are either both in the stable regime (for $k_2 < k_r$ where $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$), or the first is in the stable regime and the second in the unstable (for $k_2 > k_r$ where $P_1 Q_{11} < 0$ and $P_2 Q_{22} > 0$). Note that $k_r$ depends on the particular value of the spectral index $\kappa$ in accordance with the inset of Fig. 3a

Fig. 8

Maps of the growth rate $\Gamma$ on the $k_2 - K$ plane for a $\kappa =1.75$; b $\kappa =2.00$; c $\kappa =2.25$; d $\kappa =2.50$. The other parameters as in Fig. 7. The vertical black-solid line indicates the boundary between two different regimes of the decoupled CNLS equations, i.e., the stable-stable regime for which $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$ ($k_2 < k_r$, left from the vertical line) and the stable–unstable regime for which $P_1 Q_{11} < 0$ and $P_2 Q_{22} > 0$ ($k_2 > k_r$, right from the vertical line). The stability situation in these maps is the same as that in Figs. 5 and 6. Note that $k_r$ depends weakly on the spectral index $\kappa$, but the differences cannot be observed in this scale

Generally speaking, the decrease of the spectral index $\kappa$ increases the areas on the $k_2 - K$ plane in which MI occurs. Moreover, the maximum values of the growth rate $\Gamma$ seem to increase considerably with decreasing $\kappa$ (note the different scales in the colorbars). Note also the difference in the modulational instability patterns for values of $\kappa$ in the far- and near-equilibrium region, i.e., for $\kappa =2$ and $\kappa =3,4,5,6,100$, respectively, which are separated by a rough empirical boundary at around $\kappa \simeq 2.5$. Indeed, for $\kappa =2$, the growth rate $\Gamma$ exhibits very large values, and the CNLS system is modulationally unstable in the larger part of the $k_2 - K$ plane in which the decoupled CNLS equations are in the stable-stable regime ($P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$). For the next higher value of $\kappa$, i.e., for $\kappa =3$, the CNLS system is modulationally stable in the most part of the area in which the decoupled CNLS equations are in the stable-stable regime. With further increasing the value of $\kappa$, the areas of the $k_2 - K$ plane in which the CNLS system is modulationally unstable gradually shrink slightly, while the higher values of the growth index $\Gamma$ also gradually decrease.

In Fig. 5, as well as in Figs. 7 and 9, it is evident that the most significant variation in the patterns of $\Gamma$ seems to occur for values of the spectral index $\kappa$ within the strongly non-thermal region, i.e., for $1.5< \kappa < 2.5$. To the contrary, the variation of the $\Gamma$ pattern for $\kappa =3$ and up to infinity is rather slight, at least as long as the size of the modulational instability areas on the $k_2 - K$ plane and the magnitude of $\Gamma$ in these areas are concerned. In Fig. 6, maps of $\Gamma$ on the $k_2 - K$ plane are shown for more values of $\kappa$ within the strongly non-thermal region, i.e., for $\kappa =1.75$, 2.25, and 2.50. In the figure, the map of the already shown map for $\kappa =2$ is also shown along with the other three. Inspection of the four subfigures of Fig. 6 readily reveals the dramatic variations of the modulational instability $\Gamma$ patterns with the variation of $\kappa$. For $\kappa =1.75$ (Fig. 6a), in particular, modulational instability accompanied by very high values of $\Gamma$ is apparent over almost the whole of the $k_2 - K$ plane shown. As we shall see also below, this is true for the other case studies presented here. Empirically we find that this the situation for $\kappa$ up to 1.90, where some modulationally stable islands begin to appear on the $k_2 - K$ plane. When $\kappa$ is increased to 2, as we have also discussed in the previous figure, a substantial modulationally stable appears on the $k_2 - K$ plane that extends to both the stable-stable and stable–unstable regions of the decoupled CNLS equations. At the same time, the modulationally unstable areas, which remain large, are localized to two basic lobes, the one in the stable-stable and the other in the stable–unstable region of the decoupled CNLS equations. In the centers of these lobes, the highest values of $\Gamma$ occur. With further increasing $\kappa$, the modulationally stable area increases against the modulationally unstable ones. Moreover, the strongly modulationally unstable areas gradually concentrate in the stable–unstable region of the decoupled CNLS equations, while another strongly modulationally unstable area remains for low $k_2$. Remnants of the latter can be even observed in Fig. 5b (for $\kappa =3$).

Fig. 9

Maps of the growth rate $\Gamma$ on the plane of the wavenumber of the second carrier wave $k_2$ and the wavenumber of the perturbation K for $k_1 =1.6$, $\Psi _{1,0} =\Psi _{2,0} =0.15$, and a $\kappa =2$; b $\kappa =3$; c $\kappa =4$; d $\kappa =5$; e $\kappa =6$; f $\kappa =100$. For the selected value of $k_1$, the two single NLS equations resulting from decoupling the CNLS equations (e.g., by setting $Q_{12} =Q_{21} =0$ in Eqs. (63) and (64) are either both in the unstable regime (for $k_2 > k_r$ where $P_1 Q_{11} > 0$ and $P_2 Q_{22} > 0$), or the first is in the unstable regime and the second in the stable (for $k_2 < k_r$ where $P_1 Q_{11} > 0$ and $P_2 Q_{22} < 0$). Note that $k_r$ depends on the particular value of the spectral index $\kappa$ in accordance with the inset of Fig. 3a

The results shown in Fig. 7 have been obtained with the same parameters as those used in Fig. 5, except that in this case $k_1 =0.7$. Thus, as long as the stability of the decoupled CNLS equations is concerned, the situation is exactly the same as that in Fig. 5, i.e., the decoupled CNLS equations are in the stable-stable regime ($P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$) for $k_2 < k_r (\kappa )$, while they are in the stable–unstable regime for $k_2 > k_r (\kappa )$ ($P_1 Q_{11} < 0$ and $P_2 Q_{22} > 0$). In comparison with Fig. 5, we observe that for $\kappa =3,4,5,6,100$, areas of strong instability with relatively high values of the growth rate $\Gamma$ occur at low $k_2$ for most of the perturbation wavenumbers shown in these figures. Again, these strongly unstable areas shrink slightly with increasing spectral index from $\kappa =3$ to 100. A similar situation can be described for $\kappa =2$, where high values of the growth rate $\Gamma$ occur at low $k_2$ as in the case of higher $\kappa$; however, the values of $\Gamma$ are significantly higher in this case (note again the difference in the scales of colorbars). Also, in a large part of the stable-stable area of the $k_2 - K$ plane modulational instability with moderate values of $\Gamma$ occurs. Generally speaking, the strength of the modulational instability is weaker and the areas where that instability occurs are smaller in Fig. 7 for $k_1 =0.7$ than in Fig. 5 for $k_1 =0.4$ (except at low $k_2$). This can be observed more clearly for $\kappa \ge 3$.

As above, we also present maps of $\Gamma$ for a few more values of $\kappa$ in the strongly non-thermal region, i.e., in the interval $1.5< \kappa < 2.5$ in Fig. 8. Roughly, the remarks made for the patterns of $\Gamma$ in Fig. 6 also hold here. For $\kappa =1.75$ (Fig. 8a), almost all of the shown area of the $k_2 - K$ plane is modulationally unstable, with the growth rate achieving very high values of the same order as those in Fig. 6a. Again, with increasing $\kappa$, the modulationally stable areas on the $k_2 - K$ plane grow to the expense of the modulationally unstable ones. The pattern of $\Gamma$ in Fig. 8b is similar to that in Fig. 6b with the two modulationally unstable lobes and the strongly modulationally unstable area for low $k_2$. In Fig. 8c, the two lobes disappear, while a strongly modulationally unstable area at low $k_2$ remains, along with another modulationally unstable area which is located in the stable–unstable region of the decoupled CNLS equations, i.e., in the area with $k_2 > k_r (\kappa )$. Peculiarly, the modulationally unstable areas in Fig. 8d are larger to those in Fig. 8c. However, the general tendency of shrinking of the modulationally unstable areas with increasing $\kappa$ continuous for $\kappa > 2.5$. Note that in this case the strongly modulationally unstable area for low $k_2$ persists, although becoming much smaller with increasing $\kappa$, even for very large values of $\kappa$, i.e., $\kappa =100$ (Fig. 7f).

Fig. 10

Maps of the growth rate $\Gamma$ on the $k_2 - K$ plane for a $\kappa =1.75$; b $\kappa =2.00$; c $\kappa =2.25$; d $\kappa =2.50$. The other parameters as in Fig. 9. The vertical black-solid line indicates the boundary between two different regimes of the decoupled CNLS equations, i.e., the unstable-stable regime for which $P_1 Q_{11} > 0$ and $P_2 Q_{22} < 0$ ($k_2 < k_r$, left from the vertical line) and the unstable–unstable regime for which $P_1 Q_{11} > 0$ and $P_2 Q_{22} > 0$ ($k_2 > k_r$, right from the vertical line). Note that $k_r$ depends weakly on the spectral index $\kappa$, but the differences cannot be observed in this scale

The results shown in Fig. 9 have been obtained with the same parameters as those used in Figs. 5 and 7, except that the value of $k_1$ is now $k_1 =1.6 > k_r (\kappa )$. That means that the decoupled CNLS equations are either in the unstable-stable regime ($P_1 Q_{11} > 0$ and $P_2 Q_{22} < 0$) for $k_2 < k_r (\kappa )$, i.e., to the left from the black-solid vertical line, while they are in the unstable–unstable regime ($P_1 Q_{11} > 0$ and $P_2 Q_{22} > 0$) for $k_2 > k_r (\kappa )$, i.e., to the right of the black-solid vertical line. In this case, we observe a change in the obtained instability patterns, especially for $\kappa \ge 3$. For all values of $\kappa$, we again observe strong modulational instability with high values of $\Gamma$ for low $k_2$. For $\kappa =2$, modulational instability occurs in most parts of the areas of the $k_2 - K$ plane in which the decoupled CNLS equations are either in the unstable-stable or the unstable–unstable regime. For $\kappa \ge 3$ we again observe some shrinkage of the instability areas with increasing $\kappa$. We can also observe for these values of $\kappa$ that the modulationally unstable areas are mostly in the unstable-stable regime than in the unstable–unstable regime of the decoupled CNLS equations.

In the case shown in Fig. 10, also, the patterns of the growth rate $\Gamma$ on the $k_2 - K$ plane for a few values of $\kappa$ are in the strongly non-thermal region, i.e., for small values of $\kappa$. The evolution of these patterns is similar to the corresponding evolution described in Fig. 10. Thus, from Figs. 5, 6, 7, 8, 9, and 10 we can safely conclude that the most dramatic variation in the onset (region) of modulational instability on the $k_2 - K$ plane occurs in the interval of $\kappa$ values within the strongly non-thermal region.

Fig. 11

The growth rate $\Gamma$ of the CNLS system (black curves) and the growth rates $\Gamma _1$ and $\Gamma _2$ (red and green curves, respectively) of the first and second decoupled CNLS Eqs. (63) and (64 as a function of the wavenumber of the perturbation K for $\kappa =3$, $\Psi _{1,0} =\Psi _{2,0} =0.15$, and a $k_1 =1$ and $k_2 =0.6$, for which $P_1 Q_{11} < 0$ and $P_2 Q_{22} < 0$ (stable-stable); b $k_1 =1.6$ and $k_2 =1.35$, for which $P_1 Q_{11} > 0$ and $P_2 Q_{22} < 0$ (unstable-stable); c $k_1 =1.6$ and $k_2 =1.45$, for which $P_1 Q_{11} > 0$ and $P_2 Q_{22} > 0$ (unstable–unstable). Note the difference in the horizontal scales. The growth rates $\Gamma _1$ and $\Gamma _2$ are always zero in (a), while $\Gamma _2$ is always zero in (b)

4.1 Representative examples of growth rate variation

It may be interesting to present some illustrative examples for the growth rate $\Gamma$ as a function of the perturbation wavenumber K which may be distinctly different from those one may observe in a single NLS equation. In Fig. 11$\Gamma (K)$ curves are shown in three cases that differ in respect of the stability regime of the decoupled CNLS equations, for $\kappa =3$. Along with these curves, we also show the corresponding growth rates $\Gamma _1$ and $\Gamma _2$ obtained for the first and the second decoupled CNLS equation, respectively. In Fig. 11a, in which $k_1 =1 < k_r (\kappa )$ and $k_2 =0.6 < k_r (\kappa )$, i.e., in the stable-stable regime of the decoupled CNLS equations, we obtain a $\Gamma (K)$ curve with two instability lobes. Interestingly, stronger modulational instability occurs in the second lobe, for K between 3 and 4, than in the first lobe for K between 0 and 0.5 (low K). Since both the decoupled equations are modulationally stable, the corresponding growth rates $\Gamma _1$ and $\Gamma _2$ are both zero. In Fig. 11b, in which $k_1 =1.6 > k_r (\kappa )$ and $k_2 =1.35 > k_r (\kappa )$, i.e., in the unstable-stable regime of the decoupled CNLS equations, we obtain a $\Gamma (K)$ curve with two humps. Moreover, we obtain a nonzero $\Gamma _1 (\kappa )$ curve which has the commonly observed shape. A comparison between the two indicates that besides the difference in shape, the values of $\Gamma _1 (\kappa )$ are always significantly smaller than those of $\Gamma (\kappa )$. Moreover, the modulationally unstable interval in K is much smaller in the first decoupled NLS equation than that of the coupled CNLS system. In Fig. 11c, in which $k_1 =1.6 > k_r (\kappa )$ and $k_2 =1.45 > k_r (\kappa ) =1.42$, i.e., in the unstable–unstable regime of the decoupled CNLS equations, we obtain three curves for the growth rates $\Gamma (K)$, $\Gamma _1$, and $\Gamma _2$ which have the same shape but very different size. As a result, the interval of the perturbation wavenumber K in which the coupled CNLS system is modulationally unstable, is much larger that the corresponding one of either the first or the second decoupled NLS equation.

5 Discussion and conclusions

A pair of CNLS equations was derived for two co-propagating and interacting electrostatic wavepackets in a plasma fluid, comprising cold inertial ions evolving against a thermalized, kappa-distributed electron background. A multiple-scale technique has been adopted, similar to the well-known Newell’s method in nonlinear optics, for the reduction of the original plasma fluid model to the pair of CNLS equations which is generally non-integrable since the dispersion, nonlinearity, and coupling coefficients $P_j$ and $Q_{ij}$ ($j=1,2$) depend on the carrier wavenumbers $k_1$ and $k_2$ (both assumed arbitrary) of the two interacting wavepackets. The exact mathematical expressions for those coefficients have been analytically obtained and in fact depend parametrically on the plasma parameters too. Although $P_j$ for the particular model considered here is negative, while it approaches asymptotically zero for large $k_j$, the coefficients $Q_{jj}$ can be either positive or negative. The value of $k_j$ that separates positive from negative $Q_{jj}$ values, $k_r$, depends on the value of the spectral index $\kappa$ which characterizes the kappa distribution of the electrons, i.e., $k_r =k_r (\kappa )$. The spectral index enters into the expressions of $Q_{jj}$ through the coefficients $c_1$, $c_2$, and $c_3$ of the Mc Laurin expansion of that distribution. Interestingly, the $\kappa$-dependence of $k_r$ is not monotonous, but it exhibits a minimum around $\kappa \simeq 2.5$ which has been set as a rough boundary between electrons far- and near-equilibrium by empirical investigations of Space plasmas. The $k_r (\kappa )$ dependence is weak for most values of $\kappa$, while it becomes stronger for $\kappa < 2$ where it increases abruptly until its divergence at $\kappa =3/2$. For very large values of $\kappa$, on the other hand, $k_r$ converges slowly to 1.47 from below.

The coupling coefficients $Q_{12}$ and $Q_{21}$, which depend on both wavenumbers $k_1$ and $k_2$, may also be either positive or negative. While $P_j$ and $Q_{jj}$ have values of the order of unity, the values of $Q_{12}$ and $Q_{21}$ may also become very large positive or negative, implying very strong coupling for the interacting electrostatic wavepackets in the plasma fluid. All this prescribes a multifaceted dynamical profile with strong interconnection among the various physical parameters. A compatibility condition was derived through standard modulational instability analysis, in the form of a fourth-degree polynomial in the frequency of the perturbation. By numerically calculating the roots of the compatibility condition and identifying the one with the largest imaginary part (growth rate), modulationally stable and unstable areas on the $k_2 - K$ plane have been identified. The instability growth rate $\Gamma$, mapped on that plane, reveals that modulational instability occurs in areas of the $k_2 - K$ plane (say, for fixed $k_1$), actually for all four stability regimes of the decoupled CNLS equation (i.e., those resulting by setting $Q_{12} =Q_{21} =0$), for all values of $\kappa$ used here.

Modulational instability in fact may occur even if both waves of the decoupled system are stable (stable-stable regime), since their strong nonlinear coupling may potentially destabilize the system in regions with large perturbation wavenumbers K. The instability that results from the nonlinear coupling between the two wavepackets is more intense in the case of equal amplitudes of the two waves (as those used in the present work); instability areas also occupy larger areas (“windows”) on the $k_2 - K$ plane in the latter case. When one or both the waves of the decoupled system are unstable, their nonlinear coupling leads again to an unstable pair of wavepackets. A comparison of the growth rates of the two waves of the decoupled system with that of the waves in the coupled one reveals that the latter is always larger than the former; furthermore, the unstable areas on the $k_2 - K$ plane are larger than those of the waves in the decoupled system. Also, as it becomes obvious from Figs. 5, 6, 7, 8, 9, and 10, the most dramatic variation of the $\Gamma$ patterns on the $k_2 - K$ plane occurs for values of the spectral index $\kappa$ within the strongly non-thermal region, i.e., in the interval $1.5< \kappa < 2.5$. Moreover, as the numerical calculation of the growth rate $\Gamma$ indicates, the CNLS equations are modulationally unstable in almost all of the $k_2 - K$ plane shown in the figures below $\kappa \sim 1.9$. For these values of $\kappa$, i.e., for $\kappa < 1.9$, the values of $\Gamma$ increase fast with decreasing $\kappa$ and diverge in the limit of $\kappa \rightarrow 1.5$.

Extensive numerical search supports the conclusion that the nonlinear wave modes of the CNLS equations are apparently always partly modulationally unstable, i.e., that there is an interval in the perturbation wavenumber K for which modulational instability occurs. Although it cannot be considered as a definite proof, our investigations show that it is highly possible. As mentioned above, the instability is probably due to the large values of the coupling coefficients $Q_{12}$ and $Q_{21}$ (as compared with the values of the coefficients $P_j$ and $Q_{jj}$). Note that it is actually the product of the two, i.e., $Q_{12} Q_{21}$ which enters into $\Omega _c^4$ that appears in the right-hand side of compatibility condition Eq. (76). However, it is possible to have modulationally stable nonlinear wave modes by “eliminating” $\Omega _c^4$ from the right-hand side of Eq. (76). This is possible if we set one of the two coefficients $Q_{12}$ and $Q_{21}$ equal to zero (in the considered model it is not possible to find $k_1$ and $k_2$ such as both these coefficients become zero). In fact, $Q_{12}$ is for example, zero along the curves shown in Fig. 3b or as the contours shown in 4 on the $k_1 - k_2$ plane. Along these curves $Q_{12} =0$ so that the CNLS equations are still at least partially coupled, but their perturbation frequencies can be calculated from Eq. (80) which are the same as for the two decoupled CNLS equations. Thus, for modulational stability in this special case we can assert that $P_1 Q_{11} < 0$ and $P_2 Q_{2} < 0$ simultaneously. This condition can be clearly satisfied within the considered model for $k_1, k_2 < k_r (\kappa )$. A bare look at Figs. 3b and 4 is enough to see that there are available $k_1$ and $k_2$ that satisfy the latter inequality.

The occurrence of very broad modulational instability areas in the parameter space of $k_1$, $k_2$, and K, may on the other hand favor the emergence of vector solitons which may emerge in combinations of bright and dark components. The possible existence of such vector solitons, the determination of their parameters such as their width and amplitudes, as well as their stability, and how these are affected by the spectral index $\kappa$, will be the focus of future work.

Appendices

Appendix A Coefficients—analytical expressions

$$\begin{aligned} C_{n,2,j}^{(2)}= & {} \frac{(k_j^2 +c_1)}{6 k_j^2} \left[ 3 (4 k_j^2 +c_1) (k_j^2 +c_1) -2 c_2 \right] , \end{aligned}$$

(A1)

$$\begin{aligned} C_{u,2,j}^{(2)}= & {} \frac{\sqrt{k_j^2 +c_1}}{6 k_j^2} \left[ 3 (k_j^2 +c_1) (2 k_j^2 +c_1) -2 c_2 \right] , \end{aligned}$$

(A2)

$$\begin{aligned} C_{\phi ,2,j}^{(2)}= & {} \frac{1}{6 k_j^2} \left[ 3 (k_j^2 +c_1)^2 -2 c_2 \right] , \end{aligned}$$

(A3)

$$\begin{aligned} C_{n,2,\pm }^{(1)}= & {} \frac{1}{D_\pm } \left\{ \left[ (k_1 \pm k_2)^2 +c_1 \right] \right. \nonumber \\{} & {} \left. \left[ (k_1 \pm k_2) f_2^{(\pm )} +(\omega _1 \pm \omega _2) f_1^{(\pm )} \right] \right. \nonumber \\{} & {} \left. +(k_1 \pm k_2)^2 f_3^{(\pm )} \right\} , \nonumber \\ C_{u,2,\pm }^{(1)}= & {} \frac{1}{D_\pm } \left\{ (k_1 \pm k_2) \left[ f_1^{(\pm )} +(\omega _1 \pm \omega _2) f_3^{(\pm )} \right] \right. \nonumber \\{} & {} \left. +(\omega _1 \pm \omega _2) \left[ (k_1 \pm k_2)^2 +c_1 \right] f_2^{(\pm )} \right\} , \nonumber \\ C_{\phi ,2,\pm }^{(1)}= & {} \frac{1}{D_\pm } \left\{ (\omega _1 \pm \omega _2) \left[ f_1^{(\pm )} +(\omega _1 \pm \omega _2) f_3^{(\pm )} \right] \right. \nonumber \\{} & {} \left. +(k_1 \pm k_2) f_2^{(\pm )} \right\} , \end{aligned}$$

(A4)

where

$$\begin{aligned} D_\pm =(k_1 \pm k_2)^2 -(\omega _1 \pm \omega _2)^2 \left[ (k_1 \pm k_2)^2 +c_1 \right] . \end{aligned}$$

(A5)

The quantities $f_m^{(\pm )}$ ($m=1,2,3$) are defined in Eqs. (33)–(33).

$$\begin{aligned}{} & {} C_{n,2,j}^{(0)} =\left( c_1 C_{\phi ,2,j}^{(0)} +2 c_2 \right) , \nonumber \\{} & {} C_{u,2,j}^{(0)} =\frac{1}{v_{g,j}} \left[ C_{\phi ,2,j}^{(0)} +\frac{k_j^2}{\omega _j^2} \right] , \nonumber \\{} & {} C_{\phi ,2,j}^{(0)} =\rho _j \frac{1}{1 -c_1 v_{g,j}^2}, \end{aligned}$$

(A6)

where

$$\begin{aligned} \rho _j =-( k_j^2 +c_1 ) -2 c_1 +2 c_2 v_{g,j}^2. \end{aligned}$$

(A7)

Appendix B Right-hand sides of the perturbative equations

$$\begin{aligned} \mathcal{F}_1= & {} -\frac{\partial (n_1)}{\partial t_1} -\frac{\partial (u_1)}{\partial x_1} -\frac{\partial (n_1 u_1)}{\partial x_0}, \nonumber \\ \mathcal{F}_2= & {} -\frac{\partial u_1}{\partial t_1} -\frac{\partial \phi _1}{\partial x_1} -u_1 \frac{\partial u_1}{\partial x_0}, \nonumber \\ \mathcal{F}_3= & {} +c_2 \phi _1^2 -2 \frac{\partial ^2 \phi _1}{\partial x_0 \partial x_1}. \end{aligned}$$

(B8)

$$\begin{aligned} \mu _{1,j}= & {} -\left( \frac{k_j}{\omega _j} \right) ^2 \frac{\partial \Psi _j}{\partial t_1} -\frac{k_j}{\omega _j} \frac{\partial \Psi _j}{\partial x_1}, \end{aligned}$$

(B9)

$$\begin{aligned} \mu _{2,j}= & {} -\frac{k_j}{\omega _j} \frac{\partial \Psi _j}{\partial t_1} -\frac{\partial \Psi _j}{\partial x_1}, \nonumber \\ \mu _{3,j}= & {} -2 i k_j \frac{\partial \Psi _j}{\partial x_1}. \end{aligned}$$

(B10)

$$\begin{aligned} f_1^{(+)}= & {} -(k_1 +k_2) \frac{k_1 k_2}{\omega _1 \omega _2} \left( \frac{k_1}{\omega _1} +\frac{k_2}{\omega _2} \right) , \end{aligned}$$

(B11)

$$\begin{aligned} f_2^{(+)}= & {} -(k_1 +k_2) \frac{k_1 k_2}{\omega _1 \omega _2}, \end{aligned}$$

(B12)

$$\begin{aligned} f_3^{(+)}= & {} +2 c_2. \end{aligned}$$

(B13)

$$\begin{aligned} f_1^{(-)}= & {} -(k_1 -k_2) \frac{k_1 k_2}{\omega _1 \omega _2} \left( \frac{k_1}{\omega _1} +\frac{k_2}{\omega _2} \right) , \end{aligned}$$

(B14)

$$\begin{aligned} f_2^{(-)}= & {} -(k_1 -k_2) \frac{k_1 k_2}{\omega _1 \omega _2}, \end{aligned}$$

(B15)

$$\begin{aligned} f_3^{(-)}= & {} +2 c_2. \end{aligned}$$

(B16)

$$\begin{aligned} \mathcal{G}_1= & {} -\frac{\partial (n_2)}{\partial t_1} -\frac{\partial (u_2)}{\partial x_1} -\frac{\partial (n_1)}{\partial t_2} -\frac{\partial (u_1)}{\partial x_2}\nonumber \\{} & {} -\frac{\partial (n_1 u_2 +n_2 u_1)}{\partial x_0} -\frac{\partial (n_1 u_1)}{\partial x_1}, \end{aligned}$$

(B17)

$$\begin{aligned} \mathcal{G}_2= & {} -\frac{\partial u_2}{\partial t_1} -\frac{\partial \phi _2}{\partial x_1} -\frac{\partial u_1}{\partial t_2} -\frac{\partial \phi _1}{\partial x_2} -\frac{\partial u_1 u_2}{\partial x_0} -u_1 \frac{\partial u_1}{\partial x_1}, \end{aligned}$$

(B18)

$$\begin{aligned} \mathcal{G}_3= & {} -2 \frac{\partial ^2 \phi _2}{\partial x_0 \partial x_1} -2 \frac{\partial ^2 \phi _1}{\partial x_0 \partial x_2}\nonumber \\{} & {} -\frac{\partial ^2 \phi _1}{\partial x_1^2} +2 c_2 \phi _1 \phi _2 +c_3 \phi _1^3. \end{aligned}$$

(B19)

$$\begin{aligned} \mathcal{R}_{1,j}= & {} -\left( \frac{\partial n_{2,j}^{(1)} }{\partial t_1} +\frac{\partial u_{2,j}^{(1)} }{\partial x_1} +\frac{\partial n_{1,j}^{(1)} }{\partial t_2} +\frac{\partial u_{1,j}^{(1)} }{\partial x_2} \right) \nonumber \\{} & {} -i k_j \left( n_{1,j}^{(-1)} u_{2,j}^{(2)} +n_{1,j}^{(1)} u_{2}^{(0)} +n_{1,k_j}^{(-1)} u_{2,p}^{(1)} +n_{1,k_j}^{(1)} u_{2,m}^{(\ell _j)} \right) \nonumber \\{} & {} -i k_j \left( u_{1,j}^{(-1)} n_{2,j}^{(2)} +u_{1,j}^{(1)} n_{2}^{(0)} +u_{1,k_j}^{(-1)} n_{2,p}^{(1)} +u_{1,k_j}^{(1)} n_{2,m}^{(\ell _j)} \right) , \nonumber \\ \end{aligned}$$

(B20)

$$\begin{aligned} \mathcal{R}_{2,j}= & {} -\left( \frac{\partial u_{2,j}^{(1)} }{\partial t_1} +\frac{\partial \phi _{2,j}^{(1)} }{\partial x_1} +\frac{\partial u_{1,j}^{(1)} }{\partial t_2} +\frac{\partial \Psi _j }{\partial x_2} \right) \nonumber \\{} & {} -i k_j \left( u_{1,j}^{(-1)} u_{2,j}^{(2)} +u_{1,j}^{(1)} u_{2}^{(0)} +u_{1,k_j}^{(-1)} u_{2,p}^{(1)} +u_{1,k_j}^{(1)} u_{2,m}^{(\ell _j)} \right) , \nonumber \\ \end{aligned}$$

(B21)

$$\begin{aligned} \mathcal{R}_{3,j}= & {} -2 i k_j \left( \frac{\partial \phi _{2,j}^{(1)} }{\partial x_1} +\frac{\partial \Psi _j }{\partial x_2} \right) \nonumber \\{} & {} -\frac{\partial ^2 \Psi _j }{\partial x_1^2} +2 c_2 \left( \Psi _j^\star \phi _{2,j}^{(2)} +\Psi _j \phi _{2}^{(0)} +\Psi _{k_j}^\star \phi _{2,p}^{(1)} +\Psi _{k_j} \phi _{2,m}^{(\ell _j)} \right) \nonumber \\{} & {} +3 c_3 \Psi _j \left( |\Psi _j|^2 +2 |\Psi _{k_j}|^2 \right) , \end{aligned}$$

(B22)

where $j=1,2$, and $k_j$, $\ell _j$ defined as $\ell _1 =1$, $\ell _2 =-1$, $k_1 =2$, and $k_2 =1$.