1 Introduction

The structural integrity of many engineering structures, such as bridges, buildings, and power lines, has been a central area of study for several decades. However, one phenomenon that plagues the structural integrity of these infrastructures is unwanted high-amplitude vibration [1,2,3,4]. Researchers have employed linear and nonlinear models of these structures to understand the dynamics and, accordingly, design efficient solutions to mitigate the vibration-induced damages to these structures. A linear model of a structure tends to be favored over a nonlinear model as the former has a lower complexity level [5, 6]. However, to capture the essential dynamics of a system that can exhibit large amplitude oscillations, a nonlinear model is preferred [7, 8].

The development of improved models of civil structures has helped in the design of an efficient vibration control system. For a linear system, a tuned mass damper (TMD), initially introduced by Fram et al. [9], has been widely used to mitigate and sometimes eliminate undesired vibrations. Also, significant improvements have been made to the original design of TMD via passive [10,11,12,13], semi-active [14,15,16] and active [17,18,19] means. However, TMDs are only effective in a narrow range of operating frequencies. To alleviate this limitation, multiple approaches have been used. One of the efficient solutions to overcome this limitation is to incorporate inerters [20, 21], a mass amplification device with negligible physical weight, in TMDs’ design [22,23,24,25,26,27]. The inclusion of inerter in TMD’s design increases the effective operating frequency range without increasing the overall weight of the absorber and hence improves the performance. Another solution is the development of a nonlinear vibration absorber, which is designed to enhance the performance of TMD by extending the concept of Den’s Hartog equal peak method for nonlinear oscillations [28, 29]. The nonlinear tuned mass dampers (NTMDs) have proven to perform better than linear TMDs to mitigate vibrations in primary nonlinear systems [30,31,32].

Although TMDs and NTMDs are proven to be efficient solutions for controlling undesirable vibrations in a primary system, they do not take advantage of the energy generated by ambient vibrations. Indeed, most of the vibration energy in TMDs and NTMDs is dissipated through heat. However, many systems have essential energy requirements that can be met by energy harvesting techniques. One device that has the potential to perform both vibration control and energy harvesting is the shunt damper (SD), initially introduced by Forward et al. [33]. They demonstrated the use of passive circuit shunting for the narrow-band reduction of resonant mechanical response.

Further, Hagood and von Flotow [34] theoretically and experimentally proved that a piezoelectric shunt with an RL circuit would act as a TMD. The use of SD incorporating piezoelectric material and the electromagnetic transducer is well established in the literature [35,36,37,38]. The benefit of having an electromagnetic device for SDs is that it enables energy harvesting for given circuit parameters. Tuned SD, for both vibration control and energy harvesting, further led to the development of electromagnetic resonant shunt-tuned mass dampers (ERS-TMD) [39] and, more recently, electromagnetic resonant shunt-tuned mass damper with inerters (ERS-TMDI) [40, 41] to further take advantage of the inerter devices. The latest development in an ERS-TMDI is the improved design of the conventional ERS-TMDI by Joubaneh and Barry [42] for linear oscillators, which optimized simultaneous vibration control and energy harvesting. On a similar line, Paul and Barry [43] presented an optimal configuration for a nonlinear ERS-TMDI (NERS-TMDI) to enhance the performance in terms of vibration control and energy harvesting for a given value of excitation amplitude. The optimal configuration of the NERS-TMDI was also compared to conventional solutions such as the ERS-TMDI and NTMD, and the results demonstrated that the NERS-TMDI was superior to the other designs.

Given the significant advantages, our novel NERS-TMDI provides for simultaneous vibration control and energy harvesting in a nonlinear system, and it is crucial to investigate the impact of its parameters on the primary structure under various operating conditions. To address this, the present study introduces a pioneering analysis of both the linear and nonlinear stability of the optimized NERS-TMDI. By employing linear and nonlinear stability methods, including geometric (the Floquet multiplier, phase-portraits, Lyapunov exponent) and statistical (0–1 chaos test, global sensitivity analysis), our research offers design guidelines that ensure the safe operation of NERS-TMDI within predetermined frequency ranges and amplitudes, supplementing the findings presented in [43]. The remainder of this paper is organized as follows. In Sect. 2, the mathematical model for the optimal configuration [43] of the NERS-TMDI is presented briefly, along with the linear and nonlinear formulation required for the stability analysis. The multi-parametric recursive method is also detailed in Sect. 2 as a tool to track bifurcation points on increased parameter space. In Sect. 4, the aforementioned recursive method is used to detect isolated solutions (ISs). In Sect. 5, the linear stability of the steady-state periodic solutions is presented. In Sect. 6, the linear stability of the periodic solution is extended to a nonlinear stability analysis via Lyapunov exponents (LEs) [44,45,46,47] and Poincaré maps to help characterize the type of instability the system is subject on the force and natural frequency parameter space. In Sect. 7, a well-established global sensitivity framework is used to assess the uncertainty of the NERS-TMDI key parameters. Final remarks on this study and the next steps are provided in Sect. 8.

2 Mathematical modeling

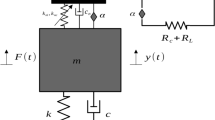
Figure 1 shows the schematic of the NERS-TMDI configuration [43] attached to a nonlinear primary system, in our case, a Duffing oscillator. In the schematic, the mass of the primary system is represented by \(m_s\), the viscous damping coefficient by \(c_s\), and the linear and the nonlinear stiffness of the Duffing oscillator is represented as \(k_s\) and \(k_{sn}\), respectively. It should be noted that the nonlinear stiffness \(k_{sn}\) exhibits cubic nonlinearity. Furthermore, the tuned mass of NERS-TMDI, \(m_t\), connects to the Duffing oscillator via spring with linear and nonlinear stiffness as \(k_t\) and \(k_{tn}\), respectively, and the damper with the damping coefficient of \(c_t\). For improved vibration control performance, \(k_{tn}\) exhibits cubic nonlinearity similar to \(k_{sn} \) [28, 29].

In the current design of NERS-TMDI, NERS-TMDI is equipped with an electromagnetic resonant shunt component that behaves like a damping structure and provides additional vibration control. Hence, \(c_t\) becomes redundant in the system, and we can put \(c_t=0\) for the analysis of our system. Also, it has been well established that the better performance of vibration absorber yields when it exhibits the same characteristics as the primary structure [28, 29]. Therefore, we assume that in the NERS-TMDI nonlinear stiffness, \(k_{sn}\) is also cubic in nature. The electrical circuit resistance, inductance, and capacitance are represented as \({\bar{R}}\), \({\bar{L}}\), and \({\bar{C}}\), respectively, in Fig. 1. \(k_f\) and \(k_v\) indicate the transducer’s force constant and voltage constant, respectively. Note that the analysis assumes no energy loss through the conductor; hence, \(k_f= k_v\). Therefore, the governing equations of motion for the coupled system can be written as

$$\begin{aligned}{} & {} m_s\ddot{x}_s+c_s\dot{x}_s+k_sx_s+k_{sn}x_s^3\nonumber \\{} & {} \quad +k_t(x_s-x_t)+k_{tn}(x_s-x_t)^3=F_w, \end{aligned}$$
(1a)
$$\begin{aligned}{} & {} (m_t+b)\ddot{x}_t+k_t(x_t-x_s)\nonumber \\{} & {} \quad +k_{tn}(x_t-x_s)^3+k_f\dot{q}=0, \end{aligned}$$
(1b)
$$\begin{aligned}{} & {} {\bar{L}}\ddot{q}+{\bar{R}}\dot{q}\nonumber \\{} & {} \quad +\frac{1}{{\bar{C}}}q-k_v\dot{x}_t=0. \end{aligned}$$
(1c)
Fig. 1
figure 1

The schematic of the Duffing oscillator attached to the optimal configuration of NERS-TMDI

Full size image

In the above equations of motion, \(F_w\) represents an external excitation acting on the primary system. In real-life scenarios, \(F_w\) can take complex forms such as random excitation, impulse, and stochastic excitation. However, for the sake of simplicity in our analysis, we assume sinusoidal form for \(F_w\), and accordingly, assume \(F_w=F\sin (\omega \,t)\) with the excitation amplitude of F and excitation frequency of \(\tilde{\omega }\). Furthermore, to reduce the number of effective parameters in the subsequent analysis, we introduce the following nondimensional scales and parameters in the system

$$\begin{aligned}{} & {} x_0=\frac{F_0}{k_s},\,\xi _s=\frac{x_s}{x_0},\, \xi _t=\frac{x_t}{x_0},\, \tau =\omega _p t,\,\omega _p=\sqrt{\frac{k_s}{m_s}},\,\nonumber \\{} & {} \mu =\frac{m_t+b}{m_s},\,\zeta =\frac{c_s}{\sqrt{k_sm_s}},\, \alpha =\frac{k_{sn}F_0^2}{k_s^3},\,\nonumber \\{} & {} \beta =\frac{k_t}{k_s},\, \gamma =\frac{k_{tn}F_0^2}{k_s^3},\, \lambda =\frac{k_f}{F_0},\, \sigma =\frac{{\bar{R}}}{{\bar{L}} \omega _p},\, \nonumber \\{} & {} \kappa =\frac{1}{{\bar{L}}{\bar{C}}\omega _p^2},\, \rho =\frac{k_vF_0}{k_s{\bar{L}}\omega _p },\, \nonumber \\{} & {} \tilde{\omega }=\frac{\omega }{\omega _p},\, {\bar{F}}=\frac{F}{F_0}, \end{aligned}$$
(2)

where \(F_0\) represents a constant force that causes a static displacement \(x_0\) in the linear spring of the primary system. Using aforementioned nondimensional scales and parameters, Eq. (1a) is nondimensionalized to get

$$\begin{aligned}{} & {} \ddot{\xi }_s+\zeta \dot{\xi }_s+\xi _s\nonumber \\{} & {} \quad +\alpha \xi _s^3-\beta (\xi _t-\xi _s)-\gamma (\xi _t-\xi _s)^3= {\bar{F}} \sin (\tilde{\omega } \tau ), \end{aligned}$$
(3a)
$$\begin{aligned}{} & {} \ddot{\xi }_t+\frac{\beta }{\mu }(\xi _t-\xi _s)\nonumber \\{} & {} \quad +\frac{\gamma }{\mu }(\xi _t-\xi _s)^3+\frac{\lambda }{\mu } \dot{q}=0 , \end{aligned}$$
(3b)
$$\begin{aligned}{} & {} \ddot{q}+\sigma \dot{q}\nonumber \\{} & {} \quad +\kappa q-\rho \dot{\xi }_t=0. \end{aligned}$$
(3c)

In the above nondimensional governing equations of motion, \((\dot{)}\) represents the derivate with respect to nondimensional time \(\tau \). Next, to get the steady-state periodic solutions of Eq. (3), we use the method of harmonic balance (HBM) and, accordingly, assume that solutions for the motion of the primary mass (\(\xi _{s}\)), the absorber mass (\(\xi _{t}\)), and the charge q of the RLC circuit are periodic and synchronous with the external excitation. With these assumptions, \(\xi _{s}\), \(\xi _{t}\) and q are given by

$$\begin{aligned}{} & {} \xi _s=A_{s0}+A_s\cos (\tilde{\omega } \tau )+B_s\sin (\tilde{\omega } \tau )+A_{s3}\cos (3\,\tilde{\omega } \tau )\nonumber \\{} & {} \quad \quad \ +B_{s3} \sin (3\,\tilde{\omega } \tau ), \end{aligned}$$
(4a)
$$\begin{aligned}{} & {} \xi _{t}=A_{t0}+A_t\cos (\tilde{\omega } \tau )+B_t\sin (\tilde{\omega } \tau )+A_{t3}\cos (3\,\tilde{\omega }\tau )\nonumber \\{} & {} \quad \quad \ +B_{t3}\sin (3\,\tilde{\omega } \tau ), \end{aligned}$$
(4b)
$$\begin{aligned}{} & {} q=A_{i0}+A_i \cos (\tilde{\omega } \tau )+B_i \sin (\tilde{\omega } \tau )+A_{i3}\cos (3\,\tilde{\omega } \tau )\nonumber \\{} & {} \quad \quad \ +B_{i3}\sin (3\,\tilde{\omega } \tau ). \end{aligned}$$
(4c)

We emphasize that these assumed solutions include constant terms for DC and asymmetric motions. Furthermore, higher harmonics of cosine and sine terms are considered to improve the accuracy of the solutions for the current nonlinear system. On substituting these assumed forms of the solutions in Eq. (3) and collecting the coefficients for different harmonics and constant terms, we get fifteen nonlinear algebraic simultaneous equations. Since these equations are lengthy and involved, we do not report these for brevity. It should be noted that due to the highly nonlinear characteristics of these algebraic equations, it is difficult to solve them analytically. Therefore, we employ the fixed-arc-length continuation method to solve the nonlinear simultaneous equations to get the solutions for different values of excitation amplitude and frequency.

To capture the global dynamics of the system, the multi-parametric recursive continuation method introduced by Grenat et al., [48] is employed in the current analysis. For the sake of brevity, the mathematical methodology is not presented here. Please refer to [48] for more details about the method.

Having obtained the steady-state periodic solutions of the system numerically through the continuation scheme, next, we perform the linear stability analysis of the system to explore the local or linear stability of these steady states in the parametric space of excitation amplitude and frequency. To perform linear stability analysis, we first rewrite Eq. (3) in the following state-space form:

$$\begin{aligned} S= \begin{pmatrix} x_2\\ {\bar{F}} \sin (\tilde{\omega } \tau ) - \zeta x_2 - x_1 - \beta (x_1 - x_3) - \alpha x_1^3 - \gamma (x_1 - x_3)^3\\ x_4\\ \frac{\beta }{\mu } (x_1 - x_3) - \frac{\lambda }{\mu } x_6 + \frac{\gamma }{\mu } (x_1 - x_3)^3\\ x_6\\ \rho x_4 - \kappa x_5 - \sigma x_6 \end{pmatrix},\nonumber \\ \end{aligned}$$
(5)

with

$$\begin{aligned} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \end{bmatrix}=\begin{bmatrix} \xi _s \\ \dot{\xi _s} \\ \xi _t \\ \dot{\xi _t} \\ q \\ \dot{q} \end{bmatrix}. \end{aligned}$$
(6)

This state-space formulation facilitates the derivation of the following Jacobian matrix,

$$\begin{aligned} J= \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ - \beta - 3\alpha _{s1}^2 - 3\gamma (x_{s1} - x_{s3})^2 - 1 &{} -\zeta &{} \beta + 3\gamma (x_{s1} - x_{s3})^2 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ \frac{\beta }{\mu } + (3\gamma (x_{s1} - x_{s3})^2)/\mu &{} 0 &{} - \frac{\beta }{\mu } - (3\gamma \hspace{0.8mm}(x_{s1} - x_{s3})^2)/\mu &{} 0 &{} 0 &{} -\frac{\lambda }{\mu }\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} \rho &{} -\kappa &{} -\sigma \end{bmatrix}, \end{aligned}$$
(7)

where \(x_{s1}\), \(x_{s3}\), and \(x_{s5}\) are the steady-state periodic solutions of the coupled system obtained from the HBM.

The Floquet multipliers are then extracted from the eigenvalues of the Jacobian evaluated at the steady-state periodic solution and then are used to determine the linear stability of the steady-state periodic solution of the coupled system. If the dominant Floquet multiplier for a given steady state lies with the unit circle in the Re–Im space, then the steady-state periodic solution is considered to be stable, otherwise unstable.

Note that the Floquet multipliers are only helpful in determining the linear or local stability of the steady-state periodic solutions. However, to explore the dynamics of the nonlinear system (in our case, Duffing oscillator) attached to the NERS-TMDI beyond periodic motions, it is necessary to extend our analysis by performing nonlinear stability analysis and determine the Lyapunov Exponents (LE) of the coupled nonlinear system. We evolve Eq. 3 coupled with the tangent space equations for each degree of freedom of the system. (In the current analysis, we have six degrees of freedom.) For instance, one degree-of-freedom tangent space equation can be written as:

$$\begin{aligned} \begin{bmatrix} \dot{\delta x_1} \\ \dot{\delta x_2} \\ \dot{\delta x_3} \\ \dot{\delta x_4} \\ \dot{\delta x_5} \\ \dot{\delta x_6} \end{bmatrix} = \begin{bmatrix} \delta x_1\\ \delta x_3\hspace{0.8mm}(\beta + 3\hspace{0.8mm}\gamma (x_1 - x_3)^2) - \delta x_2\hspace{0.8mm}\zeta - \delta x_1\hspace{0.8mm}(\beta + 3\hspace{0.8mm}\alpha \hspace{0.8mm}x_1^2 + 3\hspace{0.8mm}\gamma \hspace{0.8mm}(x_1 - x_3)^2 + 1)\\ \delta x_4\\ \delta x_1\hspace{0.8mm}(\beta /\mu + (3\hspace{0.8mm}\gamma (x_1 - x_3)^2)/\mu ) - \delta x_3\hspace{0.8mm}(\beta /\mu + (3\hspace{0.8mm}\gamma (x_1 - x_3)^2)/\mu ) - (\delta x_6\hspace{0.8mm}\lambda )/\mu \\ \delta x_6\\ \delta x_4\hspace{0.8mm}\rho - \delta x_5\hspace{0.8mm}\kappa - \delta x_6\hspace{0.8mm}\sigma \end{bmatrix}. \end{aligned}$$
(8)

Therefore, eventually, we solve 42 equations simultaneously to obtain the evolution of the LE. To deal with the exponential growth of the exponents, we use the Gram–Schmidt procedure (QR decomposition). Then, we average the instantaneous LE to get the average LE for each degree of freedom and select the largest LE to observe the system behavior. The 0–1 test for chaos introduced by Gottwald et al. [49] is also considered for the nonlinear stability analysis. It is more computationally efficient than the LE method since it requires a total of 4 equations to determine the behavior of the system. However, before proceeding further, we present the validation of the steady-state periodic solutions obtained through the harmonic balance method. This is presented next.

3 Validation of analytical solution

As mentioned earlier, the HBM is used to validate the analytical results, i.e., Eq. (4) by comparing them against the numerical simulations of Eq. (3) for the parameter values listed in Table 1. We will use these parameter values for the remainder of the analysis unless otherwise stated. The Duffing oscillator with parameters \(\zeta =0.01\) and \(\alpha =1\) is connected to the NERS-TMDI. The numerical results were generated using ‘ode45’ in MATLAB with high values of absolute tolerance and relative tolerances (\(1e^{-8}\)). Figure 2 shows the comparison of frequency response curves of the NERS-TMDI obtained using analytical and numerical approaches. We observe a good agreement between both approaches with a maximum error of \(0.2\%\). Hence, the analytical solutions will be used in the subsequent analysis unless otherwise stated.

4 Detection of isolas and NERS-TMDI safe operation

Having established the accuracy of the analytical solution through the HBM, we now proceed to analyze the complex stability behavior of the NERS-TMDI attached to the primary system. In our previous paper [43], we observed a significant jump in the amplitude/response of the primary system as we increased the excitation amplitude after a threshold value. In some cases, this jump in amplitude/response of the system can be attributed to the merge of isolated solutions, which exist on a detached resonant curve, also known as Isola (IS), with the primary response curve. It should be noted that such a complex phenomenon has already been observed by Habib et al. [29] for a Duffing oscillator attached to an NLTVA. To show the existence of Isolas for the proposed NERS-TMDI, we plot the frequency response curve for two different values of excitation amplitude, in particular for \(\tilde{F}=0.023\) and \(\tilde{F}=0.06 \) which are shown in Fig. 3a and b, respectively. From Fig.  3a, we can observe the birth of Isola in the system at \(\tilde{F}=0.023\), which grows toward the primary frequency response curve as \(\tilde{F}\) increases to \(\tilde{F}=0.06\).

It should be noted that the existence of an Isola in a system causes high-amplitude vibration, further detrimental to the performance of the vibration absorber to control vibration. Therefore, it is necessary to track the points corresponding to the birth and merging of Isola to the primary response curve and, accordingly, define the safe and unsafe operating regions. This step can be achieved by using a numerical continuation technique, where the system’s limit point (LP) branch for selected parameters can be projected on the parametric space of \(\tilde{F}-\xi _s\). Figure 3c shows a 3-D view of the LP branch as well as the evolution of the frequency response of the primary system for \(\tilde{F}\)=0.023, 0.06, and 0.1. The birth of the Isola is represented by a diamond marker, while a square marker represents the merging with the primary response curve.

Table 1 Parameters of the NERS-TMDI
Full size table

Furthermore, the LP branch in \(\tilde{F}-\xi _s\) can be classified into different regions depending on the birth and merging of the Isola with the primary frequency response curve. The three regions with different dynamical behaviors, initially defined by Detroux et al. [50], are characterized as follows: (1) ‘Safe’ when the frequency response curve has no Isola in the system, (2) ‘Unsafe’ when the frequency response curve exhibits an Isola, and (3) ‘Unacceptable’ when the Isola has merged with the primary response curve and becomes a part of it. Since there are no Isolas for any value of the excitation amplitude \(\tilde{F}\), there is no sudden jump to a higher amplitude stable solution for any frequency value in the ‘Safe’ region. However, for the ‘Unsafe’ region, Isola exists for a given frequency range. Therefore, the system can settle down to high-amplitude stable solutions or low-amplitude stable solutions depending on the initial conditions for the operation. Eventually, in the ‘Unacceptable’ region, the Isola merges with the primary frequency response curve, and irrespective of initial conditions, high-amplitude solutions exist in the system as frequency changes. Using this classification, we observe from Fig. 3d that in our system, the ‘Safe’ region exists for forcing amplitudes before the birth of Isolas where \(\tilde{F}<0.023\). After this value, the system exhibits Isola; hence, it operates within the unsafe region until the merging point at \(\tilde{F}=0.0849\). Beyond this merging point, the operation of the system becomes unacceptable.

Fig. 2
figure 2

Comparison of the frequency response curves obtained using the analytical and numerical approach with \(\tilde{F}=0.05\), \(\alpha =1\) and \(\zeta =0.01\). The other parameters for simulations are listed in Table 1

Full size image

To identify these regions of operation, it is essential to locate the points corresponding to the birth and merging of the Isola to the primary resonance curve. From Fig. 3c, we can easily observe that in the 2-D Projection of the LP branch in \(F-\xi _s\) space, the points of the birth and merging of the Isola

Fig. 3
figure 3

Frequency response curves of the primary system for a \(\tilde{F}\)=0.023 and b \( \tilde{F}\)=0.06. c The continuation of the LP branch and primary frequency response curves with stable solutions (Brown), unstable solutions (light blue), and LP (dark blue). d shows the classification regions per [48] for the proposed system

Full size image

correspond to \(\Delta F=0\). Therefore, in the 2-D Projection of the LP branch, if we can identify the points where \(\Delta F\) becomes 0, then we will be able to locate the birth and merging of an Isola and, hence, can precisely establish the different regions of operation. To perform this task, we use the multi-parametric recursive method as detailed by Grenat et al. [48] and track the birth and the merging of an Isola for a specific parameter variation. We emphasize that as the current system contains many parameters, varying one parameter to track the birth and merging will provide only one optimization solution and, hence, cannot be treated as a unique optimum solution. Furthermore, since the current system is a 3-DOF system, this analysis has to be conducted more carefully as it is more complex than the NLTVA mentioned in [50].

In the next step, we select the parameters for the parametric analysis. It should be noted here that the parameters chosen for the investigation should not detune the NERS-TMDI with the primary system. This limitation eliminates \(\mu , \beta , \sigma , \kappa \), and \(\rho \) as changing any of these parameters will either detune the absorber or RLC circuit, which further interferes with vibration control and energy harvesting. Therefore, we choose \(\gamma \) and \(\lambda \) for this parametric analysis.

We start with the parameter \(\gamma \), which relates to the absorber’s nonlinear stiffness. Figure 4a shows the locus of points corresponding to the birth and merging of Isola for different values of \(\gamma \) in 2-D space of \(\tilde{F}-\gamma \), while Fig. 4b extends the analysis in 3-D space of \(\tilde{F}-\gamma -\xi _s\). From Fig. 4a, we can easily observe that as the value of \(\gamma \) increases, \(\tilde{F}\) corresponding to the merging of Isola also increases. This further implies the delay in the occurrence of the ‘Unacceptable’ region with higher values of \(\gamma \) (nonlinear stiffness of the absorber). Furthermore, we observe that for the initial increase in \(\gamma \), there is no significant impact on the birth points of Isola. However, for relatively higher values of \(\gamma \), \(\tilde{F}\) corresponding to the birth of Isola also increases. From these observations, we can conclude that higher values of \(\gamma \) can lead to a wider ‘Safe’ and ‘Unsafe’ region.

Fig. 4
figure 4

a Variation of the birth and merging point of Isola with \(\gamma \) in 2-D space of \(\tilde{F}-\gamma \), and t should be n 3-D view of the variation of the birth and merging point of Isola

Full size image
Fig. 5
figure 5

a Variation of the birth and merging point of Isola with \(\lambda \) in 2-D space of \(\tilde{F}-\gamma \), and b 3-D view of the variation of the birth and merging point of Isola

Full size image
Fig. 6
figure 6

a Existence of three LP branches corresponding to the primary system response for \(\gamma \)=0.0013, b variation of the birth and merging point of Isola for second LP with \(\gamma \), and c a zoomed view of the variation of the birth and merging of the ISs in \(\tilde{F}-\gamma \) plane

Full size image

Similar to \(\gamma \), we extend our analysis to \(\lambda \), which relates to the force constant between the physical system and the circuit. Figure 5a shows the locus of points corresponding to the birth and merging of Isola in 2-D space of \(\tilde{F}-\lambda \), while Fig. 5b shows the locus in 3-D space of \(\tilde{F}-\lambda -\xi _s\). From Fig. 5a, we can observe that the initial increase in \(\lambda \) causes an increase in the value of \(\tilde{F}\) corresponding to the merging of Isola, and hence, an increase in the ‘Unsafe’ region. However, after \(\lambda =0.5\), any increase in \(\lambda \) does not significantly impact \(\tilde{F}\) for the merging point. At the same instant, an increase in \(\lambda \) leads to a slow and approximately linear increase in the \(\tilde{F}\) corresponding to the birth of Isola. These observations further imply that an initial increase in \(\lambda \) can lead to a wider ‘Unsafe’ region; however, relatively high values of \(\lambda \) can increase the ‘Safe’ region with a decrement in the ‘Unsafe region.’

Furthermore, due to the existence of three peaks in the primary resonance curve and the complex behavior of the system, there can be more than one LP branch in the system. For instance, Fig. 6a shows the existence of three LP branches for \(\gamma =0.0013\) in 2-D space. The third LP branch in Fig. 6a corresponds to the birth and merging points as observed in Fig. 4a for \(\gamma =0.0013\). We further emphasize that the only second LP branch exhibits the birth and merging of an Isola in the remaining two branches. For the sake of completeness, we track Isola’s birth and merging points corresponding to the second LP branch with \(\gamma \) as shown in Fig. 6b. From Fig. 6b, we can observe that at low values of \(\gamma \), the birth and merging points are well separated in the space, hence, providing a clear definition of the ‘Safe’ and ‘Unsafe’ region. However, as the value of \(\gamma \) increases, these two points become close, and the width of the ‘Unsafe’ region decreases. Eventually, at \(\gamma \approx 0.2\), the birth and merging points coincide, leading to the disappearance of the ‘Unsafe’ region.

Furthermore, these results indicate that varying \(\gamma \) for given system parameters does not provide an optimum condition at which the birth of Isola can be delayed and enable an acceptable range of forcing for which the system can be considered to operate safely. To get the improved results, a complete set of parameters must first be optimized as in Joubaneh et al., [42] using, for example, an H2 optimization scheme while additionally considering the nonlinear parameters in the primary system and in the NERS-TMDI. However, H2 Optimization is out of the scope of this paper and is left for future work. Overall, although the NERS-TMDI provides improved vibration control and energy harvesting compared to the NLTVA [51], it is more difficult to tune the system and eliminate Isola.

5 Linear stability analysis of the NERS-TMDI

The multi-parametric recursive analysis helped us to establish Isola’s existence in our system, further developing essential safety concerns for the current NERS-TMDI operation. However, this analysis does not provide any information about the local or global stability of the periodic solutions in the frequency response of our system. Therefore, we first investigate the linear stability of our approach in this section. To do so, we take advantage of Floquet theory [52] to analyze the stability of the periodic analytical solutions obtained during the HBM.

Fig. 7
figure 7

Projection of limit points tracking: Linear stability of the primary system in the \(\tilde{\omega }-\tilde{F}\) parameter space

Full size image

It should be noted here that the continuation process presented in Sect. 4 depends on Floquet multipliers to determine the occurrence of Limit Point Cycles and is identical to the method employed by Xie et al. [53]. At the LP branch boundary, the Floquet multipliers are equal to, smaller, or greater than 1. Therefore, by projecting the LP branch initially obtained in Fig. 3 into the \(\tilde{\omega }-\tilde{F}\) parameter space, we obtain two distinct stability regions as shown in Fig. 7. The area within the LP branch is unstable, denoted by ‘U,’ while the area outside the LP branch is stable, denoted by ‘S.’ In the next step, we perform the parametric analysis of the linear stability of the steady-state periodic solutions.

We first start with the variation of linear stability curves for varying values of nondimensional parameter \(\gamma \) on the stability of our system, which is shown in Fig. 8. From Fig. 8, we can easily observe that any change, increase or decrease, in the value of \(\gamma \) from its optimal value (reported in Table 1) does not change the stability region significantly. We emphasize that these observations contrast the impact of \(\gamma \) on an NLTVA, as observed by Grenat et al., [48], where increasing the nonlinear parameter significantly reduces the instability region while decreasing as the opposite impact.

Fig. 8
figure 8

Projection of limit points tracking: Comparison of the stability regions for varying \(\gamma \)

Full size image

Finally, the effect of \(\lambda \) on the system’s stability is also analyzed and is shown in Fig. 9. From Fig. 9, we can easily observe that for values of \(\lambda \) lower than the optimal value, the onset of the unstable region happens at the lower value of excitation amplitude for a given value of the frequency. However, as \(\lambda \) increases beyond \(\lambda _{opt}\), the unstable region shrinks in size and, in turn, increases the stable region. These results indicate that higher values of \(\lambda \) can help reduce the instability in the primary system response.

Fig. 9
figure 9

Projection of limit points tracking: Comparison of the stability regions for varying \(\lambda \)

Full size image

6 Lyapunov exponents, time response, and Poincaré Map

The linear stability analysis presented in Sect. 5 only provides information about the local stability of the steady-state periodic solutions. However, the time evolution of a perturbation to these steady-state periodic solutions (quasi-periodic, chaotic, or periodic motion with amplitude other than steady-state) truly depends on the nonlinearity present in the system.

Fig. 10
figure 10

Nonlinear stability of the primary system attached to the NERS-TMDI for parameter values listed in Table 1

Full size image

To demonstrate the significance of this analysis, we present the nonlinear stability curves for the parameter values listed in Table 1 in Fig. 10. From Fig. 10, we can easily observe that the nonlinear stable region is significantly different from the linear stable region presented in Sect. 5. This is because nonlinear stability analysis can differentiate the chaotic and quasi-periodic solutions from periodic solutions, unlike linear stability analysis, which only dictates whether a given steady-state periodic solution is stable or not. We further observe from Fig. 10 that two major nonlinear unstable regions exist in the parametric space of \(\tilde{F}-\omega \) for given system parameters. One lies between \(\tilde{\omega }\)=1\(-\)1.5 at lower forcing values 0.1\(<\tilde{F}<\)0.3, while the other unstable region exists between \(\tilde{\omega }\)=1.5\(-\)1.75 for higher forcing amplitude \(\tilde{F}>\)0.5. We emphasize that as the stable periodic solutions cross the nonlinear stability boundary, they become unstable and settle down to quasi-periodic motions, whereas within the unstable region, only chaotic solutions exist. To verify our findings, we next present our system’s time evolution and corresponding Poincaré maps for different operating conditions corresponding to stable and unstable regions shown in Fig.  11. Figure 11 depicts the time responses and corresponding Poincaré maps for different values of \(\tilde{F}\) with \(\tilde{\omega }=1.25\). We selected \(\tilde{\omega }=1.25\) for the analysis; considering this value, we observe a significant variation in the system’s stability. From Fig.  11, we can easily observe that as \(\tilde{F}\) increases at \(\tilde{\omega }=1.25\), the stable periodic solution loses its stability through the quasi-periodic solution and settles down to the chaotic motion as observed in Fig. 10.

Fig. 11
figure 11

Time response and Poincaré maps of the Duffing oscillator for \(\tilde{\omega }\)=1.25 and varying forcing amplitudes

Full size image

This observation further verifies our nonlinear stability analysis. Further, we observe that the response of the primary system doubles as the system transitions from the stable periodic solution to the quasi-periodic or chaotic solution. Since high amplitude solutions are not desirable in the system, our nonlinear stability analysis helps us to identify the safe region of operation.

Another approach to determining the nonlinear stability of a nonlinear system is the 0–1 test for chaos presented by Gottwald et al., [49]. In this test, we determine a variation of parameter K, which relates to the asymptotic growth rate of the system. For \(K=0\), the system exhibits nonchaotic behavior, while a value closer to \(K=1\) highlights a system with chaotic behavior. To compare the above nonlinear dynamics through LE with the 0–1 chaos test, we plot the variation of K with varying values of forcing \(\tilde{F}\) and \(\tilde{\omega }\)=1.25 shown in Fig. 12. We can observe that the variation of parameter K is consistent with our analysis through the Lyapunov exponent and Poincaré sections (Figs. 10 and 11). Therefore, the Lyapunov exponent is used in the remainder of the study. However, in future work, the 0–1 test for chaos will be used to explore forcing amplitude beyond \(\tilde{F}\)=1 given that this formulation is more computationally efficient than deriving the largest LE.

Similar to the linear stability analysis, we also perform a parametric analysis for the nonlinear stability region. The effects of \(\gamma \) and \(\lambda \) on the nonlinear stability region are shown in Figs. 13 and 14, respectively. From Fig. 13, we can observe that an increase in \(\gamma \) from its optimum value causes an increase in the instability region. In contrast, a decrease from its optimum value decreases the instability region. This further implies that the lower value of nonlinear stiffness of NERS-TMDI can benefit the system from the aspect of stability. In the case of \(\lambda \), increasing the parameter value from its optimum value results in decreased instability regions, as can be seen from Fig. 14. However, as \(\lambda \) decreases from its optimum value, the instability region corresponding to lower values of \(\tilde{F}\) grows, but the instability region corresponding to higher forcing amplitude decreases and essentially disappears. Therefore, to increase the nonlinear stable region, it is favorable to decrease \(\gamma \) and increase \(\lambda \) for the given set of parameters in this analysis.

Fig. 12
figure 12

01 Test for chaos for the NERS-TMDI for \(\tilde{\omega }\) ( [49])

Full size image
Fig. 13
figure 13

Nonlinear stability of the primary system attached to the NERS-TMDI for varying \(\gamma \)

Full size image

7 Global sensitivity analysis

It should be noted that the earlier linear and nonlinear stability analyses were performed for the fixed set of parameters. However, these parameters may vary during real-world operations; hence, we perform a global sensitivity analysis to assess the impact of parameter uncertainties on system dynamics. Our approach employs a variance decomposition method, wherein the system’s response is expressed as the sum of individual and combined contributions from each input variable. For this, we use Sobol indices, as established by Sobol [54], to quantify each parameter’s contribution to the model’s total [55,56,57,58]. It is worth noting that global sensitivity analyses can be conducted using various metrics, such as bifurcation diagrams or frequency responses. In this study, we focus exclusively on the frequency response of the system. For this, we fix the forcing, and analysis is performed relative to \(\gamma \), \(\lambda \), \(\sigma \), \(\kappa \), and \(\rho \). We compute the area under the curve for each sample to evaluate the corresponding Sobol indices. Lower areas indicate better vibration control in the primary system, implying that parameters sensitive to this metric are likely to cause significant changes in system dynamics. Figure 15 presents the uncertainty plot and Sobol indices distribution for the combined system at \(\tilde{F} =0.07\). Our findings reveal that the uncertainty distribution for \(\lambda \), \(\kappa \), and \(\rho \) exceeds 20\(\%\), indicating higher sensitivity. In contrast, the system shows lower sensitivity to \(\sigma \) and \(\gamma \). Moreover, even slight variations in these sensitive parameters can lead to significant changes in system response. Thus, reducing uncertainties in \(\lambda \), \(\kappa \), and \(\rho \) is crucial for ensuring the safe operation of the NERS-TMDI system under forces near \(\tilde{F}\)=0.07.

Fig. 14
figure 14

Nonlinear stability of the primary system attached to the NERS-TMDI for varying \(\lambda \)

Full size image
Fig. 15
figure 15

Uncertainty plot and Sobol total (ST) indices for variation in the area under the FRF for varying system parameters

Full size image

8 Conclusions and final remarks

In this work, we analyzed the linear and nonlinear dynamics of the novel NERS-TMDI attached to the classical Duffing oscillator. The linear analysis included the detection of Isolas in the system’s frequency response using the multi-parametric recursive method. Through a detailed analysis of the LP branch of the system, extracted from the level 1 continuation, we observed the existence of Isolas in the Duffing oscillator attached to NERS-TMDI. Furthermore, the parametric study showed that varying \(\gamma \) (nonlinear stiffness of the absorber) or \(\lambda \) (transducer force constant) at the Level 2 continuation is insufficient to improve the global stability of the system by removing Isola for the given system parameters. The system will, therefore, operate in an ‘unsafe’ manner as the possibility of higher Isola solutions cannot be avoided for the selected parameters.

The linear stability of the system through Floquet multipliers was also conducted in the parametric space of excitation amplitude and frequency for different values of \(\gamma \) and \(\lambda \). These results showed that \(\gamma \), i.e., the nonlinear stiffness of the absorber, had a minimal impact on the linear instability region of the system. However, high values of \(\lambda \) could increase the stable region and, hence, are desirable.

The nonlinear parametric stability analysis of the system was also conducted through the Lyapunov exponent for different values of \(\gamma \) and \(\lambda \). The results showed that lower values of \(\gamma \) and higher values of \(\lambda \) could help reduce the system’s nonlinear instability region. Time response plots and Poincaré maps were used as verification tools to show the existence of quasi-periodic and moderate chaotic behavior.

Overall, the results of this study showed that although the NERS-TMDI provides simultaneous vibration control and energy harvesting, it is subject to complex global stability behavior that renders it unsafe for a wider range of forcing amplitude and frequency. The stability analysis also showed that the system could exhibit quasi-periodic and moderate chaotic behavior. The parametric study showed that lower values of nonlinear stiffness of the absorber and higher values of transducer force constant could help improve the system’s stability. Furthermore, the global sensitivity analysis presented showed that the system is more sensitive toward the transducer force constant, the capacitance, and the voltage constant for the given value of forcing. Future work will focus on expanding the global sensitivity analysis to various forcing values and additional system responses like bifurcation diagrams. This aims to identify critical behaviors influenced by parameter uncertainties. We also intend to conduct a global optimization of NERS-TMDI parameters to improve system safety and performance, particularly near critical merging points. Experimental validation to confirm these theoretical findings is also planned.