1 Introduction

Thermo-acoustic instabilities pose a severe challenge in the development of clean burning techniques using lean fully premixed laminar flames. These instabilities can typically be divided in two types, namely unstable modes (i) with a duct acoustic origin and (ii) with a burner/flame intrinsic thermo-acoustic (ITA) origin [21]. In the first type, an duct acoustic mode of the system is perturbed by the heat-release rate oscillation of the flames and, in turn perturbs the flames. If the heat-release rate is in phase with the pressure, a positive feedback is established between the acoustic mode and the flames. Due to this feedback the acoustic mode is destabilised by the flames. The second type of modes originates from an internal feedback loop in the burner/flame configuration as shown by Bomberg et al. [3] and Emmert et al. [9]. For premixed gaseous velocity-sensitive flames, which are considered in this research, the heat-release rate generated by the flames depends on the oscillations of acoustic velocity of the unburned mixture, which in turn is perturbed by the heat-release rate of the flames and consequently establishing an internal feedback mechanism in the burner/flame configuration. By its nature, the physics of the ITA modes are not affected by the acoustic embedding of the flames [19].

Thermo-acoustic instabilities manifest themselves often as limit cycle oscillations. The amplitude of the unstable oscillations saturates due to nonlinear processes, which renders thermo-acoustic systems as nonlinear dynamical systems. In general, the flames are believed to contribute as the main nonlinear element in thermo-acoustic systems [13, 15, 18, 20]. Besides limit cycle oscillations, a variety of other nonlinear oscillations are observed. Bifurcation analyses conducted by Kabiraj et al. [14] and Kashinath et al. [15] reveal that thermo-acoustic systems also exhibit quasi-periodic and chaotic behaviour. These bifurcation analyses are conducted on a system where the acoustics of the appliance vessel are coupled to the flame dynamics. Hence, it remains unclear if these nonlinear features of the oscillations are purely generated by the flame nonlinearity or resulting from the coupling between the flames and the acoustics, which is essentially a coupling between two oscillators. To elucidate this problem, an experimental setup that decouples the flame dynamics from the acoustics was built by Wildemans et al. [29]. With this setup the nonlinear behaviour of pure ITA modes, reflecting the self-excited dynamics of the flames, are studied by means of a bifurcation analysis. This bifurcation analysis revealed that the flames are able to generate limit cycle, period-2 limit cycle and quasi-periodic oscillations.

Accurate models of the flame dynamics are of key importance in designing clean and thermo-acoustically stable burning appliances. These models can be used to investigate the instability mechanisms and broaden the understanding of these mechanisms. Furthermore, they can be used to analyse the stability of burning appliances in an early design phase. Finally, these models can be used to design active and passive instability mitigation strategies. The success of these strategies depends on the quality of the models that describe the dynamical behaviour of the system. Besides the accuracy of the models, computation time is also important. Especially, when mitigation strategies or application designs need to be optimised. In these cases the performance of the complete system needs to be evaluated for a lot of different parameter values, which is a computational heavy task. Hence, accurate low-order models of the flame dynamics are required.

Thermo-acoustic systems are typically modelled by dividing the full system in two subsystems, namely the acoustic and the flame dynamics. The acoustics are considered to be linear and are typically modelled by the linearised wave equation. The flame dynamics of velocity sensitive flames, as considered in this paper, are described by a relation between the acoustic velocity perturbations just upstream of the flames and the heat-release rate oscillations of the flames. To describe and predict the nonlinear oscillations as for example observed in bifurcation analyses, a nonlinear model of the flame dynamics is required.

In theory, a low-order model that describes the dynamics of the flames can be derived starting from first principles. Next, these governing equations should be simplified analytically to the level where the main observable quantities (e.g., heat-release rate) are described by a low-order dynamical model that captures the essential dynamics. Since such a model is derived from governing equations, it is based on physics and its parameters have a physical interpretation. In case of premixed flames, the governing equations are the fluid dynamical conservation equations coupled to strongly nonlinear (detailed or reduced) chemical reactions and an appropriate diffusion model. In fact, analytical models are mostly developed for stationary problems in simplified geometries. The flame-acoustic interaction has analytical solutions for a few simplified cases such as 1-D flames (burner surface stabilised flat flames). In case of 2-D flames (such as conical flames as investigated in this paper) flame front tracking equations like the G-equation [30] are used and only analytical results are obtained incorporating a number of significantly restricting assumptions [26]. Among those are the neglection of flame to flow interaction, forced flame anchoring and the neglection of flame curvature and flow strain effects. Relaxation of such restrictions to incorporate for example nonlinear effects require numerical simulations since the equations cannot be solved analytically. To conclude, the state-of-the-art of the description of flame-acoustics interaction does not provide analytical solutions with physics-based description of the nonlinear flame dynamics.

In absence of physics-based low-order dynamical models phenomenological models of different complexity are typically used to describe the experimentally observed flame dynamics. In general these models are proven to be useful in understanding the destabilising mechanisms and designing stable combustion systems. Furthermore, phenomenological models can also facilitate the development of analytical low-order descriptions of the flame-acoustic interaction, since they provide a set of resulting equations that captures the essential dynamics that could be aimed for. Next, a number of different phenomenological models is discussed.

The nonlinear response of the flames is often modelled by a Flame Describing Function (FDF) [18, 20]. An FDF is a weakly nonlinear model which assumes a-priori that the output responds at the same frequency as the input. FDF do not include the energy transfer between different frequencies and higher harmonics in the response are not accounted for. Hence, an FDF is not able to describe the limit cycles where higher harmonics are clearly present. Furthermore, due to the quasi-linear frequency assumption it also fails to predict other nonlinear oscillations that are observed in thermo-acoustic systems, such as period-2 limit cycle, quasi-periodic and chaotic oscillations. The concept of an FDF is extended by Haeringer et al. [12] by incorporating the response at higher harmonics. This enables the prediction of limit cycle oscillations in which the contribution of higher harmonics is not negligible. However, the extended FDF is also a weakly nonlinear model and thus not able to describe aperiodic oscillations.

Another type of nonlinear models used to study thermo-acoustic instabilities is based on low-order oscillator models [4, 11, 16]. In these models, the acoustic mode is described by a Van der Pol oscillator. The flame dynamics are modelled by a static nonlinear function that describes the relation between the acoustic velocity perturbations and the heat-release rate. It is shown that these time-domain models are capable of reproducing a rich variety of nonlinear oscillations. A slightly different approach is taken by Weng et al. [28], in which the flame is modelled as a nonlinear oscillator that is nonlinearly coupled to the oscillator that described the acoustic field. This phenomenological model of two coupled oscillators is able to qualitatively describe the nonlinear oscillations of the bifurcation experiment conducted by Kabiraj et al. [14]. However, these flame models require the coupling to the acoustic oscillators to generate nonlinear oscillations. These flame models are not able to describe the self-excited ITA modes which are independent on the acoustic modes due to the static nature of the flame models. Hence, these flame models are not capable to describe all experimentally observed behaviour.

A new data-driven modelling approach is applied to describe the nonlinear flame response in time-domain [27]. An artificial neural network is trained on CFD simulation data. This model accounts for energy transfer between different frequencies and is thus more general then a FDF. Furthermore, it was shown that this model is able to reproduce both the forced and the self-excited flame dynamics. The main drawback of this modelling approach is its black-box nature, which makes it difficult to make a physical interpretation of the model.

Recently, a grey-box modelling approach is successfully applied. Doehner et al. [8] introduced a low-order time-domain model of two coupled oscillators to describe the forced response of the flames. This model was able to provide an accurate representation of the forced flame dynamics. Since this model is a low-order time-domain model, it is well suited for inexpensive time-domain simulations of thermo-acoustic systems.

Since the model of Doehner et al. [8] is identified based on the acoustic forced dynamics of the flames, it remains unclear if the model is also capable of reproducing the rich variety of nonlinear oscillations originated from the self-excited ITA mode as shown by Wildemans et al. [29]. In Wildemans et al. [29], however, a phenomenological model of two coupled oscillators was introduced that is able to qualitatively reproduce all the different regimes observed in the experimental bifurcation analysis. Hence, a model of two coupled oscillators provides a promising model structure for nonlinear time-domain flame models.

The main goal of this paper is to investigate if the phenomenological model, as introduced in Wildemans et al. [29], is able to quantitatively describe the nonlinear self-excited oscillations exhibited by a pure ITA mode. Thereto, the nonlinear model of two nonlinearly coupled oscillators is investigated in detail to understand the exhibited oscillations. Furthermore, a parameter estimation is conducted to show that, besides the qualitative match, there is also a quantitative match between the model response and the experimental time-series for all four regimes.

The paper is structured as follows. First, the experimental setup to observe pure ITA modes is introduced and the experimental bifurcation analysis is discussed. Thereafter, the model of two coupled oscillators is introduced and explained. In the fourth section, the parameter estimation procedure is explained. Subsequently, the results of the parameter estimation are presented and discussed. In this section it is also investigated if the model introduced in Doehner et al. [8] is able to reproduce the oscillations of the four different regimes in the bifurcation diagram. Finally, a discussion of the results is presented in the seventh section followed by conclusions in the last section.

2 Experimental bifurcation analysis

Pure ITA modes are observed when the burner/flame configuration are completely decoupled from the duct acoustic modes of the thermo-acoustic system. This is typically realised by using anechoic up- and downstream conditions, such that the acoustic waves are not reflected back to the flames. A setup is developed to experimentally observe an unstable pure ITA mode. With this setup an experimental bifurcation study of the pure ITA mode is executed. Below, the setup is explained in more detail and thereafter the main findings of the bifurcation analysis are presented.

2.1 Experimental setup

In Wildemans et al. [29] a setup is introduced to experimentally observe pure ITA modes. This setup is schematically depicted in Fig. 1. It consists of three main parts: the burner and an up- and downstream duct with their mufflers (denoted by G and H, respectively). The burner consists of a water cooled burner deck holder in which a 1 mm thick perforated brass burner deck (A) is placed. This burner deck has 109 holes with a diameter of 2 mm which are arranged in a hexagonal pattern with a pitch of 4.5 mm. The up- and downstream mufflers provide close to anechoic conditions over a wide frequency range including the typical frequencies of pure ITA modes. The setup is equipped with three sensors, namely a Constant Temperature Anemometer (CTA, denoted by B) to measure the acoustic velocity oscillations just upstream of the burner deck, a Photomultiplier (PMT, denoted by C) with an OH\({}^*\) light filter (\(310 \pm 10\) nm) to measure the OH chemiluminescence as an indicator for the heat-release rate and a pressure transducer (D) to measure the pressure oscillations in the upstream duct. The flames could externally be forced by a loudspeaker (E), however, in this work only self-excited oscillations of the flames are considered. In this research a fully premixed methane-air mixture is used which is injected into the system at the inlet in the upstream duct (F). The equivalence ratio \(\phi \) and the mean upstream velocity of the mixture can easily be controlled by the means of mass flow controllers. In this research the equivalence ratio is kept constant at \(\phi =0.70\). The mean upstream velocity of the mixture in the holes of the burner deck is used as a bifurcation parameter and denoted by V. An increase of this velocity at a constant equivalence ratio is similar to an increase of thermal power. A more detailed discussion of the experimental setup can be found in Wildemans et al. [29].

Fig. 1
figure 1

Schematic overview of experimental setup: A—burner deck, B—CTA sensor, C—PMT sensor, D—pressure transducer, E—loudspeaker inlet, F—mixture inlet, G—upstream muffler and H—downstream muffler. All dimensions are in mm

Full size image

2.2 Bifurcation analysis

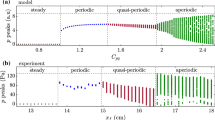
The setup reveals self-excited oscillations for a broad range of mean velocities V. These oscillations originate from an unstable ITA mode as shown in Wildemans et al. [29]. By slowly varying the mean velocity in the burner deck holes, V, qualitative changes of the self-excited oscillations are observed. In Wildemans et al. [29] the nonlinear dynamics of the pure ITA mode are experimentally investigated by means of a bifurcation diagram.

Fig. 2
figure 2

Bifurcation diagram of pure ITA mode with \(u'/{\bar{u}}\) the normalised acoustic velocity fluctuations amplitude and the bifurcation parameter V denoting the mean upstream velocity of the air–fuel mixture

Full size image

The bifurcation diagram is depicted in Fig. 2. The dots represent the local maxima of the time-series of the normalised acoustic velocity just upstream of the burner deck, \(u'/{\bar{u}}\). Here, \(u'\) represents the velocity perturbation and \({\bar{u}}\) the mean velocity. This bifurcation diagram reveals four distinct regimes. Regime I, located at \(V<0.50\) m/s, represents a stable flame characterised by a velocity perturbation of \(u'=0\). Note that a zero velocity perturbation implies a zero heat-release rate perturbation. When the bifurcation parameter is increased, the flame looses stability through a supercritical Hopf bifurcation and limit cycles emerge. Regime II of the limit cycles is observed in the range \(V=0.50{-}1.50\) m/s. In the bifurcation diagram, limit cycles are typically characterised by a single dot. However, in Fig. 2 a small spread of dots is observed in regime II, which is caused by the small differences of local maxima due to noise. When the bifurcation parameter V increases to a certain value, the limit cycles bifurcate into quasi-periodic oscillations. This bifurcation is named a Neimark–Sacker bifurcation, which describes the birth of a second oscillation frequency. The quasi-periodic oscillations are characterised by a low frequent amplitude and frequency modulation. The corresponding frequency spectrum reveals a distinct peak at the low modulation frequency, which turns out to be quite special. This is elaborated in more detail in Sect. 5.3. The amplitude modulation results in local maxima of the time-series with varying peak values characterised by a large spread of points in Fig. 2 in the range of \(V=1.60{-}2.40\) m/s. Thereafter, period-2 limit cycles are observed which are reached via a period doubling bifurcation. The signature of this regime is characterised by two distinct dots representing the two distinct local maxima of the time-series. The bifurcation analysis reveals that an unstable pure ITA mode exhibits a rich variety of different nonlinear oscillations. Hence, a proper flame model should be able to describe all observed regimes. In the next section, a model of two coupled oscillators is introduced that produces all four regimes.

3 Model of coupled oscillators

A proper flame model should be able to describe the nonlinear oscillations produced by the internal feedback loop of the ITA mode. Such a new flame model can be obtained due to system identification. A first step in the identification of a model is the selection of a model structure that is capable of describing the nonlinear dynamics of the flames of all four regimes. Dynamical models that exhibit self-excited oscillations are typically described by nonlinear differential equations, also known as oscillators. Many of such dynamical models exhibit limit cycle and period-2 limit cycle oscillations. However, quasi-periodic oscillations are less common, especially those with a distinct peak in the frequency spectrum at the low modulation frequency. Most dynamical system that reveal quasi-periodic oscillations does not show a distinct peak at the low modulation frequency, e.g., the system in Kuznetsov et al. [17]. In Wildemans et al. [29], it was shown that the frequency spectrum corresponding to the quasi-periodic oscillations reveal a clear peak at the low modulation frequency, which turns out to be quite special feature of the flame dynamics and thus can be used as a guide in selecting a proper model structure. The dynamic model proposed in Anishchenko et al. [1] is able to describe quasi-periodic oscillations characterised by a peak at the low modulation frequency. Furthermore, this model is also able to describe the other observed attractors, namely a stable fixed point, limit cycle and period-2 limit cycle oscillations as shown in Wildemans et al. [29]. Hence, this dynamical model provides a promising model structure to describe the flame dynamics.

In the remainder of this section the structure and important features of the model, as introduced in Anishchenko et al. [1], are discussed. This model represents two nonlinearly coupled oscillators and is given by

$$\begin{aligned}&\ddot{y} - \left( m-d{\dot{y}}^2\right) {\dot{y}} + y = -{\dot{y}}{\dot{z}}, \end{aligned}$$
(1)
$$\begin{aligned}&\ddot{z} + \gamma {\dot{z}} + gz = \gamma \varPhi (-{\dot{y}}), \end{aligned}$$
(2)

with

$$\begin{aligned} \varPhi (x) = I(x)x^2, \quad I(x)=\left\{ \begin{array}{c} 1,\quad x>0\\ 0,\quad x\le 0 \end{array}\right. . \end{aligned}$$
(3)

Equation (1) represents the Rayleigh oscillator, that is characterised by the cubic damping term \(d{\dot{y}}^3\). This oscillator is linearly unstable for small values of \({\dot{y}}\) (\(|{\dot{y}}|<\sqrt{m/d}\)) and consequently produces self-excited oscillations. For large values of \({\dot{y}}\) (\(|{\dot{y}}|>\sqrt{m/d}\)), the damping becomes positive and the amplitude of the oscillations saturates. Hence, the amplitude of the oscillations is determined by the ratio m/d. The Rayleigh oscillator is closely related to the classical Van der Pol oscillator and can easily be transformed to the latter. The second oscillator is described by Eq. (2) and represents a linear damped oscillator. This oscillator is equivalent to a linear mass-spring-damper system. The damping constant is represented by \(\gamma \) and the spring constant by g. This linear oscillator is not able to generate stable self-excited oscillations by itself due to its linear nature. Both oscillators are nonlinearly coupled to each other through the terms \(-{\dot{y}}{\dot{z}}\) and \(\gamma \varPhi (-{\dot{y}})\). The coupling in the first oscillator affects the damping of the first oscillator with the magnitude of the first time derivative of the state variable of the second oscillator. When the time-series of \({\dot{y}}\) and \({\dot{z}}\) are in phase, positive damping is added and the amplitude of the first oscillator will decrease depending on the oscillations of the second oscillator. When \({\dot{y}}\) and \({\dot{z}}\) are out of phase, the additional negative damping will result in growth of the amplitude of \({\dot{y}}\). Hence, this coupling will result in a variable damping constant. The coupling in the second oscillator is only active when \({\dot{y}}<0\), due to the Heaviside function I(x). This coupling will add a positive value to the second derivative of z and potentially destabilises the second oscillator. Due to this destabilisation, the second oscillator can produce oscillations, which in turn affect the first oscillator. This destabilisation occurs when \({\dot{y}}\) and \({\dot{z}}\) are in phase, because in that case a positive value is added to the derivative when the amplitude of its state is positive. When both states are in anti-phase, the amplitude of \({\dot{z}}\) is damped due to the coupling.

This dynamical system of two coupled oscillators is able to generate complex dynamical oscillations due to their mutual interaction. For example, quasi-periodic oscillations can be generated in an oscillatory system with two independent frequencies in which the variable damping constant (\(\alpha -\mu _1 {\dot{x}}_2\)) is periodically modulated [1]. These conditions are satisfied by the system of Eqs. (4) and (5), which is thus due to the nonlinear coupling able to generate quasi-periodic oscillations.

To obtain better fitting results, the Rayleigh oscillator is transformed into the Van der Pol oscillator. Furthermore, all terms in both oscillators are uniquely parametrised to increase the flexibility in describing the experimental data. This results in the following set of differential equations:

$$\begin{aligned}&\ddot{x}_1 - \left( \alpha -\delta x_1^2\right) {\dot{x}}_1+\beta x_1=-\mu _1 {\dot{x}}_1 {\dot{x}}_2, \end{aligned}$$
(4)
$$\begin{aligned}&\ddot{x}_2 +\varepsilon {\dot{x}}_2 + \zeta x_2 = \mu _2\varPhi ({\dot{x}}_1). \end{aligned}$$
(5)

In these equations, \(\beta \) and \(\zeta \) represent the stiffness parameters of both oscillators and mainly determine the oscillation frequencies. The parameters \(\alpha \), \(\delta \) and \(\varepsilon \) are all related to the damping of both oscillators and \(\mu _1\) and \(\mu _2\) describe the coupling strength. Furthermore, the non-smooth function \(\varPhi ({\dot{x}}_1)\) remains unchanged and is given by Eq. (3). As explained, this model is a phenomenological model which is not derived from first principles. Consequently, the states and parameters do not have a straightforward physical interpretation as well as the nonlinear (coupling) terms. However, in the next section it is explained in more detail that the state \({\dot{x}}_1\) reveals a remarkable similarity with the acoustic velocity oscillations. This indicates that the state variable \(x_1\) represents a displacement of the acoustic medium and \({\dot{x}}_1\) the acoustic velocity. The second oscillator is thus destabilised by a perturbation of the acoustic velocity in downstream direction (\({\dot{x}}_1>0\)). Furthermore, when a flame is perturbed it will return to its stable equilibrium after some time. This indicates a restoring force which is equivalent to a spring force in the dynamical model as mentioned in Doehner et al. [8].

4 Parameter estimation

In the previous section, it is explained that the presented model of two coupled oscillators is able to describe the experimentally observed oscillations qualitatively. To find a quantitative match between the experimental data and the model, the correct parameters for the different regimes should be estimated. Thereto, a cost function is required to evaluate a certain parameter set. A natural choice for such a function is to compare the time-series of a certain model output with measured time-series. Such a cost function directly enforces a physical meaning to the model output. A similarity is observed between the time-series of the state \({\dot{x}}_1\) of the model and the experimental acoustic velocity perturbations in the limit cycle regime. Both time-series reveal an asymmetric limit cycle characterised by a relatively fast rise and a relatively slow decay. This feature of the signal shape is also observed in CFD simulations of a pure ITA mode by Courtine et al. [7] and Silva et al. [25]. Hence, the state \({\dot{x}}_1\) is chosen as the output of the model to describe the measured acoustic velocity. More specific, the time evolution of the state \({\dot{x}}_1\) should match the experimental time-series data as close as possible. This requirement results in the minimisation of cost function

$$\begin{aligned} J(\theta )=\sum _{j=1}^{N_t}\left( {\tilde{y}}_j-h(x(t_j,\theta ),t_j,\theta )\right) ^2, \end{aligned}$$
(6)

subject to the dynamical system as given in Eqs. (4)–(5). In the cost function, \({\tilde{y}}_j\) is the jth sample of the experimental time-series, \(N_t\) is the total number of samples, h is the model output given by \(h(x,t)={\dot{x}}_1(\theta ,t)\) and \(\theta \) is the vector with unknown parameters that should be estimated. The unknown parameters consist of all model parameters including the initial conditions of the states \(x_1\), \(x_2\) and \({\dot{x}}_2\). The parameter vector \(\theta \) is given by

$$\begin{aligned} \theta = \left[ \begin{array}{cccccccccc} \alpha&\quad \beta&\quad \delta&\quad \mu _1&\quad \varepsilon&\quad \zeta&\quad \mu _2&\quad x_1(0)&\quad x_2(0)&\quad {\dot{x}}_2(0) \end{array}\right] ^\textrm{T}.\nonumber \\ \end{aligned}$$
(7)

Note that the initial conditions of the state \({\dot{x}}_1\) is equal to the first value of the experimental time-series due to the definition of the cost function. Since the experimental data originates from self-excited oscillations, the parameter estimation is based on output data only.

Parameter estimation of nonlinear dynamical models is known to be a difficult problem with a variety of possible pitfalls [22, 23]. Among the pitfalls are a lack of identifiability, local solutions, oscillating dynamics, badly scaled parameters, noisy data and overfitting. Especially, the oscillating dynamics of Eqs. (4) and (5) poses difficulties to the parameter estimation, since the cost function will have multiple local minima and an irregular structure [23]. A local (gradient based) optimisation method will likely converge to a local minima. Hence, finding the global minimum is highly dependent on the initialisation of the algorithm. Several global optimisation approaches are developed to find the global minimum of a cost function subject to an oscillator. The simplest algorithm uses a multi-start approach, which is potentially inefficient if there are many parameters to identify. Another approach combines a global search phase with a local (e.g., gradient based) search. A well-known algorithm of this class is the enhanced scattering search (eSS), that outperforms the simple multi-start algorithm in many occasions [10, 22]. Furthermore, experimental data is always subjected to noise which poses the problem of overfitting the data. In an overfitted model the noise is fitted rather than the signal. The value of the cost function of an overfitted model can be small, but that does not mean that the obtained model has good predictive power. One remedy against overfitting is to reduce the amount of noise in the data. This can typically be achieved by filtering the data. However, filtering highly nonlinear experimental time-series with a low pass filter will filter out the higher harmonics and consequently alters the nonlinear oscillations. Therefore, the experimental data is filtered with a nonlinear filter as described in Schreiber [24]. Another method to reduce overfitting, is to use regularisation techniques [10, 22]. To minimise model complexity and penalise wild behaviour of the model, a regularisation term is added to the cost function. The regularisation term adds some regularity to the minimisation problem and can be used to add some prior knowledge about the parameters.

The AMIGO toolbox is used for the parameter estimation [2], since this toolbox provides several good features for parameter estimation. A hybrid algorithm that combines a global search phase with a local optimization phase, known as eSS, is used to minimise the cost function. Furthermore, the toolbox enables the use of the exact Jacobian, which improves and speeds up the convergence of the local gradient based algorithms. This, however, requires model equations that are continuous in the states and parameters. The function \(\varPhi (x)\) in the second oscillator, given by Eq. (3), is discontinuous due to the Heaviside function. Therefore, this function is substituted by the following continuous approximation:

$$\begin{aligned} {\tilde{\varPhi }}(x)=\frac{1}{1+e^{-40x}}x^2. \end{aligned}$$
(8)

Finally, the AMIGO toolbox enables to use Tikhonov regularisation to improve the parameter estimation procedure [10]. The regularisation adds a penalty term \(\varGamma (\theta )\) to the cost function, which results in the regularised cost function

$$\begin{aligned} J_R(\theta ) = J(\theta )+\lambda \varGamma (\theta ), \end{aligned}$$
(9)

where \(\lambda \) is the non-negative regularisation parameter. The penalty function is given by the following quadratic penalty function

$$\begin{aligned} \varGamma (\theta ) = \left( \theta -\theta _\textrm{ref}\right) ^\textrm{T}W^\textrm{T}W\left( \theta -\theta _\textrm{ref}\right) . \end{aligned}$$
(10)

Herein, W is a diagonal scaling matrix and \(\theta _\textrm{ref}\) is a reference parameter vector. In Gabor and Banga [10], different scenarios of selecting W and \(\theta _\textrm{ref}\) are discussed depending on the prior knowledge of the parameters. Since the model parameters are roughly of \({\mathcal {O}}(1)\) due to the scaling, a reliable initial guess of the parameters within one order of magnitude is known. Hence, in Gabor and Banga [10] it is advised to select for W the identity matrix and for \(\theta _\textrm{ref}\) the parameter guess which is chosen as a vector with all its elements equal to 0.1. The regularisation parameter \(\lambda \) determines the balance between the prior knowledge and the information of the data. This parameter is automatically selected by a generalised cross validation algorithm, which was shown to produce good results [10].

Furthermore, the experimental time-series reveal dominant oscillations in the range of 100–200 Hz, indicating that the response of the model should be in the order of milliseconds. An oscillator with such a response time should have parameter values that differ several orders in magnitude. Large differences between parameter values will make the minimisation of the cost function with a gradient based algorithm a challenging task. To avoid these problems, the time variable of the model is scaled to a dimensionless time \(\tau \) such that the parameter values of the scaled model are roughly of the same order. The dimensionless time is given by \(\tau =t/T_\textrm{ref}\), in which \(T_\textrm{ref}\) describes a typical time scale of the oscillating flames. A Van der Pol oscillator with mass and spring values of \({\mathcal {O}}(1)\) and a strength of the nonlinear damping that provides limit cycle oscillations with a comparable shape as observed in the experimental data, has a typical period time of \(\tau =5\). Several characteristic times can be used to obtain a suitable reference time. For example, in Doehner et al. [8] the restoration time is used, which is the typical time for a flame to recover to its initial position after a perturbation. In this paper, the period time of a typical limit cycle is used. The limit cycle frequency at a velocity of 1.00 m/s is 150.3 Hz, which corresponds with a characteristic time of 6.7 ms. Hence, the reference time to slow down the flame dynamics is given by

$$\begin{aligned} T_\textrm{ref} = \frac{t}{\tau }=\frac{6.7\times 10^{-3}}{5}=\frac{1}{751.5} s. \end{aligned}$$
(11)

Applying this time scaling to the model of Eqs. (4) and (5) will result in a model with the same structure with the parameters as given in Table 1. Note that the coupling parameters \(\mu _1\) and \(\mu _2\) are not changed due to the time-scaling. Furthermore, the time of the experimental data is similarly scaled to match the new dimensionless time of the model equations.

Table 1 Relation between parameters of scaled and non-scaled model
Full size table

Besides the time-scaling, also the sampling frequency is adapted to obtain better parameter estimation results. The experimental data is sampled with a frequency of 3000 Hz. It was found that an increased sampling frequency improves the parameter estimation. With a higher sampling frequency, the oscillations are more precisely covered by the reference data and due to the higher number of data points around the maxima a mismatch in the maxima results in a larger value of the cost function. The sampling frequency of the experimental data is increased by a factor 4 by using the Modified Akima cubic Hermite interpolation (makima) function in MATLAB.

The parameters are estimated for the experimental data sets corresponding to all values of the bifurcation parameter V, starting from the low values. Based on preliminary results, it was observed that the convergence of the algorithm for the data in the limit cycle regime hardly depends on the initialisation of the parameter vector and almost always converge to a proper solution. However, for the other two regimes, with quasi-periodic and period-2 limit cycle oscillations, the algorithm does often not converge to a proper solution with the same qualitative type of oscillations. The data sets in a specific regime obtained with the subsequent value of the bifurcation parameter are visually almost similar. Hence, it is expected that the estimated parameters hardly change between those data sets. Even when the algorithm was initialised with the estimated parameters based on the previous data set, it was often not able to converge to a proper solution. Therefore, a staged optimisation is applied in which different sets of parameters are estimated separately. The main idea behind this staged optimisation is to reduce the number of unknowns to simplify the optimisation. The parameters \(\beta \) and \(\zeta \) determine the frequency of both oscillators and consequently have the largest influence on the cost function. First, the initial conditions are estimated, then the values of \(\beta \) and \(\zeta \) to ensure that the oscillation frequencies of both oscillators match the experimental data and subsequently the other parameters are estimated. Note that the initialisation between the different runs is updated with the newly estimated parameters. Finally, in the last run all parameters are estimated at the same time to check if parameters updated in earlier stages should be updated based on the new parameters of the later stages.

For the parameter estimation the data is divided into a training and validation set. The training set consists of 8000 samples and is used for the parameter estimation. The validation set is used to investigate the predictive power of the model with the identified parameters. The normalised root-mean-square error (NRMSE) between the model output and the experimental data set is used as a metric to quantify and therefore to evaluate the quality of the estimated parameters and the predictive power of the model. The NRMSE is calculated as

$$\begin{aligned} \hbox {NRMSE}(\theta )=\sqrt{\frac{1}{N_t}\sum _{j=1}^{N_t}\left( \frac{{\tilde{y}}_j-h(x(t_j,\theta ),t_j,\theta )}{\max {{\tilde{y}}}-\min {{\tilde{y}}}}\right) ^2}.\nonumber \\ \end{aligned}$$
(12)

The NRMSE is scaled by the number of samples \(N_t\) to enable the comparison between the quality of the model based on the training and validation data set. Furthermore, the error is scaled with the amplitude of the oscillations to make the NRMSE of different data sets comparable. Note that only the initial condition of the state \({\dot{x}}_1\) is known in both the training and validation data sets. Hence, for an adequate validation of the estimated model parameters, for the validation set the initial conditions of the other states are estimated with the same procedure as described above.

5 Results

In this section, the results of the parameter estimation for the different regimes are presented. The model parameters are identified with the AMIGO toolbox, as discussed in the previous section, based on the time-scaled experimental data. These identified parameters are transformed back to the non-scaled form according to the relations in Table 1. Thereafter, the model is simulated and the results are compared with the corresponding experimental data sets.

5.1 Regime I: stable fixed point

The first regime, observed for \(V<0.50\) m/s, is characterised by stable flames. This regime indicates a constant heat-release rate and acoustic velocity just upstream of the burner deck. Hence, the velocity perturbation \(u'=0\) which implies that the time-derivative of the second state equals to zero, \(\ddot{x}_1=0\). This condition is only satisfied when the system given by Eqs. (4) and (5) has a stable equilibrium. The model actually has a single equilibrium at \(x_0=[ x_1 \; {\dot{x}}_1 \; x_2 \; {\dot{x}}_2]^\textrm{T}=[ 0 \; 0 \; 0 \; 0]^\textrm{T}\), which stability is given by the eigenvalues of the Jacobian matrix of the system evaluated at the equilibrium point. This results in the following expressions for the eigenvalues of the Jacobian matrix:

$$\begin{aligned} \lambda _{1,2}&= \frac{\alpha }{2}\pm \frac{1}{2}\sqrt{\alpha ^2-4\beta }, \end{aligned}$$
(13)
$$\begin{aligned} \lambda _{3,4}&= -\frac{\varepsilon }{2}\pm \sqrt{\varepsilon ^2-4\zeta }. \end{aligned}$$
(14)

Based on these eigenvalues, it is concluded that the equilibrium point is linearly stable iff \(\alpha <0\) and \(\varepsilon >0\). Hence, this is the minimal requirement on the parameters to obtain the stable attractor as observed in regime I.

5.2 Regime II: limit cycles

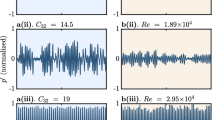
When the velocity increases, a regime of limit cycles is exhibited by the flames in the range of \(V\in \left[ 0.50,\, 1.50\right] \) m/s. Experimentally, this regime is reached after a supercritical Hopf bifurcation as shown in Wildemans et al. [29]. The nature of the Hopf bifurcation as produced by the model when \(\alpha \) becomes positive is also supercritical. Hence, the nature of the bifurcation is adequately described by the model. For the parameter estimation a typical response with limit cycle oscillations at \(V=1.00\) m/s is selected. In Fig. 3a the time-series of the experiment and the identified model (state \({\dot{x}}_1\)) are depicted. This results shows that the model is able of describing the limit cycle oscillations accurately. The frequency and the shape of the limit cycle are both described precisely by the model. The limit cycle is asymmetric since the absolute values of its maxima are larger compared to the minima. Furthermore, the limit cycle is characterised by a bend close before its minimum, which is also described by the model. The Power Spectral Densities (PSDs) of both time-series are depicted in Fig. 3b. As expected based on the time-series, the dominant frequency and its higher harmonics are well captured by the model. Especially, the dominant and first harmonic reveal a similar strength compared to the experimental data. The second and third harmonic are slightly less strongly present in the model response. The NRMSE of the fit confirms the good match between the model output and the experimental data and is given by 0.0161. Besides this good fit, the model reveals also a strong predictive power since the NRMSE based on the validation data set (0.0138) is approximately similar to the NRMSE based on the training data. Based on these results, we can also conclude that the model is not overfitted.

Fig. 3
figure 3

Limit cycle oscillations of the normalised acoustic velocity at \(V=1.00\) m/s. In a the time-series of the experimental data () and the model () are shown and in b the corresponding PSDs

Full size image
Table 2 Estimated parameter values of time-scaled model for data sets corresponding to oscillatory regimes II to IV
Full size table

The corresponding estimated parameter values of the scaled model are shown in Table 2. The parameters \({\tilde{\beta }}\) and \({\tilde{\zeta }}\) represents the stiffness of both oscillators and are closely related to the oscillator frequencies. Both parameters have approximately the same value, which indicates that both oscillators have almost the same frequency. This is also confirmed by the oscillation frequencies of both oscillators in the simulated model response, which are both 149.6 Hz.

5.3 Regime III: quasi periodicity

The third regime is characterised by quasi-periodic oscillations and is experimentally observed in the range of \(V\in \left[ 1.60,\,2.40\right] \) m/s. The oscillations in this regime reveal both amplitude and frequency modulation by a low frequency. The amplitude modulation is clearly visible in the time-series as depicted in Fig. 4a, while the presence of frequency modulation can be deduced from the PSD as shown in Fig. 4b. Frequency modulation is characterised by a frequency spectrum with multiple sidebands at \(f_\textrm{ITA}\pm nf_L\), with \(n=1,2,\ldots \) and \(f_\textrm{ITA}\) the dominant oscillating frequency and \(f_L\) the low frequent modulation frequency.

Fig. 4
figure 4

Quasiperiodic oscillations of the normalised acoustic velocity at \(V=1.60\) m/s. In a the time-series of the experimental data () and the model () are shown, in b the corresponding PSDs and in c the instantaneous frequencies

Full size image

The experimental data corresponding to \(V=1.60\) m/s is used to perform the parameter estimation. In Fig. 4a it is shown that the model is able to capture both the dominant oscillation frequency and the amplitude modulation. In general the maxima and minima of the model response are slightly larger compared to the experimental data. However, the minima of the model are smaller when the modulated amplitude is minimal. Both time-series reveal a similar frequency spectrum as depicted in Fig. 4b. The PSD of the model response shows that the model also describes the frequency modulation. Furthermore, the dominant oscillation frequency and its sidebands are reveal a similar strength as in the experimental data. The higher harmonics and their sidebands are well predicted by the model, but their strength are in general slightly over predicted by the model. The model is also able to describe the characteristic peak at the low modulation frequency \(f_L\). However, its peak is much higher in the experimental data. To verify how well the frequency modulation is described by the model, the instantaneous frequency of both signals is computed. Thereto, the Hilbert transform is used, which enables the calculation of instantaneous attributes of time-series, such as amplitude, phase and frequency. This transform extends a real valued signal \(x_r(t)\) into an analytical signal \(x(t)=x_r(t)+ix_i(t)\), in which i represents the imaginary unit. The imaginary part of the signal \(x_i\) is similar to the real part \(x_r\), but with a phase shift of \(90^{\circ }\). The instantaneous phase and frequency are closely related, since the latter is the time rate of change of the first. The instantaneous phase is given by

$$\begin{aligned} \phi (t)=\arctan \left( \frac{x_i(t)}{x_r(t)}\right) . \end{aligned}$$
(15)

Hence, the instantaneous frequency is given by \(\omega (t)=\text {d}\phi /\text {d}t\). This derivative is numerically computed using total-variation regularisation [6]. The instantaneous frequencies of the experimental data and model response are shown in Fig. 4c. Both lines reveal a similar pattern of the frequency modulation. However, the maximal frequency of the model response is slightly lower than in the experimental data. Based on the results in Fig. 4 it is concluded that the model is able to describe the complex oscillations with amplitude and frequency modulation rather well.

In Table 2 the corresponding parameter values are given. Compared to the limit cycle oscillations, the dominant oscillation frequency is increased which is reflected by an increase of \({\tilde{\beta }}\). However, the estimated value for \({\tilde{\zeta }}\) is only slightly increased. This indicates that both oscillators have a different oscillation frequency. Furthermore, the values of both coupling parameters, \(\mu _1\) and \(\mu _2\), are more than doubled. Hence, the coupling between both oscillators is intensified to produce quasi-periodic oscillations. Finally, the damping values are changed for which the drop of \({\tilde{\delta }}\) is most notable.

The quality of the fit and the predictive power are good as can be seen from the NRMSE values computed on both data sets. The NRMSE of the training data equals 0.1068 and of the validation data 0.1029. These values are roughly a factor seven higher compared to the limit cycle oscillations, indicating that the model can describe the limit cycle oscillations more accurately. This is also expected since the quasi-periodic oscillations are rather complex due to the frequency and amplitude modulation and therefore more difficult to describe.

5.4 Regime IV: period-2 limit cycles

The oscillations in the last regime are period-2 limit cycles, which repeats itself after two oscillations. This regime is observed in the range of \(V\in \left[ 2.50,\,3.50\right] \) m/s. A typical response at \(V=3.00\) m/s is selected for the parameter identification and depicted in Fig. 5a. The model is able to describe the oscillations accurately, however, there is a small mismatch in the extrema. The PSDs in Fig. 5b show that the dominant frequency is well captured by the model, but the sub- and higher harmonics are in general less strongly present in the model response. This indicates that the shape of the oscillations are not perfectly matching, which is also visible in Fig. 5a. Overall, it is concluded that the model is also able to describe the period-2 limit cycle oscillations rather accurately. The oscillation frequencies of both oscillators reveal an interesting relation, namely the frequency of the first oscillator is exactly twice the frequency of the second oscillator. The difference in oscillation frequency is also visible in the estimated parameters, since \({\tilde{\zeta }}\) is much lower compared to \({\tilde{\beta }}\). Furthermore, \({\tilde{\zeta }}\) is also much lower compared to its values for the limit cycle and quasi-periodic regime, indicating that the second oscillator changed its behaviour significantly to generate period-2 limit cycle oscillations. Besides, the coupling parameter \(\mu _2\) is equal to zero, indicating that the second oscillator is not affected by the first oscillator. Furthermore, the damping constant \({\tilde{\varepsilon }}\) of the second oscillator equals to zero. Since \({\tilde{\varepsilon }}\) and \(\mu _2\) are equal to zero, the second oscillator is able to generate oscillations with a constant amplitude depending on its initialisation. The oscillations of this second generator produce an oscillating damping in the first oscillator through the coupling term. Due to the specific ratio between the oscillation frequencies of both oscillators and the oscillating damping in the first oscillator, the system is able to produce period-2 limit cycle oscillations.

Fig. 5
figure 5

Period-2 limit cycle oscillations of the normalised acoustic velocity at \(V=3.00\) m/s. In a the time-series of the experimental data () and the model () are shown and in b the corresponding PSDs

Full size image

5.5 Estimated parameter values

The relation between the model parameters with the experimental bifurcation parameter can provide some insight in the working of the model and the effect of its model parameters. This clearly reveals which parameters mainly change when the model bifurcates from one regime to an other. As mentioned earlier, the oscillation frequency of the models is mainly determined by the parameters \(\beta \) and \(\zeta \) for the first and second oscillator, respectively. In Fig. 6 the undamped natural frequency of both oscillators is depicted along the dominant frequency of the experimental data. The undamped natural frequency of both oscillators is calculated by

$$\begin{aligned} f_i = \frac{1}{2\pi T_\textrm{ref}}\sqrt{\varPsi _i}, \end{aligned}$$
(16)

with \(\varPsi \in [{\tilde{\beta }}, {\tilde{\zeta }}]\) and the index i denotes the first or second oscillator. Figure 6 reveals that for the limit cycle oscillations (regime II) the natural frequency of both oscillators is roughly similar and show a good correspondence with the frequency of the experimental limit cycle. When the model bifurcates to quasi-periodic oscillations (regime III), the natural frequencies of both oscillators are not equal to each other and to the experimental frequency. The natural frequency of the first oscillator is significantly higher compared to the experimental dominant frequency and the natural frequency of the second oscillator is significantly lower. Hence, in this regime we have two coupled oscillators with significantly different frequencies. These coupled oscillators are able to generate amplitude and frequency modulation. Finally, in the regime with period-2 limit cycle oscillations (regime IV), the natural frequency of the first oscillator is similar to the dominant frequency of the experimental data. The natural frequency of the second oscillator is exactly half of the frequency of the first oscillator. Hence, the coupled oscillators are able to produce period-2 limit cycle when the ratio between both natural frequencies is exactly two.

Fig. 6
figure 6

Frequencies of oscillations against bifurcation parameter V, with the dominant experimental ITA frequency (), the undamped natural frequency of the first oscillator, \(f_1=\frac{1}{2\pi T_\textrm{ref}}\sqrt{{\tilde{\beta }}}\) () and the undamped natural frequency of the second oscillator, \(f_2=\frac{1}{2\pi T_\textrm{ref}}\sqrt{{\tilde{\zeta }}}\) ()

Full size image

The coupling strength between both oscillators depends on the values of \(\mu _1\) and \(\mu _2\). In Fig. 7 their values are shown for different values of the bifurcation parameter V. These results reveal a clear difference of the coupling strength between the different regimes. In regime II with the limit cycle oscillations, the coupling parameters have approximately a similar strength and are all below 1. In the next regime, with quasi-periodic oscillations, the coupling parameters have a significantly higher value compared to the other two regimes. This indicates that in regime III a strong interaction between both oscillators is required to generate the quasi-periodic oscillations with frequency and amplitude modulation. In the last regime, with the period-2 limit cycles, only \(\mu _1\) has non zero values. As already mentioned, this indicates that the second oscillator affects the first one, but not the other way around. The values of \(\mu _1\) are slightly lower compared to regime II. However, this does not necessarily mean that the effect on the dynamics of the first oscillator is weaker, since this is also determined by the amplitude of the states \({\dot{x}}_1\) and \({\dot{x}}_2\).

Fig. 7
figure 7

Parameter values of the coupling parameters \(\mu _1\) () and \(\mu _2\) () for different values of V

Full size image

In the standard Van der Pol oscillator, the amplitude is governed by the ratio \(\sqrt{{\tilde{\delta }}/{\tilde{\alpha }}}\) as explained in Sect. 3. This ratio is calculated for all values for the bifurcation parameter and depicted in Fig. 8. This ratio is small in the region of the limit cycle oscillations and reveals a slightly increasing trend with increasing V. This indicates an increase in amplitude, which was also observed in the experiments as depicted in Fig. 2. When the model enters regime III, a drastic increase of the ratio is observed. Thereafter, ratio decreases with increasing V and remains approximately constant during the last regime. In the experiments, the oscillation amplitude increases with increasing V in regime III. This is not reflected in the ratio, that determines the amplitude in a standard Van der Pol oscillator. This indicates that in regime III the strong coupling between both oscillators plays a dominant role in the determination of the maximal amplitude. Furthermore, the value of the ratio is higher in the regime of period-2 limit cycles compared to the regime of limit cycle oscillations. This is in line with the maxima of the experimentally observed oscillations as shown in Fig. 2.

Fig. 8
figure 8

The ratio \(\sqrt{{\tilde{\alpha }}/{\tilde{\delta }}}\) for different values of V

Full size image

Finally, the damping parameter of the second oscillator \({\tilde{\varepsilon }}\) is depicted in Fig. 9. It is observed that the value of this parameter reveals a slightly increasing trend for the limit cycle oscillations. Furthermore, the trend is approximately similar to the values of the coupling parameters. This is likely due to the possible destabilising effect of the coupling term in the second oscillator, such that the increase in negative damping is compensated by positive damping. In the regime of quasi-periodic oscillations, this damping value is significantly higher compared to the other regimes and shows a decreasing trend for increasing V. Finally, in the regime of period-2 limit cycles this damping vanishes. In this last regime the second oscillator should produce oscillations with a constant amplitude which is only possible when there is no damping in that oscillator, otherwise these oscillations will damp out over time and the first oscillator will no longer produce period-2 limit cycles.

Fig. 9
figure 9

Values of \({\tilde{\varepsilon }}\) for different values of V

Full size image

Overall, the proposed phenomenological model shows a good quantitative match with all datasets corresponding to different values of the experimental bifurcation parameter V. Contrary to the slowly varying experimental bifurcation parameter between different experiments, some model parameters reveal a jump between two distinct regimes of oscillations reflecting the experimentally observed sudden qualitative change of type of oscillations. This may indicate that the proposed phenomenological model do not directly reproduce the structure of, at the moment unknown, the ontological model which may follows from first principle considerations. However, it provides important insights in the essential features that a dynamical model should have to describe all different regimes.

5.6 Comparison with linearly coupled Van der Pol oscillators

Recently, a new nonlinear time-domain model for laminar premixed flames was introduced by Doehner et al. [8]. This model consists of two linearly coupled Van der Pol oscillators. It was calibrated based on external acoustic forcing and mainly describes the effect of acoustic perturbations on the heat-release rate of the flames. However, it is interesting to investigate if this model is also able to describe the self-excited ITA oscillations. Thereto, a parameter estimation of this model is conducted based on the experimental data presented in the previous sections.

The differential equations of the model read as follows:

$$\begin{aligned}&\ddot{z}_1 + \alpha _1 {\dot{z}}_1 + \beta _1 {\dot{z}}_1 z_1^2 + \eta _1 z_1 = \delta _1\left( z_2-z_1\right) +\gamma F, \end{aligned}$$
(17)
$$\begin{aligned}&\ddot{z}_2 +\alpha _2 {\dot{z}}_2 + \beta _2{\dot{z}}_2z_2^2 + \eta _2z_2= -\delta _2\left( z_2-z_1\right) , \end{aligned}$$
(18)
$$\begin{aligned}&\dot{{\tilde{z}}}_2 = {\dot{z}}_2 +\frac{2}{\zeta }\left( z_2-{\tilde{z}}_2\right) . \end{aligned}$$
(19)

Herein, F is the external acoustic forcing, \(z_1\) and \({\dot{z}}_1\) are the state variables of the first oscillator and \(z_2\) and \({\dot{z}}_2\) the state variables of the second oscillator. The notation \({\tilde{z}}\) denotes a time-delayed variable. In this model \(\dot{{\tilde{z}}}_2\) describes the heat-release rate. This model has clear similarities with the model given by Eqs. (4) and (5). Namely, it also consists of two coupled oscillators and the first oscillator also resembles a Van der Pol oscillator. The main difference between both models is the coupling between the oscillators. The model introduced in this paper is characterised by nonlinear coupling between both oscillators, while the model of Doehner et al. [8] has linear coupling. Since we are only considering self-excited oscillations, the external forcing F is set to zero for the parameter estimation routine. Due to the similarities between both models, it is assumed that the state \({\dot{z}}_1\) describes the self-excited acoustic velocity perturbations just upstream of the flames similar as the state \({\dot{x}}_1\) in the model of Eqs. (4) and (5). Hence, to investigate if the model of Eqs. (17)–(19) is able to reproduce the experimentally observed nonlinear oscillations of pure ITA modes, the parameters are estimated such that state \({\dot{z}}_1\) mimics the experimental time-series of \(u'/{\bar{u}}\).

In Doehner et al. [8] the oscillators are chosen to be identical to reduce the model complexity in terms of parameters to estimate. Equations (17)–(19) are equivalent to the model from Doehner et al. [8] for the following parameter constraints, namely \(\alpha _1=\alpha _2\), \(\beta _1=\beta _2\), \(\delta _1=\delta _2\) and \(\eta _1=\eta _2=1\). The latter parameter constraint is obtained for a specific definition of \(T_\textrm{ref}\). In case of positive parameter values, the model of Eqs. (17)–(19) will have a single stable fixed point at \(z_0=[ z_1 \; {\dot{z}}_1 \; z_2 \; {\dot{z}}_2]^\textrm{T}=[ 0 \; 0 \; 0 \; 0]^\textrm{T}\). To let the system exhibit self-excited oscillations, the sign of \(\alpha _1\) is changed in the subsequent analysis.

First, it is investigated if the model with two identical oscillators is able to describe the limit cycle oscillations of regime II. Thereto, the typical time-series of \(V=1.00\) m/s is selected to estimate the model parameters. The result is depicted in Fig. 10. The dominant oscillation frequency is well described by the model. However, the shape of the limit cycle is less accurately captured compared to the model of Eqs. (4) and (5) as shown in Fig. 3. It is concluded that the model with two identical Van der Pol oscillators is not able to describe the asymmetric shape of the limit cycle. Furthermore, it was observed that this model was also not able to describe more complex nonlinear oscillations as the quasi-periodic and period-2 limit cycle oscillations. Hence, the model with two identical linearly coupled Van der Pol oscillators is not able to describe the rich variety of self-excited oscillations produced by an unstable pure ITA mode.

Fig. 10
figure 10

Time-series of limit cycle oscillations of the normalised acoustic velocity at \(V=1.00\) m/s of experimental data () and of model with two identical Van der Pol oscillators ()

Full size image
Fig. 11
figure 11

Time-series of limit cycle oscillations of the normalised acoustic velocity at \(V=1.00\) m/s of experimental data () and of model with two non-identical Van der Pol oscillators ()

Full size image
Table 3 NRMSE for different data sets obtained with the model as introduced in this paper (model I) and the full parametrised model as introduced by Doehner et al. [8] (model II)
Full size table

Next, it is investigated if a model of two non-identical linear coupled Van der Pol oscillators is able to describe the nonlinear oscillations of an unstable ITA mode. Therefore, the same model structure of Eqs. (17)–(19) is used but the requirement that the parameters of both oscillators are need to be similar is relaxed. Note, that also \(\eta _1\) and \(\eta _2\) are not necessarily equal to 1. Firstly, parameters are identified to investigate how accurate the non-identical Van der Pol oscillators can describe the limit cycle oscillations. Therefore, the experimental data corresponding to \(V=1.00\) m/s is used. The result is shown in Fig. 11. Again, the dominant oscillation frequency is well captured by the model. Furthermore, the asymmetric limit cycle shape is accurately described. The performance of the non-identical Van der Pol oscillators in describing the limit cycle oscillations is very well comparable to the results obtained with the non-linearly coupled oscillators as shown in Fig. 3. This is also confirmed by the NRMSE values as given in Table 3, which are approximately similar compared to the results obtained with the nonlinearly coupled oscillators.

Fig. 12
figure 12

Quasiperiodic oscillations of the normalised acoustic velocity at \(V=1.60\) m/s. In a the time-series of the experimental data () and the model of two non-identical Van der Pol oscillators () are shown, in b the corresponding PSDs and in c the instantaneous frequencies

Full size image

Thereafter, the parameters are estimated for a data set of quasi-periodic oscillations obtained with \(V=1.60\) m/s. In Fig. 12a the result is shown. The dominant oscillation frequency is well described and the amplitude modulation is clearly present. In general the maxima are slightly underestimated by the model, while the minima are over estimated. In Fig. 12b the PSDs are depicted, which reveal clear differences between the model and the experiments. The dominant frequency and its sidebands are similarly present, indicating the presence of frequency modulation. However, the higher harmonics with their sidebands are almost absent. Furthermore, the characteristic peak at the low modulation frequency is not produced by the model. The instantaneous frequencies of both time-series are given in Fig. 12c and reveal a frequency modulation with an approximately similar frequency, but a different shape. The frequency modulation in the experimental data is close to symmetrical, while the modulation of the model is highly asymmetrical. When the amplitude of the time-series is minimal, the frequency reveals a narrow peak which exceeds the maximum frequency of the experimental data. During the rest of the amplitude modulation, the frequency remains almost constant at a value that is significantly higher than the minimal frequency observed in the experimental data. Hence, it is concluded that the model of two linearly coupled non-identical Van der Pol oscillators is not able to describe the quasi-periodic oscillations accurately. The NRMSE values obtained by this model are also significantly higher compared to the model as introduced in Sect. 3. This also shows that the linearly coupled non-identical Van der Pol oscillators have a lower capability of describing the quasi-periodic oscillations.

Finally, the ability of the non-identical oscillator model to describe the period-2 limit cycle oscillations is investigated. Thereto, the parameters are identified based on a data set obtained with \(V=3.00\) m/s. The result is shown in Fig. 13 and reveals a good agreement between the model response and the experimental time-series. The dominant oscillation frequency is described accurately. Comparable to the results obtained with the model of Eqs. (4) and (5), the shape of the oscillations is captured accurately, but there is a small mismatch in the extrema.

Based on the above results, it is concluded that a model of two coupled non-identical oscillators is able to describe quasi-periodic and period-2 limit cycle oscillations. However, to describe the experimentally observed quasi-periodic oscillations accurately including the correct frequency modulation and the peak at low frequency, the nonlinear coupling between the oscillators turns out to be necessary. Nonlinear, asymmetric functions, such as \(\varPhi (x)\), are able to demodulate amplitude modulated signals and thus can extract the low frequent modulation frequency from such a signal. When both oscillators produce oscillations with a small difference in frequency, this can lead to an amplitude modulated signal due to the coupling. When this modulated signal is fed into the function \(\varPhi \), it is demodulated and the low frequent oscillation is extracted from the signal. Hence, this can produce a distinct peak at this low modulation frequency in the frequency spectrum of the model response.

Fig. 13
figure 13

Time-series of period-2 limit cycle oscillations of the normalised acoustic velocity at \(V=3.00\) m/s of experimental data () and of model with two non-identical Van der Pol oscillators ()

Full size image

6 Discussion

A model of two coupled oscillators provides a promising model structure to describe the flame dynamics. Such a model is of low-order, which makes it useful for time-domain simulations. Such simulations are important in the design of a combustion application and the design of instability mitigation strategies. In this paper it is shown that a two coupled oscillator model is able to describe and predict the self-excited nonlinear oscillations of an unstable ITA mode, which reflects the self-excited flame dynamics. In Doehner et al. [8] it is shown that such a model is also capable of describing the acoustically forced flame dynamics. Hence, with a model of two coupled oscillators both the self-excited and the forced flame dynamics can be described accurately. Despite that both mentioned models are coupled oscillators, there are some important differences.

The main difference between both models is the coupling. The coupling in the model of Doehner et al. [8] is on the displacement level and is linear. In the model introduced in this paper, the coupling is on the level of velocity and is nonlinear. Both models are capable of describing the limit cycle and period-2 limit cycle oscillations rather accurate. However, there is a significant difference in their ability to produce the quasi-periodic oscillations with the amplitude and frequency modulation. Only the model with the nonlinear coupling is able to produce a similar frequency modulation and frequency spectrum including the peak at the low modulation frequency as observed in the experiments. The presence of the peak at the low frequency spectrum is likely due to the demodulation of the asymmetric coupling in the second oscillator. Hence, the nonlinear coupling is important in describing all observed regimes accurately. Furthermore, the model as introduced in this paper consists of a Van der Pol oscillator coupled to a linear damped oscillator, while the model of Doehner et al. [8] consists of two coupled Van der Pol oscillators. Van der Pol oscillators are able to produce self-excited oscillations, while linear damped oscillators cannot. Hence, coupled Van der Pol oscillators provides a bit more flexibility in describing the period-2 limit cycle oscillations.

The proposed phenomenological model provides an accurate description of the observed nonlinear regimes and a solid base to continue its development and include the heat-release rate as a state variable, leading to a time-domain description of the relationship between acoustic velocity perturbations and heat-release rate perturbations. This extension of the time-domain model could for example be realised by a novel technique named sparse identification of nonlinear dynamics [5]. When the time-domain description of the relation between the acoustic velocity and heat-release perturbations is established, this model can be coupled to an acoustic domain and used for the (stability) analysis of a complete thermo-acoustic system.

7 Conclusions

In this paper, a phenomenological model is proposed that is able to describe the nonlinear self-excited nonlinear dynamics of pure ITA modes. This model consists of two nonlinearly coupled oscillators, where the first represents a Van der Pol oscillator and the second one a standard mass-damper-spring oscillator. In an experimental bifurcation analysis, it was observed that the fully premixed flames reveal subsequently four different attractors, namely a fixed point and limit cycle, quasi-periodic and period-2 limit cycle oscillations. For all four regimes, model parameters are identified such that the presented phenomenological model is able to qualitatively and quantitatively describe the experimentally observed nonlinear attractors. The regime with quasi-periodic oscillations is characterised by low frequency amplitude and frequency modulation, which phenomena are both accurately captured by the model. A comparable model, proposed by Doehner et al. [8], is also investigated. This model was able to describe the limit cycle and period-2 limit cycle accurately, however, it was not able to describe quasi-periodic oscillations with a similar frequency spectrum. It is believed that this is mainly due to the difference in the coupling between both oscillators, which is linear in the model of Doehner et al. [8] and nonlinear in the model of this paper. Hence, the model with nonlinear coupling, as presented in this paper, provides a promising model structure to represent the internal nonlinear flame dynamics.

Although the presented phenomenological model is able to describe the nonlinear flame dynamics accurately, it does not yet provide a full description of acoustic behaviour of the flames. Therefore, the model should be extended such that it can describe the heat-release rate oscillations as well. The extension of this model is an interesting question for future research. Other interesting questions are how to couple this model to an acoustic domain and what is the physical meaning of the states and model parameters?