Skip to main content
SpringerLink
Log in

A hybrid averaging and harmonic balance method for weakly nonlinear asymmetric resonators

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

Models for nonlinear vibrations commonly employ polynomial terms that arise from series expansions about an equilibrium point. The analysis of symmetric systems with cubic stiffness terms is very common, and the inclusion of asymmetric quadratic terms is known to modify the effective cubic nonlinearity in weakly nonlinear systems. When using low (second, in this case)-order perturbation methods, the net effect in these cases is found to be a monotonic dependence of the free vibration frequency on the amplitude squared, with a single term that depends on the coefficients of the quadratic and cubic terms. However, in many applications, such a monotonic dependence is not observed, necessitating the use of techniques for strongly nonlinear systems, or the inclusion of higher-order terms and perturbation methods in weakly nonlinear formulations. In either case, the analysis involves very tedious and/or numerical approaches for determining the system response. In the present work, we propose a method that is a hybrid of the methods of averaging and harmonic balance, which provides, with relatively straightforward calculations, good approximations for the free and forced vibration response of weakly nonlinear asymmetric systems. For free vibration, it captures the correct amplitude–frequency dependence, including cases of non-monoticity. The method can also be used to determine the steady-state response of damped, harmonically driven vibrations, including information about stability. The method is described, and general results are obtained for an asymmetric system with up to quintic nonlinear terms. The results are applied to a numerical example and validated using simulations. This approach will be useful for analyzing a variety of system models with polynomial nonlinearities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability

Data will be made available by reasonable requests.

Notes

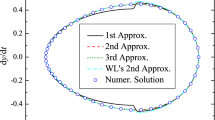
  1. Note that the exact solution of the free oscillation given in Eq. (11) of Ref. [41] is obtained from an elliptic integral of the conservative system, and is expressed in terms of the total energy of the system \(E_\textrm{tot}\) rather than in terms of the amplitude of oscillation a. However, the relation between these two quantities is simply \(E_\textrm{tot}=\omega _0^2x_\textrm{max}^2/2+\alpha _2x_\textrm{max}^3/3+\alpha _3x_\textrm{max}^4/4\), where \(x_\textrm{max}=a+\sum _{k=0,k\ne 1}^{5}a_k\), and therefore, we can easily compute \(\omega _\textrm{exact}\) in terms of a.

References

  1. Tiwari, S., Candler, R.N.: Using flexural MEMS to study and exploit nonlinearities: a review. J. Micromech. Microeng. 29(8), 083002 (2019)

    Article  Google Scholar 

  2. Chakraborty, G., Jani, N.: Nonlinear dynamics of resonant microelectromechanical system (mems): a review. Mech. Sci. (2021). https://doi.org/10.1007/978-981-15-5712-5_3

    Article  Google Scholar 

  3. Shoshani, O., Shaw, S.W.: Resonant modal interactions in micro/nano-mechanical structures. Nonlinear Dyn. 104(3), 1801–1828 (2021)

    Article  Google Scholar 

  4. Bachtold, A., Moser, J., Dykman, M.: Mesoscopic physics of nanomechanical systems. arXiv preprint arXiv:2202.01819 (2022)

  5. Touzé, C., Vizzaccaro, A., Thomas, O.: Model order reduction methods for geometrically nonlinear structures: a review of nonlinear techniques. Nonlinear Dyn. 105(2), 1141–1190 (2021)

    Article  Google Scholar 

  6. Rosenberg, S., Shoshani, O.: Amplifying the response of a driven resonator via nonlinear interaction with a secondary resonator. Nonlinear Dyn. 105(2), 1427–1436 (2021)

    Article  Google Scholar 

  7. Miller, N.J., Shaw, S.W., Dykman, M.: Suppressing frequency fluctuations of self-sustained vibrations in underdamped nonlinear resonators. Phys. Rev. Appl. 15(1), 014024 (2021)

    Article  Google Scholar 

  8. Tepsic, S., Gruber, G., Møller, C., Magén, C., Belardinelli, P., Hernández, E.R., Alijani, F., Verlot, P., Bachtold, A.: Interrelation of elasticity and thermal bath in nanotube cantilevers. Phys. Rev. Lett. 126(17), 175502 (2021)

    Article  Google Scholar 

  9. Krakover, N., Ilic, B.R., Krylov, S.: Micromechanical resonant cantilever sensors actuated by fringing electrostatic fields. J. Micromech Microeng. 32(5), 054001 (2022)

    Article  Google Scholar 

  10. Defoort, M., Hentz, S., Shaw, S.W., Shoshani, O.: Amplitude stabilization in a synchronized nonlinear nanomechanical oscillator. Commun. Phys. 5(1), 1–7 (2022)

    Article  Google Scholar 

  11. Perl, T., Maimon, R., Krylov, S., Shimkin, N.: Control of vibratory MEMS gyroscope with the drive mode excited through parametric resonance. J. Vib. Acoust. (2021). https://doi.org/10.1115/1.4050351

    Article  Google Scholar 

  12. Xu, Q., Younis, M.I.: Micromachined threshold inertial switches: a review. J. Micromech. Microeng. (2022). https://doi.org/10.1088/1361-6439/ac6192/meta

    Article  Google Scholar 

  13. Yaqoob, U., Jaber, N., Alcheikh, N., Younis, M.I.: Selective multiple analyte detection using multi-mode excitation of a MEMS resonator. Sci. Rep. 12(1), 1–14 (2022)

    Article  Google Scholar 

  14. Rosłoń, I.E., Japaridze, A., Steeneken, P.G., Dekker, C., Alijani, F.: Probing nanomotion of single bacteria with graphene drums. Nat. Nanotechnol. 17, 1–6 (2022)

    Article  Google Scholar 

  15. Lee, J., Shaw, S.W., Feng, P.X.L.: Giant parametric amplification and spectral narrowing in atomically thin MoS2 nanomechanical resonators. Appl. Phys. Rev. 9(1), 011404 (2022)

    Article  Google Scholar 

  16. Mistry, K., Nguyen, V.H., Arabi, M., Ibrahim, K.H., Asgarimoghaddam, H., Yavuz, M., Muñoz-Rojas, D., Abdel-Rahman, E., Musselman, K.P.: Highly sensitive self-actuated zinc oxide resonant microcantilever humidity sensor. Nano Lett. (2022). https://doi.org/10.1021/acs.nanolett.1c04378

    Article  Google Scholar 

  17. Potekin, R., Asadi, K., Kim, S., Bergman, L.A., Vakakis, A.F., Cho, H.: Ultrabroadband microresonators with geometrically nonlinear stiffness and dissipation. Phys. Rev. Appl. 13(1), 014011 (2020)

    Article  Google Scholar 

  18. Houri, S., Asano, M., Okamoto, H., Yamaguchi, H.: Self-sustained libration regime in nonlinear microelectromechanical devices. Phys. Rev. Appl. 16(6), 064015 (2021)

    Article  Google Scholar 

  19. Miller, J.M., Gomez-Franco, A., Shin, D.D., Kwon, H.K., Kenny, T.W.: Amplitude stabilization of micromechanical oscillators using engineered nonlinearity. Phys. Rev. Res. 3(3), 033268 (2021)

    Article  Google Scholar 

  20. Czaplewski, D.A., Strachan, S., Shoshani, O., Shaw, S.W., López, D.: Bifurcation diagram and dynamic response of a MEMS resonator with a 1: 3 internal resonance. Appl. Phys. Lett. 114(25), 254104 (2019)

    Article  Google Scholar 

  21. Keşkekler, A., Shoshani, O., Lee, M., van der Zant, H.S., Steeneken, P.G., Alijani, F.: Tuning nonlinear damping in graphene nanoresonators by parametric-direct internal resonance. Nat. Commun. 12(1), 1–7 (2021)

    Article  Google Scholar 

  22. Asadi, K., Yeom, J., Cho, H.: Strong internal resonance in a nonlinear, asymmetric microbeam resonator. Microsyst. Nanoeng. 7(1), 1–15 (2021)

  23. Kacem, N., Hentz, S., Pinto, D., Reig, B., Nguyen, V.: Nonlinear dynamics of nanomechanical beam resonators: improving the performance of NEMS-based sensors. Nanotechnology 20(27), 275501 (2009)

    Article  Google Scholar 

  24. Kacem, N., Hentz, S.: Bifurcation topology tuning of a mixed behavior in nonlinear micromechanical resonators. Appl. Phys. Lett. 95(18), 183104 (2009)

    Article  Google Scholar 

  25. Sobreviela, G., Vidal-Álvarez, G., Riverola, M., Uranga, A., Torres, F., Barniol, N.: Suppression of the Af-mediated noise at the top bifurcation point in a MEMS resonator with both hardening and softening hysteretic cycles. Sens. Actuator A Phys. 256, 59–65 (2017)

    Article  Google Scholar 

  26. Polunin, P.M., Yang, Y., Dykman, M.I., Kenny, T.W., Shaw, S.W.: Characterization of MEMS resonator nonlinearities using the ringdown response. J. Microelectromech. Syst. 25(2), 297–303 (2016)

    Article  Google Scholar 

  27. Huang, L., Soskin, S., Khovanov, I., Mannella, R., Ninios, K., Chan, H.B.: Frequency stabilization and noise-induced spectral narrowing in resonators with zero dispersion. Nat. Commun. 10(1), 1–10 (2019)

    Article  Google Scholar 

  28. Qiao, W., Guo, T., Kang, H., Zhao, Y.: Softening-hardening transition in nonlinear structures with an initial curvature: a refined asymptotic analysis. Nonlinear Dyn. 107(1), 357–374 (2022)

    Article  Google Scholar 

  29. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, vol. 42. Springer, Cham (2013)

    MATH  Google Scholar 

  30. Dykman, M., Mannella, R., McClintock, P.V., Soskin, S.M., Stocks, N.: Noise-induced narrowing of peaks in the power spectra of underdamped nonlinear oscillators. Phys. Rev. A 42(12), 7041 (1990)

    Article  Google Scholar 

  31. Soskin, S.M., Mannella, R., McClintock, P.V.E.: Zero-dispersion phenomena in oscillatory systems. Phys. Rep. 373(4–5), 247–408 (2003)

    Article  Google Scholar 

  32. Landau, L., Lifshitz, E.: Mechanics: Volume 1. Elsevier, New York (1982)

    Google Scholar 

  33. Nayfeh, A., Mook, D.: Nonlinear Oscillations. Wiley, New York (1995)

    Book  MATH  Google Scholar 

  34. Krack, M., Gross, J.: Harmonic Balance for Nonlinear Vibration Problems. Springer, Cham (2019)

    Book  MATH  Google Scholar 

  35. Cochelin, B., Vergez, C., Karkar, S.: Manlab, an Interactive Series-Expansion Approach for Continuation-Focus on Periodic Solutions. Galway, ESMC (2009)

    Google Scholar 

  36. Košata, J., del Pino, J., Heugel, T.L., Zilberberg, O.: HarmonicBalance. jl: A Julia suite for nonlinear dynamics using harmonic balance. arXiv preprint arXiv:2202.00571 (2022)

  37. Shoshani, O., Dykman, M.I., Shaw, S.W.: Tuning linear and nonlinear characteristics of a resonator via nonlinear interaction with a secondary resonator. Nonlinear Dyn. 99(1), 433 (2020)

  38. Nayfeh, A.H.: Perturbation Methods. Wiley, New York (2008)

  39. Lifshitz, R., Cross, M.C.: Nonlinear dynamics of nanomechanical and micromechanical resonators. In: Schuster, H.G. (ed.) Reviews of Nonlinear Dynamics and Complexity. Wiley, New York (2008)

  40. Volvert, M., Kerschen, G.: Phase resonance nonlinear modes of mechanical systems. J. Sound Vib. 511, 116355 (2021)

    Article  Google Scholar 

  41. Rosenberg, S., Shoshani, O.: Zero-dispersion point in curved micro-mechanical beams. Nonlinear Dyn. 107(1), 1–14 (2022)

  42. Wang, S., Tang, B.: A comparative study of parameter identification methods for asymmetric nonlinear systems with quadratic and cubic stiffness. Sensors 22(15), 5854 (2022)

Download references

Funding

This work is supported by BSF under Grant No. 2018041. SWS is also supported by NSF grant CMMI-1662619. OS is also supported by the Pearlstone Center of Aeronautical Engineering Studies at Ben-Gurion University of the Negev. S.R. acknowledges the financial support of the Kreitman school of advanced graduate studies at Ben-Gurion University of the Negev under the Negev-Tzin Scholarship. Just prior to submission, we learned of a concurrent formulation of a very similar technique by Mark Dykman that will be used in a forthcoming paper; discussions with him helped to clarify and expand our understanding of the approach.

Author information

Authors and Affiliations

  1. Florida Institute of Technology, 150 W University Blvd, Melbourne, FL, USA

    Steven W. Shaw

  2. Ben-Gurion University of the Negev, 84105, Beer Sheva, Israel

    Sahar Rosenberg & Oriel Shoshani

Authors
  1. Steven W. Shaw
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sahar Rosenberg
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Oriel Shoshani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Steven W. Shaw.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Transient dynamics

Transient dynamics

Here, we demonstrate the main shortcoming of the proposed approach, namely its inability to correctly capture the full transient dynamics. To this end, we numerically integrated both Eq. (2) and Eqs. (8)-(9) with identical initial conditions and compared their transient dynamics. To extract the amplitude a(t) and phase \(\phi (t)\) of the fundamental harmonic from Eq. (2), we heterodyned the numerically obtained signal x(t) with the in-phase and quadrature components at the drive frequency \(\omega \), and passed the mixed signals through a band-pass filter to remove the overtones and DC components [26]. We then use the resulting slowly-varying (with respect to \(\omega ^{-1}\)) quadratures of the fundamental harmonics, u(t) and v(t), to construct the amplitude and phase. The top panel of Fig. 4 depicts this process. The simulation results shown in the bottom panel of Fig. 4 clearly demonstrate that the transient dynamics from our analysis [Eqs. (8)-(9)] are distinctly different from those of the original system [Eq. (2)].

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shaw, S.W., Rosenberg, S. & Shoshani, O. A hybrid averaging and harmonic balance method for weakly nonlinear asymmetric resonators. Nonlinear Dyn 111, 3969–3979 (2023). https://doi.org/10.1007/s11071-022-08065-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-08065-3

Keywords

Search

Navigation