1 Introduction

Microelectromechanical systems (MEMS) [1,2,3] have been drawing significant attention over the last decade thanks to their small size, low power consumption, high sensitivity, and low cost [4]. These devices have widespread important applications in environmental monitoring [5], air quality measurement [6, 7], mass sensors [8, 9], pressure sensors [10], communications [11, 12], logic/memory [13, 14], and energy harvesting [15,16,17]. Electrostatically driven resonators have been the subject of ongoing research since the early work of Nathanson et al. [18]. The use of the electrostatic force is to drive the MEMS resonators statically or dynamically in the linear or nonlinear regimes. Electrostatically actuated MEMS resonators were proposed for various applications such as tunable resonators [19], synchronisation [20], sensing [21, 22], and micromirrors [23].

Commonly, these MEMS resonators consist of a movable electrode and a fixed electrode, mainly based on slender silicon microbeams. The movable electrode is mainly modelled as a microbeam (whose length is much higher than its width and thickness) deflecting towards the fixed electrode as applying a bias voltage [24]. A sudden collapse into the fixed electrode, also known as the pull-in instability, occurs if the voltage exceeds a critical value. The static and dynamic behaviours were investigated in depth in the literature theoretically and experimentally due to the continuously increasing exploitation of these microsystems [19, 24,25,26,27,28]. Analysing the behaviour of these resonators is commonly based on the classical model (Euler–Bernoulli beam theory) or the nonclassical mechanical model of the beam.

The main difficulty of the theoretical modelling of these movable structures is the accurate prediction of the nonlinear vibration of these resonators as driven electrostatically, which is crucial for various potential applications [29,30,31]. One of the key factors to be considered in modelling MEMS resonators is damping, which can be intrinsic, such as thermoelastic [32,33,34,35], or extrinsic, such as squeeze film [33, 36,37,38,39,40,41,42,43,44] damping. Damping lowers the quality factor of MEMS resonators affecting adversely their performance, making the quality factor a key parameter design for a wide range of applications such as timing and sensing. More recently, Alcheikh et al. [45] investigated the effect of air damping on the quality factor of in-plane nano- and microresonators actuated by two stationary electrodes (for actuation and sensing).

On the other hand, as the oscillation amplitude increases, the energy dissipation tends to deviate from the linear viscous dissipation and start to vary nonlinearly. The nonlinear energy dissipation (or nonlinear damping) has drawn specific attention in the last decade. For instance, Amabili [46,47,48] studied the nonlinear damping in large-amplitude vibrations of rectangular plates, both theoretically and experimentally. Li and Shaw [49] examined the effect of nonlinear damping in the dynamic response of a single-degree-of-freedom system subject to both direct and parametric excitations. Croy et al. [50] proposed and studied a microscopic mechanism for energy dissipation in electrically actuated nanomechanical resonators; they found that the coupling between flexural modes and in-plane phonons results in nonlinear damping for out-of-plane oscillations. An in-depth theoretical and experimental investigation highlighting the effect of different damping sources (e.g. thermoelastic, anchor losses, and Akhiezer) on the quality factor of MEMS silicon resonators was conducted by Kenny and co-authors [51,52,53]. More recently, nonlinear damping in graphene nanoresonators motivated several interesting studies [50, 54,55,56,57,58]. For instance, Eichler et al. [56] studied the damping of mechanical resonators based on graphene membranes and carbon nanotubes and found that damping strongly and nonlinearly depends on the amplitude of motion. Keşkekler et al. [58] studied experimentally nonlinear damping in graphene nanoresonators; they investigated the parametric resonance tuning of a graphene nanodrum by monitoring nonlinear dissipation over a wide frequency range. Furthermore, Dolleman et al. [57] investigated multimode parametric resonance in opto-thermally excited graphene membranes and showed that nonlinear damping is essential for examining their large-amplitude parametric resonance. Nonlinear damping was used recently for different applications in sensing [59], energy harvesting [60], vibration isolation [61, 62], and was shown experimentally for graphene [58].

Despite these valuable studies, there is still no comprehensive study on nonlinear damping in in-plane MEMS resonators with relatively large gaps. The present study conducts a thorough investigation on the nonlinear damping in in-plane micromachined electromechanical resonators using carefully conducted experiments and an accurate nonlinear theoretical model. It should be noted that the main aim of this study is to develop a damping model that accurately captures MEMS resonators' nonlinear response without focusing on or specifically identifying the sources of nonlinear dissipation (e.g. thermoelastic, viscoelastic, anchor losses). More specifically, detailed procedures are provided for calibrating different nonlinear damping models using minimum number of experimental frequency responses, which can be applied to any micro-/nano-resonator irrespective of the type of nonlinear damping. The experimental set-up is explained in Sect. 2, followed by a detailed nonlinear model development in Sect. 3. The theoretical and experimental results are presented for various cases and discussed in detail in Sect. 4. Finally, a summary of the key findings is presented in Sect. 5.

2 Experimental set-up

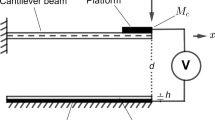
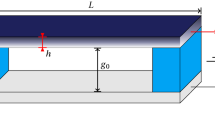
The clamped–clamped in-plane microbeam under consideration (shown in Fig. 1a) is fabricated from SOI (Silicon on Insulator) wafers with a highly conductive Si device layer. The geometric parameters of the microbeam are given in Table 1.

Fig. 1
figure 1

a Optical image of the electrostatically actuated in-plane microbeam. b A 3D schematic of the microbeam. c Experimental set-up

Full size image
Table 1 Geometrical properties of the silicon clamped–clamped microbeam
Full size table

To excite the microbeam, the resonator is actuated electrostatically by a DC polarisation voltage \({V}_{\mathrm{DC}}\) and an AC harmonic voltage of amplitude \({V}_{\mathrm{AC}}\) and frequency \(\omega \). The resonance frequencies and the frequency response curves of the resonating microbeam were measured experimentally using the stroboscopic video microscopy from Polytec, as shown in Fig. 1c. To minimise the effect of squeeze film damping, the microbeam is placed in a vacuum chamber with a pressure of 950mTorr set throughout the experiments. Even though the microbeam is actuated by one stationary electrode, one should note that the microbeam is sandwiched between two electrodes, as shown in Fig. 1a. The damping models are considered in a general way to capture any dissipation in the system, either structural or those associated with the airgap.

3 System model development

In this section, the nonlinear equation of motion for the MEMS resonator under consideration is derived using the Euler–Bernoulli beam theory. More specifically, due to the clamped–clamped configuration of the microbeam, the midplane-stretching nonlinearity is considered. This study utilises a Kelvin–Voigt model, resulting in a nonlinear damping mechanism due to the presence of geometric nonlinearity. Apart from the Kelvin–Voigt damping, a general nonlinear damping mechanism (for the transverse motion) is modelled as well. These damping mechanisms will be examined in detail in Sect. 4.

Based on the Kelvin–Voigt model, the stress–strain relationship is given by:

$$ \sigma_{xx} = E\varepsilon_{xx} + \eta \partial_{t} \varepsilon_{xx} , $$
(1)

where \(E\) is the microbeam’s Young’s modulus and \(\eta\) is its material damping coefficient.

Denoting the longitudinal and transverse displacements by \(u\) and \(w\), respectively, and accounting for the midplane-stretching nonlinearity, the axial strain can be formulated as:

$$ \varepsilon_{xx} = \partial_{x} u + \frac{1}{2}\left( {\partial_{x} w} \right)^{2} - z\partial_{xx} w. $$
(2)

The variation of the potential energy of the microbeam and the virtual work of the viscous component of the axial stress are expressed as:

$$ \delta \Pi = \mathop \int \limits_{0}^{L} \mathop \int \limits_{A} E\varepsilon_{xx} \delta \varepsilon_{xx} {\text{d}}A{\text{d}}x, $$
(3)
$$ \delta W_{V} = - \mathop \int \limits_{0}^{L} \mathop \int \limits_{A} \eta \partial_{t} \varepsilon_{xx} \delta \varepsilon_{xx} {\text{d}}A{\text{d}}x, $$
(4)

in which \(\delta\) is the variational operator. The variation of the kinetic energy of the microbeam is given by:

$$ \delta K = \rho A\mathop \smallint \limits_{0}^{L} \left[ {\partial_{t} u\delta \left( {\partial_{t} u} \right) + \partial_{t} w\delta \left( {\partial_{t} w} \right)} \right]{\text{d}}x, $$
(5)

where \(\rho \) is the mass density and \(A\) is the cross-sectional area of the microbeam.

The bridge resonator is actuated through the electrostatic capacitance load, which is modelled using the Meijs–Fokkema formula [63] given by

$$ f_{e} = \frac{1}{2}\varepsilon V^{2} \left[ {\frac{b}{{\left( {d - w} \right)^{2} }} + 0.265\frac{{b^{\frac{1}{4}} }}{{\left( {d - w} \right)^{\frac{5}{4}} }} + 0.53\frac{{h^{\frac{1}{2}} }}{{\left( {d - w} \right)^{\frac{3}{2}} }}} \right], $$
(6)

in which \(V={V}_{\text{DC}}+{V}_{\text{AC}}\text{cos}\left(\omega t\right)\). The Meijs–Fokkema formula accounts for the fringing field effect via two additional terms (i.e. the second and third terms in Eq. (6)) and provides reliable predictions with less than 2% deviation from the results of a finite element model, for the case when b/d ≥ 1 and 0.1 ≤ h/d ≤ 4 [63]. As such, the virtual work of the electrostatic load can be formulated as:

$$ \delta W_{E} = \mathop \smallint \limits_{0}^{L} \frac{1}{2}\varepsilon \left( {V_{{{\text{DC}}}} + V_{{{\text{AC}}}} \cos \left( {\omega t} \right)} \right)^{2} \left[ {\frac{b}{{\left( {d - w} \right)^{2} }} + 0.265\frac{{b^{\frac{1}{4}} }}{{\left( {d - w} \right)^{\frac{5}{4}} }} + 0.53\frac{{h^{\frac{1}{2}} }}{{\left( {d - w} \right)^{\frac{3}{2}} }}} \right]\delta w{\text{d}}x, $$
(7)

where \(\varepsilon \) is the medium’s permittivity.

Substituting Eqs. (3–5) and Eq. (7) into the generalised Hamilton’s principle, neglecting the longitudinal inertia, and taking into account the work of a general nonlinear cubic damping mechanism for \(w\)

$$ \delta W_{D} = - \mathop \int \limits_{0}^{L} \left[ {c_{1} \partial_{t} w + c_{2} \partial_{t} w\left| {\partial_{t} w} \right| + c_{3} \left( {\partial_{t} w} \right)^{3} } \right] \delta w{\text{d}}x, $$
(8)

yield the following nonlinear equation governing the transverse motion of the MEMS resonator:

$$ \rho A\partial_{tt} w + c_{1} \partial_{t} w + c_{2} \partial_{t} w\left| {\partial_{t} w} \right| + c_{3} \left( {\partial_{t} w} \right)^{3} + EI\partial_{xxxx} w + \eta I\partial_{txxxx} w - \frac{EA}{{2L}}\partial_{xx} w\mathop \int \limits_{0}^{L} \left( {\partial_{x} w} \right)^{2} {\text{d}}x - \frac{\eta A}{{2L}}\partial_{xx} w\mathop \int \limits_{0}^{L} 2\partial_{x} w\partial_{tx} w{\text{d}}x - \frac{1}{2}\varepsilon \left( {V_{{{\text{DC}}}} + V_{{{\text{AC}}}} \cos \left( {\omega t} \right)} \right)^{2} \left[ {\frac{b}{{\left( {d - w} \right)^{2} }} + 0.265\frac{{b^{\frac{1}{4}} }}{{\left( {d - w} \right)^{\frac{5}{4}} }} + 0.53\frac{{h^{\frac{1}{2}} }}{{\left( {d - w} \right)^{\frac{3}{2}} }}} \right] = 0. $$
(9)

Defining the following dimensionless quantities

$$ \hat{x} = \frac{x}{L}, \hat{w} = \frac{w}{d}, \alpha_{1} = \frac{{Ad^{2} }}{2I}, \eta_{d} = \frac{\eta }{ET}{, }\tau = \frac{t}{T}, {\Omega } = \omega T,c_{d}^{\left( 1 \right)} = \frac{{c_{1} L^{4} }}{EIT},c_{d}^{\left( 2 \right)} = \frac{{c_{2} L^{4} d}}{{EIT^{2} }},\;c_{d}^{\left( 3 \right)} = \frac{{c_{3} L^{4} d^{2} }}{{EIT^{3} }},\beta_{1} = \frac{b}{d},\beta_{2} = \frac{b}{h} , $$
(10)

where \(T = L^{2} \sqrt {\rho A/\left( {EI} \right)}\), and defining the coefficient of the electrostatic load term as \(\alpha_{2} = \varepsilon bL^{4} /\left( {2EId^{3} } \right)\), the dimensionless equation of motion of the MEMS resonator can be written as:

$$ \begin{gathered} \partial_{\tau \tau } \hat{w} + c_{d}^{\left( 1 \right)} \partial_{\tau } \hat{w} + c_{d}^{\left( 2 \right)} \partial_{\tau } \hat{w}\left| {\partial_{\tau } \hat{w}} \right| + c_{d}^{\left( 3 \right)} \left( {\partial_{\tau } \hat{w}} \right)^{3} + \partial_{{\hat{x}\hat{x}\hat{x}\hat{x}}} \hat{w} + \eta_{d} \partial_{{\tau \hat{x}\hat{x}\hat{x}\hat{x}}} \hat{w} - \alpha_{1} \partial_{{\hat{x}\hat{x}}} \hat{w}\mathop \int \limits_{0}^{1} \left( {\partial_{{\hat{x}}} \hat{w}} \right)^{2} {\text{d}}\hat{x} \hfill \\ - \alpha_{1} \eta_{d} \partial_{{\hat{x}\hat{x}}} \hat{w}\mathop \int \limits_{0}^{1} 2\partial_{{\hat{x}}} \hat{w} \partial_{{\tau \hat{x}}} \hat{w}{\text{d}}\hat{x} - \alpha_{2} \left[ {V_{{{\text{DC}}}} + V_{{{\text{AC}}}} \cos \left( {{\Omega }\tau { }} \right)} \right]^{2} \left[ {\frac{1}{{\left( {1 - \hat{w}} \right)^{2} }} + 0.265\frac{1}{{\beta_{1}^{\frac{3}{4}} \left( {1 - \hat{w}} \right)^{\frac{5}{4}} }} + 0.53\frac{1}{{\beta_{1}^{\frac{1}{2}} \beta_{2}^{\frac{1}{2}} \left( {1 - \hat{w}} \right)^{\frac{3}{2}} }}} \right] = 0 \hfill \\ \end{gathered} $$
(11)

To solve Eq. (11) numerically, first it needs to be discretised in the spatial domain and reduced to a set of nonlinear ordinary differential equations (ODEs). To this end, the transverse displacement is defined as:

$$ \hat{w}\left( {\hat{x},\tau } \right) = \mathop \sum \limits_{k = 1}^{N} {\Xi }_{k} \left( {\hat{x}} \right)q_{k} \left( \tau \right), $$
(12)

where \({q}_{k}(\tau )\) denotes the kth unknown time-dependent generalised coordinate for the transverse motion and \({\Xi }_{k}(\widehat{x})\) represents the corresponding dimensionless eigenfunction for a linear clamped–clamped beam. Next, the finite series expansion defined for \(\widehat{w}\) in Eq. (12) is substituted into Eq. (11), and then, the Galerkin method is applied resulting in:

$$ \begin{gathered} \mathop \sum \limits_{k = 1}^{N} \left( {\partial_{\tau \tau } q_{k} \left( \tau \right) + c_{d}^{\left( 1 \right)} \partial_{\tau } q_{k} \left( \tau \right)} \right)\left( {\mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right){\Xi }_{k} \left( {\hat{x}} \right){\text{d}}\hat{x}} \right) + \mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right)\left( {c_{d}^{\left( 2 \right)} \mathop \sum \limits_{k = 1}^{N} {\Xi }_{k} \left( {\hat{x}} \right)\partial_{\tau } q_{k} \left( \tau \right)\left| {\mathop \sum \limits_{k = 1}^{N} {\Xi }_{k} \left( {\hat{x}} \right)\partial_{\tau } q_{k} \left( \tau \right)} \right|} \right){\text{d}}\hat{x} \hfill \\ + c_{d}^{\left( 3 \right)} \mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l = 1}^{N} \mathop \sum \limits_{m = 1}^{N} \partial_{\tau } q_{k} \left( \tau \right)\partial_{\tau } q_{l} \left( \tau \right)\partial_{\tau } q_{m} \left( \tau \right)\left( {\mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right){\Xi }_{k} \left( {\hat{x}} \right){\Xi }_{l} \left( {\hat{x}} \right){\Xi }_{m} \left( {\hat{x}} \right){\text{d}}\hat{x}} \right) + \mathop \sum \limits_{k = 1}^{N} \left( {q_{k} \left( \tau \right) + \eta_{d} \partial_{\tau } q_{k} \left( \tau \right)} \right)\left( {\mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right)\partial_{{\hat{x}\hat{x}\hat{x}\hat{x}}} {\Xi }_{k} \left( {\hat{x}} \right){\text{d}}\hat{x}} \right) \hfill \\ - \alpha_{1} \mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l = 1}^{N} \mathop \sum \limits_{m = 1}^{N} q_{k} \left( \tau \right)q_{l} \left( \tau \right)q_{m} \left( \tau \right)\left( {\mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right)\partial_{{\hat{x}\hat{x}}} {\Xi }_{k} \left( {\hat{x}} \right)\left( {\mathop \smallint \limits_{0}^{1} \partial_{{\hat{x}}} {\Xi }_{l} \left( {\hat{x}} \right)\partial_{{\hat{x}}} {\Xi }_{m} \left( {\hat{x}} \right){\text{d}}\hat{x}} \right){\text{d}}\hat{x}} \right) \hfill \\ - \alpha_{1} \eta_{d} \mathop \sum \limits_{k = 1}^{N} \mathop \sum \limits_{l = 1}^{N} \mathop \sum \limits_{m = 1}^{N} q_{k} \left( \tau \right)q_{l} \left( \tau \right)\partial_{\tau } q_{m} \left( \tau \right)\left( {\mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right)\partial_{{\hat{x}\hat{x}}} {\Xi }_{k} \left( {\hat{x}} \right)\left( {\mathop \smallint \limits_{0}^{1} 2\partial_{{\hat{x}}} {\Xi }_{l} \left( {\hat{x}} \right)\partial_{{\hat{x}}} {\Xi }_{m} \left( {\hat{x}} \right){\text{d}}\hat{x}} \right){\text{d}}\hat{x}} \right) \hfill \\ - \alpha_{2} \left[ {V_{{{\text{DC}}}} + V_{{{\text{AC}}}} \cos \left( {{\Omega }\tau { }} \right)} \right]^{2} \mathop \smallint \limits_{0}^{1} {\Xi }_{j} \left( {\hat{x}} \right)\left[ {\frac{1}{{\left( {1 - \mathop \sum \nolimits_{k = 1}^{N} {\Xi }_{k} \left( {\hat{x}} \right)q_{k} \left( \tau \right)} \right)^{2} }} + \frac{0.265}{{\beta_{1}^{\frac{3}{4}} \left( {1 - \mathop \sum \nolimits_{k = 1}^{N} {\Xi }_{k} \left( {\hat{x}} \right)q_{k} \left( \tau \right)} \right)^{\frac{5}{4}} }} + \frac{0.53}{{\beta_{1}^{\frac{1}{2}} \beta_{2}^{\frac{1}{2}} \left( {1 - \mathop \sum \nolimits_{k = 1}^{N} {\Xi }_{k} \left( {\hat{x}} \right)q_{k} \left( \tau \right)} \right)^{\frac{3}{2}} }}} \right]{\text{d}}\hat{x} = 0 \hfill \\ j = 1, 2, \ldots , N \hfill \\ \hfill \\ \end{gathered} $$
(13)

The discretisation procedure for the proposed MEMS model with nonlinear damping is challenging due to the presence of terms that cannot be integrated in closed form, namely the damping term involving \(\left|{\partial }_{\tau }\widehat{w}\right|\) and the electrostatic load term involving \(w\)-dependent components in the denominator. Hence, to ensure accuracy when applying the Galerkin technique, these terms are kept intact and spatial integrations are conducted numerically while retaining sufficient number of terms. This procedure leads to very large discretised equations of motion, but ensures accurate results. Furthermore, \(N\) is set to 10, resulting in a 10-degree-of-freedom (dof) model, ensuring converged results. The resultant discretised 10-dof model is solved numerically using a continuation method; the simulation results are discussed in detail in Sect. 4.

4 Results and discussion

In this section, the nonlinear resonance response of the MEMS resonator is examined in detail and extensive comparisons are conducted between the theoretical and experimental results. Different linear and nonlinear damping models are examined to determine the model that works best for various DC and AC voltage levels when calibrated only once. In other words, the goal is to find a damping model that can be calibrated once using experimental data at a specific level of excitation and then used reliably at other excitation levels and vibration amplitudes.

Two sets of experiments are conducted, one at \({V}_{\mathrm{DC}}=5\) V and the other at \({V}_{\mathrm{DC}}=30\) V. The primary resonance response of the MEMS resonator is captured at various AC voltage levels for each case, i.e. at \({V}_{\mathrm{AC}}=0.4, 5.5, 10,\) and \(20\) V for the case of \({V}_{\mathrm{DC}}=5\) V, and at \({V}_{\mathrm{AC}}=0.5, 1.0, 2.0,\) and \(7.0\) V for the case of \({V}_{\mathrm{DC}}=30\) V.

The geometric properties of the fabricated microbeam are given in Table 1, resulting in \({\alpha }_{1}=42.667\) and \({\alpha }_{2}=1.049\times {10}^{-2}\) considering a flexural rigidity of \(8.44\times {10}^{-12} \;{\text {Nm}}^2\) and a mass density of 2350 kg/m3. These values lead to a good match with the experimental linear and nonlinear responses, and hence, the residual stress is neglected. In the results shown in this section, \({\omega }_{1}\) indicates the first dimensionless natural frequency of the resonator, which is related to its dimensional counterpart \({\widetilde{\omega }}_{1}\) via \({\omega }_{1}={\widetilde{\omega }}_{1}T\). Additionally, \({w}_{d}\) denotes the midpoint transverse oscillation amplitude measured from the deflected state caused by the DC voltage. Furthermore, in all the theoretical results, solid lines indicate stable periodic solutions, while dashed lines represent unstable periodic solutions.

4.1 Linear viscous damping model

First, the Kelvin–Voigt damping coefficient \({\eta }_{d}\) and the nonlinear damping coefficients, i.e. \({c}_{d}^{(2)}\) and \({c}_{d}^{(3)}\), are set to zero in order to examine the performance of the linear viscous damping model in predicting the peak vibration amplitude at higher excitation levels when calibrated based on the results at relatively low excitation magnitudes. For this case, only the experimental results conducted at \({V}_{\mathrm{DC}}=5\) V are used. Two cases are considered to examine the performance of the linear viscous damping model as discussed in detail next.

For the first case, the linear damping coefficient, \({c}_{d}^{(1)}\), is calibrated using the experimental frequency response at \({V}_{\mathrm{AC}}=0.4\) V, resulting in \({c}_{d}^{(1)}=0.107\). Then, the AC voltage is increased to 5.5 V while keeping \({c}_{d}^{(1)}\) fixed, and the resultant theoretical frequency response is constructed and compared to the experimental one, as shown in Fig. 2a. As seen, the linear damping model significantly overestimates the peak amplitude when it is calibrated for very small oscillation amplitudes and kept intact for higher-amplitude oscillation predictions.

Fig. 2
figure 2

Frequency responses of the MEMS resonator at \({V}_{\mathrm{DC}}=5\) V, and different AC voltages (denoted on the curves). Circles: experimental data; lines: theoretical predictions using the linear damping model with a coefficient of a \({c}_{d}^{(1)}=0.107\) calibrated based on the experimental results for \({V}_{\mathrm{AC}}=0.4\) V and b \({c}_{d}^{(1)}=0.305\) calibrated based on the experimental results for \({V}_{\mathrm{AC}}=5.5\) V

Full size image

For the second case, the experimental frequency response for \({V}_{\mathrm{AC}}=5.5\) V is used to calibrate the linear damping model and then the frequency response for \({V}_{\mathrm{AC}}=10\) is obtained while keeping \({c}_{d}^{(1)}\) intact. The initial calibration for this case results in \({c}_{d}^{(1)}=0.305\), and the result of the comparison is shown in Fig. 2b. A similar behaviour is seen for this case in which the linear damping model overestimates the peak oscillation amplitude for the higher AC excitation level of 10 V. Furthermore, the comparison between the values of \({c}_{d}^{(1)}\) for the two cases examined shows that the calibrated coefficient for the case \({V}_{\mathrm{AC}}=5.5\) V is almost three times larger than that for the case of 0.4 V AC excitation level. This shows that as the AC voltage is increased from 0.4 to 5.5 V, the linear damping coefficient needs to be increased from 0.107 to 0.305 so that the theoretical model predictions match the experimental ones, which again shows the inaccuracy of the linear damping model.

It is evident from the linear damping analysis that irrespective of which excitation level is chosen to calibrate the damping model, as the excitation magnitude is increased, the linear damping model overestimates the peak amplitude. Hence, a nonlinear damping mechanism must be used to capture this nonlinearly increasing energy dissipation at higher oscillation amplitudes.

4.2 Kelvin–Voigt model

In this section, a comparison similar to the one in Sect. 4.1 is conducted, while replacing the linear damping model with a Kelvin–Voigt model; hence, \({c}_{d}^{(1)}\), \({c}_{d}^{(2)}\), and \({c}_{d}^{(3)}\) are set to zero, and the value of \({\eta }_{d}\) is obtained using the experimental frequency response at \({V}_{\mathrm{AC}}=0.4\) V for the first case and using the one at \({V}_{\mathrm{AC}}=5.5\) V for the second case. It should be noted that the Kelvin–Voigt model has both linear and nonlinear components; however, the coefficient of damping for both components is the same and equal to \({\eta }_{d}\); hence, it does not allow for separate calibration of the linear and the nonlinear damping coefficients.

First, the Kelvin–Voigt model is calibrated based on the low-amplitude frequency–response at 0.4 AC voltage, resulting in \({\eta }_{d}=2.10\times {10}^{-4}\). Then, \({\eta }_{d}\) is kept fixed and the AC voltage is increased to 5.5 V. The result of the comparison is shown in Fig. 3a. As seen, while the Kelvin–Voigt model works better than the linear damping (i.e. as seen from comparison of Fig. 3a to Fig. 2a), it still overestimates the peak amplitude by a large margin. To investigate whether this is due to calibration with a very small oscillation amplitude, for the next case, the Kelvin–Voigt damping coefficient is calibrated using the experimental frequency response for \({V}_{\mathrm{AC}}=5.5\) V, resulting in \({\eta }_{d}=5.80\times {10}^{-4}\). Obtaining the frequency response for \({V}_{\mathrm{AC}}=10\) using the new value of \({\eta }_{d}\) and plotting against the experimental one in Fig. 3b show that the Kelvin–Voigt model again overestimates the peak amplitudes at higher AC excitation levels. Hence, although the Kelvin–Voigt model works better than the linear damping model owing to its nonlinear parts, it still cannot reliably predict the peak amplitude at excitation levels higher than the one it is calibrated for.

Fig. 3
figure 3

Frequency responses of the MEMS resonator at \({V}_{\mathrm{DC}}=5\) V, and different AC voltages (denoted on the curves). Circles: experimental data; lines: theoretical predictions using the Kelvin–Voigt model with a coefficient of a \({\eta }_{d}=2.10\times {10}^{-4}\) calibrated based on the experimental results for \({V}_{\mathrm{AC}}=0.4\) V and b \({\eta }_{d}=5.80\times {10}^{-4}\) calibrated based on the experimental results for \({V}_{\mathrm{AC}}=5.5\) V

Full size image

4.3 Modified Kelvin–Voigt model with two damping coefficients

In the previous section, it was shown that the Kelvin–Voigt model cannot be used to predict peak amplitudes at different excitation levels reliably with a fixed damping coefficient for both linear and nonlinear terms. More specifically, even though the Kelvin–Voigt model used in this study is a nonlinear damping model, it still underestimates the energy dissipation at higher oscillation amplitudes, which indicates the presence of a strong nonlinear damping in the MEMS resonator. Hence, to have more flexibility in adjusting the nonlinear damping in the Kelvin–Voigt model, a modified version is examined in this section with two damping coefficients. More specifically, the coefficient of the linear damping term in the Kelvin–Voigt model is replaced by \({\eta }_{d}^{\left(l\right)}\) and that of the nonlinear damping term is replaced by \({\eta }_{d}^{\left(n\right)}\). This allows for adjusting each coefficient separately and provides more flexibility in modelling the damping for both small- and large-amplitude oscillations as explained in the following.

For such a damping model, two experimental frequency responses are needed to calibrate the coefficients: one at very low excitation level where the response is mostly linear and one at larger excitation level where the system clearly shows a nonlinear behaviour. To this end, the frequency responses at \({V}_{\mathrm{AC}}=0.4\) and \(5.5\) V (for the case with \({V}_{\mathrm{DC}}=5\) V) are used to calibrate the two coefficients of the modified Kelvin–Voigt model. The calibration procedure is as follows: first, an initial estimate of the value of linear damping coefficient, i.e. \({\eta }_{d}^{\left(l\right)}\), is obtained by setting \({\eta }_{d}^{\left(n\right)}\) to zero and calibrating \({\eta }_{d}^{\left(l\right)}\) using the resonance response at \({V}_{\mathrm{AC}}=0.4\) V. This provides a relatively accurate initial estimate for \({\eta }_{d}^{\left(l\right)}\) as the response of the system is mostly linear at this low excitation level. Then, while keeping \({\eta }_{d}^{\left(l\right)}\) fixed, the value of \({\eta }_{d}^{\left(n\right)}\) is chosen such that a match is obtained between the theoretical and experimental frequency responses at 5.5 V AC excitation level. Since the addition of \({\eta }_{d}^{\left(n\right)}\) will slightly affect the oscillation amplitude for the case \({V}_{\mathrm{AC}}=0.4\) V, both \({\eta }_{d}^{\left(l\right)}\) and \({\eta }_{d}^{\left(n\right)}\) coefficients are slightly modified until good matches are obtained at both 0.4 V and 5.5 V AC excitation levels.

This calibration procedure results in \({\eta }_{d}^{\left(l\right)}=2.0\times {10}^{-4}\) and \({\eta }_{d}^{\left(n\right)}=8.5\times {10}^{-3}\). The values of \({\eta }_{d}^{(l)}\) and \({\eta }_{d}^{\left(n\right)}\) are then kept fixed, while the AC voltage is increased to 10 and then 20 V. The result of the comparison between experimental and theoretical frequency responses at various AC voltage levels is shown in Fig. 4. The good fit between the results at \({V}_{\mathrm{AC}}=0.4\) V and 5.5 V is expected, as the experimental results at these excitation levels were used to calibrate the damping model. However, as seen in the figure, the new modified Kelvin–Voigt model does an excellent job at predicting correct peak oscillation amplitudes at larger AC voltage excitations, even though both damping coefficients were kept fixed. Hence, Fig. 4 shows that the procedure used for calibrating the damping coefficients is robust, as it uses a very small-amplitude frequency response to almost eliminate the nonlinear effects and calibrates the linear part; the nonlinear part can then be calibrated using any relatively large-amplitude experimental frequency response.

Fig. 4
figure 4

Frequency responses of the MEMS resonator at \({V}_{\mathrm{DC}}=5\) V, and various AC voltages (denoted on the curves). Circles: experimental data; lines: theoretical predictions using the modified Kelvin–Voigt model with the two damping coefficients calibrated based on the experimental data for \({V}_{\mathrm{AC}}=0.4\) and \(5.5\) V

Full size image

To further examine the reliability of the proposed modified Kelvin–Voigt model, another set of experimental data is considered, which was conducted at \({V}_{\mathrm{DC}}=30\) V and several AC voltages, namely \({V}_{\mathrm{AC}}=0.5\), \(1.0\), \(2.0\), and \(7.0\) V. The material damping coefficients, i.e. \({\eta }_{d}^{\left(l\right)}\) and \({\eta }_{d}^{\left(n\right)}\), are kept fixed, and the frequency responses of the MEMS resonator at these AC voltage levels are constructed numerically. A comparison between the numerical and experimental results is shown in Fig. 5. As seen, even though the modified Kelvin–Voigt model was calibrated using a completely different set of experimental results, it still works very well in capturing the primary resonance response and peak amplitudes at these new DC-AC excitation levels. It is noticed that the modified Kelvin–Voigt model predicts generally smaller peak amplitudes compared to the experimental results; the maximum error in estimating the peak amplitude is less than 9% and the average percentage error in estimating the peak amplitude for all AC voltage levels is 6.5%.

Fig. 5
figure 5

Frequency responses of the MEMS resonator at \({V}_{\mathrm{DC}}=30\) V, and for various AC voltages (denoted on the curves). Circles: experimental data; lines: theoretical predictions using the modified Kelvin–Voigt model with the same damping coefficients as the ones used in Fig. 4

Full size image

4.4 Cubic nonlinear damping model

In this section, the performance of the cubic nonlinear damping model is examined in detail. To this end, the Kelvin–Voigt damping is removed from the MEMS model so as to examine only the cubic damping model. Two formulations of the cubic damping model are investigated: one with the linear and cubic terms (i.e. neglecting the quadratic term) and one with all linear, quadratic, and cubic terms being considered. The former is referred to as the cubic model, and the latter as the general quadratic–cubic model.

Starting with the cubic model, a procedure similar to the one used in Sect. 4.3 is followed here to calibrate the two damping coefficients, i.e. \({c}_{d}^{(1)}\) and \({c}_{d}^{(3)}\). More specifically, the model is calibrated using the experimental results conducted at \({V}_{\mathrm{DC}}=5\) V, making use of the two lower-amplitude frequency responses. The damping coefficients are then kept fixed, and the frequency responses at other AC and DC voltages are obtained and compared to the experimental results.

Similar to the previous section, the cubic damping model has a linear and a nonlinear term; hence, the damping coefficients can be calibrated using two frequency responses, i.e. the ones conducted at \({V}_{\mathrm{AC}}=0.4\) and \(5.5\) V. Following a calibration procedure similar to the one in Sect. 4.3 results in \({c}_{d}^{(1)}=0.100\) and \({c}_{d}^{(3)}=0.038\). These damping coefficients are then kept fixed, and two sets of numerical simulations are conducted; one set at 5 V DC voltage and \({V}_{\mathrm{AC}}=10\) and 20 V, and another set at 30 V DC voltage and \({V}_{\mathrm{AC}}=0.5\), \(1.0\), \(2.0\), and \(7.0\) V. The comparisons between numerical and experimental results are shown in Fig. 6. More specifically, Fig. 6a shows the comparison for the set of results at \({V}_{\mathrm{DC}}=5\) V, while Fig. 6b shows that at \({V}_{\mathrm{DC}}=30\) V. As seen in Fig. 6a, the cubic damping model works well in capturing the peak amplitudes at \({V}_{\mathrm{AC}}=10\) and 20 V once calibrated using the results at \({V}_{\mathrm{AC}}=0.4\) and 5.5 V. However, it is seen that the cubic damping model slightly underestimates the peak amplitude, and this becomes more visible at higher AC voltage levels. Nevertheless, it still does a very good job in capturing the nonlinear damping in the system.

Fig. 6
figure 6

Frequency responses of the MEMS resonator at a \({V}_{\mathrm{DC}}=5\) V and b \({V}_{\mathrm{DC}}=30\) V, and various AC voltages (denoted on the curves). Circles: experimental data; lines: theoretical predictions using the cubic damping model with the two damping coefficients calibrated based on the experimental data for \({V}_{\mathrm{AC}}=0.4\) and \(5.5\) V (sub-figure (a))

Full size image

Looking at the set of results conducted at a higher level of DC voltage, Fig. 6b, a similar behaviour is observed, i.e. the cubic model captures the peak amplitude correctly at relatively lower AC voltages; however, as the AC voltage is increased, it tends to underestimate the peak amplitude. Similar to the modified Kelvin–Voigt model, for the case of Fig. 6b the maximum error is less than 9% but the average error is slightly lower at 5%. The underestimation of the peak amplitude at higher AC voltages can be attributed to the fact that the only nonlinear term in the damping model is of cubic order, which increases very rapidly as the oscillation amplitude (and hence velocity) increases. To further study this, the general quadratic–cubic model will be examined next to investigate whether the addition of a quadratic term can improve the overall performance of the damping model.

The general quadratic–cubic model consists of three damping coefficients, i.e. \({c}_{d}^{(1)}\), \({c}_{d}^{(2)}\), and \({c}_{d}^{(3)}\), which need to be determined using the experimental data. Since there are three unknown coefficients, three experimental frequency responses are required to calibrate the model. It should be noted that the three coefficients might also be determined using, for instance, two frequency responses, but in that case optimum values cannot be found and hence the model might not work as intended. Hence, the experimental frequency responses at \({V}_{\mathrm{AC}}=0.4\), \(5.5\), and \( {10} \) V (at 5 V DC voltage) are selected for the calibration process. It should be noted that the calibration procedure for this case is not as straightforward as the previous case and is more iterative. The goal is to achieve an optimised mix of quadratic and cubic terms that can lead to larger peak amplitudes at higher AC voltages, while maintaining accurate predictions at smaller oscillation amplitudes. To this end, first a procedure similar to the previous case is followed by only considering \({c}_{d}^{(1)}\) and \({c}_{d}^{(2)}\) (i.e. a quadratic model), using the curves for \({V}_{\mathrm{AC}}=0.4\) and \(5.5\), which leads to optimum values of \(0.074\) and \(0.100\) for \({c}_{d}^{(1)}\) and \({c}_{d}^{(2)}\), respectively. We also know from the previous case that the optimum values for a cubic model are \(0.100\) and \(0.038\) for \({c}_{d}^{(1)}\) and \({c}_{d}^{(3)}\), respectively. Hence, it is assumed that the optimised case for the general quadratic–cubic model is a linear combination of these two cases. Therefore, a weight factor \(\mu \) in the range [0 1] is considered and the damping coefficients are defined as: \({c}_{d}^{(1)}=\mu \times 0.100+(1-\mu )\times 0.074\), \({c}_{d}^{(2)}=(1-\mu )\times 0.100\), and \({c}_{d}^{(3)}=\mu \times 0.038\). Knowing that the cubic model already provided good results, it is expected that a \(\mu \) closer to 1 (than 0) would be ideal as it slightly reduces the effect of the cubic term and introduces a quadratic term which has less damping effect at larger amplitudes (since it grows at a quadratic rate rather a cubic one). Hence, different values of \(\mu \) are tested to see which value gives best fit for all three frequency responses. Following this procedure leads to \(\mu =0.765\) as the optimum value, which results in the following damping coefficient values for the general quadratic–cubic damping model: \({c}_{d}^{(1)}=0.094\), \({c}_{d}^{(2)}=0.024\), and \({c}_{d}^{(3)}=0.029\). Similar to the previous case, the damping coefficients are kept fixed and the frequency responses at other AC/DC voltage levels are constructed and compared to the experimental results, as illustrated in Fig. 7 through (a) for the set of results at \({V}_{\mathrm{DC}}=5\) V and (b) that at \({V}_{\mathrm{DC}}=30\) V.

Fig. 7
figure 7

Frequency responses of the MEMS resonator at a \({V}_{\mathrm{DC}}=5\) V and b \({V}_{\mathrm{DC}}=30\) V, and various AC voltages (denoted on the curves). Circles: experimental data; lines: theoretical predictions using the general quadratic-cubic damping model with the three damping coefficients calibrated based on the experimental data for \({V}_{\mathrm{AC}}=0.4\), \(5.5\), and \(10\) V (sub-figure (a))

Full size image

Starting with Fig. 7a, it is seen that the general quadratic–cubic damping model does an excellent job at predicting correct peak amplitudes at various AC voltage levels. Furthermore, the model also works well for the set of results at an increased DC voltage level, as seen in Fig. 7b. In fact, for the case of Fig. 7b, the maximum error in estimating the peak amplitude is less than 6% and the average error is 3.3%, both of which are less than those of the other nonlinear damping models examined in this study.

Hence, it is shown that once calibrated, the general quadratic–cubic damping model works best in predicting the primary resonance response amplitudes at various AC and DC voltages. However, compared to the cubic model and the modified Kelvin–Voigt model, it requires more experimental frequency responses for optimal calibration.

5 Conclusions

This study conducted a thorough theoretical–experimental investigation on the nonlinear damping in in-plane MEMS resonators. Precise experimental measurements were conducted to examine the primary resonance response of an in-plane electrically actuated clamped–clamped microbeam for various AC and DC voltages. More specifically, the frequency responses of the system were constructed at various AC voltage levels for two different statically deflected configurations (i.e. DC voltage levels). For the theoretical part, a nonlinear model was developed for the microbeam taking into account nonlinearities associated with midplane stretching, electrostatic load, and damping. In particular, two different damping mechanisms were considered: the general quadratic–cubic nonlinear damping model and the Kelvin–Voigt model. The nonlinear continuous model of the MEMS resonator was discretised utilising the Galerkin method while retaining 10 modes and while ensuring that the electrostatic load term with nonlinearities in the denominator and the damping term in the absolute function are kept intact in the discretisation procedure.

Various damping models were examined and compared to experimental data including the linear damping model, the Kelvin–Voigt model, the modified Kelvin–Voigt model with two damping coefficients, the cubic model (including linear and cubic terms), and the general quadratic–cubic damping model. It should be highlighted that the goal was to investigate whether a damping model is capable of capturing correct resonance amplitudes at various excitation levels with fixed damping coefficients without focusing on the nonlinear damping sources. Thorough investigations were conducted, and it was found that:

  • The linear damping model significantly overestimates the peak amplitude at higher excitation levels when it is calibrated using the experimental data at a lower excitation level.

  • The Kelvin–Voigt model works better than the linear damping model, but still overestimates the response at higher excitation levels.

  • The modified Kelvin–Voigt model with two damping coefficients (one for linear and one for nonlinear terms) does an excellent job at capturing the correct peak resonance amplitudes at various AC voltages when calibrated using the two lowest amplitude experimental data. When the DC voltage is increased, this model tends to slightly underestimate the peak amplitude.

  • The cubic model works well, but it slightly underestimates the peak amplitude as the AC voltage level is increased (at different DC voltage levels)

  • The general quadratic–cubic model works better than the other nonlinear models and captures the peak amplitude at various AC and DC voltage levels with a minimum error.

Hence, this study clearly shows the presence of a strong nonlinear damping in in-plane clamped–clamped silicon MEMS resonators and proposes suitable nonlinear damping models (along with robust calibration procedures) to capture such a nonlinear behaviour. In summary, both quadratic–cubic and modified Kelvin–Voigt models work really well, noting that the former is more complicated to calibrate as it requires three experimental frequency responses for optimal calibration, while the modified Kelvin–Voigt model has two coefficients and can be calibrated using only two experimental frequency responses.