Nonlinear dynamic modelling and analysis of multiple thin plates connected by long hinges

Abstract

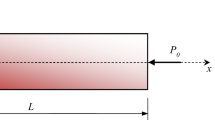
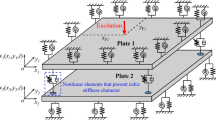
The dynamical modelling method and nonlinear characteristics of the multi-plate structure are investigated in this paper. The structure presents as a chain, which consists of multiple plates and adjacent plates are connected by a long hinge. The length of the hinge should be considered therefore the boundary conditions of each plate are discontinuous. A novel constraining method based on the power series polynomial is proposed to establish the mathematical model of the connection and constraint for the plate with the local restrained boundary. The characteristic equation of the multi-plate structure is derived by using the Rayleigh–Ritz method and then natural frequencies are obtained. The discrete nonlinear dynamical equation is established by using the obtained linear modal shapes. By comparing natural characteristics with the result of the finite element model, the correctness of the present model and the validation of the proposed method are verified. The modal analysis shows that the complex frequency phenomena are due to the different influence of the long hinge on symmetric and antisymmetric modes of each plate. The parameter analysis reveals nonlinear characteristics of the whole multi-plate structure. Numerical results demonstrate that the proposed constraining method can impose constraints on interval discontinuous boundaries of the plate, which goes beyond the traditional Lagrange multiplier method.

Appendix

The detailed expression of the elastic potential energy Eq. (4) is written as

$$\begin{aligned} U_{total} &= \frac{1}{2}\sum\limits_{i = 1}^{3} {\int_{ - L}^{L} {\int_{ - b}^{b} {\left\{ {Q_{11} \left[ {2h\left( {\frac{{\partial u_{i} }}{{\partial x_{i} }}} \right)^{2} + \frac{{2h^{3} }}{3}\left( {\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}} \right)^{2} + 2h\frac{{\partial u_{i} }}{{\partial x_{i} }}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} + \frac{h}{2}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{4} } \right]} \right.} } } \\ &\quad + Q_{12} \left[ {4h\left( {\frac{{\partial u_{i} }}{{\partial x_{i} }}} \right)\left( {\frac{{\partial v_{i} }}{{\partial y_{i} }}} \right) + \frac{{4h^{3} }}{3}\left( {\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}} \right)\left( {\frac{{\partial^{2} w_{i} }}{{\partial y_{i}^{2} }}} \right) + h\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} } \right]\\ &\quad \left. { + 2h\frac{{\partial u_{i} }}{{\partial x_{i} }}\left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} + 2h\frac{{\partial v_{i} }}{{\partial y_{i} }}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} } \right]\\ &\quad + Q_{22} \left[ {2h\left( {\frac{{\partial v_{i} }}{{\partial y_{i} }}} \right)^{2} + \frac{{2h^{3} }}{3}\left( {\frac{{\partial^{2} w_{i} }}{{\partial y_{i}^{2} }}} \right)^{2} + 2h\frac{{\partial v_{i} }}{{\partial y_{i} }}\left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} + \frac{h}{2}\left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{4} } \right] \\ &\quad + Q_{66} \left[ {2h\left( {\frac{{\partial u_{i} }}{{\partial y_{i} }}} \right)^{2} + 2h\left( {\frac{{\partial v_{i} }}{{\partial x_{i} }}} \right)^{2} + 4h\left( {\frac{{\partial u_{i} }}{{\partial y_{i} }}} \right)\left( {\frac{{\partial v_{i} }}{{\partial x_{i} }}} \right) + \frac{{8h^{3} }}{3}\left( {\frac{{\partial^{2} w_{i} }}{{\partial x_{i} \partial y_{i} }}} \right)^{2} } \right.\\ &\quad \left. {\left. { + 4h\frac{{\partial u_{i} }}{{\partial y_{i} }}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)\left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right) + 4h\frac{{\partial v_{i} }}{{\partial x_{i} }}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)\left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right) + 2h\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} } \right]} \right\}{\text{d}}y_{i} {\text{d}}x_{i}\\ \quad + \frac{1}{2}k_{t} (\Delta \theta_{y01}^{2} + \Delta \theta_{y12}^{2} + \Delta \theta_{y23}^{2} ), \\ \end{aligned}$$

(A1)

The maximum values of energy expressions in Eq. (15) are given as

$$\begin{gathered} T_{\max } = \frac{1}{2}\omega^{2} \rho \sum\limits_{i = 1}^{3} {\int_{ - L}^{L} {\int_{ - b}^{b} {\left[ {H_{1} \left( {U_{i}^{2} + V_{i}^{2} + W_{i}^{2} } \right) + H_{2} \left( {\frac{{\partial W_{i} }}{{\partial x_{i} }}} \right)^{2} + H_{2} \left( {\frac{{\partial W_{i} }}{{\partial y_{i} }}} \right)^{2} } \right]{\text{d}}y_{i} {\text{d}}x_{i} } } } , \hfill \\ U_{\max } = \frac{1}{2}\sum\limits_{i = 1}^{3} {\int_{ - L}^{L} {\int_{ - b}^{b} {\left[ {Q_{11} H_{1} \left( {\frac{{\partial U_{i} }}{{\partial x_{i} }}} \right)^{2} + Q_{11} H_{2} \left( {\frac{{\partial^{2} W_{i} }}{{\partial x_{i}^{2} }}} \right)^{2} + 2Q_{12} H_{1} \left( {\frac{{\partial U_{i} }}{{\partial x_{i} }}} \right)\left( {\frac{{\partial V_{i} }}{{\partial y_{i} }}} \right)} \right.} } } \hfill \\ \, + 2Q_{12} H_{2} \left( {\frac{{\partial^{2} W_{i} }}{{\partial x_{i}^{2} }}} \right)\left( {\frac{{\partial^{2} W_{i} }}{{\partial y_{i}^{2} }}} \right) + Q_{22} H_{1} \left( {\frac{{\partial V_{i} }}{{\partial y_{i} }}} \right)^{2} + Q_{22} H_{2} \left( {\frac{{\partial^{2} W_{i} }}{{\partial y_{i}^{2} }}} \right)^{2} + Q_{66} H_{1} \left( {\frac{{\partial V_{i} }}{{\partial x_{i} }}} \right)^{2} \hfill \\ \, \left. { + Q_{66} H_{1} \left( {\frac{{\partial U_{i} }}{{\partial y_{i} }}} \right)^{2} { + }2Q_{66} H_{1} \left( {\frac{{\partial U_{i} }}{{\partial y_{i} }}} \right)\left( {\frac{{\partial V_{i} }}{{\partial x_{i} }}} \right) + 4Q_{66} H_{2} \left( {\frac{{\partial^{2} W_{i} }}{{\partial x_{i} \partial y_{i} }}} \right)^{2} } \right]{\text{d}}y_{i} {\text{d}}x_{i} \hfill \\ \, + \frac{1}{2}k_{t} (\Delta \theta_{y01}^{2} + \Delta \theta_{y12}^{2} + \Delta \theta_{y23}^{2} ), \hfill \\ \end{gathered}$$

(A2)

where

$$H_{1} = 2h, \, H_{2} = \frac{{2h^{3} }}{3}, \, H_{3} = h.$$

(A3)

The element detailed expression of the characteristic stiffness and mass matrices in Eq. (18) are given as

$$\begin{gathered} \left\{ {K_{ii}^{(u)} } \right\}_{rs} = H_{1} \int_{ - b}^{b} {\int_{ - L}^{L} {\left[ {Q_{11} \frac{{\partial^{2} \varphi_{{m_{r} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{r} }}^{(1)} \frac{{\partial^{2} \varphi_{{m_{s} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{s} }}^{(i)} + Q_{66} \frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\frac{{\partial \varphi_{{n_{r} }}^{(i)} }}{\partial y}\frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\frac{{\partial \varphi_{{n_{s} }}^{(i)} }}{\partial y}} \right]} } {\text{d}}x{\text{d}}y, \hfill \\ \left\{ {K_{ii}^{(v)} } \right\}_{rs} = H_{1} \int_{ - b}^{b} {\int_{ - L}^{L} {\left[ {Q_{22} \frac{{\partial^{2} \varphi_{{m_{r} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{r} }}^{(1)} \frac{{\partial^{2} \varphi_{{m_{s} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{s} }}^{(i)} + Q_{66} \frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\frac{{\partial \varphi_{{n_{r} }}^{(i)} }}{\partial y}\frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\frac{{\partial \varphi_{{n_{s} }}^{(i)} }}{\partial y}} \right]} } {\text{d}}x{\text{d}}y, \hfill \\ \left\{ {K_{ii}^{(uv)} } \right\}_{rs} = H_{1} \int_{ - b}^{b} {\int_{ - L}^{L} {\left[ {Q_{12} \frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\varphi_{{n_{r} }}^{(1)} \varphi_{{m_{s} }}^{(i)} \frac{{\partial \varphi_{{n_{s} }}^{(i)} }}{\partial y} + Q_{66} \varphi_{{m_{r} }}^{(i)} \frac{{\partial \varphi_{{n_{r} }}^{(i)} }}{\partial y}\frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\varphi_{{n_{s} }}^{(i)} } \right]} } {\text{d}}x{\text{d}}y, \hfill \\ \end{gathered}$$

(A4)

$$\begin{gathered} \left\{ {K_{ii}^{(w)} } \right\}_{rs} = H_{2} \int_{ - b}^{b} {\int_{ - L}^{L} {\left\{ {Q_{11} \frac{{\partial^{2} \varphi_{{m_{r} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{r} }}^{(i)} \frac{{\partial^{2} \varphi_{{m_{s} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{s} }}^{(i)} } \right.} } \hfill \\ + Q_{12} \left[ {\frac{{\partial^{2} \varphi_{{m_{r} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{r} }}^{(i)} \varphi_{{m_{s} }}^{(i)} \frac{{\partial^{2} \varphi_{{n_{s} }}^{(i)} }}{{\partial y^{2} }} + \varphi_{{m_{r} }}^{(i)} \frac{{\partial^{2} \varphi_{{n_{r} }}^{(i)} }}{{\partial y^{2} }}\frac{{\partial^{2} \varphi_{{m_{s} }}^{(i)} }}{{\partial x^{2} }}\varphi_{{n_{s} }}^{(i)} } \right] \hfill \\ \left. { + Q_{22} \varphi_{{m_{r} }}^{(i)} \frac{{\partial^{2} \varphi_{{n_{r} }}^{(i)} }}{{\partial y^{2} }}\varphi_{{m_{s} }}^{(i)} \frac{{\partial^{2} \varphi_{{n_{s} }}^{(i)} }}{{\partial y^{2} }}{\kern 1pt} + 4Q_{66} \frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\frac{{\partial \varphi_{{n_{r} }}^{(i)} }}{\partial y}\frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\frac{{\partial \varphi_{{n_{s} }}^{(i)} }}{\partial y}} \right\}{\text{d}}x{\text{d}}y \hfill \\ + k_{t} \left[ {\left. {\frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\varphi_{{n_{r} }}^{(i)} \frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\varphi_{{n_{s} }}^{(i)} } \right|_{\begin{subarray}{l} x = - L \\ y = 0 \end{subarray} } + \left. {\frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\varphi_{{n_{r} }}^{(i)} \frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\varphi_{{n_{s} }}^{(i)} } \right|_{\begin{subarray}{l} x = - L \\ y = 0 \end{subarray} } } \right], \hfill \\ \end{gathered}$$

(A5)

$$\left\{ {K_{ij}^{(w)} } \right\}_{rs} = - k_{t} \left( {\left. {\frac{{\partial \varphi_{{m_{r} }}^{(j)} }}{\partial x}\varphi_{{n_{r} }}^{(j)} } \right|_{\begin{subarray}{l} x = - L \\ y = 0 \end{subarray} } } \right)\left( {\left. {\frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\varphi_{{n_{s} }}^{(i)} } \right|_{\begin{subarray}{l} x = L \\ y = 0 \end{subarray} } } \right),\;\;\;(i < j),\;\;\;K_{ji} = K_{ij} .$$

(A6)

$$\begin{gathered} \left\{ {M_{ii}^{(u)} } \right\}_{rs} = \rho H_{1} \int_{ - b}^{b} {\int_{ - L}^{L} {\left[ {\varphi_{{m_{r} }}^{(i)} \varphi_{{n_{r} }}^{(i)} \varphi_{{m_{s} }}^{(i)} \varphi_{{n_{s} }}^{(i)} } \right]{\text{d}}x{\text{d}}y} } \hfill \\ \left\{ {M_{ii}^{(v)} } \right\}_{rs} = \rho H_{1} \int_{ - b}^{b} {\int_{ - L}^{L} {\left[ {\varphi_{{m_{r} }}^{(i)} \varphi_{{n_{r} }}^{(i)} \varphi_{{m_{s} }}^{(i)} \varphi_{{n_{s} }}^{(i)} } \right]{\text{d}}x{\text{d}}y} } \hfill \\ \left\{ {M_{ii}^{(w)} } \right\}_{rs} = \rho \int_{ - h}^{h} {\int_{ - b}^{b} {\int_{ - L}^{L} {\left[ {H_{2} \frac{{\partial \varphi_{{m_{r} }}^{(i)} }}{\partial x}\varphi_{{n_{r} }}^{(i)} \frac{{\partial \varphi_{{m_{s} }}^{(i)} }}{\partial x}\varphi_{{n_{s} }}^{(i)} } \right.} } } \hfill \\ \;\left. {\left. { + H_{2} \varphi_{{m_{r} }}^{(i)} \frac{{\partial \varphi_{{n_{r} }}^{(i)} }}{\partial x}\varphi_{{m_{s} }}^{(i)} \frac{{\partial \varphi_{{n_{s} }}^{(i)} }}{\partial x} + H_{1} \varphi_{{m_{r} }}^{(i)} \varphi_{{n_{r} }}^{(i)} \varphi_{{m_{s} }}^{(i)} \varphi_{{n_{s} }}^{(i)} } \right]} \right\}{\text{d}}x{\text{d}}y{\text{d}}z, \hfill \\ \end{gathered}$$

(A7)

where the superscripts (i) and (j) denote the number of the plate, respectively. The subscripts r and s denote the serial number of the general term of the Chebyshev polynomial $\varphi_{m} (x)$ and $\varphi_{n} (y)$.

Elements of matrices in Eq. are listed as follows

$$\begin{gathered} {\mathbf{M}}_{u} = \rho H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {{\mathbf{U}}_{1}^{{\text{T}}} {\mathbf{U}}_{1} { + }{\mathbf{U}}_{2}^{{\text{T}}} {\mathbf{U}}_{2} + {\mathbf{U}}_{3}^{{\text{T}}} {\mathbf{U}}_{3} } \right){\text{d}}y{\text{d}}x} } \hfill \\ {\mathbf{M}}_{v} = \rho H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {{\mathbf{V}}_{1}^{{\text{T}}} {\mathbf{V}}_{1} { + }{\mathbf{V}}_{2}^{{\text{T}}} {\mathbf{V}}_{2} + {\mathbf{V}}_{3}^{{\text{T}}} {\mathbf{V}}_{3} } \right){\text{d}}y{\text{d}}x} } \hfill \\ {\mathbf{M}}_{w} = \rho \int_{ - L}^{L} {\int_{ - b}^{b} {\left[ {H_{1} \left( {{\mathbf{W}}_{1}^{{\text{T}}} {\mathbf{W}}_{1} { + }{\mathbf{W}}_{2}^{{\text{T}}} {\mathbf{W}}_{2} + {\mathbf{W}}_{3}^{{\text{T}}} {\mathbf{W}}_{3} } \right){ + }H_{2} \left( {\frac{{\partial {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial x_{1} }}\frac{{\partial {\mathbf{W}}_{1} }}{{\partial x_{1} }}{ + }\frac{{\partial {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial y_{1} }}\frac{{\partial {\mathbf{W}}_{1} }}{{\partial y_{1} }}} \right)} \right.} } \hfill \\ \, \left. {{ + }H_{2} \left( {\frac{{\partial {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial x_{2} }}\frac{{\partial {\mathbf{W}}_{2} }}{{\partial x_{2} }}{ + }\frac{{\partial {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial y_{2} }}\frac{{\partial {\mathbf{W}}_{2} }}{{\partial y_{2} }}} \right){ + }H_{2} \left( {\frac{{\partial {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial x_{3} }}\frac{{\partial {\mathbf{W}}_{3} }}{{\partial x_{3} }}{ + }\frac{{\partial {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial y_{3} }}\frac{{\partial {\mathbf{W}}_{3} }}{{\partial y_{3} }}} \right)} \right]{\text{d}}y{\text{d}}x \hfill \\ \end{gathered}$$

(A8)

$$\begin{gathered} {\mathbf{K}}_{u} = Q_{11} H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial {\mathbf{U}}_{1}^{{\text{T}}} }}{{\partial x_{1} }}\frac{{\partial {\mathbf{U}}_{1} }}{{\partial x_{1} }}{ + }\frac{{\partial {\mathbf{U}}_{2}^{{\text{T}}} }}{{\partial x_{2} }}\frac{{\partial {\mathbf{U}}_{2} }}{{\partial x_{2} }} + \frac{{\partial {\mathbf{U}}_{3}^{{\text{T}}} }}{{\partial x_{3} }}\frac{{\partial {\mathbf{U}}_{3} }}{{\partial x_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + Q_{66} H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial {\mathbf{U}}_{1}^{{\text{T}}} }}{{\partial y_{1} }}\frac{{\partial {\mathbf{U}}_{1} }}{{\partial y_{1} }}{ + }\frac{{\partial {\mathbf{U}}_{2}^{{\text{T}}} }}{{\partial y_{2} }}\frac{{\partial {\mathbf{U}}_{2} }}{{\partial y_{2} }} + \frac{{\partial {\mathbf{U}}_{3}^{{\text{T}}} }}{{\partial y_{3} }}\frac{{\partial {\mathbf{U}}_{3} }}{{\partial y_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ {\mathbf{K}}_{v} = Q_{22} H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial {\mathbf{V}}_{1}^{{\text{T}}} }}{{\partial y_{1} }}\frac{{\partial {\mathbf{V}}_{1} }}{{\partial y_{1} }}{ + }\frac{{\partial {\mathbf{V}}_{2}^{{\text{T}}} }}{{\partial y_{2} }}\frac{{\partial {\mathbf{V}}_{2} }}{{\partial y_{2} }} + \frac{{\partial {\mathbf{V}}_{3}^{{\text{T}}} }}{{\partial y_{3} }}\frac{{\partial {\mathbf{V}}_{3} }}{{\partial y_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + Q_{66} H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial {\mathbf{V}}_{1}^{{\text{T}}} }}{{\partial x_{1} }}\frac{{\partial {\mathbf{V}}_{1} }}{{\partial x_{1} }}{ + }\frac{{\partial {\mathbf{V}}_{2}^{{\text{T}}} }}{{\partial x_{2} }}\frac{{\partial {\mathbf{V}}_{2} }}{{\partial x_{2} }} + \frac{{\partial {\mathbf{V}}_{3}^{{\text{T}}} }}{{\partial x_{3} }}\frac{{\partial {\mathbf{V}}_{3} }}{{\partial x_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ {\mathbf{K}}_{uv} = Q_{12} H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial {\mathbf{U}}_{1}^{{\text{T}}} }}{{\partial x_{1} }}\frac{{\partial {\mathbf{V}}_{1} }}{{\partial y_{1} }}{ + }\frac{{\partial {\mathbf{U}}_{2}^{{\text{T}}} }}{{\partial x_{2} }}\frac{{\partial {\mathbf{V}}_{2} }}{{\partial y_{2} }} + \frac{{\partial {\mathbf{U}}_{3}^{{\text{T}}} }}{{\partial x_{3} }}\frac{{\partial {\mathbf{V}}_{3} }}{{\partial y_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + Q_{66} H_{1} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial {\mathbf{U}}_{1}^{{\text{T}}} }}{{\partial y_{1} }}\frac{{\partial {\mathbf{V}}_{1} }}{{\partial x_{1} }}{ + }\frac{{\partial {\mathbf{U}}_{2}^{{\text{T}}} }}{{\partial y_{2} }}\frac{{\partial {\mathbf{V}}_{2} }}{{\partial x_{2} }} + \frac{{\partial {\mathbf{U}}_{3}^{{\text{T}}} }}{{\partial y_{3} }}\frac{{\partial {\mathbf{V}}_{3} }}{{\partial x_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \end{gathered}$$

(A9)

$$\begin{gathered} {\mathbf{K}}_{w} = Q_{11} H_{2} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial^{2} {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial x_{1}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{1} }}{{\partial x_{1}^{2} }}{ + }\frac{{\partial^{2} {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial x_{2}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{2} }}{{\partial x_{2}^{2} }} + \frac{{\partial^{2} {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial x_{3}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{3} }}{{\partial x_{3}^{2} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + Q_{22} H_{2} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial^{2} {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial y_{1}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{1} }}{{\partial y_{1}^{2} }}{ + }\frac{{\partial^{2} {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial y_{2}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{2} }}{{\partial y_{2}^{2} }} + \frac{{\partial^{2} {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial y_{3}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{3} }}{{\partial y_{3}^{2} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + Q_{12} H_{2} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial^{2} {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial x_{1}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{1} }}{{\partial y_{1}^{2} }}{ + }\frac{{\partial^{2} {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial x_{2}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{2} }}{{\partial y_{2}^{2} }} + \frac{{\partial^{2} {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial x_{3}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{3} }}{{\partial y_{3}^{2} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + Q_{12} H_{2} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial^{2} {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial y_{1}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{1} }}{{\partial x_{1}^{2} }}{ + }\frac{{\partial^{2} {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial y_{2}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{2} }}{{\partial x_{2}^{2} }} + \frac{{\partial^{2} {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial y_{3}^{2} }}\frac{{\partial^{2} {\mathbf{W}}_{3} }}{{\partial x_{3}^{2} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \, + 4Q_{66} H_{2} \int_{ - L}^{L} {\int_{ - b}^{b} {\left( {\frac{{\partial^{2} {\mathbf{W}}_{1}^{{\text{T}}} }}{{\partial x_{1} \partial y_{1} }}\frac{{\partial^{2} {\mathbf{W}}_{1} }}{{\partial x_{1} \partial y_{1} }}{ + }\frac{{\partial^{2} {\mathbf{W}}_{2}^{{\text{T}}} }}{{\partial x_{2} \partial y_{2} }}\frac{{\partial^{2} {\mathbf{W}}_{2} }}{{\partial x_{2} \partial y_{2} }} + \frac{{\partial^{2} {\mathbf{W}}_{3}^{{\text{T}}} }}{{\partial x_{3} \partial y_{3} }}\frac{{\partial^{2} {\mathbf{W}}_{3} }}{{\partial x_{3} \partial y_{3} }}} \right){\text{d}}y{\text{d}}x} } \hfill \\ \end{gathered}$$

(A10)

$$ \begin{aligned} {\mathbf{N}}_{u} \left[ {{\mathbf{p}}_{u} (t)} \right] = & \sum\limits_{{i = 1}}^{3} {\int_{{ - L}}^{L} {\int_{{ - b}}^{b} {\left[ {Q_{{11}} H_{3} \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \frac{{\partial {\mathbf{U}}_{i}^{{\text{T}}} }}{{\partial x_{i} }} + Q_{{12}} H_{3} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} \frac{{\partial {\mathbf{U}}^{{\text{T}}} }}{{\partial x_{i} }} + Q_{{66}} H_{1} \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{U}}_{i}^{{\text{T}}} }}{{\partial x_{i} }}} \right]} } } {\text{d}}y_{i} {\text{d}}x_{i} , \\ {\mathbf{N}}_{v} \left[ {{\mathbf{p}}_{v} (t)} \right] = & \sum\limits_{{i = 1}}^{3} {\int_{{ - L}}^{L} {\int_{{ - b}}^{b} {\left[ {Q_{{22}} H_{3} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} \frac{{\partial {\mathbf{V}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{{12}} H_{3} \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \frac{{\partial {\mathbf{V}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{{66}} H_{1} \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{V}}_{i}^{{\text{T}}} }}{{\partial y_{i} }}} \right]} } } {\text{d}}y_{i} {\text{d}}x_{i} , \\ \end{aligned} $$

(A11)

$$\begin{gathered} {\mathbf{N}}_{w} \left[ {{\mathbf{p}}_{w} (t)} \right] = \sum\limits_{i = 1}^{3} {\int_{ - L}^{L} {\int_{ - b}^{b} {\left[ {Q_{11} H_{1} \frac{{\partial u_{i} }}{{\partial x_{i} }}\frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }} + Q_{11} H_{3} \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{3} \frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }}{ + }Q_{12} H_{1} \frac{{\partial v_{i} }}{{\partial y_{i} }}\frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }}} \right.} } } \hfill \\ { + }Q_{22} H_{1} \frac{{\partial v_{i} }}{{\partial y_{i} }}\frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{22} H_{3} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{3} \frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{12} H_{1} \frac{{\partial u_{i} }}{{\partial x_{i} }}\frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} \hfill \\ { + }Q_{12} H_{1} \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{12} H_{1} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }} \hfill \\ { + }Q_{66} H_{1} \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{66} H_{1} \left( {\frac{{\partial w_{i} }}{{\partial y_{i} }}} \right)^{2} \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }} \hfill \\ \, + Q_{66} H_{1} \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial u_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{66} H_{1} \frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial u_{i} }}{{\partial y_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }} \hfill \\ \, \left. { + Q_{66} H_{1} \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial v_{i} }}{{\partial x_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial y_{i} }} + Q_{66} H_{1} \frac{{\partial w_{i} }}{{\partial y_{i} }}\frac{{\partial v_{i} }}{{\partial x_{i} }}\frac{{\partial {\mathbf{W}}_{i}^{{\text{T}}} }}{{\partial x_{i} }}} \right]{\text{d}}y_{i} {\text{d}}x_{i} . \hfill \\ \end{gathered}$$

(A12)