Skip to main content
SpringerLink
Log in

Gait transition and orbital stability analysis for a biped robot based on the V-DSLIP model with torso and swing leg dynamics

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

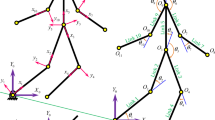
In this paper, the variable legs stiffness damper-spring-loaded inverted pendulum with a rigid torso and swing leg dynamics is proposed. First, the dynamic equations are derived using the Euler–Lagrange method, and the impact model is derived based on momentum theorem. Second, the feedback linearization controller is designed to track the desired trajectory and regulate the swing leg orientation and the attitude of the torso. Third, the gait switching strategy is presented to realize waking gait transition by controlling the legs stiffness and the hip torques; thus, the average walking speed can be changed. Fourth, the Poincaré mapping method is used to analyze the orbital stability of the biped robot system. Finally, computer simulations are carried out to verify the effectiveness of the presented method. The simulation results show that the controller is effective for the transition between two natural gaits, it can track the desired walking gait and keep the torso upright simultaneously. Since all the eigenvalues of the Jacobian matrix are located inside the unit circle, it is also concluded that the proposed controller is robust against external disturbances and the system is orbital stable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

References

  1. McGeer, T.: Passive dynamic walking. Int. J. Robot. Res. 9(2), 62–82 (1990)

    Article  Google Scholar 

  2. Collins, S., Ruina, A., Tedrake, R., Wisse, M.: Efficient bipedal robots based on passive-dynamic walkers. Science 307(5712), 1082–1085 (2005)

    Article  Google Scholar 

  3. Blickhan, R.: The spring-mass model for running and hopping. J. Biomech. 22(11), 1217–1227 (1989)

    Article  Google Scholar 

  4. Geyer, H., Seyfarth, A., Blickhan, R.: Compliant leg behaviour explains basic dynamics of walking and running. Biol. Sci. 273(1603), 2861–2867 (2006)

    Google Scholar 

  5. Peuker, F., Seyfarth, A., Grimmer, S.: Inheritance of SLIP running stability to a single-legged and bipedal model with leg mass and damping. In: Proceedings of the 4th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, pp. 395–400 (2012)

  6. Hao, M., Chen, K., Fu, C.L.: Effects of hip torque during step-to-step transition on center-of-mass dynamics during human walking examined with numerical simulation. J. Biomech. 90(2019), 33–39 (2019)

    Article  Google Scholar 

  7. Rummel, J., Blum, Y., Seyfart, A.: Robust and efficient walking with spring-like legs. Bioinspir. Biomim. (2010). https://doi.org/10.1088/1748-3182/5/4/046004

    Article  Google Scholar 

  8. Visser, L.C., Stramigioli, S., Carloni, R.: Robust bipedal walking with variable leg stiffness. In: Proceedings of the 4th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, pp. 1626–1631 (2012)

  9. Visser, L.C., Stramigioli, S., Carloni, R.: Control strategy for energy-efficient bipedal walking with variable leg stiffness. In: Proceedings of IEEE International Conference on Robotics and Automation, pp. 5644–5649 (2013)

  10. Pelit, M.M., Chang, J., Takano, R., Yamakita, M.: Bipedal walking based on improved spring loaded inverted pendulum model with swing leg (SLIP-SL). In: Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics, pp. 72–77 (2020)

  11. Xie, S., et al.: Compliant bipedal walking based on variable spring-loaded inverted pendulum model with finite-sized foot*. In: Proceedings of the 6th IEEE International Conference on Advanced Robotics and Mechatronics, pp. 667–672 (2021)

  12. Maus, H.M., Lipfert, S.W., Gross, M., Rummel, J., Seyfarth, A.: Upright human gait did not provide a major mechanical challenge for our ancestors. Nat. Commun. (2010). https://doi.org/10.1038/ncomms1073

    Article  Google Scholar 

  13. Sharbafi, M.A., Seyfarth, A.: FMCH: a new model for human-like postural control in walking. In: Proceedings of IEEE/RSJ International Conference on Intelligent Robots & Systems, pp.5742–5747 (2015)

  14. Maufroy, C., Maus, H.M., Seyfarth, A.: Simplified control of upright walking by exploring asymmetric gaits induced by leg damping. In: Proceedings of IEEE International Conference on Robotics and Biomimetics, pp. 491–496 (2011)

  15. Vu, M.N., Lee, J. Oh, Y.: Control strategy for stabilization of the biped trunk-SLIP walking model. In: Proceedings of the 14th International Conference on Ubiquitous Robots and Ambient Intelligence, (2017). https://doi.org/10.1109/URAI.2017.7992875

  16. Westervelt, E.R., Grizzle, J.W., Wit, C.D.: Switching and PI control of walking motions of planar biped walkers. IEEE Trans. Autom. Control 48(2), 308–312 (2003)

    Article  MathSciNet  Google Scholar 

  17. Hobbelen, D.G.E., Wisse, M.: Controlling the walking speed in limit cycle walking. Int. J. Robot. Res. 27(9), 989–1005 (2008)

    Article  Google Scholar 

  18. Haarnoja, T., Cabezas, J.L.P., Halme, A.: Model-based velocity control for limit cycle walking. In: Proceedings of IEEE/RSJ International Conference on Intelligent Robots & Systems, pp. 2255–2260 (2011)

  19. Huang, Y., Vanderborght, B., Ham, R.V., Wang, Q.N., Damme, M.V., Xie, G.M., Lefeber, D.: Step length and velocity control of a dynamic bipedal walking robot with adaptable compliant joints. IEEE/ASME Trans. Mechatron. 18(2), 598–611 (2013)

    Article  Google Scholar 

  20. Roozing, W., Carloni, R.: Bipedal walking gait with variable stiffness knees. In: Proceedings of the 5th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, pp. 924–930 (2014)

  21. Roozing, W., Carloni, R.: Variable bipedal walking gait with variable leg stiffness. In: Proceedings of the 5th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, pp. 931–938 (2014)

  22. Shahbazi, M., et al.: Unified modeling and control of walking and running on the spring-loaded inverted pendulum. IEEE Trans. Robot. A Publ. IEEE Robot. Autom. Soc. 32(5), 1178–1195 (2015)

    MathSciNet  Google Scholar 

  23. Grizzle, J.W., et al.: Asymptotically stable walking for biped robots: analysis via systems with impulse effects. IEEE Trans. Autom. Control 46(1), 51–64 (2001)

    Article  MathSciNet  Google Scholar 

  24. Westervelt, E.R., Grizzle, J.W., Koditschek, D.E.: Hybrid zero dynamics of planar biped walkers. IEEE Trans. Autom. Control 48(1), 42–56 (2003)

    Article  MathSciNet  Google Scholar 

  25. Kuznetsov, S.V.: The motion of the elastic pendulum. Regul. Chaot. Dyn. 4(3), 3–12 (1999)

    Article  MathSciNet  Google Scholar 

  26. Goswami, A., Thuilot, B., Espiau, B.: Study of the passive gait of a compass-like biped robot: symmetry and chaos. Int. J. Robot. Res. 17(12), 1282–1301 (1998)

    Article  Google Scholar 

  27. Plestan, F., et al.: Stable walking of a 7-dof biped robot. IEEE Trans. Robot. Autom. 19(4), 653–668 (2003)

    Article  Google Scholar 

  28. Grizzle, J.W., Plestan, F., Abba, G.: Poincare’s method for systems with impulse effects: application to mechanical biped locomotion. In: Proceedings of the 38th IEEE Conference on Decision and Control, pp. 3869–3876 (1999)

  29. McGeer, T.: Passive dynamic biped catalogue. In: Proc. Experimental Robotics II: The 2nd International Symposium, pp. 465–490 (1992)

  30. Wafa, Z., Hassène, G., Safya, B.: Stabilization of the passive walking dynamics of the compass-gait biped robot by developing the analytical expression of the controlled Poincaré map. Nonlinear Dyn. 101(2), 1061–1091 (2020)

    Article  Google Scholar 

  31. Kant, N., Mukherjee, R.: Orbital stabilization of underactuated systems using virtual holonomic constraints and impulse controlled poincaré maps. Syst. Control Lett. 146, 104813 (2020)

    Article  Google Scholar 

  32. Kant, N., Mukherjee, R.: Energy-based orbital stabilization of underactuated systems using impulse controlled poincaré maps. In: Proceedings of the 2021 American Control Conference (ACC), pp. 1724–1729 (2021)

  33. Kant, N., Mukherjee, R.: Juggling a devil-stick: hybrid orbit stabilization using the impulse controlled poincaré map. IEEE Control Syst. Lett. (2021)

  34. Kant, N., Mukherjee, R.: Non-prehensile manipulation of a devil-stick: planar symmetric juggling using impulsive forces. Nonlinear Dyn. 103(3), 2409–2420 (2021)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation (NNSF) of China under Grant 12172059.

Funding

Liao has received research support from the National Natural Science Foundation(NNSF) of China under Grant 12172059.

Author information

Authors and Affiliations

  1. School of Automation, Beijing Information Science and Technology University, Beijing, 100192, China

    Fakang Liao, Yali Zhou & Qizhi Zhang

Authors
  1. Fakang Liao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yali Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qizhi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fakang Liao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Data availability

Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Single support model

First, calculate the kinetic energy K and the potential energy P of the biped robot system, then the Lagrangian function L can be written as:

$$ \begin{aligned} L = & \frac{{M + m + m_{f} }}{2}\left( {\dot{x}^{2} + \dot{y}^{2} } \right) + \frac{1}{2}I\dot{\alpha }^{2} \\ & + \frac{m}{2}\left( {l^{2} \dot{\alpha }^{2} + 2l\dot{x}\dot{\alpha }\cos \alpha - 2l\dot{y}\dot{\alpha }\sin \alpha } \right) \\ & + \frac{{m_{f} }}{2}\left( {L_{0}^{2} \dot{\beta }^{2} + 2L_{0} \dot{x}\dot{\beta }\cos \beta + 2L_{0} \dot{y}\dot{\beta }\sin \beta } \right) \\ & - Mgy - mg\left( {y + l\cos \alpha } \right) - m_{f} g\left( {y - L_{0} \cos \beta } \right) \\ & - \frac{1}{2}\left( {k_{0} + u_{1} } \right)\left( {L_{0} - \sqrt {x^{2} + y^{2} } } \right)^{2} \\ \end{aligned} $$
(A1)

where g is the gravitational acceleration.

Secondary, substitute (A1) into (2), then the dynamic equations for the SS phase can be obtained as follows:

$$ \begin{gathered} (M + m + m_{f} )\ddot{x} + ml\ddot{\alpha }\cos \alpha - ml\dot{\alpha }^{2} \sin \alpha \hfill \\ \quad + m_{f} L_{0} \ddot{\beta }\cos \beta - m_{f} L_{0} \dot{\beta }^{2} \sin \beta \hfill \\ \quad - (k_{0} + u_{1} )\left( {\frac{{L_{0} }}{{L_{1} }} - 1} \right)x - \frac{{c\dot{L}_{1} }}{{L_{1} }}x = F_{1} \hfill \\ \end{gathered} $$
(A2)
$$ \begin{gathered} (M + m + m_{f} )\ddot{y} - ml\ddot{\alpha }\sin \alpha - ml\dot{\alpha }^{2} \cos \alpha \hfill \\ \quad \quad \quad + m_{f} L_{0} \ddot{\beta }\sin \beta + m_{f} L_{0} \dot{\beta }^{2} \cos \beta + (M + m + m_{f} )g \hfill \\ \quad \quad - (k_{0} + u_{1} )\left( {\frac{{L_{0} }}{{L_{1} }} - 1} \right)y - \frac{{c\dot{L}_{1} }}{{L_{1} }}y = F_{2} \hfill \\ \end{gathered} $$
(A3)
$$ \begin{gathered} (I + ml^{2} )\ddot{\alpha } + ml(\ddot{x}\cos \alpha - \ddot{y}\sin \alpha ) \hfill \\ \quad \quad - mgl\sin \alpha = F_{3} \hfill \\ \end{gathered} $$
(A4)
$$ \begin{gathered} m_{f} L_{0}^{2} \ddot{\beta } + m_{f} L_{0} \left( {\ddot{x}\cos \beta + \ddot{y}\sin \beta } \right) \hfill \\ \quad \quad + m_{f} gL_{0} \sin \beta = F_{4} \hfill \\ \end{gathered} $$
(A5)

where \(L_{1} = \sqrt {x^{2} + y^{2} }\) is the length of the left leg.

Third, according to the principle of virtual work, the generalized force is computed as:

$$ \begin{aligned} F_{1} = & \frac{y}{{x^{2} + y^{2} }}\tau_{1} \\ F_{2} = & - \frac{x}{{x^{2} + y^{2} }}\tau_{1} \\ F_{3} = & - \tau_{1} - \tau_{2} \\ F_{4} = & - \tau_{2} \\ \end{aligned} $$
(A6)

Then, the dynamic equations in compact matrix form can be written as:

$$ \begin{gathered} {\varvec{M}}_{{{\varvec{ss}}}} {\ddot{\mathbf q}}_{{{\varvec{ss}}}} + {\varvec{C}}_{{{\varvec{ss}}}} \dot{\mathbf{q}}_{{{\varvec{ss}}}} - {\varvec{F}}_{{{\varvec{ss}}}} + {\varvec{G}}_{{{\varvec{ss}}}} \hfill \\ \quad \quad = {\varvec{B}}_{{{\varvec{ss}}1}} \tau_{1} + {\varvec{B}}_{{{\varvec{ss}}2}} \tau_{2} + {\varvec{B}}_{{{\varvec{ss}}3}} u_{1} \hfill \\ \end{gathered} $$
(A7)

where

$$ {\varvec{M}}_{{{\varvec{ss}}}} = \left[ {\begin{array}{*{20}c} {M + m + m_{f} } & 0 & {ml\cos \alpha } & {m_{f} L_{0} \cos \beta } \\ 0 & {M + m + m_{f} } & { - ml\sin \alpha } & {m_{f} L_{0} \sin \beta } \\ {ml\cos \alpha } & { - ml\sin \alpha } & {ml^{2} + I} & 0 \\ {m_{f} L_{0} \cos \beta } & {m_{f} L_{0} \sin \beta } & 0 & {m_{f} L_{0}^{2} } \\ \end{array} } \right] $$
$$ {\varvec{C}}_{{{\varvec{ss}}}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\begin{array}{*{20}c} { - ml\dot{\alpha }\sin \alpha } & { - m_{f} L_{0} \dot{\beta }\sin \beta } \\ { - ml\dot{\alpha }\cos \alpha } & {m_{f} L_{0} \dot{\beta }\cos \beta } \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \\ \end{array} } \right],\quad {\varvec{G}}_{{{\varvec{ss}}}} = \left[ {\begin{array}{*{20}c} 0 \\ {\left( {M + m + m_{f} } \right)g} \\ { - mgl\sin \alpha } \\ {m_{f} gL_{0} \sin \beta } \\ \end{array} } \right] $$
$$ {\varvec{F}}_{{{\varvec{ss}}}} = \left[ {k_{0} \left( {\frac{{L_{0} }}{{L_{1} }} - 1} \right) - \frac{{c\dot{L}_{1} }}{{L_{1} }}} \right]\left[ {\begin{array}{*{20}c} x \\ y \\ 0 \\ 0 \\ \end{array} } \right] $$
$$ {\varvec{B}}_{{{\varvec{ss}}1}} = \left[ {\begin{array}{*{20}c} {\frac{y}{{x^{2} + y^{2} }}} \\ { - \frac{x}{{x^{2} + y^{2} }}} \\ { - 1} \\ 0 \\ \end{array} } \right],\quad {\varvec{B}}_{{{\varvec{ss}}2}} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - 1} \\ { - 1} \\ \end{array} } \right],\quad {\varvec{B}}_{{{\varvec{ss}}3}} = \left( {\frac{{L_{0} }}{{L_{1} }} - 1} \right)\left[ {\begin{array}{*{20}c} x \\ y \\ 0 \\ 0 \\ \end{array} } \right] $$

Appendix B: Double support model

Using the derivation method used in the SS phase, the dynamic equations of the DS phase can be obtained as:

$$ \begin{gathered} {\varvec{M}}_{{{\varvec{ds}}}} {\ddot{\mathbf q}}_{{{\varvec{ds}}}} + {\varvec{C}}_{{{\varvec{ds}}}} \dot{\mathbf {q}}_{{{\varvec{ds}}}} - {\varvec{F}}_{{{\varvec{ds}}1}} - {\varvec{F}}_{{{\varvec{ds}}2}} + {\varvec{G}}_{{{\varvec{ds}}}} \hfill \\ \quad = {\varvec{B}}_{{{\varvec{ds}}1}} \tau_{1} + {\varvec{B}}_{{{\varvec{ds}}2}} u_{1} + {\varvec{B}}_{{{\varvec{ds}}3}} u_{2} \hfill \\ \end{gathered} $$
(B1)

where

$$ {\varvec{M}}_{{{\varvec{ds}}}} = \left[ {\begin{array}{*{20}c} {M + m} & 0 & {ml\cos \alpha } \\ 0 & {M + m} & { - ml\sin \alpha } \\ {ml\cos \alpha } & { - ml\sin \alpha } & {ml^{2} + I} \\ \end{array} } \right],\quad {\varvec{C}}_{{{\varvec{ds}}}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\begin{array}{*{20}c} { - ml\dot{\alpha }\sin \alpha } \\ { - ml\dot{\alpha }\cos \alpha } \\ 0 \\ \end{array} } \\ \end{array} } \right] $$
$$ {\varvec{F}}_{{{\varvec{ds}}{1}}} = \left[ {k_{0} \left( {\frac{{L_{0} }}{{L_{1} }} - 1} \right) - \frac{{c\dot{L}_{1} }}{{L_{1} }}} \right]\left[ {\begin{array}{*{20}c} x \\ y \\ 0 \\ \end{array} } \right],\quad {\varvec{F}}_{{{\varvec{ds}}{2}}} = \left[ {k_{0} \left( {\frac{{L_{0} }}{{L_{2} }} - 1} \right) - \frac{{c\dot{L}_{2} }}{{L_{2} }}} \right]\left[ {\begin{array}{*{20}c} {x - a} \\ y \\ 0 \\ \end{array} } \right] $$
$$ {\varvec{G}}_{{{\varvec{ds}}}} = \left[ {\begin{array}{*{20}c} 0 \\ {\left( {M + m} \right)g} \\ { - mgl\sin \alpha } \\ \end{array} } \right],\quad {\varvec{B}}_{{{\varvec{ds}}1}} = \left[ {\begin{array}{*{20}c} {\frac{y}{{x^{2} + y^{2} }}} \\ {\begin{array}{*{20}c} { - \frac{x}{{x^{2} + y^{2} }}} \\ { - 1} \\ \end{array} } \\ \end{array} } \right],\quad {\varvec{B}}_{{{\varvec{ds}}2}} = \left( {\frac{{L_{0} }}{{L_{1} }} - 1} \right)\left[ {\begin{array}{*{20}c} x \\ y \\ 0 \\ \end{array} } \right] $$
$$ {\varvec{B}}_{{{\varvec{ds}}3}} = \left( {\frac{{L_{0} }}{{L_{2} }} - 1} \right)\left[ {\begin{array}{*{20}c} {x - a} \\ y \\ 0 \\ \end{array} } \right],\quad L_{2} = \sqrt {(x - a)^{2} + y^{2} } $$

L2 is the length of the right leg and a is the step size, a = x + L0cosθ.

Appendix C: State space representation

The SS phase:

$$ \dot{\mathbf{z}}_{{{\varvec{ss}}}} = {\varvec{f}}\left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right) + {\varvec{g}}_{{\tau_{1} }} \left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right)\tau_{1} + {\varvec{g}}_{{\tau_{2} }} \left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right)\tau_{2} + {\varvec{g}}_{1} \left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right)u_{1} $$
(C1)

where

$$ {\varvec{f}}\left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right) = \left( {\begin{array}{*{20}c} {\dot{\mathbf{q}}_{{{\varvec{ss}}}} } \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} \left( { - {\varvec{C}}_{{{\varvec{ss}}}} \dot{\mathbf{q}} + {\varvec{F}}_{{{\varvec{ss}}}} - {\varvec{G}}_{{{\varvec{ss}}}} } \right)} \\ \end{array} } \right),\quad {\varvec{g}}_{{\tau_{1} }} \left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}1}} } \\ \end{array} } \right) $$
$$ {\varvec{g}}_{{\tau_{2} }} \left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}2}} } \\ \end{array} } \right),\quad {\varvec{g}}_{1} \left( {{\varvec{z}}_{{{\varvec{ss}}}} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}3}} } \\ \end{array} } \right) $$

The DS phase:

$$ \dot{\mathbf{z}}_{{{\varvec{ds}}}} = {\varvec{f}}\left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right) + {\varvec{g}}_{{\tau_{1} }} \left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right)\tau_{1} + {\varvec{g}}_{1} \left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right)u_{1} + {\varvec{g}}_{2} \left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right)u_{2} $$
(C2)

where

$$ {\varvec{f}}\left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right) = \left( {\begin{array}{*{20}c} {\dot{\mathbf{q}}_{{{\varvec{ds}}}} } \\ {{\varvec{M}}_{{{\varvec{ds}}}}^{ - 1} \left( {{\varvec{F}}_{{{\varvec{ds}}1}} + {\varvec{F}}_{{{\varvec{ds}}2}} - {\varvec{G}}_{{{\varvec{ds}}}} - C_{{{\varvec{ds}}}} \dot{\mathbf{q}}} \right)} \\ \end{array} } \right),\quad {\varvec{g}}_{{\tau_{1} }} \left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\varvec{M}}_{{{\varvec{ds}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ds}}1}} } \\ \end{array} } \right) $$
$$ {\varvec{g}}_{1} \left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\varvec{M}}_{{{\varvec{ds}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ds}}2}} } \\ \end{array} } \right),\quad {\varvec{g}}_{2} \left( {{\varvec{z}}_{{{\varvec{ds}}}} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\varvec{M}}_{{{\varvec{ds}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ds}}3}} } \\ \end{array} } \right) $$

Appendix D: Relative degree derivation

In order to convert this nonlinear system into a standard linear form, first the relative degree γss = {γp, γα, γβ} of the error system needs to be determined.

For the position error (ep) system:

$$ \begin{aligned} \dot{e}_{p} = & \frac{{\partial e_{p} }}{{\partial {\varvec{z}}}}\dot{\mathbf{z}}_{ss} = \left( {\begin{array}{*{20}c} {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} & {\frac{{\partial e_{p} }}{{\partial \dot{\mathbf{q}}}}} \\ \end{array} } \right)\left( {{\varvec{f}} + {\varvec{g}}_{{\tau_{1} }} \tau_{1} + {\varvec{g}}_{{\tau_{2} }} \tau_{2} + {\varvec{g}}_{1} u_{1} } \right) \\ = & \underbrace {{\left( {\begin{array}{*{20}c} {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\dot{\mathbf{q}}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} \left( {{\varvec{F}}_{{{\varvec{ss}}}} - {\varvec{G}}_{{{\varvec{ss}}}} - C_{{{\varvec{ss}}}} \dot{\mathbf{q}}} \right)} \\ \end{array} } \right)}}_{{L_{f} e_{p} }} \\ & + \underbrace {{\left( {\begin{array}{*{20}c} {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}1}} } \\ \end{array} } \right)}}_{{L_{{g\tau_{1} }} e_{p} = 0}}\tau_{1} \\ & + \underbrace {{\left( {\begin{array}{*{20}c} {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}2}} } \\ \end{array} } \right)}}_{{L_{{g\tau_{2} }} e_{p} = 0}}\tau_{2} \\ & + \underbrace {{\left( {\begin{array}{*{20}c} {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}3}} } \\ \end{array} } \right)}}_{{L_{{g_{1} }} e_{p} = 0}}u_{1} \\ = & L_{f} e_{p} ({\varvec{q}},\dot{\mathbf{q}}) \\ \end{aligned} $$
(D1)

where \(L_{{g\tau_{1} }} e_{p} = L_{{g\tau_{2} }} e_{p} = \, L_{{g_{1} }} e_{p} = 0\). We proceed by calculating the second-order derivative:

$$ \begin{aligned} \ddot{e}_{p} = & \left( {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{q}}}}\left( {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}\dot{\mathbf{q}}} \right)} & {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} \\ \end{array} } \right)\left( {{\varvec{f}} + {\varvec{g}}_{{\tau_{1} }} \tau_{1} + {\varvec{g}}_{{\tau_{2} }} \tau_{2} + {\varvec{g}}_{1} u_{1} } \right) \\ = & \underbrace {{\left( {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{q}}}}\left( {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}\dot{\mathbf{q}}} \right)} & {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\dot{\mathbf{q}}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} \left( {{\varvec{F}}_{{{\varvec{ss}}}} - {\varvec{G}}_{{{\varvec{ss}}}} - C_{{{\varvec{ss}}}} \dot{\mathbf{q}}} \right)} \\ \end{array} } \right)}}_{{L_{f}^{2} e_{p} }} \\ & + \underbrace {{\left( {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{q}}}}\left( {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}\dot{\mathbf{q}}} \right)} & {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}1}} } \\ \end{array} } \right)}}_{{L_{{g\tau_{1} }} L_{f} e_{p} }}\tau_{1} \\ & + \underbrace {{\left( {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{q}}}}\left( {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}\dot{\mathbf{q}}} \right)} & {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{2} } \\ \end{array} } \right)}}_{{L_{{g\tau_{2} }} L_{f} e_{p} }}\tau_{2} \\ & + \underbrace {{\left( {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{q}}}}\left( {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}\dot{\mathbf{q}}} \right)} & {\frac{{\partial e_{p} }}{{\partial {\varvec{q}}}}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\varvec{M}}_{{{\varvec{ss}}}}^{ - 1} {\varvec{B}}_{{{\varvec{ss}}3}} } \\ \end{array} } \right)}}_{{L_{g1} L_{f} e_{p} }}u_{1} \\ =\, & L^{2}_{f} e_{p} ({\varvec{q}},\dot{\mathbf{q}}) + L_{{g\tau_{1} }} L{}_{f}e_{p} ({\varvec{q}})\tau_{1} \\ & + L_{{g\tau_{2} }} L{}_{f}e_{p} ({\varvec{q}})\tau_{2} + L_{g1} L{}_{f}e_{p} ({\varvec{q}})u_{1} \\ \end{aligned} $$
(D2)

where \(L_{{g\tau_{1} }} L_{f} e_{p} \ne 0,\quad L_{{g\tau_{2} }} L_{f} e_{p} \ne 0,\), and \(L_{{g_{1} }} L_{f} e_{p} \ne 0\) denote the (repeated) Lie-derivatives of the error functions along the vector fields of dynamics system. So the relative degree γp = 2. In the same way, we can get the relative degrees γα = γβ = 2. So, in the SS phase, the relative degree of the error system γss = {γp, γα, γβ} = {2, 2, 2}.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liao, F., Zhou, Y. & Zhang, Q. Gait transition and orbital stability analysis for a biped robot based on the V-DSLIP model with torso and swing leg dynamics. Nonlinear Dyn 108, 3053–3075 (2022). https://doi.org/10.1007/s11071-022-07364-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07364-z

Keywords

Search

Navigation